1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 1, 2022

Известия РАН. Механика твердого тела, 2022, № 1, стр. 122-132

МОДЕЛЬ ДЛЯ АНАЛИЗА НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ТРЕХСЛОЙНЫХ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК С ПРЯМОУГОЛЬНЫМИ ВЫРЕЗАМИ

В. Н. Бакулин a, *

a Институт прикладной механики РАН
Москва, Россия

* E-mail: vbak@yandex.ru

Поступила в редакцию 20.03.2021
После доработки 22.03.2021
Принята к публикации 29.03.2021

Полный текст (PDF)

Аннотация

Рассматривается построение модели для послойного анализа напряженно-деформированного состояния трехслойных цилиндрических оболочек вращения с прямоугольными вырезами. Провести послойный анализ для оболочек с прямоугольными вырезами аналитическими методами, как правило, не удается из-за математических трудностей, поэтому применяется конечно-элементный подход. Модели послойного анализа отличаются большой размерностью, а наличие вырезов приводит к необходимости измельчения сетки разбиений, что еще более увеличивает размерность задачи, для уменьшения которой применены эффективные функции аппроксимаций деформаций и перемещений внутри конечных элементов. Рассмотренная модель позволяет учесть особенности слоисто-неоднородного строения, а также наличие вырезов. В качестве примера проведено исследование напряженно–деформированного состояния в слоях трехслойных цилиндрических оболочек вращения с прямоугольными вырезами.

Ключевые слова: трехслойные цилиндрические оболочки вращения, прямоугольные вырезы, напряженно-деформированное состояние, послойный подход, конечно-элементные модели, аппроксимирующие функции обобщенных деформаций и перемещений

1. Введение. Актуальность темы в теоретическом плане связана с недостаточной исследованностью проблемы анализа напряженно-деформированного состояния (НДС) трехслойных цилиндрических оболочек с учетом неоднородности структуры при наличии вырезов. Интерес с практической точки зрения объясняется увеличивающимся распространением в современной ракетной, авиакосмической, судостроительной, строительной и других отраслях указанных элементов конструкций трехслойных оболочек, отличающихся высокими показателями весовой эффективности, удельной жесткости и прочности, несущей способности и многих других важных характеристик [1–4].

Недостаточное развитие моделей для уточненного анализа НДС с учетом указанных выше особенностей оказывает сдерживающее влияние на распространение трехслойных оболочек. Поэтому построение адекватных моделей, позволяющих учесть отмеченные особенности является актуальной научной проблемой, имеющей важное прикладное значение.

Теорий расчета напряженно-деформированного состояния неоднородных и трехслойных оболочек достаточно много. Значительно меньше публикаций, в которых разработанные модели позволяют с необходимой точностью и степенью детализации провести расчет НДС трехслойных оболочек с указанными выше особенностями.

В работах [5–8] рассмотрены некоторые последние обзоры расчетных моделей слоисто-неоднородных и в том числе трехслойных оболочек.

С требуемой точностью и степенью детализации провести расчет НДС трехслойных нерегулярных оболочек вращения с указанными выше особенностями позволяет послойный анализ [7, 9–12], при котором в случае необходимости стенка оболочки, в том числе заполнитель, может моделироваться по толщине слоями, стыкуемыми между собой. При этом могут быть разные по сложности модели для расчета слоев с применением аналитических и численных методов в зависимости от условий задач.

Обзоры по расчету оболочек, ослабленных отверстиями, приведены, например, в работах [13–15]. Большая часть работ по исследованию оболочек с вырезами посвящена однородным оболочкам, меньшая часть – оболочкам из композиционных материалов и совсем в небольшом числе работ рассмотрены трехслойные оболочки с вырезами. В значительной части этих работ приведены исследования трехслойных сферических оболочек с круговыми отверстиями. При этом почти отсутствуют результаты расчетов трехслойных оболочек, ослабленных прямоугольными в плане вырезами [15].

Аналитическими методами решение подобных задач с учетом указанных особенностей для оболочек с прямоугольными вырезами сталкивается с непреодолимыми математическими сложностями. Это приводит к необходимости применять численные методы и особенно метод конечных элементов (МКЭ) [16–18].

Краткий обзор конечно-элементных моделей (КЭМ) для расчета оболочек, включая трехслойные и слоисто-неоднородные оболочки, рассмотрен в статье [7].

Strang G., Fix G.J. отмечали [19] “…конечные элементы стали наиболее употребительным средством вычислительной математики во всем мире, но будет еще лучше, если мы научимся решать те же задачи с меньшими затратами…”.

Похожие мысли высказывал академик И.Ф. Образцов в статье [20] “…основная проблема при рассмотрении сложных конструкций заключается в создании эффективных математических моделей исследуемых систем, которые не только обеспечивают выполнение заданных требований к информативности и точности исследований, но и одновременно являются экономичными, способствуя, в частности, минимизации затрат машинного времени и памяти ЭВМ…”.

2. Постановка задачи. Размерность конечно-элементных моделей оболочек при послойном анализе определяется числом слоев по толщине оболочки, количеством конечных элементов, на которые разбиваются слои, числом степеней свободы конечных элементов. Количество конечных элементов (КЭ), с помощью которых моделируются слои, зависит от эффективности функций формы КЭ, то есть от того, как быстро численные результаты будут приближаться к точным решениям при увеличении числа разбиений на КЭ. При послойном моделировании трехслойных и слоисто-неоднородных нерегулярных оболочек это чрезвычайно важно.

Увеличение размерности модели приводит к росту вычислительных операций, а следовательно к повышению вычислительных погрешностей расчета, увеличению расчетного времени и ужесточению требований к вычислительным ресурсам.

Оптимальным для повышения скорости сходимости численных алгоритмов и получаемых результатов и уменьшения требуемого для решения задач числа КЭ было бы построение функций формы КЭ на основе аналитических решений [21–26]. Такой подход удалось реализовать для круговых слоистых арок [21] и осесимметричных конечных элементов трехслойных и слоистых цилиндрических оболочек [22–26].

Наличие вырезов приводит к необходимости измельчения сеток разбиений, что еще более увеличивает размерность задач, для уменьшения которой применены эффективные функции аппроксимации деформаций в конечных элементах несущих слоев рассматриваемых трехслойных цилиндрических оболочек.

В отличие от работ по моделированию НДС в оболочках конической формы [10, 27–30] и оболочках двоякой кривизны [31–35], в которых используются аппроксимирующие функции перемещений, в данной работе рассмотрим алгоритм построения конечно-элементной модели с применением функций, аппроксимирующих обобщенные деформации, для анализа НДС в несущих слоях трехслойных нерегулярных цилиндрических оболочках вращения. Рассмотрение алгоритмов построения конечно-элементных моделей несущих слоев и слоя заполнителя проведем на примере конечных элементов естественной кривизны прямоугольной в плане формы, что позволит более просто моделировать НДС в слоях трехслойных цилиндрических оболочек вращения, ослабленных прямоугольными вырезами.

3. Алгоритм построения модели для исследования напряженно-деформированного состояния в несущих слоях трехслойных нерегулярных цилиндрических оболочек вращения. Будем рассматривать несущие слои как тонкие моментные оболочки, к которым применима классическая теория Кирхгофа–Лява, тогда запишем [36]

(3.1)
$\begin{gathered} \varepsilon _{1}^{{}} = \frac{{\partial u}}{{\partial x}},\quad \varepsilon _{2}^{{}} = \frac{1}{R}\frac{{\partial {v}}}{{\partial \varphi }} + \frac{w}{R},\quad \gamma = \frac{1}{R}\frac{{\partial u}}{{\partial \varphi }} + \frac{{\partial {v}}}{{\partial x}} \\ \unicode{230} _{1}^{{}} = - \frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}},\quad {{\unicode{230} }}_{{\text{2}}}^{{}} = \frac{1}{{{{R}^{2}}}}\frac{{\partial {v}}}{{\partial \varphi }} - \frac{1}{{{{R}^{2}}}}\frac{{{{\partial }^{2}}w}}{{\partial {{\varphi }^{2}}}},\quad \chi = \frac{1}{R}\frac{{\partial {v}}}{{\partial x}} - \frac{1}{R}\frac{{{{\partial }^{2}}w}}{{\partial x\partial \varphi }} \\ \end{gathered} $
где х – линейная координата вдоль меридиана на срединной поверхности каждого несущего слоя, φ – угловая координата в плоскости, перпендикулярной оси оболочки, R – радиус кривизны для каждого из несущих слоев.

Одним из требований к аппроксимирующим функциям конечных элементов для расчета оболочек является учет перемещений как твердых тел [37–40]. Для получения перемещений как твердого тела проинтегрируем (3.1) при нулевых значениях деформаций. При этом появятся шесть констант интегрирования, назовем их неопределенными коэффициентами и обозначим α1, …, α6. Они будут задействованы при записи выражений для перемещений как твердого тела.

Рассмотрим конечный элемент несущих слоев трехслойной в общем случае нерегулярной цилиндрической оболочки вращения, полученный сечением оболочки двумя плоскостями, проходящими через ось оболочки, и двумя плоскостями, перпендикулярными оси вращения. За узловые параметры в четырех угловых точках конечного элемента примем три линейных перемещения точек срединной поверхности и два угла поворота нормали к срединной поверхности относительно осей координат в осевом и кольцевом направлениях. Конечный элемент имеет двадцать степеней свободы (по пять степеней свободы в узлах) и следовательно для записи аппроксимирующих функций обобщенных деформаций остается четырнадцать неопределенных коэффициентов (первые шесть неопределенных коэффициентов α1, …, α6 использованы при записи выражений для перемещений как твердого тела).

При выборе полиномов для записи выражений аппроксимирующих функций обобщенных деформаций исходим из предполагаемого характера изменения параметров напряженно–деформированного состояния в несущих слоях трехслойных нерегулярных цилиндрических оболочек вращения. Так как несущие слои считаем тонкими моментными оболочками, то параметры изменения кривизны ${{\unicode{230} }}_{1}^{{}}{\text{,\unicode{230} }}_{2}^{{}}$ срединной поверхности, отвечающие за моментное состояние, будем представлять полиномами более высоких порядков по сравнению с другими параметрами вектора обобщенных деформаций ${{\varepsilon }_{1}},{{\varepsilon }_{2}},\gamma {\text{,}}\chi $.

Для удовлетворения уравнениям неразрывности (совместности) деформаций [36] в полиномы выражений аппроксимирующих функций обобщенных деформаций добавим функции, которые определяются совместным интегрированием уравнений неразрывности деформаций.

После проведения математических операций получим выражения для компонент вектора деформаций, который будет иметь вид

(3.2)
$\varepsilon _{i}^{c} = {\mathbf{\Omega }}_{i}^{c}{\mathbf{\alpha }}_{i}^{c}$
где $\varepsilon _{i}^{c} = {{\{ \varepsilon _{1}^{{}},\varepsilon _{2}^{{}},\gamma ,{{\unicode{230} }}_{1}^{{}},{{\unicode{230} }}_{2}^{{}},\chi \} }^{Т}}$, i = 1, 2, 3 номер слоя, считая от внутренней поверхности трехслойной оболочки, индекс “c” означает, что слой является несущим, $\Omega _{i}^{c}$ (6 × 20) – матрица аппроксимирующих функций деформаций конечного элемента несущих слоев трехслойной нерегулярной цилиндрической оболочки вращения (табл. 1), ${\mathbf{\alpha }}_{i}^{c}$ – вектор неопределенных коэффициентов α1, …, α20.

Таблица 1.

Матрица аппроксимирующих функций деформаций конечного элемента несущих слоев трехслойной нерегулярной цилиндрической оболочки вращения

            1 φ                        
                1 x   –x2/2R –x3/6R –x2φ/2R –x3φ/6R          
                    1                  
                      1 х φ xφ          
                              1 x φ xφ  
              –x/R2           x/R x2/2R   Rφ   R φ2/2 1

Коэффициенты в первых шести столбцах матрицы (табл. 1) нулевые из-за того, что при записи аппроксимирующих функций деформаций конечного элемента несущих слоев использованы четырнадцать неопределенных коэффициентов, начиная с седьмого по двадцатый.

Дальнейшее решение задачи проводится с помощью хорошо разработанных и отлаженных алгоритмов метода перемещений МКЭ. Поэтому переходим к функциям, аппроксимирующим перемещения конечного элемента несущих слоев, которые состоят из перемещений, вызванных деформированием конечного элемента, и перемещений как твердых тел. Аппроксимирующие функции перемещений, определяемые деформированием КЭ, находятся интегрированием (3.1) при полученных выражениях (3.2).

Аппроксимирующие функции перемещений (АФП) конечного элемента несущих слоев, записанные в матричной форме с помощью вектора неопределенных коэффициентов αic, будут иметь вид

(3.3)
${\mathbf{\delta }}_{{\mathbf{i}}}^{{\mathbf{c}}} = {\mathbf{T}}_{{\mathbf{i}}}^{{\mathbf{c}}}{\mathbf{\alpha }}_{{\mathbf{i}}}^{{\mathbf{c}}}$
где ${\mathbf{\delta }}_{{\mathbf{i}}}^{{\mathbf{c}}} = {{\left\{ {u,{v},w} \right\}}^{T}}$ – вектор перемещений точек срединной поверхности несущих слоев, ${\mathbf{T}}_{{\mathbf{i}}}^{{\mathbf{c}}}$ (3 × 20)-матрица АФП конечного элемента несущих слоев.

С учетом (3.2), используя физические соотношения (закон Гука) для несущих слоев, легко записать выражения для усилий и моментов через вектор неопределенных коэффициентов ${\mathbf{\alpha }}_{{\mathbf{i}}}^{{\mathbf{c}}}$, а затем через вектор узловых перемещений. Из условия минимума полной потенциальной энергии (вариационный принцип Лагранжа) [17, 36] находятся выражения для записи матрицы жесткости конечного элемента несущих слоев аналогично [23].

4. Тестовый пример. Эффективность рассмотренного подхода и приведенной модели, высокая скорость сходимости полученных с помощью этой модели решений (график 4 рис. 1) показана сравнением с известными КЭ и аналитическим решением С.П. Тимошенко [41] (график 6 рис. 1) на примере оболочки при действии самоуравновешенных диаметрально противоположных радиальных сосредоточенных сил Р. Приведены зависимости прогиба $\bar {w} = - wDl{\text{/}}P{{R}^{3}}$ в точке приложения сил от порядка решаемой системы уравнений N для распространенных цилиндрических конечных элементов c аппроксимирующими функциями перемещений [42]: КЭ (Cantin G., Glagh R.W. [42]) с 24 степенями свободы с учетом (график 3) и без учета (график 1) перемещений как твердого тела; КЭ (Bogner F.K., Fox R.L. and Schmit L.A. [42]) с 48 степенями свободы (график 2); оболочечный КЭ нулевой кривизны с 20 степенями свободы [10, 27] (график 5). Из-за симметрии рассматривалась восьмая часть цилиндрической оболочки. Из сравнения видно, что практически точное значение достигается при N = 20 для конечного элемента c аппроксимирующими функциями деформаций (то есть при моделировании рассматриваемого сегмента одним КЭ с 20 степенями свободы), при ~N = 140 для КЭ c аппроксимирующими функциями перемещений (АФП) с 48 степенями свободы, при ~N = 200 для КЭ с АФП и 24 степенями свободы и при ~N = 333 для оболочечного КЭ нулевой кривизны с 20 степенями свободы. Следует отметить, что решение С.П. Тимошенко [41] получено для нерастяжимой срединной поверхности, поэтому оно находится ниже точного значения, к которому сходятся конечно-элементные решения.

Рис. 1.

Зависимости прогиба оболочки от порядка системы уравнений при расчете различными конечными элементами.

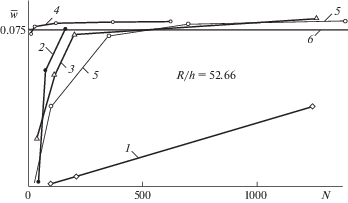
Были проведены также и другие сравнения с большим числом различных КЭ. Эти сопоставления подтвердили эффективность рассмотренного подхода и приведенной модели, а также высокую скорость сходимости полученных с помощью этой модели решений, что позволило, как показали сравнения, значительно уменьшить необходимое для расчета число КЭ. Для приведенного здесь примера (рис. 1) уменьшение порядка решаемой системы уравнений N для конечного элемента c аппроксимирующими функциями деформаций произошло в ~ 7–17 раз соответственно в сравнении с рассмотренными конечными элементами c аппроксимирующими функциями перемещений.

Достоверность и эффективность приведенной модели конечного элемента несущих слоев показана и на примерах исследования НДС цилиндрических, в том числе ортотропных композитных оболочек, ослабленных прямоугольными отверстиями [43, 44].

5. Алгоритм построения трехмерной модели для исследования напряженно-деформированного состояния в слое заполнителя трехслойных нерегулярных цилиндрических оболочек вращения. Подход при построении модели трехмерного оболочечного конечного элемента для исследования НДС слоя заполнителя состоит в следующем. За узловые поверхности этого КЭ принимаются поверхности стыковки с несущими слоями с узлами в угловых точках трехмерного оболочечного конечного элемента слоя заполнителя. К этим поверхностям со срединных поверхностей несущих слоев приводятся узловые перемещения КЭ несущих слоев с помощью матриц перехода подобно [17]. Таким образом, КЭ заполнителя (КЭЗ) будет иметь восемь узлов по четыре узла на внутренней и внешней цилиндрических поверхностях, а аппроксимирующими функциями перемещений будут функции, аппроксимирующие перемещения конечных элементов несущих слоев. Такая схема построения КЭ слоя заполнителя свободна от погрешностей расчета, связанных с разрывом перемещений на цилиндрических поверхностях стыковки КЭ заполнителя с конечными элементами несущих слоев.

Обозначим как ${\mathbf{\bar {\delta }}}_{i}^{c}$ вектор перемещений КЭ несущих слоев на поверхностях сопряжения с КЭ слоя заполнителя, где i = 1 для внутреннего и i = 3 для внешнего несущих слоев. Тогда условия стыковки в векторной форме примут следующий вид для случая одного КЭЗ по толщине слоя заполнителя

(5.1)
${\mathbf{\delta }}_{{}}^{1} = {\mathbf{\bar {\delta }}}_{1}^{c};\quad {\mathbf{\delta }}_{{}}^{2} = {\mathbf{\bar {\delta }}}_{3}^{c}$
где ${\mathbf{\delta }}_{{}}^{{\mathbf{1}}}$, ${\mathbf{\delta }}_{{}}^{{\mathbf{2}}}$ векторы перемещений соответственно внутренней и внешней цилиндрических поверхностей КЭ заполнителя.

Вектор перемещений трехмерного КЭ слоя заполнителя ${\mathbf{\delta }}_{i}^{{\mathbf{f}}} = {{\{ u,{v},w\} }^{T}}$ (f означает, что рассматривается слой заполнителя, i = 2 для слоя заполнителя и этот индекс далее не указывается) будет иметь вид

(5.2)
${\mathbf{\delta }}_{{}}^{{\mathbf{f}}} = {\mathbf{\delta }}_{{}}^{{\mathbf{1}}}\varphi _{{}}^{1} + {\mathbf{\delta }}_{{}}^{{\mathbf{2}}}\varphi _{{}}^{2}$
где φ1 = (1– 2zf/hf )/2, φ2 = 1– φ1, zf – нормальная к срединной поверхности КЭЗ координата, hf – толщина конечного элемента заполнителя.

С учетом (5.1), (5.2), зная АФП КЭ несущих слоев (3.3), запишем в матричной форме выражение для вектора перемещений трехмерного КЭ слоя заполнителя

(5.3)
${\mathbf{\delta }}_{{}}^{{\mathbf{f}}}{\mathbf{ = T}}_{{}}^{{\mathbf{f}}}{\mathbf{\alpha }}_{{}}^{{\mathbf{f}}}$
где ${\mathbf{T}}_{{}}^{{\mathbf{f}}}$ (3 × 40), ${{{\mathbf{\alpha }}}^{{\mathbf{f}}}}$ – соответственно матрица аппроксимирующих функций перемещений и вектор неопределенных коэффициентов конечных элементов слоя заполнителя.

После подстановки (5.3) в геометрические соотношения для трехмерного тела, записанные в цилиндрических координатах, будет иметь выражение для вектора обобщенных деформаций КЭ слоя заполнителя в матричной форме

(5.4)
${\mathbf{\varepsilon }}_{{}}^{f} = \Omega _{{}}^{f}{\mathbf{\alpha }}_{{}}^{f}$

Используя для КЭ слоя заполнителя физические соотношения (закон Гука), с учетом (5.4) получим запись выражений для напряжений с помощью вектора неопределенных коэффициентов, а затем с помощью вектора узловых перемещений. Из условия минимума полной потенциальной энергии (вариационный принцип Лагранжа) [36, 17 ] находятся выражения для записи матрицы жесткости конечного элемента слоя заполнителя подобно [23].

Определив выражения для матриц жесткости конечных элементов несущих слоев и слоя заполнителя, дальнейшее решение задачи проводится с помощью хорошо разработанных и отлаженных алгоритмов метода перемещений МКЭ.

6. Числовой пример. Разработанную модель применим для исследования напряженно-деформированного состояния в слоях трехслойной цилиндрической композитной оболочки, нагруженной равномерно распределенным внутренним давлением и ослабленной двумя диаметрально противоположными прямоугольными вырезами. Несущие слои оболочки выполнены из стеклопластика, а заполнитель – из пенопласта.

Рассматриваются два варианта оболочки с вырезами:

1 – вырезы сквозные;

2 – вырезы закрыты крышками, которые служат для герметизации отсека и не воспринимают нагрузку, действующую на них, а та часть давления, которая приходится на площадь крышки при расчете заменялась распределенными по периметру выреза перерезывающими силами.

Вырезы располагаются на равном расстоянии от торцов оболочки. Длина вырезов составляет 40% от длины образующей. Угол раствора вырезов равен 0.84 рад.

Принимается, что граничные условия на торцах несущих слоев оболочки соответствуют случаю жесткой заделки с разрешением осевых перемещений.

Геометрические параметры оболочки следующие:

$L = 2{\text{ м}},\quad R = 1.5{\text{ м}},\quad {{h}_{1}} = 0.002{\text{ м}},\quad {{h}_{3}} = 0.002{\text{ м,}}\quad H = 0.05{\text{ м}}$
где L – длина, R – радиус срединной поверхности заполнителя оболочки; h1, h3 – толщина внутреннего и наружного несущих слоев соответственно; H – толщина трехслойного пакета.

Физико-механические характеристики трехслойной оболочки следующие:

– для внутреннего и наружного ортотропных несущих слоев: E1 = 20594 Мпа, E2 = = 18632.6 Мпа, G12 = 3432.3 Мпа, μ2 = 0.1;

– для заполнителя: E3 = 23.53 Мпа, G13 = G23 = 9.81 Мпа.

Вследствие симметрии в осевом и окружном направлениях при расчете рассматривалась 1/8 симметричная часть оболочки, которая разбивалась на 20 трехслойных блоков (состоящих из конечных элементов внутреннего и наружного несущих слоев и слоя заполнителя) в осевом направлении и на 30 блоков в окружном.

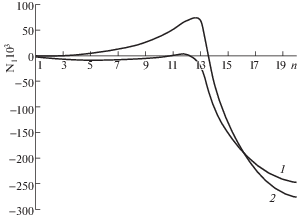
Наибольшими по абсолютной величине в несущих слоях являются мембранные усилия N1 во внутреннем несущем слое на середине прямолинейного края выреза (рис. 2). Максимальные значения мембранных усилий N2 наблюдаются в окрестности угловой точки выреза во внутреннем несущем слое. Эти максимальные значения усилий N2 почти на 20% меньше наибольших усилий N1 для варианта 2 оболочки с вырезами. Максимальные значения мембранных напряжений в несущих слоях превышают максимальные значения моментных напряжений.

Рис. 2

Изменение усилий N1 вдоль прямолинейного края выреза трехслойной цилиндрической оболочки: 1 – сквозные вырезы; 2 – вырезы закрыты крышками.

Наибольшими в заполнителе являются напряжения τ31, τ23 вблизи угловой точки выреза (рис. 3). Причем максимальные значения τ31 на ~33% больше наибольших напряжений τ23 для варианта 2 оболочки с вырезами и почти в 3 раза выше напряжений σ33. В заполнителе напряжения σ11, σ22, которыми обычно пренебрегают, сопоставимы с σ33.

Рис. 3

Изменение напряжений τ31 вдоль прямолинейного края выреза трехслойной цилиндрической оболочки: 1 – сквозные вырезы; 2 – вырезы закрыты крышками.

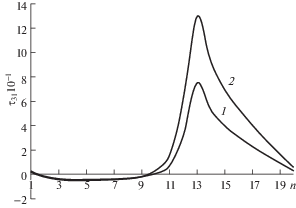
Изменение наибольших усилий N1 (Н/м) и напряжений τ31 (Мпа) вдоль прямолинейного края выреза представлено на рис. 2, 3. По оси абсцисс откладывается номер КЭ, начиная от торца оболочки к середине выреза.

Цифрами 1, 2 обозначены графики для двух вариантов оболочки, указанных выше.

Как видно из приведенных графических зависимостей, напряженно-деформированного состояние оболочки, ослабленной вырезами, характеризуется ярко выраженным краевым эффектом в окрестности выреза и вблизи его угловых точек, быстро затухающим по мере удаления от выреза. Учет нагрузок от крышки (вариант 2) значительно повышает напряжения возле выреза.

7. Заключение. Рассмотрено построение модели для послойного анализа напряженно-деформированного состояния трехслойных нерегулярных цилиндрических оболочек вращения, при котором стенка оболочки моделируется по толщине конечными элементами, которые затем стыкуются между собой. Модель позволяет адекватно моделировать особенности слоисто-неоднородного строения, моментное состояние несущих слоев, трехмерное напряженно-деформированное состояние в заполнителе, а также учесть наличие прямоугольных вырезов. Для уменьшения размерности модели послойного анализа применены функции аппроксимаций деформаций. Приведено исследование напряженно-деформированного состояния в слоях трехслойных цилиндрических оболочек вращения с прямоугольными вырезами, в том числе закрытыми крышками.

Статья посвящается светлой памяти Ученого и Учителя, Героя Социалистического Труда, лауреата Ленинской и Государственной премий, чл.-кор. АН СССР В.И. Феодосьева (05.05.1916–24.09.1991) от его благодарного студента, дипломника, аспиранта, ученика.

Работа выполнена в рамках государственного задания ИПРИМ РАН.

Список литературы

  1. Васильев В.В. Механика конструкций из композиционных материалов. М.: Машиностроение, 1988. 272 с.

  2. Бакулин В.Н., Образцов И.Ф., Потопахин В.А. Динамические задачи нелинейной теории многослойных оболочек: Действие интенсивных термосиловых нагрузок, концентрированных потоков энергии. М.: Наука. Физматлит, 1998. 464 с.

  3. Бакулин В.Н., Острик А.В. Комплексное действие излучений и частиц на тонкостенные конструкции с гетерогенными покрытиями. М.: Физматлит, 2015. 280 с.

  4. Bakulin V. N. Investigation of the Influence of the Cutout Dimensions on the Stress-strain State of Three-layer Shells with Load-bearing Layers of Composite Materials // J. Phys.: Conf. Ser.: Mater. Sci. Eng. 2020. V. 714. P. 012002. https://doi.org/10.1088/1757-899X/714/1/012002

  5. Паймушин В.Н. Теория среднего изгиба подкрепленных на контуре трехслойных оболочек с трансверсально-мягким заполнителем // Мех. композ. материалов. 2017. Т. 53. № 1. С. 3–26.

  6. Григоренко Я.М., Григоренко A.Я. Статические и динамические задачи для анизотропных неоднородных оболочек с переменными параметрами и их числовым решением (обзор) // Прикладная механика. 2013. Т. 49. № 2. С. 3–70.

  7. Бакулин В.Н. Послойный анализ напряженно-деформированного состояния нерегулярных трехслойных оболочек вращения ненулевой гауссовой кривизны // ПММ. 2021. Т. 85. № 1. С. 90–106.

  8. Аннин Б.Д., Волчков Ю.М. Неклассические модели теории пластин и оболочек // ПМТФ. 2016. Т. 57. № 5. С. 5–14.

  9. Бакулин В.Н. Уточненные модели послойного анализа трехслойных нерегулярных оболочек // Всероссийская научно-техническая конференция. “Механика и математическое моделирование в технике”, посвященная 100-летию со дня рождения В.И. Феодосьева. Сб. материалов. М.: МГТУ им. Н.Э. Баумана, 2016. С. 278–281.

  10. Bakulin V. N. A Corrected model of level-by-level analysis of three-layer irregular conical shells // Dokl. Phys. 2017. V. 62. № 1. P. 37–41.

  11. Bakulin V.N. Block based finite element model for layer analysis of stress strain state of three-layered shells with irregular structure // Mech. Solids. 2018. V. 53. No. 4. P. 411–417. https://doi.org/10.3103/S0025654418040064

  12. Бакулин В.Н. Уточненный послойный анализ НДС слоисто-неоднородных, в общем случае нерегулярных оболочечных элементов конструкций // Материалы XIII Международной конференции по Прикладной математике и механике в аэрокосмической отрасли (AMMAI'2020), посвященной 90-летию МАИ и 100-летию со дня рождения академика И.Ф. Образцова, 6–13 сентября 2020 г. Алушта. М.: Изд-во МАИ, 2020. С. 259–261.

  13. Гузь А.Н., Чернышенко И.С., Чехов Вал.Н., Чехов Вик.Н., Шнеренко К.И. Методы расчета оболочек. Т. 1. Теория тонких оболочек, ослабленных отверстиями. Киев: Наукова думка, 1980. 636 с.

  14. Бакулин В.Н., Ревенко В.П. Аналитико-численный метод конечных тел решения краевой задачи для цилиндрической ортотропной оболочки с немалым прямоугольным отверстием // Изв. вузов. Математика. 2016. № 6. С. 3–14.

  15. Bakulin V.N. Layer-by-layer analysis of the stress-strain state of three-layer shells with cutouts // Mech. Solids. 2019. V. 54. № 3. P. 448–460. https://doi.org/10.3103/S0025654419020092

  16. Образцов И.Ф., Савельев Л.М., Хазанов Х.С. Метод конечных элементов в задачах строительной механики летательных аппаратов. М.: Высшая школа, 1985. 392 с.

  17. Бакулин В.Н., Рассоха А.А. Метод конечных элементов и голографическая интерферометрия в механике композитов. М.: Машиностроение, 1987. 312 с.

  18. Бакулин В.Н. Построение конечно-элементных моделей для уточненного прочностного анализа слоистых оболочек. Материалы XII Международной конференции по Прикладной математике и механике в аэрокосмической отрасли (NPNJ'2018), посвященной памяти академика Ю.А. Рыжова. 24–31 мая 2018 г. Алушта, Крым. M.: МАИ, 2018. С 330–332.

  19. Strang G., Fix G.J. An Analysis of the Finite Element Method. Englewood Cliffs, N. J.: Prentice-Hall, 1973 = Стренг Г., Фикс Д. Теория метода конечных элементов. М.: Мир, 1977. 392 с.

  20. Образцов И.Ф. О некоторых перспективных прикладных проблемах механики, имеющих народнохозяйственное значение // Изв. АН СССР. МТТ. 1982. № 4. С. 3–9.

  21. Бакулин В.Н., Каледин Вл.О. Конечный элемент круговой арки с конечной сдвиговой жесткостью // Мех. композ. матер. 1988. № 5. С. 915–919.

  22. Бакулин В.Н. Аппроксимации для моделирования напряженно-деформированного состояния слоистых цилиндрических оболочек // Матем. моделир. 2004. Т. 16. № 6. С. 101–105.

  23. Бакулин В.Н. Конечно-элементная модель для анализа напряженно-деформированного состояния трехслойных оболочек // Матем. моделир. 2006. Т. 18. № 1. С. 3–9.

  24. Образцов И.Ф., Бакулин В.Н. Уточненные модели для исследования напряженно-деформированного состояния трехслойных цилиндрических оболочек // ДАН. 2006. Т. 407. № 1. С. 36–39.

  25. Бакулин В.Н. Неклассические уточненные модели в механике трехслойных оболочек // Вест. Нижегородского университета им. Н.И. Лобачевского. 2011. № 4. Ч. 5. С. 1989–1991.

  26. Каледин Вл.О., Шпиталь С.В. Выбор расчетной схемы при исследовании осесимметричного краевого эффекта в трехслойных цилиндрических оболочках с легким заполнителем // Мех. композ. материалов. 1993. № 5. С. 657–665.

  27. Бакулин В.Н., Репинский В.В. Конечно-элементные модели деформации однослойных и трехслойных конических оболочек // Матем. моделир. 2001. Т. 13. № 6. С. 39–46.

  28. Бакулин В.Н. Уточненная модель для расчета напряженно-деформированного состояния трехслойных конических оболочек вращения // Вестник Московского авиац. ин-та, 2011. Т. 18. № 2. С. 211–218.

  29. Bakulin V.N. Analysis of the influence of rectangular cutouts on the stress-strain state of three-layer shells // 18th International Conference “Aviation and Cosmonautics – 2019”. Abstracts. Moscow: Moscow State Institute of Aviation (National Research University), 2019. P. 435–436.

  30. Bakulin V.N. A Model for Refined Calculation of the Stress-Strain State of Sandwich Conical Irregular Shells // Mech. Solids. 2019. V. 54. № 5. P. 786–796. https://doi.org/10.3103/S0025654419050054

  31. Бакулин В.Н., Кривцов В.С., Рассоха А.А. Алгоритм получения матрицы жесткости конечного элемента анизотропной оболочки // Изв. вузов. Авиац. техника. 1983. № 4. С. 14–18.

  32. Бакулин В. Н. Конечно-элементные модели для расчета слоистых оболочек вращения ненулевой гауссовой кривизны // Матем. моделир. 2002. Т. 14. № 8. С. 37–43.

  33. Бакулин В.Н., Репинский В.В. Сравнение конечно-элементного решения с аналитическим в задачах механики деформирования сферических оболочек. Материалы XII Международной конференции по Прикладной математике и механике в аэрокосмической отрасли (NPNJ'2018), посвященной памяти академика Ю.А. Рыжова. 24–31 мая 2018 г. Алушта, Крым. M.: МАИ, 2018. С 338–340.

  34. Bakulin V.N. Block finite-element model of layer-by-layer analysis of the stress–strain state of three-layer generally irregular shells of double-curvature revolution // Dokl. Phys., 2019. V. 64. No. 1. P. 9–13. https://doi.org/10.1134/S1028335819010026

  35. Bakulin V.N. Model for Layer-by-Layer Analysis of the Stress-Strain State of Three-Layer Irregular Shells of Revolution of Double Curvature // Mech. Solids. 2020. V. 55. № 2. P. 248–257. https://doi.org/10.3103/S0025654420020077

  36. Балабух Л.И., Колесников К.С., Зарубин В.С. и др. Основы строительной механики ракет. М.: Высшая школа, 1969. 494 с.

  37. Bakulin V.N. Effective model of load-bearing layers for layer-by-layer analysis of the stress-strain state of three-layer cylindrical irregular shells of revolution // Mech. Solids. 2020. V. 55. № 3. P. 357–365. https://doi.org/10.3103/S0025654420030048

  38. Кантин Г. Смещение криволинейных элементов как жесткого целого // Ракетная техника и космонавтика. 1970. № 7. С. 84–88.

  39. Железнов Л.П., Кабанов В.В. Функции перемещений конечных элементов оболочки вращения как твердых тел // Изв. РАН. МТТ. 1990. № 1. С. 131–136

  40. Клочков Ю.В. Учет жестких смещений конечного элемента в неявном виде на основе использования векторной интерполяции перемещений // Вестник РУДН. 2002. Спецвыпуск. № 1. С. 123–127.

  41. Timoshenko S., Woinowsky-Krieger S. Theory of plates and shells. 2d ed. New York: Mc Graw-Hill, 1959. = Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки. М.: Физматгиз, 1963. 635 с.

  42. Голованов А.И., Тюленева О.Н., Шигабутдинов А.Ф. Метод конечных элементов в статике и динамике тонкостенных конструкций. М.: Физматлит, 2006. 392 с.

  43. Bakulin V.N. Research of the influence of rectangular cutout dimensions on the stress-strain state of shells using an effective finite element model // IOP Conf. Ser.: Mater. Sci. Eng. 2020. V. 868. P. 012034. https://doi.org/10.1088/1757-899X/868/1/012034

  44. Bakulin V.N. Investigation of the stress-strain state of the composite cylindrical shell with rectangular cutouts // IOP Conf. Ser.: Mater. Sci. Eng. 2020. V. 927. P. 012066. https://doi.org/10.1088/1757-899X/927/1/012066

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал