1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 5, 2021

Известия РАН. Механика твердого тела, 2021, № 5, стр. 113-126

ТЕОРЕТИЧЕСКИЕ АСПЕКТЫ ПРИМЕНЕНИЯ ВОЛН ПОХГАММЕРА–КРИ К ЗАДАЧАМ ОПРЕДЕЛЕНИЯ ДИНАМИЧЕСКОГО КОЭФФИЦИЕНТА ПУАССОНА

Т. А. Гаджибеков a, А. В. Ильяшенко b, *

a Московский государственный технический университет им. Баумана
Москва, Россия

b Московский государственный строительный университет
Москва, Россия

* E-mail: avi_56@mail.ru

Поступила в редакцию 20.06.2020
После доработки 28.07.2020
Принята к публикации 31.08.2020

Полный текст (PDF)

Аннотация

Анализируются теоретические аспекты применения акустических волн Похгаммера–Кри в неразрушающей диагностике. Основное внимание уделяется продольным аксиально симметричным гармоническим модам. Впервые дается анализ дисперсионных кривых для стержней, выполненных из ауксетиков (материалов с отрицательным коэффициентом Пуассона). Получены дисперсионные кривые в окрестности второй предельной скорости, обнаруживающие чувствительность значений второй предельной скорости к вариации коэффициента Пуассона.

Ключевые слова: волны Похгаммера–Кри, поляризация, дисперсия, коэффициент Пуассона, предельная скорость

1. Введение. Впервые дисперсионные уравнения, описывающие распространение гармонических волн в цилиндрическом стержне, называемых волнами Похгаммера–Кри, получены в [1–3].

Однако, решения этих уравнений, связывающие фазовую (или групповую) скорость с частотой оставались практически неизученными вплоть до середины прошлого века, когда в [4–23] с помощью численного анализа дисперсионных уравнений [1–3, 8] были найдены нижние ветви дисперсионных кривых.

Надо отметить, что в [4–21] исследовались в основном продольные аксиально симметричные моды, тогда как в [22, 23] рассматривались изгибные и крутильные моды.

1.1. Дисперсионные соотношения, сплошной цилиндрический стержень. С помощью асимптотических методов в [4–12] были найдены длинноволновой и коротковолновой пределы для фазовой скорости фундаментальной продольной аксиально симметричной моды. При этом, коротковолновой предел при $\omega \to \infty $

(1.1)
${{c}_{{1,lim}}} = {{c}_{R}}$
совпал со скоростью волны Рэлея (${{c}_{R}}$), а длинноволновой предел дал следующее значение фазовой скорости ${{c}_{{{\text{2,}}lim}}}$
(1.2)
${{c}_{{{\text{2,}}lim}}} = \sqrt {\frac{E}{\rho }} $
где E и ρ – модуль упругости и плотность материала стержня, соответственно.

Дисперсионные кривые высших мод в терминах безразмерных фазовой частоты и волнового числа с помощью численных методов исследовались в [4–20], причем в [8], по-видимому, впервые были вычислены корни дисперсионного уравнения и построены первые три дисперсионные кривые, отвечающие низшим продольным аксиально симметричным модам. Соответствующие дисперсионные кривые, определенные в [19], показаны на рис. 1. $L(0,m)$ обозначает аксиально симметричную продольную моду $m$-го порядка, см. [16]. На вертикальной и горизонтальной осях на этом рисунке отложены, соответственно, безразмерная частота ($\Omega = \omega a{\text{/}}{{v}_{s}}$) и волновое число ($\gamma $); $a$ – радиус стержня; ${{v}_{s}}$ – скорость объемной поперечной волны в среде.

Рис. 1.

Дисперсионные кривые аксиально симметричных гармонических волн Похгаммера–Кри в цилиндрическом стержне [16]: сплошной линией обозначены действительные или чисто мнимые кривые, а пунктирной линией – комплексные.

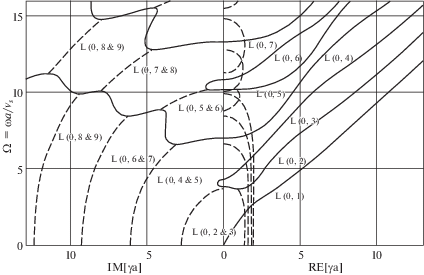
Одна из интересных особенностей незатухающих высших мод ($L(0,m),$ $m > 1$) соответствующих дисперсионных кривых, появляется при $\gamma \to 0$:

(1.3)
$\mathop {\lim }\limits_{\gamma \to 0} \frac{{\partial \Omega }}{{\partial \gamma }} = 0$

Фактически, условие (1.3) означает наличие в высших модах горизонтальной асимптоты в дисперсионной зависимости $\omega (c)$ при фазовой скорости $c \to \infty $. Здесь обнаруживается связь с незатухающими высшими модами соответствующих дисперсионных кривых волн Лэмба [24, 25], для которых также выполняется соотношение (1.3).

1.2. Родственные задачи. Исследование по распространению ангармонических продольных волн в полуограниченном цилиндрическом стержне и, в частности, импульсов в виде временной $\delta $-функции, по-видимому, впервые осуществлено в [26]. В этой работе, также как и в последующих исследованиях [17, 27–29], основное внимание уделялось распространению длинноволновой асимптотики, дисперсионные составляющие не исследовались. Необходимость учета (геометрической) дисперсии при распространении ангармонических импульсов в цилиндрических стержнях отмечена в [30], где с помощью экспериментальных сейсмограмм, отвечающих распространению продольных волн от δ-образного импульса, приложенного к одному из торцов стержня, прослежена деформация импульса, вызванная дисперсией соответствующих волн.

Вопросам распространения волн Похгаммера–Кри в цилиндрическом стержне из вязкоупругого материала посвящены исследования [31–37]. В [31] впервые обнаружена и описана, так называемая, физическая дисперсия волн Похгаммера–Кри, вызванная вязкостью материала и проявляющаяся даже на тех участках дисперсионных кривых, где в случае упругого материала геометрическая дисперсия практически отсутствует.

Исследование дисперсии волн Похгаммера–Кри в коаксиальных стержнях (трубах) проводилось в [38–43] с применением той же техники, что и для сплошных стержней, но с удержанием в построенном решении бесселевых функций как первого, так и второго рода, так как для коаксиальных стержней отпадает необходимость ставить ограничение конечности перемещений на оси стержня.

С помощью техники замены переменных в конических стержнях исследовались продольные аксиально симметричные волны и соответствующие колебания [44–49], причем в этих работах для исключения сингулярных решений вершина конуса исключалась из рассмотрения.

В [50, 51] с помощью приближенной одномерной теории Рэлея–Лява и точной теории, основанной на уравнениях Похгаммера–Кри, исследовались негармонические волны Похгаммера–Кри, вызванные продольным ударом по сплошному цилиндрическому стержню. В этих работах возможная перекачка энергии на высшие аксиально симметричные моды не исследовалась, а предполагалось, что при продольном ударе вся энергия локализована в продольной фундаментальной моде. При этом для рассмотренного случая отмечена значительная дисперсия.

Волны в трансверсально изотропных стержнях кругового поперечного сечения исследовались в [52–57] с применением той же техники, что использовалась для изотропных стержней. В этой связи более общие случаи цилиндрической анизотропии, по-видимому, не исследовались, за исключением различных мод волн Похгаммера–Кри в цилиндрически ортотропной упругой слоистой трубе [58] исследованной с помощью метода конечных элементов. Надо отметить, что применение метода конечных элементов для получения дисперсионных соотношений в стержнях наталкивается на определенные трудности, связанные с необходимостью исключения начальной негармонической фазы [58, 59]. Аналогичные трудности отмечены и в случае применения метода конечных элементов для определения дисперсионных соотношений волн Лэмба [60].

Волны Похгаммера–Кри в стержнях некруговой формы исследовались в работах [61–63] с помощью метода конечных элементов, причем в [62, 63] наряду с действительными решениями дисперсионного уравнения анализировались и комплексные ветви высших мод. Для этого в работах [62, 63] были соответствующим образом модифицированы Лагранжиан и принцип Гамильтона, что позволило учесть комплексные поля перемещений.

Известны и другие приближенныe методы, применяемые для анализа волновых процессов в стержнях, основанные на различного рода приближенных теориях, по аналогии с технической теорией изгиба балок. В этой связи надо отметить обзоры [64–66].

1.3. Применения волн Похгаммера–Кри к задачам неразрушающей диагностики. Продольные аксиально симметричные волны Похгаммера–Кри часто применяются в качестве метода как для (i) неразрушающего определения механических свойств материалов, так и для (ii) диагностики наличия дефектов.

В первом случае, как правило, используют два цилиндрических длинных стержня Гопкинсона (называемых иногда стержнями Кольского), между которыми размещают исследуемый образец, как правило, также цилиндрической формы; рис. 2.

Рис. 2.

Принципиальная схема двух стержней Гопкинсона: (1) ударник; (2) первый стержень Гопкинсона, передающий ударное воздействие на образец; (3) образец; (4) второй стержень Гопкинсона, в котором распространяются рефрагированные волны.

При ударном воздействии, приложенном к левому торцу первого стержня Гопкинсона, распространяется импульс со скоростью близкой ко второй предельной скорости ${{c}_{{{\text{2,}}lim}}}$, далее на интерфейсной границе между первым стержнем и образцом часть энергии, отвечающей рефрагированной волне, переходит в образец, а часть отражается, при этом энергия отраженной и рефрагированной волн зависит от соотношения импедансов материала стержня и образца. На следующей границе между образцом и вторым стержнем Гопкинсона происходит аналогичное явление; см. обзорную монографию [68]. Использование длинных стержней Гопкинсона с отношением длины стержня $L$ к его диаметру d, $L{\text{/}}d > 100$ необходимо для исключения, во-первых нераспространяющихся мод волн Похгаммера–Кри, и, во-вторых, для обеспечения возможно большей локализации энергии аксиально симметричной волны Похгаммера–Кри в области малых частот [67–70]. Роль длительности ударной нагрузки, приложенной к одному из торцов стержня Гопкинсона, исследовалась в [71–73]; было установлено, что в случае более продолжительных импульсов, низкочастотные составляющие фундаментальной моды, распространяющиеся с большей скоростью, имеют и большие амплитуды. Известны обобщения на случай применения стержней Гопкинсона для экспериментальных исследований, связанных с возбуждением и распространением крутильных мод волн Похгаммера–Кри [74].

Задачи обнаружения дефектов в трубах и слоистых коаксиальных цилиндрах также основаны на генерировании в основном продольных аксиально симметричных (как правило, гармонических) волн Похгаммера–Кри и исследовании либо их отражения от локализованных дефектов [75–77], либо изменения их дисперсионных кривых при распространении по участкам с измененными свойствами [78–80]. C помощью этих волн могут исследоваться как упругие, так и вязкоупругие свойства сплошных стержней и цилиндрических оболочек, в том числе слоистых, состоящих из вложенных друг в друга и находящихся в контакте коаксиальных цилиндров [81, 82]. Как отмечено выше, при неразрушающем контроле дефектных зон в стержнях и трубах, как правило, используют источники, возбуждающие гармонические волны Похгаммера–Кри. Это необходимо для возможности сопоставления теоретических дисперсионных кривых (определяемых для гармонических волн) с полученными в ходе экспериментальных исследований. Диапазон частот, применяемых для экспериментального обнаружения и исследования участков сплошного цилиндра или трубы с измененными свойствами, обычно варьируется в диапазоне от 30 КГц до 100 МГц [82, 83]. Общие свойства решений дисперсионных уравнений для волн Похгаммера–Кри, а так же других типов дисперсионных поверхностных волн обсуждаются в работах [84–87].

В последние годы для возбуждения различных мод волн Похгаммера–Кри получили методы, основанные на применении электромагнитно-акустических преобразователей (ЭМАП) поверхностных волн, причем наряду с продольными модами могут возбуждаться изгибные и крутильные моды [88–90].

В исследованиях [91–94] отражены некоторые теоретические аспекты, связанные с анализом дисперсионных соотношений волн Похгаммера–Кри. Следует отметить также некоторые родственные задачи: в работах [95, 96] исследовались вторые предельные скорости в пластинах, в [97] анизотропные ауксетки, в [98, 99] рассматривались спиральные волны в стержнях.

1.4. Краткое содержание последующих разделов. В разделе 2 вводятся основные уравнения, определяются потенциалы смещений, выписываются решения для потенциалов в терминах бесселевых функций, определяются дисперсионные уравнения.

В третьем разделе по дисперсионному уравнению осуществляется построение дисперсионных кривых, основное внимание уделено аксиально симметричной фундаментальной моде. Впервые дается анализ дисперсионных кривых для стержней, выполненных из ауксетиков (материалов с отрицательным коэффициентом Пуассона). Анализируется чувствительность аксиально симметричной фундаментальной моды к вариации упругих свойств во всем допустимом диапазоне фазовых скоростей и, в частности, в окрестности первой (${{c}_{{{\text{1,}}lim}}}$) и второй предельной скорости (${{c}_{{{\text{2,}}lim}}}$). Приводятся расчетные формулы для определения упругих характеристик материала по значениям соответствующих предельных скоростей.

2. Основные соотношения. Ниже, в основном, используется нотация [84, 85]. Уравнения движения для изотропного упругого тела в отсутствии массовых сил представимы в виде

(2.1)
$c_{1}^{2}\nabla {\text{div}}\,{\mathbf{u}} - c_{2}^{2}{\text{rot}}\,{\text{rot}}\,{\mathbf{u}} = \partial _{{tt}}^{2}{\mathbf{u}}$
где u – поле перемещений, c1, c2 – скорости продольной и поперечной объемных волн в среде, определяемые выражениями

(2.2)
${{c}_{1}} = \sqrt {\frac{{\lambda + 2\mu }}{\rho }} ,\quad {{c}_{2}} = \sqrt {\frac{\mu }{\rho }} $

В (2.2) λ, μ – константы Ламе, $\rho $ – плотность среды.

Как правило, в рассматриваемом классе задач для векторного поля ${\mathbf{u}}$ применяется представление Гельмгольца

(2.3)
${\mathbf{u}} = \nabla \Phi + {\text{rot}}\Psi $
где $\Phi $ и $\Psi $ соответственно скалярный и векторный потенциалы. В цилиндрических координатах представление Гельмгольца (2.3) для физических компонент вектора перемещений имеет вид
(2.4)
$\begin{gathered} {{u}_{r}} = \frac{{\partial \Phi }}{{\partial r}} + \frac{1}{r}\frac{{\partial {{\Psi }_{z}}}}{{\partial \theta }} - \frac{{\partial {{\Psi }_{\theta }}}}{{\partial z}} \\ {{u}_{\theta }} = \frac{1}{r}\frac{{\partial \Phi }}{{\partial \theta }} + \frac{{\partial {{\Psi }_{r}}}}{{\partial z}} - \frac{{\partial {{\Psi }_{z}}}}{{\partial r}} \\ {{u}_{z}} = \frac{{\partial \Phi }}{{\partial z}} + \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r{{\Psi }_{\theta }}} \right) - \frac{1}{r}\frac{{\partial {{\Psi }_{r}}}}{{\partial \theta }} \\ \end{gathered} $
причем из условия аксиальной симметрии следует

(2.5)
${{u}_{\theta }} = 0$

Подстановка представления (2.3) в уравнения движения (2.1) дает

(2.6)
$c_{1}^{2}\Delta \Phi = \partial _{{tt}}^{2}\Phi ,\quad c_{2}^{2}\Delta \Psi = \partial _{{tt}}^{2}\Psi $

Для гармонической волны, распространяющейся в направлении оси z, потенциалы (2.6) представимы в виде

(2.7)
$\Phi = {{\Phi }_{0}}({\mathbf{x}}{\kern 1pt} '){{e}^{{i\gamma (z - ct)}}},\quad \Psi = {{\Psi }_{0}}({\mathbf{x}}{\kern 1pt} '){{e}^{{i\gamma (z - ct)}}}$
где $\gamma $ – волновое число, связанное с фазовой скоростью c и круговой частотой $\omega $ соотношением

(2.8)
$\gamma = \frac{\omega }{c}$

В (2.7) ${\mathbf{x}}{\kern 1pt} '$ – координата в поперечном сечении (${\mathbf{x}}{\kern 1pt} ' = {\mathbf{x}} - ({\mathbf{n}} \cdot {\mathbf{x}}){\mathbf{n}}$), ${\mathbf{n}}$ – волновой вектор, $z = {\mathbf{n}} \cdot {\mathbf{x}}$, t – время.

Подстановка представлений (2.7) в уравнения (2.6) дает уравнения Гельмгольца для соответствующих потенциалов

(2.9)
$\Delta {{\Phi }_{0}} + \left( {\frac{{{{c}^{2}}}}{{c_{1}^{2}}} - 1} \right){{\gamma }^{2}}{{\Phi }_{0}} = 0,\quad \Delta {{\Psi }_{0}} + \left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}}{{\Psi }_{0}} = 0$

Переход в (2.9) к цилиндрическим координатам для скалярного потенциала Φ0 с учетом аксиальной симметрии потенциала Φ0

(2.10)
$\frac{{\partial {{\Phi }_{0}}}}{{\partial \theta }} = 0$

  • приводит к уравнению Бесселя

    (2.11)
    $\frac{1}{r}\frac{d}{{dr}}r\frac{d}{{dr}}{{\Phi }_{0}}(r) + \left( {\frac{{{{c}^{2}}}}{{c_{1}^{2}}} - 1} \right){{\gamma }^{2}}{{\Phi }_{0}}(r) = 0$

где c – фазовая скорость. Решения уравнения (2.11) выражается через функции Бесселя первого и второго рода нулевого порядка
(2.12)
${{\Phi }_{0}}(r) = {{C}_{1}}{{J}_{0}}({{q}_{1}}r) + {{C}_{2}}{{Y}_{0}}({{q}_{1}}r)$
где ${{C}_{k}},k = 1,2$ – неизвестные, вообще говоря, комплексные коэффициенты и

(2.13)
$q_{{_{1}}}^{2} = \left( {\frac{{{{c}^{2}}}}{{c_{1}^{2}}} - 1} \right){{\gamma }^{2}}$

Уравнения (1.10) для векторного потенциала ${{\Psi }_{0}}$ при учете аксиальной симметрии компонент потенциала ${{\Psi }_{0}}$, что обеспечивается условиями

(2.14)
$\frac{{\partial {{\Psi }_{r}}}}{{\partial \theta }} = \frac{{\partial {{\Psi }_{\theta }}}}{{\partial \theta }} = \frac{{\partial {{\Psi }_{z}}}}{{\partial \theta }} = 0$
дают следующие уравнения Бесселя (для соответствующих физических компонент)

(2.15)
$\begin{gathered} \frac{1}{r}\frac{d}{{dr}}r\frac{d}{{dr}}{{\Psi }_{r}}(r) + \left( {\left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}} - \frac{1}{{{{r}^{2}}}}} \right){{\Psi }_{r}}(r) = 0 \\ \frac{1}{r}\frac{d}{{dr}}r\frac{d}{{dr}}{{\Psi }_{\theta }}(r) + \left( {\left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}} - \frac{1}{{{{r}^{2}}}}} \right){{\Psi }_{\theta }}(r) = 0 \\ \frac{1}{r}\frac{d}{{dr}}r\frac{d}{{dr}}{{\Psi }_{z}}(r) + \left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}}{{\Psi }_{z}}(r) = 0 \\ \end{gathered} $

Решение уравнений (2.15) имеет вид

(2.16)
$\begin{gathered} {{\Psi }_{\theta }}(r) = {{C}_{3}}{{J}_{1}}({{q}_{2}}r) + {{C}_{4}}{{Y}_{1}}({{q}_{2}}r) \\ {{\Psi }_{r}}(r) = {{C}_{5}}{{J}_{1}}({{q}_{2}}r) + {{C}_{6}}{{Y}_{1}}({{q}_{2}}r) \\ {{\Psi }_{z}}(r) = {{C}_{7}}{{J}_{0}}({{q}_{2}}r) + {{C}_{8}}{{Y}_{0}}({{q}_{2}}r) \\ \end{gathered} $

В (2.16) ${{C}_{k}},k = 3,...,8$ неизвестные, вообще говоря, комплексные коэффициенты, и

(2.17)
$q_{{_{2}}}^{2} = \left( {\frac{{{{c}^{2}}}}{{c_{2}^{2}}} - 1} \right){{\gamma }^{2}}$

Условие аксиальной симметрии векторного потенциала $\Psi $ накладывает еще одно ограничение [14, 16]:

(2.18)
${{\Psi }_{r}} = {{\Psi }_{z}} = 0$

С учетом (2.4), (2.5) (2.12), (2.16), (2.18), векторное поле, отвечающее распространению продольной аксиально симметричной гармонической незатухающей волны в цилиндрическом стержне, представимо в виде [19]

(2.19)
$\begin{gathered} {{u}_{r}} = - \left[ {{{q}_{1}}\left( {{{C}_{1}}{{J}_{1}}({{q}_{1}}r) + {{C}_{2}}{{Y}_{1}}({{q}_{1}}r)} \right) + i\gamma \left( {{{C}_{3}}{{J}_{1}}({{q}_{2}}r) + {{C}_{4}}{{Y}_{1}}({{q}_{2}}r)} \right)} \right]{{e}^{{i\gamma (z - ct)}}} \\ {{u}_{\theta }} = 0 \\ {{u}_{z}} = \left[ {i\gamma \left( {{{C}_{1}}{{J}_{0}}({{q}_{1}}r) + {{C}_{2}}{{Y}_{0}}({{q}_{1}}r)} \right) + {{q}_{2}}\left( {{{C}_{3}}{{J}_{0}}({{q}_{2}}r) + {{C}_{4}}{{Y}_{0}}({{q}_{2}}r)} \right)} \right]{{e}^{{i\gamma (z - ct)}}} \\ \end{gathered} $

С учетом необходимой ограниченности поля перемещений на оси $r = 0$ и неограниченности при $r \to 0$ бесселевых функций второго рода, из (2.19) получаем

(2.20)
$\begin{gathered} {{u}_{r}} = - \left[ {{{q}_{1}}{{C}_{1}}{{J}_{1}}({{q}_{1}}r) + i\gamma {{C}_{2}}{{J}_{1}}({{q}_{2}}r)} \right]{{e}^{{i\gamma (z - ct)}}} \\ {{u}_{\theta }} = 0 \\ {{u}_{z}} = \left[ {i\gamma {{C}_{1}}{{J}_{0}}({{q}_{1}}r) + {{q}_{2}}{{C}_{2}}{{J}_{0}}({{q}_{2}}r)} \right]{{e}^{{i\gamma (z - ct)}}} \\ \end{gathered} $

При получении (2.20) из (2.19) константа C3 обозначена C2.

Условие равенства нулю поверхностных усилий на боковой поверхности цилиндра при $r = R$ представимо в виде

(2.21)
${{\left. {{{{\mathbf{t}}}_{\nu }} \equiv \left( {\lambda ({\text{tr}}\varepsilon )\nu + 2\mu \varepsilon \cdot \nu } \right)} \right|}_{{r = R}}} = 0$
где $\nu $ – вектор единичной внешней нормали к боковой поверхности, $\varepsilon $ – инфинитезимальный тензор деформаций.

Условие (2.21) позволяет записать граничные условия (с точностью до экспоненциального множителя ${{e}^{{i\gamma (z - ct)}}}$) в терминах соответствующих бесселевых функций

(2.22)
$\begin{gathered} {{t}_{{rr}}} \equiv \lambda {{I}_{\varepsilon }} + 2\mu {{\varepsilon }_{{rr}}} = - {{\left[ \begin{gathered} \lambda (q_{1}^{2} + {{\gamma }^{2}}){{J}_{0}}({{q}_{1}}r){{C}_{1}} + \\ + \frac{{2\mu }}{r}\left[ \begin{gathered} {{q}_{1}}{{C}_{1}}\left( {{{q}_{1}}r{{J}_{0}}({{q}_{1}}r) - {{J}_{1}}({{q}_{1}}r)} \right) + \\ + \,i\gamma {{C}_{2}}\left( {{{q}_{2}}r{{J}_{0}}({{q}_{2}}r) - {{J}_{1}}({{q}_{2}}r)} \right) \\ \end{gathered} \right] \\ \end{gathered} \right]}_{{r = R}}} = 0 \\ {{t}_{{rz}}} \equiv 2\mu {{\varepsilon }_{{rz}}} = - \mu {{\left[ \begin{gathered} i\gamma \left[ {{{q}_{1}}{{C}_{1}}{{J}_{1}}({{q}_{1}}r) + i\gamma {{C}_{2}}{{J}_{1}}({{q}_{2}}r)} \right] \\ + \,[i\gamma {{q}_{1}}{{C}_{1}}{{J}_{1}}({{q}_{1}}r) + q_{2}^{2}{{C}_{2}}{{J}_{1}}({{q}_{2}}r)] \\ \end{gathered} \right]}_{{r = R}}} = 0 \\ \end{gathered} $

Условия (2.22) дают искомое дисперсионное уравнение, записываемое в виде

(2.23)
$\det {\mathbf{A}} = 0$
где A – квадратная матрица второго порядка с комплексными коэффициентами

${{A}_{{11}}} = - \lambda (q_{1}^{2} + {{\gamma }^{2}}){{J}_{0}}({{q}_{1}}R) - \frac{{2\mu }}{R}{{q}_{1}}\left( {{{q}_{1}}R{{J}_{0}}({{q}_{1}}R) - {{J}_{1}}({{q}_{1}}R)} \right)$
(2.24)
$\begin{gathered} {{A}_{{12}}} = - \frac{{2\mu i\gamma }}{R}\left( {{{q}_{2}}R{{J}_{0}}({{q}_{2}}R) - {{J}_{1}}({{q}_{2}}R)} \right) \\ {{A}_{{21}}} = - 2\mu i\gamma {{q}_{1}}{{J}_{1}}({{q}_{1}}R) \\ \end{gathered} $
${{A}_{{22}}} = - \mu (q_{2}^{2} - {{\gamma }^{2}}){{J}_{1}}({{q}_{2}}R)$

При заданной частоте $\omega $ дисперсионным уравнением (2.23) определяется фазовая скорость продольных аксиально симметричных мод волн Похгаммера–Кри, а двумерные, вообще говоря, комплексные собственные векторы, отвечающие нулевым собственным числам матрицы (2.23), определяют поляризацию соответствующих волн.

3. Некоторые аспекты применения аксиально симметричной фундаментальной моды. По дисперсионному уравнению (2.23) осуществляется построение дисперсионных кривых для нижней (фундаментальной) аксиально симметричной моды волн Похгаммера–Кри, распространяющихся в цилиндрическом стержне.

Рассматривается два основных случая: (1) вариация коэффициента Пуассона и (2) вариация модуля упругости материала стержня.

3.1. Вариация коэффициента Пуассона. Приведенный на рис. 4 график изменения относительного значения первой предельной скорости ${{c}_{{{\text{1,}}lim}}}{\text{/}}{{c}_{2}}$, определенной по дисперсионному уравнению (2.23), при вариации коэффициента Пуассона (при фиксированном модуле упругости и плотности), показывает, что в области высоких частот фазовая скорость является информативной для определения коэффициента Пуассона материала. В частности, при вариации коэффициента Пуассона во всем допустимом диапазоне значений (–1; 0.5) относительная фазовая скорость ${{c}_{{{\text{1,}}lim}}}{\text{/}}{{c}_{2}}$ изменяется почти в два раза.

Рис. 3.

График изменения первой предельной скорости в зависимости от изменения коэффициента Пуассона.

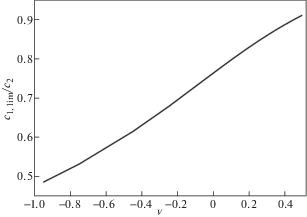
Рис. 4.

Изменение фундаментальной моды аксиально симметричных волн Похгаммера–Кри в окрестности второй предельной скорости при вариации модуля упругости.

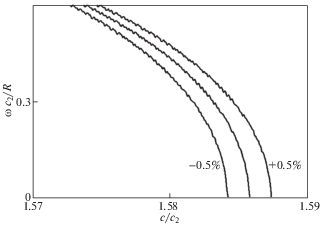
В то же время, проведенные расчеты показывают, что в области низких частот и, в особенности, в окрестности второй предельной скорости ${{c}_{{{\text{2,}}lim}}}$, все дисперсионные кривые сливаются в одну кривую.

Замечание 3.1. Надо отметить, что в случае ауксетиков известные аппроксимационные дробно-рациональные формулы для скорости волны Рэлея [86, 87] (совпадающей со скоростью ${{c}_{{{\text{1,}}lim}}}$) дают неверные результаты. Поэтому в случае ауксетиков скорость ${{c}_{{{\text{1,}}lim}}}$ должна определяться либо непосредственно по дисперсионному уравнению (2.23), либо с помощью регрессионных формул. Например, полиномиальная регрессия вида

(3.1)
$\begin{gathered} {{c}_{{{\text{1,}}lim}}}(\nu ) \approx ({{a}_{1}} + {{a}_{2}}\nu + {{a}_{3}}{{\nu }^{2}}){{c}_{2}} \\ {{a}_{1}} = 0.7622,\quad {{a}_{2}} = 0.3119,\quad {{a}_{3}} = 0.0129 \\ \end{gathered} $
обеспечивает приближение к точному значению ${{c}_{{{\text{1,}}lim}}}$, найденному по уравнению (2.23), с относительной ошибкой в равномерной норме, не превышающей 0.6% в интервале значений коэффициента Пуассона ν ∈ (–0.75; 0.45).

Пример 3.1. Определение коэффициента Пуассона по скорости ${{c}_{{{\text{1,}}lim}}}$.

А) Предположим, что наряду со скоростью ${{c}_{{{\text{1,}}lim}}}$ известна также скорость ${{c}_{2}}$. С использованием регрессионного уравнения (3.1) в предположении, что объемная скорость поперечной волны ${{c}_{2}}$ известна, получаем следующее выражение для определения коэффициента Пуассона

(3.2)
$\nu = \frac{{ - {{a}_{2}} + \sqrt {a_{2}^{2} - 4{{a}_{1}}{{a}_{3}} + 4{{a}_{3}}{{c}_{{1,\lim }}}{\text{/}}{{c}_{2}}} }}{{2{{a}_{3}}}}$
где коэффициенты ${{a}_{1}},\,{{a}_{2}},\,{{a}_{3}}$ определены по регрессионному уравнению (3.1).

Б) Предположим, что наряду со скоростью ${{c}_{{{\text{1,}}lim}}}$ известна скорость ${{c}_{{{\text{2,}}lim}}}$. В этом случае, ограничиваясь первыми тремя членами тейлоровского разложения по $\nu $ правой части регрессионного уравнения (3.1)

(3.3)
$\begin{gathered} {{c}_{{{\text{1,}}lim}}} \approx ({{b}_{1}} + {{b}_{2}}\nu + {{b}_{3}}{{\nu }^{2}}){{c}_{{{\text{2,}}lim}}} \\ {{b}_{1}} = \frac{{{{a}_{1}}}}{{\sqrt 2 }},\quad {{b}_{2}} = \frac{{ - {{a}_{1}} + 2{{a}_{2}}}}{{2\sqrt 2 }},\quad {{b}_{3}} = \frac{{3{{a}_{1}} - 4{{a}_{2}} + 8{{a}_{3}}}}{{8\sqrt 2 }} \\ \end{gathered} $
получаем следующее выражение для коэффициента Пуассона

(3.4)
$\nu = \frac{{ - {{b}_{2}} + \sqrt {b_{2}^{2} - 4{{b}_{1}}{{b}_{3}} + 4{{b}_{3}}\,{{c}_{{1,\lim }}}{\text{/}}{{c}_{{2,\lim }}}} }}{{2{{b}_{3}}}}$

Надо отметить, что коэффициенты тейлоровского разложения ${{b}_{1}},{{b}_{2}},{{b}_{3}}$ в (3.3) определены через коэффициенты ${{a}_{1}},{{a}_{2}},{{a}_{3}}$ по аналитическим формулам. В свою очередь, коэффициенты ${{a}_{1}},{{a}_{2}},{{a}_{3}}$ определены по регрессионному уравнению (3.1). В (3.4) учтено выражение (1.2) для длинноволновой асимптотики ${{c}_{{{\text{2,}}lim}}}$.

3.2. Вариация модуля упругости. На рис. 4 в окрестности второй предельной скорости ${{c}_{{{\text{2,}}lim}}}$ построены дисперсионные кривые, отвечающие аксиально симметричным фундаментальным модам при вариации модуля упругости материала стержня, коэффициент Пуассона в этом случае считался фиксированным (ν = 0.25).

На рис. 4 по вертикальной оси отложены значения безразмерной частоты $\omega {{c}_{2}}{\text{/}}R$, а по горизонтальной оси – значения относительной фазовой скорости волн Похгаммера–Кри ($c{\text{/}}{{c}_{2}}$). Графики соответствуют дисперсионным кривым при уменьшении (‒0.5%) и увеличении (+0.5%) модуля упругости, по сравнению с референсным значением (средняя кривая). Приведенные графики показывают, что в окрестности второй предельной скорости исследуемые дисперсионные кривые являются информативными для определения модуля упругости материала (в предположении, что плотность фиксирована). Здесь надо отметить, что, как показывает асимптотическая формула (1.2), значение второй предельной скорости ${{c}_{{{\text{2,}}lim}}}$ не зависит от коэффициента Пуассона.

Пример 3.2. Определение модуля упругости и коэффициента Пуассона по скоростям ${{c}_{{{\text{1,}}lim}}}$ и ${{c}_{{{\text{2,}}lim}}}$.

Предполагается, что плотность материала известна. Асимптотическое выражение (1.2) для скорости ${{c}_{{{\text{2,}}lim}}}$ дает

(3.5)
$E = {{\left( {{{c}_{{{\text{2,}}lim}}}} \right)}^{2}}\rho $

Далее, по известным значениям предельных скоростей ${{c}_{{{\text{1,}}lim}}}$ и ${{c}_{{{\text{2,}}lim}}}$ и формуле (3.4) определяется коэффициент Пуассона.

Отметим, что также как и для рассмотренных волн Похгаммера–Кри, в случае волн Лэмба, распространяющихся в упругом слое, по скорости ${{c}_{{{\text{2,}}lim}}}$ оказывается возможным анализировать вариацию модуля Юнга, см. [92].

4. Выводы. Проведен анализ продольных аксиально симметричных гармонических волн Похгаммера–Кри в стержнях. Рассмотрены точные решения волнового уравнения Похгаммера–Кри.

Исследована зависимость дисперсионных кривых, отвечающих аксиально симметричным модам и, в частности, симметричной фундаментальной моде, от вариации коэффициента Пуассона и модуля упругости. На численных примерах показана информативность аксиально симметричной фундаментальной моды для неразрушающей диагностики физико-механических свойств материалов и, в частности, для обнаружения участков с измененными свойствами.

Впервые проведен анализ вариации первой предельной скорости для стержней, выполненных из ауксетиков (материалов с отрицательным коэффициентом Пуассона).

Благодарность. Авторы благодарят Российский научный фонд, грант 20-49-08002 за финансовую поддержку.

Список литературы

  1. Pochhammer L. Ueber die Fortpflanzungsgeschwindigkeiten kleiner Schwingungen in einem unbegrenzten isotropen Kreiscylinder // J. Reine Angew. Math. 1876. V. 81. S. 324–336.

  2. Chree C. Longitudinal vibrations of a circular bar // Quart. J. Pure Appl. Math. 1886. V. 21. P. 287–298.

  3. Chree C. The equations of an isotropic elastic solid in polar and cylindrical coordinates, their solutions and applications // Trans. Cambridge Philos. Soc. 1889. V. 14. P. 250–309.

  4. Field G.S. Velocity of sound in cylindrical rods // Canadian J. Research. 1931. V. 5. P. 619–624.

  5. Field G.S. Longitudinal waves in cylinders of liquid, in hollow tubes and in solid rods // Canadian J. Research. 1934. V. 11. P. 254–263.

  6. Field G.S. Dispersion of supersonic waves in cylindrical rods // Phys. Rev. 1940. V. 57. P. 1188.

  7. Shear S.K., Focke A.B. The dispersion of supersonic waves in cylindrical rods of polycrystalline silver, nickel, and magnesium // Phys. Rev. 1940. V. 57. P. 532–537.

  8. Bancroft D. The velocity of longitudinal waves in cylindrical bars // Phys. Rev. 1941. V. 59. P. 588–593.

  9. Hudson G.E. Dispersion of elastic waves in solid circular cylinders // Phys. Rev. 1943. V. 63. P. 46–51.

  10. Holden A.H. Longitudinal modes of elastic waves in isotropic cylinders and slabs // Bell System Tech. J. 1951. V. 30. P. 956–969.

  11. Adem J. On the axially-symmetric steady wave propagation in elastic circular rods // Quart. Appl. Math. 1954. V. 12. P. 261–275.

  12. Redwood M., Lamb J. On propagation of high frequency compressional waves in isotropic cylinders // Proc. Phys. Soc. London. 1957. B. 70. P. 136–143.

  13. Mindlin R.D., McNiven H.D. Axially symmetric waves in elastic rods // Trans. ASME. J. Appl. Mech. 1960. V. 27. P. 145–151.

  14. McNiven H.D., Perry D.C. Axially symmetric waves infinite, elastic rods // J. Acoust. Soc. Amer. 1962. V. 34. P. 433–437.

  15. Onoe M., McNiven H.D., Mindlin R.D. Dispersion of axially symmetric waves in elastic rods // Trans. ASME. J. Appl. Mech. 1962. V. 29. P. 729–734.

  16. Meeker T.R., Meitzler A.H. Guided wave propagation in elongated cylinders and plates // Physical acoustics. Principles and methods. New York: Acad. Press. 1964. V. 1A. P. 111–167.

  17. Kolsky H. Stress waves in solids // J. Sound Vibr. 1964. V. 1. P. 88–110.

  18. Hutchinson J.R., Percival C.M. Higher modes of longitudinal wave propagation in thin rod // J. Acoust. Soc. Amer. 1968. V. 44. P. 1204–1210.

  19. Zemanek J. An experimental and theoretical investigation of elastic wave propagation in a cylinder // J. Acoust. Soc. Amer. 1972. V. 51. P. 265–283.

  20. Thurston R.N. Elastic waves in rods and clad rods // J. Acoust. Soc. Amer. 1978. V. 64. P. 1–37.

  21. Graff K.F. Wave motion in elastic solids. New York: Dover, 1991. 692 p.

  22. Abramson H.N. Flexural waves in elastic beams of circular cross section // J. Acoust. Soc. Amer. 1957. V. 29. P. 1284–1286.

  23. Pao Y.-H., Mindlin R.D. Dispersion of flexural waves in an elastic, circular cylinder // Trans. ASME. J. Appl. Mech. 1960. V. 27. P. 513–520.

  24. Kuznetsov S.V. Subsonic Lamb waves in anisotropic plates // Quart. Appl. Math. 2002. V. 60. P. 577–587.

  25. Kuznetsov S.V. Lamb waves in anisotropic plates (Review) // Acoust. Physics. 2014. V. 60. P. 95–103.

  26. Davis R.M. A critical study of the Hopkinson pressure bar // Philos. Trans. R. Soc. London Ser. 1948. V. A240. P. 375–457.

  27. Kolsky H. Stress Waves in Solids. Dover Publications, New York, 1963. P. 59–60.

  28. Kolsky H. Experimental results of stress wave investigations. In: Mandel J., Brun L. (Eds.), Mechanical Waves in Solids. Springer, New York. 1976.

  29. Gregory R.D., Gladwell I. Axisymmetric waves in a semi-infinite elastic rod // Q. J. Mech. Appl. Math. 1989. V. 42. P. 327–337.

  30. Puckett A.D., Peterson M.L. Individual longitudinal Pochhammer-Chree modes in observed experimental signals // Acoustics Research Letters Online. 2005. V. 6 (4). P. 268–273.

  31. Kolsky H. The propagation of stress pulses in viscoelastic solids // Philos. Mag. 1956. V. 1. P. 693–710.

  32. Coquin G.A. Attenuation of guided waves in isotropic viscoelastic materials // J. Acoust. Soc. Am. 1964. V. 36. P. 1074–1080.

  33. Sogabe Y., Kishida K. Wave propagation analysis for determining the dynamic properties of high damping alloys // Bull. JSME. 1982. V. 25. P. 321–327.

  34. Sogabe Y., Tsuzuki M. Identification of the dynamic properties of linear viscoelastic materials by the wave propagation testing // Bull. JSME. 1986. V. 29. P. 2410–2417.

  35. Zhao H. Gary G. A three dimensional analytical solution of the longitudinal wave propagation in an infinite linear viscoelastic cylindrical bar. Applications to experimental techniques // J. Mech. Phys. Solids. 1995. V. 43. P. 1335–1348.

  36. Bacon C. An experimental method for considering dispersion and attenuation in a viscoelastic Hopkinson bar // Exp. Mech. 1998. V. 38. P. 242–249.

  37. Benatar A., Rittel D., Yarin A.L. Theoretical and experimental analysis of longitudinal wave propagation in cylindrical viscoelastic rods // Journal of the Mechanics and Physics of Solids. 2003. V. 51. P. 1413–1431.

  38. Gazis D.C. Three-dimensional investigation of the propagation of waves in hollow circular cylinders. I. Analytical foundation // Journal of the Acoustical Society of America. 1959. V. 31 (5). P. 568–578.

  39. Viktorov I.A., Zubova O.M. Normal waves in a solid cylindrical layer (in Russian) // Akust. Zhurnal. 1963. V. 9. P. 19–22.

  40. Ditri J.J., Rose J.L. Excitation of guided elastic wave modes in hollow cylinders by applied surface tractions // Journal of Applied Physics. 1992. V. 72 (7). P. 2589–2597.

  41. Ditri J.J. Utilization of guided elastic waves for the characterization of circumferential cracks in hollow cylinders // Journal of the Acoustical Society of America. 1994. V. 96 (6). P. 3769–3775.

  42. Aristegui C., Lowe M.J.S., Cawley P. Guided waves in fluid-filled pipes surrounded by different fluids // Ultrasonics. 2001. V. 39 (5). P. 367–375.

  43. Seco F., Jiménez A.R. Modelling the Generation and Propagation of Ultrasonic Signals in Cylindrical Waveguides // In: Ultrasonic Waves InTechOpen. 2012. P. 1–28.

  44. Suh N.P. Stress-wave propagation in truncated cones against a “rigid” wall // Experimental Mechanics. 1967. V. 7. P. 541–544.

  45. Hettche L.R. Theoretical and experimental study on longitudinal impact of tapered rods // Journal of Research of the National Bureau of Standards. C. Engineering and Instrumentation. 1968. V. 72C. P. 231–241.

  46. Höschl C., Okrouhlik M., Červ J., Beneš J. Analytical, computational and experimental investigations on stress wave propagation // Appl. Mech. Rev. 1994. V. 47. P. 77–99.

  47. Abrate S. Vibration of non-uniform rods and beams // Journal of Sound and Vibration. 1995. V.185. P. 703–716.

  48. Barat C.N. Vibration of rods with uniformly tapered sections // Journal of Sound and Vibration 1995. V. 185. P. 185–189.

  49. Eberhard P., Hu B., Schiehlen W. Longitudinal wave propagation in conical rods subject to impacts // In: Multifield Problems. State of the Art. Springer. 2000. P. 246–253.

  50. Vales F., Moravka S., Brepta R., Cerv J. Wave propagation in a thick cylinder bar due to longitudinal impact // JSME International Journal, Series A 1996. V. 39 (1). P. 60–70.

  51. Gabriel D., Plesek J., Kolman R., Vales F., Dispersion of elastic waves in the contact-impact problem of a long cylinder // Journal of Computational and Applied Mathematics. 2010. V. 234. P. 930–1936.

  52. Mirsky I. Vibrations of orthotropic, thick, cylindrical shells // Journal of the Acoustical Society of America. 1964. V. 36 (1). P. 41–51.

  53. Mirsky I. Wave propagation in transversely isotropic circular cylinders Part I: Theory // Journal of the Acoustical Society of America. 1965. V. 37. P. 1016–1021.

  54. Mirsky I. Wave propagation in transversely isotropic circular cylinders Part II: Numerical Results // Journal of the Acoustical Society of America. 1965. V. 37. P. 1022–1026.

  55. Spies M. Elastic waves in homogeneous and layered transversely isotropic media: Plane waves and Gaussian wave packets. A general approach // Journal of the Acoustical Society of America. 1994. V. 95. P. 1748–1760.

  56. Nagy P.B. Longitudinal guided wave propagation in a transversely isotropic rod immersed in fluid // Journal of the Acoustical Society of America. 1995. V. 98 (1). P. 454–457.

  57. Nayfeh A.H. and Nagy P.B. General study of axisymmetric waves in layered anisotropic fibers and their composites // Journal of the Acoustical Society of America. 1996. V. 99. P. 931–941.

  58. Predoi M.V. Guided waves dispersion equations for orthotropic multilayered pipes solved using standard finite elements code // Ultrasonics. 2014. V. 54. P. 1825–1831.

  59. Biot M.A. Propagation of elastic waves in a cylindrical bore containing a fluid // Journal of Applied Physics. 1952. V. 23. P. 997–1005.

  60. Ilyashenko A.V., Kuznetsov S.V. Theoretical aspects of applying Lamb waves in nondestructive testing of anisotropic media // Russian Journal of Nondestructive Testing. 2017. V. 53. № 4. P. 243–259.

  61. Gavric L. Computation of propagative waves in free rail using a finite element technique // J. Sound Vib. 1995. V. 185. P. 531–543.

  62. Damljanovic V., Weaver R.L. Propagating and evanescent elastic waves in cylindrical waveguides of arbitrary cross section // J. Acoust. Soc. Am. 2004. V. 115. № 4. P. 1572–1581.

  63. Hayashi T., Tamayama C., Murase M. Wave structure analysis of guided waves in a bar with an arbitrary cross-section // Ultrasonics. 2006. V. 44. P. 17–24.

  64. Hayashi T., Song W.-J., Rose J.L. Guided wave dispersion curves for a bar with an arbitrary cross-section, a rod and rail example // Ultrasonics. 2003. V. 41. P. 175–183.

  65. Shatalov M., Marais J., Fedotov I., Tenkam M.D., Schmidt M. Longitudinal vibration of isotropic solid rods: from classical to modern theories // In: Advances in Computer Science and Engineering, InTechOpen. 2011. P. 187–214.

  66. Valsamos G., Casadei F., Solomos G. A numerical study of wave dispersion curves in cylindrical rods with circular cross-section // Applied and Computational Mechanics. 2013. V. 7. P. 99–114.

  67. Parry D.J., Walker A.G., Dixon P.R. Hopkinson bar pulse smoothing // Measur. Sci. Technol. 1995. V. 6. P. 443–446.

  68. Weinong Chen, Bo Song Split Hopkinson (Kolsky) Bar. Springer. 2011. ISBN: 978-1-4419-7981-0.

  69. Ramesh K.T., Narasimhan S. Finite deformations and the dynamic measurement of radial strains in Kolsky bar experiments // Int. J. Solids Struct. 1996. V. 33. P. 3723–3738.

  70. Bragov A.M., Lomunov A.K. Methodological aspects of studying dynamic material properties using the Kolsky method // Int. J. Impact Eng. 1995. V. 16. P. 321–330.

  71. Mohr D., Gary G. M-shaped specimen for the high strain rate tensile testing using a split Hopkinson pressure bar apparatus // Exp. Mech. 2007. V. 47. P. 681–692.

  72. Martin B.E., Chen W., Song B., Akers S.A. Moisture effects on the high strain-rate behavior of sand // Mech. Mater. 2009. V. 41. P. 786–798.

  73. Gilat A., Schmidt T.E., Walker A.L. Full field strain measurement in compression and tensile split Hopkinson bar experiments // Exp. Mech. 2009. V. 49. P. 291–302.

  74. Rajagopalan S., Prakash V. A modified torsional Kolsky bar for investigating dynamic friction. Exp. Mech. 1999. V. 39. P. 295–303.

  75. Ma S., Wu Z., Wang Y., Liu K. The reflection of guided waves from simple dents in pipes // Ultrasonics. 2014. V. 57. P. 190–197.

  76. Huthwaite P., Ribichini R., Cawley P., Lowe M.J.S. Mode selection for corrosion detection in pipes and vessels via guided wave tomography // IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2013 V. 60. P. 1165–1177.

  77. Leinov E., Lowe M.J.S., Cawley P. Investigation of guided wave propagation and attenuation in pipe buried in sand // J. Sound Vib. 2015. V. 347. P. 96–114.

  78. Farhidzadeh A., Salamone S. Reference-free corrosion damage diagnosis in steel strands using guided ultrasonic waves // Ultrasonics 2015. V. 57. P. 198–208.

  79. Barshinger J.N., Rose J.L. Guided wave propagation in an elastic hollow cylinder coated with a viscoelastic material // IEEE Trans. Ultrason. Ferroelectr. Freq. Control. 2004. V. 51. P. 1547–1556.

  80. Lu Y., Li J., Ye L., Wang D. Guided waves for damage detection in rebar-reinforced concrete beams // Constr. Build. Mater. 2013. V. 47. P. 370–378.

  81. Raišutis R., Kažys R., Žukauskas E., Mažeika L., Vladišauskas A. Application of ultrasonic guided waves for non-destructive testing of defective CFRP rods with multiple delaminations // NDT E Int. 2010. V. 43. P. 416–424.

  82. Castaings M., Hosten B. Guided waves propagating in sandwich structures made of anisotropic, viscoelastic, composite materials // J. Acoust. Soc. Am. 2003. V. 113 (5). P. 2622–2634.

  83. Rostami J., Chen J., Tse P.W. A Signal Processing Approach with a Smooth Empirical Mode Decomposition to Reveal Hidden Trace of Corrosion in Highly Contaminated Guided Wave Signals for Concrete-Covered Pipes // Sensors. 2017. V. 17. P. 1–21.

  84. Gurtin M.E. The Linear Theory of Elasticity. In: Handbuch der Physik, Bd. VIa/2. Springer, New York, 1972.

  85. Graff K.F. Wave Motion in Elastic Solids. Dover, 1991.

  86. Freund L.B. Dynamic Fracture Mechanics. Cambridge University Press. 1998.

  87. Viktorov I.A. Rayleigh and Lamb Waves: Physical Theory and Applications, Springer. 2013.

  88. Hirao M., Ogi H. EMATs for Science and Industry – Noncontacting Ultrasonic Measurements, Dordrecht: Kluwer Academic Publishers, 2003.

  89. Kundu T. Ultrasonic and electromagnetic waves for nondestructive evaluation and structural health monitoring // Procedia Engineering. 2014. V. 86. P. 395–405.

  90. Placko D., Kundu T. Ultrasonic Nondestructive Evaluation: Engineering and Biological Material Characterization, Boca Raton: CRC Press, 2004.

  91. Mokryakov V.V. Maxima of the stresses in the longitudinal Pochhammer–Chree waves // Mech. Solids. 2019. V. 54. P. 1063–1075.

  92. Kuznetsov S.V. Pochhammer-Chree waves: Spectral analysis of axially symmetric modes // J. Appl. Mech. Eng. 2018. V. 7. № 301. P. 1–9. https://doi.org/10.4172/2168-9873.1000301

  93. Kuznetsov S.V. Pochhammer–Chree waves in rods: degeneracy at the bulk wave velocities // ZAMP. 2018. V. 69 (6). P. 142–148.

  94. Ilyashenko A.V. Pochhammer–Cree longitudinal waves: Anomalous polarization // Mech. Solids. 2019. V. 54. P. 598–606.

  95. Kuznetsov S.V. Love waves in stratified monoclinic media // Quart. Appl. Math. 2004. V. 62 (4). P. 749–766.

  96. Djeran-Maigre I. et al. Solitary SH waves in two-layered traction-free plates // Comptes Rendus. Mechanique. 2008. V. 336 (1–2). P. 102–107.

  97. Городцов В.А., Лисовенко Д.С. Ауксетики среди материалов с кубической анизотропией // Известия РАН. МТТ. 2020. № 4. С. 7–24.

  98. Tyutekin V.V., Boiko A.I. Helical normal waves near a cylindrical cavity in an elastic medium // Acoustical Physics. 2010. V. 56 (2). P. 141–144.

  99. Tyutekin V.V. Properties of circumferential and helical waves of a cylindrical waveguide // Acoustical Physics. 2008. V. 54 (1). P. 13–14.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал