Известия РАН. Механика твердого тела, 2021, № 5, стр. 152-164

1. Постановка задачи и основные обозначения. Рассмотрим движение твердого тела $\mathcal{B}$ вокруг неподвижной точки O в осесимметричном силовом поле с направленным вдоль него единичным вектором ${\mathbf{\gamma }} = {{({{{\mathbf{\gamma }}}_{1}},{{{\mathbf{\gamma }}}_{2}},{{{\mathbf{\gamma }}}_{3}})}^{T}}.$ Пусть ${\mathbf{I}} = {\text{diag}}({{I}_{1}},{{I}_{2}},{{I}_{3}})$ – тензор инерции тела относительно точки O, ${\mathbf{\omega }} = {{({{\omega }_{1}},{{\omega }_{2}},{{\omega }_{3}})}^{T}}$ – вектор угловой скорости тела, U_N = = ${{U}_{N}}\left( {\mathbf{\gamma }} \right)$ – потенциал силового поля. Здесь и далее все векторы и тензорные величины задаются в подвижной системе отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, оси которой направлены вдоль главных осей инерции тела, задаваемых собственными векторами тензора инерции I.

Тогда уравнения движения твердого тела могут быть записаны как уравнения Эйлера–Пуассона

Помимо интеграла энергии

эти уравнения обладают интегралом площадей и геометрическим интегралом

На перманентных вращениях угловая скорость твердого тела неизменна как в абсолютных осях, так и в осях $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, связанных с телом. Тогда ${\mathbf{\omega }} = {{\omega }}{\mathbf{\gamma }} = {\text{const}}$, и согласно первой подсистеме из (1.1) положение осей перманентных вращений определяется алгебраическими уравнениями

Ставится задача исследования существования и устойчивости перманентных вращений и, прежде всего, равновесий для твердого тела в виде симметричного равногранного тетраэдра с равными массами в вершинах. Оригинальный подход к изучению установившихся движений в задачах динамики твердого тела, опирающийся на эффективное использование симметрий в распределении масс, предложен в [1] (см. также [2]). Согласно исследованиям Р.С. Суликашвили [3–5] в случае правильного тетраэдра, являющегося частным случаем равногранного, наблюдаются достаточно непривычные свойства равновесий. Чувствительность этих свойств к деформациям правильного тетраэдра является основным предметом настоящего исследования.

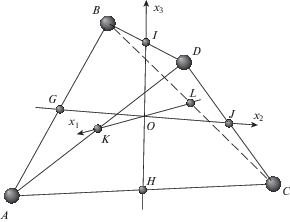
2. Определение равногранного тетраэдра и его свойства. Согласно определению (см., например, [6]), тетраэдр называется равногранным, если все грани – равные между собой треугольники. Известно, что у равногранного тетраэдра бимедианы попарно перпендикулярны и делятся точкой пересечения пополам. Пусть $\mathcal{B}$ – равногранный тетраэдр с равными массами m в вершинах, совершающий вращение вокруг неподвижной точки O, совпадающей с точкой пересечения бимедиан. Зададим жестко связанную с тетраэдром правую систему отсчета $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ с началом в точке O и осями, направленными вдоль бимедиан. Если длины бимедиан равны 2a₁, 2a₂, 2a₃ соответственно, то в этой системе отсчета вершины тетраэдра A, B, C и D задаются радиус-векторами (рис. 1)

причем

Середины ребер тетраэдра задаются как

Оси $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ являются главными центральными осями инерции тела $\mathcal{B}$, в них главные центральные моменты инерции записываются как

3. Потенциал поля притяжения и его разложение в ряд. Пусть единицы размерности выбраны так, что гравитационная постоянная, масса в точке N и расстояние от N до O равны единице. Тогда потенциал притяжения имеет вид

где $(a,b,c,d)$ – циклическая перестановка индексов.

Следуя подходу, предложенному в [7], разложим потенциал (3.1) в ряд по степеням параметров

Такое разложение имеет вид

В разложении (3.2), слагаемое U₀ постоянно, а слагаемое U₁ равно нулю, так как тетраэдр подвешен в центре масс.

4. Равновесия равногранного тетраэдра в центральном поле сил: существование. Прежде всего зададимся решением вопроса о существовании равновесий тетраэдра.

4.1. Уравнения равновесий. В разложении потенциала примем во внимание лишь два первых нетривиальных слагаемых, т.е. в качестве приближенного потенциала примем функцию

В силу соотношений (1.3) приближенные уравнения равновесий имеют вид

Эти уравнения, естественно, следует рассматривать вместе с уравнением (1.2), выражающим единичность вектора ${\mathbf{\gamma }}.$

Уравнения (1.2), (4.1) всегда обладают решениями

Этим шести решениям отвечают равновесия, на которых тетраэдр “смотрит” на притягивающий центр одной из полуосей подвижной системы отсчета.

4.2. Случай правильного тетраэдра. В случае правильного тетраэдра α₁ = α₂ = α₃ и первые слагаемые в уравнениях (4.1) обращаются в нуль. Сами уравнения принимают вид

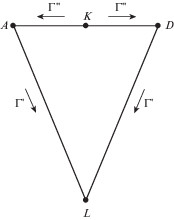
Эти уравнения совместно с (1.2) помимо равновесий (4.2) определяют равновесия $\mathcal{I}\mathcal{I}$, на которых тетраэдр “смотрит” на притягивающий центр одной из своих вершин, и равновесия $\mathcal{I}\mathcal{I}\mathcal{I}$, на которых тетраэдр “смотрит” на притягивающий центр центром одной из граней. Так, например, на равновесии

из класса $\mathcal{I}\mathcal{I}$ тетраэдр “смотрит” на точку N вершиной D, а на равновесии из класса $\mathcal{I}\mathcal{I}\mathcal{I}$ тетраэдр “смотрит” на точку N центром грани ABC. Остальные равновесия из классов $\mathcal{I}\mathcal{I}$ и $\mathcal{I}\mathcal{I}\mathcal{I}$ выписываются аналогично.

Равновесия правильного тетраэдра в центральном ньютоновском поле сил изучались в работах Р.С. Суликашвили. В частности, было доказано, что других решений изучаемых уравнений, а вместе с ними – и равновесий, у правильного тетраэдра нет.

Как сказано выше, равновесия вида (4.2) имеются у равногранного тетраэдра и в общем случае. Спрашивается, существуют ли в общем случае классы равновесий равногранного тетраэдра, которым принадлежат равновесия из классов $\mathcal{I}\mathcal{I}$ и $\mathcal{I}\mathcal{I}\mathcal{I}$ правильного тетраэдра.

4.3. Случай равенства двух бимедиан. В дальнейшем ограничимся рассмотрением случая, когда две бимедианы равны, например, ${{\alpha }_{2}} = {{\alpha }_{3}} = {{\alpha }_{ \star }}$. В этом случае плоскости ${{{\mathbf{x}}}_{2}} = \pm {{{\mathbf{x}}}_{3}}$ являются плоскостями симметрии. Кроме того, в силу первого уравнения (4.1) либо ${{{\mathbf{\gamma }}}_{1}} = 0,$ либо ${\mathbf{\gamma }}_{2}^{2} = {\mathbf{\gamma }}_{3}^{2}.$

Пусть ${{{{\gamma }}}_{1}} = 0.$ Тогда второе и третье уравнения (4.1) принимают вид

откуда либо ${{{{\gamma }}}_{2}} = 0$, либо ${{{{\gamma }}}_{3}} = 0$, и имеют место либо решение ${{\mathcal{I}}_{3}}$, либо решение ${{\mathcal{I}}_{2}}$ из (4.2).

Пусть теперь ${{\gamma }}_{2}^{2} = {{\gamma }}_{3}^{2}$. Тогда ${{{{\gamma }}}_{2}} = {{\varepsilon }}{{{{\gamma }}}_{3}}$, $\varepsilon = \pm 1$, а второе и третье уравнения (4.1) совпадают и приводятся к виду

Это уравнение относительно ${{{{\gamma }}}_{3}}$ надо рассматривать вместе с уравнением (1.2), принимающим вид

Случай ${{{{\gamma }}}_{3}} = 0$ дает решение ${{\mathcal{I}}_{1}}$. В другом случае, когда обращается в нуль второй сомножитель из (4.3), выразим ${{\gamma }}_{3}^{2}$ из (4.4) и подставим в (4.3). Имеем

где $p = 2({{\alpha }}_{ \star }^{2} - {{\alpha }}_{1}^{2})$.

Замечание. Из соотношения $p = 2({{\alpha }}_{ \star }^{2} - {{\alpha }}_{1}^{2})$ можно однозначно выразить параметр ${{a}_{ \star }}$ как функцию от величин a₁ и p:

Таким образом, для любых наперед заданных значений a₁ и p однозначно определяется значение параметра ${{a}_{ \star }} > 0$, и, следовательно, параметр p может принимать любые действительные значения.

Равновесия, удовлетворяющие соотношениям (4.4), (4.5) в дальнейшем будем называть “косыми”, противопоставляя их тем самым “прямым” равновесиям ${{\mathcal{I}}_{k}}$.

В пространстве $\left( {{{{{\gamma }}}_{1}},{{{{\gamma }}}_{2}},{{{{\gamma }}}_{3}},p} \right)$ найденные зависимости задают кривые, заполненные равновесиями. Ограничимся рассмотрением случая, когда ε = 1, т.е. ${{{{\gamma }}}_{2}} = {{{{\gamma }}}_{3}}.$ В этом случае притягивающий центр N располагается в плоскости, содержащей ребро AD и проходящей через точку L – середину ребра BC, а потому и перпендикулярной этому ребру¹¹. В силу (4.5) и указанной симметрии изучаемые равновесия описываются соотношениями

причем, $\mathcal{I}\mathcal{I}\left( 0 \right) = \mathcal{I}\mathcal{I}$ и $\mathcal{I}\mathcal{I}\mathcal{I}(0) = \mathcal{I}\mathcal{I}\mathcal{I}$.

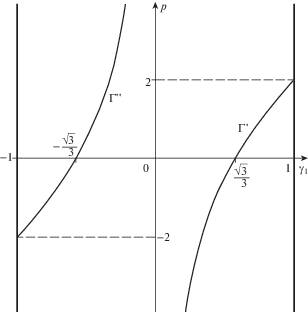
Проекции задаваемых этими соотношениями кривых на плоскости $\left( {{{{{\gamma }}}_{1}},p} \right)$ и $\left( {{{{{\gamma }}}_{3}},p} \right)$ изображены на рис. 2, 3.

Рассмотрим сначала проекции изучаемых кривых на плоскость $\left( {{{{{\gamma }}}_{1}},p} \right)$ (рис. 2). При $p \ll 0$ имеется единственная ветвь ${{\Gamma }}'$. Вдоль ветви ${{\Gamma }}'$ в пределе $\mathop {{\text{lim}}}\limits_{p \to - \infty } {{{{\gamma }}}_{1}} = {{0}^{ + }}$, $\mathop {{\text{lim}}}\limits_{p \to - \infty } {{{{\gamma }}}_{2}}$ = $\mathop {{\text{lim}}}\limits_{p \to - \infty } {{{{\gamma }}}_{3}} = \pm \frac{{\sqrt 2 }}{2}$. При этом положительным предельным значениям γ₂ и γ₃ отвечает случай, когда тетраэдр “смотрит” на точку N вершиной A, а отрицательным предельным значениям – случай, когда тетраэдр смотрит на точку N вершиной D.

Пусть теперь параметр p возрастает. Вдоль ветви ${{\Gamma }}'$ значение γ₁ также возрастает и достигает величины $\frac{{\sqrt 3 }}{3}$ при p = 0. Между тем при $p = - 2$ в точке ${{{{\gamma }}}_{1}} = - 1$ возникает ветвь $\Gamma {\kern 1pt} ''$, заполненная равновесиями. Вдоль ветви $\Gamma {\kern 1pt} ''$ значение γ₁ также возрастает и достигает значения $ - \frac{{\sqrt 3 }}{3}$ при p = 0. Пересечениям ветвей ${{\Gamma }}'$ и $\Gamma {\kern 1pt} ''$ с осью p = 0 отвечают случаи, когда правильный тетраэдр обращен к притягивающему центру серединами граней и вершинами соответственно.

Для ветви ${{\Gamma }}'$ с возрастанием параметра p значение γ₁ также возрастает и достигает физически осмысленного предела ${{{{\gamma }}}_{1}} = 1$ при $p = 2$. Тем самым при p = 2 получаем равновесие вида ${{\mathcal{I}}_{1}}$. Для ветви $\Gamma {\kern 1pt} ''$ с возрастанием параметра p величина γ₁ тоже возрастает, причем $\mathop {{\text{lim}}}\limits_{p \to + \infty } {{{{\gamma }}}_{1}} = {{0}^{ - }}$. Равновесия из этого класса в пределе стремятся к положениям, когда тетраэдр “смотрит” на притягивающий центр одной из вершин A или D, не достигая этих положений.

Поведение при изменении параметра p проекций тех же кривых на плоскость $\left( {{{{{\gamma }}}_{3}},p} \right)$ проиллюстрировано на рис. 3.

Схематически изменения положений равновесия с возрастанием параметра $p$ изображено на рис. 4.

Замечание. Зависимости, изображенные на рис. 2 и 3, обладают очевидными свойствами нечетности и четности, и, казалось бы это обстоятельство так или иначе должно проявляться в геометрии тетраэдра. Однако это не так. Напомним, что в рассматриваемом случае грани тетраэдра – равнобедренные треугольники. Обозначим ${{\varphi }}$ угол при их вершинах. При p = 0 грани тетраэдра – правильные треугольники, и ${{\varphi }} = \frac{{{\pi }}}{3}.$ Однако при p < 0 угол φ принимает значения на интервале от 0 до $\frac{{{\pi }}}{3}$, в то время как p > 0 угол ${{\varphi }}$ принимает значения на интервале от $\frac{{{\pi }}}{3}$ до $\frac{{{\pi }}}{2}$. Иными словами, геометрия треугольников, расположенных в гранях, сильно разнится в случаях p < 0 и p > 0.

5. Равновесия: устойчивость. Зададимся решением вопроса об устойчивости равновесий тетраэдра.

Для исследования устойчивости, следуя методу Рауса ([8, 9], см. также [10]) выпишем функцию

и исследуем знакоопределенность ограничения ее второй вариации на линейное многообразие

Если обозначить

то вторые производные имеют вид где (1, 2, 3) – циклическая перестановка индексов.

Неопределенный множитель Лагранжа λ в общем случае имеет вид

5.1. Случай, когда равны все бимедианы. Согласно результатам Р.С. Суликашвили для равновесий, на которых тетраэдр “смотрит” на притягивающий центр вершиной, например, вершиной D, имеем

Квадратичная форма (5.3) положительно определена, степень неустойчивости равна нулю $\left( {{{\chi }} = 0} \right)$. Рассматриваемое равновесие доставляет минимум измененному потенциалу, оно устойчиво по Ляпунову по теореме Лагранжа об устойчивости [11, 12].

Для равновесий, на которых тетраэдр “смотрит” на притягивающий центр серединой ребра, например, для решения ${{\mathcal{I}}_{3}}$, имеем

Рассматриваемое равновесие отвечает седловой точке измененного потенциала (степень неустойчивости равна единице, χ = 1), и потому неустойчиво [11, 12].

Для равновесий, на которых тетраэдр “смотрит” на притягивающий центр центром грани, например, центром грани ABC, имеем

Квадратичная форма (5.5) отрицательно определена, степень неустойчивости равна двум (χ = 2). Рассматриваемое равновесие неустойчиво по теореме, обратной теореме Лагранжа об устойчивости [12].

5.2. Случай, когда равны две бимедианы. Прежде всего изучим условия устойчивости равновесий ${{\mathcal{I}}_{k}}$ в условиях раздела 4.3, т.е. ${{\alpha }_{2}} = {{\alpha }_{3}} = {{\alpha }_{ \star }}$ (${{a}_{2}} = {{a}_{3}} = {{a}_{ \star }}$).

Для равновесия ${{\mathcal{I}}_{1}}$ ограничение квадратичной формы на линейное многообразие принимает вид

Это равновесие устойчиво $\left( {{{\chi }} = 0} \right)$, если выполнено условие $p < - 2$. Если $p > - 2,$ то равновесие неустойчиво, причем χ = 1, если $p < 2,$ и ${{\chi }} = 2,$ если $p > 2$.

Для изучения устойчивости равновесия ${{{{\gamma }}}_{2}} = {{{{\gamma }}}_{3}} = 0$, ${{{{\gamma }}}_{1}} = - 1$ при $p = - 2$ в потенциале выполним замену ${{{{\gamma }}}_{1}} = - {\kern 1pt} {\kern 1pt} \sqrt {1 - {{\gamma }}_{2}^{2} - {{\gamma }}_{3}^{2}} $ и разложим получившееся выражение в ряд Маклорена по ${{{{\gamma }}}_{2}}$ и ${{{{\gamma }}}_{3}}$ вплоть до слагаемых четвертого порядка малости. Имеем

Для исследования типа особой точки ${{{{\gamma }}}_{2}} = {{{{\gamma }}}_{3}} = 0$ функции (5.6) введем полярные координаты

В них после преобразований функция (5.6) примет вид

Выражение в квадратных скобках при ${{\rho }} \ne 0$ принимает только положительные значения. Поэтому в точке ${{{{\gamma }}}_{2}} = {{{{\gamma }}}_{3}} = 0$ функция (5.6) достигает своего строгого минимума, и равновесие устойчиво по Ляпунову.

Аналогично при p = 2 в потенциале с помощью замены ${{{{\gamma }}}_{1}} = \sqrt {1 - {{\gamma }}_{2}^{2} - {{\gamma }}_{3}^{2}} $ и разложения получившейся функции в ряд Маклорена по ${{\gamma }_{2}}$ и ${{\gamma }_{3}}$ вплоть до слагаемых четвертого порядка малости, имеющего вид

доказывается, что при ${{{{\gamma }}}_{2}} = {{{{\gamma }}}_{3}} = 0$, ${{{{\gamma }}}_{3}} = 1$ функция (5.7) достигает своего строгого максимума, и равновесие неустойчиво.

Замечание. Общие методы, касающиеся распределения свойств устойчивости вдоль ветвей установившихся движений, а также устойчивости установившихся движений, отвечающих точкам бифуркации, изучались в [13, 14].

Для равновесия ${{\mathcal{I}}_{2}}$ ограничение квадратичной формы на линейное многообразие принимает вид

Коэффициенты Пуанкаре записываются как

Коэффициент c_– всегда отрицателен, в то время как коэффициент c₊ всегда положителен. Это означает, что равновесие неустойчиво $\left( {{{\chi }} = 1} \right)$. Так как ${{{{\alpha }}}_{2}} = {{{{\alpha }}}_{3}}$, то тоже самое справедливо и для равновесия ${{\mathcal{I}}_{3}}$. Впрочем, в этом случае свободный член характеристического уравнения отрицателен, и, следовательно, корни имеют разные знаки, и их можно было не вычислять.

Обратимся теперь к изучению условий устойчивости равновесий, задаваемых соотношением (4.5) при ${{\varepsilon }} = 1$. Ограничимся рассмотрением решений, для которых γ₂ = ${{{{\gamma }}}_{3}} = {{{{\gamma }}}_{ \star }}$ > 0. Случай ${{{{\gamma }}}_{2}} = {{{{\gamma }}}_{3}} = {{{{\gamma }}}_{ \star }} < 0$ рассматривается аналогично.

Для исследуемых равновесий линейное многообразие задается, например, как

Подстановка этого соотношения и соотношения для ${{{{\gamma }}}_{ \star }}$ в выражение (5.1), а также последующее приведение подобных позволяет представить изучаемое ограничение квадратичной формы на линейное многообразие в виде

При этом коэффициенты Пуанкаре имеют вид

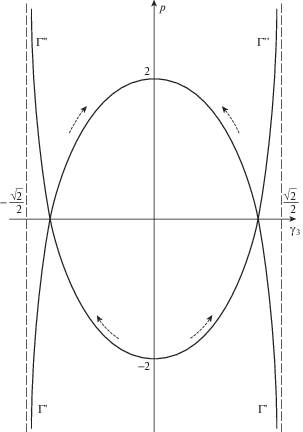
На рис. 5 приведена бифуркационная картина на плоскости $\left( {{{{{\gamma }}}_{1}},p} \right)$. Штриховые линии разделяют области, в которых оба коэффициента Пуанкаре c₁ и c₂ имеют один и тот же знак, сами знаки этих коэффициентов прорисованы по периметру фигуры. Сплошными линиями отмечены равновесия ${{\Gamma }}'$ и ${{\Gamma ''}}$. Нетрудно видеть, что для равновесий, заполняющих кривую ${{\Gamma }}',$ степень неустойчивости равна двум, и эти равновесия неустойчивы. Также нетрудно видеть, что для равновесий, заполняющих кривую ${{\Gamma ''}}$, степень неустойчивости равна нулю, и эти равновесия устойчивы по Ляпунову.

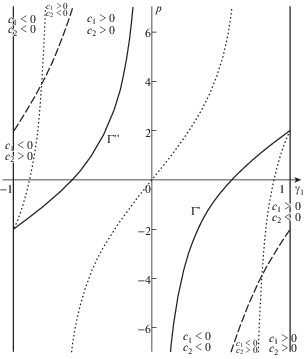
Замечание. В то время, как проекции кривых ${{\Gamma }}'$ и ${{\Gamma ''}}$ на плоскость $\left( {{{{{\gamma }}}_{1}},p} \right)$ центрально симметричны относительно начала координат, относительно свойств устойчивости, допуская вольность речи, можно сказать, что они “антисимметричны” относительно начала координат на этой плоскости: для двух центрально симметричных точек значения коэффициентов Пуанкаре имеют противоположные знаки.

Замечание. Исследование коэффициентов Пуанкаре можно выполнить явно: подставляя в выражения (5.8) в качестве параметра p выражение из (4.5), имеем

Тогда на изучаемых равновесиях коэффициенты Пуанкаре принимают вид

На равновесиях ${{\Gamma }}'$ выполнены неравенства $0 < {{{{\gamma }}}_{1}} < 1$. Поэтому в силу (5.9) на этих равновесиях ${{c}_{1}} < 0,$ ${{c}_{2}} < 0,$ причем ${{c}_{1}} = 0$ лишь при ${{{{\gamma }}}_{1}} = 1$.

Аналогично, на равновесиях ${{\Gamma ''}}$ выполнены неравенства $ - 1 < {{{{\gamma }}}_{1}} < 0.$ Поэтому на этих равновесиях ${{c}_{1}} > 0,$ ${{c}_{2}} > 0,$ причем ${{c}_{1}} = 0$ лишь при ${{{{\gamma }}}_{1}} = - 1$.

6. Перманентные вращения равногранного тетраэдра. Как было показано выше, уравнения перманентных вращений твердого тела в рассматриваемой задаче имеют вид (1.3). В случае, когда в разложении потенциала удерживаются лишь слагаемые второго и третьего порядка малости, эти уравнения представимы в виде

где

Отметим, что эти уравнения совпадают с уравнениями (4.1).

Таким образом, все рассуждения, выполненные выше при отыскании равновесий, дословно переносятся и на случай перманентных вращений. Следует заметить, что при заданном значении угловой скорости ω перманентные вращения могут быть найдены как критические точки измененного (augmented) потенциала, имеющего вид

и рассмотренного как функция на сфере (1.2). Здесь и далее $I\left( {\mathbf{\gamma }} \right) = \left( {{\text{I}}{\mathbf{\gamma }},{\mathbf{\gamma }}} \right)$ – момент инерции тела относительно оси вращения. Однако определение типа критических точек при фиксированном значении ω не дает возможности в общем случае сделать выводы об устойчивости движения. Исключения составляют движения, существующие при любом значении угловой скорости, такие как вращения типа I_k вокруг бимедиан (см. [15]).

Для “косых” перманентных вращений, на которых положение оси вращения в теле зависит от величины угловой скорости, перманентные вращения определяются как критические точки приведенного (amended) потенциала, имеющего вид

и также рассмотренного как функция на сфере (1.2). При этом величина угловой скорости ${{\omega }}$ и постоянная интеграла площадей связаны соотношением ${{p}_{{{\psi }}}} = I\left( {\mathbf{\gamma }} \right)\,{{\omega }}$.

7. Выводы. Выполненное исследование показало, что при описанных выше деформациях правильного тетраэдра в классе равногранных тетраэдров равновесия вида ${{\mathcal{I}}_{k}}$ существуют всегда, но их свойства устойчивости зависят от размеров тетраэдра. Так, при $p \leqslant - 2$ равновесия ${{\mathcal{I}}_{1}}$ устойчивы, при $ - 2 < p < 2$ эти равновесия неустойчивы со степенью неустойчивости $\chi = 1$, при $p \geqslant 2$ равновесия неустойчивы со степенью неустойчивости $\chi = 2$. Равновесия ${{\mathcal{I}}_{2}}$ и ${{\mathcal{I}}_{3}}$ неустойчивы со степенью неустойчивости $\chi = 2$ при любом значении параметра p.

Равновесия вида $\mathcal{I}\mathcal{I}$ принадлежат однопараметрическому семейству $\mathcal{I}\mathcal{I}\left( p \right)$, причем эти равновесия устойчивы по Ляпунову при любом значении параметра p. Наконец, равновесия типа $\mathcal{I}\mathcal{I}\mathcal{I}$ также принадлежат однопараметрическому семейству $\mathcal{I}\mathcal{I}\mathcal{I}\left( p \right)$, и при любом значении параметра p эти решения неустойчивы со степью неустойчивости равной два.

Являющееся на первый взгляд чисто академическим, такое исследование приобретает определенный смысл, поскольку для некоторых малых небесных тел таких как, например, комета (67P) Чурюмова–Герасименко, поле притяжения хорошо приближается с помощью образующих тетраэдр четырех массивных точек [16] (см. также работу [17], касающуюся качества приближения).

Представляют интерес изучение относительного движения тел, имеющих схожее распределение масс, на кеплеровской орбите, а также исследование точек либрации в случае равномерного вращения таких тел.