Известия РАН. Механика твердого тела, 2021, № 4, стр. 98-108
УСТОЙЧИВОСТЬ БЕСКОНЕЧНО ДЛИННОЙ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ, НАГРУЖЕННОЙ НАРУЖНЫМ ДАВЛЕНИЕМ, СОЗДАВАЕМЫМ ЖЕСТКОЙ ВНЕШНЕЙ СРЕДОЙ
В. В. Васильев a, *, В. А. Салов b
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
b Центр перспективных разработок АО Центрального НИИ специального машиностроения
Хотьково, Россия
* E-mail: vvvas@dol.ru
Поступила в редакцию 25.01.2021
После доработки 26.01.2021
Принята к публикации 27.01.2021
Аннотация
В статье рассматривается задача устойчивости бесконечно длинной цилиндрической оболочки, находящейся в абсолютно жесткой среде, сжимающей оболочку так, что она может потерять устойчивость деформируясь только во внутреннюю полость. С помощью уравнений нелинейной теории оболочек, учитывающей из нелинейных эффектов только изменения радиусов кривизны срединной поверхности оболочки в процессе деформации, получено точное решение, определяющее критическое давление или предельную величину докритической деформации оболочки. Установлено, что критическое давление и деформация в значительной степени зависят от связи между оболочкой и наружной средой в кольцевом направлении. Исследовано два предельных случая – оболочка жестко связанная со средой и оболочка свободная от тангенциальной кольцевой поверхностной нагрузки. Полученное решение сопоставляется с результатами эксперимента, проведенного на композитных оболочках с металлическим и полимерным внутренним слоем.
1. Введение. Задача, рассматриваемая в статье, имеет длинную историю. Погруженные в грунт трубопроводы, и тоннели, имеющие облицовку, испытывают давление со стороны грунта, усаживающегося в силу различных причин, и могут потерять устойчивость. Как известно, критическое значение внешнего давления, действующего на бесконечно длинную цилиндрическую оболочку, определяется равенством
(1.1)
${{q}_{{cr}}} = \frac{{\bar {E}{{h}^{3}}}}{{4{{R}^{3}}}},\quad \bar {Е} = \frac{Е}{{1 - {{\nu }^{2}}}}$Здесь E, $\nu $ – модуль упругости и коэффициент Пуассона материала и $R$, $h$ – радиус и толщина оболочки. Для рассматриваемой задачи удобно ввести вместо давления величину докритической кольцевой деформации оболочки, которая связана с давлением следующим образом:
В соответствие с равенством (1.1), критическая деформация ${{\varepsilon }_{{cr}}} = {{(h{\text{/}}2R)}^{2}}.$ При такой деформации сечение оболочки принимает эллиптическую форму. Однако для оболочки, находящейся в жесткой среде, такая форма потери устойчивости невозможна. Существенной особенностью рассматриваемой задачи является односторонний характер связи между оболочкой и окружающей средой, при котором оболочка может потерять устойчивость, если она приобретает местный прогиб, направленный к центру сечения. При этом на отслоившийся от среды участок оболочки давление не действует. Как показывают результаты эксперимента, критическое давление при этом оказывается значительно больше давления, соответствующего равенству (1.1). Традиционные линеаризованные уравнения устойчивости не позволяют найти критическое давление – из них следует, что оболочка не теряет устойчивости. Исключение составляет задача, рассмотренная в работе [1], посвященной устойчивости погруженной в грунт оболочки при действии давления жидкости, а не грунта. Еще одно традиционное приложение рассматриваемой задачи связано с устойчивостью слоистых оболочек при нагреве. Если оболочка состоит из двух слоев таких, что жесткость наружного слоя больше, а коэффициент линейного температурного расширения (КЛТР) меньше чем у внутреннего слоя, то при нагреве во внутреннем слое появляется сжимающее напряжение, которое может вызвать его отслоение от наружного слоя. Если наружный слой является абсолютно жестким, то критическая температурная деформация внутреннего слоя имеет вид
Здесь $\alpha _{T}^{i}$ и $\alpha _{T}^{e}$ – КЛТР внутреннего и наружного слоя и $\Delta T$ – критическое приращение температуры. И наконец, в последние годы появилось еще одно приложение рассматриваемой задачи, связанное с потерей устойчивости лейнера в композитных баллонах давления. Композитные баллоны, как правило, имеют внутренний герметизирующий слой (лейнер), изготовленный из металла или термопласта. Композиты допускают сравнительно большие упругие деформации, при которых материал лейнера оказывается упруго-пластическим. При разгрузке баллона остаточная деформация лейнера вызывает появление в нем сжимающих напряжений, которые могут вызвать отслоение лейнера. На рис. 1 показано отслоение лейнера из стали (a), и термопласта (b) в баллонах из углепластика.
Рис. 1.
Потеря устойчивости внутренней оболочки из стали (а) и полипропилена (б) (наружный слой – углепластик)

История рассматриваемой задачи обсуждается в работе [2]. Для решения традиционно используется два подхода. В первом подходе основные уравнения получаются с помощью вариационного принципа [2, 7]. При этом для приближенного определения критического давления используются различные аппроксимации для прогиба отслоившейся части оболочки (или кольца) [3, 4]. Второй подход основан на аналитическом или численном решении нелинейных уравнений теории оболочек [5, 6]. Заметим, что численное решение рассматриваемой задачи связано с принципиальными трудностями. Интегрирование по параметру нагрузки для идеальной оболочки сводится к задаче Коши с нулевыми начальными условиями и приводит к тривиальному решению. Для получения нетривиального решения необходимо вводить начальные несовершенства, а они неизвестны. В работах [8, 9] предлагается вводить помимо давления фиктивную сосредоточенную силу, вызывающую местный изгиб оболочки. Для оценки устойчивости оболочки выделяется ее равновесное состояние, соответствующее нулевой фиктивной силе. Следует отметить, что рассматриваемая задача принципиально отличается от другой известной аналогичной задачи об устойчивости цилиндрической оболочки под действием натяжения наматываемых на нее нитей [10]. В этой задаче потеря устойчивости оболочки сопровождается отклонением ее формы от цилиндрической по всей поверхности. Оболочка, теряющая устойчивость в жесткой среде, рассматриваемая ниже, сохраняет цилиндрическую форму на всей поверхности за исключением зоны отслоения.
В настоящей работе используются нелинейные уравнения теории оболочек, которые из всех возможных нелинейных эффектов учитывают только изменения радиусов кривизны срединной поверхности оболочки [11]. В такой постановке получено точное в рамках принятых гипотез аналитическое решение задачи.
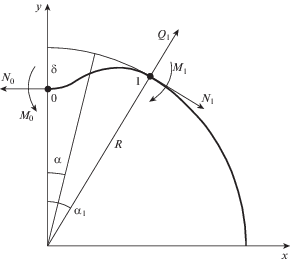
2. Исходные уравнения. Рассмотрим отслоившийся участок оболочки, показанный на рис. 1. Нелинейные уравнения, которые учитывают только изменение радиуса кривизны в процессе деформации, имеют вид [11]
(2.1)
$N{\text{'}} + Q(1 + \omega _{\alpha }^{'}) = 0,\quad Q{\text{'}} - N(1 + \omega _{\alpha }^{'}) = 0,\quad M{\text{'}} - RQ = 0\quad ( \cdots ){\text{'}} = d( \cdots ){\text{/}}d\alpha $(2.2)
$N = B{{\varepsilon }_{\alpha }},\quad M = \frac{D}{R}\omega _{\alpha }^{'},\quad B = \bar {E}h,\quad D = \frac{1}{{12}}\bar {E}{{h}^{3}}$(2.3)
${{\varepsilon }_{\alpha }} = \frac{1}{R}(u_{\alpha }^{'} + w),\quad {{\omega }_{\alpha }} = \frac{1}{R}\left( {u - w{\text{'}}} \right)\quad (1,2),$Здесь $N$, Q, $M$ – кольцевое усилие, поперечное усилие и изгибающий момент, положительные направления которых показаны на рис. 2, ${{u}_{\alpha }}$, $w$ – кольцевое перемещение и прогиб, направленный по наружной нормали. Уравнения (2.2) соответствуют бесконечно длинной цилиндрической оболочке. Для кольца в них следует принять $\nu = 0$. Как уже отмечалось, из возможных нелинейных эффектов уравнения (2.1)–(2.3) учитывают только изменение кривизны $\omega _{\alpha }^{'}$. Эти уравнения справедливы если отношениями ${{u}_{\alpha }}{\text{/}}R$, $u_{\alpha }^{'}{\text{/}}R$ и $w{\text{/}}R$, $w{\text{'/}}R$ можно пренебречь по сравнению с единицей.
Уравнения (2.1) можно дополнить уравнениями равновесия участка 0–1 (рис. 2) как твердого тела. Приравнивая нулю равнодействующие сил, действующих на этот участок, и суммарный момент относительно начала координат, получим
(2.4)
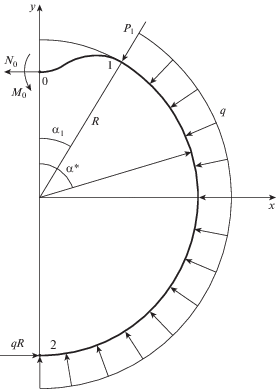
$\begin{gathered} - {{N}_{0}} + {{Q}_{1}}\sin {{\alpha }_{1}} + {{N}_{1}}\cos {{\alpha }_{1}} = 0,\quad {{Q}_{1}}\cos {{\alpha }_{1}} - {{N}_{1}}\sin {{\alpha }_{1}} = 0 \\ - {{N}_{0}}(R - \delta ) + {{N}_{1}}R - {{M}_{0}} + {{M}_{1}} = 0 \\ \end{gathered} $Рассмотрим равновесие оболочки, отделенной от среды (рис. 3). Предполагается, что на участке 1–2 оболочка сохраняет круговую форму, т.е. на этом участке на оболочку действует равномерное внешнее давление q, а в точке 2 действует только кольцевое усилие равное qR. Существенной особенностью задачи является наличие сосредоточенной силы ${{Р}_{1}}$ в точке 1, где соединяются участки. Эта сила появляется в контактных задачах для оболочек, описываемых классической теорией. Для иллюстрации рассмотрим опертую по концам балку, нагруженную в середине пролета через жесткий штамп. Уравнение изгиба балки имеет вид $D{{w}^{{(4)}}} = q$, где q – контактное давление. Если поверхность штампа описывается полиномом, степень которого меньше четырех, то контактное давление оказывается равным нулю и для обеспечения равновесия штампа на границе области контакта появляются сосредоточенные силы. Эти силы отсутствуют, если оболочка описывается неклассическими уравнениями, учитывающими деформацию поперечного сдвига. В этом случае на границах области контакта возникает локальное давление [12]. На существование обсуждаемой сосредоточенной силы в рассматриваемой задаче указывается в работах [2, 6]. Уравнения равновесия аналогичные уравнениям (2.4) имеют вид
Решение этих уравнений совместно с уравнениями (2.4) дает
(2.5)
${{N}_{0}} = - \frac{{qR}}{{\cos {{\alpha }_{1}}}},\quad {{N}_{1}} = - qR,\quad {{Q}_{1}} = - {{P}_{1}} = - qR\tan {{\alpha }_{1}},\quad {{M}_{1}} = 0$Преобразуем уравнения (2.1)–(2.3). Во-первых, будем считать контур поперечного сечения оболочки нерастяжимым. Тогда из первого равенства (2.3) имеем $u{{_{\alpha }^{'}}_{{}}} = - w$. Во-вторых, введем безразмерные переменные
(2.6)
$\bar {N} = \frac{N}{{qR}},\quad \bar {M} = \frac{M}{{q{{R}^{2}}}},\quad {{\bar {u}}_{\alpha }} = \frac{{{{u}_{\alpha }}}}{R},\quad \bar {w} = \frac{w}{R}$В результате, система уравнений (2.1)–(2.3) и равенства (2.5) принимают следующий вид:
(2.7)
$\bar {N}{\text{'}} + \bar {Q}(1 + \omega _{\alpha }^{'}) = 0,\quad \bar {Q}{\text{'}} - \bar {N}(1 + \omega _{\alpha }^{'}) = 0,\quad \bar {M}{\text{'}} = \bar {Q}$(2.8)
$\bar {M} = \frac{1}{{12\lambda }}\omega _{\alpha }^{'},\quad \omega _{\alpha }^{'} = - (\bar {w} + \bar {w}{\text{''}}),\quad \lambda = \frac{{q{{R}^{3}}}}{{\bar {E}{{h}^{3}}}}$(2.9)
${{\bar {N}}_{0}} = - \frac{1}{{\cos {{\alpha }_{1}}}},\quad {{\bar {N}}_{1}} = - 1,\quad {{\bar {Q}}_{1}} = - \operatorname{tg} {{\alpha }_{1}},\quad {{\bar {M}}_{1}} = 0$В заключение этого раздела преобразуем параметр $\lambda $. Используя равенство (1.2), выразим этот параметр через деформацию, то есть
3. Определение критической деформации. Рассмотрим уравнения (2.7). Умножим первое уравнение на $\bar {N}$ и прибавим к нему второе уравнение, умноженное на $\bar {Q}$. В результате получим $\bar {N}\bar {N}{\text{'}} + \bar {Q}\bar {Q}{\text{'}} = 0$. Интегрируя, имеем ${{\bar {N}}^{2}} + {{\bar {Q}}^{2}} = {{C}^{2}}$. Постоянную $С$ найдем с помощью граничных условий при $\alpha = 0$ (рис. 2), согласно которым $\bar {N}(\alpha = 0) = - {{\bar {N}}_{0}}$ и $\bar {Q}(\alpha = 0) = 0$. Учитывая равенства (2.9), окончательно получим
Удовлетворим это уравнение, введя новую функцию $\theta (\alpha )$ такую, что
(3.1)
$\bar {N} = - \frac{{\cos \theta }}{{\cos {{\alpha }_{1}}}},\quad \bar {Q} = - \frac{{\sin \theta }}{{\cos {{\alpha }_{1}}}}$Учитывая равенства (2.9), можно установить пределы изменения функции $\theta (\alpha )$, то есть
Рассмотрим первое уравнение (2.7). Подставляя в него равенства (3.1) и выражая $\omega _{\alpha }^{'}$ через $\bar {М}$ с помощью первого равенства (2.8), получим
Из третьего уравнения (2.7) и второго равенства (3.1) имеем
Дифференцируя уравнение (3.3) и исключая $\bar {М}{\text{'}}$ с помощью равенства (3.4) придем к следующему уравнению:
(3.5)
$\theta {\text{''}} + {{k}^{2}}\sin \theta = 0,\quad {{k}^{2}} = \frac{{12\lambda }}{{\cos {{\alpha }_{1}}}}$Решение уравнения (3.5) выражается через эллиптический интеграл. Однако оно неудобно для дальнейшего анализа так как не позволяет получить явного выражения $\theta (\alpha )$. В связи с этим упростим это уравнение, считая, что угол ${{\alpha }_{1}}$ много меньше $\pi $ (рис. 1, 3). Учитывая равенства (3.2), можно заключить, что тогда можно считать что угол $\theta $ также много меньше $\pi $ и использовать приближенное соотношение $\sin \theta \approx \theta $. В результате, уравнение (3.5) упрощается следующим образом:
Решение этого уравнения, удовлетворяющее граничным условиям (3.2), имеет вид
Подставляя решение (3.6) в равенство (3.3), найдем изгибающий момент
(3.7)
$\bar {M} = \frac{1}{{12\lambda }}\left( {\frac{{\eta \cos k\alpha }}{{\sin \eta }} - 1} \right)$Определим момент, действующий на концах участка 1–2 (рис. 2). Имеем
(3.8)
${{\bar {M}}_{0}} = \bar {M}(\alpha = 0) = \frac{1}{{12\lambda }}\left( {\frac{\eta }{{\sin \eta }} - 1} \right),\quad {{\bar {M}}_{1}} = \bar {M}(\alpha = {{\alpha }_{1}}) = \frac{1}{{12\lambda }}\left( {\frac{\eta }{{\operatorname{tg} \eta }} - 1} \right)$Для дальнейшего анализа воспользуемся равенствами (2.8), (2.10), (3.5) и (3.6) и запишем развернутое выражение для параметра $\eta ,$ то есть
(3.9)
$\eta = 2{{\alpha }_{1}}\sqrt {\frac{{3\lambda }}{{\cos {{\alpha }_{1}}}}} = 2{{\alpha }_{1}}\frac{R}{h}\sqrt {\frac{{3qR}}{{\bar {E}h\cos {{\alpha }_{1}}}}} = 2{{\alpha }_{1}}\frac{R}{h}\sqrt {\frac{{3\varepsilon }}{{\cos {{\alpha }_{1}}}}} $Отсюда следует, что параметры $\eta $ и $\lambda $ являются параметрами нагружения. Рассмотрим первое соотношение (3.8). При малых значениях параметра $\eta $ имеем $\sin \eta > 0$ и ${{\bar {М}}_{0}} > 0$. При таком моменте оболочка изгибается наружу, что не соответствует условиям ее закрепления. Как следует из рис. 2, для того, чтобы оболочка изгибалась внутрь, необходимо, чтобы выполнялось условие ${{\bar {М}}_{0}} < 0$. Для этого в первом равенстве (3.8) должно быть $\sin \eta < 0$, что возможно если нагрузка достигает значения, при котором $\pi < \eta < 2\pi .$ Конкретное значение $\eta $ следует из второго равенства (3.8). Согласно соответствующему уравнению (2.9), ${{\bar {М}}_{1}} = 0$. В результате, получим следующее уравнение для $\eta $:
Заметим, что при этом условии $d{{\bar {M}}_{0}}{\text{/}}d\eta = 0$, то есть если параметр $\eta $ удовлетворяет уравнению (3.10), то момент ${{\bar {М}}_{0}}$ принимает минимальное абсолютное значение. Минимальный ненулевой корень уравнения (3.10) – $\eta = 4.4934$.
Определим прогиб оболочки. Из равенств (2.8) и (3.7) имеем
(3.11)
$\omega {{_{\alpha }^{'}}_{{}}} = 12\lambda \bar {M} = \frac{{\eta \cos k\alpha }}{{\sin \eta }} - 1$Угол поворота должен удовлетворять граничному условию (рис. 2): ${{\omega }_{\alpha }}(\alpha = 0) = 0$. Интегрируя равенство (3.11) с учетом этого условия и равенства (3.6) для $\eta ,$ получим
Отсюда следует, что ${{\omega }_{\alpha }}$ $(\alpha = {{\alpha }_{1}}) = 0$, то есть угол поворота равен нулю в точках 1 и 2 (рис. 2). Из второго уравнения (2.8) следует
где $\omega _{\alpha }^{'}$ определяется равенством (3.10). Решение уравнения (3.12) симметричное по координате $\alpha $ (рис. 2), имеет вид(3.13)
$\bar {w} = - {{\bar {w}}_{0}}\cos \alpha + \cos \alpha \int\limits_0^\alpha {\omega _{\alpha }^{'}} {\text{sin}}\alpha d\alpha - \sin \alpha \int\limits_0^\alpha {\omega _{\alpha }^{'}} \cos \alpha d\alpha $Здесь ${{\bar {w}}_{0}} = \bar {w}(\alpha = 0)$ определяет максимальный прогиб оболочки, который находится из условия $\bar {w}(\alpha = {{\alpha }_{1}}) = 0$ (рис. 2). В результате получим
(3.14)
${{\bar {w}}_{0}} = \tan {{\alpha }_{1}}\int\limits_0^{{{\alpha }_{1}}} {\omega _{\alpha }^{'}} \cos \alpha d\alpha - \int\limits_0^{{{\alpha }_{1}}} {\omega _{\alpha }^{'}} \sin \alpha d\alpha $Подставляя выражение (3.11) в равенства (3.13) и (3.14) и интегрируя, окончательно найдем
(3.15)
$\bar {w} = {{\bar {w}}_{0}}\cos \alpha + \frac{{\sin \eta ({{\eta }^{2}} - \alpha _{1}^{2})\left( {1 - \cos \alpha } \right) - \eta \alpha _{1}^{2}\left( {\cos \alpha - \cos k\alpha } \right)}}{{\sin \eta ({{\eta }^{2}} - \alpha _{1}^{2})}}$(3.16)
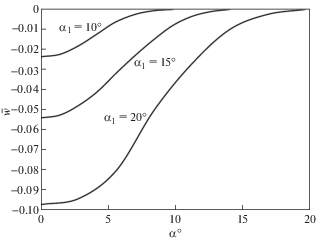
${{\bar {w}}_{0}} = \frac{{\sin \eta ({{\eta }^{2}} - \alpha _{1}^{2})\left( {\cos {{\alpha }_{1}} - 1} \right) + \eta \alpha _{1}^{2}\left( {\cos {{\alpha }_{1}} - \cos \eta } \right)}}{{\sin \eta ({{\eta }^{2}} - \alpha _{1}^{2})\cos {{\alpha }_{1}}}}$Зависимости $\bar {w}(\alpha ),$ соответствующие ${{\alpha }_{1}} = 10^\circ ,15^\circ ,20^\circ $ показаны на рис. 4.
Для завершения решения необходимо найти угол α1 (рис. 2). Для этого воспользуемся условием недеформируемости оболочки в кольцевом направлении. При образовании прогиба оболочки на участке 0–1 (рис. 2) точка 1 смещается в кольцевом направлении на величину $\Delta S$, которое с учетом принятых ранее гипотез имеет вид
Поскольку оболочка имеет предварительную деформацию сжатия ε, эта деформация релаксирует так, что $\Delta S = \varepsilon l{\text{*}}$. Здесь $l* = R\alpha {\text{*}}$ – длина по окружности, на которой происходит релаксация деформации (рис. 3). Определить эту длину и соответствующий угол $\alpha {\text{*}}$ не представляется возможным так как они зависят от величины накопленной в оболочке упругой энергии и силы трения между оболочкой и окружающей ее средой. Однако возможны два предельных случая. Если оболочка жестко связана со средой в кольцевом направлении, то проскальзывать может только ее отслоившийся участок и $\alpha {\text{*}} = {{\alpha }_{1}}$. Если трение между оболочкой и средой отсутствует, то проскальзывает вся оболочка и $\alpha * = \pi $ (рис. 3). Таким образом, имеем
Подставляя $\varepsilon $ и $\bar {w}$ из равенств (2.10) и (3.14) найдем
(3.17)
${{\left( {\frac{h}{R}} \right)}^{2}} = \frac{1}{{2\alpha {\text{*}}\lambda }}\int\limits_0^{{{\alpha }_{1}}} {{{{(\bar {w}{\text{'}})}}^{2}}} d\alpha = \frac{{6{{\alpha }_{1}}}}{{\alpha {\text{*}}\eta \cos {{\alpha }_{1}}}}\int\limits_0^{{{\alpha }_{1}}} {{{{(\bar {w}{\text{'}})}}^{2}}} d\alpha $Последнее равенство получено с учетом соотношения
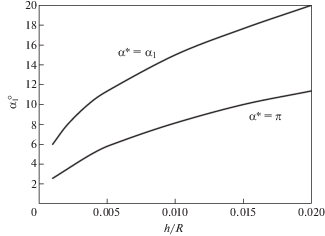
следующего из первой формулы (3.9). Используя выражение (3.15) для $\bar {w}$ и интегрируя, окончательно получим гдеЗдесь $\eta = 4.4934.$ Уравнение (3.18) позволяет найти ${{\alpha }_{1}}$ при заданных значениях отношения $h{\text{/}}R$ и угла $\alpha {\text{*}}$. Соответствующие зависимости при $\alpha * = {{\alpha }_{1}}$ и $\alpha * = \pi $ показаны на рис. 5. Критическая деформация определяется из равенств (2.10) и (3.18), то есть
(3.20)
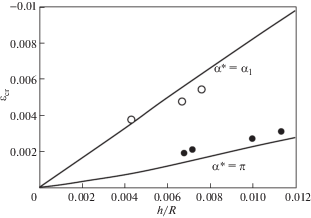
${{\varepsilon }_{{cr}}} = \frac{{\eta \cos {{\alpha }_{1}}}}{{12{{\alpha }_{1}}}}{{\left( {\frac{h}{R}} \right)}^{2}}$Зависимости критической деформации от отношения $h{\text{/}}R$ показаны для $\alpha * = {{\alpha }_{1}}$ и $\alpha * = \pi $ на рис. 6.
4. Анализ полученных результатов. На первый взгляд создается впечатление, что критическая деформация (3.20) не зависит от модуля упругости и абсолютной толщины теряющей устойчивость оболочки. Однако это не так – эти параметры влияют на критическую деформацию через угол $\alpha {\text{*}}$. Чем больше энергия деформаций докритического состояния, которая пропорциональна этим параметрам, тем больше угол $\alpha {\text{*}}$. Как следует из рис. 6, величина этого угла оказывает значительное влияние на критическую деформацию – деформации, соответствующие верхней и нижней кривой отличаются в 3.5 раза. Этим объясняется большой разброс экспериментальных результатов, полученных для различных материалов [13]. Темными точками на рис. 6 показаны средние по трем испытаниям результаты полученные на двухслойных кольцах с радиусами 45–75 мм [14] (рис. 1(a)). Наружное кольцо c толщиной 6–8 мм изготовлено методом намотки из углепластика и имеет нулевой КЛТР. Внутреннее кольцо, на которое осуществлялась намотка, изготовлено из нержавеющей стали и обладает следующими параметрами: h = 0.5 мм, $Е = 200$ ГПа, $\alpha _{T}^{i} = 16 \times {{10}^{{ - 6}}}$ 1/°C. Потеря устойчивости достигалась нагревом колец, а критическая деформация находилась по формуле (1.3). Как следует из рис. 6, сравнительно высокий модуль упругости стали и соответствующий уровень докритической энергии деформации обеспечивают критическую деформацию близкую к получаемой при отсутствии трения между кольцами ($\alpha * = \pi $). Светлые точки соответствуют аналогичному эксперименту с внутренним кольцом из полипропилена (рис. 1(b)) с характеристиками h = 0.4 мм, $Е = 0.9$ ГПа, $\alpha _{T}^{i} = 95 \times {{10}^{{ - 6}}}$ 1/°C. Результаты эксперимента близки к кривой $\alpha * = {{\alpha }_{1}},$ что соответствует жесткому скреплению колец за счет силы трения. О важности силы трения свидетельствует эксперимент с кольцом из полиэтилена с характеристиками h = 0.16 мм, $Е = 0.1$ ГПа, $\alpha _{T}^{i} = 200 \times {{10}^{{ - 6}}}$ 1/°C. При нагреве такого кольца наблюдались два взаимно независимых диаметрально расположенных отслоения внутреннего кольца.
В работах по устойчивости оболочки в жесткой среде критическая деформация оболочки аппроксимируется следующим соотношением:
где C – некоторый коэффициент. Для нижней границы полученного решения, соответствующего кривой $\alpha * = \pi $ на рис. 6, имеем $С = 0.55$. Ранее были получены следующие значения: в работе [1] – $C = 1.11$, в [3] – $C = 1.2$, в [4] $C = 0.43$, в [7] $C = 1$.Заключение. В рамках варианта нелинейной теории оболочек, учитывающего из нелинейных членов только связанные с изменением кривизны оболочки в процессе деформации, получено точное аналитическое решение, определяющее критическое значение деформации оболочки, сжимаемой бесконечно жесткой внешней средой. Установлено, что эта деформация существенно зависит от соотношения между упругой энергией в сжатой оболочке и силами трения, действующими между оболочкой и средой. Исследованы два предельных случая – отсутствие трения между средой и оболочкой и жесткая тангенциальная связь между ними. Полученное решение подтверждено экспериментально.
Список литературы
Cheney J.A. Pressure buckling of ring encased in cavity // J. Eng. Mech. Division. 1971. V. 97. Iss. 2. P. 333–343
El-Bayoumy L. Buckling of a circular elastic ring confined to a uniformly contacting circular boundary // J. Appl. Mech. Sep 1972. V. 39. № 3. P. 758–766. https://doi.org/10.1115/1.3422785
Chicurel R. Shrink buckling of thin circular rings // J. Appl. Mech. Sep 1968. V. 35. № 3. P. 608–610. https://doi.org/10.1115/1.3601259
Glock D. Post-critical behavior of a rigidly encased circular pipe subject to external water pressure and temperature rise // Der Stahlbau. 1977. V. 46. № 7. P. 212–217.
Chan H.C., McMinn S.J. The stability of a uniformly compressed ring surrounded by a rigid circular surface // Int. J. Mech. Sci. 1966. V. 8. P. 433–442.
Zagustin E.A., Herrmann G. Stability of an elastic ring in a rigid cavity // J. Appl. Mech. Jun 1967. V. 34. № 2. P. 263–270. https://doi.org/10.1115/1.3607677
Буяков И.А. Простейшее решение задачи о выпучивании кольца внутри жесткой обоймы // Космонавтика и ракетостроение. 2004. Вып. 1 (34). С. 119–130.
Буяков И.А., Березкин В.А. Выпучивание тонкой сферической оболочки внутри шаровой полости сжимающегося массивного тела // Проблемы машиностроения и надежности машин. 2014. № 5. С. 30–33.
Буяков И.А., Ермаков И.С., Сухомлинов Л.Г. Исследование выпучивания тонкой сферической оболочки внутри шаровой полости сжимающегося массивного тела // Космонавтика и ракетостроение. 2018. Вып. 4 (103). С. 46–51.
Феодосьев В.И. Избранные задачи и вопросы по сопротивлению материалов. М.: Наука–Физматлит, 1996. 368 с.
Васильев В.В. Механика конструкций из композиционных материалов. М.: Машиностроение, 1988. 270 с.
Васильев В.В. О теории тонких пластин // Изв. РАН. МТТ. 1992. № 3. С. 26–47.
Johns R.H., Kaufman A. Filament-overwrapped metallic cylindrical pressure vessels // J. Spacecr. Rockets. 1967. V. 4. № 7. P. 872–877.
Васильев В.В., Мороз Н.Г. Композитные баллоны давления – проектирование, расчет, изготовление и испытания. М.: Машиностроение, 2015. 373 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела