1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 4, 2021

Известия РАН. Механика твердого тела, 2021, № 4, стр. 151-164

ОТКЛИК НЕЛОКАЛЬНЫХ И ФАЗОВЫХ ЗАПАЗДЫВАНИЙ НА НАГРУЖЕНИЯ ЛИНЕЙНОГО ТИПА В ТЕОРИЯХ ТЕРМОУПРУГИХ МОМЕНТНЫХ НАПРЯЖЕНИЙ С УЧЕТОМ ДИФФУЗИИ

Раджниш Кумар a, Сачин Каушал b, *, Викрам b

a Университет Курукшетры, Курукшетра
Харьяна, Индия

b Школа химической инженерии и физических наук, Профессиональный университет Лавли – Пхагвара
Пенджаб, Индия

* E-mail: sachin_kuk@yahoo.co.in

Поступила в редакцию 10.09.2020
После доработки 11.12.2020
Принята к публикации 11.12.2020

Полный текст (PDF)

Аннотация

Построена новая математическая модель диффузии с учетом термоупругих моментных напряжений (ТМН), в которой рассмотрены эффекты нелокального и двухфазного запаздывания. Это обобщение анализируется в процессе термомеханического нагружения. Основные уравнения упрощаются за счет использования методов преобразования Лапласа и Фурье. Для демонстрации предложенной модели учитываются нормальная и тепловая нагрузки линейного типа. Рассчитаны и графически проанализированы перемещения, напряжения, изменения температуры и химического потенциала. Также рассмотрены частные случаи.

Ключевые слова: модифицированная моментная термоупругость, нелокальность, двухфазные запаздывания, преобразования Лапласа, преобразования Фурье, нормальная нагрузка линейного типа, тепловой источник

1. Введение. В нелокальной теории упругости напряженное состояние в точке является функцией деформации всех точек тела, тогда как классическая (локальная) теория упругости описывает напряженное состояние в данной точке посредством деформаций в той же точке. Нелокальная теория была разработана и опубликована в работах А.К. Эрингена [1–7], Д. Эделена [1, 8], К. Ло [8], Б. МакКея и М. Нарсимханa [9, 10]. Исчерпывающее исследование теории нелокальной упругости изложено в монографии А.К. Эрингена [11].

Нелокальный отклик и запаздывающий отклик среды схожи, как в пространстве, так и во времени. В работе [12] Д. Цзу объединил отклик нелокальной теплопроводности с однофазным запаздыванием и сравнил его с моделью, разработанной Б. Цао и З. Го [13] и З. Го и К. Хоу [14]. Д. Цзу и З. Го в [15] демонстрируют объединение нелокального отклика с моделью двухфазного запаздывания, предложенной Д. Цзу в работах [16, 17], и известной как новая теория, включающая оба эффекта (нелокального и запаздывающего отклика).

К. Шарма в [18] исследовал краевые задачи в обобщенной термоупругой диффундирующей среде. Влияние источников тепла и времени релаксации на распределение температуры в тканях изложено в [19]. К. Шарма и др. в [20] изучали плоские волны и фундаментальное решение в твердом теле с учетом электро-микро- растяжений. Коробление нанотрубок при неоднородной температуре на основе нелокальной термоупругости исследовано в [21]. А.Е. Абуэлригал в работе [22] показал влияние температурно-зависимых физических свойств и дробной (фрактальной) термоупругости на нелокальные нанотрубки.

Р. Кумар и соавт. в [23] провели переходный анализ нелокальной микростатической термоупругой толстой круглой пластины с фазовым запаздыванием. Р. Кумар и соавт. в [24] исследовали влияние источников теплового и химического потенциала в тонком пучке в ТМН с помощью модели термоупругой диффузии с трехфазным запаздыванием. В. Боржалилу и др. [25] представили явное соотношение для термоупругого демпфирования в нелокальных нанотрубках с учетом эффекта двухфазного запаздывания.

В этой статье исследуются нелокальные эффекты и эффекты фазового запаздывания, связанные с термомеханическими источниками при диффузии ТМН. Для исследования проблемы применяется метод интегрального преобразования. Подход был продемонстрирован на нормальной и тепловой нагрузках линейного типа. Результаты изображены графически, чтобы показать нелокальный эффект и эффект фазового запаздывания.

2. Основные уравнения. Исходя из работ [15, 26, 27], имеем

(i) Определяющие coотношения

(2.1)
${{t}_{{ij}}} = 2\mu {{e}_{{ij}}} - \frac{1}{2}{{e}_{{kij}}}{{m}_{{lk,l}}} + {{\delta }_{{ij}}}[{{\lambda }_{0}}{{e}_{{kk}}} - {{\gamma }_{1}}T - {{\gamma }_{2}}P]$
(2.2)
${{m}_{{ij}}} = 2\alpha {{\chi }_{{ij}}}$

(ii) Уравнение движения

(2.3)
$\left( {{{\lambda }_{0}} + \mu + \frac{\alpha }{4}\Delta } \right)\nabla (\nabla \cdot {\mathbf{u}}) + \left( {\mu - \frac{\alpha }{4}\Delta } \right)(\Delta {\mathbf{u}}) - {{\gamma }_{1}}\nabla T - {{\gamma }_{2}}\nabla P = \rho (1 - {{\xi }^{2}}\Delta )\frac{{{{\partial }^{2}}{\mathbf{u}}}}{{\partial {{t}^{2}}}}$

(iii) Уравнение теплопроводности

(2.4)
$\left( {1 - {{\zeta }^{2}}\Delta + {{\tau }_{q}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{q}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)({{\gamma }_{1}}{{T}_{0}}\mathop e\limits^ \bullet \; + {{l}_{1}}{{T}_{0}}\mathop T\limits^ \bullet \; + {{T}_{0}}d\mathop P\limits^ \bullet ) = K\left( {1 + {{\tau }_{t}}\frac{\partial }{{\partial t}}} \right)\Delta T$

(iv) Уравнение диффузии

(2.5)
$\left( {1 - {{\varsigma }^{2}}\Delta + {{\tau }_{u}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{u}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)({{\gamma }_{2}}\mathop e\limits^ \bullet \; + d\mathop T\limits^ \bullet \; + n\mathop P\limits^ \bullet ) = D\left( {1 + {{\tau }_{p}}\frac{\partial }{{\partial t}}} \right)\Delta P$

Здесь ${{\chi }_{{ij}}} = \frac{1}{2}({{\omega }_{{i,j}}} + {{\omega }_{{j,i}}})$, ${{\omega }_{i}} = \frac{1}{2}{{e}_{{ipq}}}{{u}_{{q,p}}}$, где ${{\lambda }_{o}} = \lambda - \frac{{\beta _{2}^{2}}}{b}$, ${{\gamma }_{1}} = {{\beta }_{1}} + \frac{a}{b}{{\beta }_{2}}$, ${{\gamma }_{2}} = \frac{{{{\beta }_{2}}}}{b}$, l1 = = $\frac{{\rho {{C}_{e}}}}{{{{T}_{o}}}} + \frac{{{{a}^{2}}}}{b}$, $d = \frac{a}{b}$, $n = \frac{1}{b}$.

В уравнениях (2.1)–(2.5), $\xi ,\;\zeta ,\;\varsigma $ – нелокальные параметры, ${{\tau }_{q}}$ и ${{\tau }_{t}}$ – времена тепловой релаксации, где ${{\tau }_{q}},{{\tau }_{t}} \geqslant 0$, и ${{\tau }_{u}}$ и ${{\tau }_{p}}$ – времена диффузионной релаксации где ${{\tau }_{u}},{{\tau }_{p}} \geqslant 0$. ${{\beta }_{1}} = (3\lambda + 2\mu ){{\alpha }_{t}}$, ${{\beta }_{2}} = (3\lambda + 2\mu ){{\alpha }_{c}}$. Здесь ${{\alpha }_{t}},\;{{\alpha }_{c}}$ соответствуют коэффициенту линейного теплового расширения и диффузионного расширения соответственно. $\Delta $ – оператор Лапласа, $\nabla $ – оператор набла (градиента). Остальные символы имеют общепринятое значение.

3. Постановка задачи. Рассматривается однородное изотропное нелокальное диффундирующее ТМН тело с двухфазным запаздыванием, занимающее область ${{x}_{3}} \geqslant 0$. Введем прямоугольную декартову систему координат $({{x}_{1}},{{x}_{2}},{{x}_{3}})$ с началом координат на x3 = 0. Полупространство подвергается нормальной и тепловой рамповой нагрузке на граничной плоскости x3 = 0.

Для предлагаемой модели запишем

(3.1)
${\mathbf{u}} = ({{u}_{1}}({{x}_{1}},{{x}_{3}},t),0,{{u}_{3}}({{x}_{1}},{{x}_{3}},t)),\quad T({{x}_{1}},{{x}_{3}},t),\quad P({{x}_{1}},{{x}_{3}},t)$

Подставляя (3.1) в (2.3)–(2.5), приходим к следующим уравнениям

(3.2)
$({{\lambda }_{o}} + \mu )\frac{{\partial e}}{{\partial {{x}_{1}}}} + \mu \Delta {{u}_{1}} + \frac{\alpha }{4}\Delta \left( {\frac{{\partial e}}{{\partial {{x}_{1}}}} - \Delta {{u}_{1}}} \right) - {{\gamma }_{1}}\frac{{\partial T}}{{\partial {{x}_{1}}}} - {{\gamma }_{2}}\frac{{\partial P}}{{\partial {{x}_{1}}}} = \rho (1 - {{\xi }^{2}}\Delta )\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}}$
(3.3)
$({{\lambda }_{o}} + \mu )\frac{{\partial e}}{{\partial {{x}_{3}}}} + \mu \Delta {{u}_{3}} + \frac{\alpha }{4}\Delta \left( {\frac{{\partial e}}{{\partial {{x}_{3}}}} - \Delta {{u}_{3}}} \right) - {{\gamma }_{1}}\frac{{\partial T}}{{\partial {{x}_{3}}}} - {{\gamma }_{2}}\frac{{\partial P}}{{\partial {{x}_{3}}}} = \rho (1 - {{\xi }^{2}}\Delta )\frac{{{{\partial }^{2}}{{u}_{3}}}}{{\partial {{t}^{2}}}}$
(3.4)
$\left( {1 - {{\zeta }^{2}}\Delta + {{\tau }_{q}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{q}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)({{\gamma }_{1}}{{T}_{o}}\mathop e\limits^ \bullet \; + {{l}_{1}}{{T}_{o}}\mathop T\limits^ \bullet \; + {{T}_{o}}d\mathop P\limits^ \bullet ) = K\left( {1 + {{\tau }_{t}}\frac{\partial }{{\partial t}}} \right)\Delta T$
(3.5)
$\left( {1 - {{\varsigma }^{2}}\Delta + {{\tau }_{u}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{u}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)({{\gamma }_{2}}\mathop e\limits^ \bullet \; + d\mathop T\limits^ \bullet \; + n\mathop P\limits^ \bullet ) = D\left( {1 + {{\tau }_{p}}\frac{\partial }{{\partial t}}} \right)\Delta P$

Введем следующие безразмерные переменные:

(3.6)
$\begin{gathered} \xi {\kern 1pt} ' = \frac{{\omega {\kern 1pt} *}}{{{{c}_{1}}}}\xi ,\quad \zeta {\kern 1pt} ' = \frac{{\omega {\kern 1pt} *}}{{{{c}_{1}}}}\zeta ,\quad \varsigma {\kern 1pt} ' = \frac{{\omega {\kern 1pt} *}}{{{{c}_{1}}}}\varsigma ,\quad x_{i}^{'} = \frac{{\omega {\kern 1pt} *}}{{{{c}_{1}}}}{{x}_{i}},\quad u_{i}^{'} = \frac{{\omega {\kern 1pt} *}}{{{{c}_{1}}}}{{u}_{i}},\quad t{\kern 1pt} ' = \omega {\kern 1pt} *t \\ \tau _{t}^{'} = \omega {\kern 1pt} *{{\tau }_{t}},\quad \tau _{q}^{'} = \omega {\kern 1pt} *{{\tau }_{q}},\quad \tau _{u}^{'} = \omega {\kern 1pt} *{{\tau }_{u}},\quad \tau _{p}^{'} = \omega {\kern 1pt} *{{\tau }_{p}},\quad t_{{ij}}^{'} = \frac{1}{{{{\gamma }_{1}}{{T}_{o}}}}{{t}_{{ij}}} \\ m_{{ij}}^{'} = \frac{{\omega {\kern 1pt} *}}{{{{\gamma }_{1}}{{T}_{o}}{{c}_{1}}}}{{m}_{{ij}}},\quad T{\kern 1pt} ' = \frac{{{{\gamma }_{1}}}}{{\rho c_{1}^{2}}}T,\quad P{\kern 1pt} ' = \frac{1}{{b{{\gamma }_{2}}}}P \\ \end{gathered} $
где
$\omega {\kern 1pt} {{*}^{2}} = \frac{{\lambda _{ \circ }^{2}}}{{{{\mu }^{2}}{{t}^{2}} + \rho \alpha }},\quad c_{1}^{2} = \frac{{{{\lambda }_{o}} + 2\mu }}{\rho }$
$\omega {\kern 1pt} *$ – характерная частота, ${{c}_{1}}$ – скорость продольной волны в среде.

Уравнения (3.2)–(3.5) с помощью (3.6) сводятся путем опускания штрихов к следующим

(3.7)
$\frac{{({{\lambda }_{o}} + \mu )}}{{\rho c_{1}^{2}}}\frac{{\partial e}}{{\partial {{x}_{1}}}} + \frac{\mu }{{\rho c_{1}^{2}}}\Delta {{u}_{1}} + \frac{\alpha }{4}\frac{{\omega {\kern 1pt} {{*}^{2}}}}{{\rho c_{1}^{4}}}\Delta \left( {\frac{{\partial e}}{{\partial {{x}_{1}}}} - \Delta {{u}_{1}}} \right) - \frac{{\partial T}}{{\partial {{x}_{1}}}} - \frac{{b\gamma _{2}^{2}}}{{\rho c_{1}^{2}}}\frac{{\partial P}}{{\partial {{x}_{1}}}} = (1 - {{\xi }^{2}}\Delta )\frac{{{{\partial }^{2}}{{u}_{1}}}}{{\partial {{t}^{2}}}}$
(3.8)
$\frac{{({{\lambda }_{o}} + \mu )}}{{\rho c_{1}^{2}}}\frac{{\partial e}}{{\partial {{x}_{3}}}} + \frac{\mu }{{\rho c_{1}^{2}}}\Delta {{u}_{3}} + \frac{\alpha }{4}\frac{{\omega {\kern 1pt} {{*}^{2}}}}{{\rho c_{1}^{4}}}\Delta \left( {\frac{{\partial e}}{{\partial {{x}_{3}}}} - \Delta {{u}_{3}}} \right) - \frac{{\partial T}}{{\partial {{x}_{3}}}} - \frac{{b\gamma _{2}^{2}}}{{\rho c_{1}^{2}}}\frac{{\partial P}}{{\partial {{x}_{3}}}} = (1 - {{\xi }^{2}}\Delta )\frac{{{{\partial }^{2}}{{u}_{3}}}}{{\partial {{t}^{2}}}}$
(3.9)
$\left( {1 - {{\zeta }^{2}}\Delta + {{\tau }_{q}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{q}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)\left( {\frac{{\gamma _{1}^{2}}}{{K\rho \omega {\kern 1pt} *}}{{T}_{o}}\mathop e\limits^ \bullet \; + \frac{{{{l}_{1}}c_{1}^{2}}}{{K\omega {\kern 1pt} *}}{{T}_{o}}\mathop T\limits^ \bullet \; + \frac{{b{{\gamma }_{2}}{{\gamma }_{1}}}}{{K\rho \omega {\kern 1pt} *}}{{T}_{o}}d\mathop P\limits^ \bullet } \right) = \left( {1 + {{\tau }_{t}}\frac{\partial }{{\partial t}}} \right)\Delta T$
(3.10)
$\left( {1 - {{\varsigma }^{2}}\Delta + {{\tau }_{u}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{u}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)\left( {\frac{{c_{1}^{2}}}{{Db\omega {\kern 1pt} *}}\mathop e\limits^ \bullet \; + \frac{{c_{1}^{4}d\rho }}{{Db\omega {\kern 1pt} *{{\gamma }_{1}}{{\gamma }_{2}}}}\mathop T\limits^ \bullet \; + \frac{{nc_{1}^{2}}}{{D\omega {\kern 1pt} *}}\mathop P\limits^ \bullet } \right) = \left( {1 + {{\tau }_{p}}\frac{\partial }{{\partial t}}} \right)\Delta P$
где

$\Delta = \frac{{{{\partial }^{2}}}}{{\partial x_{1}^{2}}} + \frac{{{{\partial }^{2}}}}{{\partial x_{3}^{2}}},\quad e = \frac{{\partial {{u}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{u}_{3}}}}{{\partial {{x}_{3}}}}$

4. Метод решения. Компоненты вектора перемещений ${{u}_{1}}({{x}_{1}},{{x}_{3}},t)$ и ${{u}_{3}}({{x}_{1}},{{x}_{3}},t)$ относятся к скалярным потенциалам $\phi ({{x}_{1}},{{x}_{3}},t)$ и $\psi ({{x}_{1}},{{x}_{3}},t)$ в безразмерной форме как

(4.1)
${{u}_{1}} = \frac{{\partial \phi }}{{\partial {{x}_{1}}}} + \frac{{\partial \psi }}{{\partial {{x}_{3}}}},\quad {{u}_{3}} = \frac{{\partial \phi }}{{\partial {{x}_{3}}}} - \frac{{\partial \psi }}{{\partial {{x}_{1}}}}$

С помощью (4.1) уравнения (3.7)–(3.10) записываются в виде

(4.2)
$({{a}_{1}} + {{a}_{2}})\Delta \phi - T - {{a}_{4}}P - (1 - {{\xi }^{2}}\Delta )\frac{{{{\partial }^{2}}\phi }}{{\partial {{t}^{2}}}} = 0$
(4.3)
$({{a}_{2}} - {{a}_{3}}\Delta )\Delta \psi - (1 - {{\xi }^{2}}\Delta )\frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}} = 0$
(4.4)
$\left( {1 - {{\zeta }^{2}}\Delta + {{\tau }_{q}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{q}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)({{a}_{5}}\Delta \mathop \phi \limits^ \bullet \; + {{a}_{6}}\mathop T\limits^ \bullet \; + {{a}_{7}}\mathop P\limits^ \bullet ) = \left( {1 + {{\tau }_{t}}\frac{\partial }{{\partial t}}} \right)\Delta T$
(4.5)
$\left( {1 - {{\varsigma }^{2}}\Delta + {{\tau }_{u}}\frac{\partial }{{\partial t}} + \frac{1}{2}\tau _{u}^{2}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}} \right)({{a}_{8}}\Delta \mathop \phi \limits^ \bullet + {{a}_{9}}\mathop T\limits^ \bullet + {{a}_{{10}}}\mathop P\limits^ \bullet ) = \left( {1 + {{\tau }_{p}}\frac{\partial }{{\partial t}}} \right)\Delta P$
где

$\begin{gathered} {{a}_{1}} = \frac{{({{\lambda }_{o}} + \mu )}}{{\rho c_{1}^{2}}},\quad {{a}_{2}} = \frac{\mu }{{\rho c_{1}^{2}}},\quad {{a}_{3}} = \frac{\alpha }{4}\frac{{\omega {\kern 1pt} {{*}^{2}}}}{{\rho c_{1}^{4}}},\quad {{a}_{4}} = \frac{{b\gamma _{2}^{2}}}{{\rho c_{1}^{2}}},\quad {{a}_{5}} = \frac{{\gamma _{1}^{2}}}{{K\rho \omega {\kern 1pt} *}}{{T}_{o}} \\ {{a}_{6}} = \frac{{{{l}_{1}}c_{1}^{2}}}{{K\omega {\kern 1pt} *}}{{T}_{o}},\quad {{a}_{7}} = \frac{{b{{\gamma }_{2}}{{\gamma }_{1}}}}{{K\rho \omega {\kern 1pt} *}}{{T}_{o}}d,\quad {{a}_{8}} = \frac{{c_{1}^{2}}}{{Db\omega {\kern 1pt} *}},\quad {{a}_{9}} = \frac{{c_{1}^{4}d\rho }}{{Db\omega {\kern 1pt} *{{\gamma }_{1}}{{\gamma }_{2}}}},\quad {{a}_{{10}}} = \frac{{nc_{1}^{2}}}{{D\omega {\kern 1pt} *}} \\ \end{gathered} $

Определим преобразования Лапласа и Фурье согласно

(4.6)
$\begin{gathered} \overline f ({{x}_{{1,}}}{{x}_{3}},s) = \int\limits_0^\infty {f({{x}_{1}},{{x}_{3}},t)\exp ( - st)dt} \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{f} ({{x}_{{1,}}}{{x}_{3}},s) = \int\limits_{ - \infty }^\infty {\overline f ({{x}_{1}},{{x}_{3}},s)\exp (i{{\xi }_{1}}{{x}_{1}})d{{x}_{1}}} \\ \end{gathered} $

Используя преобразование (4.6) в (4.2)–(4.5), после упрощения получаем:

(4.7)
$({{R}_{1}}D_{1}^{6} + {{R}_{2}}D_{1}^{4} + {{R}_{3}}D_{1}^{2} + {{R}_{4}})(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} ) = 0$
(4.8)
$(D_{1}^{4} + {{R}_{5}}D_{1}^{2} + {{R}_{6}})\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\psi } = 0$
где

${{R}_{1}} = {{R}_{{11}}}{{R}_{{13}}}{{R}_{{15}}} - {{R}_{{33}}}{{R}_{{35}}}{{R}_{{11}}}{{\zeta }^{2}}{{\varsigma }^{2}} + {{R}_{{31}}}{{R}_{{15}}}{{\zeta }^{2}} - {{R}_{{33}}}{{R}_{{34}}}{{\zeta }^{2}}{{\varsigma }^{2}} - {{R}_{{31}}}{{R}_{{35}}}{{a}_{4}}{{\zeta }^{2}}{{\varsigma }^{2}} + {{R}_{{34}}}{{R}_{{13}}}{{a}_{4}}{{\varsigma }^{2}},$
${{R}_{2}} = {{R}_{{01}}} - 3\xi _{1}^{2}{{R}_{1}},\quad {{R}_{3}} = 3\xi _{1}^{4}{{R}_{1}} - 2\xi _{1}^{2}{{R}_{{01}}} + {{R}_{{02}}},\quad {{R}_{4}} = {{R}_{{01}}}\xi _{1}^{4} - {{R}_{1}}\xi _{1}^{6} - {{R}_{{02}}}\xi _{1}^{2} - {{R}_{{03}}},$
${{R}_{5}} = - \frac{{{{a}_{2}} + {{\xi }^{2}}{{s}^{2}} + 2\xi _{1}^{2}{{a}_{3}}}}{{{{a}_{3}}}},$
${{R}_{6}} = \frac{{{{a}_{3}}\xi _{1}^{4} + {{a}_{2}}\xi _{1}^{2} + {{s}^{2}} + \xi _{1}^{2}{{\xi }^{2}}{{s}^{2}}}}{{{{a}_{3}}}}$
$\begin{gathered} {{R}_{{01}}} = - {{R}_{{11}}}{{R}_{{22}}}{{R}_{{15}}} - {{R}_{{11}}}{{R}_{{13}}}{{R}_{{26}}} - {{R}_{{13}}}{{R}_{{15}}}{{s}^{2}} + {{R}_{{33}}}{{R}_{{11}}}{{R}_{{25}}}{{\zeta }^{2}} + {{R}_{{35}}}{{R}_{{23}}}{{R}_{{11}}}{{\varsigma }^{2}} + {{R}_{{33}}}{{R}_{{35}}}{{\zeta }^{2}}{{\varsigma }^{2}}{{s}^{2}} - \\ \, - {{R}_{{31}}}{{R}_{{26}}}{{\zeta }^{2}} - {{R}_{{21}}}{{R}_{{15}}} + {{R}_{{33}}}{{R}_{{24}}}{{\zeta }^{2}} + {{R}_{{34}}}{{R}_{{23}}}{{\varsigma }^{2}} + {{R}_{{31}}}{{R}_{{24}}}{{a}_{4}}{{\zeta }^{2}} + {{R}_{{35}}}{{R}_{{21}}}{{a}_{4}}{{\varsigma }^{2}} - \\ \, - {{R}_{{13}}}{{R}_{{24}}}{{a}_{4}} - {{R}_{{34}}}{{R}_{{22}}}{{\varsigma }^{2}}{{a}_{4}} \\ \end{gathered} $
$\begin{gathered} {{R}_{{02}}} = {{R}_{{11}}}{{R}_{{22}}}{{R}_{{26}}} + {{R}_{{13}}}{{R}_{{26}}}{{s}^{2}} + {{R}_{{22}}}{{R}_{{15}}}{{s}^{2}} - {{R}_{{11}}}{{R}_{{23}}}{{R}_{{25}}} - {{R}_{{33}}}{{R}_{{25}}}{{\zeta }^{2}}{{s}^{2}} - {{R}_{{35}}}{{R}_{{23}}}{{\varsigma }^{2}}{{s}^{2}} + \\ \, + {{R}_{{21}}}{{R}_{{26}}} - {{R}_{{23}}}{{R}_{{24}}} - {{R}_{{21}}}{{R}_{{25}}}{{a}_{4}} + {{R}_{{22}}}{{R}_{{24}}}{{a}_{4}} \\ {{R}_{{03}}} = - {{s}^{2}}{{R}_{{26}}}{{R}_{{22}}} + {{s}^{2}}{{R}_{{23}}}{{R}_{{25}}},\quad {{R}_{{11}}} = {{a}_{1}} + {{a}_{2}} + {{\xi }^{2}}{{s}^{2}} \\ \end{gathered} $
$\begin{gathered} {{R}_{{12}}} = 1 + s{{\tau }_{q}} + \frac{{{{s}^{2}}}}{2}\tau _{q}^{2},\quad {{R}_{{13}}} = {{a}_{6}}s{{\zeta }^{2}} + 1 + s{{\tau }_{t}},\quad {{R}_{{14}}} = 1 + s{{\tau }_{u}} + \frac{{{{s}^{2}}}}{2}\tau _{u}^{2} \\ {{R}_{{15}}} = 1 + s{{\tau }_{p}} + s{{\zeta }^{2}}{{a}_{{10}}},\quad {{R}_{{21}}} = {{R}_{{31}}}{{R}_{2}},\quad {{R}_{{22}}} = {{R}_{{32}}}{{R}_{2}},\quad {{R}_{{23}}} = {{R}_{{33}}}{{R}_{2}} \\ \end{gathered} $
$\begin{gathered} {{R}_{{24}}} = {{R}_{{34}}}{{R}_{4}},\quad {{R}_{{25}}} = {{R}_{{35}}}{{R}_{4}},\quad {{R}_{{26}}} = {{R}_{{36}}}{{R}_{4}},\quad {{R}_{{31}}} = {{a}_{5}}s,\quad {{R}_{{32}}} = {{a}_{6}}s \\ {{R}_{{33}}} = {{a}_{7}}s,\quad {{R}_{{34}}} = {{a}_{8}}s,\quad {{R}_{{35}}} = {{a}_{9}}s,\quad {{R}_{{36}}} = {{a}_{{10}}}s \\ \end{gathered} $

Связанное решение уравнений (4.7) и (4.8) имеет вид

(4.9)
$(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\phi } ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} )({{x}_{3}},{{\xi }_{1}},s) = \sum\limits_{i = 1}^3 {(1,R_{i}^{*},S_{i}^{*}){{A}_{i}}} \exp ( - {{m}_{i}}{{x}_{3}})$
(4.10)
$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\psi } ({{x}_{3}},{{\xi }_{1}},s) = \sum\limits_{i = 4}^5 {{{A}_{i}}} \exp ( - {{m}_{i}}{{x}_{3}})$

Здесь ${{m}_{i}}(i = 1,2, \ldots ,5)$ – корни уравнений (4.7) и (4.8), а константы связи определяются выражениями

$R_{i}^{*} = \frac{\begin{gathered} {{(m_{i}^{2} - \xi _{1}^{2})}^{3}}({{R}_{{33}}}{{R}_{{34}}}{{\zeta }^{2}}{{\varsigma }^{2}} - {{R}_{{31}}}{{R}_{{15}}}{{\zeta }^{2}}) + {{(m_{i}^{2} - \xi _{1}^{2})}^{2}}({{R}_{{31}}}{{R}_{{26}}}{{\zeta }^{2}} + {{R}_{{21}}}{{R}_{{15}}} - {{R}_{{33}}}{{R}_{{24}}}{{\zeta }^{2}} \\ - {{R}_{{35}}}{{R}_{{21}}}{{\varsigma }^{2}}) + (m_{i}^{2} - \xi _{1}^{2})({{R}_{{21}}}{{R}_{{25}}} - {{R}_{{23}}}{{R}_{{24}}}) \\ \end{gathered} }{\begin{gathered} {{(m_{i}^{2} - \xi _{1}^{2})}^{2}}({{R}_{{13}}}{{R}_{{15}}} - {{R}_{{33}}}{{R}_{{35}}}{{\zeta }^{2}}{{\varsigma }^{2}}) + (m_{i}^{2} - \xi _{1}^{2})( - {{R}_{{22}}}{{R}_{{15}}} - {{R}_{{13}}}{{R}_{{26}}} + {{R}_{{33}}}{{R}_{{25}}}{{\zeta }^{2}} \\ + {{R}_{{35}}}{{R}_{{23}}}{{\varsigma }^{2}}) + ({{R}_{{22}}}{{R}_{{26}}} - {{R}_{{23}}}{{R}_{{25}}}) \\ \end{gathered} }$
$S_{i}^{*} = \frac{\begin{gathered} {{(m_{i}^{2} - \xi _{1}^{2})}^{3}}({{R}_{{31}}}{{R}_{{35}}}{{\zeta }^{2}}{{\varsigma }^{2}} - {{R}_{{34}}}{{R}_{{13}}}{{\varsigma }^{2}}) + {{(m_{i}^{2} - \xi _{1}^{2})}^{2}}({{R}_{{34}}}{{R}_{{22}}}{{\varsigma }^{2}} + {{R}_{{13}}}{{R}_{{24}}} - {{R}_{{31}}}{{R}_{{25}}}{{\zeta }^{2}} \\ - {{R}_{{35}}}{{R}_{{21}}}{{\varsigma }^{2}}) + (m_{i}^{2} - \xi _{1}^{2})({{R}_{{21}}}{{R}_{{25}}} - {{R}_{{22}}}{{R}_{{24}}}) \\ \end{gathered} }{\begin{gathered} {{(m_{i}^{2} - \xi _{1}^{2})}^{2}}({{R}_{{13}}}{{R}_{{15}}} - {{R}_{{33}}}{{R}_{{35}}}{{\zeta }^{2}}{{\varsigma }^{2}}) + (m_{i}^{2} - \xi _{1}^{2})( - {{R}_{{22}}}{{R}_{{15}}} - {{R}_{{13}}}{{R}_{{26}}} + {{R}_{{33}}}{{R}_{{25}}}{{\zeta }^{2}} \\ + {{R}_{{35}}}{{R}_{{23}}}{{\varsigma }^{2}}) + ({{R}_{{22}}}{{R}_{{26}}} - {{R}_{{23}}}{{R}_{{25}}}) \\ \end{gathered} }$
$i = 1,2,3$

5. Термомеханические условия. Рассмотрим нормальную нагрузку линейного типа с тепловым источником, пренебрегая при этом касательным моментным напряжением и химическим потенциалом:

(5.1)
${{t}_{{33}}} = - {{F}_{1}}(t)\delta (x),\quad {{t}_{{31}}} = 0,\quad {{m}_{{32}}} = 0,\quad T = {{F}_{2}}(t)\delta (x),\quad P = 0$
(5.2)
$[{{F}_{1}}(t),{{F}_{2}}(t)] = ({{F}_{0}},{{F}_{{01}}})\left\{ \begin{gathered} 0\quad t \leqslant 0 \hfill \\ \frac{t}{{{{t}_{0}}}}\quad 0 < t \leqslant {{t}_{0}} \hfill \\ 1\quad t > {{t}_{0}} \hfill \\ \end{gathered} \right.$
где F0 и F01 определяют величину силы и стационарную температуру, $\delta (x)$ обозначает дельта-функцию Дирака, а ${{t}_{0}}$ – линейный параметр.

Безразмерные компоненты напряжения определяются выражением

(5.3)
${{t}_{{33}}} = \frac{{2\mu }}{{{{\gamma }_{1}}{{T}_{o}}}}\left( {\frac{{\partial {{u}_{3}}}}{{\partial {{x}_{3}}}}} \right) + \frac{{{{\lambda }_{o}}}}{{{{\gamma }_{1}}{{T}_{o}}}}\left( {\frac{{\partial {{u}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{u}_{3}}}}{{\partial {{x}_{3}}}}} \right) - \frac{{\rho c_{1}^{2}}}{{{{\gamma }_{1}}{{T}_{o}}}}T - \frac{{\gamma _{2}^{2}b}}{{{{\gamma }_{1}}{{T}_{o}}}}P$
(5.4)
${{t}_{{31}}} = \frac{\mu }{{{{\gamma }_{1}}{{T}_{o}}}}\left( {\frac{{\partial {{u}_{1}}}}{{\partial {{x}_{3}}}} + \frac{{\partial {{u}_{3}}}}{{\partial {{x}_{1}}}}} \right) - \frac{\alpha }{4}\frac{{\omega {\kern 1pt} {{*}^{2}}}}{{c_{1}^{2}{{\gamma }_{1}}{{T}_{o}}}}\Delta \left( {\frac{{\partial {{u}_{1}}}}{{\partial {{x}_{3}}}} - \frac{{\partial {{u}_{3}}}}{{\partial {{x}_{1}}}}} \right)$
(5.5)
${{m}_{{32}}} = \frac{\alpha }{2}\frac{{\omega {\kern 1pt} {{*}^{2}}}}{{c_{1}^{2}{{\gamma }_{1}}{{T}_{o}}}}\frac{\partial }{{\partial {{x}_{3}}}}\left( {\frac{{\partial {{u}_{1}}}}{{\partial {{x}_{3}}}} - \frac{{\partial {{u}_{3}}}}{{\partial {{x}_{1}}}}} \right)$

Используя (4.6) в уравнениях (5.1) и (5.2), получим

(5.6)
${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} }_{{33}}} = - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }_{1}}(s),\quad {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} }_{{31}}} = 0,\quad {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m} }_{{32}}} = 0,\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} = {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }_{2}}(s),\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} = 0$
(5.7)
${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }_{1}}(s) = \frac{{{{F}_{0}}(1 - \exp ( - s{{t}_{0}}))}}{{{{t}_{0}}{{s}^{2}}}},\quad {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }_{2}}(s) = \frac{{{{F}_{{01}}}(1 - \exp ( - s{{t}_{0}}))}}{{{{t}_{0}}{{s}^{2}}}}$

Учитывая (4.9) и (4.10) в (5.7) вместе с (4.1), (4.6) и (5.3)–(5.5) имеем

(5.8)
${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} }_{1}} = - \frac{{i{{\xi }_{1}}}}{\Delta }\sum\limits_{i = 1}^3 {{{\Delta }_{i}}} \exp ( - {{m}_{i}}{{x}_{3}}) + \frac{1}{\Delta }\sum\limits_{i = 4}^5 {{{m}_{i}}{{\Delta }_{i}}\exp ( - {{m}_{i}}{{x}_{3}})} $
(5.9)
${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u} }_{3}} = - \frac{1}{\Delta }\sum\limits_{i = 1}^3 {{{m}_{i}}{{\Delta }_{i}}} \exp ( - {{m}_{i}}{{x}_{3}}) - \frac{{i{{\xi }_{1}}}}{\Delta }\sum\limits_{i = 4}^5 {{{\Delta }_{i}}\exp ( - {{m}_{i}}{{x}_{3}})} $
(5.10)
${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} }_{{33}}} = \frac{1}{\Delta }\sum\limits_{i = 1}^5 {{{a}_{{1i}}}{{\Delta }_{i}}\exp ( - {{m}_{i}}{{x}_{3}})} $
(5.11)
${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{t} }_{{31}}} = \frac{1}{\Delta }\sum\limits_{i = 1}^5 {{{a}_{{2i}}}{{\Delta }_{i}}\exp ( - {{m}_{i}}{{x}_{3}})} $
(5.12)
${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{m} }_{{32}}} = \frac{1}{\Delta }\sum\limits_{i = 1}^5 {{{a}_{{3i}}}{{\Delta }_{i}}\exp ( - {{m}_{i}}{{x}_{3}})} $
(5.13)
$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{T} = \frac{1}{\Delta }\sum\limits_{i = 1}^3 {R_{i}^{*}{{\Delta }_{i}}\exp ( - {{m}_{i}}{{x}_{3}})} $
(5.14)
$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} = \frac{1}{\Delta }\sum\limits_{i = 1}^3 {S_{i}^{*}{{\Delta }_{i}}\exp ( - {{m}_{i}}{{x}_{3}})} $
здесь

$\Delta = (S_{2}^{*}R_{1}^{*} - S_{1}^{*}R_{2}^{*}){{n}_{1}} + (S_{1}^{*}R_{3}^{*} - S_{3}^{*}R_{1}^{*}){{n}_{2}} + (S_{3}^{*}R_{2}^{*} - S_{2}^{*}R_{3}^{*}){{n}_{3}}$
$\begin{gathered} {{n}_{1}} = {{a}_{{13}}}{{a}_{{24}}}{{a}_{{35}}} - {{a}_{{13}}}{{a}_{{34}}}{{a}_{{25}}} - {{a}_{{14}}}{{a}_{{23}}}{{a}_{{35}}} + {{a}_{{14}}}{{a}_{{33}}}{{a}_{{25}}} + {{a}_{{15}}}{{a}_{{23}}}{{a}_{{34}}} - {{a}_{{15}}}{{a}_{{33}}}{{a}_{{24}}} \\ {{n}_{2}} = {{a}_{{12}}}{{a}_{{24}}}{{a}_{{35}}} - {{a}_{{12}}}{{a}_{{34}}}{{a}_{{25}}} - {{a}_{{14}}}{{a}_{{22}}}{{a}_{{35}}} + {{a}_{{14}}}{{a}_{{32}}}{{a}_{{25}}} + {{a}_{{15}}}{{a}_{{22}}}{{a}_{{34}}} - {{a}_{{15}}}{{a}_{{32}}}{{a}_{{24}}} \\ {{n}_{3}} = {{a}_{{11}}}{{a}_{{24}}}{{a}_{{35}}} - {{a}_{{11}}}{{a}_{{32}}}{{a}_{{25}}} - {{a}_{{14}}}{{a}_{{21}}}{{a}_{{35}}} + {{a}_{{14}}}{{a}_{{31}}}{{a}_{{25}}} + {{a}_{{15}}}{{a}_{{21}}}{{a}_{{34}}} - {{a}_{{15}}}{{a}_{{31}}}{{a}_{{24}}} \\ \end{gathered} $
$\begin{gathered} {{a}_{{1i}}} = (2{{r}_{1}} + {{r}_{2}})m_{i}^{2} - \xi _{1}^{2}{{r}_{2}} - {{r}_{3}}R_{i}^{*} - {{r}_{4}}S_{i}^{*},\quad {{a}_{{1j}}} = 2i{{\xi }_{1}}{{r}_{1}}{{m}_{j}} \\ {{a}_{{2i}}} = 2i{{\xi }_{1}}( - {{r}_{5}}m_{i}^{3} + {{r}_{1}}{{m}_{i}} + {{r}_{5}}\xi _{1}^{2}{{m}_{i}}),\quad {{a}_{{2j}}} = {{r}_{5}}m_{j}^{4} - {{r}_{1}}m_{j}^{2} - {{r}_{1}}\xi _{1}^{2} - {{r}_{5}}\xi _{1}^{4} \\ \end{gathered} $
$\begin{gathered} {{a}_{{3i}}} = 4i{{\xi }_{1}}{{r}_{5}}{{m}_{i}},\quad {{a}_{{3j}}} = - 2{{r}_{5}}(m_{j}^{2} + \xi _{1}^{2}),\quad {{r}_{1}} = \frac{\mu }{{{{\gamma }_{1}}{{T}_{o}}}},\quad {{r}_{2}} = \frac{{{{\lambda }_{o}}}}{{{{\gamma }_{1}}{{T}_{o}}}} \\ {{r}_{3}} = \frac{{\rho c_{1}^{2}}}{{{{\gamma }_{1}}{{T}_{o}}}},\quad {{r}_{4}} = \frac{{\gamma _{2}^{2}b}}{{{{\gamma }_{1}}{{T}_{o}}}},\quad {{r}_{5}} = \frac{\alpha }{4}\frac{{\omega {\kern 1pt} {{*}^{2}}}}{{{{\gamma }_{1}}{{T}_{o}}c_{1}^{2}}},\quad i = 1,2,3,\quad j = 4,5 \\ \end{gathered} $

Помещая $[ - {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }_{1}}(s),0,0,{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{F} }_{2}}(s),0)]'$ в i-й столбец $\Delta $ соответственно, определим ${{\Delta }_{i}}$ (i = 1, 2, ..., 5).

6. Проверка и особые случаи. (a) Для нормальной нагрузки линейного типа ${{F}_{2}} = 0$ соответствующие значения определяются из уравнений (5.8)–(5.14).

(b) Для теплового источника линейного типа ${{F}_{1}} = 0$ значения величин определяются из уравнений (5.8)–(5.14).

Особые случаи:

(1). Принимая $\xi ,\zeta ,\varsigma = 0$, получим соответствующие выражения из (5.8)–(5.14) в отсутствие нелокальных параметров.

(2). Принимая ${{\tau }_{t}},{{\tau }_{q}},{{\tau }_{u}},{{\tau }_{p}} = 0$, получим соответствующие выражения из (5.8)–(5.14) без двухфазного запаздывания.

7. Обратное преобразование. Обращаем преобразования в (5.8)–(5.14) с помощью методов, изложенных в работе [28].

8. Обcуждение численных результатов. Для численных расчетов, следуя работе [29], рассмотрим в качестве термоупругого диффундирующего твердого тела медь с соответствующими параметрами:

$\begin{gathered} \lambda = 7.76 \times {{10}^{{10}}}\;{\text{Kг}} \cdot {{{\text{м}}}^{{ - 1}}} \cdot {{{\text{с}}}^{{ - 2}}},\quad \mu = 3.86 \times {{10}^{{10}}}\;{\text{Kг}} \cdot {{{\text{м}}}^{{ - 1}}} \cdot {{{\text{с}}}^{{ - 2}}},\quad {{T}_{o}} = 0.293 \times {{10}^{3}}\;{\text{K}} \\ {{C}_{e}} = 0.3891 \times {{10}^{3}}\;{\text{Дж}} \cdot {\text{к}}{{{\text{г}}}^{{ - 1}}} \cdot {{{\text{K}}}^{{ - 1}}},\quad {{\alpha }_{t}} = 1.78 \times {{10}^{{ - 5}}}\;{{{\text{K}}}^{{ - 1}}},\quad {{\alpha }_{c}} = 1.98 \times {{10}^{{ - 4}}}\;{{{\text{м}}}^{3}} \cdot {\text{K}}{{{\text{г}}}^{{ - 1}}} \\ a = 1.02 \times {{10}^{4}}\;{{{\text{м}}}^{2}} \cdot {{{\text{с}}}^{{ - 2}}} \cdot {{{\text{K}}}^{{ - 1}}},\quad b = 9 \times {{10}^{5}}\;{\text{K}}{{{\text{г}}}^{{ - 1}}} \cdot {{{\text{м}}}^{5}} \cdot {{{\text{с}}}^{{ - 2}}},\quad D = 0.85 \times {{10}^{{ - 8}}}\;{\text{Kг}} \cdot {{{\text{м}}}^{{ - 3}}} \cdot {\text{с}} \\ \end{gathered} $
$\begin{gathered} \rho = 8.954 \times {{10}^{3}}\;{\text{Kг}} \cdot {{{\text{м}}}^{{ - 3}}},\quad K = 0.386 \times {{10}^{3}}\;{\text{Вт}} \cdot {{{\text{м}}}^{{ - 1}}}{{{\text{K}}}^{{ - 1}}},\quad \alpha = 0.05\;{\text{Кг}} \cdot {\text{м}} \cdot {{{\text{с}}}^{{ - 2}}} \\ t = 0.01\;{\text{с}},\quad {{t}_{o}} = 0.2\;{\text{с}},\quad {{\tau }_{t}} = 0.6\;{\text{с}},\quad {{\tau }_{q}} = 0.7\;{\text{с}},\quad {{\tau }_{p}} = 0.8\,{\text{s}},\quad {{\tau }_{u}} = 0.9\;{\text{с}} \\ \xi = 0.395 \times {{10}^{{ - 9}}}\;{\text{м}},\quad \zeta = 0.2 \times {{10}^{{ - 9}}}\;{\text{м}},\quad \varsigma = 0.15 \times {{10}^{{ - 9}}}\;{\text{м}},\quad {{F}_{0}} = 1,\quad {{F}_{{01}}} = 1 \\ \end{gathered} $

Для вычислений использовался Matlab (R2016a). Численное моделирование проводилось в следующих случаях:

(i) Диффузия ТМН с нелокальным и двухфазным запаздыванием (MNP).

(ii) Диффузия ТМН с двухфазным запаздыванием (NP).

(iii) Диффузия ТМН с нелокальным запаздыванием и без учета диффузионного запаздывания (MNWDP).

(iv) Диффузия ТМН с нелокальным запаздыванием и без учета теплового запаздывания (MNWTP).

(v) Диффузия ТМН с нелокальным запаздыванием (MH).

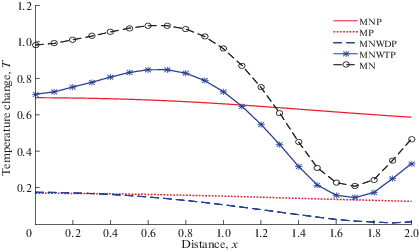
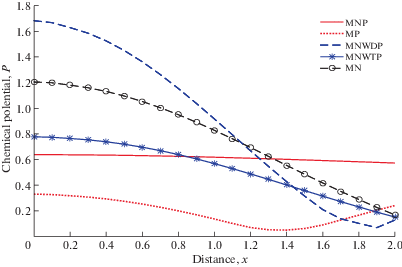
На рис. 1–5 показано влияние нормальной нагрузки линейного типа для всех случаев. На рис. 6–10 показано влияние теплового источника линейного типа для всех случаев.

Рис. 1.

Зависимость нормального напряжения ${{t}_{{33}}}$ от расстояния x

На всех рисунках линия (──) соответствует диффузии ТМН с нелокальным и двухфазным запаздыванием (MNP), линия (- – -) представляет диффузию ТМН с двухфазным запаздыванием (NP), линия (─ ─) соответствует диффузии ТМН с нелокальным запаздыванием и без запаздывания диффузионной фазы (MNWDP), линия (─ * ─) соответствует диффузии ТМН с нелокальным запаздыванием и без запаздывания термической фазы (MNWTP), линия (─ 0 ─) соответствует диффузии ТМН с нелокальным запаздыванием (MH).

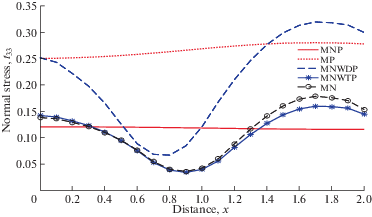
8.1. Нормальная нагрузка. На рис. 1 показана зависимость ${{t}_{{33}}}$ от x. Вариация ${{t}_{{33}}}$ остается для MNP стационарной. Значения ${{t}_{{33}}}$ увеличиваются для ограниченного интервала x и уменьшаются за пределами этого интервала для NP. ${{t}_{{33}}}$ показывает аналогичное поведение для MNWDP, MNWTP и MH с разницей в значениях магнитуды.

На рис. 2 показана зависимость ${{t}_{{31}}}$ от x. Величина ${{t}_{{31}}}$ увеличивается для ограниченной области и уменьшается вдали от источника для Ф. ${{t}_{{31}}}$ показывает тенденцию к снижению для ограниченного региона и после этого показывает колебания для MNP, MNWDP, MNWTP и MH.

Рис. 2.

Зависимость касательного напряжения ${{t}_{{31}}}$ от расстояния x

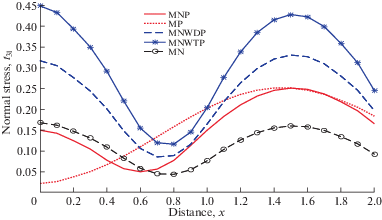
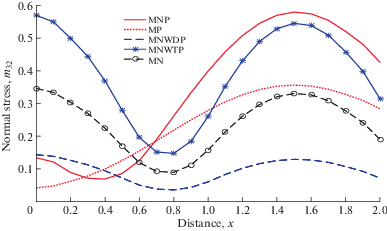
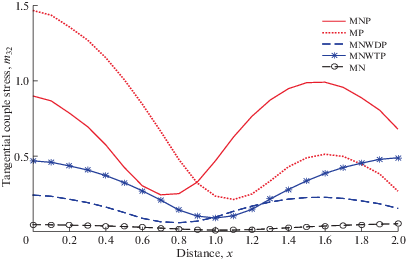
На рис. 3 показана зависимость ${{m}_{{32}}}$ от $x$. Поведение ${{m}_{{32}}}$ в случае MNWDP, MNWTP и MH аналогично для всех значений $x$, но величина ${{m}_{{32}}}$ в случае MNWDP меньше по сравнению с MNWTP и MH. Профиль ${{m}_{{32}}}$ для NP и MNP остается таким же для $x > 0.9$, хотя величина для MNP больше, чем для NP.

Рис. 3.

Зависимость касательного моментного напряжения ${{m}_{{32}}}$ от расстояния x

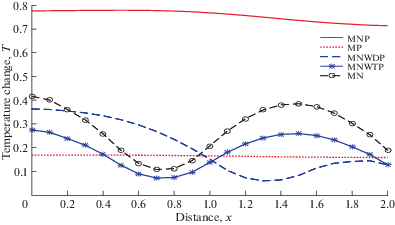
На рис. 4 показана зависимость $T$ от x. $T$ показывает тенденцию к уменьшению в MNP и NP с разницей в значениях величины. Величина $T$ постепенно уменьшается вблизи источника и увеличивается вдали от источника для MNWDP. $T$ уменьшается для ограниченной области, и после этого наблюдается колебательное поведение для MNWDP и MH.

Рис. 4.

Зависимость температуры $T$ от расстояния x

На рис. 5 показана зависимость $P$ от $P$. Вариация $P$ постепенно уменьшается для MNP и NP. $P$ обозначают тенденцию к уменьшению около источника, а вдали от источника наблюдается тенденция к увеличению для MNWDP. Поведение $P$ для MNWTP и NP аналогично, хотя значение $P$ для MNWTP больше, чем для NP.

Рис. 5.

Зависимость химического потенциала $P$ от расстояния x

Рис. 6.

Зависимость нормального напряжения ${{t}_{{33}}}$ от расстояния x

8.2. Тепловой источник. На рис. 6 показана зависимость ${{t}_{{33}}}$ от x. Поведение ${{t}_{{33}}}$ противоположно для MP и MN. Значения ${{t}_{{33}}}$ монотонно уменьшаются для MNWTP, тогда как для MNP наблюдается стационарное изменение. ${{t}_{{33}}}$ демонстрирует колебательное поведение для модели MNWDP.

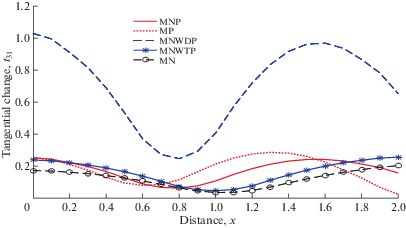
На рис. 7 показана зависимость ${{t}_{{31}}}$ от x. Тенденция ${{t}_{{31}}}$ аналогична для MNP и MNWDP с разницей в значениях уровня исследуемых величин. Вблизи источника величина ${{t}_{{31}}}$ уменьшается, после чего наблюдается колебательное поведение для модели ТМН. ${{t}_{{31}}}$ показывает аналогичное поведение для всех значений x для MNWTP и MNP.

Рис. 7.

Зависимость касательного напряжения ${{t}_{{31}}}$ от расстояния x

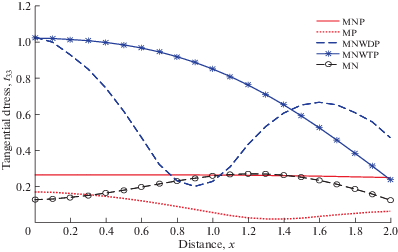
На рис. 8 показана зависимость ${{m}_{{32}}}$ от x. Величина ${{m}_{{32}}}$ уменьшается с начальными значениями ${{m}_{{32}}}$ и для промежуточного интервала x колебательное поведение ${{m}_{{32}}}$ наблюдается для всех случаев. Вдали от ограничивающей поверхности тренд ${{m}_{{32}}}$ уменьшается, за исключением MNWTP и MNP.

Рис. 8.

Зависимость касательного парного напряжения ${{m}_{{32}}}$ от расстояния x

На рис. 9 показана зависимость $T$ от x. $T$ демонстрирует тенденцию к снижению для MNP, MP и MNWDP. Величина $T$ уменьшается вблизи источника, и после этого поведение $T$ исследуется для MNWTP и MNP.

Рис. 9.

Зависимость изменения температуры $T$ от расстояния x

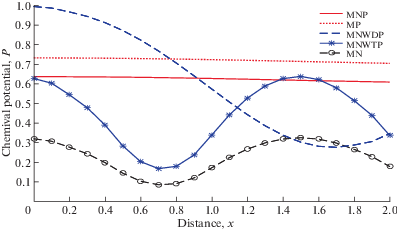
Рис. 10 показана зависимость $P$ от x. Поведение $P$ аналогично для MNWDP, MNWTP и MN, за исключением того, что он находится вдали от источника. Значения $P$ монотонно увеличиваются для MNP и MP.

Рис. 10.

Зависимость химического потенциал $P$ от расстояния x

9. Заключение. Рассмотрена проблема определения физических величин с помощью методов интегрального преобразования с учетом нормальной и тепловой нагрузки. Интегральное преобразование включает преобразование Лапласа по времени и преобразование Фурье по пространственной переменной. Нелокальные параметры и параметры фазового запаздывания существенно влияют на получаемые величины. Обнаружено, что эти величины очень чувствительны к нелокальным параметрам и параметрам фазового запаздывания.

Отмечено, что значения величин составляющих напряжений для нормальной нагрузки линейного типа больше по сравнению с термической нагрузкой линейного типа. В заданное время распределение заданных величин ограничено. Результаты этой модели заметно различаются для разных случаев. Для всех случаев показано, что определенные величины в точке приложения источника проявляют тенденцию к снижению и отклонению от нее при колебательном поведении. Также наблюдается сильное колебание всех результирующих величин из-за отличия нормальной нагрузки от термической. Полученные результаты важны для исследователей, работающих в области модифицированной термоупругости учитывающей моментные напряжения с диффузионными и нелокальными параметрами. Проблема имеет важное и практическое значение для конструкций или устройств в микромасштабе, подверженных переходным механическим и тепловым нагрузкам.

Список литературы

  1. Eringen A.C., Edelen D.G.B. On nonlocal elasticity // Int. J. Eng. Sci. 1972. V. 10. P. 233–248.

  2. Eringen A.C. On nonlocal fluid mechanics // Int. J. Eng. Sci. 1972. V. 10. № 6. P. 561–575.

  3. Eringen A.C. Nonlocal polar elastic continua // Int. J. Eng. Sci. 1972. V. 10. № 1. P. 1–16.

  4. Eringen A.C. Nonlocal continuum theory of liquid crystals // Mol. Cryst. Liq. Cryst. 1981. V. 75. P. 321–343.

  5. Eringen A.C. Nonlocal inviscid magneto-hydrodynamics and dispersion of Alfven waves // Bull. Tech. Univ. Istanb. 1986. V. 39. P. 393–408.

  6. Eringen A.C. Memory dependent nonlocal electrodynamics // Proceedings of IUTAM Symposium on mechanical modelling of new electromagnetic materials, Stockholm, Sweden, 1990. Ed. by Hsieh R.K.T. Amsterdam: Elsevier, 1990. P. 45–59.

  7. Eringen A.C. Memory dependent nonlocal electromagnetic elastic solids and superconductivity // J. Math. Phy. 1991. V. 32. № 3. P. 787–796.

  8. Edelen D.G.B., Laws N. On the thermodynamics of systems with nonlocality // Arch. Ration. Mech. Anal. 1971. V. 43. P. 24–35.

  9. McCay B.M., Narsimhan M.L.N. Theory of nonlocal electromagnetic fluids // Arch. Mech. 1981. V. 33. № 3. P. 365–384.

  10. Narsimhan M.L.N., McCay B.M. Dispersion of surface waves in nonlocal dielectric fluids // Arch. Mech. 1981. V. 33. № 3. P. 385–400.

  11. Eringen A.C. Nonlocal continuum field theories. New York: Springer, 2002. 367 p.

  12. Tzou D.Y. Thermal shock phenomena under high rate response in solids // Annual Rev. Heat Transf. 1992. V. 4. P. 111–185.

  13. Cao B.Y., Guo Z.Y. Equation of motion of a phonon gas and non-Fourier heat conduction // J. Appl. Phys. 2007. V. 5. P. 053503.

  14. Guo Z.Y., Hou Q.W. Thermal wave based on the thermomass model // J. Heat Transf. 2010. V. 5. P. 072403.

  15. Tzou D.Y., Guo Z.Y. Nonlocal behavior in thermal lagging // Int. J. Therm. Sci. 2010. V. 49. № 7. P. 1133–1137.

  16. Tzou D.Y. A unified field approach for heat conduction from macro to micro scales // J. Heat Transf. 1995. V. 117. № 1. P. 8–16.

  17. Tzou D.Y. The generalised lagging response in small scale and high rate heating // Int. J. Heat Mass Transf. 1995. V. 38 (17). P. 3231–3240.

  18. Sharma K. Boundary value problems in generalised thermodiffusive elastic medium // J. Solid Mech. 2010. V. 2. № 4. P. 348–362.

  19. Sharma S., Sharma K. Influence of heat sources and relaxation time on temperature distributions in tissues // Int. J. Appl. Mech. Eng. 2014. V. 19. № 2. P. 427–433.

  20. Sharma S., Sharma K., Bhargava R.R. Plane waves and fundamental solution in an electro-microstretch elastic solids // Afr. Math. 2014. V. 25. № 2. P. 483–497.

  21. Yu Y.J., Xue Z.N., Li C.L., Tian X.G. Buckling of nanobeams under nonuniform temperature based on nonlocal thermoelasticity // Compos. Struct. 2016. V. 146. P. 108–113.

  22. Abouelregal A.E. The effect of temperature dependent physical properties and fractional thermoelasticity on nonlocal nanobeams // Open Acc. J. Math Theor. Phy. 2018. V. 1. № 2. P. 46–55.

  23. Kumar R., Miglani A., Rani R. Transient analysis of nonlocal microstretch thermoelastic thick circular plate with phase lags // Med. J. Simul. 2018. V. 9. P. 25–42.

  24. Kumar R., Devi S., Sharma V. Resonance of nanoscale beam due to various sources in modified couple stress thermoelastic diffusion with phase lags // Mech. Mech. Eng. 2019. V. 23. P. 36–49.

  25. Borjalilou V., Asghari M., Taati E. Thermoelastic damping in nonlocal nanobeams considering dual phase lagging effect // J. Vib. Contr. 2020. V. 26. № 11–12. P. 1042–1053.

  26. Sherief H.H., Hamza F.A., Saleh H.A. The theory of generalised thermoelastic diffusion // Int. J. Eng. Sci. 2004. V. 42. P. 591–608.

  27. Yu Y.J., Tian X.-G., Xiong Q.-L. Nonlocal thermoelasticity based on nonlocal heat conduction and nonlocal elasticity // Eur. J. Mech. / A Solids. 2016. V. 60. P. 238–253.

  28. Kumar R., Devi S., Sharma V. Effect of hall current and rotation in modified couple stress generalised thermoelastic half space due to ramp type heating // J. Solid Mech. 2017. V. 9. № 3. P. 527–542.

  29. Sherief H.H., Saleh H. A half space problem in the theory of generalised thermoelastic diffusion // Int. J. Solids Struct. 2005. V. 42. P. 4484–4493.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал