Известия РАН. Механика твердого тела, 2021, № 4, стр. 109-120

ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНОЕ РАЗРУШЕНИЕ ЦИЛИНДРИЧЕСКОЙ ОБОЛОЧКИ ПРИ НЕСТАЦИОНАРНОМ СЛОЖНОМ НАПРЯЖЕННОМ СОСТОЯНИИ В ПРИСУТСТВИИ АГРЕССИВНОЙ ОКРУЖАЮЩЕЙ СРЕДЫ

Ю. Г. Басалов^a, *, А. М. Локощенко^a, **, Л. В. Фомин^a, b, ***

^a Научно-исследовательский институт механики Московского государственного университета им. М.В. Ломоносова
Москва, Россия

^b Самарский государственный технический университет
Самара, Россия

^* E-mail: basalov@yandex.ru
^** E-mail: loko@imec.msu.ru
^*** E-mail: fleonid1975@mail.ru

Поступила в редакцию 21.05.2020
После доработки 12.06.2020
Принята к публикации 25.06.2020

DOI: 10.31857/S0572329921040048

Полный текст (PDF)

Аннотация

Исследование основано на результатах испытаний на ползучесть до разрушения растягиваемых образцов титанового сплава ВТ6 при 600°C, в которые предварительно был внедрен водород различной концентрации. В данной работе проведено теоретическое обобщение полученных данных на нестационарное сложное напряженное состояние. Рассматривается моделирование ползучести цилиндрической оболочки вплоть до разрушения при двух программах зависимости осевого и поперечного напряжений от времени. Предполагается, что материал оболочки предварительно насыщался внедренным водородом различной концентрации. Описание ползучести проводится при учете физической и геометрической нелинейности. Для описания длительного разрушения используется кинетическая теория Ю.Н. Работнова с векторным параметром поврежденности. В первой части рассматривается кусочно-постоянная зависимость осевого и поперечного растягивающих напряжений от времени. Показано, что времена до разрушения оболочки при ступенчатом увеличении и уменьшении одинаковых значений напряжений совпадают. Во второй части рассматривается нагружение оболочки, при котором осевое и поперечное напряжения возрастают пропорционально времени. Получены кривые осевой ползучести оболочки вплоть до разрушения при различных скоростях увеличения напряжений.

Ключевые слова: ползучесть, длительное разрушение, цилиндрическая оболочка, сложное напряженное состояние, нестационарное нагружение, агрессивная среда, векторный параметр поврежденности, кривые осевой ползучести

1. Введение. В данной статье рассматривается ползучесть вплоть до разрушения цилиндрической оболочки при переменных осевом ${{\sigma }_{z}}$ и поперечном ${{\sigma }_{\theta }}$ растягивающих напряжениях в присутствии агрессивной среды. В качестве основы приняты результаты испытаний цилиндрических образцов из двухфазного (α + β) титанового сплава ВТ6 (Ti-6Al-4V) на ползучесть при растяжении вплоть до разрушения при температуре 600°C в присутствии предварительно внедрённого водорода [1–2].

2. Ползучесть оболочки вплоть до разрушения при кусочно-постоянной зависимости осевого и поперечного напряжений от времени. 2.1. Экспериментально-теоретическое исследование ползучести титанового сплава ВТ6 при растяжении вплоть до разрушения в присутствии агрессивной среды [1, 2]. Перед механическими испытаниями образцы титанового сплава насыщались водородом термодиффузионным способом в аппаратуре Сивертса. Данная аппаратура позволяет получать высокочистый газообразный водород и проводить гидрирование в высоком вакууме при температуре 600°C, что исключает окисление поверхности образцов.

Перед проведением механических испытаний в образцы вводился водород до концентрации $c$ = 0.1, 0.2 и 0.3%. При $c$ = 0, 0.1, 0.2 и 0.3% количество $\beta $-фазы составляло соответственно γ = 28%, 35%, 45% и $55\% $.

В испытаниях при постоянной растягивающей силе P использовались цилиндрические образцы диаметром ${{d}_{0}} = 5$ мм и рабочей длиной ${{l}_{0}} = 25$ мм. Поскольку титановые сплавы характеризуются при ползучести значительным увеличением длины l от времени t, то в качестве характеристики осевой деформации ползучести в [1, 2] принималась логарифмическая деформация:

${{p}_{z}}(t) = \ln \left( {l(t){\text{/}}{{l}_{0}}} \right)$

Из условия несжимаемости материала при однородном деформировании $lF = l{{F}_{0}}$ ($F(t)$ – площадь поперечного сечения образцов, ${{F}_{0}} = F\left( 0 \right)$) и соотношения для растягивающей силы $P = {{\sigma }_{0}}{{F}_{0}} = \sigma F$ ($\sigma (t)$ – осевое напряжение, ${{\sigma }_{0}} = \sigma (0)$) получаем, что зависимость осевого напряжения $\sigma $ от времени имеет вид:

$\sigma (t) = {{\sigma }_{0}}\exp ({{p}_{z}}(t))$

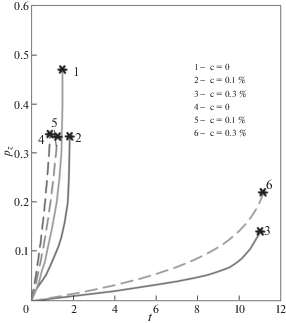
Испытания [1, 2] показали, что все кривые ползучести характеризуются установившейся стадией с последующим разупрочнением вплоть до разрушения. Испытания проводились в широком диапазоне начальных напряжений ${{\sigma }_{0}}$ от 47 до 217 МПа. В качестве примера на рис. 1–2 сплошными линиями обозначены экспериментальные кривые осевой ползучести ${{p}_{z}}(t)$ при различных концентрациях c и осевых напряжениях ${{\sigma }_{0}} = 167$ и 217 МПа соответственно. Поскольку на поверхности титановых образцов, испытываемых на воздухе, всегда присутствует слой, препятствующий выходу водорода из сплава, то концентрация водорода $c$ не меняется во времени $t$ (измеряется в часах). Испытания показали, что увеличение доли предварительно внедренного водорода $c$ приводит к систематическому уменьшению в несколько раз скорости установившейся ползучести ${{\dot {p}}_{z}}$, увеличению времени до разрушения $t{\kern 1pt} *$ и, как правило, к уменьшению предельной деформации $p_{z}^{*} = {{p}_{z}}(t{\kern 1pt} *)$.

Рис. 1

Рис. 2

Для теоретического описания реологического процесса деформирования титанового сплава с предварительно внедренным водородом в [1, 2] применялся вариант кинетической теории Ю.Н. Работнова с использованием скалярного параметра поврежденности $\omega $. При этом скорость деформаций ползучести ${{\dot {p}}_{z}}$ и скорость накопления поврежденности $\dot {\omega }$ являются функциями не только $\sigma $ и $\omega $, но и концентрации c водорода в сплаве. Так как скорость деформации ползучести при разрушении ($t \to t{\kern 1pt} *$) не бесконечна, то для зависимостей ${{\dot {p}}_{z}}$ и $\dot {\omega }$ от поврежденности $\omega $ вместо пионерской модели Ю.Н. Работнова [3] со степенной функцией ${{\left( {1 - \omega } \right)}^{{ - 1}}}$ в [1, 2] была использована экспоненциальная функция $\exp (\omega )$.

(2.1)

$\begin{array}{*{20}{c}} {\frac{{d{{p}_{z}}}}{{dt}} = {{A}^{{ - 1}}}{{{\left[ {\sigma (t) \cdot \exp (\omega )} \right]}}^{m}} \cdot {{f}_{1}}(c),\quad {{p}_{z}}(t = 0) = 0} \\ {\frac{{d\omega }}{{dt}} = {{B}^{{ - 1}}}{{{\left[ {\sigma (t) \cdot \exp (\omega )} \right]}}^{n}} \cdot {{f}_{2}}(c),\quad \omega (t = 0) = 0} \end{array}$

Функция ${{f}_{1}}(c)$ характеризует уменьшение скорости деформации $\frac{{d{{p}_{z}}}}{{dt}}$ при увеличении концентрации c. Функция ${{f}_{2}}(c)$ определяет зависимость скорости накопления поврежденности $\frac{{d\omega }}{{dt}}$ от величины c.

Значения ${{f}_{1}}(c)$ и ${{f}_{2}}(c)$ приведены в табл. 1.

Таблица 1.

Зависимости характеристик ползучести и длительной прочности титанового сплава ВТ6 от уровня предварительно внедренного водорода [1, 2]

$c$ (%)	$\gamma $ (%)	f₁	f₂
0	0.28	1	1
0.1	0.35	0.71	0.73
0.2	0.45	0.23	0.54
0.3	0.55	0.03	0.11

Анализ приведенных в [1, 2] испытаний привел к следующим значениям материальных констант:

$m = 3.07,\quad n = 3.25,\quad A = 3 \times {{10}^{7}}\;{{({\text{МПа}})}^{m}}{\text{/}}час,\quad B = 7 \times {{10}^{7}}\;{{({\text{МПа}})}^{n}}{\text{/}}час.$

На рис. 1–2 штриховыми линиями обозначены теоретические кривые ползучести при различных уровнях c при ${{\sigma }_{0}} = 167$ и 217 МПа соответственно.

2.2. Накопление поврежденности в цилиндрической оболочке при кусочно-постоянном сложном напряженном состоянии в присутствии агрессивной окружающей среды. В данном параграфе исследуется накопление поврежденности в цилиндрической оболочке в процессе ползучести при одновременном действии осевого ${{\sigma }_{z}}$ и поперечного ${{\sigma }_{\theta }}$ напряжений, величины которых являются кусочно-постоянными функциями времени t. Рассмотрим этот процесс применительно к ползучести оболочек из титанового сплава ВТ6 при температуре 600°C в присутствии предварительно внедренного водорода.

Для простоты вычислений примем, что при любом значении времени t значения ${{\sigma }_{z}}$ и ${{\sigma }_{\theta }}$ равны:

(2.2)

$\begin{gathered} {{\sigma }_{z}}(t) = {{\sigma }_{\theta }}(t) = {{\sigma }_{1}} > 0,\quad {{\sigma }_{r}} = 0\quad {\text{при}}\quad 0 \leqslant t \leqslant {{t}_{1}} \\ {\text{и}}\quad {{\sigma }_{z}}(t) = {{\sigma }_{\theta }}(t) = {{\sigma }_{2}} > 0,\quad {{\sigma }_{r}} = 0\quad {\text{при}}\quad {{t}_{1}} \leqslant t \leqslant t{\text{*}} \\ \end{gathered} $

(t* – время до разрушения оболочки при сложном напряженном состоянии).

В данном случае интенсивность напряжений ${{\sigma }_{u}}$ и компоненты девиатора напряжений s_z, ${{s}_{\theta }}$, s_r принимают следующие значения:

(2.3)

$\begin{gathered} {{\sigma }_{u}} = \frac{1}{{\sqrt 2 }}\sqrt {{{{\left( {{{\sigma }_{z}} - {{\sigma }_{\theta }}} \right)}}^{2}} + {{{\left( {{{\sigma }_{\theta }} - {{\sigma }_{r}}} \right)}}^{2}} + {{{\left( {{{\sigma }_{z}} - {{\sigma }_{r}}} \right)}}^{2}}} = \frac{1}{{\sqrt 2 }}\sqrt {2{{\sigma }^{2}}} = \sigma \\ {{s}_{z}} = {{s}_{\theta }} = \frac{1}{3}\sigma ,\quad {{s}_{r}} = - \frac{2}{3}\sigma \\ \end{gathered} $

Рассмотрим обобщение уравнений (2.1) на случай сложного напряженного состояния:

(2.4)

$\begin{gathered} \frac{{d{{p}_{z}}}}{{dt}} = \frac{3}{2} \cdot \frac{{{{F}_{1}}\left( {{{\sigma }_{u}}} \right)}}{{{{\sigma }_{u}}}}{{s}_{z}}{{\left[ {\exp \left( \omega \right)} \right]}^{m}}{{f}_{1}}(c) \hfill \\ \frac{{d{{p}_{\theta }}}}{{dt}} = \frac{3}{2} \cdot \frac{{{{F}_{1}}\left( {{{\sigma }_{u}}} \right)}}{{{{\sigma }_{u}}}}{{s}_{\theta }}{{\left[ {\exp \left( \omega \right)} \right]}^{m}}{{f}_{1}}(c) \hfill \\ \frac{{d{{p}_{r}}}}{{dt}} = \frac{3}{2} \cdot \frac{{{{F}_{1}}\left( {{{\sigma }_{u}}} \right)}}{{{{\sigma }_{u}}}}{{s}_{r}}{{\left[ {\exp \left( \omega \right)} \right]}^{m}}{{f}_{1}}(c),\quad {{F}_{1}} = {{A}^{{ - 1}}}\sigma _{u}^{m} \hfill \\ \end{gathered} $

(2.5)

$\begin{array}{*{20}{l}} {\frac{{d{{\omega }_{z}}}}{{dt}} = \frac{3}{2} \cdot \frac{{{{F}_{2}}\left( {{{\sigma }_{u}}} \right)}}{{{{\sigma }_{u}}}}{{s}_{z}}{{{\left[ {\exp \left( \omega \right)} \right]}}^{n}}{{f}_{2}}(c)} \\ {\frac{{d{{\omega }_{\theta }}}}{{dt}} = \frac{3}{2} \cdot \frac{{{{F}_{2}}\left( {{{\sigma }_{u}}} \right)}}{{{{\sigma }_{u}}}}{{s}_{\theta }}{{{\left[ {\exp \left( \omega \right)} \right]}}^{n}}{{f}_{2}}(c)} \\ {\frac{{d{{\omega }_{r}}}}{{dt}} = 0,\quad {{F}_{2}} = {{B}^{{ - 1}}}\sigma _{u}^{n}} \end{array}$

В (2.5) ${{\omega }_{z}}$, ${{\omega }_{\theta }}$, ${{\omega }_{r}}$ представляют собой компоненты вектора поврежденности.

Система уравнений (2.4) представляет собой гипотезу пропорциональности девиаторов напряжений и скоростей деформаций ползучести. Система уравнений (2.5) построена по аналогичному принципу.

В качестве ${{F}_{1}}\left( {{{\sigma }_{u}}} \right)$ и ${{F}_{2}}\left( {{{\sigma }_{u}}} \right)$ рассматриваются степенные функции интенсивности напряжений ${{\sigma }_{u}}$. Производная $\frac{{d{{\omega }_{r}}}}{{dt}}$ равна нулю, так как радиальная компонента девиатора напряжений отрицательна (${{s}_{r}} < 0$), при этом предполагается [3], что поврежденность материала при сжатии не накапливается.

В рассматриваемом случае проекции вектора поврежденности на главные оси и величина вектора $\omega $ принимают следующие значения:

${{\omega }_{z}} = {{\omega }_{\theta }},\quad {{\omega }_{r}} = 0,\quad \omega = \sqrt {\omega _{z}^{2} + \omega _{\theta }^{2} + \omega _{r}^{2}} = {{\omega }_{z}}\sqrt 2 $

Проведем интегрирование первого уравнения (2.5) при ${{\sigma }_{u}} = {{\sigma }_{1}}$ и начальном условии ${{\omega }_{z}}(t = 0) = 0$.

$\frac{{d{{\omega }_{z}}(t)}}{{dt}} = \frac{1}{2}{{B}^{{ - 1}}}{{[{{\sigma }_{1}}\exp ({{\omega }_{z}}\sqrt 2 )]}^{n}}{{f}_{2}}(c)$

$\int\limits_0^{{{\omega }_{z}}} {{{{[\exp ({{\omega }_{z}}\sqrt 2 )]}}^{{ - n}}}d{{\omega }_{z}} = } \frac{1}{2}{{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)\,t$

$\begin{gathered} \frac{1}{{\sqrt 2 }}\int\limits_0^{{{\omega }_{z}}} {{{{[\exp ({{\omega }_{z}}\sqrt 2 )]}}^{{ - n}}}d({{\omega }_{z}}\sqrt 2 ) = } \frac{1}{{\sqrt 2 }}\int\limits_0^{{{\omega }_{z}}} {{{{[\exp ({{\omega }_{z}}\sqrt 2 )]}}^{{ - n - 1}}}d[exp({{\omega }_{z}}\sqrt 2 )] = } \\ \, = \left. {\frac{1}{{\sqrt 2 }}\frac{{{{{[\exp ({{\omega }_{z}}\sqrt 2 )]}}^{{ - n}}}}}{{( - n)}}} \right|_{{{{\omega }_{z}} = 0}}^{{{{\omega }_{z}}}} = \frac{1}{{n\sqrt 2 }} \cdot \{ 1 - {{[\exp ({{\omega }_{z}}\sqrt 2 )]}^{{ - n}}}\} = \frac{1}{2}{{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)t \\ \end{gathered} $

$1 - {{[\exp ({{\omega }_{z}}\sqrt 2 )]}^{{ - n}}} = \frac{{n\sqrt 2 }}{2}{{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)t$

Определим зависимость ω_z от t.

$\exp ({{\omega }_{z}}\sqrt 2 ) = {{\left[ {1 - \frac{{n\sqrt 2 }}{2}{{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)t} \right]}^{{ - \left( {\frac{1}{n}} \right)}}}\quad {{\omega }_{z}}\sqrt 2 = - \frac{1}{n}\ln \left[ {1 - \frac{{n\sqrt 2 }}{2}{{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)t} \right]$

(2.6)

${{\omega }_{z}} = - \frac{1}{{n\sqrt 2 }}\ln \left[ {1 - \frac{{n\sqrt 2 }}{2}{{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)t} \right]$

Определим значение $t_{1}^{*}$, при котором наступит разрушение в случае постоянного значения ${{\sigma }_{1}}$.

Из (2.6) при учете $\omega {\kern 1pt} * = 1$ $\left( {\omega _{z}^{*} = \frac{{\sqrt 2 }}{2}} \right)$ получаем:

(2.7)

$(1 - {{e}^{{ - n}}}) = \frac{{n\sqrt 2 }}{2}{{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)t_{1}^{*},\quad t_{1}^{*} = \frac{{2(1 - {{e}^{{ - n}}})}}{{n\sqrt 2 {{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)}}$

Пусть первая стадия ползучести оболочки ${{\sigma }_{z}} = {{\sigma }_{\theta }} = {{\sigma }_{u}} = {{\sigma }_{1}}$ заканчивается при t₁ = $\frac{1}{2}t_{1}^{*}$.

Значение поврежденности ${{\omega }_{z}}$ в момент времени ${{t}_{1}} = \frac{1}{2}t_{1}^{*}$ согласно (2.7) равно:

${{\omega }_{{z1}}} = {{\omega }_{z}}({{t}_{1}}) = - \frac{1}{{n\sqrt 2 }}\ln \left\{ {1 - \frac{{n\sqrt 2 }}{2}B_{1}^{{ - 1}}\sigma _{1}^{n}{{f}_{2}}(c) \cdot \frac{{(1 - {{e}^{{ - n}}})}}{{[n\sqrt 2 {{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)]}}} \right\}$

${{\omega }_{{z1}}} = - \frac{1}{{n\sqrt 2 }}\ln \left\{ {1 - \frac{{(1 - {{e}^{{ - n}}})}}{2}} \right\}$

При $t = {{t}_{1}}$ напряжения ${{\sigma }_{z}} = {{\sigma }_{\theta }} = {{\sigma }_{1}}$ мгновенно изменяют свои значения и становятся равными ${{\sigma }_{2}}$.

С помощью интегрирования первого уравнения (2.5) определим зависимость $\omega _{z}^{{}}\left( t \right)$ на II стадии нагружения (${{t}_{1}} \leqslant t \leqslant t{\kern 1pt} *$):

$\frac{{d{{\omega }_{z}}}}{{dt}} = \frac{1}{2}{{B}^{{ - 1}}}{{[{{\sigma }_{2}}\exp ({{\omega }_{z}}\sqrt 2 )]}^{n}}{{f}_{2}}(c)$

$\int\limits_{{{\omega }_{{z1}}}}^{{{\omega }_{z}}} {{{{[\exp ({{\omega }_{z}}\sqrt 2 )]}}^{{ - n}}}d{{\omega }_{z}}} = \int\limits_{{{t}_{1}}}^t {\frac{1}{2}{{B}^{{ - 1}}}\sigma _{2}^{n}{{f}_{2}}(c)} dt = \frac{1}{2}{{B}^{{ - 1}}}\sigma _{2}^{n}{{f}_{2}}(c)\left( {t - {{t}_{1}}} \right)$

$\left. {\frac{1}{{\sqrt 2 }} \cdot \frac{{{{{[\exp ({{\omega }_{z}}\sqrt 2 )]}}^{{ - n}}}}}{{\left( { - n} \right)}}} \right|_{{{{\omega }_{{z1}}}}}^{{{{\omega }_{z}}}} = \frac{{{{{[\exp ({{\omega }_{{z1}}}\sqrt 2 )]}}^{{ - n}}} - {{{[\exp ({{\omega }_{z}}\sqrt 2 )]}}^{{ - n}}}}}{{n\sqrt 2 }}$

$\begin{gathered} {{[\exp ({{\omega }_{z}}\sqrt 2 )]}^{{ - n}}} = {{\left[ {\exp \left( { - \frac{1}{n}\ln \left( {1 - \frac{{1 - {{e}^{{ - n}}}}}{2}} \right)} \right)} \right]}^{{ - n}}} - \\ \, - \frac{{n\sqrt 2 }}{2}{{B}^{{ - 1}}}\sigma _{2}^{n}{{f}_{2}}(c)\left( {t - {{t}_{1}}} \right) = C - D\left( {t - {{t}_{1}}} \right) \\ \end{gathered} $

$С = {{\left[ {\exp \left( { - \frac{1}{n}\ln \left( {1 - \frac{{1 - {{e}^{{ - n}}}}}{2}} \right)} \right)} \right]}^{{ - n}}} = \left( {1 - \frac{{1 - {{e}^{{ - n}}}}}{2}} \right),\quad D = \frac{{n\sqrt 2 }}{2}{{B}^{{ - 1}}}\sigma _{2}^{n}{{f}_{2}}(c)$

(2.8)

${{\omega }_{z}} = - \frac{{\ln \left[ {C - D\left( {t - {{t}_{1}}} \right)} \right]}}{{n\sqrt 2 }}$

При разрушении ${{\omega }_{z}}(t{\kern 1pt} *) = \frac{1}{{\sqrt 2 }}$, при этом

$\ln \left[ {C - D\left( {t{\kern 1pt} * - {{t}_{1}}} \right)} \right] = - n;\quad C - D\left( {t{\kern 1pt} * - {{t}_{1}}} \right) = \exp \left( { - n} \right);\quad D\left( {t{\kern 1pt} * - {{t}_{1}}} \right) = C - \exp \left( { - n} \right)$

Таким образом, время до разрушения оболочки после обеих стадий нагружения равно

(2.9)

$\begin{gathered} t{\kern 1pt} * = {{t}_{1}} + \frac{{C - \exp \left( { - n} \right)}}{D} = {{t}_{1}} + \frac{{(1 - {{e}^{{ - n}}})}}{{2D}} \\ t{\kern 1pt} * = \frac{{(1 - {{e}^{{ - n}}})}}{{n\sqrt 2 {{B}^{{ - 1}}}\sigma _{1}^{n}{{f}_{2}}(c)}} + \frac{{(1 - {{e}^{{ - n}}})}}{{n\sqrt 2 {{B}^{{ - 1}}}\sigma _{2}^{n}{{f}_{2}}(c)}} \\ \end{gathered} $

Соотношение (2.9) действительно как при ${{\sigma }_{1}} > {{\sigma }_{2}} > 0$, так и при $0 < {{\sigma }_{1}} < {{\sigma }_{2}}$.

Отсюда следует, что времена до разрушения оболочки при ступенчатом увеличении (${{\sigma }_{1}} < {{\sigma }_{2}}$) и ступенчатом уменьшении (${{\sigma }_{1}} > {{\sigma }_{2}}$) напряжений совпадают.

2.3. Ползучесть цилиндрической оболочки при кусочно-постоянных напряжениях. Для определения осевой ползучести рассматриваемой оболочки воспользуемся первым дифференциальным уравнением (2.4) при учете (2.3)

$\frac{{d{{p}_{z}}}}{{dt}} = \frac{1}{2}{{A}^{{ - 1}}}{{\left[ {{{\sigma }_{u}}\exp (\omega )} \right]}^{m}}{{f}_{1}}(c),\quad {{p}_{z}}(t = 0) = 0$

На первой стадии при $0 \leqslant t \leqslant {{t}_{1}}$ согласно (2.6) и (2.7) получаем:

$\begin{gathered} {{p}_{z}} = \frac{1}{2}{{A}^{{ - 1}}}\sigma _{1}^{m}{{f}_{1}}(c)\int\limits_0^t {{{{\left[ {1 - \frac{{n\sqrt 2 }}{2}B_{{}}^{{ - 1}}\sigma _{1}^{m}{{f}_{2}}(c)t} \right]}}^{{( - m/n)}}}} dt = \\ \, = \frac{1}{2}A\sigma _{1}^{m}{{f}_{1}}(c)\frac{{\left\{ {1 - {{{\left[ {1 - \frac{{n\sqrt 2 }}{2}B_{{}}^{{ - 1}}\sigma _{1}^{m}{{f}_{2}}(c)t} \right]}}^{{\left( {1 - \frac{m}{n}} \right)}}}} \right\}}}{{\left( {1 - \frac{m}{n}} \right)\frac{{n\sqrt 2 }}{2}B_{{}}^{{ - 1}}\sigma _{1}^{m}{{f}_{2}}(c)}} \\ \end{gathered} $

На второй стадии при ${{t}_{1}} \leqslant t \leqslant t{\kern 1pt} *$ согласно (2.8) получаем:

${{p}_{z}} = - \frac{1}{2}{{A}^{{ - 1}}}\sigma _{2}^{m}{{f}_{1}}(c) \cdot \int\limits_{{{t}_{1}}}^t {{{{\left\{ {\exp \left[ { - \frac{{\ln (C - D \cdot (t - {{t}_{1}}))}}{n}} \right]} \right\}}}^{m}}} dt$

2.4. Получение кривых ползучести, соответствующих кусочно-постоянным зависимостям ${{\sigma }_{z}}(t) = {{\sigma }_{\theta }}(t)$ при мгновенном увеличении и уменьшении напряжений. В этом параграфе в качестве примера рассмотрим два варианта нагружения оболочек, при которых напряжения σ₁ и σ₂ удовлетворяют неравенствам $0 < {{\sigma }_{1}} < {{\sigma }_{2}}$ или ${{\sigma }_{1}} > {{\sigma }_{2}} > 0$. В первом варианте нагружения рассмотрим значения ${{\sigma }_{1}} = 167$ МПа и ${{\sigma }_{2}} = 217$ МПа. При этом характерные значения приведены в табл. 2.

Таблица 2.

Характеристики длительной прочности при ${{\sigma }_{1}} = 167$ МПа и ${{\sigma }_{2}} = 217$ МПа

$c$ (%)	$t_{1}^{*}$, час	${{t}_{1}}$, час	$t_{2}^{*}$, час	${{\omega }_{{z1}}}$	t*, час
0	1.749	0.874	0.747	0.143	1.248
0.1	2.396	1.198	1.023	0.143	1.709
0.2	3.238	1.619	1.383	0.143	2.31
0.3	15.898	7.949	6.787	0.143	11.342

Во втором варианте нагружения рассмотрим значения ${{\sigma }_{1}} = 217$ МПа и ${{\sigma }_{2}} = 167$ МПа. В этом случае характеристики длительной прочности приведены в табл. 3.

Таблица 3.

Характеристики длительной прочности при ${{\sigma }_{1}} = 217$ МПа и ${{\sigma }_{2}} = 167$ МПа

$c$ (%)	$t_{1}^{*}$, час	${{t}_{1}}$, час	$t_{2}^{*}$, час	${{\omega }_{{z1}}}$	t*, час
0	0.747	0.373	1.749	0.143	1.248
0.1	1.023	0.511	2.396	0.143	1.709
0.2	1.383	0.691	3.238	0.143	2.31
0.3	6.787	3.393	15.898	0.143	11.342

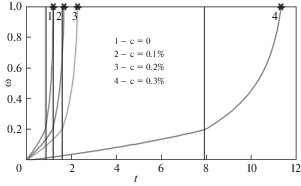
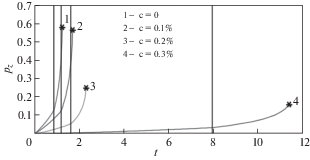
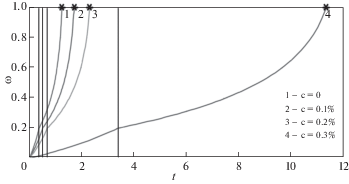
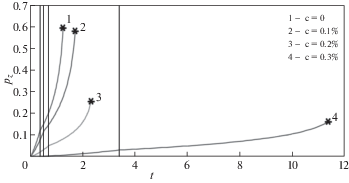
На рис. 3–4 приведены зависимости $\omega (t)$ и ${{p}_{z}}(t)$ при мгновенном увеличении напряжений (${{\sigma }_{1}} = 167$ МПа, ${{\sigma }_{2}} = 217$ МПа) при использовании материальных констант (2.2). На рис. 5–6 приведены аналогичные зависимости $\omega (t)$ и ${{p}_{z}}(t)$ при мгновенном уменьшении напряжений (${{\sigma }_{1}} = 217$ МПа и ${{\sigma }_{2}} = 167$ МПа).

Рис. 3

Рис. 4

Рис. 5

Рис. 6

3. Ползучесть цилиндрической оболочки при линейной зависимости осевого и поперечного напряжений от времени вплоть до разрушения. Рассмотрим ползучесть цилиндрической оболочки вплоть до разрушения, в которой осевое и окружное напряжения возрастают пропорционально времени:

${{\sigma }_{z}} = {{U}_{0}}k\,t,\quad {{\sigma }_{\theta }} = a{{\sigma }_{z}} = a{{U}_{0}}kt,\quad {{\sigma }_{r}} = 0$

U₀ – скорость увеличения напряжений.

Интенсивность напряжений ${{\sigma }_{u}}$ равна

${{\sigma }_{u}} = \frac{1}{{\sqrt 2 }}{{\sigma }_{z}}\sqrt {{{{\left( {a - 1} \right)}}^{2}} + {{a}^{2}} + 1} = g{{\sigma }_{z}},\quad g = \sqrt {{{a}^{2}} - a + 1} $

Компоненты девиатора напряжений равны

${{s}_{z}} = \frac{{\left( {2 - a} \right)}}{3}{{\sigma }_{z}},\quad {{s}_{\theta }} = \frac{{\left( {2a - 1} \right)}}{3}{{\sigma }_{z}},\quad {{s}_{r}} = - \frac{{\left( {a + 1} \right)}}{3}{{\sigma }_{z}}$

Для рассмотрения длительного разрушения материала оболочки воспользуемся кинетической теорией ползучести и длительной прочности с векторным параметром поврежденности.

В случае пропорционального нагружения оболочки уравнения (2.4)–(2.5) принимают следующую форму:

(3.1)

$\begin{array}{*{20}{c}} \begin{gathered} \frac{{d{{p}_{z}}}}{{dt}} = \frac{3}{2}{{A}^{{ - 1}}}\sigma _{u}^{{m - 1}}{{s}_{z}}{{\left( {\exp \omega } \right)}^{m}}{{f}_{1}}(c) = \hfill \\ \, = \frac{{(2 - a)}}{2}{{A}^{{ - 1}}}{{g}^{{m - 1}}}\sigma _{z}^{m}{{\left( {\exp \omega } \right)}^{m}}{{f}_{1}}(c),\quad {{p}_{z}}(t = 0) = 0 \hfill \\ \end{gathered} \\ \begin{gathered} \frac{{d{{p}_{\theta }}}}{{dt}} = \frac{3}{2}{{A}^{{ - 1}}}\sigma _{u}^{{m - 1}}{{s}_{\theta }}{{\left( {\exp \omega } \right)}^{m}}{{f}_{1}}(c) = \hfill \\ \, = \frac{{(2a - 1)}}{2}{{A}^{{ - 1}}}{{g}^{{m - 1}}}\sigma _{z}^{m}{{\left( {\exp \omega } \right)}^{m}}{{f}_{1}}(c),\quad {{p}_{\theta }}(t = 0) = 0 \hfill \\ \end{gathered} \\ \begin{gathered} \frac{{d{{p}_{r}}}}{{dt}} = \frac{3}{2}{{A}^{{ - 1}}}\sigma _{u}^{{m - 1}}{{s}_{r}}{{\left( {\exp \omega } \right)}^{m}}{{f}_{1}}(c) = \hfill \\ \, = - \frac{{(a + 1)}}{2}{{A}^{{ - 1}}}{{g}^{{m - 1}}}\sigma _{z}^{m}{{\left( {\exp \omega } \right)}^{m}}{{f}_{1}}(c),\quad {{p}_{r}}(t = 0) = 0 \hfill \\ \end{gathered} \end{array}$

(3.2)

$\begin{array}{*{20}{l}} \begin{gathered} \frac{{d{{\omega }_{z}}}}{{dt}} = \frac{3}{2}{{B}^{{ - 1}}}\sigma _{u}^{{n - 1}}{{s}_{z}}{{\left( {\exp \omega } \right)}^{n}}{{f}_{2}}(c) = \frac{{(2 - a)}}{2}{{B}^{{ - 1}}}{{g}^{{n - 1}}}\sigma _{z}^{n}{{\left( {\exp \omega } \right)}^{n}}{{f}_{2}}(c) \hfill \\ при\quad a < 2,\quad {{\omega }_{z}}(t = 0) = 0 \hfill \\ \end{gathered} \\ {\frac{{d{{\omega }_{z}}}}{{dt}} = 0,\quad при\quad a \geqslant 2} \\ \begin{gathered} \frac{{d{{\omega }_{\theta }}}}{{dt}} = \frac{3}{2}{{B}^{{ - 1}}}\sigma _{u}^{{n - 1}}{{s}_{\theta }}{{\left( {\exp \omega } \right)}^{n}}{{f}_{2}}(c) = \frac{{(2a - 1)}}{2}{{B}^{{ - 1}}}{{g}^{{n - 1}}}\sigma _{z}^{n}{{\left( {\exp \,\omega } \right)}^{n}}\,{{f}_{2}}(c) \hfill \\ при\quad a \geqslant 0.5,\quad {{\omega }_{\theta }}(t = 0) = 0 \hfill \\ \end{gathered} \\ {\frac{{d{{\omega }_{\theta }}}}{{dt}} = 0,\quad при\quad a < 0.5} \\ {\frac{{d{{\omega }_{r}}}}{{dt}} = 0,\quad {{\omega }_{r}}(t = 0) = 0,\quad {{\omega }_{r}}(t) \equiv 0} \end{array}$

Сравнивая ω_z и ${{\omega }_{\theta }}$, согласно (3.2) при $0.5 < a < 2$ получаем:

$\frac{{{{\omega }_{z}}}}{{{{\omega }_{\theta }}}} = \frac{{(2 - a)}}{{(2a - 1)}},\quad {{\omega }_{\theta }} = \frac{{(2a - 1)}}{{(2 - a)}}{{\omega }_{z}}$

$\omega = \sqrt {\omega _{z}^{2} + \omega _{\theta }^{2} + \omega _{r}^{2}} = \sqrt {1 + {{{\left( {\frac{{2a - 1}}{{2 - a}}} \right)}}^{2}}} {{\omega }_{z}} = \frac{{\sqrt {4 - 4a + {{a}^{2}} + 4{{a}^{2}} - 4a + 1} }}{{\left( {2 - a} \right)}}{{\omega }_{z}} = b{{\omega }_{z}}$

$b = \frac{{\sqrt {5{{a}^{2}} - 8a + 5} }}{{\left( {2 - a} \right)}}$

(3.3)

$\frac{{d{{\omega }_{z}}}}{{dt}} = \frac{{\left( {2 - a} \right)}}{2}{{B}^{{ - 1}}}{{g}^{{n - 1}}}{{\left( {\exp b{{\omega }_{z}}} \right)}^{n}}{{f}_{2}}(c) \cdot {{\left( {{{U}_{0}}kt} \right)}^{n}},\quad {{\omega }_{z}}(t = 0) = 0$

Интегрируя уравнение (3.3), получаем:

$\left. {\frac{{{{{\left[ {\exp \left( {b{{\omega }_{z}}} \right)} \right]}}^{{ - n}}}}}{{ - n \cdot b}}} \right|_{0}^{{{{\omega }_{z}}}} = \frac{1}{{bn}}\{ 1 - {{\left[ {\exp \left( {b{{\omega }_{z}}} \right)} \right]}^{{ - n}}}\} = \frac{{\left( {2 - a} \right)}}{2}{{B}^{{ - 1}}}{{g}^{{n - 1}}} \cdot {{f}_{2}}(c) \cdot \frac{{{{{\left( {{{U}_{0}}k} \right)}}^{n}} \cdot {{t}^{{n + 1}}}}}{{\left( {n + 1} \right)}}$

$1 - {{\left[ {\exp \left( {b{{\omega }_{z}}} \right)} \right]}^{{ - n}}} = \frac{{b \cdot n\left( {2 - a} \right)}}{2}{{B}^{{ - 1}}}{{g}^{{n - 1}}}{{f}_{2}}(c) \cdot \frac{{{{{\left( {{{U}_{0}}k} \right)}}^{n}}{{t}^{{n + 1}}}}}{{\left( {n + 1} \right)}} = G{{t}^{{n + 1}}}$

$G = \frac{{b \cdot n\left( {2 - a} \right)}}{2}{{B}^{{ - 1}}}{{f}_{2}}(c) \cdot \frac{{{{{\left( {{{U}_{0}}k} \right)}}^{n}}}}{{\left( {n + 1} \right)}}$

(3.4)

$\begin{gathered} \exp \left( {b{{\omega }_{z}}} \right) = {{[1 - G{{t}^{{n + 1}}}]}^{{ - \left( {1/n} \right)}}},\quad b{{\omega }_{z}} = - \frac{1}{n}ln[1 - G{{t}^{{n + 1}}}] \\ {{\omega }_{z}}(t) = - \frac{1}{{bn}}ln[1 - G{{t}^{{n + 1}}}],\quad t = {{\left\{ {\frac{{1 - {{{\left[ {\exp \left( {b{{\omega }_{z}}} \right)} \right]}}^{{ - n}}}}}{G}} \right\}}^{{\left( {\frac{1}{{n + 1}}} \right)}}} \\ \end{gathered} $

При разрушении оболочки $\omega {\kern 1pt} * = \omega (t{\kern 1pt} *) = b\omega _{z}^{*} = 1$.

Следовательно, время t* до разрушения оболочки определяется следующим соотношением:

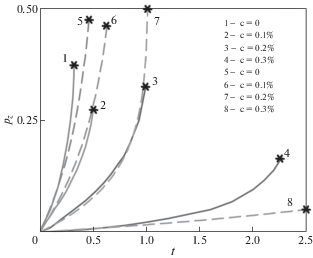
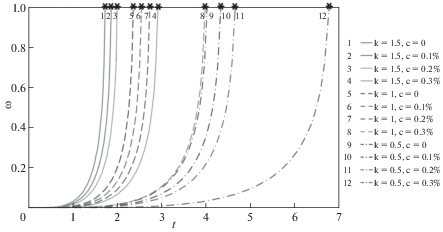
$t{\kern 1pt} * = {{\left[ {\frac{{1 - {{e}^{{ - n}}}}}{G}} \right]}^{{\left( {\frac{1}{{n + 1}}} \right)}}}$

Зависимости $\omega (t)$ при ${{U}_{0}} = 100$ МПа/час, a = 1, различных значениях k и уровнях концентрации $c$ приведены на рис. 7.

Рис. 7

Перейдем к вычислениям продольной деформации ползучести ${{p}_{z}}(t)$.

С помощью (3.1) и (3.4) получаем зависимость ${{p}_{z}}(t)$:

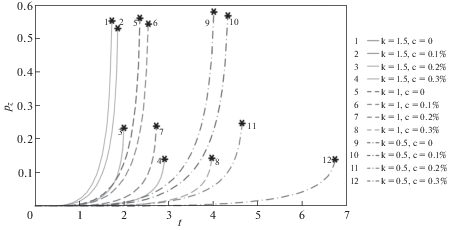
${{p}_{z}} = \frac{{\left( {2 - a} \right)}}{2}{{A}^{{ - 1}}}{{g}^{{m - 1}}}{{f}_{1}}(c)\int\limits_0^t {{{{[1 - G{{t}^{{n + 1}}}]}}^{{ - \left( {m/n} \right)}}}{{{\left( {{{U}_{0}}kt} \right)}}^{m}}dt} $

Кривые ползучести ${{p}_{z}}(t)$ при t от 0 до t* при различных значениях исходных параметров приведены на рис. 8.

Рис. 8

Зависимости $\omega (t)$, ${{p}_{z}}(t)$ на рис. 7–8 при $k = 0.5$ нанесены сплошными линиями, при $k = 1.0$ – штриховыми линиями, при $k = 1.5$ – штрих-пунктирными линиями.

Из рис. 7–8 следует, что при уменьшении параметра k (то есть скорости возрастания напряжений во времени) время t* до разрушения оболочки увеличивается, а значение деформации ползучести при разрушении ${{p}_{z}}(t{\kern 1pt} *)$ уменьшается. Увеличение уровня концентрации предварительно внедренного водорода здесь, так же как и при одноосном растяжении титанового сплава [1, 2], приводит к увеличению времени до разрушения t* и уменьшению предельной деформации $p_{z}^{*} = {{p}_{z}}(t{\kern 1pt} *)$.

4. Заключение. Проведено моделирование ползучести цилиндрической оболочки вплоть до разрушения в присутствии агрессивной среды при двух программах нестационарного сложного напряженного состояния.

В качестве первой программы нагружения рассматривается кусочно-постоянная зависимость осевого и окружного напряжений от времени. Во второй программе нагружения осевое и окружное напряжения возрастают пропорционально времени. Для описания длительного разрушения используется кинетическая теория Ю.Н. Работнова с векторным параметром поврежденности. Построены кривые осевой ползучести при различных значениях исходных параметров. Вычисления показали, что зависимость времени до разрушения t* от уровня предварительно внедренной агрессивной среды c имеют тот же характер, который наблюдается в испытаниях растягиваемых образцов титанового сплава ВТ6 с предварительно внедренным водородом. Увеличение уровня агрессивной среды приводит к увеличению значений t* и уменьшению значений $p_{z}^{*}$.

Работа выполнена при финансовой поддержке Российского научного фонда, проект № 19-19-00062.

Список литературы

Локощенко А.М., Ильин А.А., Мамонов А.М., Назаров В.В. Анализ ползучести и длительной прочности титанового сплава ВТ6 с предварительно внедренным водородом // Физико-химическая механика материалов. 2008. № 5. С. 98–104. (Lokoshchenko А.M., Il’in A.A., Mamo-nov A.M., and Nazarov V.V. Analysis of the creep and long-term strength of VT6 titanium alloy with preliminarily injected hydrogen // Materials Science. 2008. Volume 44, pages 700–707).
Локощенко А.М. Ползучесть и длительная прочность металлов. М.: Физматлит, 2016. 504 с. (перевод: A.M. Lokoshchenko. Creep and long term strength of metals. CISP. CRC Press. Taylor & Francis Group. Boca. Raton. London. New York. 2018. 545 p.).
Работнов Ю.М. О механизме длительного разрушения // Вопросы прочности материалов и конструкций. М.: Изд-во АН СССР, 1959. С. 5–7.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал