1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 4, 2021

Известия РАН. Механика твердого тела, 2021, № 4, стр. 3-17

ДИСПЕРСИЯ И ПРОСТРАНСТВЕННАЯ ЛОКАЛИЗАЦИЯ ИЗГИБНЫХ ВОЛН, РАСПРОСТРАНЯЮЩИХСЯ В БАЛКЕ ТИМОШЕНКО, ЛЕЖАЩЕЙ НА НЕЛИНЕЙНО-УПРУГОМ ОСНОВАНИИ

В. И. Ерофеев a, *, А. В. Леонтьева a, **

a Институт проблем машиностроения РАН – филиал Федерального государственного бюджетного научного учреждения “Федеральный исследовательский центр Институт прикладной физики Российской академии наук”
Нижний Новгород, Россия

* E-mail: erof.vi@yandex.ru
** E-mail: aleonav@mail.ru

Поступила в редакцию 25.05.2020
После доработки 07.06.2020
Принята к публикации 25.06.2020

Полный текст (PDF)

Аннотация

В настоящей работе рассматриваются изгибные волны, распространяющиеся в однородной балке, закрепленной на нелинейно-упругом основании. Динамическое поведение балки определяется теорией Тимошенко. Система уравнений, описывающая изгибные колебания балки, сводится к одному нелинейному уравнению четвертого порядка относительно поперечных смещений частиц срединной линии балки. Показано, что в случае, если жесткость балки мала по сравнению с линейной жесткостью основания, эволюционное уравнение представляет собой модифицированное уравнение Островского с дополнительным кубично-нелинейным слагаемым. Для эволюционного уравнения найдены точные солитонные решения из класса стационарных волн в виде кинка и антикинка.

Ключевые слова: изгибная волна, балка Тимошенко, нелинейно-упругое основание, эволюционное уравнение, обобщение модифицированного уравнения Островского, нелинейная стационарная волна, дисперсия

1. Введение. В задачах динамики упругих конструкций традиционно уделяется большое внимание распространению изгибных волн в стержнях и стержневых системах. В качестве базовой модели для проведения анализа часто выбирается математическая модель балки, предложенная С.П. Тимошенко [1–30]. Эта модель, уточняющая техническую теорию изгиба стержней, предполагает, что поперечные сечения остаются плоскими, но не перпендикулярными деформируемой срединной линии стержня; нормальные напряжения на площадках, параллельных оси, равны нулю; учитываются инерционные составляющие, связанные с поворотом поперечных сечений [4, ‎6, ‎20, ‎31].

Модель балки Тимошенко занимает особое место в механике: позволяя хорошо описывать многие процессы, происходящие в реальных конструкциях, она остается достаточно простой, доступной для аналитических исследований.

Непрерывное увеличение быстродействия и удельной мощности машин и механизмов, забота о снижении веса конструкции при сохранении ее надежности в работе, а также широкое внедрение в современную технику новых композиционных материалов требуют более полного исследования реального напряженно-деформированного состояния. Для этого часто оказывается недостаточно классических линейных теорий и необходимо рассматривать теории более высоких приближений, учитывающих, в частности, геометрическую и физическую нелинейности.

Нелинейные искажения, возникающие при распространении интенсивных изгибных волн, могут накапливаться с течением времени и при определенных условиях приведут к сильному укручению волновых фронтов и существенному изменению всего волнового процесса. Это, в свою очередь, может вызвать появление больших напряжений, необратимых деформаций в материале и привести к локальной потере устойчивости. Интерес к изучению нелинейных волновых процессов связан с возможностью возникновения даже в простых элементах упругих конструкций специфических нелинейных режимов. С одной стороны, эффекты формирования нелинейных волн с большими градиентами напряжений и деформаций оказываются нежелательными, поскольку могут приводить к разрушению или пластическому течению материала, но, с другой стороны, – они могут быть полезными и найти применение в технологиях обработки материалов, в дефектоскопии и технической диагностике. Теоретические расчеты параметров нелинейных волн необходимы для изучения свойств новых конструкционных материалов, в частности, измерения нелинейных модулей упругости.

Целью данной работы является исследование влияния нелинейно-упругого основания на распространение изгибных волн в балке Тимошенко в рамках математической модели, сформулированной в [32].

2. Математическая модель. В рамках теории Тимошенко динамическое поведение стержня, закрепленного на нелинейно-упругом основании, описывается системой уравнений [32]:

(2.1)
$\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} - \kappa c_{\tau }^{2}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + \kappa c_{\tau }^{2}\frac{{\partial \varphi }}{{\partial x}} + {{h}_{1}}w + {{h}_{2}}{{w}^{3}} = 0$
(2.2)
$\frac{{{{\partial }^{2}}\varphi }}{{\partial {{t}^{2}}}} - c_{0}^{2}\frac{{{{\partial }^{2}}\varphi }}{{\partial {{x}^{2}}}} + \frac{{\kappa c_{\tau }^{2}}}{{r_{y}^{2}}}\left( {\varphi - \frac{{\partial w}}{{\partial x}}} \right) = 0$
где w(x, t) – поперечное смещение частиц срединной линии стержня; φ(x, t) – угол отклонения сечения стержня от вертикального положения; ${{c}_{\tau }} = \sqrt {{\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0em} \rho }} $, ${{c}_{0}} = \sqrt {{E \mathord{\left/ {\vphantom {E \rho }} \right. \kern-0em} \rho }} $ – скорости распространения сдвиговых волн в неограниченной среде и продольных волн в стержне, соответственно; ρ – плотность материала стержня; $\mu $ – модуль сдвига; E – модуль Юнга; ${{r}_{y}} = \sqrt {{{{{I}_{y}}} \mathord{\left/ {\vphantom {{{{I}_{y}}} F}} \right. \kern-0em} F}} $ – осевой радиус инерции; Iy – осевой момент инерции (для прямоугольного поперечного сечения ${{I}_{y}} = {{{{a}^{3}}b} \mathord{\left/ {\vphantom {{{{a}^{3}}b} {12}}} \right. \kern-0em} {12}}$); F – площадь поперечного сечения стержня; κ – поправочный коэффициент, учитывающий отклонение от теории плоских сечений, его величина зависит от способа определения среднего значения для угла сдвига и характера распределения сдвигов по сечению (для стержня прямоугольного сечения κ = 5/6); ${{h}_{1}}$, ${{h}_{2}}$ – коэффициенты, характеризующие нелинейно-упругое основание.

Предполагаем, что балка является бесконечной. Такая идеализация допустима, если на ее границах находятся оптимальные демпфирующие устройства, т.е. параметры граничного закрепления таковы, что падающие на него возмущения не будут отражаться. В [33] на основе точного аналитического решения обосновано существование согласованного концевого гасителя изгибных колебаний балки Тимошенко, не дающего отраженных возмущений в системе. Это позволяет рассматривать модель балки (2.1), (2.2) без учета граничных условий, а вибрации, распространяющиеся по балке, рассматривать как бегущие изгибные волны.

Система уравнений (2.1), (2.2) сводится к одному уравнению относительно поперечного смещения частиц $w$:

(2.3)
$\begin{gathered} \left( {1 + \frac{{{{h}_{1}}r_{y}^{2}}}{{\kappa c_{\tau }^{2}}}} \right)\frac{{{{\partial }^{2}}w}}{{\partial {{t}^{2}}}} - \frac{{c_{0}^{2}{{h}_{1}}r_{y}^{2}}}{{\kappa c_{\tau }^{2}}}\frac{{{{\partial }^{2}}w}}{{\partial {{x}^{2}}}} + c_{0}^{2}r_{y}^{2}\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{4}}}} - \frac{{r_{y}^{2}}}{{\kappa c_{\tau }^{2}}}(c_{0}^{2} + \kappa c_{\tau }^{2})\frac{{{{\partial }^{4}}w}}{{\partial {{x}^{2}}\partial {{t}^{2}}}} + \hfill \\ + \;\frac{{r_{y}^{2}}}{{\kappa c_{\tau }^{2}}}\frac{{{{\partial }^{4}}w}}{{\partial {{t}^{4}}}} + {{h}_{1}}w + {{h}_{2}}{{w}^{3}} + \frac{{{{h}_{2}}r_{y}^{2}}}{{\kappa c_{\tau }^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{t}^{2}}}}({{w}^{3}}) - \frac{{c_{0}^{2}{{h}_{2}}r_{y}^{2}}}{{\kappa c_{\tau }^{2}}}\frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}({{w}^{3}}) = 0 \hfill \\ \end{gathered} $

В безразмерных переменных уравнение (2.3) принимает вид:

(2.4)
$\begin{gathered} \left( {1 + {{m}_{1}}} \right)\frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}} - {{m}_{1}}\frac{{{{\partial }^{2}}W}}{{\partial {{z}^{2}}}} + \frac{{{{\partial }^{4}}W}}{{\partial {{z}^{4}}}} - \left( {1 + {{m}_{2}}} \right)\frac{{{{\partial }^{4}}W}}{{\partial {{z}^{2}}\partial {{\tau }^{2}}}} + {{m}_{2}}\frac{{{{\partial }^{4}}W}}{{\partial {{\tau }^{4}}}} + \\ + \;\frac{{{{m}_{1}}}}{{{{m}_{2}}}}W + \frac{{{{m}_{3}}}}{{{{m}_{2}}}}{{W}^{3}} + {{m}_{3}}\left( {\frac{{{{\partial }^{2}}}}{{\partial {{\tau }^{2}}}}({{W}^{3}}) - \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}}({{W}^{3}})} \right) = 0 \\ \end{gathered} $
где $W = {w \mathord{\left/ {\vphantom {w {{{w}_{0}}}}} \right. \kern-0em} {{{w}_{0}}}}$, $z = {x \mathord{\left/ {\vphantom {x {{{r}_{y}}}}} \right. \kern-0em} {{{r}_{y}}}}$, $\tau = {{{{c}_{0}}t} \mathord{\left/ {\vphantom {{{{c}_{0}}t} {{{r}_{y}}}}} \right. \kern-0em} {{{r}_{y}}}}$ – безразмерные величины перемещения, координаты и времени, соответственно. Безразмерные комплексы параметров
${{m}_{1}} = \frac{{{{h}_{1}}r_{y}^{2}}}{{\kappa c_{\tau }^{2}}},$ ${{m}_{2}} = \frac{{c_{0}^{2}}}{{\kappa c_{\tau }^{2}}},$ ${{m}_{3}} = \frac{{{{h}_{2}}r_{y}^{2}w_{0}^{2}}}{{\kappa c_{\tau }^{2}}}$
характеризуют линейную жесткость основания (${{m}_{1}} > 0$), отношение скоростей (${{m}_{2}} > 1$) и нелинейность системы. Для жесткой нелинейности основания параметр ${{m}_{3}} > 0$ (по терминологии Рейснера – “упрочняющееся основание” [34]), для мягкой нелинейности – ${{m}_{3}} < 0$ (“размягченное” основание [34]). Параметр ${{m}_{1}} \to 0$, если линейная жесткость основания существенно уступает жесткости балки ${{h}_{1}} \ll {{\kappa c_{\tau }^{2}} \mathord{\left/ {\vphantom {{\kappa c_{\tau }^{2}} {r_{y}^{2}}}} \right. \kern-0em} {r_{y}^{2}}}$. Если  линейная жесткость основания существенно превосходит жесткость балки ${{h}_{1}} \gg {{\kappa c_{\tau }^{2}} \mathord{\left/ {\vphantom {{\kappa c_{\tau }^{2}} {r_{y}^{2}}}} \right. \kern-0em} {r_{y}^{2}}}$, то ${{m}_{1}} \to \infty $. Параметр ${{m}_{1}} \to 1$, если линейная жесткость основания и жесткость балки сопоставимы ${{h}_{1}} \approx {{\kappa c_{\tau }^{2}} \mathord{\left/ {\vphantom {{\kappa c_{\tau }^{2}} {r_{y}^{2}}}} \right. \kern-0em} {r_{y}^{2}}}$.

3. Линеаризованное уравнение. Для изучения дисперсионных свойств системы отбросим нелинейную часть уравнения (2.4) и получим следующее уравнение

(3.1)
$\frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}} - \frac{{{{m}_{1}}}}{{1 + {{m}_{1}}}}\frac{{{{\partial }^{2}}W}}{{\partial {{z}^{2}}}} + \frac{1}{{1 + {{m}_{1}}}}\frac{{{{\partial }^{4}}W}}{{\partial {{z}^{4}}}} - \frac{{1 + {{m}_{2}}}}{{1 + {{m}_{1}}}}\frac{{{{\partial }^{4}}W}}{{\partial {{z}^{2}}\partial {{\tau }^{2}}}} + \frac{{{{m}_{2}}}}{{1 + {{m}_{1}}}}\frac{{{{\partial }^{4}}W}}{{\partial {{\tau }^{4}}}} + \frac{{{{m}_{1}}}}{{{{m}_{2}}\left( {1 + {{m}_{1}}} \right)}}W = 0$
решение которого ищем в виде бегущей гармонической волны
$W\left( {z,\tau } \right) = {{W}_{0}}{{e}^{{i\left( {\omega \tau - kz} \right)}}} + к.с.$
где W0 – комплексная амплитуда волны, $\omega $ – частота, k – волновое число, к.с. – комплексно‑сопряженная величина. Уравнение (3.1) принимает вид

(3.2)
${{m}_{2}}({{\omega }^{2}} - {{k}^{2}})({{m}_{1}} - {{m}_{2}}{{\omega }^{2}} + {{k}^{2}}) = {{m}_{1}} - {{m}_{2}}{{\omega }^{2}}$

Дисперсионное уравнение содержит два параметра и имеет четвертый порядок по частоте и волновому числу. Разрешая (3.2) относительно $\omega $, получим

(3.3)
$\omega = \pm \frac{1}{{\sqrt {2{{m}_{2}}} }}\sqrt {{{k}^{2}}(1 + {{m}_{2}}) + 1 + {{m}_{1}} \pm \sqrt {{{k}^{4}}{{{({{m}_{2}} - 1)}}^{2}} + 2{{k}^{2}}(1 + {{m}_{2}} - {{m}_{1}}({{m}_{2}} - 1)) + {{{(1 - {{m}_{1}})}}^{2}}} } $

Дисперсионная кривая имеет две ветви, и при ненулевых значениях параметров у каждой ветви существует частота отсечки. Качественно разный вид имеет дисперсионная кривая при различных значениях параметра ${{m}_{1}}$: ${{m}_{1}} \to 0$, ${{m}_{1}} \to 1$ и ${{m}_{1}} \to \infty $. Значение параметра ${{m}_{2}}$ существенным образом не влияет на вид дисперсионной кривой. При увеличении этого параметра дисперсия смещается в более низкий частотный диапазон.

В отсутствие упругого основания (${{m}_{1}} = 0$) уравнение (3.1) является классическим уравнением Тимошенко

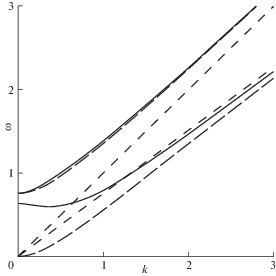
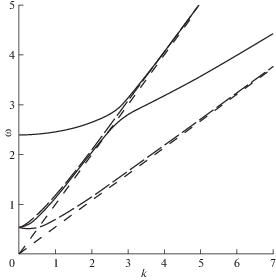
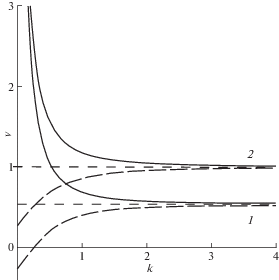
$\frac{{{{\partial }^{2}}W}}{{\partial {{\tau }^{2}}}} + \frac{{{{\partial }^{4}}W}}{{\partial {{z}^{4}}}} - \left( {1 + {{m}_{2}}} \right)\frac{{{{\partial }^{4}}W}}{{\partial {{z}^{2}}\partial {{\tau }^{2}}}} + {{m}_{2}}\frac{{{{\partial }^{4}}W}}{{\partial {{\tau }^{4}}}} = 0$
описывающим изгибные колебания балки. Дисперсионные свойства этой модели хорошо изучены, например, в [4, 6, 20, 35].

Зависимости (3.3) в первой четверти при различных значениях параметра ${{m}_{1}}$ изображены на рис. 1, 2: ${{m}_{1}} < 1$ (рис. 1, сплошная линия), ${{m}_{1}} = 0$ (рис. 1, длинный пунктир), ${{m}_{1}} > 1$ (рис. 2, сплошная линия), ${{m}_{1}} = 1$ (рис. 2, длинный пунктир). Асимптоты на всех рисунках в статье отмечены коротким пунктиром.

Рис. 1
Рис. 2

На рисунке при ${{m}_{1}} < 1$ (рис. 1) частоты отсечек верхней и нижней ветвей, соответственно, равны $\omega = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{m}_{2}}} }}} \right. \kern-0em} {\sqrt {{{m}_{2}}} }}$ и $\omega = \sqrt {{{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} $ (k = 0). При ${{m}_{1}} = 0$ нижняя ветвь берет начало в нуле. При ${{m}_{1}} > 1$ (рис. 2) верхняя и нижняя ветви исходят (k = 0) из значений частот $\omega = \sqrt {{{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} $ и $\omega = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{m}_{2}}} }}} \right. \kern-0em} {\sqrt {{{m}_{2}}} }}$, соответственно. При ${{m}_{1}} = 1$ частоты отсечек обеих ветвей совпадают. На бесконечности верхняя и нижняя ветви дисперсионной кривой стремятся к прямым $\omega = k$ и $\omega = {k \mathord{\left/ {\vphantom {k {\sqrt {{{m}_{2}}} }}} \right. \kern-0em} {\sqrt {{{m}_{2}}} }}$, соответственно. При ${{m}_{1}} = 0$ на низких частотах вблизи нуля справедливо $\omega = {{k}^{2}}$, а для верхней ветви на низких частотах выполняется $\omega = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{m}_{2}}} }}} \right. \kern-0em} {\sqrt {{{m}_{2}}} }} + {{\left( {1 + {{m}_{2}}} \right){{k}^{2}}} \mathord{\left/ {\vphantom {{\left( {1 + {{m}_{2}}} \right){{k}^{2}}} {(2\sqrt {{{m}_{2}}} )}}} \right. \kern-0em} {(2\sqrt {{{m}_{2}}} )}}$.

Верхняя ветвь дисперсионной кривой расположена выше своей асимптоты при любых значениях параметра ${{m}_{1}}$. Расположение нижней ветви кривой относительно своей асимптоты зависит от значения параметра. Нижняя ветвь лежит выше асимптоты при ${{m}_{1}} > {1 \mathord{\left/ {\vphantom {1 {\left( {{{m}_{2}} - 1} \right)}}} \right. \kern-0em} {\left( {{{m}_{2}} - 1} \right)}}$ и ниже – при ${{m}_{1}} = 0$. Если значение параметра находится в интервале $0 < {{m}_{1}} < {1 \mathord{\left/ {\vphantom {1 {\left( {{{m}_{2}} - 1} \right)}}} \right. \kern-0em} {\left( {{{m}_{2}} - 1} \right)}}$, то у нижней ветви дисперсионной кривой существует точка пересечения со своей асимптотой (${{k}_{ * }},{{\omega }_{ * }}$), где ${{k}_{ * }} = \sqrt {{{m}_{2}}} {{\omega }_{ * }}$, ${{\omega }_{ * }} = \sqrt {{{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {\left( {{{m}_{2}}\left( {1 + {{m}_{1}} - {{m}_{1}}{{m}_{2}}} \right)} \right)}}} \right. \kern-0em} {\left( {{{m}_{2}}\left( {1 + {{m}_{1}} - {{m}_{1}}{{m}_{2}}} \right)} \right)}}} $. В этом случае ветка расположена ниже асимптоты на частотах $\omega > {{\omega }_{ * }}$.

При значении параметра $0 < {{m}_{1}} < 1 + {1 \mathord{\left/ {\vphantom {1 {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}$ у нижней ветви дисперсионной кривой есть точка минимума, которая расположена ниже частоты отсечки. Минимальное значение частоты и соответствующее значение волнового числа равны $\omega _{{\min }}^{2} = {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {\left( {{{m}_{2}} - 1} \right)}}} \right. \kern-0em} {\left( {{{m}_{2}} - 1} \right)}}$ + + ${{2(\sqrt {1 - {{m}_{1}} + {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} - 1)} \mathord{\left/ {\vphantom {{2(\sqrt {1 - {{m}_{1}} + {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} - 1)} {{{{({{m}_{2}} - 1)}}^{2}}}}} \right. \kern-0em} {{{{({{m}_{2}} - 1)}}^{2}}}}$, $k_{{\min }}^{2} = {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {\left( {{{m}_{2}} - 1} \right)}}} \right. \kern-0em} {\left( {{{m}_{2}} - 1} \right)}}$ + (1 + m2)$(\sqrt {1 - {{m}_{1}} + {{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} - 1)$/(m2 – – 1)2. На частоте отсечки нижней ветви ненулевое значение волнового числа равно $k = \sqrt {{{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} $ (при $0 < {{m}_{1}} \leqslant 1$) или $k = \sqrt {{{\left( {1 + {{m}_{2}} - {{m}_{1}}{{m}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {1 + {{m}_{2}} - {{m}_{1}}{{m}_{2}}} \right)} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} $ (при $1 \leqslant {{m}_{1}} < 1 + {1 \mathord{\left/ {\vphantom {1 {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}$).

При любых значениях параметра m1 нижняя ветвь пересекает асимптоту верхней ветви $\omega = k$, значение частоты при этом равно $\omega = \sqrt {{{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} $.

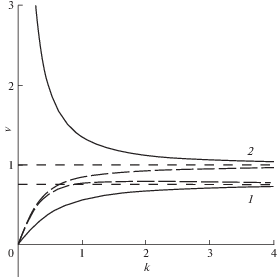
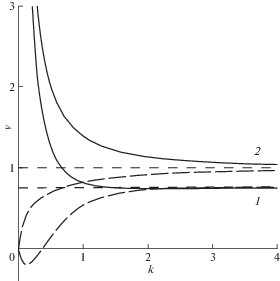
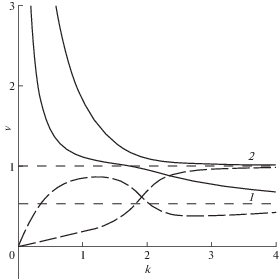
Зависимости фазовой ${{{v}}_{{ph}}} = {\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0em} k}$ и групповой ${{{v}}_{{gr}}} = {{d\omega } \mathord{\left/ {\vphantom {{d\omega } {dk}}} \right. \kern-0em} {dk}}$ скоростей от волнового числа и частоты определяются из выражения (3.3). На рис. 3–6 представлены зависимости ${{{v}}_{{ph}}}\left( k \right)$ (сплошная линия) и ${{{v}}_{{gr}}}\left( k \right)$ (длинный пунктир) при различных значениях параметра m1: ${{m}_{1}} = 0$ (рис. 3), ${{m}_{1}} < 1$ (рис. 4), ${{m}_{1}} = 1$ (рис. 5), ${{m}_{1}} > 1$ (рис. 6).

Рис. 3
Рис. 4
Рис. 5
Рис. 6

Нижней ветви дисперсионной кривой $\omega \left( k \right)$ соответствуют нижние ветви (“1” на рис. 3–6), а верхней – верхние ветви фазовой и групповой скоростей (“2” на рис. 3–6). Для последней пары кривых значения фазовой скорости больше значений групповой скорости при любых значениях волнового числа и всех допустимых значениях частоты.

Кривые фазовой и групповой скоростей нижней пары меняют свое расположение относительно друг друга в зависимости от значений параметра. При ${{m}_{1}} = 0$ кривая групповой скорости расположена выше кривой фазовой скорости. При $0 < {{m}_{1}} < 1$ + + 1/m2 дисперсионная кривая $\omega \left( k \right)$ имеет точку минимума, а кривая групповой скорости ${{{v}}_{{gr}}}(k)$ уходит в отрицательную полуплоскость. При $0 < {{m}_{1}} < {1 \mathord{\left/ {\vphantom {1 {\left( {{{m}_{2}} - 1} \right)}}} \right. \kern-0em} {\left( {{{m}_{2}} - 1} \right)}}$ кривые фазовой и групповой скоростей пересекаются. При ${{m}_{1}} > {1 \mathord{\left/ {\vphantom {1 {\left( {{{m}_{2}} - 1} \right)}}} \right. \kern-0em} {\left( {{{m}_{2}} - 1} \right)}}$ фазовая скорость больше групповой во всем диапазоне частот и волновых чисел.

На бесконечности (при больших значениях частоты или волнового числа) пары кривых “1”, “2” (рис. 3–6) стремятся к значениям ${{{v}}_{{ph}}} = {{{v}}_{{gr}}} = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{m}_{2}}} }}} \right. \kern-0em} {\sqrt {{{m}_{2}}} }}$ и ${{{v}}_{{ph}}} = {{{v}}_{{gr}}} = 1$, соответственно.

Кривые фазовой скорости ${{{v}}_{{gr}}}(k)$ имеют вертикальную асимптоту k = 0. Кривые групповой скорости ${{{v}}_{{gr}}}(k)$ берут свое начало в нуле, за исключением случая, когда ${{m}_{1}} = 1$ и кривые на вертикальной оси имеют отметки ${{{v}}_{{gr}}} = \pm {1 \mathord{\left/ {\vphantom {1 {(2\sqrt {{{m}_{2}}} )}}} \right. \kern-0em} {(2\sqrt {{{m}_{2}}} )}}$. Значения частот $\omega = \sqrt {{{{{m}_{1}}} \mathord{\left/ {\vphantom {{{{m}_{1}}} {{{m}_{2}}}}} \right. \kern-0em} {{{m}_{2}}}}} $, $\omega = {1 \mathord{\left/ {\vphantom {1 {\sqrt {{{m}_{2}}} }}} \right. \kern-0em} {\sqrt {{{m}_{2}}} }}$ являются точками исхода кривых групповой скорости ${{{v}}_{{gr}}}(\omega )$ и вертикальными асимптотами кривых фазовой скорости ${{{v}}_{{ph}}}(\omega )$.

Кривая фазовой скорости “2” лежит выше кривой фазовой скорости “1” при любых значениях частоты, волнового числа и параметра m1. Кривые групповых скоростей при определенных значениях параметра имеют точку пересечения и кривая “1” оказывается выше кривой “2”.

4. Нелинейная стационарная волна. В случае малости жесткости балки по сравнению с линейной жесткостью основания (${{m}_{1}} \to \infty $), задача позволяет отследить эволюционные изменения профиля волны. Перейдем в уравнении (2.4) в движущуюся систему координат $\xi = z - c\tau $, $\theta = \varepsilon \tau $, где c – скорость волны, заранее неизвестна, $\varepsilon $ – малый параметр ($\varepsilon \ll 1$). Выбор переменных объясняется тем, что возмущение, распространяясь со скоростью c вдоль оси z, медленно эволюционирует во времени из-за нелинейности, дисперсии и диссипации.

Учитывая, что нелинейные и дисперсионные слагаемые малы, в нулевом приближении находим скорость c:

${{c}^{2}} = \frac{{{{m}_{1}}}}{{1 + {{m}_{1}}}}$

В первом приближении по малому параметру имеем:

(4.1)
$\frac{\partial }{{\partial \xi }}\left( {\frac{{\partial W}}{{\partial \theta }} + {{d}_{1}}{{W}^{2}}\frac{{\partial W}}{{\partial \xi }} + {{d}_{2}}\frac{{{{\partial }^{3}}W}}{{\partial {{\xi }^{3}}}}} \right) - {{d}_{3}}W - {{d}_{4}}{{W}^{3}} = 0$
где коэффициенты уравнения равны

$\begin{gathered} {{d}_{1}} = \frac{{3{{m}_{3}}}}{{2\varepsilon c{{{\left( {1 + {{m}_{1}}} \right)}}^{2}}}},\quad {{d}_{2}} = \frac{{{{m}_{1}}{{m}_{2}} - \left( {1 + {{m}_{1}}} \right)}}{{2\varepsilon c{{{\left( {1 + {{m}_{1}}} \right)}}^{3}}}} \\ {{d}_{3}} = \frac{{{{m}_{1}}}}{{2\varepsilon c\left( {1 + {{m}_{1}}} \right){{m}_{2}}}},\quad {{d}_{4}} = \frac{{{{m}_{3}}}}{{2\varepsilon c\left( {1 + {{m}_{1}}} \right){{m}_{2}}}} \\ \end{gathered} $

Заметим, что уравнение (4.1) отличается от известного в нелинейной волновой динамике уравнения Островского [36–40] наличием во втором слагаемом кубической нелинейности вместо квадратичной и дополнительным нелинейным слагаемым (последнее слагаемое в уравнении).

Уравнение (4.1) будем классифицировать как модифицированное уравнение Островского с дополнительным нелинейным слагаемым. При этом, естественно назвать уравнение (4.1) без последнего слагаемого модифицированным уравнением Островского, по аналогии, с известными модифицированным уравнением Кортевега–де Вриза (мКдВ) и модифицированным уравнением Бюргерса. Однако понятие “модифицированное” в случае уравнения КдВ имеет несколько иное значение и связано с наличием преобразования Миуры [‎41], которое переводит решения модифицированного уравнения в решения классического уравнения. Похожих преобразований относительно классических и модифицированных уравнений Бюргерса и Островского пока не найдено.

В [‎40] показано, что уравнение Островского и его модификации имеют отношение к широкому кругу нелинейных систем, характеризующихся наличием бездисперсионной полосы в спектре частот, разделяющей области с низко- и высокочастотной дисперсиями.

Как и уравнение Островского, модифицированное уравнение Островского не имеет точных решений, но допускает анализ качественными методами исследования динамических систем [39, ‎40]. Далее увидим, что наличие дополнительного кубично-нелинейного слагаемого позволяет найти точные решения уравнения (4.1) в виде солитонов.

Для стационарных волн $W\left( {\xi ,\theta } \right) = W\left( \chi \right)$, $\chi = \xi - {v}\theta $ уравнение (4.1) запишется так:

(4.2)
$( - {v}W{\text{'}} + {{d}_{1}}{{W}^{2}}W{\text{'}} + {{d}_{2}}W{\text{'''}}){\text{'}} - {{d}_{3}}W - {{d}_{4}}{{W}^{3}} = 0$
где ${v}$ имеет смысл скорости нелинейной волны. Cчитаем, что волна распространяется в положительном направлении оси ξ.

Будем искать решение уравнения (4.2) методом простейших уравнений [42], используя в качестве простейшего уравнения – уравнение Риккати с постоянными коэффициентами в виде

(4.3)
$Y{\text{'}}\left( \chi \right) = - {{Y}^{2}}\left( \chi \right) + {{B}_{0}}$
которое имеет решение

(4.4)
$Y\left( \chi \right) = \sqrt {{{B}_{0}}} th(\sqrt {{{B}_{0}}} \chi )$

Решение уравнения (4.2) имеет полюс первого порядка, и поэтому решение типа уединенных волн будем искать в виде

(4.5)
$W\left( \chi \right) = {{b}_{0}}Y\left( \chi \right) + {{b}_{1}}$
где Y(χ) – решение (4.4) уравнения (4.3).

Подставляя решение (4.5) в уравнение (4.2) и учитывая уравнение Риккати, получаем полином относительно Y(χ). Приравнивая нулю выражения при одинаковых степенях Y(χ), получаем систему алгебраических уравнений, из которой находим значения коэффициентов

$b_{0}^{2} = - \frac{{6{{d}_{2}}}}{{{{d}_{1}}}},\quad {{b}_{1}} = 0,\quad {{B}_{0}} = \frac{{{{d}_{1}}{{d}_{3}}}}{{6{{d}_{2}}{{d}_{4}}}}$

Кроме того, находим выражение для скорости нелинейной волны

${v} = - \frac{{{{d}_{1}}{{d}_{3}}}}{{3{{d}_{4}}}} + \frac{{3{{d}_{2}}{{d}_{4}}}}{{{{d}_{1}}}}$

Учитывая значения найденных коэффициентов, решение (4.5) принимает вид

(4.6)
$W\left( \chi \right) = \pm \sqrt { - \frac{{{{d}_{3}}}}{{{{d}_{4}}}}} th\left( {\sqrt {\frac{{{{d}_{1}}{{d}_{3}}}}{{6{{d}_{2}}{{d}_{4}}}}} \chi } \right)$

Будем считать, что ${{W}_{1}} = {{W}_{ + }}$, ${{W}_{2}} = {{W}_{ - }}$ при подстановке ${{b}_{{0 + }}}$ и ${{b}_{{0 - }}}$, соответственно. Решения ${{W}_{1}}$, ${{W}_{2}}$ отличаются только знаком коэффициента перед гиперболическим тангенсом.

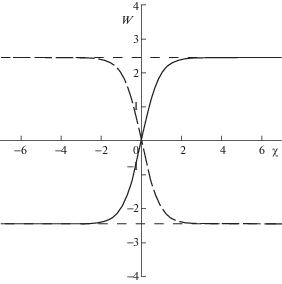
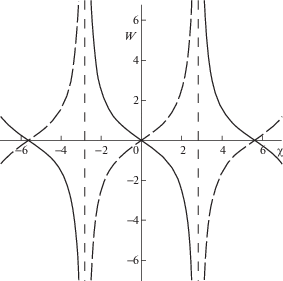
Очевидно, что для существования действительных решений, коэффициенты d1 и d2 должны быть разных знаков. Для существования ограниченных действительных решений коэффициенты в парах d1, d2 и ${{d}_{3}}$, ${{d}_{4}}$ должны быть разных знаков. Профили ограниченных и неограниченных решений ${{W}_{1}}\left( \chi \right)$ (сплошная линия) и ${{W}_{2}}\left( \chi \right)$ (длинный пунктир) при различных значениях ${{d}_{1}}$–${{d}_{4}}$ изображены на рис. 7 и рис. 8, соответственно. При положительных подкоренных выражениях в (4.6) решение ${{W}_{1}}\left( \chi \right)$, как и решение ${{W}_{2}}\left( \chi \right)$, является уединенной волной и имеет профиль кинка – плавного перепада между двумя значениями функции (рис. 7). При отрицательных подкоренных выражениях решения ${{W}_{1}}\left( \chi \right)$, ${{W}_{2}}\left( \chi \right)$ являются периодическими неограниченными (рис. 8). Наибольший интерес представляют ограниченные решения.

Рис. 7
Рис. 8

Решения в виде кинков существуют на плоскости одновременно, причем каждый из кинков является симметричным относительно точки перегиба, совпадающей с началом координат. Один из кинков монотонно возрастающий, другой – монотонно убывающий. Кинки имеют одинаковые амплитуды и ширины: $A = 2\sqrt { - {{{{d}_{3}}} \mathord{\left/ {\vphantom {{{{d}_{3}}} {{{d}_{4}}}}} \right. \kern-0em} {{{d}_{4}}}}} $, Δ = = $\sqrt {{{6{{d}_{2}}{{d}_{4}}} \mathord{\left/ {\vphantom {{6{{d}_{2}}{{d}_{4}}} {\left( {{{d}_{1}}{{d}_{3}}} \right)}}} \right. \kern-0em} {\left( {{{d}_{1}}{{d}_{3}}} \right)}}} $.

Возвращаясь к безразмерным параметрам задачи, запишем выражения для скорости, амплитуды и ширины волны в виде:

(4.7)
${v} = - \frac{1}{{2\varepsilon {{m}_{2}}\sqrt {{{m}_{1}}\left( {1 + {{m}_{1}}} \right)} }},\quad A = 2\sqrt { - \frac{{{{m}_{1}}}}{{{{m}_{3}}}}} ,\quad \Delta = \sqrt {\frac{{2\left( {{{m}_{1}}{{m}_{2}} - {{m}_{1}} - 1} \right)}}{{{{m}_{1}}\left( {1 + {{m}_{1}}} \right)}}} $

Учитывая, что параметры ${{m}_{1}} > 0$ и ${{m}_{2}} > 1$, получаем ограничение на параметр m3, ${{m}_{3}} < 0$. При увеличении значения m1 амплитуда растет, нелинейная скорость падает, причем волна распространяется в отрицательном направлении оси $\xi $. Ширина фронта волны сначала увеличивается, затем уменьшается. Максимальная ширина фронта волны достигается в точке ${{\left( {{{m}_{1}}} \right)}_{{\max }}} = {{(1 + \sqrt {{{m}_{2}}} )} \mathord{\left/ {\vphantom {{(1 + \sqrt {{{m}_{2}}} )} {\left( {{{m}_{2}} - 1} \right)}}} \right. \kern-0em} {\left( {{{m}_{2}} - 1} \right)}}$ и равна ${{\Delta }_{{\max }}} = \sqrt 2 (\sqrt {{{m}_{2}}} - 1)$, минимальная – при ${{m}_{1}} \to + \infty $ или ${{m}_{1}} \to {1 \mathord{\left/ {\vphantom {1 {\left( {{{m}_{2}} - 1} \right)}}} \right. \kern-0em} {\left( {{{m}_{2}} - 1} \right)}}$. При увеличении m2 точка максимума сдвигается влево, максимальное значение ширины фронта волны при этом увеличивается.

5. Частный случай эволюционного уравнения. Уравнение (4.1) содержит по два дисперсионных и нелинейных слагаемых, отношения их коэффициентов d2/d3 ~ 1/(1 + m1)2, ${{{{d}_{1}}} \mathord{\left/ {\vphantom {{{{d}_{1}}} {{{d}_{4}}}}} \right. \kern-0em} {{{d}_{4}}}}\sim {1 \mathord{\left/ {\vphantom {1 {\left( {1 + {{m}_{1}}} \right)}}} \right. \kern-0em} {\left( {1 + {{m}_{1}}} \right)}}$ показывают, что наибольший вклад в дисперсионный процесс вносит слагаемое с коэффициентом d3, а главным нелинейным является слагаемое с коэффициентом d4.

В частном случае, если в уравнении (4.1) ограничиться отбрасыванием дисперсионного слагаемого (${{d}_{2}} = 0$), получим следующее уравнение

(5.1)
$\frac{\partial }{{\partial \xi }}\left( {\frac{{\partial W}}{{\partial \theta }} + {{d}_{1}}{{W}^{2}}\frac{{\partial W}}{{\partial \xi }}} \right) - {{d}_{3}}W - {{d}_{4}}{{W}^{3}} = 0$
которое в переменных бегущей волны ($W\left( {\xi ,\theta } \right) = W\left( \chi \right)$, $\chi = \xi - {v}\theta $) примет вид

(5.2)
${{W}_{{\chi \chi }}} + \frac{{{{d}_{3}}}}{{v}}W - \frac{{{{d}_{1}}}}{{3{v}}}{{({{W}^{3}})}_{{\chi \chi }}} + \frac{{{{d}_{4}}}}{{v}}{{W}^{3}} = 0$

Уравнение (5.2) описывает колебания ангармонического осциллятора и содержит три типа кубической нелинейности, одна из которых та же, что и в уравнении Дуффинга. Если в уравнении (4.1) пренебречь малыми дисперсионным и нелинейным слагаемыми и положить ${{d}_{1}} = {{d}_{2}} = 0$, то в переменных бегущей волны получится само уравнение Дуффинга.

После интегрирования по координате уравнение (5.2) запишется следующим образом

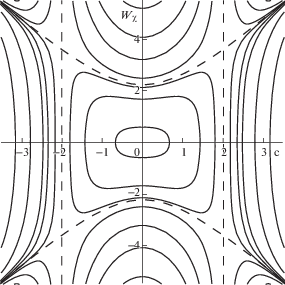
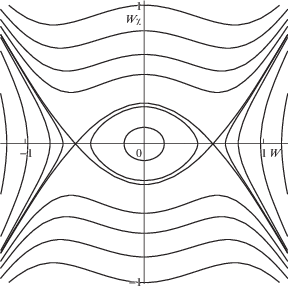
${{\left( {\frac{{dW}}{{d\chi }}} \right)}^{2}} = \frac{{({{d}_{1}}{{d}_{4}}{\text{/}}(3{{{v}}^{2}})){{W}^{6}} + \left( {{{\left( { - {{d}_{4}} + {{{{d}_{1}}{{d}_{3}}} \mathord{\left/ {\vphantom {{{{d}_{1}}{{d}_{3}}} {v}}} \right. \kern-0em} {v}}} \right)} \mathord{\left/ {\vphantom {{\left( { - {{d}_{4}} + {{{{d}_{1}}{{d}_{3}}} \mathord{\left/ {\vphantom {{{{d}_{1}}{{d}_{3}}} {v}}} \right. \kern-0em} {v}}} \right)} {\left( {2{v}} \right)}}} \right. \kern-0em} {\left( {2{v}} \right)}}} \right){{W}^{4}} - \left( {{{{{d}_{3}}} \mathord{\left/ {\vphantom {{{{d}_{3}}} {v}}} \right. \kern-0em} {v}}} \right){{W}^{2}} + {{C}_{0}}}}{{{{{(1 - \left( {{{{{d}_{1}}} \mathord{\left/ {\vphantom {{{{d}_{1}}} {v}}} \right. \kern-0em} {v}}} \right){{W}^{2}})}}^{2}}}}$
где ${{C}_{0}}$ – константа интегрирования, имеет смысл полной энергии системы.

Фазовые портреты ($W$, ${{W}_{\chi }}$) при разных значениях параметра нелинейной жесткости основания m3 изображены на рис. 9 (${{m}_{3}} > 0$) и рис. 10 (${{m}_{3}} < 0$). На фазовых плоскостях присутствуют замкнутые траектории. Области движений разделяют две прямые ${v} - {{d}_{1}}{{W}^{2}} = 0$ и две параболы ${{\left( {{{W}_{\chi }}} \right)}^{2}} = \left( {{{{{d}_{4}}} \mathord{\left/ {\vphantom {{{{d}_{4}}} {\left( {3{{d}_{1}}} \right)}}} \right. \kern-0em} {\left( {3{{d}_{1}}} \right)}}} \right){{W}^{2}} + {{{{d}_{3}}} \mathord{\left/ {\vphantom {{{{d}_{3}}} {\left( {2{{d}_{1}}} \right)}}} \right. \kern-0em} {\left( {2{{d}_{1}}} \right)}} + {{{v}{{d}_{4}}} \mathord{\left/ {\vphantom {{{v}{{d}_{4}}} {(6d_{1}^{2})}}} \right. \kern-0em} {(6d_{1}^{2})}}$ (на рис. 9 отмечены пунктиром). Знак параметра ${{m}_{3}}$ влияет на существование сепаратрисы, так при положительных значениях параметра она отсутствует на фазовой плоскости. Замкнутые траектории вблизи начала координат имеют эллипсовидную форму, а вблизи асимптот искажаются и имеют форму “бабочки”. При отрицательных значениях параметра, фазовый портрет (рис. 10) аналогичен фазовому портрету осциллятора с кубической нелинейностью (описывается уравнением Дуффинга) в условиях “мягкой пружины”.

Рис. 9
Рис. 10

6. Заключение. Таким образом, в работе показано, что учет внешнего нелинейно-упругого основания влияет на распространение гармонических и нелинейных волн в балке Тимошенко, совершающей поперечные колебания.

Наличие упругого основания способствует появлению зоны непропускания по частоте при распространении линейных волн. Как и в балке Тимошенко без упругого основания, на низких частотах у обеих ветвей проявляется дисперсия, а на высоких частотах она отсутствует. Однако тип дисперсии зависит от величины линейной жесткости основания. При больших значениях параметра линейной жесткости низкочастотная волна обладает нормальной дисперсией, в то время как у балки Тимошенко в отсутствие упругого основания, низкочастотная ветка имеет аномальную дисперсию. Высокочастотная волна показывает нормальную дисперсию вне зависимости от наличия или отсутствия упругого основания.

При небольших значениях (вблизи единицы) параметра линейной жесткости у длинных волн (длина которых кратно превосходит осевой радиус инерции) фазовая и групповая скорости имеют разные знаки. На небольших промежутках частоты (при любых значениях параметра линейной жесткости) и волнового числа (при больших значениях параметра) большим значениям фазовой скорости соответствуют меньшие значения групповой скорости.

В случае, когда линейная жесткость внешнего основания существенно больше жесткости балки, тип нелинейности (мягкая, жесткая) основания влияет на существование локализованных волн и форму периодических волн, распространяющихся в балке Тимошенко. Нелинейные и дисперсионные процессы, создающие укручение и расплывание волнового фронта, формируют стационарные волны солитонного типа в виде кинка и антикинка.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 20-19-00613).

Список литературы

  1. Achenbach J.D., Sun C.T. Moving load on a flexible supported Timoshenko beam // International Journal of Solid and Structures. 1965. V. 1. P. 353–370.

  2. Слепян Л.И. Нестационарные упругие волны. Л.: Судостроение, 1972. 376 с.

  3. Вольмир А.С. Нелинейная динамика пластинок и оболочек. М.: Наука, 1972. 432 с.

  4. Григолюк Э.И., Селезов И.Т. Неклассические теории стержней, пластин и оболочек. М.: ВИНИТИ, 1973. 272 с.

  5. Abbas B.A.H., Thomas J. Dynamic stability of Timoshenko beams resting on an elastic foundation // Journal of Sound and Vibration. 1978. V. 60. № 1. P. 33–44.

  6. Артоболевский И.И., Бобровницкий Ю.И., Генкин М.Д. Введение в акустическую динамику машин. М.: Наука, 1979. 296 с.

  7. Сагомонян А.Я. Волны напряжения в сплошных средах. М.: Изд-во МГУ, 1985. 416 с.

  8. Eisenberger M., Clastomik J. Beams on variable two-parameter elastic foundation // Computers and Structures. 1986. V. 23. P. 351–356.

  9. Каплунов Ю.Д., Муравский Г.Б. Действие равнопеременно движущейся силы на балку Тимошенко, лежащую на упругом основании. Переходы через критические скорости // Прикладная математика и механика. 1987. Т. 51. № 3. С. 475–482.

  10. Yokoyama T. Parametric instability of Timoshenko beams resting on an elastic foundation // Computers and Structures. 1988. V. 28. № 2. P. 207–216.

  11. Kar R.C., Sujata T. Parametric instability of Timoshenko beam with thermal gradient resting on a variable Pasternak foundation // Computers and Structures. 1990. V. 36. № 4. P. 659–665.

  12. Gutierrez R.H., Laura P.A., Rossi R.E. Fundamental frequency of vibration of a Timoshenko beam of non-uniform thickness // Journal of Sound and Vibration. 1991. V. 145. P. 241–245.

  13. Lee S.Y., Kuo Y.H., Lin F.Y. Stability of a Timoshenko beam resting on a Winkler elastic foundation // Journal of Sound and Vibration. 1992. V. 153. № 2. P. 193–202.

  14. Cleghorn W.L., Tabarrok B. Finite element formulation of tapered Timoshenko beam for free lateral vibration analysis // Journal of Sound and Vibration. 1992. V. 152. P. 461–470.

  15. Felszeghy S.F. The Timoshenko beam on an elastic foundation and subject to a moving step load // Journal of Vibration and Acoustics. 1996. V. 118. № 3. P. 277–284.

  16. Kim J.H., Choo Y.S. Dunamic stability of a free-free Timoshenko beam subjected to a pulsating follower force // Journal of Sound and Vibration. 1998. V. 216. № 4. P. 623–636.

  17. Lee H.P. Dynamic response of a Timoshenko beam on a Winkler foundation subjected to a moving mass // Applied Acoustics. 1998. V. 55. № 3. P. 203–215.

  18. Suiker A.S.J., de Borst R., Esveld C. Critical behavior of a Timoshenko beam half plane system under a moving load // Archive of Applied Mechanics. 1998. V. 68. № 3–4. P. 158–168.

  19. Wang C.M., Lam K.Y., He X.O. Exact solution for Timoshenko beams on elastic foundations using Green’s functions // Mechanics of Structures & Machines. 1998. V. 26. P. 101–113.

  20. Вибрации в технике: Справочник в 6-ти томах / Ред. cовет: Фролов К.В. (пред.). Т. 1: Колебания линейных систем. 2-е изд., испр. и доп. / Под ред. Болотина В.В. М.: Машиностроение. 1999. 504 с.

  21. Wu T.X., Thompson D.J. A double Timoshenko beam model for vertical vibration analists of railway track at high frequencies // Journal of Sound and Vibration. 1999. V. 224. № 2. P. 329–348.

  22. Chen Y.H., Huang Y.H. Dynamic stiffness of infinite Timoshenko beam on viscoelastic foundation in moving co-ordinate // International Journal for Numerical Methods in Engineering. 2000. V. 48. № 1. P. 1–18.

  23. Chen Y.H., Huang Y.H., Shih C.T. Response of an infinite Timoshenko beam on a viscoelastic foundation to a harmonic moving load // Journal of Sound and Vibration. 2001. V. 241. № 5. P. 809–824.

  24. Весницкий А.И. Волны в системах с движущимися границами и нагрузками. М.: Наука, Физматлит, 2001. 320 с.

  25. Metrikine A.V., Verichev S.N. Instability of a moving two-mass oscillator on a flexibly supported Timoshenko beam // Archive of Applied Mechanics. 2001. V. 71. P. 613–624.

  26. Veritchev S.N. Instability of a vehicle moving on an elastic structure. The Netherlands: Delft University Press, 2002. 190 p.

  27. Suiker A.S.J. The mechanical behaviour of ballasted railway tracks. The Netherlands: Delft University Press, 2002. 236 p.

  28. Иванченко И.И. Динамика транспортных сооружений: высокоскоростные подвижные, сейсмические и ударные нагрузки. М.: Наука, 2011. 574 с.

  29. Метрикин А.В., Веричев С.Н., Вострухов А.В. Фундаментальные задачи высокоскоростного наземного транспорта. Saarbrucken, Deutschland: Lambert Academy Publishing. 2014. 200 с.

  30. Гафуров У.С., Земсков А.В., Тарлаковский Д.В. Алгоритм построения поверхностных функций Грина в задаче о нестационарных колебаниях балки Тимошенко с учетом диффузии // Динамические и технологические проблемы механики конструкций и сплошных сред. Материалы XXV международного симпозиума им. А.Г. Горшкова. М.: МАИ, 2019. С. 55–57.

  31. Тимошенко С.П. Статические и динамические проблемы теории упругости. Киев: Наукова думка, 1975. 563 с.

  32. Ерофеев В.И., Кажаев В.В., Лисенкова Е.Е., Семерикова Н.П. Несинусоидальные изгибные волны в балке Тимошенко, лежащей на нелинейно-упругом основании // Проблемы машиностроения и надежности машин. 2008. № 3. С. 30–36.

  33. Весницкий А.И., Романов Н.Д. К построению демпфера гашения изгибных колебаний балки // Прикладная механика. 1988. Т. 26. № 6. С. 122–124.

  34. Reissner E. On postbuckling behavior and imperfection sensitivity of thin elastic plates on a non-linear elastic foundation // Studies in Appl. Math. 1970. V. XLIX. № 1. P. 45–57.

  35. Ерофеев В.И., Кажаев В.В., Семерикова Н.П. Волны в стержнях. Дисперсия. Диссипация. Нелинейность. М.: Физматлит, 2002. 208 с.

  36. Островский Л.А. Нелинейные внутренние волны во вращающемся океане // Океанология. 1978. Т. 18. № 2. С. 181–191.

  37. Островский Л.А., Степанянц Ю.А. Нелинейные волны во вращающейся жидкости // Нелинейные волны: физика и астрофизика. М.: Наука, 1993. С. 132–153.

  38. Гандариас М.Л., Брузон М.С. Симметрийный анализ и точные решения для некоторых уравнений Островского // Теоретическая и математическая физика. 2011. Т. 168. № 1. С. 49–64.

  39. Stepanyants Y.A. On stationary solutions of the reduced Ostrovsky equation: Periodic waves, compactons and compound solitons // Chaos, Solitons and Fractals. 2006. V. 28. P. 193–204.

  40. Степанянц Ю.А. Нелинейные волны во вращающемся океане (уравнение Островского, его обобщения и приложения) // Известия РАН. Физика атмосферы и океана. 2020. Т. 56. № 1. С. 20–42.

  41. Рыскин Н.М., Трубецков Д.И. Нелинейные волны. М.: Ленанд, 2017. 312 с.

  42. Кудряшов Н.А. Методы нелинейной математической физики: Учебное пособие. Долгопрудный: Интеллект, 2010. 368 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал