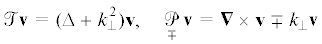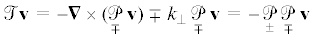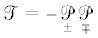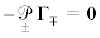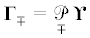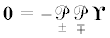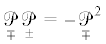Известия РАН. Механика твердого тела, 2021, № 2, стр. 148-156

ПРЕДСТАВЛЕНИЕ ПЕРЕМЕЩЕНИЙ В ПРОСТРАНСТВЕННОЙ ГАРМОНИЧЕСКОЙ ЗАДАЧЕ ТЕОРИИ УПРУГОСТИ С ПОМОЩЬЮ ДВУХ ВИНТОВЫХ ВЕКТОРОВ

Ю. Н. Радаев^a, *, **

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

^* E-mail: radayev@ipmnet.ru
^** E-mail: y.radayev@gmail.com

Поступила в редакцию 11.11.2019
После доработки 18.11.2019
Принята к публикации 20.11.2019

DOI: 10.31857/S057232992102015X

Аннотация

Рассматриваются дифференциальные уравнения для потенциалов, обеспечивающие выполнение основного векторного дифференциального уравнения линейной теории упругости в случае гармонической зависимости поля перемещений от времени. Развивается альтернативная схема расщепления векторного дифференциального уравнения линейной теории упругости на несвязанные уравнения. Она основана на понятии о гамма-векторе, удовлетворяющем винтовому уравнению. В результате проблема нахождения вихревой составляющей поля перемещений сводится к последовательному решению несвязанных между собой винтовых дифференциальных уравнений первого порядка с частными производными. Сформулирована и доказана теорема о полноте представления поля перемещений с помощью двух винтовых вихревых векторных полей.

Ключевые слова: теория упругости, вектор перемещения, скалярный потенциал, векторный потенциал, гамма-вектор, вихревой вектор, винтовое уравнение, полнота представления

1. Предварительные сведения и вводные замечания. Пространственная гармоническая задача теории упругости за свою многолетнюю историю не потеряла своей актуальности и по-прежнему может характеризоваться как важнейший инструмент исследования целого спектра прикладных задач механики деформируемого твердого тела, строительной механики, механики кораблестроения, механики грунтов, моделирования работы механизмов и машин. Ей посвящена обширная научная литература (см., например, [1–6]). Родственные проблемы и постановки задач возникают также в термоупругости [7] и особенно в вопросах распространения гармонических волн в гиперболических термоупругих средах [8]. В настоящей работе развивается альтернативная (по отношению к обычно применяемым в прикладных проблемах) схема расщепления основного векторного дифференциального уравнения гармонической линейной теории упругости на несвязанные уравнения. Последние будут иметь форму винтовых уравнений, поэтому ниже будут приведены необходимые сведения, касающиеся таких уравнений (см., например, [9]).

Векторное поле $\Upsilon $ называется винтовым (screw field), если оно удовлетворяет следующему свойству:

$\Upsilon \times (\nabla \times \Upsilon ) = 0$

т.е. вихрь векторного поля оказывается коллинеарным направлению поля

$\nabla \times \Upsilon = A\Upsilon $

где множитель $A$ характеризуется термином анормальность (abnormality) поля. В том случае, когда множитель $A$ есть постоянная величина, все кратные вихри поля $\Upsilon $

$\nabla \times \Upsilon ,\quad \nabla \times (\nabla \times \Upsilon ),\quad \nabla \times (\nabla \times (\nabla \times \Upsilon )),\; \ldots $

также будут винтовыми полями с той же самой анормальностью A; поле $\Upsilon $ будет удовлетворять векторному уравнению Гельмгольца

$\Delta \Upsilon + {{A}^{2}}\Upsilon = 0$

винтовое поле $\Upsilon $ с постоянной анормальностью A представимо в форме

$\Upsilon = A(\nabla h) \times {\mathbf{d}} + {{A}^{2}}h{\mathbf{d}} + ({\mathbf{d}} \times \nabla )\nabla h$

где d – постоянный единичный директор, $h$ – скалярное поле, удовлетворяющее уравнению Гельмгольца

$\Delta h + {{A}^{2}}h = 0$

Скажем несколько слов о содержании работы. Сразу после вводной части, во втором разделе, рассматриваются основные уравнения линейной теории упругости в терминах вектора перемещения в случае его гармонической зависимости от времени. Вводятся скалярный и векторный потенциалы, из которых складывается представление поля перемещений в форме Ламе. Приводятся дифференциальные уравнения (уравнения Гельмгольца) для потенциалов, обеспечивающие выполнение основного векторного дифференциального уравнения линейной теории упругости (дифференциального уравнения Ламе), и обсуждаются условия калибровки векторного потенциала.

В третьем разделе статьи развивается альтернативная схема расщепления дифференциального уравнения Ламе на независимые уравнения, в основе которой лежит вектор, представляющий собой вихревую составляющую поля перемещений. В отличии от векторного потенциала указанный вектор заведомо удовлетворяет естественному калибровочному условию, устанавливающему его нулевую расходимость. В этом же разделе вводится понятие о гамма-векторах в гармонической задаче теории упругости. Получено уравнение первого порядка, которому должен удовлетворять гамма-вектор (так называемое винтовое уравнение (screw equation)). С помощью полученных результатов проблема нахождения вихревой составляющей поля перемещений сводится к последовательному решению двух (с учетом чередования знаков – четырех) дифференциальных уравнений первого порядка с частными производными.

Четвертый раздел посвящен исследованию одного общего представления гамма-вектора через вихревое векторное поле. Показано, что, если указанное вихревое поле удовлетворяет уравнению Гельмгольца, то дифференциальное уравнение для гамма-вектора будет выполнено в силу самого представления гамма-вектора. Здесь изложение может быть в значительной степени упрощено, если ввести два дифференциальных оператора, действующих в линейном пространстве вихревых (т.е. обладающих нулевой расходимостью) векторных полей: один из операторов имеет второй порядок, а другой – первого.

Содержание пятого раздела целиком связано с формулировкой и доказательством полноты построенных в предыдущих разделах работы представлений поля перемещений. Результаты, полученные в этом направлении, завершают описание рассматриваемой схемы решения гармонической задачи теории упругости в перемещениях.

2. Основное векторное дифференциальное уравнение гармонической линейной теории упругости. Рассмотрим трехмерную систему дифференциальных уравнений гармонической линейной теории упругости в стандартной векторной форме [6]:

(2.1)

$(\lambda + 2\mu )\nabla \nabla \times {\mathbf{u}} - \mu \nabla \times (\nabla \times {\mathbf{u}}) = \rho {{\partial }_{ \cdot }}{{\partial }_{ \cdot }}{\mathbf{u}}$

где $\rho $ – плотность; u – вектор перемещения; $\lambda $, $\mu $ – определяющие постоянные (упругие постоянные Ламе); $\nabla $ – трехмерный оператор Гамильтона; ${{\partial }_{ \cdot }}$ – частное дифференцирование по времени при фиксированных пространственных переменных.

Векторное дифференциальное уравнение (2.1) будет исследоваться в областях трехмерного пространства, обладающих свойством поверхностной односвязанности: любая замкнутая поверхность, целиком расположенная в области может быть стянута в точку, не выходя за границу области. Такое требование совершенно необходимо для того, чтобы любое безвихревое векторное поле имело бы потенциал, а любое векторное поле с нулевой расходимостью оказывалось бы вихревым, т.е. имело бы векторный потенциал.

В дальнейшем изложении зависимость от времени предполагается гармонической, т.е. физические поля представляются как произведения комплексных амплитуд (за которыми мы сохраним те же обозначения, что и для самих полей) на комплексную гармоническую экспоненту ${{e}^{{i\omega t}}}$, где $\omega $ – циклическая частота.

Поле перемещений ${\mathbf{u}}$ при любых обстоятельствах может быть представлено в форме разложения (разложения Ламе) на потенциальную и вихревую части

(2.2)

${\mathbf{u}} = \nabla \Phi + \nabla \times \Psi $

где Φ – скалярный потенциал перемещений, $\Psi $ – векторный потенциал перемещений. Необходимо отметить, что разложение Ламе обычно сопровождается тем или иным калибровочным условием на векторный потенциал. Оно, в принципе, не является обязательным и мы пока не будем выставлять никакого условия калибровки. Разложение Ламе, как известно, обладает необходимой степенью полноты [6], т.е. любое решение основного векторного дифференциального уравнения теории упругости представимо в форме (2.2).

Прежде чем переходить к уравнениям для потенциалов перемещений введем фазовые скорости двух основных типов волн в упругой среде и соответствующие волновые числа

(2.3)

$c_{\parallel }^{2} = \frac{{\lambda + 2\mu }}{\rho },\quad k_{\parallel }^{2} = \frac{{{{\omega }^{2}}}}{{c_{\parallel }^{2}}};\quad c_{ \bot }^{2} = \frac{\mu }{\rho },\quad k_{ \bot }^{2} = \frac{{{{\omega }^{2}}}}{{c_{ \bot }^{2}}}$

Дальнейший стандартный ход рассуждений состоит в следующем. Подстановка представления Ламе (2.2) в векторное дифференциальное уравнение (2.1) позволяет перейти к уравнению

(2.4)

$\nabla (k_{\parallel }^{{ - 2}}\Delta \Phi + \Phi ) + \nabla \times ( - k_{ \bot }^{{ - 2}}\nabla \times (\nabla \times \Psi ) + \Psi ) = 0$

или – к эквивалентному уравнению

(2.5)

$\nabla (k_{\parallel }^{{ - 2}}\Delta \Phi + \Phi ) + \nabla \times (k_{ \bot }^{{ - 2}}\Delta \Psi + \Psi ) = 0$

откуда получаются скалярное и векторное уравнения Гельмгольца для потенциалов поля перемещений:

(2.6)

$\Delta \Phi + k_{\parallel }^{2}\Phi = 0,\quad \Delta \Psi + k_{ \bot }^{2}\Psi = 0$

Как видно из проведенного вывода, если потенциалы $\Phi $ и $\Psi $ удовлетворяют уравнениям (2.6), то поле (2.2) удовлетворяет дифференциальному уравнению (2.1). При этом нет необходимости привлекать какое бы то ни было условие калибровки. Ясно, что приведенное выше заключение актуально также при навязывании того или иного калибровочного условия; в частности, стандартного условия калибровки (когда расходимость векторного потенциала объявляется равной нулю)

(2.7)

$\nabla \cdot \Psi = 0$

или более общего условия –

(2.8)

$\nabla \cdot \Psi = H$

где H – произвольная a priori заданная функция пространственных переменных и времени.

Заключая этот раздел работы обратим внимание также на то, что, несущественно изменяя ход рассуждений, вместо уравнений Гельмгольца для потенциалов (2.6) можно установить несколько более общие уравнения (h – произвольная функция пространственных переменных и времени)

(2.9)

$\Delta \Phi + k_{\parallel }^{2}\Phi = 0,\quad \Delta \Psi + k_{ \bot }^{2}\Psi = \nabla h$

3. Вихревая составляющая поля перемещений и гамма-векторы. Интересную теорию гармонической задачи линейной теории упругости удается построить, если вместо векторного потенциала в качестве фундаментального элемента теории рассматривать вихревую составляющую поля перемещений, т.е. исходить из следующего представления:

(3.1)

${\mathbf{u}} = \nabla \Phi + \Upsilon $

Здесь $\Upsilon $ — вихревая часть перемещений u, которая заведомо обладает нулевой расходимостью:

$\nabla \cdot \Upsilon = 0$

В терминах векторного потенциала вихревая часть перемещений, очевидно, вычисляется как

$\Upsilon = \nabla \times \Psi $

откуда также следует данное выше равенство.

Векторное поле $\Upsilon $ с формальной точки зрения удовлетворяет точно таким же дифференциальным уравнениям, что и векторный потенциал $\Psi $. Действительно, как нетрудно видеть уравнение (2.4) эквивалентно

(3.2)

$\nabla (k_{\parallel }^{{ - 2}}\Delta \Phi + \Phi ) - k_{ \bot }^{{ - 2}}\nabla \times (\nabla \times \Upsilon ) + \Upsilon = 0$

а это уравнение, в свою очередь, – уравнению

(3.3)

$\nabla (k_{\parallel }^{{ - 2}}\Delta \Phi + \Phi ) - k_{ \bot }^{{ - 2}}\Delta \Upsilon + \Upsilon = 0$

Таким образом, новая пара $\Phi $, $\Upsilon $ должна удовлетворять тем же самым уравнениям Гельмгольца, что и пара потенциалов $\Phi $, $\Psi $:

(3.4)

$\Delta \Phi + k_{\parallel }^{2}\Phi = 0,\quad \Delta \Upsilon + k_{ \bot }^{2}\Upsilon = 0$

правда, с уже естественным калибровочным условием

(3.5)

$\nabla \cdot \Upsilon = 0$

Стоит указать на то обстоятельство, что вектор $\Upsilon $ значительно более удобен, чем векторный потенциал $\Psi $, поскольку формулировка, например, граничных условий в случае использования $\Upsilon $ не будет содержать лишних дифференцирований по пространственным координатам. Однако наиболее важное преимущество вектора $\Upsilon $ заключается в том, что с его помощью появляется возможность развития альтернативного подхода к исследованию уравнений гармонической линейной теории упругости.

Будем исходить из дифференциального уравнения (3.2). В левой части указанного уравнения произведем следующее формальное преобразование: добавим и отнимем одно и то же слагаемое

$ \mp {{k}_{ \bot }}\nabla \times \Upsilon $

Умножая уравнение на $k_{ \bot }^{2}$ и группируя затем очевидным образом слагаемые, приходим к уравнению

$k_{ \bot }^{2}\nabla (k_{\parallel }^{{ - 2}}\Delta \Phi + \Phi ) - (\nabla \times (\nabla \times \Upsilon ) \mp {{k}_{ \bot }}\nabla \times \Upsilon ) \mp {{k}_{ \bot }}(\nabla \times \Upsilon \mp {{k}_{ \bot }}\Upsilon ) = 0$

Из полученного уравнения находится еще одно уравнение для определения вихревой части поля перемещений:

(3.6)

$ - \nabla \times (\nabla \times \Upsilon \mp {{k}_{ \bot }}\Upsilon ) \mp {{k}_{ \bot }}(\nabla \times \Upsilon \mp {{k}_{ \bot }}\Upsilon ) = 0$

Если далее ввести вектор (точнее, два вектора, которые мы будем в дальнейшем называть гамма-векторами)

(3.7)

${{\Gamma }_{ \mp }} = \nabla \times \Upsilon \mp {{k}_{ \bot }}\Upsilon $

то в результате уравнение (3.6) приобретет форму

(3.8)

$ - \nabla \times {{\Gamma }_{ \mp }} \mp {{k}_{ \bot }}{{\Gamma }_{ \mp }} = 0$

Уравнение (3.8) в механике и математической физике называется винтовым. Оно имеет основное значение во всем последующем изложении. Сейчас лишь заметим, что каждое решение дифференциального уравнения первого порядка (3.8) будет на основании уравнения (3.11) определять вихревую часть поля перемещений $\Upsilon $. Следовательно, указанная вихревая часть получается последовательным интегрированием (если оно оказывается возможным) двух дифференциальных уравнений в частных производных первого порядка.

Точно так же, как и $\Upsilon $, гамма-вектор ${{\Gamma }_{ \mp }}$ заведомо будет удовлетворять естественному калибровочному условию

(3.9)

$\nabla \cdot {{\Gamma }_{ \mp }} = 0$

В изложенной выше схеме важным является то, что речь идет по существу о двух независимых векторах ${{\Upsilon }_{ - }}$ и ${{\Upsilon }_{ + }}$, сумма которых также может выступать в качестве вихревой составляющей поля перемещений, т.е. о решениях основного векторного дифференциального уравнения следующего вида:

(3.10)

${\mathbf{u}} = \nabla \Phi + {{\Upsilon }_{ - }} + {{\Upsilon }_{ + }}$

В качестве простого примера рассмотрим случай нулевого гамма-вектора ${{\Gamma }_{ \mp }}$:

${{\Gamma }_{ \mp }} = 0$

Ясно, что дифференциальное уравнение (3.8) удовлетворяется, поэтому вихревая составляющая поля перемещений будет интегралом векторного дифференциального уравнения

(3.11)

$\nabla \cdot \Upsilon \mp {{k}_{ \bot }}\Upsilon = 0$

который обладает естественной калибровкой (3.5). Точнее, здесь речь идет о паре независимых интегралов уравнений

(3.12)

$\begin{gathered} \nabla \times \Upsilon - {{k}_{ \bot }}\Upsilon = 0 \\ \nabla \times \Upsilon + {{k}_{ \bot }}\Upsilon = 0 \\ \end{gathered} $

4. Гамма-вектор и уравнение Гельмгольца для вихревого поля. Проведенные в предыдущем разделе работы рассуждения, а именно определение гамма-векторов и вывод дифференциальных уравнений для них¹ ¹, на самом деле оказываются тесно связанными с решениями векторного уравнения Гельмгольца с естественной калибровкой. Сейчас мы точно сформулируем соответствующее утверждение.

Если гамма-вектор $\Gamma $ представим с помощью вихревого векторного поля $\Upsilon $ в форме

(4.1)

$\Gamma = \nabla \times \Upsilon \mp {{k}_{ \bot }}\Upsilon $

с вектором $\Upsilon $, удовлетворяющим уравнению Гельмгольца и естественному условию калибровки, то гамма-вектор (4.1) является решением дифференциального уравнения с частными производными первого порядка

(4.2)

$ - \nabla \times \Gamma \mp {{k}_{ \bot }}\Gamma = 0$

и также удовлетворяет естественному условию калибровки.

Сформулированное утверждение допускает простое доказательство. Действительно, поскольку вектор $\Upsilon $ удовлетворяет уравнению Гельмгольца и обладает нулевой расходимостью, то

$\begin{gathered} \Delta \Upsilon + k_{ \bot }^{2}\Upsilon = - \nabla \times (\nabla \times \Upsilon ) + k_{ \bot }^{2}\Upsilon = \\ = \; - (\nabla \times (\nabla \times \Upsilon ) \mp {{k}_{ \bot }}\nabla \times \Upsilon ) \mp {{k}_{ \bot }}(\nabla \times \Upsilon \mp {{k}_{ \bot }}\Upsilon ) = 0 \\ \end{gathered} $

откуда на основании (4.1) следует (4.2).

Ситуация становится намного более ясной, если принять более компактные обозначения. С этой целью введем в рассмотрение два дифференциальных оператора, действующих в линейном пространстве вихревых векторных полей, согласно

(4.3)

где v – произвольное вихревое векторное поле.

Прежде всего заметим, что для любого вихревого векторного поля выполняется

т.е. для дифференциального оператора Гельмгольца справедливо следующее мультипликативное разложение:

(4.4)

Дифференциальное уравнение для гамма-вектора (4.2) в операторной форме будет иметь вид

(4.5)

Ясно, что последнее уравнение имеет решение в форме

только при условии

и в силу (4.4), только при условии

$0 = \mathcal{T}\Upsilon $

т.е. когда векторное поле $\Upsilon $ удовлетворяет уравнению Гельмгольца.

Заключая этот раздел работы, заметим, что

5. Представление с помощью винтовых векторных полей. Полнота представления поля перемещений. Как следует из полученных в предыдущих разделах работы результатов интерес представляют решения уравнений гармонической задачи теории упругости в перемещениях в форме (3.10), в которой вихревые составляющие удовлетворяют дифференциальным уравнениям первого порядка (3.12), скалярный потенциал $\Phi $ уравнению Гельмгольца:

(5.1)

$\Delta \Phi + k_{\parallel }^{2}\Phi = 0$

Ясно, прежде всего, что такая форма представления вектора перемещений должна быть весьма ограниченной, поскольку она характеризуется нулевыми гамма-векторами. В принципе, набор гамма-векторов значительно шире, но даже этот вариант обладает необходимой полнотой: любое решение гармонического векторного уравнения линейной теории упругости может быть представлено в форме

(5.2)

${\mathbf{u}} = \nabla \Phi + {{\Upsilon }_{ - }} + {{\Upsilon }_{ + }}$

с потенциалом $\Phi $ и вихревыми винтовыми полями (screw fields) ${{\Upsilon }_{ - }}$, ${{\Upsilon }_{ + }}$, удовлетворяющими несвязанным дифференциальным уравнениям

(5.3)

$\begin{gathered} \Delta \Phi + k_{\parallel }^{2}\Phi = 0 \\ \nabla \times {{\Upsilon }_{ - }} - {{k}_{ \bot }}{{\Upsilon }_{ - }} = 0 \\ \nabla \times {{\Upsilon }_{ + }} + {{k}_{ \bot }}{{\Upsilon }_{ + }} = 0 \\ \end{gathered} $

Приведем формальное доказательство сформулированного утверждения о полноте. Допустим, что u – произвольное решение гармонических уравнений теории упругости. На основании векторного гармонического уравнения теории упругости разложим поле перемещений на две составляющие (вихревую и безвихревую):

${\mathbf{u}} = \mathop {\mathbf{u}}\limits^* \, + \mathop {\mathbf{u}}\limits_* $

где

$\begin{gathered} \mathop {\mathbf{u}}\limits^* = - \frac{1}{{k_{\parallel }^{2}}}\nabla \nabla \cdot {\mathbf{u}} \\ \mathop {\mathbf{u}}\limits_* = \frac{1}{{k_{ \bot }^{2}}}\nabla \times (\nabla \times {\mathbf{u}}) \\ \end{gathered} $

Поскольку

$\nabla \cdot {\mathbf{u}} = \nabla \cdot \mathop {\mathbf{u}}\limits^* ,\quad \nabla \times {\mathbf{u}} = \nabla \times \mathop {\mathbf{u}}\limits_* $

то данные выше формулы преобразуются к виду

$\begin{gathered} \mathop {\mathbf{u}}\limits^* = - \frac{1}{{k_{\parallel }^{2}}}\nabla \nabla \cdot \mathop {\mathbf{u}}\limits^* \\ \mathop {\mathbf{u}}\limits_* = \frac{1}{{k_{ \bot }^{2}}}\nabla \times (\nabla \times \mathop {\mathbf{u}}\limits_* ) \\ \end{gathered} $

т.е. записываются только в терминах безвихревой $\mathop {\mathbf{u}}\limits^* $ и вихревой $\mathop {\mathbf{u}}\limits_* $ составляющих поля перемещений.

Обозначим через $\mathop \Phi \limits^* $ потенциал безвихревого векторного поля $\mathop {\mathbf{u}}\limits^* $ так, что

$\mathop {\mathbf{u}}\limits^* = \nabla \mathop \Phi \limits^* $

Как нетрудно заметить

$\nabla (\Delta \mathop \Phi \limits^* \, + k_{\parallel }^{2}\mathop \Phi \limits^* ) = 0$

откуда (C – произвольная постоянная)

$\Delta \mathop \Phi \limits^* \, + k_{\parallel }^{2}\mathop \Phi \limits^* = k_{\parallel }^{2}C$

и, вводя функцию

$\Phi = \mathop \Phi \limits^* \, - C$

находим, что

$\mathop {\mathbf{u}}\limits^* = \nabla \Phi $

с потенциалом, удовлетворяющим уравнению Гельмгольца

$\Delta \Phi + k_{\parallel }^{2}\Phi = 0$

Остается рассмотреть вихревую часть поля перемещений $\mathop {\mathbf{u}}\limits_* $. Она удовлетворяет уравнению

$ - \nabla \times (\nabla \times \mathop {\mathbf{u}}\limits_* ) + k_{ \bot }^{2}\mathop {\mathbf{u}}\limits_* = 0$

или также

$ - (\nabla \times (\nabla \times \mathop {\mathbf{u}}\limits_* ) - {{k}_{ \bot }}\nabla \times \mathop {\mathbf{u}}\limits_* ) - {{k}_{ \bot }}(\nabla \times \mathop {\mathbf{u}}\limits_* \, - {{k}_{ \bot }}\mathop {\mathbf{u}}\limits_* ) = 0$

Полученное уравнение, обозначая

${{{\mathbf{P}}}_{ - }} = \nabla \times \mathop {\mathbf{u}}\limits_* \, - {{k}_{ \bot }}\mathop {\mathbf{u}}\limits_* $

переписываем в форме

$ - \nabla \times {{{\mathbf{P}}}_{ - }} - {{k}_{ \bot }}{{{\mathbf{P}}}_{ - }} = 0$

Рассуждая аналогично, введем вектор

${{{\mathbf{P}}}_{ + }} = \nabla \times \mathop {\mathbf{u}}\limits_* \, + {{k}_{ \bot }}\mathop {\mathbf{u}}\limits_* $

для которого, в свою очередь, получается уравнение

$ - \nabla \times {{{\mathbf{P}}}_{ + }} + {{k}_{ \bot }}{{{\mathbf{P}}}_{ + }} = 0$

Замечая, наконец, что

$\mathop {\mathbf{u}}\limits_* = \frac{{{{{\mathbf{P}}}_{ + }} - {{{\mathbf{P}}}_{ - }}}}{{2{{k}_{ \bot }}}}$

и производя переобозначения

${{{\mathbf{P}}}_{ + }} = 2{{k}_{ \bot }}{{\Upsilon }_{ - }},\quad {{{\mathbf{P}}}_{ - }} = - 2{{k}_{ \bot }}{{\Upsilon }_{ + }}$

приходим к следующему соотношению для вихревой части поля перемещений:

$\mathop {\mathbf{u}}\limits_* = {{\Upsilon }_{ - }} + {{\Upsilon }_{ + }}$

Таким образом, произвольное решение гармонического векторного уравнения теории упругости всегда представляется в форме (5.2), составляющие которой должны удовлетворять несвязанным уравнениям (5.3).

6. Заключение. 1. Исследуется трехмерное векторное дифференциальное уравнение линейной теории упругости в случае гармонической зависимости поля перемещений от времени.

2. Обсуждаются уравнения для скалярного и векторного потенциала, задающих поле перемещений в соответствии с представлением Ламе, выполнение которых обеспечивает выполнение основного векторного уравнения линейной теории упругости.

3. Показано, что теория гармонической задачи может быть развита, не опираясь на какое бы то ни было калибровочное условие, навязываемое на векторный потенциал поля перемещений.

4. Предложена альтернативная схема расщепления векторного дифференциального уравнения Ламе сначала на два, а затем на три несвязанных дифференциальных уравнения.

5. Вводится понятие о гамма-векторах, определяющих сложность форм дифференциальных уравнений в процессе расщепления уравнения Ламе. Гамма-векторы удовлетворяют винтовому уравнению и образуют винтовое векторное поле.

6. Найдено общее представление гамма-вектора через вихревое векторное поле, удовлетворяющее уравнению Гельмгольца.

7. Сформулирована и доказана теорема о полноте рассматриваемых в работе представлений гармонического поля перемещений с помощью двух винтовых векторных полей.

Работа выполнена по теме государственного задания (госрегистрации AAAA-A20-120011690132-4) и при частичной финансовой поддержке Российского фонда фундаментальных исследований (проект 18-01-00844 Моделирование термомеханических процессов в сложных средах с помощью принципа термомеханической ортогональности).

Список литературы

Саусвелл Р.В. Введение в теорию упругости для инженеров и физиков. М.: Гос. изд-во иностр. лит-ры, 1948. 676 с.
Кольский Г. Волны напряжений в твердых телах. М.: Изд-во иностр. лит-ры, 1955. 192 с.
Снеддон И.Н., Берри Д.С. Классическая теория упругости. М.: Физматгиз, 1961. 220 с.
Ландау Л.Д., Лифшиц Е.М. Теория упругости. Изд. третье. М.: Наука, 1965. 204 с.
Бреховских Л.М., Гончаров В.В. Введение в механику сплошных сред (в приложении к теории волн). М.: Наука, 1982. 336 с.
Новацкий В. Теория упругости. М.: Мир, 1975. 872 с.
Новацкий В. Динамические задачи термоупругости. М.: Мир, 1970. 256 с.
Ковалев В.А., Радаев Ю.Н. Волновые задачи теории поля и термомеханика. Саратов: Изд-во Сарат. ун-та, 2010. 328 с.
Truesdell C., Toupin R. The Classical Field Theories / Encyclopedia of Physics. V. III/1. Principles of Classical Mechanics and Field Theory. Berlin–Gottingen–Heidelberg: Springer, 1960. P. 226–902.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал