Известия РАН. Механика твердого тела, 2021, № 2, стр. 133-147

1. Введение. Идея использования в конструкции ветроустановки пары роторов, вращающихся в противоположных направлениях, наиболее популярна для турбин с горизонтальными осями вращения (например, [1–5]). В подобных устройствах ротор генератора закреплен на валу одного пропеллера, а статор – на валу другого, так что угловая скорость ротора относительно статора увеличивается при вращении пропеллеров в противоположных направлениях. Помимо этого для горизонтально-осевых турбин присутствует значительное влияние каждого пропеллера на характеристики потока воздуха, взаимодействующего с другим пропеллером. Таким образом, в подобных ветроэнергетических установках присутствует и электромеханическое и аэродинамическое взаимодействие между пропеллерами, вращающимися в противоположных направлениях.

Ситуация с вращающимися навстречу друг другу вертикально-осевыми роторами значительно отличается. Можно выделить как минимум два типа таких турбин. Предполагается, что для турбин первого типа имеет место существенное аэродинамическое взаимодействие между встречно вращающимися роторами без какого-либо электромеханического взаимодействия (например, [6, 7]). Для второго типа присутствует электромеханическое взаимодействие, тогда как аэродинамическим взаимодействием можно пренебречь: например, один ротор расположен над другим ([8]). Последний тип ветроустановок описан в литературе лишь фрагментарно.

В этой статье рассмотрим тот тип двухроторных вертикально-осевых ветроустановок, для которого можно пренебречь аэродинамическим взаимодействием между элементами. Такие установки имеют следующее преимущество по сравнению с классическими: скорость вращения ротора генератора относительно статора увеличивается без использования зубчатой передачи. Важность увеличения относительной угловой скорости обсуждалась ранее (например, в [9]). Отметим также, что вертикально-осевые ветроустановки (в частности, двухроторные) в отличие от горизонтально-осевых не нуждаются в ориентации относительно направления ветра.

В [10] была предложена малопараметрическая математическая модель для классической однороторной вертикально-осевой установки типа Дарье. Подобные модели позволяют проводить детальный параметрический анализ режимов работы турбины. В [10] для анализа поведения системы был применен метод, включающий процедуру одночастотного усреднения.

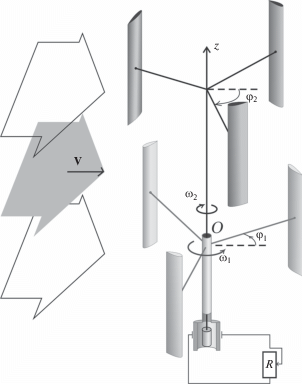
В предлагаемой работе рассматривается малая двухроторная вертикально-осевая установка типа Дарье (рис. 1). Построена замкнутая малопараметрическая математическая модель этой системы, учитывающая электрическую нагрузку в локальной цепи генератора. Для анализа режимов работы установки применено двухчастотное усреднение. Получены общие условия, при которых двухчастотное усреднение в модели двойной ветротурбины Дарье является корректным на конечном интервале времени. Проведен качественный параметрический анализ динамики усредненной системы. Получены оценки механической мощности ветротурбины. Проведено численное сравнение поведения полной и усредненной систем.

2. Описание механической системы. Рассмотрим ротор типа Дарье, который состоит из центрального вала, нескольких жестко закрепленных на нем радиальных державок, на каждой державке жестко закреплена лопасть – профилированное крыло. Как правило, на практике используют две или три лопасти. Будем рассматривать ротор с тремя лопастями. Система состоит из двух таких роторов. Роторы установлены в горизонтальном потоке воздуха один над другим так, что валы роторов соосны и вертикальны. Схема механической системы приведена на рис. 1.

Считаем, что лопасти роторов профилированы одинаково, но ориентированы “навстречу друг другу” – таким образом, чтобы по возможности обеспечивать вращение роторов в противоположных направлениях. На валу одного ротора жестко закреплен ротор электрогенератора; на валу другого – статор того же генератора. Генератор подключен к локальной электрической цепи. Внешнее сопротивление R в цепи генератора является варьируемым параметром модели.

Пусть ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$ – углы поворота нижнего и верхнего роторов. Эти углы отсчитываются от направления скорости потока против часовой стрелки и по часовой стрелке, соответственно, если наблюдать с конца оси вращения Oz.

Предполагается, что φ₁ – это угол между направлением ветра и державкой одной из лопастей нижнего ротора, которая выбрана в качестве “первой” лопасти. Тогда угол между направлением ветра и державкой лопасти “с номером k” составляет φ₁ + $2\pi (k - 1){\text{/}}3$. Заменяя φ₁ на φ₂, получаем аналогичные формулы для углов положения радиальных державок верхнего ротора.

Пусть J₁, J₂ – моменты инерции относительно оси вращения Oz для первого и второго роторов.

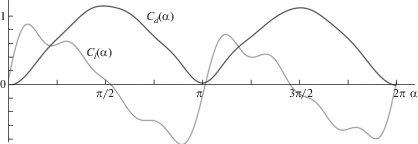
Пусть h – высота лопасти, S – характерная площадь лопасти. Аэродинамический профиль каждой лопасти характеризуется коэффициентами ${{C}_{d}}(\alpha )$ и ${{C}_{l}}(\alpha )$ силы сопротивления и подъемной силы, соответственно. Здесь α – мгновенный угол атаки. При численных расчетах будем использовать для аэродинамических коэффициентов аналитические аппроксимации (рис. 2) экспериментальных данных, которые соответствуют профилю RAF34 (результаты экспериментов взяты из [11]). Считаем, что хорда профиля лопасти перпендикулярна направлению от центра давления (точки приложения аэродинамических сил) к оси вращения ротора. Пренебрегаем возможным перемещением центра давления вдоль профиля. Расстояние от центра давления до оси Oz вращения ротора обозначим r.

Пусть V – скорость потока воздуха, ρ – плотность воздуха, ${{\omega }_{1}} = r{{\dot {\varphi }}_{1}}{\text{/}}V$ – быстроходность первого ротора, ${{\omega }_{2}} = r{{\dot {\varphi }}_{2}}{\text{/}}V$ – второго.

Для описания аэродинамических сил, действующих на каждую лопасть, используется квазистатическая модель [12–14]. Далее, D – сила сопротивления, L – подъемная сила, U – воздушная скорость центра давления лопасти, величины u и w являются промежуточными переменными, k – номер лопасти:

При вычислении величин u_k, w_k для первого/второго ротора подставляем $\varphi = {{\varphi }_{i}}$, $\omega = {{\omega }_{i}}$, соответственно.

Взаимодействие между ротором и статором генератора описывается электромеханическим моментом. Предполагается, что этот момент является линейной функцией угловой скорости ротора относительно статора [12]:

Здесь С – коэффициент электромеханического взаимодействия, σ – внутреннее сопротивление генератора, R – внешнее сопротивление в локальной электрической цепи генератора. Момент T действует со стороны первого ротора на второй и направлен так, что замедляет вращение второго ротора. Такой же по величине момент действует со стороны второго ротора на первый и направлен так, что замедляет вращение первого ротора.

3. Уравнения движения и постановка задачи. Уравнения движения системы могут быть представлены в следующем безразмерном виде:

Система (3.1) дополняется соотношениями (2.1).

Коэффициент c внешней нагрузки характеризует изменяемые условия работы ветроустановки, а именно скорость ветра и внешнее сопротивление в цепи генератора. Чем больше потребителей в цепи, тем меньше R и больше c. Решение системы уравнений (3.1) с периодическими или близкими к периодическим (например, квазипериодическими) функциями ${{\omega }_{1}}(t)$, ${{\omega }_{2}}(t)$ соответствует режиму перманентного вращения обоих роторов. Если это решение притягивающее, оно соответствует рабочему режиму устройства.

Представляет интерес найти и описать установившиеся периодические и квазипериодические решения ${{\omega }_{1}}(t)$, ${{\omega }_{2}}(t)$ системы (3.1) в предположении, что ε – малый параметр, а также оценить механическую мощность ветротурбины на соответствующих режимах. На практике достаточно малые значения ε могут быть получены путем увеличения моментов инерции роторов.

4. Усреднение по двум углам. Предположим, что ε – малый параметр системы (3.1). Рассмотрим поведение системы в фазовой области $G = \{ {{\omega }_{1}} > {{\omega }_{0}} > 0,\;{{\omega }_{2}} > {{\omega }_{0}} > 0\} $, где ${{\omega }_{0}}$ – некоторое положительное значение (не являющееся малой величиной). Тогда оба угла ${{\varphi }_{1}}$ и ${{\varphi }_{2}}$ являются быстрыми переменными, а обе безразмерные угловые скорости ${{\omega }_{1}}$ и ${{\omega }_{2}}$ – медленными.

Для проведения конструктивного параметрического анализа фазовых траекторий (3.1) удобно начать с усреднения по обеим быстрым переменным. Формальное усреднение по двум углам приводит к следующей системе:

Здесь переменные ${{\Omega }_{1}}$, ${{\Omega }_{2}}$ соответствуют осредненным значениям переменных ${{\omega }_{1}}$ и ${{\omega }_{2}}$. Решения системы (4.1) будем рассматривать в качестве первого приближения поведения переменных ${{\omega }_{1}}$ и ${{\omega }_{2}}$. Однако, если в некоторый момент времени отношение частот ${{\omega }_{1}}$ и ${{\omega }_{2}}$ станет близким к рациональному числу, то дальнейшая эволюция переменных ${{\omega }_{i}}$ может, вообще говоря, существенно отличаться от эволюции переменных ${{\Omega }_{i}}$, поскольку прохождение через резонансы зачастую приводит с весьма сложным динамическим эффектам [15–22]. Для резонансного случая построим систему первого приближения, используя подход аналогичный [16, 19].

В области G угол ${{\varphi }_{1}}$ можно принять за новое время. Тогда система (3.1) примет вид:

Здесь ${{f}_{1}}({{\varphi }_{1}},{{\omega }_{1}},{{\omega }_{2}}) = f({{\varphi }_{1}},{{\omega }_{1}}) - c({{\omega }_{1}} + {{\omega }_{2}})$, ${{f}_{2}}({{\varphi }_{2}},{{\omega }_{1}},{{\omega }_{2}}) = a(f({{\varphi }_{2}},{{\omega }_{2}}) - c({{\omega }_{1}} + {{\omega }_{2}}))$.

Обе функции f₁ и f₂ являются 2π-периодическими по отношению к первому аргументу и являются бесконечно дифференцируемыми по всем аргументам. Отметим, что дальнейшие аналитические преобразования не используют сходства функций  f₁ и f₂  друг с другом.

Предположим, что система находится в ε-окрестности резонанса:

Здесь m, n – натуральные числа, $g({{\omega }_{1}},{{\omega }_{2}})$ – некоторая бесконечно дифференцируемая функция порядка O(1) или выше.

Введем новую угловую координату:

Координата $\psi $ является медленной переменной. Перепишем систему (4.2) в переменных $\psi $, ${{\omega }_{1}}$, ${{\omega }_{2}}$:

Все переменные системы (4.3) являются медленными переменными, все функции в правой части бесконечно дифференцируемы, период правой части относительно ${{\varphi }_{1}}$ равен 2πn. Применяя классическое одночастотное усреднение [18] к системе (4.3), получаем следующие уравнения:

Отметим, что первое уравнение (4.4) отделено от двух других. Кроме того, имеет место следующее равенство:

Таким образом, два последних уравнения (4.4) преобразуются в следующую систему:

Система (4.5) с точностью до замены времени совпадает с результатом (4.1) прямого двухчастотного усреднения системы (3.1). Система (4.5) не зависит от резонансного отношения n/m. Таким образом, показано, что в области G система первого приближения для уравнений (3.1) имеет вид (4.1) в том числе и в окрестностях резонансов.

Отметим, что система вида близкого к (4.1) обсуждалась в [5] в рамках модели горизонтально-осевой турбины с двумя пропеллерами, вращающимися в противоположных направлениях.

На интервале времени порядка ε^–1 отличие между решениями ${{\omega }_{i}}(t)$ системы (3.1) и ${{\Omega }_{i}}(t)$ системы (4.1) имеет порядок ε при ${{\omega }_{i}} \in G$, если система (3.1) в соответствующей области удовлетворяет условиям теоремы об усреднении по двум углам, приведенной в [16] (в окрестности резонанса достаточно использовать результат об усреднении по времени [18]). Однако не удается применить результаты [18] для описания соответствия систем (4.3) и (4.4) на бесконечном интервале времени, поскольку отделение уравнения для $\psi $ сопряжено с дополнительным вырождением системы.

5. Неподвижные точки усредненной системы как первое приближение рабочих режимов ветроустановки. Стационарные и квазистационарные режимы работы двойной ветротурбины Дарье соответствуют периодическим и близким к периодическим решениям системы (3.1). В качестве первого приближения для таких решений рассмотрим неподвижные точки системы (4.1), а также циклы системы (4.1), если последние существуют. Подобный подход применен для описания установившихся ротационных движений твердого тела в [23, 24].

Неподвижная точка $(\Omega _{1}^{*},\Omega _{2}^{*})$ системы (4.1) определяется из соотношений:

В частности, для любого $\Omega _{1}^{*}$ существует неподвижная точка, в которой $\Omega _{2}^{*} = \Omega _{1}^{*}$. Такие неподвижные точки образуют одну из ветвей бифуркационной диаграммы $\Omega _{1}^{*}(c)$. Далее будем называть такую ветвь диаграммы неподвижных точек основной. Если функция $F(\Omega )$ немонотонна, то для $\Omega _{1}^{*}$ из некоторого диапазона существуют одно или несколько (в зависимости от числа экстремумов функции $F(\Omega )$) значений $\Omega _{2}^{*} \ne \Omega _{1}^{*}$ таких, что $F(\Omega _{1}^{*}) = F(\Omega _{2}^{*})$. Соответствующие ветви бифуркационной кривой будем называть дополнительными. Отметим, что для одиночного (классического) ротора типа Дарье, идентичного одному из роторов пары, бифуркационная диаграмма с точностью до масштабирования оси абсцисс совпадает с основной ветвью диаграммы $\Omega _{1}^{*}(c)$; при этом дополнительные ветви диаграммы стационарных режимов в случае одиночного ротора отсутствуют ([10]).

Достаточные условия асимптотической устойчивости неподвижной точки:

Здесь использованы обозначения: $F{\kern 1pt} {\text{'}}(\Omega _{1}^{*}) = {{\left. {\left( {dF{\text{/}}d\Omega } \right)} \right|}_{{\Omega = \Omega _{1}^{*}}}}$, $F{\kern 1pt} {\text{'}}(\Omega _{2}^{*}) = {{\left. {\left( {dF{\text{/}}d\Omega } \right)} \right|}_{{\Omega = \Omega _{2}^{*}}}}$.

Характеристический полином, соответствующий стационарной точке системы (4.1), имеет вид: ${{\lambda }^{2}} + \varepsilon {{G}_{1}}\lambda + a{{\varepsilon }^{2}}{{G}_{2}} = 0$.

Если выполнено хотя бы одно из неравенств ${{G}_{1}} < 0$ или ${{G}_{2}} < 0$, то соответствующая неподвижная точка неустойчива.

5.1. Случай ${{G}_{1}} = 0$. В этом случае можно ожидать бифуркацию Андронова–Хопфа. Проверим возможность ее существования в системе (4.1). Предположим, что при некоторых значениях параметров существует неподвижная точка, для которой ${{G}_{1}} = 0$ (т.е. $F{\kern 1pt} {\text{'}}(\Omega _{1}^{*})$ = $ - aF{\kern 1pt} {\text{'}}(\Omega _{2}^{*}) + c(a + 1)$). Для такой точки получаем ${{G}_{2}} = - a{{(F{\kern 1pt} {\text{'}}(\Omega _{2}^{*}) + c)}^{2}} - {{c}^{2}}$. Таким образом, ситуация ${{G}_{1}} = 0$, ${{G}_{2}} > 0$, а, следовательно, и бифуркация Андронова–Хопфа, в системе (4.1) невозможны. Случай ${{G}_{1}} = {{G}_{2}} = 0$ возможен, но является негрубым (устраняется сколь угодно малым изменением функции $F(\Omega )$).

5.2. Случай ${{G}_{2}} = 0$. Рассмотрим случай потери устойчивости неподвижной точки, сопровождающийся сменой знака коэффициента ${{G}_{2}}$ (т.е. $F{\kern 1pt} {\text{'}}(\Omega _{1}^{*})F{\kern 1pt} {\text{'}}(\Omega _{2}^{*})$ = $c(F{\kern 1pt} {\text{'}}(\Omega _{1}^{*})$ + + $F{\kern 1pt} {\text{'}}(\Omega _{2}^{*}))$). В то же время для неподвижных точек системы выполнены соотношения (5.1), а, следовательно:

Таким образом, если ${{G}_{2}} = 0$ и при этом $F{\kern 1pt} {\text{'}}(\Omega _{2}^{*})(\Omega _{1}^{*} + \Omega _{2}^{*}) \ne 0$, то выполнено $dc{\text{/}}d\Omega _{1}^{*}$ = 0, т.е. в точках смены знака коэффициента G₂ бифуркационная кривая $\Omega _{1}^{*}(c)$ имеет вертикальную касательную, по крайней мере, если $F{\kern 1pt} {\text{'}}(\Omega _{2}^{*})(\Omega _{1}^{*} + \Omega _{2}^{*}) \ne 0$. Аналогичное рассуждение справедливо для бифуркационной кривой $\Omega _{2}^{*}(c)$.

Рассмотрим отдельно случай ${{G}_{2}} = 0$, $F{\kern 1pt} {\text{'}}(\Omega _{2}^{*}) = 0$. Тогда при c > 0 выполнено $F{\kern 1pt} {\text{'}}(\Omega _{1}^{*})$ = 0. В частности, при $\Omega _{1}^{*} = \Omega _{2}^{*}$ такая неподвижная точка представляет собой седло-узел и в зависимости от направления изменения параметра с либо становится седлом, либо распадается на три неподвижные точки: два седла и устойчивый узел.

Не будем останавливаться на ситуации $F{\kern 1pt} {\text{'}}(\Omega _{1}^{*}) = F{\kern 1pt} {\text{'}}(\Omega _{2}^{*}) = 0$, $\Omega _{1}^{*} \ne \Omega _{2}^{*}$, поскольку такой случай устраняется сколь угодно малым изменением функции $F(\Omega )$.

Наконец, рассмотрим случай $\Omega _{1}^{*} + \Omega _{2}^{*} = 0$. Как видно из системы (5.1), этот случай требуется учитывать только для таких функций $F(\Omega )$, при которых существуют корни уравнения $F(\Omega ) = F( - \Omega )$. При этом значение $c$ стремится к бесконечности. Такие неподвижные точки не реализуются. При значениях $\Omega _{i}^{*}$, отвечающих корням уравнения $F(\Omega ) = F( - \Omega )$, имеет место разрыв бифуркационных кривых $\Omega _{i}^{*}(c)$ с горизонтальной асимптотой.

Из рассмотренных случаев, в частности, следует, что значения параметров a и $\varepsilon $ не влияют на то, в каких точках бифуркационных кривых $\Omega _{i}^{*}(c)$ происходит потеря устойчивости. При этом уравнения (5.1) симметричны относительно значений $\Omega _{i}^{*}$. Поэтому при построении бифуркационных кривых в зависимости от параметра c достаточно рассмотреть любую из кривых $\Omega _{i}^{*}(c)$. В связи с этим далее будем говорить об одной бифуркационной диаграмме ${{\Omega }^{*}}(c)$.

6. Пример бифуркационной диаграммы неподвижных точек усредненной системы. Стационарные значения $\Omega _{{}}^{*}(c)$ определяются уравнениями (5.1) и не зависят от параметров a и $\varepsilon $. Точки потери устойчивости определяются, как было показано, сменой знака ${{G}_{2}}$, и также не зависят от значений a и $\varepsilon $. Таким образом, значения параметров модели, определяющие величины безразмерных параметров a и ε, не влияют на вид бифуркационных кривых $\Omega _{{}}^{*}(c)$. Иными словами, первое приближение для установившихся режимов движения ветроустановки полностью определяется только аэродинамическими свойствами профиля лопасти и числом лопастей роторов (т.е. функцией $F(\Omega )$).

Рассмотрим ветроустановку с конкретными аэродинамическими характеристиками лопастей, соответствующими профилю RAF34 (рис. 2).

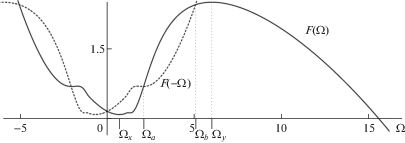
На рис. 3 приведена зависимость $F(\Omega )$, отвечающая рассматриваемому примеру. Значения, при которых достигаются локальный минимум и максимум функции $F(\Omega )$, обозначены через ${{\Omega }_{x}}$ и ${{\Omega }_{y}}$. Помимо функции $F(\Omega )$ на рис. 3 пунктирной линией показана зависимость $F( - \Omega )$ и отмечены значения ${{\Omega }_{a}}$, ${{\Omega }_{b}}$, являющиеся наряду с Ω = 0 корнями уравнения $F(\Omega ) = F( - \Omega )$. Заметим, что при других аэродинамических характеристиках профиля уравнение $F(\Omega ) = F( - \Omega )$ вполне может не иметь корней отличных от нулевого. Такой случай рассмотрен в работе [25].

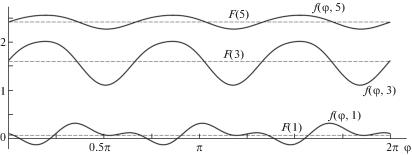
На рис. 4 приведены примеры, иллюстрирующие отклонения неосредненной функции $f(\varphi ,\Omega )$ аэродинамического момента от ее среднего значения $F(\Omega )$ при Ω = 1, 3, 5. Из рисунка видно, что отклонения функции $f(\varphi ,\Omega )$ от ее среднего значения достаточно существенны, по крайней мере, если значения Ω не очень велики. Следует отметить, что при конструировании ротора эти отклонения можно уменьшать, увеличивая число лопастей ротора.

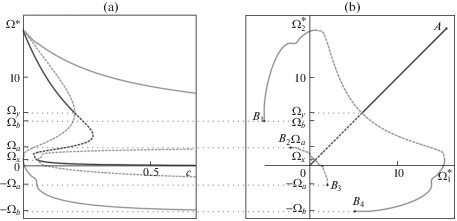
Бифуркационная кривая $\Omega {\text{*}}(c)$ – первое приближение бифуркационной диаграммы стационарных движений – приведена на рис. 5,а. На рис. 5,b показана зависимость $\Omega _{2}^{*}(\Omega _{1}^{*})$ между стационарными значениями безразмерных угловых скоростей в осредненной системе при различных значениях c. Точка A соответствует значению c = 0. Точки ${{B}_{{1 - 4}}}$ и точка $(0,0)$ отвечают предельному случаю $c \to \infty $. На рис. 5 сплошные кривые отвечают притягивающим неподвижным точкам системы (4.1), пунктирные – отталкивающим.

Точки ${{B}_{{1 - 4}}}$ на диаграмме $(\Omega _{1}^{*},\Omega _{2}^{*})$ (рис. 5,b) соответствуют корням уравнения $F(\Omega ) = F( - \Omega )$. Если последнее не имеет корней, то дополнительная ветвь диаграммы $(\Omega _{1}^{*},\Omega _{2}^{*})$ будет замкнутой. Пример соответствующей диаграммы приведен в работе [25].

На рис. 5 основная ветвь бифуркационной кривой (та, на которой $\Omega _{1}^{*} = \Omega _{2}^{*}$) показана черным цветом, дополнительные ветви ($\Omega _{1}^{*} \ne \Omega _{2}^{*}$) – серым цветом. На рис. 5,а точечными горизонтальными линиями обозначены асимптоты $\Omega * = \Omega _{a}^{{}}$, $\Omega * = \Omega _{b}^{{}}$ и точки ветвления $\Omega * = \Omega _{x}^{{}}$, $\Omega * = \Omega _{y}^{{}}$. Для рассмотренного профиля функция $F(\Omega )$ имеет еще дополнительную “слабо выраженную” пару локальных экстремумов, аргументы которых расположены между $\Omega _{x}^{{}}$ и $\Omega _{a}^{{}}$. Соответствующие им ветви бифуркационной диаграммы не приведены на рисунках, так как связанные с ними особенности поведения системы локализованы в незначительной области фазового пространства.

Отметим, что участки диаграмм $\Omega {\text{*}}(c)$ и $\Omega _{2}^{*}(\Omega _{1}^{*})$, характеризующиеся достаточно малыми значениями хотя бы одной из величин $\Omega _{i}^{*}$, не соответствуют поведению полной системы, так как вне области G процедура усреднения по двум углам некорректна.

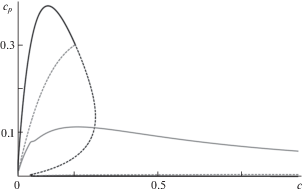
Для ветроэнергетических установок традиционно в качестве базовой характеристики эффективности выступает значение коэффициента c_p механической мощности на рабочем режиме. На рис. 6 представлена зависимость коэффициента c_p механической мощности ветротурбины от коэффициента с внешней нагрузки на установившихся режимах, построенная в первом приближении (т.е. неподвижные точки системы (4.1) используются в качестве приближения для установившихся режимов). На рисунке сплошные линии соответствуют притягивающим неподвижным точкам системы (4.1), пунктирные – отталкивающим. Черная линия соответствует основной ветви бифуркационной диаграммы неподвижных точек, серая отвечает дополнительным ветвям. Коэффициент механической мощности, отбираемой у потока, в первом приближении определен по следующей формуле:

Здесь S₀ – площадь поперечного сечения ветротурбины. Расчет c_p выполнен в предположении, что $3S{\text{/}}{{S}_{0}} = 0.01$.

Отметим, что наибольшие значения механической мощности достигаются на стационарных режимах, которые отвечают основной ветви бифуркационной диаграммы ($\Omega _{1}^{*} = \Omega _{2}^{*}$) и характеризуются значениями $\Omega {\text{*}}$, превосходящими $\Omega _{y}^{{}}$. Существенно меньше значения мощности на стационарных режимах, отвечающих дополнительной ветви ($\Omega _{1}^{*} \ne \Omega _{2}^{*}$), даже при $\Omega _{1}^{*} > \Omega _{y}^{{}}$. Стационарные режимы, на которых ни одно из значений $\Omega _{i}^{*}$ не превосходит $\Omega _{a}^{{}}$, характеризуются весьма малыми значениями мощности и для практических приложений не представляют интереса.

Отметим, что в рассмотренном примере в усредненной системе (4.1) не было обнаружено циклов.

Итак, зависимости, представленные на рис. 5, 6, в первом приближении описывают установившиеся режимы движения двухроторной ветроустановки. Справедливость предположения о соответствии между неподвижными точками системы (4.1) и периодическими/квазипериодическими траекториями полной системы (3.1) и, в особенности, вопрос о “переносе” свойств устойчивости на траектории системы (3.1) требуют дополнительного исследования. При описании аттракторов речь идет о соответствии между решениями полной и усредненной систем на бесконечном интервале времени. Аналитическое рассмотрение этого вопроса выходит за рамки данной работы. Отметим, что такого рода исследование может быть проведено на основе подходов, разработанных в [16–21]. В настоящей работе остановимся на численном исследовании соответствия между решениями ${{\omega }_{i}}(t)$ и $\Omega _{i}^{{}}(t)$ систем (3.1) и (4.1).

7. Сходство и отличия между траекториями полной и усредненной систем. Влияние величины $\varepsilon $. Численное сравнение решений ${{\omega }_{i}}(t)$ и $\Omega _{i}^{{}}(t)$, проведенное путем прямого интегрирования систем (3.1) и (4.1) при различных наборах начальных условий и различных значениях параметров a и $\varepsilon $, подтвердило следующие, вообще говоря, ожидаемые тенденции:

1) Пусть ${{\omega }_{i}}(0) = {{\Omega }_{i}}(0)$ принадлежат некоторой области W, образованной на плоскости $({{\Omega }_{1}},{{\Omega }_{2}})$ окрестностями прямых ${{\Omega }_{i}} = 0$, а также окрестностями сепаратрисных траекторий системы (4.1), и пусть ${{\varphi }_{i}}(0)$ выбраны из некоторого диапазона, зависящего от ${{\Omega }_{i}}(0)$. Тогда наблюдаются следующие варианты радикального отличия между решениями полной и усредненной систем: а) ${{\omega }_{i}}(t)$ выходит в окрестность аттрактора, расположенного около неподвижной точки системы (4.1) отличной от той, в области притяжения которой расположена точка $({{\Omega }_{1}}(0),\;{{\Omega }_{2}}(0))$; б) хотя бы одна из переменных ${{\omega }_{i}}(t)$ стремится к нулю при $t \to \infty $ или неограниченное число раз меняет знак при $t \to \infty $ (один из роторов останавливается или переходит на режим колебаний). Эта область W, в которой нецелесообразно использовать решения усредненной системы для прогнозирования поведения решений полной системы, расширяется с ростом параметра $\varepsilon $ (например, рис. 7, 8).

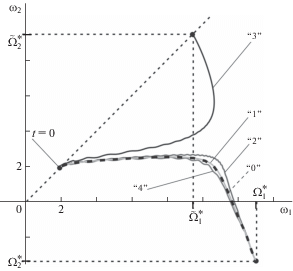
Рисунки 7, 8 построены для значения $с = 0.11$ коэффициента внешней нагрузки, поскольку именно это значение представляет особый интерес для приложений как значение, при котором достигается максимальная механическая мощность ветроустановки. Значение $a = 0.5$ выбрано для иллюстративного примера.

На рис. 7 приведен пример влияния параметра $\varepsilon $ и начальных условий по углам (${{\varphi }_{i}}(0)$) при значениях ${{\Omega }_{i}}(0)$ относительно близких к неустойчивому узлу усредненной системы ($\Omega _{i}^{*} = 1.84\; \ldots $). На рис. 7 цифрами обозначены следующие траектории: “0” – траектория усредненной системы (4.1); “1–4” – решения ${{\omega }_{i}}$ полной системы (3.1) при различных значениях параметра ε и различных начальных условиях: “1” $\varepsilon = 0.1,{{\varphi }_{i}}(0) = 1$, “2” $\varepsilon = 0.5$, ${{\varphi }_{i}}(0) = 1$, “3” ε = 1, ${{\varphi }_{i}}(0) = 1$, “4” ε = 1, ${{\varphi }_{1}}(0) = 3$, ${{\varphi }_{2}}(0)$ = 1.

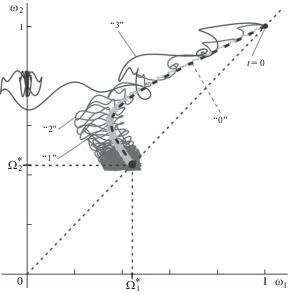
На рис. 8 приведен пример влияния параметра $\varepsilon $ при значениях ${{\omega }_{i}}$ близких к нулю. На рисунке “0” – траектория усредненной системы (4.1); “1–4” – решения ${{\omega }_{i}}$ полной системы (3.1) при различных значениях параметра ε и одних и тех же начальных условиях по угловым переменным: ${{\varphi }_{1}}(0) = 0$, ${{\varphi }_{2}}(0) = 1$. Значения параметра ε: “1” $\varepsilon = 0.1$, “2” $\varepsilon = 0.5$, “3” ε = 1. В частности, в случае ε = 1 ротор с меньшим моментом инерции переходит на режим колебаний.

2) Притягивающим неподвижным точкам (4.1) при достаточно малых $\varepsilon $ отвечают аттракторы системы (3.1). Для неподвижных точек, представляющих наибольший интерес с практической точки зрения – отвечающих режимам с большими значениями коэффициента c_p механической мощности, – диапазон по параметру ε, при котором в полной системе сохраняется соответствующий аттрактор, значительно (на несколько порядков) превосходит физически-осмысленный диапазон значений ε.

3) При $a \ne 1$ не поддерживаются резонансные соотношения между отделенными от нуля ${{\omega }_{1}}$ и ${{\omega }_{2}}$, кроме тех резонансов, которые отвечают притягивающим неподвижным точкам системы (4.1) (например, рис. 7, 8).

8. Обсуждение результатов. В качестве первого приближения для полной системы (3.1), описывающей динамику двухроторной ветроустановки типа Дарье, рассмотрена усредненная по двум углам система (4.1). Проводится аналитическое и численное исследование. При аналитическом исследовании предполагается малым значение параметра ε, который косвенно характеризует отношение плотности воздуха к средней плотности материала конструкции турбины. Отличия между медленными переменными полной системы и решениями усредненной системы имеют порядок ε на интервале времени порядка ε^–1, если полная система при нерезонансном соотношении частот удовлетворяет условиям теоремы [16] (при резонансном соотношении частот задача сводится к одночастотному усреднению и выполнены условия теоремы Крылова–Боголюбова [18]).

Для описания аттракторов полной системы в качестве первого приближения используются притягивающие неподвижные точки усредненной системы. Для оценки точности такого приближения требуется определить отличия между решениями полной и усредненной систем на бесконечном интервале времени. Эта задача выходит за рамки настоящей статьи и является одним из возможных направлений дальнейшего исследования рассмотренной системы.

Численное исследование влияния величины параметра ε на отличия между траекториями на плоскости медленных переменных полной системы и траекториями усредненной системы подтвердило, что для прикладных задач достаточно использовать данные о поведении усредненной системы (кроме движений с малыми угловыми скоростями). На практике параметр $\varepsilon $ принимает значения порядка 0.1 (или меньше).

Для неподвижных точек усредненной системы построены бифуркационные диаграммы в зависимости от параметра модели, характеризующего внешнюю электрическую нагрузку в локальной цепи генератора ветроустановки. Выявлено наличие основной ветви бифуркационной диаграммы, которая в точности аналогична бифуркационной диаграмме для одиночного ротора типа Дарье, а также продемонстрировано наличие дополнительной ветви диаграммы. Наибольшее значение коэффициента мощности достигается на основной ветви диаграммы и совпадает со значением, достижимым для однороторной ветротурбины Дарье. Основное отличие от однороторной ветротурбины на соответствующем режиме: угловая скорость ротора генератора относительно статора вдвое больше, что может снять необходимость использования дополнительной повышающей передачи в конструкции установки и тем самым значительно снизить потери энергии. Двукратное увеличение угловой скорости ротора относительно статора не приводит к росту мощности, поскольку сопровождается двукратным уменьшением эффективного электромеханического момента.

9. Заключение. Построена замкнутая математическая модель двухроторной ветротурбины типа Дарье. Выполнено двухчастотное усреднение соответствующей динамической системы по двум угловым координатам. Проанализировано влияние резонансов.

Описана область значений параметров модели и начальных условий, при которых целесообразно использовать усредненную систему для прогнозирования поведения полной системы. Построена бифуркационная диаграмма неподвижных точек усредненной системы. В первом приближении притягивающая неподвижная точка усредненной системы соответствует рабочему режиму ветротурбины.

Работа выполнена при частичной финансовой поддержке РФФИ: грант № 18-31-20029.