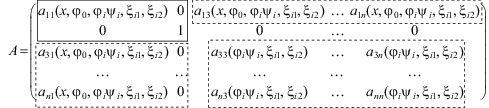Известия РАН. Механика твердого тела, 2021, № 2, стр. 72-87

1. Введение. Исследованию динамики антропоморфных систем, моделируемых системой твердых тел, посвящено значительное число работ. Исследования ведутся по проектированию экзоскелетов и созданию антропоморфных роботов. Разработке экзоскелетов на основе системы твердых тел посвящены работы [1–5]. Моделирование антропоморфных роботов системами твердых тел рассматривается в работах [6–10]. Однако, практически во всех работах, для описания движения антропоида не используются звенья переменной длины и понятие связи. Построению алгоритмов составления уравнений динамики пространственной модели экзоскелета и антропоморфного робота посвящены работы [11, 12]. В [12] был предложен рекуррентный метод построения уравнений движений экзоскелета, содержащего звенья переменной длины и управляемого моментами в суставах. Реальные условия функционирования управяемых антропоморфных систем и экзоскелетов предполагают наличие действие сил трения и наличие неголономных связей. Использование уравнений неголономной динамики [13, 14] позволяет существенно сократить размерность системы. Задачи динамики систем с трением и с неголономными связями рассмотены в работах [13–18]. В настоящей работе рассматривается модель антропоморфного механизма сложной конструкции, содержащего звенья переменной длины. Звеном переменной длины называется часть механизма между шарнирами-суставами, составляющая прямолинейную конструкцию, способную изменять расстояние между шарнирами-суставами, т.е. реализовывать растяжение-сжатие, но не подверженное деформациям изгиба и кручения.

В связи с тем, что задача моделирования неголономных систем явлется весьма сложной, для лучшего понимания модели, рассмотрим вначале модель звена переменной длины без учета неголономной связи. Отработаем на ней методику составления дифференциальных уравнений движения, получим обобщения дифференциальных уравнений движения и разработем методику составления для антропоморфной системы с произвольным числом звеньев. Далее рассмотрим задачу управления целенаправленным движением системы твердых тел, содержащей звенья переменной длины. Затем обобщим и перенесем полученные результаты на модель лыжника-сноубордиста, с учетом неголономной связи и управления движением такой неголономной модели с использованием метода стабилизации связей. Далее рассмотрим числовой пример для модели лыжника-сноубордиста с выбранным количеством звеньев и заданными числовыми параметрами.

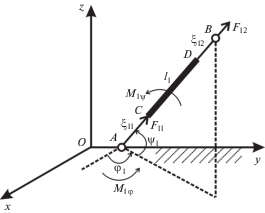
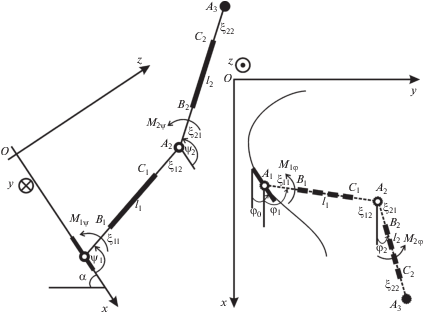
2. Описание модели закрепленного звена переменной длины и постановка задачи. Введем неподвижную правую декартову систему координат Oxyz, в которой происходит движение механизма. Пусть стержень переменной длины имеет конструкцию, показанную на рис. 1. Звено АВ переменной длины, состоящее из двух невесомых частей изменяющих свою длину AС = ξ₁₁(t) и DВ = ξ₁₂(t) и весомой абсолютно твердой части СD = l₁ [2]. На рис. 1 схематично изображено звено переменной длины и введены соответствующие обозначения.

Положение весомого участка звена зависит от трех параметров и однозначно определяется углами φ₁(t), ψ₁(t) и переменной длиной участка стержня ξ₁₁(t). Рассматриваемая система имеет три степени свободы. Обозначим через M_1φ и M_1ψ управляющие моменты, развиваемые в шарнире А. Продольную силу, действующую вдоль стержня на участке АС, обозначим F₁₁, на участке DB, обозначим F₁₂.

Длина звена складывается из суммы длин переменной части и постоянной длины:

Масса участка звена постоянной длины m₁ = ρ₁l₁, где ρ₁ – плотность материала из которого изготовлена часть стержня постоянной длины. Участки звена, в которых реализуется переменность его длины ξ₁₁(t) и ξ₁₂(t), считаем невесомыми. Это означает, что момент инерции стержня относительно точки С, расположенной на конце весомого участка, не меняется.

Координаты бесконечно малой частицы весомого участка звена, отсчитываемые от точки А, записываются в виде:

где $C_{1}^{\varphi }$ = cosφ₁, $C_{1}^{\psi }$ = cosψ₁, $S_{1}^{\varphi }$ = sinφ₁, $S_{1}^{\psi }$ = sinψ₁, х – расстояние от точки С до точки, задающей положение бесконечно малой частицы весомого участка СD звена АВ. Квадрат скорости частицы весомого участка СD равен:

Кинетическая энергия механизма, с учетом выражения момента инерции тонкого однородного стержня, если ось проходит через его конец

имеет вид: где ζ₁₁ = I₁ + m₁l₁ξ₁₁ + m₁$\xi _{{11}}^{2}$

Потенциальная энергия звена записывается в виде:

Составляя уравнения Лагранжа второго рода, получаем дифференциальные уравнения движения для модели одного подвижного звена переменной длины в трехмерном пространстве:

где ζ₁₁ = I₁ + m₁l₁ξ₁₁ + m₁$\xi _{{11}}^{2}$, λ₁₁ = ${{\xi }_{{11}}} + {{{{l}_{1}}} \mathord{\left/ {\vphantom {{{{l}_{1}}} 2}} \right. \kern-0em} 2}$, $C_{1}^{\psi }$ = cosψ₁, $S_{1}^{\psi }$ = sinψ₁.

Общее решение системы уравнений движения зависит от 6 произвольных постоянных, которые определяются заданными начальным условиями:

Таким образом, получена система дифференциальных уравнений, описывающая динамику звена переменной длины.

Задача исследования заключается в создании математической модели механизмов, составленных из таких звеньев. Требуется записать систему дифференциальных уравнений движения в векторно-матричном виде для модели с произвольным конечным количеством звеньев и получить общие формулы для матриц, входящих в дифференциальные уравнения движения. Перенести полученные результаты на систему с неголономной связью. Провести исследование ее динамики, численным методом на основе метода стабилизации связи для выбранной в качестве примера модели лыжника-сноубордиста. Для этого необходимо получить решение системы дифференциальных уравнений движения с эмпирически определенными методами биомеханики параметрами системы, соответствующими опорно-двигательному аппарату реального лыжника и сноуборда. Результатом должна быть проверка возможности получения устойчивого движения механической модели лыжника-сноубордиста за счет неголономной связи.

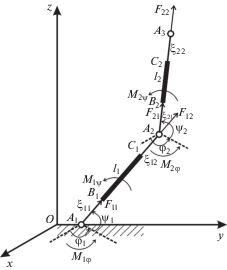
3. Модель механизма с двумя звеньями переменной длины. Составим систему дифференциальных уравнений движения для механизма с двумя последовательными подвижными звеньями переменной длины (рис. 2).

Система имеет два звена А₁A₂ и А₂A₃, состоящее каждое из двух невесомых частей изменяющих свою длину A₁B₁ = ξ₁₁(t), C₁A₂ = ξ₁₂(t), A₂В₂ = ξ₂₁(t), C₂A₃ = ξ₂₂(t) и весомых абсолютно твердых частей B₁С₁ = l₁, B₂С₂ = l₂ (рис. 2). Положение весомого участка B₁С₁ звена А₁A₂ зависит от трех параметров и однозначно определяется углами ψ₁(t), φ₁(t) и переменной длиной участка стержня ξ₁₁(t). Положение весомого участка B₂С₂ звена А₂A₃ зависит от семи параметров и определяется углами ψ₁(t), ψ₂(t), φ₁(t), φ₂(t) и переменными длинами участков стержней ξ₁₁(t), ξ₁₂(t), ξ₂₁(t). Обозначим через M_1ψ, M_1φ – управляющие моменты, развиваемые в шарнире А₁, через M_2ψ, M_2φ – в шарнире А₂. Продольную силу, действующую вдоль стержня на участке A₁B₁, обозначим F₁₁, на участке C₁A₂, обозначим F₁₂, на участке A₂В₂, обозначим F₂₁.

Кинетическая энергия звена А₁A₂, совершающего вращательное движение вокруг неподвижного шарнира А₁, имеет вид, аналогичный модели с одним звеном (2.5).

Для вычисления кинетической энергии звена А₂A₃ найдем скорость ${v}_{2}^{2}$. Весомый участок данного звена совершает сложное движение. В качестве полюса выберем точку А₂. Определим квадрат ее скорости:

где λ₁₂ = ${{\xi }_{{11}}} + {{l}_{1}} + {{\xi }_{{12}}}$, ${{\dot {\lambda }}_{{12}}}$ = ${{\dot {\xi }}_{{11}}}$ + ${{\dot {\xi }}_{{12}}}$

Тогда скорость $v_{2}^{2}$ бесконечно малой частицы участка звена А₂A₃ определяется в соответствии с теоремой о сложении скоростей.

где λ₁₂ = ${{\xi }_{{11}}} + {{l}_{1}} + {{\xi }_{{12}}}$, ${{\dot {\lambda }}_{{12}}}$ = ${{\dot {\xi }}_{{11}}}$ + ${{\dot {\xi }}_{{12}}}$, ${{C}_{{12}}} = \cos ({{\varphi }_{1}} - {{\varphi }_{2}})$, $S_{{12}}^{{}} = \sin \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right)$

Кинетическая энергия второго звена является весьма громоздким выражением равно как и система дифференциальных уравнений движения, составленных с помощью уравнений Лагранжа второго рода, состоящая из восьми уравнений. Поэтому в качестве примера, поясняющего изменения, происходящие в системе уравнений, приведем только предпоследнее, седьмое уравнение полученной системы, соответствующее обобщенной координате ξ₂₁ – нижнему невесомоу участку переменной длины второго звена.

где λ₁ = ${{\xi }_{{11}}} + {{l}_{1}}$, λ₁₁ = ${{\xi }_{{11}}} + {{{{l}_{1}}} \mathord{\left/ {\vphantom {{{{l}_{1}}} 2}} \right. \kern-0em} 2}$, λ₁₂ = ${{\xi }_{{11}}} + {{l}_{1}} + {{\xi }_{{12}}}$, λ₂ = ${{\xi }_{{21}}} + {{l}_{2}}$, λ₂₁ = ${{\xi }_{{21}}} + {{{{l}_{2}}} \mathord{\left/ {\vphantom {{{{l}_{2}}} 2}} \right. \kern-0em} 2}$, C_j = = cosφ_j, S_j = sinφ_j, j = 1, 2, $C_{{12}}^{{}} = \cos \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right)$, $S_{{12}}^{{}} = \sin \left( {{{\varphi }_{1}} - {{\varphi }_{2}}} \right)$.

В дифференциальное уравнение (3.3) входит информация о движении первого звена, к которому прикрепляется рассматриваемое второе звено. Кроме того, в сравнении с аналигичным уравнением системы (2.9) для модели с одним звеном, в уравнении для модели с двумя подвижными звеньями (3.3) возникает достаточно много новых слагаемых, связанных с тем, что движение второго звена сложное.

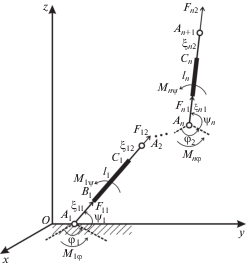
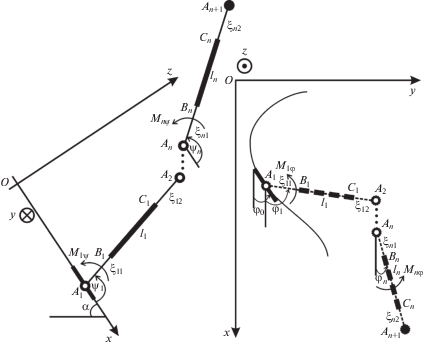
4. Обобщение модели механизма на случай произвольного количества звеньев переменной длины. Рассмотрим многозвенную стержневую модель с n звеньями. Система имеет звенья переменной длины, конструкция которых была описана выше. Все длины стержней складываются из участка постоянной длины l_i (i = 1, …, n) и переменной длины ξ_iα = ξ_iα(t) (α = 1, 2 – номер невесомого участка переменной длины на звене). На рис. 3 изображена модель со звеньями переменной длины в одноопорной фазе движения и введены соответствующие обозначения.

Положение однозначно определяется углами φ_i и участками переменной длины стержней ξ_iα. Рассматриваемая система имеет 4n – 1 степеней свободы, так как движение каждого звена описывается набором из четырех параметров: углов φ_i(t), ψ_i(t) и изменением длин невесомых участков ξ_i1(t), ξ_i2(t). При этом на конце последнего звена находится невесомый участок, который не оказывает влияния на движение звена, поэтому ξ_n2(t) не включается в обощенные координаты. Массы звеньев обозначим m_i, моменты инерции звеньев относительно осей, проходящих через один из концов весомого стержня, перпендикулярно плоскости движения – I_i. Обозначим: M_iφ, M_iψ – моменты, развиваемые в i-м шарнире; F_iα – продольные силы, действующие вдоль i‑го стержня, обеспечивающие изменение его длины требуемым образом. Моменты и продольные силы являются управлением в данной механической системе.

Уравнения движения элементов n-звенной механической системы в одноопорной фазе представляют собой систему нелинейных дифференциальных уравнений, которые в матричной форме можно записать в виде:

где нижние индексы у матриц указывают на описание соответствующей обобщенной координаты: κ = 1, …, 4, где 1 соответствует обобщенной координате φ, 2 – ψ, 3 – ξ_i1, 4 – ξ_i2; φ = (φ₁, …, φ_n)^т, ψ = (ψ₁, …, ψ_n)^т – векторы углов; ξ_α = (ξ_1α, …, ξ_nα)^т – вектор переменных длин звеньев участка α (α = 1, 2); l = (l₁, …, l_n)^т – вектор длин звеньев участков постоянной длины; $\dot {\varphi }$ – вектор угловых скоростей; $\ddot {\varphi }$ – вектор угловых ускорений; $\dot {\Phi }$ = diag(${{\dot {\varphi }}_{1}}$, …, ${{\dot {\varphi }}_{n}}$) – диагональная матрица; M, F_α – векторы управляющих моментов и сил на участке α (α = 1, 2) звена; A, B, G_α, H_α – матрицы, учитывающие инерционные свойства системы; C, K_α – матрицы, определяемые моментами силы тяжести; D₁, D₂, E₁, E₂, L_α1, L_α2, P_α1, P_α2 – матрицы, учитывающие переменную длину звеньев.

Приведем, в качестве примера, формулу для матрицы А. Матрица А = (a_ij) является симметрической: a_ij = a_ji, поэтому достаточно привести для нее только диагональные и наддиагональные элементы, т.е., если i – номер строки, j – номер столбца, то i, j = 1, 2, …, n, при этом j ≥ i.

Элементы симметрической матрицы А имеют вид:

где δ_ij – символ Кронекера, тогда ${{\tilde {\delta }}_{{ij}}}$ – половинный антикронекер:

Матричная форма записи уравнений движения (4.1) является универсальной и может быть применена к описанию движения экзоскелета или антропоморфного робота с любым числом звеньев.

Дальнейшей задачей является разработка методов управления рассмотренными выше системами с произвольным числом звеньев переменной длины.

5. Управление целенаправленным движением системы твердых тел, содержащей звенья переменной длины. Система уравнений (4.1) содержит управляющие моменты ${{M}_{\kappa }}$ и силы ${{F}_{\kappa }}$, призванные обеспечить выполнение уравнений связей, наложеннных на обобщенные координаты и скорости:

Здесь ${v} = {{dq} \mathord{\left/ {\vphantom {{dq} {dt}}} \right. \kern-0em} {dt}}$, $q = ({{q}^{1}}, \ldots ,{{q}^{{4n}}})$ – вектор обобщенных координат, соответствующих переменным φ_j, ${{\psi }_{j}}$, ${{\xi }_{{j1}}}$, ${{\xi }_{{j2}}}$, $j = 1,\; \ldots ,\;n$. В новых переменных дифференциально-алгебраические уравнения динамики замкнутой системы и уравнения возмущений связей запишутся в следующем виде:

Число S управляющих воздействий зависит от числа звеньев переменной длины, коэффициенты $h_{\mu }^{\rho }$, $k_{\sigma }^{\rho }$ уравнений (5.5) возмущений связей определяются из условий асимптотической устойчивости тривиального решения.

Из уравнений (5.2)–(5.5) следуют выражения управляющих воздействий

Здесь u⁰ – произвольная скалярная величина, $u_{s}^{\tau }$ вычисляется как определитель, первая строка которого состоит из величин ${{\delta }^{{sl}}} = 0$, $l \ne s$, ${{\delta }^{{ss}}} = 1$, $s,l = 1,\; \ldots ,\;S$, последующие строки составлены из элементов матрицы (g^ρs),

и произвольных величин ${{g}^{{\kappa s}}}$, $\kappa = r + 1,\; \ldots ,\;S - 1$, которые не обращают в нуль величину определителя. Второе слагаемое определяется выражением

Выражения (5.6) управлений соответствуют асимптотической устойчивости многообразия, определяемого уравнениями связей, и при дальнейшем уточнении коэффициентов уравнений возмущений связей позволяет обеспечить стабилизацию связей при численном решении уравнений динамики замкнутой системы [5 ] .

6. Модели лыжника-сноубордиста. В качестве примера решения прикладной задачи, модифицируем предложенный выше подход к моделированию системы с произвольным числом звеньев на случей антропоморфных систем с неголономными связями в виде лыжника-сноубордиста.

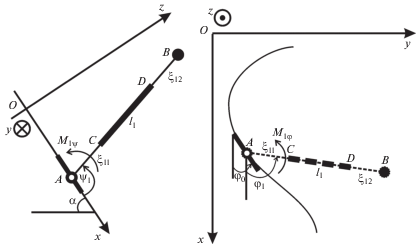
Модель лыжника-сноубордиста с одним подвижным звеном переменной длины, конструкция которого рассмотрена выше, представлена на рис. 4. Координаты крепления звена АВ к лыже x_А, y_А. Угол φ₀ определяет направление лыжи относительно оси ОХ. Масса лыжи m₀, момент инерции I₀. Положение центра масс звена АВ определяется двумя углами: φ₁ – углом между осью ОХ и проекцией звена AB на плоскость XOY, отсчитываемым от оси ОХ против часовой стрелки; ψ₁ – углом между звеном AB и его проекцией на плоскость XOY, отсчитываемым от проекции звена AB на плоскость XOY против часовой стрелки и изменением его длины, координатами крепления звена к лыже x_А, y_А и переменными длинами участков стержня ξ₁₁(t) и ξ₁₂(t). Рассматриваемая система имеет семь степеней свободы. Остальные обозначения совпадают с рис. 1.

В точке B имеется сосредоточенная масса m_G, моделирующая корпус лыжника-сноубордиста, а звено АВ моделирует ноги в целом. Рассмотрим модель с двумя звеньями переменной длины. Нижнее звено моделирует ноги в целом сноубордиста, верхнее – корпус, точечная масса – голову (рис. 5). В дополнение к рис. 4 вводится звено А₂А₃, обозначения для которого совпадают с рис. 2. Положение звена А₂А₃ описывается углами φ₂, ψ₂ и участками переменной длины ξ₂₁ и ξ₂₂. Рассматриваемая система имеет одиннадцать степеней свободы. Такая модель является более реалистичной и ближе к биомеханическому прототипу, позвляя в совокупности моделировать нижние конечности и отдельно корпус.

Рассмотрим модель с произвольным конечным количеством n звеньев переменной длины (рис. 6), с помощью которой можно моделировать динамику лыжника-сноубордиста с необходимой точностью. Количество степеней свободы такой механической системы определяется по формуле: 4n + 3.

С помощью такой модели можно моделировать лыжника-сноубордиста с нижними конечностями, состоящими из голени и бедра, корпуса из нескольких основных блоков, шеи, головы, рук. Следовательно, используя данную модель, можно описать лыжника-сноубордиста очень близко к биомеханическому прототипу.

7. Составление системы дифференциальных уравнений движения с учетом неголономной связи. Рассмотрим модель с одним звеном переменной длины (рис. 4). Процедура получения выражения для кинетической энергии с использованием бесконечно малых участков стержня и интегрированием по весомому отрезку CD описана выше.

Кинетическая энергия всего механизма складывается из кинетической энергии лыжи, звена CD и сосредоточенной массы в точке В.

Кинетическая энергия механизма в выписанном виде имеет вид:

где θ = m₀ + m₁ + m_G – масса всего механизма в виде лыжника-сноубордиста вместе с лыжей, ногами и корпусом, ζ = I₁ + m₁ξ₁₁(l₁ + $\xi _{{11}}^{{}}$) + m_G(l₁ + ($\xi _{{11}}^{{}}$ + $\xi _{{12}}^{{}}$))².

Сравнивая полученное выражение для кинетической энергии лыжника-сноубордиста (7.2) и отдельного звена (2.5) видно, что ее структура изменилась незначительно, только добавились слагаемые, соответствующие дополнительно введенным обобщенным координатам и массе лыжи и корпуса лыжника-сноубордиста.

Связь по поверхности контакта лыжи и снега является неголономной. Уравнение связи имеет вид:

Траектория сноубордиста (рис. 4) описывается синусоидой

где А – амплитуда траектории. Тогда уравнение связи принимает вид: и накладывает ограничение на вариации координат:

Для описания движения неголономной системы используем уравнения Рауса с множителями Лагранжа. В данном случае, на систему наложена одна неголономная связь (7.3). Система дифференциальных уравнений для модели, представленной на рис. 4 имеет вид:

где ζ₁ = I₁ + m₁ξ₁₁(l₁ + $\xi _{{11}}^{{}}$) + m_G(l₁ + ($\xi _{{11}}^{{}}$ + $\xi _{{12}}^{{}}$))², η₁ = m₁(ξ₁₁ + l₁/2), ϑ₁ = m_G(ξ₁₁ + l₁ + + ξ₁₂), θ = m₀ + m₁ + m_G, θ₁ = m₁ + m_G, $C_{1}^{\psi }$ = cosψ₁, $S_{1}^{\psi }$ = sinψ₁.

Были составлены также дифференциальные уравнения движения для сноубордиста с двумя звеньями переменной длины. Система дифференциальных уравнений для модели сноубордиста сохраняет вид (4.1). Однако, матрицы становятся матрицами следующего набора аргументов: A_κ(x, φ₀, φ, ψ, ξ_α), нижние индексы у матриц указывают на описание соответствующей обобщенной координаты: κ = 1, …, 6, где 1 соответствует обобщенной координате x, 2 – φ₀, 3 – φ, 4 – ψ, 5, 6 – ξ_α (α = 1, 2 – номер невесомого участка переменной длины на звене). Теперь в векторы обобщенных координат включаются дополнительные координаты: φ = (x, φ₀, φ₁, …, φ_n)^т и ψ = (x, φ₀, ψ₁, …, ψ_n)^т; ξ_α = = (x, φ₀, ξ_1α, …, ξ_nα)^т; l = (x, φ₀, l₁, …, l_n)^т. $\dot {\Phi }$ = diag($\dot {x}$, ${{\dot {\varphi }}_{0}}$, ${{\dot {\varphi }}_{1}}$, …,${{\dot {\varphi }}_{n}}$), $\dot {\Psi }$ = diag($\dot {x}$, ${{\dot {\varphi }}_{0}}$, ${{\dot {\psi }}_{1}}$, …, ${{\dot {\psi }}_{n}}$) – диагональные матрицы.

Матрицы A_κ, B_κ и т.д. распадаются на блочные матрицы, с различными блоками, соответствующими первым двум обощенным координатам, и остальным обобщенным координатам, аналогично тому, как это было в модели антропоморфного механизма в безопорной и двухопорной фазах движения, рассмотренных в работе [10].

Были получены обобщения матриц для модели n-звенного лыжника-сноубордиста. Приведем, для примера, обобщающие формулы для матрицы А. Матрица А распалась на блоки, показанные в формуле (7.13). Верхний левый блок матрицы A (показанный сплошной линией), содержащий первые две строки и столбца дает уравнения, описывающие движение точки крепления ноги к лыже

Формулу для части матрицы А блоков, содержащих информацию о движении лыжи и неголономной связи, показанных штрих-пунктирным выделением, запишем только для верхней строки, так как эти блоки являются симметрическими. Как и прежде i – номер строки,  j – номер столбца. Для верхнего правого блока: i = 1,  j = 3, 4, …, n, при этом a_1j = a_i1.

Формула для части матрицы А блока, расположенного снизу справа и выделенного пунктиром, содержащего информацию об угловых переменных представим следующим образом. Часть матрицы А является симметрической, поэтому достаточно привести для нее только диагональные и наддиагональные элементы, т.е., если i – номер строки, j – номер столбца, то i, j = 1, 2, …, n, при этом  j ≥ i.

Элементы симметрического блока матрицы А имеют вид:

где δ_ij – символ Кронекера: δ_ij = $\left\{ \begin{gathered} 1,\quad i = j, \hfill \\ 0,\quad i \ne j, \hfill \\ \end{gathered} \right.$

Остальные элементы: a_ji = a_ij. Эта формула аналогична выражению (4.2), однако, ввиду добавления элемнтов в модели и увеличившейся громоздкости записана в более компактных выражениях, а не в полностью выписанном виде.

Таким образом, на основании формулы (4.2) возможно построить выражение (7.16), что позволяет упростить получение системы дифференциальных уравнений движения.

8. Численное моделирование динамики лыжника-сноубордиста. Рассмотрим динамику модели, состоящей из двух звеньев. Для этого систему уравнений движения (7.7)–(7.12) и связей (7.3), (7.5) необходимо дополнить с целью удержания звеном околовертикального положения. Дополнительные связи позволяют однозначно определить управляющие воздействия, обеспечивающие заданное состояние звеньев.

Рассматрим следующий набор связей:

где l_c – заданное значение совместной длины.

Неголономная связь (7.3) может быть учтена, применив метод Чаплыгина. Связь (8.1) можно сразу учесть в выражении для функции Лагранжа. Таким образом, связи (8.2) и (5.5) определяют управляющие воздействия для движения по ${{\varphi }_{0}}$, ${{\xi }_{{11}}}$ и ${{\psi }_{1}}$.

Для анализа полученной системы (7.7)–(7.12), (7.3), (7.5), (8.1) и (8.2) используется численное интегрирование при помощи разностной схемы первого порядка. Для получения устойчивого численного решения применяется метод стабилизации связей.

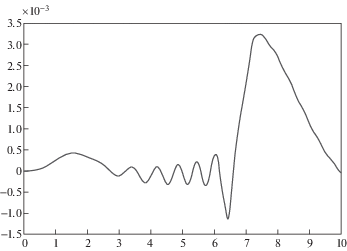
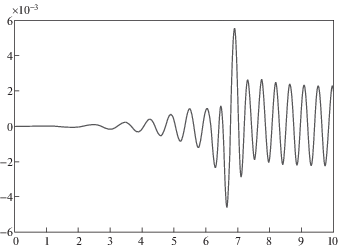
Рассмотрим значение отклонений численного решения от уравнений связей со временем, представленном на рис. 7, 8. По рисункам видно, что управляющее воздействие, полученное численным методом с учетом стабилизации связей обеспечивает почти вертикальное положение верхнего звена.

9. Заключение. Разработана динамическая модель системы твердых тел с произвольным числом звеньев переменной длины, соединенных между собой шарнирами. Предложен матричный метод записи системы дифференциальных уравнений движения и получены обобщающие формулы для матриц, одна из которых приводится в качестве примера. Поставлена задача управления такой системой на основе метода стабилизации связей.

В качестве примера использования разработанной механической системы предложена пространственная модель лыжника-сноубордиста с неголономной связью и звеньями переменной длины. Каждое звено переменной длины состоит из двух невесомых участков переменной длины и абсолютно твердого весомого звена между ними. Проведено численное моделирование управляемого движения лыжника-сноубордиста. Установлено, что метод стабилизации связи позволяет реализовывать управляемое, устойчивое, целенаправленное движение такой неустойчивой системой как лыжник-сноубордист. Результаты моделирования могут быть использованы в дальнейшем для решения задач управления антропоморфными системами с неголономными связями.

Работа выполнена при финансовой поддержке гранта РФФИ, проект № 19-08-00261 А, и Министерства образования и науки РФ по Программе повышения конкурентоспособности РУДН “5-100”.