Известия РАН. Механика твердого тела, 2021, № 1, стр. 148-162

Введение. Одним из важных разделов современной науки о прочности материалов и конструкций является линейная механика разрушения. Ее истоки заложены в работах [1, 2]. Первоосновой является наличие в материале дефектов в форме т.н. трещин, которые математически моделируются разрывом поля перемещений на некоторой части поверхности. Для упругой среды это приводит к особенностям на границе трещин. При приближении к границе трещины напряжения стремятся к бесконечности, т.е. происходит концентрация напряжений в достаточно малой окрестности границы. Поскольку в реальных материалах существование бесконечных напряжений невозможно, в окрестности краев трещины возникает область необратимых пластических деформаций. Тем не менее, в тех случаях, когда размеры данной области малы, по сравнению с размерами самой трещины, показана применимость критериев роста трещины на основе анализа полученного упругого решения [3–8]. В настоящее время линейная механика разрушения является одним из основных инструментов оценки прочности материала с дефектами. Достаточно полное представление о полученных в данной области результатах можно составить из обзоров, приведенных в работах [8–12]. В качестве основных методов исследований в механике трещин можно условно выделить аналитические, численно-аналитические и чисто численные методы решения. Каждый из них обладает своими достоинствами и недостатками. Основным преимуществом аналитических и численно-аналитических методов является возможность непосредственно оценить влияние параметров задачи на возможный рост трещин. Недостатком – применимость только для достаточно простой геометрической конфигурации задачи. В связи с ростом мощности и быстродействия современных ЭВМ, все более активно стали развиваться численные методы в применении к механике разрушения. Следует отметить, что задачи в данной области исследований имеют ряд специфических особенностей, сильно затрудняющих применение обычных численных методов, таких, например, как метод конечных элементов или сеточный метод. Наличие особенностей в малой окрестности границы трещин приводит к необходимости увеличения количества элементов вокруг особой точки. Если исследуется система трещин, которые имеют свою внутреннюю топологию и вдобавок, как-то ориентированы в пространстве, уже создание сетки элементов, адаптированной к заданной геометрии задачи, является достаточно сложной проблемой. В связи с этим, в механике трещин активно используются безсеточные численные методы, сводящие задачу к решению граничных уравнений [8, 12–15]. Очень хороший обзор разновидностей этих методов приведен во введении к монографии [12]. Один из таких методов развивают авторы настоящей статьи. По общепринятой терминологии, предлагаемый метод является непрямым методом граничных элементов. В математике употребляется название – разложение решения по базису из не ортогональных функций [16]. Близкими к рассматриваемому в данной статье методу являются работы [17–19]. В качестве базисных функций разложения используются три решения теории упругости о разрыве компонент вектора перемещений на поверхности граничного элемента. Общее решение всей задачи представляется суммой с неопределенными коэффициентами в форме конечного ряда с аналитически заданными базисными функциями. Коэффициенты ряда определяются методом коллокаций на границе (граничные условия выполняются только в центрах граничных элементов). Данный подход позволяет избежать вычисления сингулярных интегралов, которые возникают в прямых методах граничных интегральных уравнений.

Преимуществом данного метода является то, что на конечные элементы разбивается только поверхность трещин, моделирующая разрыв упругой среды. Это понижает размерности задачи на стадии ее решения. Для каждого элемента используется три независимых аналитических решения, в каждом из которых на элементе терпит разрыв одна из трех компонент вектора перемещений. Решение конкретной граничной задачи ищется в виде ряда с неопределенными коэффициентами по всему множеству элементов. Каждое элементарное решение вносит свой вклад в поле перемещений и в поле напряжений с весом, который и является соответствующим неопределенным коэффициентом ряда. Выполнение конкретных граничных условий приводит к системе линейных уравнений. После численного определения коэффициентов разложения мы имеем фактически аналитическое представление решения в виде конечного ряда внутри области. С точки зрения памяти, нам надо хранить только найденные коэффициенты разложения, позволяющие затем найти любые требуемые характеристики в любой точке области решения. Это существенно с точки зрения простоты практического использования полученного решения. Еще одним важным преимуществом предлагаемого метода является возможность решения всех типов краевых задач (задача в напряжениях, задача в перемещениях, смешанная задача).

Недостатком метода является недостаточная математическая обоснованность, поэтому необходим большой объем работы, связанный с проверкой достоверности получаемых результатов. С этой целью авторами проведено сравнение с имеющимися аналитическими решениями пространственных задач, а также с имеющимися результатами численного решения задач механики трещин, полученными с использованием других численных методов [9, 10, 20–22]. Коды программы реализованы на языке C++. Основной целью данной работы является апробация предлагаемого метода путем сравнения с известными решениями пространственных задач механики трещин. Для этого проведено численное исследование известной задачи взаимного влияния двух дискообразных плоских трещин в зависимости от расстояния между трещинами и их взаимного расположения. Результаты тестирования позволяют говорить об эффективности и удовлетворительной точности предлагаемого метода.

1. Базисные функции. Основой метода разложения решения по не ортогональным функциям [16] является построение системы линейно независимых решений основной системы уравнений задачи (базисных функций). В статической теории упругости – это решения уравнений равновесия.

Введем следующие обозначения: $({{x}_{1}},{{x}_{2}},{{x}_{3}})$ – декартовы координаты в некоторой системе координат с базисом ${{e}_{1}},\;{{e}_{2}},\;{{e}_{3}}$; ${{u}_{i}}({{x}_{1}},{{x}_{2}},{{x}_{3}})$, $(i = 1,2,3)$ – компоненты вектора перемещений; ${\lambda ,}\;{\mu },\;E,\;{\nu }$ – упругие модули (E – модуль Юнга, ν – коэффициент Пуассона); ${{{\varepsilon }}_{{ij}}},\;{{{\sigma }}_{{ij}}}$ $(i,j = 1,2,3)$ – матрицы компонент тензора деформаций и тензора напряжений; для упрощения записи воспользуемся следующим обозначением частной производной ${{\partial f} \mathord{\left/ {\vphantom {{\partial f} {\partial {{x}_{k}}}}} \right. \kern-0em} {\partial {{x}_{k}}}} = {{f}_{{,k}}}$; повторяющийся индекс в любом выражении будет означать операцию свертки; $\nabla $ – оператор градиента функции; ${{\nabla }^{2}}$ – оператор Лапласа.

Рассмотрим в упругом пространстве граничный элемент в виде плоского прямоугольника $S:$ ${{x}_{3}} = 0,$ $\left| {{{x}_{1}}} \right| \leqslant {{h}_{1}},$ $\left| {{{x}_{2}}} \right| \leqslant {{h}_{2}}$. Определим, функцию φ^(k), как потенциал двойного слоя c плотностью μ^(k)

Потенциал двойного слоя обладает следующим свойством

где $g({\mathbf{x}})$ – потенциал простого слоя.

Известно, что в статической теории упругости каждая из компонент поля перемещений, при отсутствии массовых сил, является бигармонической функцией [23, 24]. Рассмотрим три общих решения уравнений равновесия для поля перемещений в представлении Треффца [24]:

Легко проверить, что каждая компонента перемещений (1.1)–(1.3) является бигармонической функцией ${{\nabla }^{2}}{{\nabla }^{2}}{{u}_{i}}^{{(k)}} = 0,$ $i,k = 1,2,3$, а данные поля перемещений будут удовлетворять уравнениям упругости, если

Используя закон Гука ${{{\sigma }}_{{ji}}} = {\lambda }{{{\delta }}_{{ji}}}{{{\varepsilon }}_{{kk}}} + 2{\mu }{{{\varepsilon }}_{{ji}}}$ и выражения для деформаций ε_ji = = ${{({{u}_{{j,i}}} + {{u}_{{i,j}}})} \mathord{\left/ {\vphantom {{({{u}_{{j,i}}} + {{u}_{{i,j}}})} 2}} \right. \kern-0em} 2}$, можно найти компоненты вектора перемещений и тензора напряжений, соответствующие каждому решению (1.1), (1.2), (1.3).

В некоторых случаях потенциалы простого и двойного слоя можно вычислить аналитически. Например, в случае постоянной единичной плотности они соответственно равны:

В формулах (1.4) использовано символическое равенство

а функции ${{g}_{0}}\left( {{\mathbf{x}},{{{\xi }}_{1}},{{{\xi }}_{2}}} \right),$ ${{{\varphi }}_{0}}\left( {{\mathbf{x}},{{{\xi }}_{1}},{{{\xi }}_{2}}} \right)$ соответственно представлены в аналитической форме

Аналитическое представление базисных функций в методе граничных элементов позволяет значительно упростить процедуру решения, поскольку отпадает необходимость вычисления сингулярных интегралов в системе граничных интегральных уравнений. Следует помнить, что решения (1.1)–(1.3) получены в локальной системе координат каждого граничного элемента. Для построения численной схемы обозначим поля перемещений и напряжений, соответствующие каждому из базисных решений, следующим образом:

В выражениях (1.5) верхний индекс $k = 1,2,3$ означает номер решения, индекс m соответствует номеру граничного элемента, индекс i – соответствующей проекции вектора перемещений. Каждое из решений имеет разрыв соответствующей компоненты вектора перемещения на данном граничном элементе.

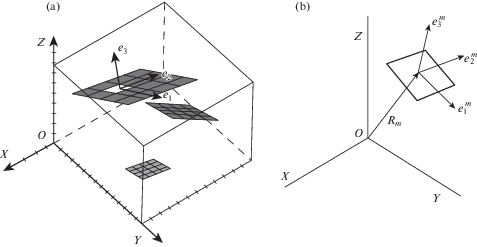
2. Описание метода. Рассмотрим типичную задачу механики трещин для бесконечного пространства. В пространстве глобальной системы координат (X, Y, Z) с базисом $({{э}_{1}},{{э}_{2}},{{э}_{3}})$ расположены несколько трещин, которые моделируются поверхностями разрыва перемещений (рис. 1,a).

Будем, для определенности, ставить задачу в напряжениях. Для бесконечного пространства могут быть поставлены две типичные краевые задачи. В первой краевой задаче на бесконечности может быть задан ненулевой вектор напряжений ${{\sigma }_{\infty }}$, а на берегах трещин вектор напряжений равен нулю. Во второй краевой задаче вектор напряжений на бесконечности равен нулю, а на берегах трещин действует заданный вектор напряжений ${{{\mathbf{P}}}_{{\mathbf{0}}}}$. В линейном случае первая задача может быть сведена ко второй использованием суперпозиции решений. Действительно, можно представить поле перемещений u и тензор напряжений $\sigma $ в виде суммы двух решений ${\mathbf{u}} = {{{\mathbf{u}}}_{\infty }} + {\mathbf{\tilde {u}}},$ $\sigma = {{\sigma }_{\infty }} + \tilde {\sigma }$, где ${{{\mathbf{u}}}_{\infty }},{{{\hat {\sigma }}}_{\infty }}$ решение для пространства с заданными условиями на бесконечности при отсутствии трещин, а решение ${\mathbf{\tilde {u}}},\;\tilde {\sigma }$ стремится к нулю на бесконечности и удовлетворяет на границах трещин условию $\tilde {\sigma } = - {{\sigma }_{{\mathbf{0}}}}$.

Построение первого решения будем считать известным. Остановимся подробно на построении решения с нулевыми условиями на бесконечности и с заданным вектором напряжений на поверхности трещин.

Это означает, что на берегу трещины задан вектор напряжений, как функция точек поверхности. Пусть ${{{\mathbf{R}}}^{{(m)}}} = \left( {{{X}_{m}},{{Y}_{m}},{{Z}_{m}}} \right)$ – радиус вектор центра граничного элемента с номером m в глобальной системе координат, $(e_{1}^{m},e_{2}^{m},e_{3}^{m})$ – локальный базис данного элемента (рис. 1,b). Введем в рассмотрение ортогональные матрицы, ${{F}^{{(m)}}}$, ${{F}^{{(mn)}}}$, позволяющие выразить векторы в глобальном базисе и переходить из одного локального базиса в другой

Для каждого граничного элемента с номером n в его локальном базисе $e_{i}^{n}$ можно считать заданными три компоненты вектора напряжений на площадке с нормалью $e_{3}^{n}$:

Рассмотрим три поля перемещений и напряжений, соответствующих (1.1)–(1.3):

Эти поля являются решениями уравнений теории упругости в локальном базисе ${{e}_{1}}^{m},{{e}_{2}}^{m},{{e}_{3}}^{m}$. Задавая координаты пробной точки M в данном базисе, мы можем найти компоненты вектора перемещений и компоненты тензора напряжений, которые возникают в этой точке от данного элемента, взятого с единичной плотностью соответствующих потенциалов простого и двойного слоя. Выражения (2.3) называются коэффициентами влияния граничного элемента в локальной системе координат данного элемента.

Выберем в качестве пробной точки – центр другого граничного элемента с номером n. Подстановка его локальных координат (в базисе ${{e}_{i}}^{{(m)}}$) в формулы (2.3), позволяет найти вклад (влияние) граничного элемента с номером m в поле перемещений и напряжений в центре граничного элемента с номером n.

В нашей постановке надо выполнить граничные условия (2.2), заданные в локальном базисе. Поэтому необходимо напряжения (2.3) пересчитать в базисе ${{e}_{i}}^{{(n)}}$. Для этого необходимо воспользоваться формулами перехода от одного базиса к другому (2.1). При этом мы получим вклады от граничного элемента с номером $m$ в поле напряжений в базисе ${{e}_{i}}^{{(n)}}$. Обозначим это поле напряжений от первого, второго и третьего решения, соответственно:

Суммируя (2.4) с неопределенными коэффициентами по всем граничным элементам, получим в локальном базисе ${{e}_{i}}^{{(n)}}$ суммарное поле напряжений

где N – общее количество граничных элементов, $D_{l}^{{(k)}}$, $\left( {k = 1,2,3} \right)$, $\left( {l = 1,2, \cdots ,N} \right)$ – неопределенные коэффициенты. Если нам необходимо выполнить граничные условия (2.2), получим $3N$ уравнений

Вид матрицы полученной системы линейных уравнений будет зависеть от порядка выполнения каждого из граничных условий. Если выбрать порядок (2.2) для всех элементов, получим систему уравнений в форме

Введем девять матриц $(N \times N)$ и шесть векторов-столбцов:

где символ ${{( \cdots )}^{Т}}$означает операцию транспонирования вектора.

В обозначениях (2.6) система (2.5) может быть переписана в блочной форме

Решение полученной системы уравнений относительно неизвестных коэффициентов $D_{i}^{k},\left( {k = 1,2,3} \right),\;\left( {i = 1,2, \cdots N} \right)$, позволяет получить коэффициенты разложения поля перемещений по базисным функциям, т.е. фактически разрывы поля перемещений, и затем вычислить все необходимые величины в любой пробной точке тела.

3. Задачи тестирования. Изложенный метод был реализован в виде программы на языке С++. Для проверки работоспособности метода было проведено тестирование и верификация с имеющимися аналитическими и численными решениями других авторов [8, 10, 20–22]. Результаты тестирования изложены в работах [26–30]. Здесь мы приводим результаты сравнения численного решения, полученного авторами, с аналитическими решениями пространственных задач.

В качестве задач тестирования были выбраны следующие аналитические результаты:

1. Круглая плоская трещина радиуса $R = a$ находится под внутренним давлением $p$ и расположена в плоскости z = 0. Теоретическое решение [21] для компоненты напряжений ${{{\sigma }}_{0}}(r) = {{\left. {{{{\sigma }}_{{zz}}}(r,z)} \right|}_{{z = 0}}}$ на продолжении трещины $r > a$ имеет вид

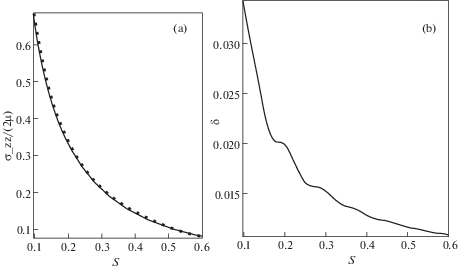
На рис. 2 представлены результаты сравнения аналитического решения (3.1) с численным решением для трещины a = 1, $p = 0.1:$ (z = 0, $r = \sqrt {{{x}^{2}} + {{y}^{2}}} < a$). Значения компоненты напряжений ${{{\sigma }}_{{zz}}}$ вычислялись в точках прямой линии $y = 0$, $z = 0$, расположенных на продолжении трещины (x > 1).

На рис. 2,а представлены графики зависимости напряжения ${{{{{\sigma }}_{{zz}}}} \mathord{\left/ {\vphantom {{{{{\sigma }}_{{zz}}}} {(2{\mu }}}} \right. \kern-0em} {(2{\mu }}})$ от расстояния s до края трещины. Сплошная линия соответствует кривой аналитического решения для функции ${{{\sigma }_{{zz}}^{{(T)}}} \mathord{\left/ {\vphantom {{{\sigma }_{{zz}}^{{(T)}}} {(2{\mu }}}} \right. \kern-0em} {(2{\mu }}})$. Точечная кривая – соответствует численным результатам ${{{\sigma }_{{zz}}^{{(N)}}} \mathord{\left/ {\vphantom {{{\sigma }_{{zz}}^{{(N)}}} {(2{\mu }}}} \right. \kern-0em} {(2{\mu }}})$. Напряжения определялись в плоскости трещины z = 0 для точек с координатами $М(x,0,0)$, x > 1. На рис. 2,b приведено распределение относительной ошибки δ = ${{({\sigma }_{{zz}}^{{(N)}} - {\sigma }_{{zz}}^{{(T)}})} \mathord{\left/ {\vphantom {{({\sigma }_{{zz}}^{{(N)}} - {\sigma }_{{zz}}^{{(T)}})} {{\sigma }_{{zz}}^{{(T)}}}}} \right. \kern-0em} {{\sigma }_{{zz}}^{{(T)}}}}$, в зависимости от расстояния $s$. Ошибка растет с уменьшением расстояния до края трещины, но не превышает 3.5%. Как видим, она максимальна около края трещины и уменьшается с ростом расстояния от края трещины.

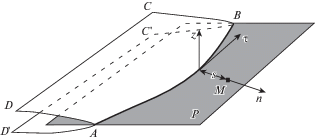
Важнейшими характеристиками упругого решения в линейной механике разрушения являются три коэффициента интенсивности напряжений (КИН), соответствующие трем элементарным нагрузкам поверхности трещины (рис. 3). На рис. 3 изображен фрагмент пространственной плоской трещины $\Pi $. Ось $z$ перпендикулярна плоскости $(x,y)$ локальной системы координат. Кривая $AB$ является частью края трещины, поверхность $ABCD$ – верхним берегом трещины (поверхность $ABC'D'$ – нижний берег трещины), ${\mathbf{\tau }}$ – единичным вектором, касательным к краю AB. Единичный вектор ${\mathbf{n}}$ расположен в плоскости трещины Π, а расстоянием от пробной точки M до трещины называется расстояние s, указанное на рис. 3.

По определению, коэффициенты интенсивности напряжений соответственно равны:

где s – расстояние от точки вычисления напряжений до границы. В аналитическом решении для круглой трещины, находящейся под действием внутреннего давления, отличен от нуля коэффициент ${{K}_{I}}$, а его величина равна

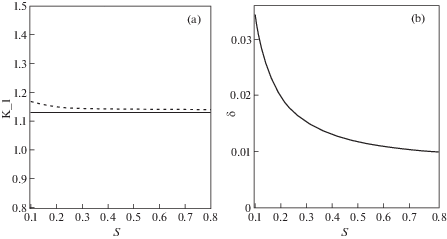
Для единичного давления внутри трещины единичного радиуса ${{K}_{I}} = 1.1284$. Численное значение K_I, соответствующее расчетам, определялось с использованием (3.2) для разных расстояний до фронта трещины.

На рис. 4 приведены численные значения K_I, найденные по определению (3.2) для разных значений расстояния $s$ (рис. 3). Сплошная линия рис. 4,а соответствует теоретическому решению $K_{I}^{{(T)}}$, точечная кривая – расчетным значениям $K_{I}^{{(N)}}(s)$, определенным для разных расстояний $s$. На рис. 4,b показаны значения относительной ошибки ${\delta }(s) = {{(K_{I}^{{(N)}}(s) - K_{I}^{{(T)}})} \mathord{\left/ {\vphantom {{(K_{I}^{{(N)}}(s) - K_{I}^{{(T)}})} {K_{I}^{{(T)}}}}} \right. \kern-0em} {K_{I}^{{(T)}}}}$, в зависимости от величины s. Видно, что дальняя асимптотика является более точной. С уменьшением расстояния до края трещины ошибка растет, но не превышает 3.5%. Как видим, численные значения всегда больше, чем теоретическое значение K_I.

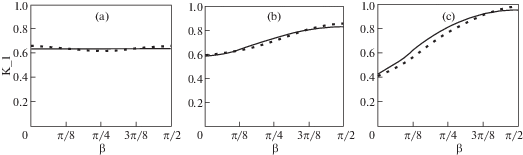
2. Метод позволяет работать с любой заданной в плане геометрией трещин. На рис. 5 показано сравнение кривых распределения коэффициента интенсивности K_I вдоль границы эллиптической трещины в упругом пространстве. Постоянная внешняя нагрузка $\sigma $ действует в направлении ортогональном плоскости трещины. Сплошные кривые соответствуют аналитическому решению [10]

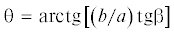где a, b – полуоси эллипса, $a \geqslant b,$ $k = \sqrt {1 - {{{\left( {b{\text{/}}a} \right)}}^{2}}} $, , E(k) – полный эллиптический интеграл второго рода. Точечные кривые являются результатом расчетов. По оси абсцисс отложен угол β, по оси ординат – безразмерный коэффициент ${{K\_1 = {{K}_{I}}} \mathord{\left/ {\vphantom {{K\_1 = {{K}_{I}}} {{\sigma }\sqrt {{\pi }b} }}} \right. \kern-0em} {{\sigma }\sqrt {{\pi }b} }}$.

Пары кривых соответствуют разному отношению полуосей: рис. 5,a – a/b = 1; рис. 5,b – a/b = 2; рис. 5,с – a/b = 5. Видно, что для сравнительно малых значений величины ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} \leqslant 2$ кривые почти совпадают (отличие соствляет менее 1%). Для значений отношения ${a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b} \geqslant 2$ ошибка мала для углов β = 0 и ${\beta } = {{\pi } \mathord{\left/ {\vphantom {{\pi } 2}} \right. \kern-0em} 2}$, но для промежуточных углов начинает увеличиваться (максимальное значение ошибки равно 10%). Возрастание ошибки, по нашему мнению, связано с использованной в расчетах одинаковой сеткой граничных элементов. По всей вероятности, увеличение кривизны кривой границы трещины требует модификации сетки в сторону уменьшения размера граничных элементов.

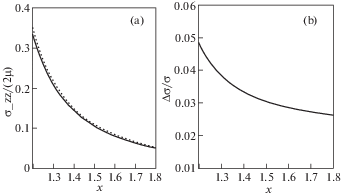
3. Задача для двух круглых плоских параллельных, одноосных трещин одинакового радиуса $R = a$, которые находятся под давлением P на расстоянии 2h друг от друга, рассмотрена в монографии [20]. Ее решение сведено к системе двух интегральных уравнений Фредгольма второго рода. Нам удалось, после решения интегральных уравнений восстановить аналитическую зависимость напряжения ${{{\sigma }}_{0}}(r) = {{\left. {{{{\sigma }}_{{zz}}}(r,z)} \right|}_{{z = 0}}}$. Результаты одного из тестовых сравнений для значений параметров R = 1, $2h = 0.6,$ $P = {p \mathord{\left/ {\vphantom {p {(2{\mu )}}}} \right. \kern-0em} {(2{\mu )}}}$ = 0.1 представлены на рис. 6. Трещины радиуса R = 1 расположены параллельно плоскости z = 0 одна над другой на расстоянии $2h = 0.6$ между их плоскостями. Обе трещины находятся под внутренним давлением P = 0.1.

На рис. 6,a показаны результаты сравнения аналитического ${{{\sigma }_{{zz}}^{{(T)}}} \mathord{\left/ {\vphantom {{{\sigma }_{{zz}}^{{(T)}}} {(2{\mu }}}} \right. \kern-0em} {(2{\mu }}})$ и численного решения ${{{\sigma }_{{zz}}^{{(N)}}} \mathord{\left/ {\vphantom {{{\sigma }_{{zz}}^{{(N)}}} {(2{\mu }}}} \right. \kern-0em} {(2{\mu }}})$. На оси абсцисс отложена координата x, на оси ординат – значение напряжения. Сплошная линия соответствует теоретическому решению, точечная кривая – численным расчетам. Зависимость относительной ошибки Δσ/σ = = ${{({\sigma }_{{zz}}^{{(N)}} - {\sigma }_{{zz}}^{{(T)}})} \mathord{\left/ {\vphantom {{({\sigma }_{{zz}}^{{(N)}} - {\sigma }_{{zz}}^{{(T)}})} {{\sigma }_{{zz}}^{{(T)}}}}} \right. \kern-0em} {{\sigma }_{{zz}}^{{(T)}}}}$ от координаты $x$ приведена на рис. 6,b. Как и в случае одиночной трещины, ошибка нарастает с приближением к краю трещины (координата края x = 1). Для данного расчета максимальное значение ошибки не превышает 5%.

Одним из основных недостатков численных решений является их привязка к конкретным значениям параметров задачи. Исследование зависимости решения от внешних данных приводит к необходимости проведения большого количества расчетов. Это накладывает достаточно жесткие требования на расчетное время, которое требуется для обработки одного конкретного набора параметров. Если это время велико, то задача определения характера зависимости решения от параметров становится громоздкой по времени. С этой точки зрения, предлагаемый метод имеет ряд преимуществ. Фактически, после решения системы (2.7), решение представлено конечным рядом. Исследование любой характеристики полученного решения сводится к суммированию соответствующего этой характеристике ряда.

Для выяснения эффективности метода рассмотрим задачи взаимного влияния двух параллельных трещин в упругом пространстве. Такие задачи рассматривались в работах [20, 21, 31–33]. В монографии [20] методом парных интегральных уравнений построено решение для двух одноосных трещин в упругом слое. В статье [21] приведено решение для двух эллиптических трещин, лежащих в одной плоскости. В работе [31] на основе асимптотического поведения решения для больших расстояний от трещины предложен механизм и геометрия зарождения новых трещин. В статье [32] приведены исследования взаимного влияния эллиптических трещин. В работе [33] излагается метод определения коэффициентов влияния для системы трещин и получены аналитические формулы данного коэффициента для двух круглых трещин. С целью проверки метода для системы трещин было проведено сравнение с некоторыми результатами этих работ.

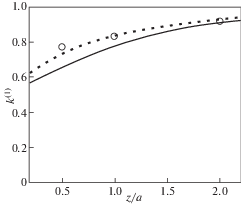
4.Коэффициент влияния для двух круглых параллельных трещин. Основой данного раздела является сравнение с результатами [20, 33] для одноосных круглых параллельных трещин. В работе [33], наряду с более общими результатами, приведена полученная аналитическая зависимость коэффициента влияния двух круглых одноосных трещин радиуса a, в зависимости от расстояния $z$ между их плоскостями

Величина коэффициента влияния k⁽¹⁾ равна отношению КИН ${{K}_{I}}$ для двух трещин к его значению для одиночной трещины. На рис. 7 приведены результаты сравнения. На оси абсцисс отложено безразмерное расстояние между трещинами z/a, на оси ординат – коэффициент влияния k⁽¹⁾. Сплошная кривая соответствует формуле (3.3), точечная кривая – результатам наших расчетов. Кружками приведены три значения коэффициентов влияния, полученные Я.С. Уфляндом [20].

В [33] также приведена аналитическая формула для предельного значения коэффициента влияния, когда расстояние между трещинами стремится к нулю

Численный метод не позволяет нам приблизить трещины на бесконечно близкое расстояние. Он ограничен характерным размером используемого граничного элемента (в наших расчетах использовался размер 0.05). Предельное расстояние достоверности результатов для данного масштаба граничного элемента z = 0.1. Численное значение коэффициента влияния для данного расстояния получилось равным ${{k}^{{(1)}}} = 0.594$.

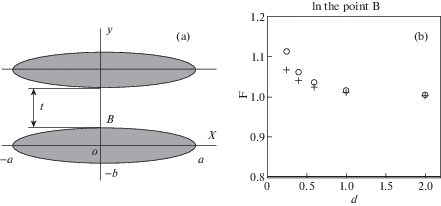
5. Коэффициент влияния двух эллиптических трещин, лежащих в одной плоскости. В работах [21, 32] проведено взаимное влияние двух эллиптических трещин, лежащих в одной плоскости. Показано, что наибольшее влияние характерно для такого взаимного расположения, когда большие полуоси эллипсов параллельны (рис. 8,a), а две другие полуоси расположены на одной прямой. На рис. 8,b приведены результаты сравнения с работой [32]. На оси абсцисс отложено приведенное расстояние между трещинами $d = t{\text{/}}(2b)$ (рис. 8,a). По оси ординат отложен коэффициент влияния F = ${{{{K}_{I}}(B)} \mathord{\left/ {\vphantom {{{{K}_{I}}(B)} {{{K}_{{I0}}}(B)}}} \right. \kern-0em} {{{K}_{{I0}}}(B)}}$, где ${{K}_{{I0}}}\left( B \right)$ – значение коэффициента интенсивности напряжений для одной эллиптической трещины в точке B, ${{K}_{I}}\left( B \right)$ – соответствующее значение коэффициента интенсивности напряжений для двух трещин. Символом “круг” отмечены точки, приведенные в [32], символом “крест” обозначены наши результаты. Расхождение результатов растет по мере сближения трещин, но максимальная ошибка составляет 4%. Как видим, результаты наших расчетов соответствуют работе [32].

Существенной особенностью метода является то, что матрица системы линейных уравнений для определения скачков поля перемещений является всюду плотной. У нее нет глобального преобладания диагональных элементов. Для решения системы использовался итерационный метод, предложенный в работе [30] – “стабилизированный метод бисопряженных градиентов”.

Предложенный авторами метод численного расчета характеристик упругого тела с системой трещин в приложении к некоторым частным задачам представлен в работах [31–35]. Следует также отметить, что трехмерная программа хорошо сохраняет симметрию задачи (если она есть), что также является косвенной проверкой корректности ее работы. Одним из достоинств метода является достаточно малое время варианта расчета и мобильность программы. Под мобильностью мы понимаем возможность быстрого выбора формы каждой трещины (реализованы эллипсы, полуэллипсы, прямоугольники), ее размеров и положения в пространстве. Предусмотрен выбор типа граничных условий (в перемещениях или в напряжениях). Практика использования программы показала, что при характерном размере трещины 1 для хорошего количественного описания требуется ~500 граничных элементов. Программа работает достаточно быстро. Статистика для расчетов на ноутбуке MSI GF63 (Intel Core i7-8750h, 32Гб) такова. Время одного расчета (в секундах) зависит от использованного числа граничных элементов (г.э.). Среднее время, которое требуется для расчета одного варианта задачи, соответственно равно:

для 749 г.э. – 3 с; для 2539 г.э. – 26 с; для 3869 г.э. – 103 с; для 6509 г.э. – 292 с; для 9689 г.э. – 687 с; для 13485 г.э. – 1306 с; для 17905 г.э. – 2389 с.

Сам пакет находится в активной стадии разработки. Продолжается работа по расширению возможных геометрических форм трещин, по улучшению пользовательского интерфейса, по внедрению параллельных вычислений.

Заключение. Подводя итоги работы, можно сказать следующее:

1. Предложенный метод позволяет достаточно эффективно решать задачи механики системы трещин в упругом пространстве. Он может быть хорошим инструментом, дополняющим другие методы исследования.

2. Тестовые расчеты показали вполне удовлетворительное количественное и качественное совпадение численных и аналитических результатов, как для напряжений, так и для коэффициентов интенсивности.

3. Количественное сравнение с результатами для простейшей системы двух трещин можно также считать удовлетворительным. Это показано для эллиптических в плане трещин, лежащих в одной плоскости, а также для системы двух одноосных круглых трещин.

Работа выполнена при поддержке гранта РФФИ № 19-07-01111.