1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 1, 2021

Известия РАН. Механика твердого тела, 2021, № 1, стр. 3-5

ПЛОСКАЯ ДИНАМИКА ОДНОРОДНОГО ПАРАЛЛЕЛЕПИПЕДА С СУХИМ ТРЕНИЕМ

В. Ф. Журавлёв *

Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: zhurav@ipmnet.ru

Поступила в редакцию 11.03.2020
После доработки 15.03.2020
Принята к публикации 19.03.2020

Полный текст (PDF)

Аннотация

Рассмотрена задача о динамике твердого тела в форме параллелепипеда на плоскости при наличии двумерного сухого трения (обобщенная модель сухого трения Кулона–Контенсу [1]). Поскольку в этой модели трения нет разрывов первого рода по скорости, то в математическом плане задача проще, чем задачи с одномерным (по Кулону) сухим трением. В этом примере увеличение размерности приводит к регуляризации задачи.

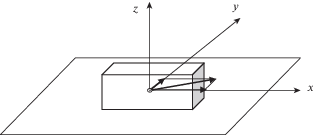
Ключевые слова: динамика, сухое трение, параллелепипед, плоскость

Уравнения динамики прямоугольного однородного параллелепипеда, движущегося по горизонтальной плоскости с сухим трением (рис. 1) имеют вид [2]:

(1)
$\begin{gathered} J\dot {u} = - f{{l}^{2}}\sigma \iint\limits_D {\frac{{({{r}^{2}}u + x{{\nu }_{y}} - y{{\nu }_{x}})dxdy}}{{\sqrt {{{r}^{2}}{{u}^{2}} + {{\nu }^{2}} + 2u(x{{\nu }_{y}} - y{{\nu }_{x}})} }}} \\ m{{{\dot {\nu }}}_{x}} = - f{{l}^{2}}\sigma \iint\limits_D {\frac{{({{\nu }_{x}} - uy)dxdy}}{{\sqrt {{{r}^{2}}{{u}^{2}} + {{\nu }^{2}} + 2u(x{{\nu }_{y}} - y{{\nu }_{x}})} }}} + P \\ m{{{\dot {\nu }}}_{y}} = - f{{l}^{2}}\sigma \iint\limits_D {\frac{{({{\nu }_{y}} + ux)dxdy}}{{\sqrt {{{r}^{2}}{{u}^{2}} + {{\nu }^{2}} + 2u(x{{\nu }_{y}} - y{{\nu }_{x}})} }}} + Q \\ \end{gathered} $
Рис. 1

Здесь обозначено: J – момент инерции тела вокруг оси z, $m$ – масса тела, $u = \omega l$, где $\omega $ – угловая скорость параллелепипеда вокруг оси $z$, а l – его длина, $h$ – ширина, (νx, νy) – скорость центра масс,  f – коэффициент сухого трения по Кулону, $\sigma $ – равномерное распределение давления тела на плоскость, ${{r}^{2}} = {{x}^{2}} + {{y}^{2}}$, $(P,Q)$ – приложенная к телу горизонтальная сила.

Стационарное решение

(2)
$u \equiv 0,\quad {{\nu }_{x}} \equiv p,\quad {{\nu }_{y}} \equiv q$

Удовлетворяет уравнениям стационарного движения

(3)
$\begin{gathered} \iint\limits_D {\frac{{(xq - yp)dxdy}}{{\sqrt {{{p}^{2}} + {{q}^{2}}} }} \equiv 0} \\ - F\iint\limits_D {\frac{{pdxdy}}{{\sqrt {{{p}^{2}} + {{q}^{2}}} }} + P \equiv - \frac{{Fphl}}{{\sqrt {{{p}^{2}} + {{q}^{2}}} }} + P \equiv 0} \\ - F\iint\limits_D {\frac{{qdxdy}}{{\sqrt {{{p}^{2}} + {{q}^{2}}} }} + Q \equiv - \frac{{Fqhl}}{{\sqrt {{{p}^{2}} + {{q}^{2}}} }} + Q \equiv 0} \\ \end{gathered} $
где $F = f{{l}^{2}}\sigma $.

Откуда следует:

$\frac{p}{P} = \frac{q}{Q}$
т.е. любое стационарное движение происходит в направлении приложенной силы. Соотношения (3) позволяют выразить компоненты установившейся скорости $(p,q)$ через компоненты приложенной силы $(P,Q)$.

Для исследования устойчивости стационарного решения (2) проварьируем его

$u = \delta u,\quad {{\nu }_{x}} = p + \delta {{\nu }_{x}},\quad {{\nu }_{y}} = q + \delta {{v}_{y}}$
и запишем уравнения в вариациях
(4)
$\begin{gathered} J\delta \dot {u} = - \frac{{f{{l}^{2}}N({{p}^{2}}{{l}^{2}} + {{q}^{2}}{{h}^{2}})}}{{12\sqrt {{{{({{p}^{2}} + {{q}^{2}})}}^{3}}} }}\delta u \\ m\delta {{{\dot {\nu }}}_{x}} = - \frac{{f{{l}^{2}}qN(q\delta {{v}_{x}} - p\delta {{v}_{y}})}}{{\sqrt {{{{({{p}^{2}} + {{q}^{2}})}}^{3}}} }} \\ m\delta {{{\dot {\nu }}}_{y}} = \frac{{f{{l}^{2}}pN(q\delta {{v}_{x}} - p\delta {{v}_{y}})}}{{\sqrt {{{{({{p}^{2}} + {{q}^{2}})}}^{3}}} }} \\ \end{gathered} $
где $N = \sigma lh$ – величина силы, прижимающей трущиеся тела друг к другу (вес параллелепипеда).

Уравнения в вариациях (4) распались. Уравнение по угловой скорости $\delta u$ отделилось от уравнений по линейной скорости. Стационарное решение $\delta u = 0$ в первом уравнении является, с очевидностью, асимптотически устойчивым.

Устойчивость тривиального решения $(\delta {{\nu }_{x}},\delta {{\nu }_{y}}) = 0$ может быть изучена анализом двух последних уравнений системы (4):

(5)
$\begin{gathered} \delta {{{\dot {\nu }}}_{x}} = - а(q\delta {{\nu }_{x}} - p\delta {{\nu }_{y}}) \\ \delta {{{\dot {\nu }}}_{y}} = b(q\delta {{\nu }_{x}} - p\delta {{\nu }_{y}}) \\ \end{gathered} $
где $a = f{{l}^{2}}qN{\text{/}}m{{r}^{3}}$, $b = f{{l}^{2}}pN{\text{/}}m{{r}^{3}}$.

Устойчивость определяется корнями характеристического уравнения:

(6)
$\left\| {A - \lambda E} \right\| = 0,$
в котором

$A = \left\| {\begin{array}{*{20}{c}} { - aq}&{ap} \\ {bp}&{ - bq} \end{array}} \right\|$

Характеристическое уравнение (6), следовательно, имеет вид:

${{\lambda }^{2}} + (bp - aq)\lambda = 0$

Его корни таковы

${{\lambda }_{1}} = 0,\quad {{\lambda }_{2}} = - (bp + aq) = - \frac{{h({{p}^{2}} + {{q}^{2}})}}{{fl\sigma m}}$

Нулевой корень объясняется наличием у системы (5) стационарного интегрального многообразия $q\delta {{\nu }_{x}} - p\delta {{\nu }_{y}} \equiv 0.$

Второй корень λ2 на этом многообразии является строго отрицательным и, следовательно, система (5) является асимптотически устойчивой.

В монографии [2] уравнения (1) рассматривались приближенно посредством замены двукратных интегралов в их правых частях аппроксимациями Паде в первом приближении. Анализ этой задачи в настоящей работе показывает полное качественное соответствие выполненного ранее приближенного исследования тому, что выполнено выше.

Исследование выполнено за счет гранта Российского научного фонда (проект № АААА-А20-120011).

Список литературы

  1. Журавлёв В.Ф. О модели сухого трения в задачах динамики твердых тел // Успехи механики. 2005. № 3. С. 58–76.

  2. Андронов В.В., Журавлёв В.Ф. Сухое трение в задачах механики. М.–Ижевск: НИЦ “Регулярная и хаотическая динамика”. Институт компьютерных исследований, 2010. 184 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал