Известия РАН. Механика твердого тела, 2021, № 1, стр. 83-105

Введение. В литературе по классической механике деформируемых сред [1–9] используются тензорные характеристики механических процессов различных видов.

В работах А.А. Ильюшина [10, 11], а также У. Нолла и К. Трусделла [12, 13] впервые обращено существенное внимание на математические аспекты инвариантности тензорных характеристик и связей между ними в определяющих соотношениях: введены понятия образа процесса и свойств пятимерной изотропии, понятие материальной независимости от системы отсчета.

Эти идеи получили воплощение и развитие в дальнейших работах авторов и их последователей [2–6, 8, 9, 14–21].

Дальнейшее развитие математических основ в работах по геометрическим и алгебраическим аспектам инвариантностей [22–34] нашло приложение в работах по механике сплошной среды и ее разделам, в том числе в работах автора [35–47], послуживших основой настоящего изложения.

В настоящей работе представлена общая теория объективных тензорных процессов классической механики, включая классическую механику сплошной среды. Введены понятия объективных тензоров различных рангов, типов объективности, включая типы Ильюшина–Хилла (материально ориентированные тензоры) и Нолла–Трусделла (пространственно ориентированные тензоры) [40]. Введены понятия простых тензорных аналогов механических характеристик одного ранга и разных типов, понятия простых коммутативных диаграмм объективных тензоров. Подробно рассмотрены диаграммы тензоров второго ранга, наиболее часто используемых в механике деформируемых сред.

Среди отображений, связывающих тензорные процессы различных рангов и типов объективности, выделены отображения, не зависящие от системы отсчета. Это фундаментальное свойство, присущее отображениям, связывающим тензорные процессы в определяющих соотношениях механических свойств тел, включая свойства сопротивления деформированию. Установлена теорема о необходимых и достаточных условиях независимости отображений от системы отсчета. Теорема накладывает наименьшие ограничения (лишь требование инвариантности относительно сдвига временной переменной) на отображения, связывающие материально ориентированные тензорные процессы, – отображения типа Ильюшина.

Для двух произвольных диаграмм объективных тензорных процессов (вообще говоря, разных рангов) рассмотрен полный набор (пакет) родственных друг другу отображений (кондукторов) всевозможных аналогов одной диаграммы во всевозможные аналоги другой диаграммы – пакет кондукторов, или отображение диаграмм. Показано, что все кондукторы пакета независимы от системы отсчета лишь одновременно (вместе с порождающим отображением – индуктором). Индуктор типа Ильюшина порождает пакет кондукторов наиболее общего вида.

Для совпадающих диаграмм (одного ранга с одинаковыми переплетающими операторами) введено обобщающее понятие объективных производных на основе индуктора типа Ильюшина – материальной производной материально ориентированного тензора. Объективные производные составляют подпакет кондукторов, связывающих тензоры одинаковых (всевозможных) рангов и типов объективности.

Приведены общие формулы объективных производных скаляров, векторов и тензоров второго ранга, представленные в лагранжевом и эйлеровом видах. Показано, что этими формулами охватываются все известные производные Зарембы–Яуманна, Олдройда, Коттер–Ривлина, Трусделла, Хилла, Седова, Динса [48–56], включая производные, использованные в работах [57–64], а также семейство производных Гордона–Шоуолтера [65].

В качестве оператора, обратного к объективной производной, построен оператор объективного интегрирования.

Возможности эффективного применения представленных в настоящей работе объективных производных и объективных интегралов проиллюстрированы на примерах подходов к построению различных моделей сред при конечных деформациях [66–84].

1. Тензорные характеристики механических процессов. 1.1. Характеристики деформаций. При лагранжевом (отсчетном, относительном) описании движения сплошной среды (x и x – положения точки тела в отсчетной и актуальной конфигурациях соответственно, t – время)

основной исходной характеристикой деформаций в смысле Коши является градиент (аффинор) деформации имеющий в силу невырожденности однозначные правое и левое полярные разложения с ортогональным тензором Q, называемым тензором полярного поворота (полярной ориентации), и симметричными положительно определенными тензорами X и Y, называемыми правым и левым тензорами растяжений (чистой деформации), связанными очевидным тождеством

Одномерные собственные подпространства тензоров X и Y называют главными правыми и левыми осями деформаций соответственно.

В подходе Коши–Грина применяются мера деформаций Коши C и тензор деформаций Грина $\mathcal{E}$, определяемые формулами

а в подходе Коши–Альманси – мера Альманси B и тензор Альманси E, задаваемые равенствами

Равенства (1.5) показывают соосность тензоров X, C и $\mathcal{E}$, а равенства (1.6) – соосность тензоров Y, B и E.

В лагранжевых базисах $\left\{ {{{{\mathbf{e}}}_{{0i}}}} \right\}$, $\{ {\mathbf{e}}_{0}^{i}\} $ отсчетной и $\left\{ {{{{\mathbf{e}}}_{i}}} \right\}$, {eⁱ} актуальной конфигураций частицы тела справедливы представления (суммирование по правилу Эйнштейна)

Совпадение компонент тензоров $\mathcal{E}$ и E (в разных базисах!) равносильно тождеству

Подобно построениям (1.5), (1.6) на основе обратных к мерам деформации C Коши и B Альманси тензоров C^–1 и ${{{\mathbf{B}}}^{{ - 1}}} = {\mathbf{F}}$ (тензор F называется мерой деформаций Фингера [16]) могут быть рассмотрены “взаимные” к $\mathcal{E}$ и E тензоры деформаций ${{\mathcal{E}}_{{{\text{II}}}}}$ и E_II:

аналогично (1.8) удовлетворяющие тождеству

Скорости деформаций характеризуются тензором скоростей деформаций V (v – поле скоростей движения точек среды)

для которого справедливы тождественные представления

1.2. Тензоры напряжений. В классической механике сплошной среды используется тензор истинных напряжений Коши S, отвечающий основной формуле теории напряжений

где ${{{\mathbf{t}}}_{{\mathbf{n}}}}(x)$ – вектор напряжения на элементарной площадке, n – вектор единичной нормали этой площадки.

Применяются также тензоры условных напряжений Пиолы–Кирхгофа первого рода Π, второго рода P и тензор напряжений Ильюшина (“энергетический” тензор напряжений) Σ, определенные формулами

2. Объективные тензоры. 2.1. Замена системы отсчета. Объективные тензоры. Типы объективности. В качестве пространства конфигураций тел и их точек в механике сплошной среды принимается трехмерное аффинное евклидово пространство $\mathcal{X}$ с точками x, а в качестве пространства моментов времени – одномерное аффинное пространство $\mathcal{T}$ с точками (моментами времени) t ($\mathcal{T}$ можно отождествить с множеством действительных чисел R и считать t числом). Пара переменных (x, t) носит название эйлеровых переменных. Присоединенное векторное (трехмерное евклидово) пространство $\mathcal{V}$ пространства $\mathcal{X}$ служит для изображения векторных величин (векторов скорости, ускорения, силы и т.п.); тензорные характеристики (включая тензоры деформаций, напряжений и др.) рассматриваются над векторным пространством $\mathcal{V}$.

Замена системы отсчета выражается следующей заменой “старых” эйлеровых переменных (x, t) на “новые” $({{{\mathbf{x}}}_{*}},{{t}_{*}})$:

где параметрами замены служат a – постоянный скаляр (физической размерности времени), x₀ – постоянная точка трехмерного пространства $\mathcal{X}$, а также точечнозначная ${{{\mathbf{x}}}_{{0*}}}$ и тензорнозначная $\mathcal{Q}$ функции времени t, причем $\mathcal{Q}$ – ортогональный тензор над $\mathcal{V}$: $\mathcal{Q}{{\mathcal{Q}}^{{\text{T}}}} = {{\mathcal{Q}}^{{\text{T}}}}\mathcal{Q} = {\mathbf{I}}$, т.е. ${{\mathcal{Q}}^{{ - 1}}} = {{\mathcal{Q}}^{{\text{T}}}}$. Как правило, эти функции предполагаются не только непрерывными, но и необходимое число раз дифференцируемыми по t.

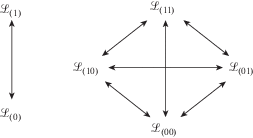
Будем для фиксированного материального объекта (точки тела x, частицы или тела в целом) рассматривать скалярные ${\varphi }$, векторные ${{{\mathbf{u}}}_{{(0)}}},{{{\mathbf{u}}}_{{(1)}}}$ и тензорные (второго ранга) ${{{\mathbf{L}}}_{{(00)}}},{{{\mathbf{L}}}_{{(10)}}},{{{\mathbf{L}}}_{{(01)}}},{{{\mathbf{L}}}_{{(11)}}}$ механические процессы, преобразующиеся при замене системы отсчета (2.1) по правилам

В пространствах ${{\mathcal{L}}_{m}}$ тензоров L_m более высоких рангов m также могут быть выделены множества тензоров, преобразующихся по формулам типа (2.2). Для набора ${{\mathfrak{A}}_{m}}$ = = $({{\mathcal{A}}_{1}},{{\mathcal{A}}_{2}}, \ldots ,{{\mathcal{A}}_{m}})$ из m тензоров второго ранга ${{\mathcal{A}}_{i}}$ определим его действие в пространстве ${{\mathcal{L}}_{m}}$ как линейного оператора (эндоморфизма) формулами (для полиад и произвольных тензоров):

где символом $\mathop \cdot \limits^m $ обозначено определяемое здесь действие оператора ${{\mathfrak{A}}_{m}}$, символом $\mathop :\limits^m $ обозначена обычная параллельная m-кратная свертка тензоров, а σ – подстановка набора чисел (1, 2, …, 2m) со значениями (1, m + 1, 2, m + 2, …, m, 2m) и T_σ – соответствующий ей оператор транспонирования [28–30, 42, 44]. Оператор ${{\mathfrak{A}}_{m}}$ с невырожденными тензорами ${{\mathcal{A}}_{i}}$ является автоморфизмом пространства ${{\mathcal{L}}_{m}}$.

Воспользуемся тензорной записью введенного в [42, 44] обобщенного представления групп в тензорах, являющегося обобщением классического представления [30]. Пусть M($\mathcal{V}$) – подгруппа группы GL($\mathcal{V}$) = Aut($\mathcal{V}$) невырожденных тензоров второго ранга над (евклидовым) пространством $\mathcal{V}$, и представление φ: G → Aut($\mathcal{V}$) группы G в векторном пространстве $\mathcal{V}$ осуществляет эпиморфизм G на M($\mathcal{V}$). Обозначим через k_m = (k₁, k₂, …, k_m) двоичный мультииндекс длины m (числа k_i равны 0 или 1). Для M ∈ M($\mathcal{V}$) примем M¹ = M, M⁰ = I, где ${\mathbf{I}}$ – единичный тензор, и составим набор ${{{\mathbf{M}}}^{{{{{\mathbf{k}}}_{m}}}}} = \left( {{{{\mathbf{M}}}^{{{{k}_{{\text{1}}}}}}},{{{\mathbf{M}}}^{{{{k}_{{\text{2}}}}}}},\,\,...,\,\,{{{\mathbf{M}}}^{{{{k}_{m}}}}}} \right)$ . Подстановка набора ${{{\mathbf{M}}}^{{{{{\mathbf{k}}}_{m}}}}}$ в (2.3), (2.4) в качестве набора ${{\mathfrak{A}}_{m}}$ (то есть невырожденных тензоров ${{{\mathbf{M}}}^{{{{{\text{k}}}_{i}}}}}$ качестве тензоров ${{\mathcal{A}}_{i}}$) показывает, что ${{{\mathbf{M}}}^{{{{{\mathbf{k}}}_{m}}}}}$ осуществляет по формулам (2.3), (2.4) автоморфизм пространства тензоров ${{\mathcal{L}}_{m}}$. Тем самым получаем, что представление φ группы G в векторном пространстве $\mathcal{V}$ порождает соответствующее представление ${{\varphi }^{{{{{\mathbf{k}}}_{m}}}}}$: G → Aut(${{\mathcal{L}}_{m}}$) группы G в пространстве ${{\mathcal{L}}_{m}}$ тензоров ${{{\mathbf{L}}}_{m}}$ ранга m над $\mathcal{V}$, называемое обобщенным k_m-представлением группы G в тензорах. Если M($\mathcal{V}$) = O($\mathcal{V}$) – ортогональная группа, то представление ${{\varphi }^{{{{{\mathbf{k}}}_{m}}}}}$ называется ортогональным k_m-представлением.

Полагая в (2.3), (2.4) ${{\mathfrak{A}}_{m}} = {{\mathcal{Q}}^{{{{{\mathbf{k}}}_{m}}}}}$, где $\mathcal{Q}$ – ортогональный тензор из (2.1), из множества ${{\mathcal{L}}_{m}}$ всех тензоров L_m ранга m над $\mathcal{V}$ выделим тензоры ${{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$, преобразующиеся подобно (2.2) по формулам автоморфизмов ортогонального k_m-представления

Определение 2.1. Назовем все механические тензорные процессы, подчиняющиеся какому-либо из правил вида (2.2), (2.5) объективными, а нижний двоичный мультииндекс k_m – типом объективности (для объективных скаляров отсутствие (мульти-) индекса формально рассматривается как пустой мультииндекс “( )”, показывающий нулевой ранг скаляра как тензора).

Примем |k_m| = k₁ + k₂ + … + k_m (m ≥ 1). Очевидно, что объективные тензоры с |k_m| = 0, то есть тензоры типа (0), (00) и аналогичные тензоры более высокого ранга, являются тензорами типа Ильюшина–Хилла [45] (известны в литературе также как “лагранжевы” [21], или “инвариантные” [62]). Будем называть их также материально ориентированными, или материальными, или правыми. Объективные тензоры с |k_m| = m, то есть тензоры типа (1), (11) и т.п., являются тензорами типа Нолла–Трусделла [45] (известны также как “не зависящие от системы отсчета” [3], или “эйлеровы” [21], или “индифферентные” [62]). Будем называть их пространственно ориентированными, или пространственными, или левыми. Остальные типы будем называть смешанными. Тип объективного тензора – его неизменный атрибут.

Нетрудно видеть, например, что векторы элементарных материальных волокон δx, ориентированных материальных площадок δS₀ и их нормалей n₀ в отсчетной конфигурации являются объективными векторами типа (0), а соответствующие векторы δx, δS и n актуальной конфигурации – объективными типа (1). Меры и тензоры деформаций ${\mathbf{C}},{{{\mathbf{C}}}^{{ - 1}}},\mathcal{E},{{\mathcal{E}}_{{{\text{II}}}}}$ из (1.5), (1.9)₁, правый тензор растяжений X из (1.3), (1.4), а также тензоры напряжений ${\mathbf{P}},\Sigma $ из (1.14) суть объективные тензоры типа (00). Меры и тензоры деформаций B, F, E, E_II из (1.6), (1.9)₂, тензор Y из (1.3), (1.4), тензор скоростей деформаций V из (1.11), (1.12), а также тензор напряжений Коши S – объективные тензоры типа (11). Аффинор деформаций A из (1.2), (1.3), тензор полярного поворота Q из (1.2), (1.3) и тензор A^–1T, а также тензор напряжений Π из (1.14) объективны типа (10), тензоры A^–1, A^T, Q^T, а также Π^T объективны типа (01).

2.2. Диаграммы. 2.2.1. Определение диаграмм. Родственные механические характеристики могут быть выражены объективными тензорами одного ранга и разных типов. Разнотипные родственные тензоры, как правило, связаны определенными взаимно однозначными (невырожденными) отображениями. Отразим это следующим формальным определением (для простоты ограничимся объективными векторами и тензорами второго ранга).

Определение 2.2. Объективные разных типов векторные характеристики ${{{\mathbf{u}}}_{{\left( 0 \right)}}},{{{\mathbf{u}}}_{{\left( 1 \right)}}}$ по отношению друг к другу, а также объективные разных типов тензорные (второго ранга) характеристики ${{{\mathbf{L}}}_{{\left( {00} \right)}}},{{{\mathbf{L}}}_{{\left( {10} \right)}}},{{{\mathbf{L}}}_{{\left( {01} \right)}}},{{{\mathbf{L}}}_{{\left( {11} \right)}}}$ по отношению друг к другу назовем простыми эквивалентными представлениями (простыми эквивалентами, простыми аналогами), если они связаны друг с другом попарно тождествами в виде отображений, составляющих коммутативные диаграммы вида

где ${{\mathcal{L}}_{{{\text{(k)}}}}}$(k = 0, 1) – линейное пространство всех (k)-объективных векторов $({{{\mathbf{u}}}_{{{\text{(k)}}}}} \in {{\mathcal{L}}_{{{\text{(k)}}}}})$, ${{\mathcal{L}}_{{{\text{(k,l)}}}}}$ (k, l = 0, 1) – линейное пространство всех (k, l)-объективных тензоров $({{{\mathbf{L}}}_{{{\text{(k,l)}}}}} \in {{\mathcal{L}}_{{{\text{(k,l)}}}}})$, а стрелками обозначены составляющие диаграмму отображения, выраженные формулами (суммирование по k, l отсутствует) с невырожденными (k', k)-объективными тензорами ${{\mathcal{A}}_{{\left( {{\text{k'}},{\text{k}}} \right)}}}$ и ${{\mathcal{A}}_{{1\left( {{\text{k'}},{\text{k}}} \right)}}},{{\mathcal{A}}_{{2\left( {{\text{k'}},{\text{k}}} \right)}}}$, связанными условиями (суммирование по повторяющимся индексам отсутствует)

Диаграммы (2.6) назовем простыми диаграммами, отображения (2.7) назовем переплетающими операторами, а тензоры (2.8) – переходными тензорами этих диаграмм.

Для диаграмм объективных тензоров ранга m примем в качестве переходных тензоров невырожденные $({\text{k}}_{i}^{'},{{{\text{k}}}_{i}})$-объективные тензоры второго ранга ${{\mathcal{A}}_{{i({\text{k}}_{i}^{'},{{{\text{k}}}_{i}})~}}}$, удовлетворяющие условиям вида (2.8)₂ для i = 1, 2, …, m. Положим в (2.3), (2.4) ${{\mathcal{A}}_{i}} = {{\mathcal{A}}_{{i({\text{k}}_{i}^{'},{{{\text{k}}}_{i}})}}}$ и обозначим их набор вида ${{\mathfrak{A}}_{m}}$ через ${{\mathfrak{A}}_{{{\mathbf{k}}_{m}^{'} \otimes {{{\mathbf{k}}}_{m}}}}}$ (где ${\mathbf{k}}_{m}^{'} = ({\text{k}}_{1}^{'},{\text{k}}_{2}^{'}, \ldots ,{\text{k}}_{m}^{'})$ и ${{{\mathbf{k}}}_{m}} = \left( {{{{\text{k}}}_{1}},{{{\text{k}}}_{2}}, \ldots ,{{{\text{k}}}_{m}}} \right)$). Тогда формула (2.4) с ${{{\mathbf{L}}}_{m}} = {{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$ определяет общий вид переплетающих операторов для объективных тензоров ранга m:

Класс простых диаграмм полностью исчерпывает все коммутативные диаграммы для векторных аналогов, класс простых диаграмм объективных тензоров второго ранга не исчерпывает множества всех коммутативных диаграмм. Тем не менее введенные классы простых диаграмм достаточно богаты для представления объективных векторных и тензорных характеристик второго ранга различными аналогами, включая аналоги типа Ильюшина–Хилла и Нолла–Трусделла [45].

2.2.2. Диаграммы тензоров второго ранга. Введем следующее определение, полезное для применения диаграмм объективных тензоров второго ранга.

Определение 2.3. Назовем простую диаграмму тензоров второго ранга, определяемую с помощью (2.2)–(2.4), квазисимметричной, если ${{\mathcal{A}}_{{2\left( {10} \right)}}} \equiv {\alpha }{{\mathcal{A}}_{{1\left( {10} \right)}}}$ с ${\alpha } \ne 0$, и симметричной, если при этом ${\alpha } \equiv 1$. Пару простых диаграмм, определяемых соответственно переходными тензорами $\mathcal{A}_{{i\left( {{\text{k}},{\text{l}}} \right)}}^{{\left( 1 \right)}}$ и $\mathcal{A}_{{i\left( {{\text{k}},{\text{l}}} \right)}}^{{\left( 2 \right)}}$ вида (2.4), назовем квазисопряженной (а сами диаграммы взаимно квазисопряженными), если $\mathcal{A}_{{1(10)}}^{{(2)}}\, \equiv \,{\beta }\mathcal{A}_{{1(10)}}^{{(1) - 1{\text{T}}}}$ и $\mathcal{A}_{{2(10)}}^{{(2)}}\, \equiv \,{{{\gamma }}^{{ - 1}}}\mathcal{A}_{{2(10)}}^{{(1) - 1{\text{T}}}}$ с ${\beta } \ne 0$ и ${\gamma } \ne 0$, и сопряженной (диаграммы – взаимно сопряженными), если при этом ${\beta } \equiv {\gamma }$ = 1.

Первая пара родственных названий в Определении 1.3 проистекает из того, что в любой квазисимметричной диаграмме материально и пространственно ориентированные аналоги симметричны лишь одновременно. Вторая пара названий соответствует тому, что для квазисопряженной пары диаграмм скалярные произведения (в классическом смысле двойной свертки ${\mathbf{M}}:{\mathbf{L}} \equiv {\text{tr}}({\mathbf{M}}{{{\mathbf{L}}}^{{\text{T}}}})$) однотипных аналогов этих диаграмм пропорциональны друг другу, а для сопряженной пары диаграмм – равны.

Заметим, что (квази-) сопряженные диаграммы (квази-) симметричны лишь одновременно.

Для каждого объективного тензора второго ранга орбита любой простой диаграммы (множество значений на этом тензоре всех композиций переплетающих операторов (2.6)₂) содержит ровно по одному элементу (включая данный тензор) в каждом из четырех пространств ${{\mathcal{L}}_{{\left( {{\text{k}},{\text{l}}} \right)}}}{\text{\;}}$ (k, l = 0, 1), то есть ровно по одному аналогу каждого типа объективности.

Рассмотрим некоторые из таких диаграмм для тензорных (второго ранга) эквивалентных представлений (аналогов) объективных механических характеристик, используя для построения переходных тензоров (2.8) невырожденный (10)-объективный тензор – аффинор (градиент) деформации A из (1.2) и его (однозначные) полярные разложения (1.3) с ортогональным тензором полярного поворота Q и тензорами растяжений X и Y [2, 3, 16].

Определим формулами (2.6)₂, (2.7), (2.8) некоторые из простых диаграмм для объективных тензоров второго ранга ${{{\mathbf{L}}}_{{\left( {{\text{k}},{\text{l}}} \right)}}} \in {{\mathcal{L}}_{{\left( {{\text{k}},{\text{l}}} \right)}}}~$, задавая определенным образом переходные тензоры ${{\mathcal{A}}_{{i\left( {{\text{k}},{\text{l}}} \right)}}}$ (i = 1, 2; k, l = 0, 1). Диаграмму Грина–Альманзи определим тензорами

диаграмму Коши–Ильюшина – тензорами

Диаграммы Грина–Альманзи и Коши–Ильюшина обе симметричны и сопряжены друг другу.

Определим диаграмму Коши–Пиолы переходными тензорами

диаграмму Коши–Хилла – тензорами

Диаграммы Коши–Пиолы и Коши–Хилла обе квазисимметричны и квазисопряжены диаграмме Грина–Альманзи.

Определим коротационные диаграммы переходными тензорами

в частности, нейтральную диаграмму (${\mathbf{R}} \equiv {\mathbf{I}}$) – тензорами

Здесь всюду A – аффинор деформации, Q – тензор полярного поворота, $J \equiv \left| {{\text{det}}{\mathbf{A}}} \right|$, R – произвольно заданный ортогональный (00)-объективный тензор.

Все коротационные диаграммы, включая нейтральную, симметричны и самосопряжены.

Нетрудно проследить [1–3, 16], что диаграмма Грина–Альманзи (2.10) связывает в качестве аналогов материально и пространственно ориентированные тензоры деформаций Грина ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv \mathcal{E}$ и Альманзи ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{E}}$, а также новые тензоры смешанных типов объективности, характеризующие деформацию: ${{{\mathbf{L}}}_{{\left( {10} \right)}}} \equiv \frac{1}{2}({\mathbf{A}} - {{{\mathbf{A}}}^{{ - 1{\text{T}}}}})$ ≡ $\frac{1}{2}{\mathbf{Q}}({\mathbf{X}} - {{{\mathbf{X}}}^{{ - 1}}})$ ≡ ≡ $\frac{1}{2}({\mathbf{Y}} - {{{\mathbf{Y}}}^{{ - 1}}}){\mathbf{Q}}$ и ${{{\mathbf{L}}}_{{\left( {01} \right)}}} \equiv \frac{1}{2}({{{\mathbf{A}}}^{{\text{T}}}} - {{{\mathbf{A}}}^{{ - 1}}})$ ≡ $\frac{1}{2}({\mathbf{X}} - {{{\mathbf{X}}}^{{ - 1}}}){{{\mathbf{Q}}}^{{\text{T}}}} \equiv \frac{1}{2}{{{\mathbf{Q}}}^{{\text{T}}}}({\mathbf{Y}} - {{{\mathbf{Y}}}^{{ - 1}}})$. Эта же диаграмма связывает в качестве аналогов материальную производную тензора деформаций Грина ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv \dot {\mathcal{E}}$ и пространственно ориентированный тензор скоростей деформаций ${{{\mathbf{L}}}_{{(11)}}}$ ≡ V, а также смешанных типов тензоры ${{{\mathbf{L}}}_{{\left( {10} \right)}}} \equiv {\mathbf{VA}} \equiv {{{\mathbf{A}}}^{{ - 1{\text{T}}}}}\dot {\mathcal{E}} \equiv \frac{1}{2}{\mathbf{Q}}({{{\mathbf{X}}}^{{ - 1}}}{\mathbf{\dot {X}X}} + {\mathbf{\dot {X}}})$ и L₍₀₁₎ ≡ A^TV ≡ ≡ $\dot {\mathcal{E}}{{{\mathbf{A}}}^{{ - 1}}} \equiv \frac{1}{2}({\mathbf{\dot {X}}} + {\mathbf{X\dot {X}}}{{{\mathbf{X}}}^{{ - 1}}}){{{\mathbf{Q}}}^{{\text{T}}}}$, характеризующие скорость деформации. Ее аналогами являются также тензоры ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {\mathbf{C}} \equiv {{{\mathbf{A}}}^{{\text{T}}}}{\mathbf{A}}$, ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{I}}$, ${{{\mathbf{L}}}_{{\left( {10} \right)}}} \equiv {\mathbf{A}},{{{\mathbf{L}}}_{{\left( {01} \right)}}} \equiv {{{\mathbf{A}}}^{{\text{T}}}}$, и тензоры ${{{\mathbf{L}}}_{{(00)}}}$ ≡ I, ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{B}} \equiv {{{\mathbf{A}}}^{{ - 1{\text{T}}}}}{{{\mathbf{A}}}^{{ - 1}}}$, ${{{\mathbf{L}}}_{{\left( {10} \right)}}} \equiv {{{\mathbf{A}}}^{{ - 1{\text{T}}}}}$, ${{{\mathbf{L}}}_{{\left( {01} \right)}}} \equiv {{{\mathbf{A}}}^{{ - 1}}}$.

Диаграмма Коши–Ильюшина (2.11) связывает в качестве аналогов пространственно и материально ориентированные тензоры истинных напряжений Коши ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{S}}$ и условных напряжений Ильюшина ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {\mathbf{\Sigma }}$, тензоры деформаций ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {{\mathcal{E}}_{{{\text{II}}}}}$ и ${{{\mathbf{L}}}_{{\left( {11} \right)}}}$ ≡ E_II, материальную производную тензора деформаций ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {{\dot {\mathcal{E}}}_{{{\text{II}}}}}$ и тензор скоростей деформаций ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{V}}$, а также тензоры ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {{{\mathbf{C}}}^{{ - 1}}}$, ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{I}}$, ${{{\mathbf{L}}}_{{\left( {10} \right)}}} \equiv {{{\mathbf{A}}}^{{ - 1{\text{T}}}}}$, ${{{\mathbf{L}}}_{{\left( {01} \right)}}} \equiv {{{\mathbf{A}}}^{{ - 1}}}$ и тензоры ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {\mathbf{I}}$, ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{F}}$, ${{{\mathbf{L}}}_{{\left( {10} \right)}}} \equiv {\mathbf{A}}$, ${{{\mathbf{L}}}_{{\left( {01} \right)}}} \equiv {{{\mathbf{A}}}^{{\text{T}}}}$.

Диаграммой Коши–Пиолы (2.12) связаны в качестве аналогов, например, тензор истинных напряжений Коши ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{S}}$, первый и второй тензоры условных напряжений Пиолы–Кирхгофа ${{{\mathbf{L}}}_{{\left( {10} \right)}}} \equiv {\mathbf{\Pi }}$, ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {\mathbf{P}}$. В диаграмме Коши–Хилла (2.13) аналогами являются, например, тензор истинных напряжений Коши ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{S}}$ и второй тензор условных напряжений Пиолы–Кирхгофа ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {\mathbf{P}}~$.

Аналогами нейтральной диаграммы вида (2.14) являются, например, тензоры, характеризующие деформацию, ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {\mathbf{X}}$, ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\mathbf{Y}}$, ${{{\mathbf{L}}}_{{\left( {10} \right)}}} \equiv {\mathbf{A}}$, ${{{\mathbf{L}}}_{{\left( {01} \right)}}} \equiv {{{\mathbf{A}}}^{{\text{T}}}}$, а также логарифмические тензоры деформации – правый тензор ${{{\mathbf{L}}}_{{\left( {00} \right)}}} \equiv {\text{ln}}{\mathbf{X}}$ и левый тензор Генки ${{{\mathbf{L}}}_{{\left( {11} \right)}}} \equiv {\text{ln}}{\mathbf{Y}}$. Нетрудно видеть, что в нейтральной диаграмме материально и пространственно ориентированными аналогами являются тензоры C и F, C^–1 и ${{{\mathbf{F}}}^{{ - 1}}} \equiv {\mathbf{B}}$. Этой же диаграммой связаны и другие наборы аналогов, характеризующих деформации, скорости деформаций и напряжения.

Диаграммы, образованные перекрестным использованием тензоров вида (2.10) и (2.11), а именно

а также наоборот назовем соответственно первой и второй “косыми” диаграммами Хилла–Седова.

Первая и вторая “косые” диаграммы Хилла–Седова не симметричны, но сопряжены друг другу.

Замечательным свойством обеих диаграмм (2.16), (2.17) является то, что они связывают в качестве материально и пространственно ориентированных аналогов тензоры деформаций перекрестно из “взаимных” пар тензоров $\mathcal{E}$, E и ${{\mathcal{E}}_{{{\text{II}}}}}$, E_II из (1.5), (1.6) и (1.9). А именно, для каждой из этих диаграмм в орбиту (набор аналогов) правого тензора $\mathcal{E}$ входит в качестве его левого аналога тензор E_II, а в орбиту ${{\mathcal{E}}_{{{\text{II}}}}}$ – тензор E. Это, в свою очередь, эквивалентно тому, что для обеих этих диаграмм правым и левым аналогами являются меры деформации Коши C и Фингера F, а также обратные к ним тензорные меры деформации C^–1 и ${{{\mathbf{F}}}^{{ - 1}}} \equiv {\mathbf{B}}$ – мера Альманзи.

Отметим специально, что для любых коротационных (2.14), включая нейтральную, а также для “косых” (2.16), (2.17) диаграмм объективных тензоров второго ранга их переплетающие операторы, связывающие пространства ${{\mathcal{L}}_{{\left( {00} \right)}}}$ и ${{\mathcal{L}}_{{\left( {11} \right)}}}$ материально и пространственно ориентированных тензоров, являются изоморфизмами ${{\mathcal{L}}_{{\left( {00} \right)}}}$ и ${{\mathcal{L}}_{{\left( {11} \right)}}}$ не только как линейных пространств, но и как линейных (некоммутативных) алгебр с единицей I. Более того, для коротационных диаграмм такие изоморфизмы также сохраняют скалярное произведение, то есть являются изоморфизмами пространств ${{\mathcal{L}}_{{\left( {00} \right)}}}$ и ${{\mathcal{L}}_{{\left( {11} \right)}}}$ как евклидовых (с обычным скалярным умножением тензоров M и L – их двойной сверткой ${\mathbf{M}}:{\mathbf{L}} \equiv {\text{tr}}({\mathbf{M}}{{{\mathbf{L}}}^{{\text{T}}}})$).

2.3. Объективные тензорные процессы. Интроспективы. Для различных тензорных процессов χ(τ) – тензорнозначных функций времени, определенных на множестве моментов времени ${\tau } \in D\left( {\chi } \right) \subseteq \mathcal{T}$, введем по отношению к произвольному фиксированному моменту времени t (моменту наблюдения) следующее

Определение 2.4. Функции

назовем соответственно t-историей и t-предысторией процесса χ(τ), или интроспективами (вторую функцию также ретроспективой) процесса χ(τ).

Очевидно, что задание процесса χ(τ) на всей области определения D(χ) (или до момента t) эквивалентно заданию пары $({\psi }(s),t)$, где ${\psi }(s) = {{{\chi }}^{t}}(s)$ (или пары $({\psi }(s),t)$, где ψ(s) = ${{{\chi }}^{{t - }}}(s)$):

Подчеркнем, что с течением времени t (то есть с изменением момента наблюдения t) t-история и t-предыстория любого заданного процесса (как функции переменного s), вообще говоря, изменяются, иными словами, взгляд на историю и предысторию процесса, вообще говоря, меняется с моментом наблюдения t.

Для объективных механических процессов χ(τ) отметим важное свойство их интроспектив в отношении действия подгруппы G_a временных сдвигов (сдвигов на временной интервал a) группы G замен системы отсчета (2.1), а именно: интроспективы любого объективного процесса χ(τ) инвариантны относительно действия подгруппы G_a, то есть имеют место тождества по s

при любых $a \in R$ (${{t}_{a}} = t + a,\;{{{\chi }}_{a}}\left( {\xi } \right) \equiv {\chi }\left( {{\xi } - a} \right)$).

Теорема 2.1. Действие всей группы G замен системы отсчета на k_m-объективные механические тензорные процессы ${{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$ из (2.5) в терминах парных представлений (2.20), (2.21) через интроспективы (2.18), (2.19) выражается формулой

3. Отображения объективных тензорных процессов. 3.1. Отображения общего вида. 3.1.1. Изотропные отображения. Обобщенная изотропия типа $\left( {{{k}_{m}},{{l}_{{m{\text{'}}}}}} \right)$. Введем некоторые специальные классы отображений тензоров и тензорных процессов. Пусть $\mathcal{F}$ – отображение тензоров ${{{\mathbf{L}}}_{m}} \in {{\mathcal{L}}_{m}}$ ранга m над n-мерным векторным пространством $\mathcal{V}$ в тензоры ${{{\mathbf{L}}}_{{m'}}} \in {{\mathcal{L}}_{{m'}}}$ ранга m' над $\mathcal{V}$, т.е. тензорнозначная функция тензорного аргумента:

Определение 3.1. Назовем функцию $\mathcal{F}$ из (3.1) изотропной типа $\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)$, или (k_m, ${{{\mathbf{l}}}_{{m'}}})$-изотропной, если для произвольных тензоров-аргументов ${{{\mathbf{L}}}_{m}} \in {{\mathcal{L}}_{m}}$ и произвольного ортогонального тензора-константы Q₀ выполнено соотношение

Рассмотрим теперь отображения тензорных процессов в тензоры:

Определение 3.2. Назовем отображение $\mathcal{F}$ из (3.3) t₀-изотропным типа $\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)$, если для произвольного аргумента L_m(t) и произвольного ортогонального тензора-процесса ${\mathbf{Q}}\left( t \right)\,\,~\left( {t \in R} \right)$ выполнено соотношение

Если (3.4) выполнено лишь для произвольного ортогонального тензора-константы ${\mathbf{Q}}\left( t \right) \equiv {{{\mathbf{Q}}}_{0}} \equiv {\text{const}}$, то отображение $\mathcal{F}$ будем подобно (3.2) называть просто изотропным типа $\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)$.

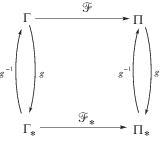
3.1.2. Отображения, связывающие объективные тензорные процессы. Независимость отображений от системы отсчета. Для множества Γ механических тензорных процессов γ рассмотрим отображение $\mathcal{F}$ этого множества в множество Π механических тензорных процессов π (процессы определены на всей временной оси $\mathcal{T} = R$ моментов времени):

Пусть ${{\gamma }_{*}},{{{\mathbf{\pi }}}_{*}},{{{\Gamma }}_{*}},{{{\Pi }}_{*}}$ – образы $\gamma ,{\mathbf{\pi }},{\Gamma },{\Pi }$ при переходе к новой системе отсчета (2.1). Заданное в новой системе отсчета отображение ${{\mathcal{F}}_{*}}$ множества ${{{\Gamma }}_{*}}$ в множество ${{{\Pi }}_{*}}$ будем называть физически тем же, что и отображение $\mathcal{F}$ в старой системе отсчета, если оно связывает физически те же процессы:

(то есть уравнения (3.5) и (3.6) физически эквивалентны), или, иначе, диаграмма коммутативна. Вертикальными стрелками в (3.7) обозначены операторы преобразования процессов $\gamma \in {\Gamma }$ и ${\mathbf{\pi }} \in {\Pi }$ в процессы ${{\gamma }_{*}} \in {{{\Gamma }}_{*}}$ и ${{{\mathbf{\pi }}}_{*}} \in {{{\Pi }}_{*}}$ при переходе к новой системе отсчета (2.1), т.е. операторы действия элементов g (и обратных к ним элементов g^–1) группы G замен системы отсчета на рассматриваемых процессах.

Будем считать аргументы γ и образы π объективными тензорами (2.5) определенных типов k_m и ${{{\mathbf{l}}}_{{m'}}}$ (и рангов m и m') соответственно:

Введем следующее фундаментальное понятие.

Определение 3.3. Отображение $\mathcal{F}$ вида (3.5), (3.6), удовлетворяющее (3.7) с ${{{\Gamma }}_{*}} = {\Gamma }$ и ${{{\Pi }}_{*}} = {\Pi }$, назовем независимым от системы отсчета, если при свободном действии группы G выполнено математическое тождество

Для равенств (3.5), (3.6) тождество (3.9) означает соответственно следующие эквиваленции

Теорема 3.1. Отображение $\mathcal{F}$ вида (3.5) объективных тензоров (3.8) не зависит от системы отсчета тогда и только тогда, когда выполнены одновременно условия:

1. отображение $\mathcal{F}$ инвариантно относительно сдвига временной переменной:

2. отображение $\mathcal{F}$ является t-изотропным типа $\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)$, то есть для любого аргумента ${\mathbf{\gamma }}\left( {\tau } \right) \equiv {{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}\left( {\tau } \right)$ и произвольного ортогонального тензорного процесса Q(τ) выполнено согласно (3.4) тождество

Теорема 3.1. Вообще говоря, накладывает на вид отображения $\mathcal{F}$ специальные ограничения, зависящие от типов объективности тензоров γ и π. Соответствующий общий вид отображения называют его общей приведенной формой.

3.1.3. Примеры независимых от системы отсчета отображений. В качестве примеров рассмотрим независимые от системы отсчета отображения, связывающие (мгновенные) значения объективных тензоров второго ранга ${\mathbf{U}} \in {{\mathcal{L}}_{{{{{\mathbf{k}}}_{2}}}}}$ и ${\mathbf{Z}} \in {{\mathcal{L}}_{{{{{\mathbf{l}}}_{2}}}}}$ как функция (первое условие теоремы выполнено)

Соответственно возможным типам объективности k₂ и l₂ тензоров U и Z (типы (00) или (01), или (10), или (11)) существуют 16 различных типов связей вида (3.14).

Пример 1. Если ${\mathbf{U}},{\mathbf{Z}} \in {{\mathcal{L}}_{{\left( {00} \right)}}}$, т.е. оба тензора U, Z материально ориентированы, то отображение (3.14) согласно Теореме 3.1 является (00;00)-объективным и имеет общий вид (теорема не накладывает ограничений).

Пример 2. Если ${\mathbf{U}} \in {{\mathcal{L}}_{{\left( {10} \right)}}},{\mathbf{Z}} \in {{\mathcal{L}}_{{\left( {00} \right)}}}$, то (3.14) (10;00)-объективно. Его общая приведенная форма имеет вид (с произвольной функцией f)

выражающий связь тензора Z лишь с неотрицательно определенной симметричной тензорной (второго ранга) комбинацией ${{{\mathbf{U}}}^{{\text{T}}}} \cdot {\mathbf{U}}$.

Случай ${\mathbf{U}} \in {{\mathcal{L}}_{{\left( {01} \right)}}},{\mathbf{Z}} \in {{\mathcal{L}}_{{\left( {00} \right)}}}$ аналогичен этому.

Пример 3. Если ${\mathbf{U}} \in {{\mathcal{L}}_{{\left( {10} \right)}}},{\mathbf{Z}} \in {{\mathcal{L}}_{{\left( {11} \right)}}}$, т.е. U – объективный тензор смешанного типа, а ${\mathbf{Z}}$ – пространственного типа, то (3.14) (10;11)-объективно и имеет приведенную форму вида

где Q_U – ортогональная часть полярного разложения тензора U, а f – произвольная тензорнозначная функция симметричного неотрицательно определенного тензорного аргумента со значениями, обеспечивающими инвариантность правой части (3.16) относительно замены Q_U в рамках неоднозначности полярного разложения.

Случай ${\mathbf{U}} \in {{\mathcal{L}}_{{\left( {01} \right)}}},{\mathbf{Z}} \in {{\mathcal{L}}_{{\left( {11} \right)}}}$ аналогичен рассмотренному здесь.

Пример 4. Пусть ${\mathbf{U}},{\mathbf{Z}} \in {{\mathcal{L}}_{{\left( {11} \right)}}}$ (оба тензора U и Z пространственно ориентированы). Тогда для (3.14) выполнено свойство изотропии типа (11; 11), совпадающее с классическим. Его приведенная форма известна для случая, когда $\mathcal{F}$ – аналитическая функция произвольного тензорного аргумента U или когда аргумент U – симметричный тензор [16]. Эта форма имеет вид

где f₀, f₁, f₂ – скалярнозначные функции совокупности ${\text{Inv\;}}({\mathbf{U}})$ собственных скалярных инвариантов тензора-аргумента U.

Применительно к конкретным моделям механики сплошной среды рассмотренные здесь случаи связей тензоров второго ранга различных типов объективности могут рассматриваться как формы определяющих соотношений сред. Так, в Примере 1, рассматривая U как тензор деформаций Грина $\mathcal{E}$, а Z как тензор напряжений Пиолы–Кирхгофа второго рода P или как тензор напряжений Ильюшина Σ, получаем, что (3.14) определяет по Ильюшину [2, 20] класс произвольных упругих материалов (вообще говоря, не линейных и не изотропных). К этому же результату приводит Пример 2, если положить в качестве U аффинор (градиент) деформации A, а в качестве Z – тензор P или Σ. Полагая в Примере 3 ${\mathbf{U}} \equiv {\mathbf{A}}$ – аффинор деформации и ${\mathbf{Z}} \equiv {\mathbf{S}}$ – тензор напряжений Коши S, получаем, что (3.14) определяет по Ноллу–Трусделлу [3, 13] тот же класс произвольных упругих материалов и имеет приведенную форму (3.16). В Примере 4, полагая ${\mathbf{U}} \equiv {\mathbf{E}}$ – тензор деформаций Альманзи и ${\mathbf{Z}} \equiv {\mathbf{S}}$, получаем, что соотношение (3.14) определяет класс изотропных упругих материалов [3, 16] и имеет приведенную форму (3.17); в этом же случае, полагая ${\mathbf{U}} \equiv {\mathbf{V}}$ – тензор скоростей деформаций и ${\mathbf{Z}} \equiv {\mathbf{S}}$, получаем, что связь (3.14) с приведенной формой (3.17) задает тензор вязких напряжений класса нелинейно вязких жидкостей с инфинитезимальной памятью первого порядка [3, 18].

Подобные примеры [40, 41, 43, 45] иллюстрируют существенное значение учета типов объективности тензоров в определяющих соотношениях сопротивления материалов деформированию.

3.2. Переплетения отображений. Отображения диаграмм. Коммутативность простых диаграмм, обеспечивающая для каждого объективного тензорного процесса типа k_m и типа ${{{\mathbf{l}}}_{{m'}}}$ единственность его аналога любого другого типа (и того же ранга), естественным образом индуцирует (порождает) для каждого конкретного отображения $\mathcal{F}:{{\mathcal{L}}_{{{{{\mathbf{k}}}_{m}}}}} \to {{\mathcal{L}}_{{{{{\mathbf{l}}}_{{m'}}}}}}$ единственную совокупность ${{2}^{{m + m'}}}$ отображений $\mathcal{F}_{{({\mathbf{k}}_{m}^{'},{\mathbf{l}}_{{m'}}^{'})}}^{{\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)}}:{{\mathcal{L}}_{{{\mathbf{k}}_{m}^{'}}}} \to {{\mathcal{L}}_{{{\mathbf{l}}_{{m'}}^{'}}}}$, связывающих всевозможные аналоги аргумента (ранга m) и образа (ранга m') исходного отображения $\mathcal{F}$, и задаваемых формулой

где использованы обозначения из (2.3), (2.4) и (2.9), причем набор $\mathfrak{A}_{{{{{\mathbf{k}}}_{m}} \otimes {\mathbf{k}}_{m}^{'}}}^{{\left( 1 \right)}}$, содержащий m тензоров, составлен из числа 4m невырожденных тензоров второго ранга $\mathcal{A}_{{i({{{\text{k}}}_{i}},{\text{k}}_{i}^{'})}}^{{(1)}}$ вида (2.8) ($i = 1,2, \ldots ,m$; ${{{\text{k}}}_{i}},{\text{k}}_{i}^{'} = 0,1$) – переходных тензоров диаграммы переплетений для объективных тензоров ранга m (тензоров-аргументов), набор $\mathfrak{A}_{{{\mathbf{l}}_{{m'}}^{'} \otimes {{{\mathbf{l}}}_{{m'}}}}}^{{\left( 2 \right)}}$, включающий m' тензоров, составлен из числа 4m' тензоров второго ранга $\mathcal{A}_{{j({{{\text{l}}}_{j}},{\text{l}}_{j}^{'})}}^{{\left( 2 \right)}}$ (j = 1, 2, ..., m'; ${{{\text{l}}}_{j}},{\text{l}}_{j}^{'} = 0,1$) – переходных тензоров диаграммы переплетений для объективных тензоров ранга m' (тензоров-образов); тензор ${{{\mathbf{L}}}_{{{{{{\mathbf{k'}}}}_{m}}}}} \equiv \mathfrak{A}_{{{{{{\mathbf{k'}}}}_{m}} \otimes {{{\mathbf{k}}}_{m}}}}^{{\left( 1 \right)}}\mathop \cdot \limits^m {{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$ – аналог типа ${\mathbf{k}}_{m}^{'}$ исходного тензора-аргумента ${{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$.

На основании (3.18) имеем также формулы

включающие (3.18) как частный случай при ${\mathbf{k}}_{m}^{{''}} = {{{\mathbf{k}}}_{{\text{m}}}},{\mathbf{l}}_{{m'}}^{{''}} = {{{\mathbf{l}}}_{{m'}}}$.

Для удобства обращения к рассматриваемым здесь отображениям введем следующие краткие названия.

Определение 3.4. Для фиксированных простых диаграмм объективных тензорных процессов ранга m и ранга m' назовем фигурирующее в (3.18) порождающее отображение $\mathcal{F} \equiv \mathcal{F}_{{\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)}}^{{\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)}}$ индуктором, каждое из отображений $\mathcal{F}_{{({\mathbf{k}}_{m}^{'},{\mathbf{l}}_{{m'}}^{'})}}^{{\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)}}$ в (3.18), (3.19) (включая индуктор) – кондуктором, а совокупность ${{\mathcal{F}}^{{\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)}}}$ всех кондукторов – пакетом (или отображением диаграмм). Верхний спаренный мультииндекс $\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{l}}}_{{m'}}}} \right)$ кондуктора (пакета) назовем порождающим типом этого кондуктора (пакета), а нижний спаренный мультииндекс кондуктора $({\mathbf{k}}_{m}^{{\text{'}}},{\mathbf{l}}_{{m'}}^{{\text{'}}})$ – его собственным типом. Равенства (3.18), (3.19) будем называть переплетениями кондукторов.

Коммутативность диаграмм и формулы переплетений показывают, что пакет в целом является однозначным отображением множества наборов из 2^m аналогов объективных тензорных процессов ранга m в множество наборов из 2^m' аналогов объективных тензоров ранга m', а детально при этом каждый элемент первого набора отображается в каждый элемент второго набора тензоров некоторым (единственным) кондуктором этого пакета. Весь пакет и его кондукторы однозначно порождаются заданием диаграмм и индуктора (заметим, что порождающий и собственный типы индуктора, конечно, совпадают). Индуктор определяет свойства всех кондукторов и пакета в целом. В частности, благодаря коммутативности диаграмм, свойство взаимной однозначности индуктора (если он им обладает) переносится на каждый из кондукторов и пакет в целом. Влияние диаграмм аргументов и образов выражается зависимостью кондукторов от переходных тензоров этих диаграмм, т.е. параметризацией кондукторов этими тензорами. Во всяком пакете параметризованные кондукторы являются независимыми от системы отсчета отображениями лишь все одновременно.

3.3. Объективные производные и интегралы. 3.3.1. Объективные производные. Для отображений диаграмм объективных тензоров из соображений наибольшей широты (нестесненности) представления в общих приведенных формах независимых от системы отсчета отображений (кондукторов) в качестве порождающего отображения (индуктора) следует выбирать (00…0; 00…0)-индуктор – отображение материально ориентированных тензоров в материально ориентированные, т.е. отображение типа Ильюшина.

Это, в частности, относится и к дифференциальным операторам по времени, среди которых первостепенную важность имеют так называемые объективные производные по времени, отображающие объективные тензорные процессы в тензоры того же типа объективности (и, конечно, того же ранга), называемые также скоростями (протекания) исходного процесса. Здесь предполагается дифференцируемость по времени самих объективных тензоров – аргументов объективных производных – и переходных тензоров диаграммы (общей для аргументов и образов).

Определение 3.5. Объективной производной по времени типа k_m назовем отображение-кондуктор ${{D}_{{{{{\mathbf{k}}}_{m}}}}}$ вида $\mathcal{F}_{{\left( {{{{\mathbf{k}}}_{m}},{{{\mathbf{k}}}_{m}}} \right)}}^{{\left( {00...0;00...0} \right)}}$ из (3.18) объективных тензорных процессов ${{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$ типа k_m в объективные тензоры типа k_m, порожденное для совпадающих диаграмм аргументов и образов ($\mathcal{A}_{{i\left( {10} \right)}}^{{\left( 1 \right)}} \equiv \mathcal{A}_{{i\left( {10} \right)}}^{{\left( 2 \right)}} = :{{\mathcal{A}}_{{\left( {10} \right)}}}$, i = 1, 2, …, m) (00…0; 00…0)-индуктором $\mathcal{F} \equiv {{D}_{{\left( {00...0} \right)}}}$ вида полной (“материальной”) производной по времени от материально ориентированного тензора ${{{\mathbf{L}}}_{{\left( {00...0} \right)}}}$ – материального аналога тензора ${{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$ – в текущий момент t:

Заметим, что материальная производная по времени материальных тензоров не зависит от системы отсчета, так как инвариантна относительно сдвигов временной переменной. Поэтому и все объективные производные (рассматриваемые как параметризованные кондукторы) являются независимыми от системы отсчета отображениями объективных тензоров.

Для объективных скалярных, векторных и тензорных второго ранга процессов (2.2) в соответствии с Определением 9 имеем:

Для $\left| {{{{\mathbf{k}}}_{m}}} \right| = 0$ объективные производные совпадают с обычными материальными производными, а для $\left| {{{{\mathbf{k}}}_{m}}} \right| > 0$ они суть дифференциальные операторы первого порядка по времени, параметризованные переходными тензорами диаграммы, и вид их целиком определяется значениями в момент t самих переходных тензоров ${{\mathcal{A}}_{{i(10)}}}$ (i = 1, 2, ..., m) и их первых полных производных по времени ${{\dot {\mathcal{A}}}_{{i\left( {10} \right)}}}$.

Другие (тождественные) представления ${{D}_{{{{{\mathbf{k}}}_{m}}}}}$ с $\left| {{{{\mathbf{k}}}_{m}}} \right| > 0$ могут оказаться удобными при эйлеровом способе описания. Для (3.21) они имеют вид:

где использованы обозначения

Введенное здесь понятие объективной производной существенно обобщает известные понятия объективных производных, относящиеся в большинстве своем к пространственно ориентированным тензорам второго ранга (см., например, [2, 16–55 ]). Так, известные объективные производные пространственно ориентированных тензоров Коттер–Ривлина [51], Олдройда [50] и Трусделла [52] суть не что иное как производная ${{D}_{{(11)}}}{{[\; \cdot \;]}^{t}}$ соответственно в диаграммах Грина–Альманзи (2.10), Коши–Ильюшина (2.11) и Коши–Пиолы (2.12) (либо в последнем случае также в диаграмме Коши–Хилла (2.13)). Производная Хилла [55] – не что иное как производная ${{D}_{{(10)}}}{{[\; \cdot \;]}^{t}}$ тензоров смешанного вида объективности (10) в диаграмме Коши–Хилла. Нейтральная производная [35, 56, 62, 63] – это производная ${{D}_{{(11)}}}{{[\; \cdot \;]}^{t}}$ в нейтральной диаграмме (2.15).

Любая объективная коротационная производная пространственно ориентированных тензоров [36, 37], включая производную Яуманна [48, 49], – производная ${{D}_{{(11)}}}{{[\; \cdot \;]}^{t}}$ в соответствующей коротационной диаграмме (2.14).

“Косые” производные Седова [53, 54] – это производная ${{D}_{{(11)}}}{{[\; \cdot \;]}^{t}}$ в “косых” диаграммах (2.16), (2.17).

Все объективные производные ${{D}_{{{{{\mathbf{k}}}_{m}}}}}$ являются линейными в отношении основного аргумента ${{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$ дифференциальными операторами. Заметим, однако, что такие привычные для обычных производных (и сохраняющиеся, конечно, для случая $\left| {{{{\mathbf{k}}}_{m}}} \right| = 0$) правила, как формула Ньютона–Лейбница и формула дифференцирования обратного тензора (для алгебры тензоров второго ранга), коммутативность с операцией транспонирования, вообще говоря, не имеют места для ${{D}_{{{{{\mathbf{k}}}_{m}}}}}$ в случаях $\left| {{{{\mathbf{k}}}_{m}}} \right| > 0$, в том числе даже для D₍₁₁₎. Широкий класс объективных производных D₍₁₁₎ (производные конвективно-коротационного типа) изучен в отношении указанных правил и способов интегрирования этих производных по времени [37]. Здесь отметим лишь, что для D₍₁₁₎ все указанные правила в их обычной формулировке имеют место в точности в случае коротационных диаграмм (2.14), т.е. в точности для производных D₍₁₁₎ коротационного типа.

3.3.2. Объективное интегрирование. В [37] для пространственно ориентированных тензоров второго ранга выведена формула интегрирования объективных производных D₍₁₁₎. Обобщением ее является формула интегрирования по времени объективной производной ${{D}_{{{{{\mathbf{k}}}_{m}}}}}$:

При этом, если производная ${{D}_{{{{{\mathbf{k}}}_{m}}}}}$ задана в виде (3.22) или подобном, то для реализации формулы (3.24) требуется предварительное интегрирование (решение относительно ${{\mathcal{A}}_{{i\left( {10} \right)}}}$) формул (3.23) с известными ${{\mathcal{D}}_{i}}$. Формула этого последнего интегрирования имеет вид

где использовано понятие хронологической экспоненты [22]. Полезные тождества для хронологических экспонент выведены в [37].

Выполнение формул (3.24) для объективных производных позволяет ввести

Определение 3.6. Объективным интегралом по времени типа k_m (или k_m-интегралом) на физическом промежутке времени ${\tau } \in \left[ {{{t}_{0}},t} \right]$ от объективного тензорного процесса ${{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$ типа k_m назовем отображение этого процесса в объективный тензор того же типа k_m, задаваемое формулой

Подобно объективным производным k_m-интегралы являются простейшими интегральными операторами в множестве процессов в ${{\mathcal{L}}_{{{{{\mathbf{k}}}_{m}}}}}$, материально порожденными (как кондукторы в данной диаграмме переплетений) обычным оператором интегрирования (как индуктором) материально ориентированного аналога ${{{\mathbf{L}}}_{{(\underbrace {0\,0\,...\,0}_m)}}}$ объективного тензора ${{{\mathbf{L}}}_{{{{{\mathbf{k}}}_{m}}}}}$.

Связь k_m-интеграла (3.26) с объективной производной ${{D}_{{{{{\mathbf{k}}}_{m}}}}}$ выражается тождествами

второе из которых совпадает с (3.24). При необходимости для реализации (3.26), (3.27) могут быть применены формулы (3.25).

Аналогично введенным k_m-интегралам могут быть построены более сложного вида объективные интегральные операторы по времени от объективных тензоров и рассмотрены соответствующие интегральные уравнения.

Подчеркнем, что понятия объективных производных и объективных интегралов (и обобщающих их операторов) позволяют исследование сложных интегро-дифференциальных связей между объективными тензорами различных типов (например, пространственных типов) свести с помощью алгебраических операций к исследованию обычных интегро-дифференциальных связей между материально ориентированными тензорами. Это касается и вопросов существования интегралов и производных, интегрируемости дифференциальных уравнений, разрешимости уравнений относительно каких-либо величин и т.п.

3.4. Приложения новых объективных производных. Распространенным способом построения определяющих соотношений сред при конечных деформациях является обобщение соотношений, известных при малых деформациях, путем замены в этих соотношениях тензоров напряжений и (малых) деформаций, и их (материальных) производных по времени новыми тензорными мерами напряжений и конечных деформаций, и их объективными производными. В 1960-м году в Москве на первом Всесоюзном съезде по теоретической и прикладной механике В. Прагер в своем докладе предупреждал исследователей от нерасчетливого использования в таких обобщениях известных к тому времени объективных производных, в первую очередь производной Яуманна. Немедленной реакцией Л.И. Седова на том же конгрессе стал его доклад, опубликованный в [53], в котором он предложил две новые объективные производные (названные здесь “косыми” производными Седова), вошедшие в его книгу [54].

Позднее подобные критические замечания об использовании производной Яуманна отмечались в работах [57, 58], причем в последней было явно отмечено нефизичное поведение моделей пластичности при конечных деформациях с производной Яуманна, получившее название “аномалии” колебаний напряжений при простом сдвиге. Реакцией на работу [58] стал ряд статей (см., например, [59, 60]), авторы которых предлагали во избежание указанной “аномалии” использовать другие объективные производные, в частности, коротационную производную, предложенную в [56] (названную здесь нейтральной). Дальнейшее развитие этой позиции нашло отражение в работах по пластичности при больших деформациях [61–64].

В последние годы в рамках представленного в настоящей работе обобщенного понятия объективных производных построены новые производные и целые их семейства (и порожденные объективным интегрированием соответствующие тензорные меры напряжений и конечных деформаций, и семейства этих мер), которые использованы в определяющих соотношениях моделей пластичности, гипоупругости, вязкоупругости, тел с памятью формы.

Так, в работах [66, 67] предложено новое подсемейство коротационных объективных производных (типа Яуманна–Динса), использованное в построении моделей гипоупругости и различных моделей пластичности при конечных деформациях. Численные эксперименты по этим моделям демонстрируют существенное влияние выбора производной из этого подсемейства на поведение тел при простом сдвиге, при кручении с растяжением цилиндра в процессах конечной деформации (до степеней деформации 600%).

В работах [68, 69] на базе семейства голономных тензорных мер напряжений и конечных деформаций [39], отвечающих производным определенного вида, построены модели тел с памятью формы (обобщением модели А.А. Мовчана [70]) при конечных деформациях, и проведена идентификация этих моделей.

В работе [71] предложена модель пластичности при конечных деформациях, основанная на использовании двух различных тензорных мер деформаций: голономной логарифмической и неголономной меры, построенной на базе нейтральной объективной производной. В работе [72] дано принципиальное уточнение основных тензорных мер конечных деформаций и напряжений, используемых в известном пакете ANSYS. Работы [73, 74] продолжают цикл исследований моделей гипоупругости, построенных на базе коротационных объективных производных и соответствующих мер.

Работы [75, 76] посвящены описанию конечных деформаций вязкоупругих тел с использованием объективных производных семейства Гордона–Шоуолтера.

В работах [77–82] изучены подходы к построению и механические свойства моделей классического и неклассического типов, включая модели Коссера. Работы [83, 84] посвящены построению и описанию моделей наполненных пористых сред при произвольных скоростях течения жидкой фазы и произвольных конечных деформациях каркаса.

Представленное в настоящей работе обобщенное понятие объективных производных включает широкий класс производных конвективно-коротационного типа [37, 38], в рамках которого в настоящее время ведутся исследования форм определяющих соотношений различных сред при конечных деформациях.

4. Заключение. Представленные в настоящей работе основы теории объективных тензоров, их диаграмм, связывающих их независимых от системы отсчета отображений, пакетов этих отображений (кондукторов) и соответствующих объективных производных и интегралов демонстрируют эффективность использования свойств инвариантности процессов и соотношений в механике сплошной среды: теория обобщает и упорядочивает известные представления и подходы, разработанные в механике сплошной среды, и составляет универсальный математический аппарат для развития современной теории определяющих соотношений.

Приведенные построения послужили основой для создания более широкой аксиоматики [9, 42, 43, 82] и построения новой теории определяющих соотношений [38, 45, 46], обобщающей подходы Ильюшина и Нолла, для построения новой обобщенной теории тензорных мер деформаций и напряжений [36, 47], существенно расширяющей возможности эффективной аппроксимации данных определяющих экспериментов и классификации свойств сред.

Работа подготовлена при финансовой поддержке Российского фонда фундаментальных исследований (грант РФФИ № 16-01-00669).