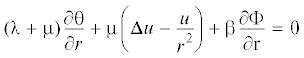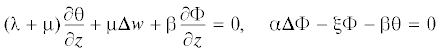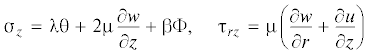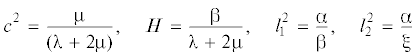Известия РАН. Механика твердого тела, 2020, № 6, стр. 116-124

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ОСЕСИММЕТРИЧНОЙ КОНТАКТНОЙ ЗАДАЧИ ДЛЯ ПОРОУПРУГОГО СЛОЯ

Е. М. Колосова^a, **, М. И. Чебаков^a, *

^a Институт математики, механики и компьютерных наук им. И.И. Воровича Южного федерального университета
Ростов-на-Дону, Россия

^** E-mail: a_lena_ch@mail.ru
^* E-mail: michebakov@yandex.ru

Поступила в редакцию 30.03.2020
После доработки 13.04.2020
Принята к публикации 23.05.2020

DOI: 10.31857/S0572329920050116

Полный текст (PDF)

Аннотация

В работе на основе уравнений теории пороупругих тел Ковина-Нунзиато рассматриваются осесимметричные контактные задачи о взаимодействии жесткого штампа с пороупругим слоем. Предполагается, что основание штампа имеет плоскую или параболическую форму, в зоне контакта отсутствует трение. Поставленные задачи сводятся относительно специальной функции, через которую выражаются контактные напряжения, к интегральным уравнениям, главной часть ядра которых является дельта-функция. Используя специальную аппроксимацию трансформанты ядра интегрального уравнения построено его асимптотическое решение для случая относительно больших толщин слоя. Такой подход к решению интегральных уравнений контактных задач был предложен И.И. Воровичем и получил дальнейшее развитие в работах его учеников. В простой аналитической форме получены выражения для контактных напряжений и области контакта в случае параболического штампа. Также в элементарных выражениях найдена связь между силой, действующей на штамп, и его перемещением, которая является одной из основных характеристик при определении механических параметров материала методом индентирования. Проведен сравнительный анализ исследуемых величин для различных значений параметров пористости и толщины слоя.

Ключевые слова: контактная задача, пористые материалы, пороупругость, модель Ковина‒Нунзиато, осесимметричная задача, слой, ассимтотический метод, индентирование

Введение. Теория Ковина-Нунзиато упругих материалов с пустотами является одним из распространенных обобщений классической теории упругости. Эта теория рассматривает упругие материалы с распределенными по объему небольшими незаполненными порами (пустотами). Практическое значение данный подход имеет при исследовании различных типов геологических, биологических и синтетических пористых материалов, для которых классическая теория не подходит. Теория упругости пористых материалов с пустыми порами была представлена Ковиным и Нунзиато в [1]. В отсутствие поля объемной доли пор данная теория сводится к классической теории упругости. Линейная теория была описана в [2]. В работе [3] приведено математическое описание линейной теории термоупругости тел с пустотами. Общая теория была довольно хорошо изучена в последние годы [4–11]. В работах [5, 6] решены контактные задачи в рамках плоской постановки для полупространства и полосы, соответственно.

Точность предложенной схемы решения задач была протестирована на аналогичных задачах для упругого слоя, решения которых для некоторых значений параметров приведены в [12].

1. Постановка задачи. В цилиндрической системе координат ($r,\phi ,z$) рассмотрим осесимметричную контактную задачу о взаимодействии жесткого штампа с пороупругим слоем $0 \leqslant z \leqslant h$, деформация которого описывается соотношениями Ковина и Нунзиато [2]. Предполагается, что основание цилиндрического штампа может быть плоским (задача 1) или иметь форму параболоида вращения (задача 2).

Теория однородного изотропного материала с пустотами, согласно теории Ковина–Нунзиато, описывается следующей системой дифференциальных уравнений в частных производных [2]

(1.1)

${\Delta } = \frac{1}{r}\frac{\partial }{{\partial r}}\left( {r\frac{\partial }{{\partial r}}} \right) + \frac{{{{\partial }^{2}}}}{{\partial {{z}^{2}}}},\quad {\theta } = \frac{u}{r} + \frac{{\partial u}}{{\partial r}} + \frac{{\partial w}}{{\partial z}}$

Здесь ${\mu }$ и λ – коэффициенты Ламэ, а α – коэффициент пустотной диффузии, ${\beta }$ – параметр связи микродилатационных и макродилатационных свойств и ${\xi }$ – пустотная жесткость, функция $\Phi (r,z)$ описывает изменение объемной части пор, u и w перемещения соответственно вдоль осей r и z. В случае ${\beta } = 0$ мы имеем упругую деформацию слоя.

Компоненты тензора напряжений определяются из следующих соотношений [2]

(1.2)

Граничные условия поставленных задач при z = h и z = 0 запишутся в следующем виде

(1.3)

$\begin{gathered} {{{\tau }}_{{rz}}}(r,z) = 0,\quad \frac{{\partial \Phi }}{{\partial z}} = 0,\quad w(r,z) = {\delta (}r{\text{)}}\,\,(z = h,r \leqslant a), \\ {{{\sigma }}_{z}}(r,z) = 0,\quad \frac{{\partial \Phi }}{{\partial z}} = 0\,\,\,(z = h,r > a) \\ \end{gathered} $

${{{\tau }}_{{rz}}}(r,z) = 0,\quad \frac{{\partial \Phi }}{{\partial z}} = 0,\quad w(r,z) = 0\quad (z = 0)$

В случае штампа с плоским основанием ${\delta }(r) = {\delta } = {\text{const}}$ (задача 1), в случае штампа с основанием в форме параболоида вращения ${\delta }(r) = {\delta } - {{r}^{2}}{\text{/}}(2R)$ (задача 2). Здесь R – радиус кривизны в вершине параболы.

2. Построение интегрального уравнения. Предварительно будем считать, что нормальные напряжения в зоне контакта известны: ${{\sigma }_{z}}(r,h) = q(r)$. В дальнейшем для их определения будет построено интегральное уравнение (2.20). Для этого найдем решение системы (1.1) с граничными условиями

(2.1)

${{{\tau }}_{{rz}}}(r,z) = 0,\quad \frac{{\partial \Phi }}{{\partial z}} = 0,\quad {{\sigma }_{z}}(r,z) = q(r)\quad (z = h,\;r \leqslant a)$

$\frac{{\partial \Phi }}{{\partial z}} = 0,\quad {{\sigma }_{z}}(r,z) = 0\quad (z = h,r > a),\quad {{{\tau }}_{{rz}}}(r,z) = 0,\quad w(r,z) = 0,\quad \frac{{\partial \Phi }}{{\partial z}} = 0\quad (z = 0)$

Представим неизвестные функции в системе (1.1) в виде преобразования Ханкеля

(2.2)

$u(r,z) = \int\limits_0^\infty {A(u,z){{J}_{1}}} (ur)udu,\quad w(r,z) = \int\limits_0^\infty {B(u,z){{J}_{0}}} (ur)udu$

$\Phi (r,z) = \int\limits_0^\infty {F(u,z){{J}_{0}}} (ur)udu$

где ${{J}_{i}}(u)$ ($i = 0,\;1$) – функции Бесселя. Тогда для отыскания неизвестных функций $A(u,z)$, $B(u,z)$, $F(u,z)$ получим систему обыкновенных дифференциальных уравнений второго порядка ($D = d{\text{/}}dz$)

(2.3)

${{c}^{2}}{{D}^{2}}A - {{u}^{2}}A - (1 - {{c}^{2}})uDB - uHF = 0,\quad (1 - {{c}^{2}})uDA + {{D}^{2}}B - {{c}^{2}}{{u}^{2}}B + HDF = 0$

$l_{1}^{2}({{D}^{2}}F - {{u}^{2}}F) - \frac{{l_{1}^{2}}}{{l_{2}^{2}}}F - uA - DB = 0$

На основе граничных условий (2.1) получим соответственно при z = h и z = 0:

(2.4)

$DA - uB = 0,\quad (1 - 2{{c}^{2}})uA + DB + HF = Q(u){{c}^{2}}{{\mu }^{{ - 1}}},\quad DF = 0\quad (z = h)$

$B(u,0) = 0,\quad DA - uB = 0,\quad DF = 0\quad (z = 0)$

(2.5)

$Q(u) = \int\limits_0^a {q(r){{J}_{0}}(ur)rdr} ,\quad q(r) = \int\limits_0^\infty {Q(u)} {{J}_{0}}(ur)udu$

Здесь использованы следующие обозначения [5]

(2.6)

Согласно теории систем обыкновенных дифференциальных уравнений второго порядка решение системы (2.3) может быть получено в виде

$A(u,z) = ({{a}_{1}} + {{a}_{2}}z){{e}^{{uz}}} + ({{a}_{3}} + {{a}_{4}}z){{e}^{{ - uz}}} + {{a}_{5}}{{e}^{{{{m}_{5}}z}}} + {{a}_{6}}{{e}^{{{{m}_{6}}z}}}$

(2.7)

$B(u,z) = ({{b}_{1}} + {{b}_{2}}z){{e}^{{uz}}} + ({{b}_{3}} + {{b}_{4}}z){{e}^{{ - uz}}} + {{b}_{5}}{{e}^{{{{m}_{5}}z}}} + {{b}_{6}}{{e}^{{{{m}_{6}}z}}}$

$F(u,z) = ({{c}_{1}} + {{c}_{2}}z){{e}^{{uz}}} + ({{c}_{3}} + {{c}_{4}}z){{e}^{{ - uz}}} + {{c}_{5}}{{e}^{{{{m}_{5}}z}}} + {{c}_{6}}{{e}^{{{{m}_{6}}z}}}$

где ${{m}_{5}} = {{\sqrt {1 - N + {{u}^{2}}l_{2}^{2}} } \mathord{\left/ {\vphantom {{\sqrt {1 - N + {{u}^{2}}l_{2}^{2}} } {{{l}_{2}}}}} \right. \kern-0em} {{{l}_{2}}}}$, ${{m}_{6}} = {{ - \sqrt {1 - N + {{u}^{2}}l_{2}^{2}} } \mathord{\left/ {\vphantom {{ - \sqrt {1 - N + {{u}^{2}}l_{2}^{2}} } {{{l}_{2}}}}} \right. \kern-0em} {{{l}_{2}}}}$, $N = {{H \cdot l_{2}^{2}} \mathord{\left/ {\vphantom {{H \cdot l_{2}^{2}} {l_{1}^{2}}}} \right. \kern-0em} {l_{1}^{2}}}$. Коэффициенты b_i, c_i ($1 \leqslant i \leqslant 6$) выражаются через a_i ($1 \leqslant i \leqslant 6$) согласно соотношениям

${{b}_{5}} = - {{a}_{5}}\frac{{\sqrt {{{u}^{2}}l_{2}^{2} - N + 1} }}{{u{{l}^{2}}}},\quad {{c}_{5}} = {{a}_{5}}\frac{{1 - N}}{{uNl_{1}^{2}}},\quad {{b}_{6}} = {{a}_{6}}\frac{{\sqrt {{{u}^{2}}l_{2}^{2} - N + 1} }}{{ul_{1}^{2}}},\quad {{c}_{6}} = {{a}_{6}}\frac{{1 - N}}{{uNl_{1}^{2}}}$

(2.8)

${{b}_{1}} = - {{a}_{1}} - {{a}_{2}}\frac{{{{c}^{2}} + 1 - N}}{{u({{c}^{2}} - 1 + N)}},\quad {{b}_{2}} = - {{a}_{2}},\quad {{c}_{1}} = {{a}_{2}}\frac{{2{{c}^{2}}l_{2}^{2}}}{{l_{1}^{2}({{c}^{2}} - 1 + N)}},\quad {{c}_{2}} = 0$

${{b}_{3}} = {{a}_{3}} - {{a}_{4}}\frac{{{{c}^{2}} + 1 - N}}{{u({{c}^{2}} - 1 + N)}},\quad {{b}_{4}} = {{a}_{4}},\quad {{c}_{3}} = - {{a}_{4}}\frac{{2{{c}^{2}}l_{2}^{2}}}{{l_{1}^{2}({{c}^{2}} - 1 + N)}},\quad {{c}_{4}} = 0$

Удовлетворяя граничным условиям (2.4), получаем уравнения для определения неизвестных коэффициентов a_i ($1 \leqslant i \leqslant 6$). Не выписывая их здесь ввиду громоздкости, приведем выражение для $B(u,0)$, которое нам понадобится для построения интегрального уравнения относительно контактных напряжений q(r)

(2.9)

$B(u,0) = \frac{{Q(u)}}{{2{\mu }(1 - {{c}^{2}})}}L(u),\quad L(u) = \frac{{{{L}_{1}}(u)}}{{{{L}_{2}}(u)}},\quad {{L}_{i}}(u) = {{\tilde {L}}_{i}}(s)\quad (i = 1,2),\quad s = u{{l}_{2}}$

$\begin{gathered} {{{\tilde {L}}}_{1}}(s) = 8\mu l_{2}^{2}(1 - {{с}^{2}})shX(ch2Y - 1){{(N - 1)}^{2}} \times \\ \times \;[2N({{s}^{4}} + T{{s}^{3}}) - (2N - 1)(N - 1){{s}^{2}} - {{(N - 1)}^{2}}] \\ \end{gathered} $

${{\tilde {L}}_{2}}(s) = 2{\text{ch}}X(2{{Z}_{1}}{\text{sh}}2Y + Z) + 4{{Z}_{2}}{\text{ch}}X({\text{ch}}2Y - 1)$

$Z = 8h(N + {{c}^{2}} - 1)(N - 1)[2N({{s}^{5}}T + {{s}^{6}}) - (2N - 1)(N - 1){{s}^{4}} - {{(N - 1)}^{2}}{{s}^{2}}]$

${{Z}_{2}} = - 4N{{c}^{2}}{{s}^{4}}{{l}_{2}}[2{{s}^{3}}N + T(2{{s}^{2}}N + N - 1)]$

${{Z}_{1}} = 2{{l}_{2}}[4{{c}^{2}}{{N}^{2}}{{s}^{7}} + 4{{c}^{2}}T{{N}^{2}}{{s}^{6}} - 2N{{(N - 1)}^{2}}(2{{c}^{2}} - 1){{s}^{5}} + $

$\begin{gathered} 2TN(N - 1)(N + {{c}^{2}} - 1){{s}^{4}} - {{(N - 1)}^{2}}(2{{N}^{2}} - 3N + 4N{{c}^{2}} + \\ + \;1 - {{c}^{2}}){{s}^{3}} - {{(N - 1)}^{3}}(N + {{c}^{2}} - 1)s] \\ \end{gathered} $

Здесь введены обозначения

$T = \sqrt {1 - N + {{s}^{2}}} ,\quad Y = hs{\text{/}}{{l}_{2}},\quad X = Th{\text{/}}{{l}_{2}}$

Из условия удовлетворения граничному условию $w(r,0) = {\delta }(r)$ при $r \leqslant a$ и z = h из (1.3) найдем

(2.10)

$w(r,h) = \frac{1}{{2{\mu }(1 - {{c}^{2}})}}\int\limits_0^\infty {Q(u)L(u)u{{J}_{0}}(ur)du = {\delta }(r)\quad (r \leqslant a)} $

Подставляя в (2.10) выражение (2.5) для Q(u) получим после несложных преобразований интегральное уравнение

(2.11)

$\int\limits_0^a {q({\rho }){\rho }k({\rho },r)d{\rho }} = \frac{{\mu }}{{{\text{1}} - {\nu }}}{\delta }(r)\quad (r \leqslant a)$

(2.12)

$k(\rho ,r) = \int\limits_0^\infty {L(u)u{{J}_{0}}(ur){{J}_{0}}(u{\rho })du} $

Здесь использовано соотношение $2(1 - {{c}^{2}}) = {{(1 - {\nu })}^{{ - 1}}}$, ν – коэффициент Пуассона.

Если N = 0, то интегральное уравнение будет соответствовать контактной задаче для упругого слоя [12].

3. Решение интегрального уравнения. Можно показать, что

(3.1)

$\lim L(u) = Ah\quad \left( {u \to 0} \right),\quad A = \frac{{(N - 1)(1 - {{c}^{2}})}}{{2(N - 1 + {{c}^{2}})}},\quad \lim L(u) = 1\quad (u \to \infty )$

В соответствии с (3.1) для получения замкнутого решения интегрального уравнения (2.17) для относительно больших толщин слоя аппроксимируем L(u) выражением [13]

(3.2)

$L{\text{*}}(hu) = th(Ahu)$

Относительная максимальная погрешность такой аппроксимации не превышает 14.5%, при некоторых значениях параметров она может быть значительно меньше.

Такая аппроксимация позволяет для решения интегрального уравнения (2.11), (2.12) с символом ядра $L(u) = L{\text{*}}(hu)$ из (3.2) использовать метод больших λ [12, 14–16], где ${\lambda } = h{\text{/}}a$, который позволяет получить окончательные выражения для контактных напряжений и других величин в компактной аналитической форме, удобной для инженерных расчетов. Для этого уравнение (2.11), (2.12) в соответствии со схемой, изложенной в [15–17], преобразуем к интегральному уравнению

(3.3)

$\varphi (t) = \frac{1}{{{\pi \lambda }}}\int\limits_{ - 1}^1 {\varphi ({\tau })k\left( {\frac{{t - {\tau }}}{{\lambda }}} \right)d{\tau } + d(t)} \quad (\left| t \right| \leqslant 1)$

(3.4)

$k(y) = \int\limits_0^\infty {[1 - L{\text{*}}(u)]\cos (uy)dy} ,\quad d(t) = \frac{d}{{dt}}\int\limits_0^t {\frac{{r{\delta }(ra)dr}}{{\sqrt {{{t}^{2}} - {{r}^{2}}} }}} = {\delta } - \frac{{{{a}^{2}}{{t}^{2}}}}{{2R}}$

Тогда контактные напряжения через $\varphi (t)$ будут выражаться соотношениями [15]

(3.5)

$q(r) = \frac{{\mu }}{{{\text{(1}} - {\nu )}a}}{\sigma }(r{\text{/}}a),\quad {\sigma }(\tau ) = - \frac{2}{{\pi }}\frac{d}{{d{\tau }}}{\tau }\int\limits_{\tau }^1 {\frac{{\varphi (t)dt}}{{t\sqrt {{{t}^{2}} - {{{\tau }}^{2}}} }}} $

Сила, действующая на штамп, может быть вычислена по формуле [15]

(3.6)

$P = 2{\pi }\int\limits_0^a {q(r)rdr} = \frac{{4{\mu }a}}{{1 - {\nu }}}\int\limits_0^1 {\varphi (t)dt} $

Представим ядро и решение интегрального уравнения (3.3), (3.4) в виде [15]

(3.7)

$k(t) = \sum\limits_{n = 0}^\infty {{{a}_{n}}{{t}^{{2k}}}} ,\quad \varphi (t) = \sum\limits_{n = 0}^\infty {{{\varphi }_{n}}(t){{{\lambda }}^{n}}} ,\quad {{a}_{n}} = \int\limits_0^\infty {\frac{{{{{( - 1)}}^{n}}{{u}^{{2n}}}}}{{(2n)!}}} [1 - L{\text{*}}(u)]du$

Тогда для нахождения функций ${{\varphi }_{n}}(t)$ получим следующие реккурентные соотношения

(3.8)

${{\varphi }_{0}}(t) = d(t),\quad {{\varphi }_{{2i + 1}}}(t) = \frac{1}{\pi }\sum\limits_{k = 0}^i {{{a}_{k}}\int\limits_{ - 1}^1 {{{\varphi }_{{2(i - k)}}}(\tau ){{{(\tau - t)}}^{{2k}}}d\tau } } \quad (i = 1,\;2,\;3, \ldots )$

${{\varphi }_{{2i}}}(t) = \frac{1}{\pi }\sum\limits_{k = 0}^{i - 1} {{{a}_{k}}\int\limits_{ - 1}^1 {{{\varphi }_{{2(i - k) - 1}}}(\tau ){{{(\tau - t)}}^{{2k}}}d\tau } } \quad (i = 1,\;2,\;3,\; \ldots )$

Отметим, что в (3.8) интегралы берутся от степенных функций и в итоге функции ${{\varphi }_{n}}(t)$ будут представлены в виде многочленов. Приведем здесь некоторые из них

${{\varphi }_{0}}(t) = {\delta } - {{t}^{2}}{{a}^{2}}{\text{/}}R,\quad {{\varphi }_{1}}(t) = \frac{{2{{a}_{0}}}}{\pi }\left( {{\delta } - \frac{{{{a}^{2}}}}{{3R}}} \right),\quad {{\varphi }_{2}}(t) = \frac{{4a_{0}^{2}}}{{{{{\pi }}^{2}}}}\left( {{\delta } - \frac{{{{a}^{2}}}}{{3R}}} \right)$

(3.9)

${{\varphi }_{3}}(t) = \frac{{\delta }}{{\pi }}\left[ {\frac{{8a_{0}^{3}}}{{{{\pi }^{2}}}} + 2{{a}_{1}}\left( {\frac{1}{3} + {{t}^{2}}} \right)} \right] - \frac{1}{{{\pi }R}}\left[ {\frac{{8a_{0}^{3}{{a}^{2}}}}{{3{{\pi }^{2}}}} + 2{{t}^{2}}{{a}^{2}}{{a}_{1}}\left( {\frac{1}{3} + {{t}^{2}}} \right)} \right]$

${{\varphi }_{4}}(t) = \frac{{8{\delta }{{a}_{0}}}}{{{{{\pi }}^{2}}}}\left[ {\frac{{2a_{0}^{3}}}{{{{{\pi }}^{2}}}} + {{a}_{1}}\left( {\frac{1}{3} + {{t}^{2}}} \right)} \right] - \frac{{4a_{0}^{{}}{{a}^{2}}}}{{R{{{\pi }}^{2}}}}\left[ {\frac{{4a_{0}^{3}}}{{3R{{{\pi }}^{2}}}} + {{a}_{1}}{{{\left( {{{t}^{2}} + \frac{1}{3}} \right)}}^{2}}} \right]$

В случае штампа с плоским основанием (${\delta }(r) = {\delta } = {\text{const}}$) с учетом (3.9) получим значения для контактных напряжений

$q(r) = \frac{{{\mu \delta }}}{{{\text{(1}} - {\nu )}a}}{{\sigma }_{0}}(r{\text{/}}a)$

(3.10)

${{\sigma }_{0}}(t) = \frac{2}{{{\pi }\sqrt {1 - {{t}^{2}}} }}\left( {1 + \frac{{2{{a}_{0}}}}{{{{{\pi }}^{{}}}{\lambda }}} + \frac{{4a_{0}^{2}}}{{{{{\pi }}^{2}}{{{\lambda }}^{2}}}} + \frac{{4(3{{{\pi }}^{2}}{{a}_{1}}{{t}^{2}} - {{{\pi }}^{3}}{{a}_{1}} + 6{\pi }a_{0}^{3})}}{{3{{{\pi }}^{4}}{{{\lambda }}^{3}}}} + } \right.$

$\left. { + \;\frac{{16{{a}_{0}}(3{{{\pi }}^{2}}{{a}_{1}}{{t}^{2}} - {{{\pi }}^{2}}{{a}_{1}} + 3a_{0}^{3})}}{{3{{{\pi }}^{4}}{{{\lambda }}^{4}}}} + O({{{\lambda }}^{{ - 5}}})} \right)$

Соотношение для силы, приложенной к штампу, примет вид

$P = 2\pi \int\limits_0^a {q(r)rdr} $

(3.11)

$P = \frac{{{\mu }a{\delta }}}{{1 - \upsilon }}\left( {4 + \frac{{8{{a}_{0}}}}{{{\pi \lambda }}} + \frac{{16a_{0}^{2}}}{{{{{\pi }}^{2}}{{{\lambda }}^{2}}}} + \frac{{16(6a_{0}^{3}{{{\pi }}^{2}} + {{a}_{1}}{{{\pi }}^{4}})}}{{3{{{\pi }}^{5}}{{{\lambda }}^{3}}}} + \frac{{64(3a_{0}^{4}{\pi } + {{a}_{0}}{{a}_{1}}{{{\pi }}^{3}})}}{{3{{\pi }^{5}}{{{\lambda }}^{4}}}} + O({{{\lambda }}^{{ - 5}}})} \right)$

В случае штампа с основанием в форме параболоида вращения (${\delta }(r) = {\delta } - {{r}^{2}}{\text{/}}(2R)$) дополнительно, кроме контактных напряжений и силы, требуется также найти радиус области контакта.

Область контакта найдем из условия обращения в ноль контактных напряжений на ее границе при r = a. Найдя выражения контактных напряжений на основе соотношений (3.5), (3.9), уравнение для определения радиуса области контакта найдем из условия

(3.12)

$\lim {\kern 1pt} (q(r)\,{\kern 1pt} \sqrt {{{a}^{2}} - {{r}^{2}}} ) = 0\quad {\text{при}}\quad r \to a$

В результате предельного перехода (3.12) получим выражение для определения области контакта с любой заданной точностью при значениях λ > 1, ниже приведем его с точностью до $O({{{\lambda }}^{{ - 5}}})$

(3.13)

$a = \sqrt {3{\delta }RB({\lambda }){\text{/}}A({\lambda })} + O({{\lambda }^{{ - 5}}})$

$A({\lambda }) = 9{{{\pi }}^{4}} + 6{{a}_{0}}{{{\pi }}^{3}}{{{\lambda }}^{{ - 1}}} + 12a_{0}^{2}{{{\pi }}^{2}}{{{\lambda }}^{{ - 2}}} + 24({{a}_{1}}{{{\pi }}^{3}} + a_{0}^{3}{{{\pi }}^{{}}}){{{\lambda }}^{{ - 3}}} + 16(4{{a}_{0}}{{a}_{1}}{{{\pi }}^{2}} + 3a_{0}^{4}){{{\lambda }}^{{ - 4}}}$

$B({\lambda }) = 3{{{\pi }}^{4}} + 6{{a}_{0}}{{{\pi }}^{3}}{{{\lambda }}^{{ - 1}}} + 12a_{0}^{2}{{{\pi }}^{2}}{{{\lambda }}^{{ - 2}}} + 8({{a}_{1}}{{{\pi }}^{3}} + 3a_{0}^{3}{\pi }){{{\lambda }}^{{ - 3}}} + 16(2{{a}_{0}}{{a}_{1}}{{{\pi }}^{2}} + 3a_{0}^{4}){{{\lambda }}^{{ - 4}}}$

Для вычисления контактных напряжений под штампом необходимо воспользоваться соотношениями (3.5), (3.9). Здесь выпишем функцию $\sigma (\tau )$ с точность до членов порядка $O({{{\lambda }}^{{ - 5}}})$

(3.14)

$\sigma ({\tau }) = \frac{{4\sqrt {\delta } (8{{a}_{1}}{{r}^{2}}{{N}_{1}} + 3{{N}_{2}})}}{{3{{{\pi }}^{2}}\sqrt {R{{D}_{1}}{{D}_{2}}} }}\sqrt {1 - {{r}^{2}}} + O({{{\lambda }}^{{ - 5}}})$

${{N}_{1}} = 3{{{\pi }}^{3}}{{{\lambda }}^{{ - 3}}} + 6{{\pi }^{2}}{{a}_{0}}{{{\lambda }}^{{ - 4}}} + 12{\pi }a_{0}^{2}{{{\lambda }}^{{ - 5}}} + (8{{a}_{1}}{{{\pi }}^{2}} + 24a_{0}^{3}){{{\lambda }}^{{ - 6}}}$

${{N}_{2}}\, = \,3{{\pi }^{4}} + 6{{a}_{0}}{{\pi }^{3}}{{{\lambda }}^{{ - 1}}} + 12a_{0}^{2}{{\pi }^{2}}{{{\lambda }}^{{ - 2}}} + 8{\pi }({{a}_{1}}{{\pi }^{2}} + 3a_{0}^{3}){{{\lambda }}^{{ - 3}}} + 8{{a}_{0}}{{a}_{1}}{{\pi }^{2}}{{\lambda }^{{ - 4}}} + 16a_{0}^{2}{{a}_{1}}\pi {{{\lambda }}^{{ - 5}}} + 32a_{0}^{3}{{a}_{1}}{{{\lambda }}^{{ - 6}}}$

${{D}_{1}} = 3{{{\pi }}^{3}} + 2{{{\pi }}^{2}}{{a}_{0}}{{{\lambda }}^{{ - 1}}} + 4{\pi }a_{0}^{2}{{\lambda }^{{ - 2}}} + 8({{a}_{1}}{{{\pi }}^{2}} + a_{0}^{3}){{{\lambda }}^{{ - 3}}}$

${{D}_{2}} = 3{{{\pi }}^{3}} + 6{{{\pi }}^{2}}{{a}_{0}}{{{\lambda }}^{{ - 1}}} + 12{\pi }a_{0}^{2}{{{\lambda }}^{{ - 2}}} + 8({{a}_{1}}{{{\pi }}^{2}} + 3a_{0}^{3}){{{\lambda }}^{{ - 3}}}$

Величину силы, действующей на штамп, на основе соотношений (3.6) можно получить с любой заданной точностью при значениях λ > 1, ниже приведем его с точностью до членов порядка $O({{{\lambda }}^{{ - 5}}})$

$P = \frac{{4a{\mu }}}{{1 - {\nu }}}\int\limits_0^1 {\varphi ({\tau })d{\tau } = \frac{{4a{\mu }}}{{1 - {\nu }}}\sum\limits_{n = 0}^4 {{{P}_{n}}{{{\lambda }}^{{ - n}}} + O({{{\lambda }}^{{ - 5}}})} } ,\quad {{P}_{0}} = {\delta } - \frac{{{{a}^{2}}}}{{3R}},\quad {{P}_{1}} = \frac{{2{{a}_{0}}(3R{\delta } - {{a}^{2}})}}{{3R{\pi }}}$

(3.15)

${{P}_{2}} = \frac{{4a_{0}^{2}(3R{\delta } - {{a}^{2}})}}{{3R{{{\pi }}^{2}}}},\quad {{P}_{3}} = \frac{{4[15R{\delta }({{a}_{1}}{{{\pi }}^{2}} + 6a_{0}^{3}) - {{a}^{2}}(7{{a}_{1}}{{{\pi }}^{2}} + 30a_{0}^{3})]}}{{45R{{{\pi }}^{3}}}}$

${{P}_{4}} = \frac{{16{{a}_{0}}[5R\delta ({{a}_{1}}{{{\pi }}^{2}} + 3a_{0}^{3}) - {{a}^{2}}(2{{a}_{1}}{{{\pi }}^{2}} + 5a_{0}^{3})]}}{{15R{{{\pi }}^{4}}}}$

4. Числовые расчеты. Для тестирования предложенной схемы решения интегрального уравнения (3.1) рассмотрен случай N = 0 (чисто упругий слой) с учетом аппроксимации соответствующей функции для упругого слоя выражением (3.2), где A = 0.5 [13]. Решение задач в этом случае в рамках классической теории упругости аналитическим методом получено в [12]. В табл. 1 для сравнения для задачи 1 приведены во второй строке значения приведенных контактных напряжений ${\sigma (\tau )}$ при λ = 4, вычисленных по формуле (3.10), а в третьей строке их соответствующие значения, взятые из табл. 27 работы [12]. В последней строке табл. 1 приведена относительная погрешность полученных значений контактных напряжений. Видим, что погрешность напряжений значительно меньше максимальной погрешности аппроксимации.

Таблица 1

1	${\tau }$	0	0.2	0.2	0.2	0.8	0.95
2	${\sigma (\tau )}$	0.827	0.843	0.897	1.019	1.344	2.556
3	${\sigma (\tau )}$ [12]	0.785	0.801	0.854	0.976	1.296	2.480
4	%	5.35	5.24	5.04	4.41	3.70	3.06

Для задачи 2 в табл. 2 приведено при λ = 4 сравнение величин ${\sigma *} = 2{\sigma }(0)R{\text{/}}a$ и $P* = P(1 - {\nu }){\text{/}}({\mu \delta }a)$ с результатами для аналогичных величин, приведенных в табл. 30 [12]. В четвертой и седьмой колонках приведены значения относительной погрешности, здесь она меньше чем в задаче 1.

Таблица 2

${\lambda }$	σ*	σ* [12]	%	P*	P* [12]	%
1	2	3	4	5	6	7
4	2.541	2.560	0.74	3.090	3.04	1.65

На основе полученного выше решения интегрального уравнения (3.3) были проведены расчеты контактных напряжений, величины силы, действующей на штамп, а также величины области контакта для задачи 2.

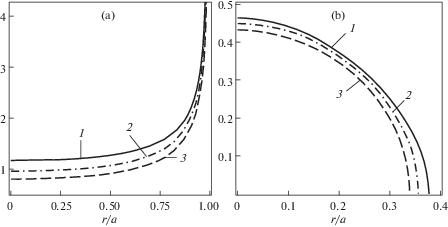
На рис. 1, a для задачи 1 при λ = 2 и с = 0.6 при некоторых значениях N приведены графики приведенных контактных напряжений $q* = q(r)(1 - {\nu }){\text{/}}({\mu \delta })$. График 1 соответствует N = 0.1 , 2 – N = 0.35, 3 – N = 0.5. При этих значениях параметров произведен также расчет величины $P* = P(1 - \nu ){\text{/}}(\mu \delta a)$, соответственно при N = 0.1 P* = 6.17, N = 0.35 P* = 5.55, N = 0.5 P* = 4.91.

Рис. 1

На рис. 1, b для задачи 2 при λ = 2, ${\delta } = 0.1$, с = 0.6 при некоторых значениях N приведены графики приведенных контактных напряжений 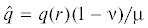. Здесь также график 1 соответствует N = 0.1 , 2 – N = 0.35, 3 – N = 0.5. При этих значениях параметров произведен также расчет величины 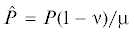и величины области контакта a, соответственно при N = 0.1 $\hat {P}$ = 0.126, a = 0.377, при N = 0.35 – $\hat {P}$ = 0.115, a = 0.356, при N = 0.5 – $\hat {P}$ = 0.103, a = 0.339.

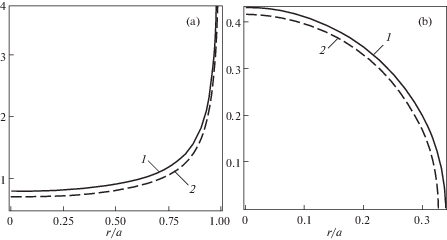
На рис. 2, a и 2, b для задач 1 и 2 соответственно приведены графики аналогичных величин, что и на рис. 1, а и 1, b при c = 0.6, N = 0.5 и различных значениях ${\lambda }$: график 1 построен при λ = 2, а график 2 при λ = 4.

Рис. 2

Расчеты показывают, что в случае штампа с плоским основанием (задача 1) при увеличении пористости при постоянной величине смещения штампа и его радиуса контактные напряжения и величина приложенной силы уменьшаются.

В случае параболического штампа (задача 2) расчеты показывают, что при постоянной величине смещения штампа с увеличением толщины слоя контактные напряжения и величина приложенной силы также уменьшаются при фиксированных значениях других параметров. Стоит также отметить, что зона контакта в случае параболического штампа с увеличением пористости или толщины слоя уменьшается при одинаковом значении смещения штампа ${\delta }$.

Работа финансово поддержана Южным федеральным университетом, 2020 (Министерство науки и высшего образования Российской Федерации). Проект № ВнГр/2020-04-ИМ.

Research was financially supported by Southern Federal University, grant No. VnGr/2020-04-IM (Ministry of Science and Higher Education of the Russian Federation).

Список литературы

Nunziato G.W., Cowin S.C. A nonlinear theory of elastic materials with voids // Arch Ration Mech Anal. 1979. V. 72. P. 175–201.
Cowin S.C., Nunziato G.W. Linear theory of elastic materials with voids // J. Elast. 1983. V. 13. P. 125–147.
Iesan D. A theory of thermoelastic materials with voids // Acta Mech. 1986. V. 60. P. 67–89.
Chandrasekharaiah D.S. Effects of surface stresses and voids on Rayleigh waves in an elastic solid // Int. J. Eng. Sci. 1987. V. 25. P. 205–211
Scalia A., Sumbatyan M.A. Contact problem for porous elastic half-plane // J. Elasticity. 2000. V. 60. P. 91–102.
Scalia A. Contact problem for porous elastic strip // Int. J. Eng. Sci. 2002. V. 40. P. 401–410.
Iovane G., Nasedkin A.V. Modal analysis of piezoelectric bodies with voids. I. Mathematical approaches // Applied Mathematical Modelling. 2010. V. 34. P. 60–71.
Iovane G., Nasedkin A.V. Finite element dynamic analysis of anisotropic elastic solids with voids // Computers and Structures. 2009. V. 87. P. 981–989.
Iovane G., Nasedkin A.V. Finite element analysis of static problems for elastic media with voids // Computers and Structures. 2005. V. 84. P. 19–24.
Kudimova A.B., Nadolin D.K., Nasedkin A.V., Nasedkina A.A., Oganesyan P.A., Soloviev A.N. Models of porous piezocomposites with 3–3 connectivity type in ACELAN finite element package // Mater. Phys. Mech. 2018. V. 37(1). C. 16–24.
Nasedkin A.V., Nasedkina A.A., Rybyanets A.N. Numerical analysis of effective properties of heterogeneously polarized porous piezoceramic materials with local alloying pore surfaces // Mater. Phys. Mech. 2018. V. 40(1). C. 12–21.
Ворович И.И., Александров В.М., Бабешко В.А. Неклассические смешанные задачи теории упругости. М.: Наука, 1974. 456 с.
Александров В.М., Чебаков М.И. Введение в механику контактных взаимодействий. Ростов-на-Дону: Изд-во ООО “ЦВВР”, 2007. 114 с.
Чебаков М.И. О дальнейшем развитии метода больших λ в теории смешанных задач // ПММ. 1976. Т. 40. Вып. 3. С. 561–565.
Александров В.М., Чебаков М.И. Аналитические методы в контактных задачах теории упругости. М.: ФИЗМАТЛИТ, 2004. 304 с.
Александров В.М., Чебаков М.И. Смешанные задачи механики сплошной среды, связанные с интегральными преобразованиями Ханкеля и Мелера–Фока // ПММ. 1972. Т. 36. Вып. 3. С. 494–504.
Александров В.М., Чебаков М.И. Об одном методе решения парных интегральных уравнений // ПММ. 1973. Т. 37. Вып. 6. С. 1088–1097.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал