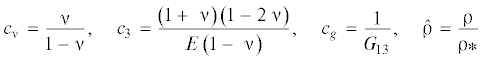Известия РАН. Механика твердого тела, 2020, № 5, стр. 7-12
ИЗГИБНАЯ ЖЕСТКОСТЬ МНОГОСЛОЙНЫХ ПЛАСТИН
Н. Ф. Морозов a, b, *, П. Е. Товстик a, b, **, Т. П. Товстик b, ***
a Санкт-Петербургский университет
Санкт-Петербург, Россия
b Институт проблем машиноведения РАН
Санкт-Петербург, Россия
* E-mail: morozov@nm1016.spb.edu
** E-mail: peter.tovstik@mail.ru
*** E-mail: tovstik_t@mail.ru
Поступила в редакцию 27.03.2020
После доработки 17.04.2020
Принята к публикации 23.04.2020
Аннотация
Рассматривается изгибная жесткость тонкой упругой многослойной пластины с трансверсально изотропными слоями. Если жесткости слоев сильно различаются, классическая модель, основанная на гипотезе прямой нормали, неприменима, и необходимо учитывать влияние поперечного сдвига. Сравниваются две модели учета влияния поперечного сдвига для многослойной пластины. Первая из них, основанная на распределении тангенциальных деформаций по толщине пластины, предложена в работе Э.И. Григолюка и Г.М. Куликова в 1988 году. Вторая модель использует асимптотическое разложение решения трехмерных уравнений теории упругости по степеням малого параметра тонкостенности. Погрешности моделей оцениваются путем сравнения с точным решением трехмерной тестовой задачи.
1. Введение. Классическая модель Кирхгофа–Лява (КЛ), основанная на гипотезе прямой недеформируемой нормали, является основной двухмерной моделью теории тонких пластин. Область применимости этой модели ограничена однослойными пластинами из однородного изотропного материала. Для анизотропных пластин с малой жесткостью на поперечный сдвиг, для пластин с косой анизотропией, для многослойных пластин с чередующимися мягкими и жесткими слоями модель КЛ приводит к большим погрешностям и возникает необходимость в использовании уточненных моделей.
Для анизотропных пластин с малой жесткостью на поперечный сдвиг и для многослойных пластин с чередующимися мягкими и жесткими слоями модель Тимошенко–Рейсснера (ТР), учитывающая поперечный сдвиг, приводит к существенному уточнению результатов по сравнению с моделью КЛ. Для многослойных пластин вводится в рассмотрение эквивалентная однослойная пластина ТР из однородного материала [1–8], моделирующая многослойную пластину при исследовании ее прогибов, колебаний и устойчивости. Если эквивалентные изгибная жесткость и массовая плотность могут быть найдены по тем же формулам, что и в модели КЛ, то определение жесткости на поперечный сдвиг представляет определенные трудности и подробно обсуждается ниже. Одним из способов определения жесткости на сдвиг является асимптотическое разложение решения трехмерной задачи в ряд по степеням малой безразмерной толщины [2–5]. Альтернативный способ основан на гипотезе о распределении деформаций поперечного сдвига по толщине пластины [6–8]. Эти способы обсуждаются на примере задачи о свободных колебаниях многослойной пластины с трансверсально изотропными слоями. Проводится сравнение с точным решением трехмерной задачи.
2. Свободные колебания многослойной пластины. Рассмотрим свободные изгибные колебания пластины с прогибом $w\left( {x,y,t} \right) = {{w}_{0}}\sin px\sin qy\sin {\omega }t$. Такую форму могут иметь колебания бесконечной пластины, а также колебания прямоугольной пластины с шарнирно опертыми сторонами длиной Lx, Ly (тогда $p = {{p}_{m}} = m{\pi /}{{L}_{x}}$, q = qn = nπ/Ly, m, n = 1, 2, ...). По модели ТР с учетом поперечного сдвига для трансверсально изотропной однородной пластины частота колебаний ω определяется из соотношений
(2.1)
${\lambda } = \frac{{{\rho }~{{h}^{2}}{{{\omega }}^{2}}}}{{{{E}_{0}}}} = \frac{{D~{{{\mu }}^{4}}}}{{1 + g~{{{\mu }}^{2}}~}},\quad {{E}_{0}} = \frac{E}{{1 - {{{\nu }}^{2}}~}},\quad {\mu } = rh,\quad {{r}^{2}} = {{p}^{2}} + {{q}^{2}}$Здесь ρ – плотность материала, h – толщина пластины, E – модуль Юнга, ν – коэффициент Пуассона, μ – малый параметр толщины, равный в силу (2.1) отношению толщины к характерной длине волны, $D = 1{\text{/}}12$ – безразмерный параметр изгибной жесткости, $g = {{E}_{0}}{\text{/}}\left( {10{{G}_{{13}}}~} \right)$ – параметр влияния поперечного сдвига, G13 – модуль упругости поперечного сдвига. Для изотропных слоев ${{G}_{{13}}} = E{\text{/}}(2(1 + ~{\nu }~))$, а для трансверсально изотропных слоев G13 – независимый параметр. При $E{\text{/}}{{G}_{{13}}}\sim 1$ слагаемым $g{{{\mu }}^{2}}$ в (2.1) можно пренебречь, а при ${{G}_{{13}}} \ll E$ поправка на сдвиг становится существенной.
Для многослойной пластины модули упругости и плотность становятся кусочно-постоянными функциями поперечной координаты z, 0 ≤ z ≤ h. В [3–5] путем асимптотического разложения решения трехмерных уравнений получено выражение для параметра частоты λ в виде, аналогичном (2.1):
(2.2)
${{D}_{*}} = \frac{1}{{{{E}_{*}}{{h}^{3}}}}\mathop \smallint \limits_0^h {{E}_{0}}\left( z \right){{\left( {z - a} \right)}^{2}}dz,\quad a = \frac{1}{{{{E}_{*}}h}}\mathop \smallint \limits_0^h {{E}_{0}}\left( z \right)zdz~$Здесь ${{E}_{*}},{{{\rho }}_{*}}$ – средние по толщине значения жесткости на растяжение и плотности, ${{D}_{*}}$ – параметр жесткости на изгиб, a – координата нейтрального слоя. Слагаемое второго порядка малости ${{q}_{*}}~{{{\mu }}^{2}}$ учитывает податливость на поперечный сдвиг (${{A}_{g}}$), пуассоновское растяжение нормального волокна (${{A}_{{\nu }}}$), инерцию его вращательного движения (J) и инерцию пуассоновского растяжения (${{J}_{{\nu }}}$) (величины ${{A}_{{\nu }}}$ и ${{J}_{{\nu }}}$ здесь не приводятся, см. [3]).
Если модули ${{G}_{{13}}}$ некоторых слоев пластины уменьшаются, то коэффициент ${{A}_{g}}$ растет в то время, как остальные коэффициенты второго порядка ${{A}_{{\nu }}},~J,~{{J}_{{\nu }}}$ остаются неизменными и существенно меньшими ${{A}_{g}}$ (см. ниже табл. 3). Поэтому положим приближенно ${{g}_{*}} = {{A}_{g}}$, возвращаясь тем самым к модели ТР. Введем параметр η, равный отношению максимального и минимального модуля Юнга слоев пластины. Расчеты [2–5] показали, что при η ≤ 1000, μ = 0.1 погрешность формулы (2.2) при ${{g}_{*}} = {{A}_{g}}$ не превосходит 4%.
Точное значение параметра частоты λ может быть найдено из краевой задачи, которая для поперечных колебаний приводится к виду [3]:
(2.3)
$\frac{{du}}{{dz}} = w + ~{{{\mu }}^{2}}{{c}_{g}}\left( z \right){\sigma },\quad \frac{{d{{{\sigma }}_{{33}}}}}{{dz}} = - {\sigma } - {\lambda \hat {\rho }}\left( z \right)w$Асимптотическое интегрирование системы (2.3) приводит к решению (2.2). Нас интересует точное значение ge сдвигового параметра g при условии, что остальные эффекты второго порядка малости не учитываются. Для его вычисления положим в системе (2.3) ${{c}_{{\nu }}} = {{c}_{3}} = 0$ и опустим слагаемое ${{{\mu }}^{2}}{\lambda \hat {\rho }}~\left( z \right)u$ в третьем уравнении. Получаем w = 1 и краевую задачу
После ее решения из условия совместности четвертого уравнения (2.3) находим
(2.4)
${\lambda } = - \mathop \smallint \limits_0^h {\sigma }\left( z \right)dz,\quad {{g}^{e}} = \frac{1}{{{{{\mu }}^{2}}}}\left( {\frac{{{{D}_{*}}}}{{\lambda }} - 1} \right)$3. Алгоритм Григолюка–Куликова. В монографии [6] был предложен алгоритм учета эффекта поперечного сдвига для многослойных пластин и оболочек. К этому алгоритму целесообразно вернуться, ибо в недавних книгах [7, 8], а также в ряде статей он был использован для решения частных задач. Этот алгоритм основан на гипотезе о распределении деформаций поперечного сдвига по толщине пластины. Он приводит к системе, порядок которой выше, чем порядок модели ТР. В [6] приведена формула для расчета частот колебаний пластины по той же форме, что и в п. 2. В наших обозначениях эта формула имеет вид:
Она отличается от формулы (2.2) наличием близкого к единице множителя ($1 + {{{\mu }}^{2}}{\theta }\tilde {g}$) (ибо параметр θ имеет порядок 0.01) и значением параметра поперечного сдвига $\tilde {g}$. Приведем алгоритм вычисления этих параметров.
Рассмотрим многослойную пластину с трансверсально изотропными слоями с толщинами hn, модулями Юнга En, коэффициентами Пуассона ${{{\nu }}_{n}}$ и модулями поперечного сдвига Gn, причем $n = 1,~ \ldots ,~N,h = \mathop \sum \limits_{n = 1}^N {{h}_{n}}$. Пусть ${{z}_{0}} = 0,{{z}_{n}} = {{z}_{{n - 1}}} + {{h}_{n}},n = 1, \ldots ,~N$, тогда для n-го слоя будет ${{z}_{{n - 1}}} \leqslant z \leqslant {{z}_{n}}$. Введем функции ${{f}_{0}}(z) = {{h}^{{ - 2}}}z(h - z))$, g0(z) = $\mathop \smallint \limits_0^z {{f}_{0}}(x)dx~$, ${{f}_{n}}\left( z \right) = h_{n}^{{ - 2}}\left( {z - {{z}_{{n - 1}}}} \right)\left( {{{z}_{n}} - z} \right)$. Получаем
(3.1)
${{{\eta }}_{1}} = \mathop \sum \limits_{n = 1}^N ({{{\pi }}_{{1n}}}{{{\gamma }}_{n}}{\xi }_{n}^{{ - 1}}) - 3c_{{12}}^{2},\quad {{{\eta }}_{2}} = \mathop \sum \limits_{n = 1}^N ({{{\pi }}_{{2n}}}{{{\gamma }}_{n}}{\xi }_{n}^{{ - 1}}) - 3{{c}_{{12}}}{{c}_{{13}}}$В работе [1] для вычисления податливости на сдвиг многослойной пластины была предложена формула
где ${{G}_{n}}$ – модули упругости поперечного сдвига слоев и ${{{\alpha }}_{n}}$ – некоторые коэффициенты. Формула (2.2) для Ag после вычисления интегралов приводится к виду (3.2) (см. [3]), а зависимость величины $\tilde {g}$ от ${{G}_{n}}$, описываемая формулой (3.1), имеет другую структуру (см. формулу для ${{q}_{{44}}}$, ибо только в нее входят модули ${{G}_{n}}$).4. Численные результаты. Рассмотрим трехслойную пластину с изотропными слоями, модули упругости крайних слоев равны ${{E}_{1}} = {{E}_{3}}$, а среднего слоя – ${{E}_{2}}$, коэффициенты Пуассона всех слоев одинаковы, ${\nu } = 0.3$. Проведем сравнение параметров g влияния поперечного сдвига, найденных по различным формулам, для ряда значений параметра ${\eta } = {{E}_{1}}{\text{/}}{{E}_{2}}~$ и при различных соотношениях между толщинами слоев.
В табл. 1 и 2 для симметричной и несимметричной по толщине пластины для пяти значений отношения модулей Юнга η = 1, 10, 100, 1000, 10000 приведены значения параметра g найденные по различным формулам: точные значения ge, найденные по формуле (2.4), и приближенные значения ${{A}_{g}}$ и $\tilde {g}$, найденные, соответственно, по формулам (2.2) и (3.1). Также приведены значения погрешностей (err) по отношению к значению ge, причем в последних столбцах в связи с большим различием величин ge и $\tilde {g}$ приведены отношения ${{g}^{e}}$/$\tilde {g}$. Разумеется, при вычислении частот погрешности существенно меньше, ибо величины g умножаются на малый множитель μ2. Поэтому приближенной формулой (2.1) при $g = {{A}_{g}}$ можно пользоваться вплоть до значений η = 1000. При η = 10000 двухмерная модель уже неприменима.
Таблица 1
| Симметричная по толщине пластина (${{h}_{1}} = {{h}_{3}} = 0.2,~~{{h}_{2}} = 0.6,~~{\mu } = 0.1$) | |||||
|---|---|---|---|---|---|
| η | ge | Ag | err | $\tilde {g}$ | Err |
| 1 | 0.2857 | 0.2857 | 0% | 0.2891 | 1.2% |
| 10 | 1.800 | 1.801 | 0.1% | 1.227 | 31.2% |
| 100 | 16.86 | 16.91 | 0.3% | 2.371 | ×7 |
| 1000 | 162.4 | 167.1 | 3.5% | 2.623 | ×62 |
| 10000 | 1244. | 1679. | 32.3% | 2.637 | ×467 |
Таблица 2
| Несимметричная по толщине пластина (${{h}_{1}} = 0.3,{{h}_{2}} = 0.6,{{h}_{3}} = 0.1,{\mu } = 0.1$) | |||||
|---|---|---|---|---|---|
| η | ${{g}^{e}}$ | Ag | err | $\tilde {g}$ | err |
| 1 | 0.2857 | 0.2857 | 0% | 0.2891 | 1.2% |
| 10 | 1.403 | 1.404 | 0.1% | 0.808 | 42.4% |
| 100 | 12.36 | 12.44 | 0.4% | 1.201 | ×10 |
| 1000 | 115.9 | 122.8 | 6.0% | 1.271 | ×91 |
| 10000 | 768.4 | 1226.0 | 58.2% | 1.279 | ×598 |
Таблица 3
| Члены второго порядка малости | ||||||
|---|---|---|---|---|---|---|
| ${{{\nu }}_{1}} = {{{\nu }}_{3}} = 0.3,{{{\nu }}_{2}} = 0.35,{{h}_{1}} = 0.3,{{h}_{2}} = 0.6,{{h}_{3}} = 0.1$ | ||||||
| η | Ag | ${{A}_{{\nu }}}$ | J | ${{J}_{{\nu }}}$ | a | ${{D}_{*}}$ |
| 1 | 0.299 | – 0.0928 | 0.1150 | 0.0308 | 0.502 | 0.0824 |
| 10 | 1.461 | – 0.0875 | 0.1114 | 0.0081 | 0.384 | 0.1202 |
| 100 | 12.921 | – 0.0844 | 0.1149 | 0.0026 | 0.354 | 0.1253 |
| 1000 | 127.515 | – 0.0840 | 0.1154 | 0.0019 | 0.350 | 0.1259 |
Последний вывод получен при μ = 0.1. Область применимости двухмерной модели зависит от совмещенного параметра ${{{\mu }}^{2}}{\eta }$. Этот вопрос нуждается в дополнительном исследовании.
Модель Григолюка–Куликова можно использовать при малых значениях η (скажем, η ≤ 10), о чем написано и в работе [6]. По-видимому, кинематические гипотезы, положенные в основу этой модели, нуждаются в корректировке. В частности, эта модель обеспечивает непрерывность тангенциальных деформаций на границе слоев в то время, как они терпят разрыв, а непрерывны тангенциальные напряжения.
Формулы (2.2) содержат выражение ${{g}_{*}} = {{A}_{g}} + {{A}_{{\nu }}} + J + {{J}_{{\nu }}}$. В табл. 3 для ряда значений η приведены значения входящих в формулу для ${{g}_{*}}$ величин.
Из результатов табл. 3 следует, что при малых η следует удерживать все члены второго порядка малости, а при больших – можно ограничиваться учетом только эффекта поперечного сдвига Ag.
При поддержке РФФИ, гранты 18-01-00884а, 19-01-00208a, 20-51-52001MHTa.
Список литературы
Hill R. A self-consistent mechanics of composite materials // J. Mech. Phys. Solids. 1965. 13(4).
Морозов Н.Ф., Товстик П.Е., Товстик Т.П. Обобщенная модель Тимошенко–Рейсснера сильно неоднородной по толщине пластины // ДАН. 2016. V. 469(5). С. 562–566.
Tovstik P.E., Tovstik T.P. Generalized Timoshenko-Reissner models for beams and plates, strongly heterogeneous in the thickness direction // ZAMM. 2017. V. 97(3). P. 296–308.
Tovstik P., Tovstik T. An elastic plate bending equation of second-order accuracy // Acta Mechanica. 2017. V. 228(10). P. 3403–3419.
Товстик П.Е., Товстик Т.П. Уравнение изгиба тонкой пластины второго порядка точности // ДАН. 2014. V. 457(60). С. 660–663.
Григолюк Э.И., Куликов Г.М. Многослойные армированные оболочки. М.: Машиностроение, 1988. 225 с.
Mikhasev G.I., Altenbach H. Thin-walled Laminated Structures. Buckling, Vibrations, and Their Suppression. Springer, 2019.
Mikhasev G.I., Tovstik P.E. Localized dynamics of thin-walled shells. CRC Press. Taylor \& Francis Group, 2020.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела