Известия РАН. Механика твердого тела, 2020, № 5, стр. 131-137

АСИМПТОТИЧЕСКИЕ МЕТОДЫ ИССЛЕДОВАНИЯ ЭЛЛИПТИЧЕСКОГО ПОГРАНСЛОЯ В ОБОЛОЧКАХ ВРАЩЕНИЯ ПРИ УДАРНЫХ ТОРЦЕВЫХ ВОЗДЕЙСТВИЯХ НОРМАЛЬНОГО ТИПА

И. В. Кириллова^a, *, Л. Ю. Коссович^a, **

^a ФГБОУ ВО “СГУ имени Н.Г. Чернышевского”
Саратов, Россия

^* E-mail: nano-bio@info.sgu.ru
^** E-mail: president@info.sgu.ru

Поступила в редакцию 12.03.2020
После доработки 02.04.2020
Принята к публикации 04.04.2020

DOI: 10.31857/S0572329920050104

Аннотация

В данной работе строятся асимметрические уравнения эллиптического погранслоя в окрестности условного фронта поверхностных волн Рэлея, имеющего место в оболочках вращения при ударных торцевых воздействиях нормального типа. Техника асимптотического вывода этих уравнений, основанная на применении символического метода Лурье и введении специальных координат, выделяющих малую прифронтовую зону, потребовала путем выделения частного решения свести исходную задачу к эквивалентной задаче для бесконечной оболочки. Рассматриваемый погранслой дополняет полное описание рассматриваемого вида напряженно-деформированного состояния (НДС) во всех участках фазовой плоскости. Здесь используется также квазистатический погранслой типа Сен-Венана в малой окрестности торца, параболический погранслой по двумерной теории Кирхгофа–Лява, квазиплоская коротковолновая составляющая и гиперболический погранслой в малой окрестности фронта волны сдвига. В заключение работы рассмотрен пример построения эллиптического погранслоя при ударном воздействии на торец цилиндрической оболочки.

Ключевые слова: оболочка вращения, асимптотические методы, метод прифронтовой асимптотики, ударные нагрузки, символический метод Лурье, волна Рэлея, погранслой

1. Введение. Асимптотические уравнения эллиптического погранслоя в оболочках вращения при ударных поверхностных воздействиях нормального типа построены в работе [1]. Эллиптический погранслой имеет место в окрестности условного фронта поверхностных волн Рэлея и дополняет полное описание рассматриваемого вида нестационарного НДС во всех участках фазовой плоскости с помощью изгибной двумерной составляющей Кирхгофа–Лява, квазистатического погранслоя типа Сен-Венана, гиперболического погранслоя в окрестности фронта волны сдвига и квазиплоской высокочастотной коротковолновой составляющей. Указанная работа [1] вместе с представленной работой завершают исследования авторов в построении асимптотической теории нестационарных процессов в тонких оболочках вращения при всех трех видах торцевых воздействий, названных, по классификации У.К. Нигула [2], продольными воздействиями тангенциального типа, продольными воздействиями изгибающего типа и нормальными воздействиями.

Представленная работа развивает результаты [3], где впервые рассматриваются уравнения эллиптического погранслоя для оболочки вращения в случае торцевого ударного воздействия. Асимптотическим методом на основе символического метода Лурье строятся уравнения погранслоя в малой окрестности условного фронта поверхностных волн Рэлея. При этом построение основывается на предварительном выделении частного решения, удовлетворяющего только граничным условиям на торце оболочки. В качестве примера рассматривается распространение нестационарных волн касательного напряжения в цилиндрической оболочке.

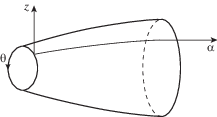
2. Постановка задачи. Рассмотрим оболочку вращения, изображенную на рис. 1.

Рис. 1

Обозначим через α длину дуги вдоль образующей срединной поверхности, через θ угол в окружном направлении и через z расстояние от срединной поверхности вдоль нормали. Через σ_ij и ${{{v}}_{i}}$ (i = 1, 2, 3) обозначим напряжения и перемещения. Рассмотрим на торце α = 0 граничные условия, определяющие осесимметричный вид НДС при ударном воздействии нормального вида [2]

(2.1)

${{\sigma }_{{13}}} = IH(t),\quad {{{v}}_{1}} = 0\quad {\text{при}}\quad \alpha = 0$

где h – полутолщина, t – время. Однородные граничные условия на лицевых поверхностях записываем в виде

(2.2)

${{\sigma }_{{33}}} = {{\sigma }_{{13}}} = 0\quad {\text{при}}\quad z = \pm h$

Рассмотрим также однородные начальные условия

(2.3)

${{{v}}_{i}} = \frac{{\partial {{{v}}_{i}}}}{{\partial t}} = 0\,\,(i = 1,2,3)\quad {\text{при}}\quad t = 0$

Введем безразмерные переменные

(2.4)

$\xi = \frac{\alpha }{h},\quad \zeta = \frac{z}{h},\quad \tau = \frac{{t{{c}_{2}}}}{h}$

где E, ν – модуль Юнга и коэффициент Пуассона материала оболочки, а c₂ – скорость волны сдвига в упругой среде: c₂ = $\sqrt {E{\text{/}}2(1 + \nu )\rho } $, где ρ – плотность. Приведенный в [1] вывод исходных разрешающих уравнений основан на предположении о типе рассматриваемого НДС: оно является коротковолновым, представляется в виде наложения симметричной и антисимметричной по ζ составляющих, причем асимптотически главной составляющей является симметричная компонента. Окончательный вид разрешающих уравнений для этой составляющей приведен в [1].

Вывод асимптотически оптимальных уравнений искомого погранслоя основывается на использовании символического метода Лурье [4]. При этом целесообразно свести задачу об ударном воздействии на торец полубесконечной оболочки вращения к эквивалетной задаче об ударном воздействии на лицевые поверхности бесконечной оболочки вращения путем выделения частного решения, удовлетворяющего только торцевым граничным условиям.

3. Частное решение и эквивалентная задача. В рассматриваемом случае уравнений для оболочки вращения с переменными коэффициентами искомое частное решение, удовлетворяющее торцевым граничным условиям, может быть получено приближенно методом прифронтовой асимптотики. Согласно простейшему варианту метода прифронтовой асимптотики искомое решение представляется в виде разложения по степеням отклонения продольной координаты от фронта волны сдвига:

(3.1)

$\sigma _{1}^{{(0)}} = 0,\quad {v}_{3}^{{(0)}} = - I{\text{*}}\sum\limits_{n = 1}^\infty {{{F}_{n}}({{\xi }_{0}}){{{({{\tau }_{0}} - {{\xi }_{0}})}}^{n}}H({{\tau }_{0}} - {{\xi }_{0}})} $

где F_n(ξ₀) – неизвестные функции, I* – некоторая постоянная, ${{{\xi }}_{0}} = {\alpha /}R$, τ₀ = tc₂/R, R – характерное значение радиусов кривизны оболочки.

Подставляя (3.1) в разрешающие уравнения, представленные в [1], получим, приравнивая нулю члены при одинаковых степенях (τ₀ – ξ₀)ⁿ, зацепляющуюся систему уравнений для неизвестных функций F_n:

(3.2)

$2\frac{{d{{F}_{n}}}}{{d{{\xi }_{0}}}} + \frac{{B{\kern 1pt} '}}{B}{{F}_{n}} = \frac{1}{n}\left( {\frac{{{{d}^{2}}{{F}_{{n - 1}}}}}{{d\xi _{0}^{2}}} + \frac{{B{\kern 1pt} '}}{B}\frac{{d{{F}_{{n - 1}}}}}{{d{{\xi }_{0}}}}} \right)$

где B – безразмерное расстояние до оси вращения (B = B*/R), B* – расстояние до оси вращения.

Частное решение (3.2) с учетом граничных условий (2.1) дает следующие выражения для перемещений и напряжений [3]

${v}_{1}^{{(0)}} = 0,\quad {v}_{3}^{{(0)}} = - I\left[ {\sqrt {\frac{{B(0)}}{B}} ({{\tau }_{0}} - {{\xi }_{0}}) + \sum\limits_{n = 2}^\infty {{{F}_{n}}({{\xi }_{0}}){{{({{\tau }_{0}} - {{\xi }_{0}})}}^{n}}} } \right]H({{\tau }_{0}} - {{\xi }_{0}})$

(3.3)

$\sigma _{{11}}^{{(0)}} = \sigma _{{33}}^{{(0)}} = 0,\quad \sigma _{{13}}^{{(0)}} = I\left[ {\sqrt {\frac{{B(0)}}{B}} + \sum\limits_{n = 2}^\infty {(n{{F}_{n}}({{\xi }_{0}}) - F_{{n - 1}}^{'}({{\xi }_{0}})){{{({{\tau }_{0}} - {{\xi }_{0}})}}^{{n - 1}}}} } \right]H({{\tau }_{0}} - {{\xi }_{0}})$

${{F}_{n}} = - \frac{1}{{2n\sqrt B }}\int\limits_0^{{{\xi }_{0}}} {\frac{1}{{\sqrt B }}\frac{d}{{d{{\xi }_{0}}}}\left( {\frac{1}{B}\frac{{d{{F}_{{n - 1}}}}}{{d{{\xi }_{0}}}}} \right)d{{\xi }_{0}},\quad n \geqslant 2,\quad I* = \frac{{2(1 + \nu )hI}}{E}} $

Представим решение исходной задачи в виде суммы

(3.4)

$\begin{array}{*{20}{c}} {{\text{НДС}} = {\text{НД}}{{{\text{С}}}^{{(0)}}} + {\text{НД}}{{{\text{С}}}^{{(1)}}}} \end{array}$

где для составляющей с верхним индексом (1) (эквивалентная задача) ставятся следующие граничные условия

(3.5)

$\frac{{\partial {v}_{3}^{{(1)}}}}{{\partial \xi }} = 0,\quad {v}_{1}^{{(1)}} = 0,\quad \xi = 0$

(3.6)

$\sigma _{{33}}^{{(1)}} = 0,\quad \sigma _{{13}}^{{(1)}} = - I\left[ {\sqrt {\frac{{B(0)}}{B}} + \sum\limits_{n = 2}^\infty {(n{{F}_{n}} - F_{{n - 1}}^{'}){{{({{\tau }_{0}} - {{\xi }_{0}})}}^{{n - 1}}}} } \right]H({{\tau }_{0}} - {{\xi }_{0}}),\quad \varsigma = \pm 1$

Анализ показывает, что для решения (3.3) деформированное торцевое сечение прямолинейно и перпендикулярно к оси ξ. Значит, составляющая с верхним индексом “1” обладает такими же свойствами. Следовательно, бесконечная оболочка вращения с симметричным относительно ς нагружением на лицевые поверхности, определенным граничными условиями (3.5), (3.6) имеет НДС, соответствующее НДС исходной полубесконечной оболочки, и задача для нее эквивалентна исходной задаче для полубесконечной оболочки.

4. Уравнения эллиптического погранслоя. Рассматриваемые уравнения строятся асимптотическим методом подобно случаю ударной нагрузки на лицевые поверхности оболочки [1]. Опишем кратко этот подход, подробно представленный в [1] для случая нормальной нагрузки на лицевые поверхности, применяемый в рассматриваемом случае для нагрузки по касательной к лицевым поверхностям. Новым здесь является и характер нагрузки, распространяющейся вдоль продольной координаты со скоростью волны сдвига.

Основой предложенного асимптотического подхода является использование символического метода Лурье: вводятся операторы ${{\partial }_{{\xi }}} = \partial {\text{/}}\partial {\xi }$, ${{\partial }_{{\tau }}} = \partial {\text{/}}\partial {\tau }$ и разрешающие уравнения рассматриваются как обыкновенные дифференциальные уравнения с аргументом ${\varsigma }$, при этом принимается, что операторы ${{\partial }_{{\xi }}}$ и ${{\partial }_{{\tau }}}$ являются алгебраическими величинами порядка единицы. Вводится также малый параметр ${\eta } = h{\text{/}}R$. Последним принципиальным шагом рассматриваемого подхода является выделение малой окрестности условного фронта поверхностных волн Рэлея путем перехода к координатам 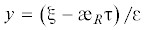и ${{{\tau }}_{0}} = {\varepsilon \tau ,}$ ε = 1/T (рассматриваются моменты времени, когда условный фронт прошел расстояние, много большее толщины оболочки).

В результате для потенциальных функций φ и ψ, определяющих движение волн от поверхности 2z = –h вглубь оболочки, получены следующие уравнения эллиптического типа:

(4.1)

$\begin{gathered} \left( {1 - \frac{{c_{R}^{2}}}{{c_{1}^{2}}}} \right)\frac{{{{\partial }^{2}}\varphi }}{{\partial {{\alpha }^{2}}}} + \frac{{{{\partial }^{2}}\varphi }}{{\partial {{z}^{2}}}} = 0 \\ \left( {1 - \frac{{c_{R}^{2}}}{{c_{2}^{2}}}} \right)\frac{{{{\partial }^{2}}\psi }}{{\partial {{\alpha }^{2}}}} + \frac{{{{\partial }^{2}}\psi }}{{\partial {{z}^{2}}}} = 0 \\ \end{gathered} $

Перемещения и напряжения выражаются при ξ > 0 через эти потенциальные функции следующим образом:

${{{v}}_{1}} = h\left( {\frac{{\partial \varphi }}{{\partial \alpha }} + b\frac{{\partial \psi }}{{\partial \alpha }}} \right),\quad {{{v}}_{3}} = h\left( {\frac{{\partial \varphi }}{{\partial z}} + \frac{1}{b}\frac{{\partial \psi }}{{\partial z}}} \right)$

(4.2)

${{\sigma }_{{33}}} = - \frac{{Eh}}{{1 + \nu }}\left( {g\frac{{{{\partial }^{2}}\varphi }}{{\partial {{\alpha }^{2}}}} + b\frac{{{{\partial }^{2}}\psi }}{{\partial {{\alpha }^{2}}}}} \right)$

${{\sigma }_{{13}}} = \frac{{Eh}}{{1 + \nu }}\left( {\frac{1}{{{{a}^{2}}}}\frac{{{{\partial }^{2}}\varphi }}{{\partial \alpha \partial z}} + \frac{{{{\unicode{230} }^{2}}\unicode{230} _{R}^{2}}}{{{{a}^{2}}{{c}_{R}}}}\frac{{{{\partial }^{2}}\varphi }}{{\partial z\partial t}} + \frac{1}{{2{{a}^{2}}}}\frac{{B'}}{B}\frac{{\partial \varphi }}{{\partial z}} + \frac{{g + \unicode{230} _{R}^{2}}}{b}\frac{{{{\partial }^{2}}\psi }}{{\partial \alpha \partial z}} + \frac{{\unicode{230} _{R}^{2}}}{{b{{c}_{R}}}}\frac{{{{\partial }^{2}}\psi }}{{\partial z\partial t}} + \frac{1}{b}\frac{{B'}}{B}\frac{{\partial \psi }}{{\partial z}}} \right)$

где a = $\sqrt {1 - {{\unicode{230} }^{2}}\unicode{230} _{R}^{2}} $, b = $\sqrt {1 - \unicode{230} _{R}^{2}} $, ${{\unicode{230} }^{2}}$ = (1 – 2ν)/(2 – 2ν), g = 2 + ${{{\unicode{230} }}_{R}}$B_ω${{B}_{{\omega }}} = 2{{\left( {\frac{{{{{\unicode{230} }}_{R}}}}{{1 - {\unicode{230} }_{R}^{2}}} + \frac{{{\unicode{230} }{{{\unicode{230} }}_{R}}}}{{1 - {{{\unicode{230} }}^{2}}{\unicode{230} }_{R}^{2}}} - \frac{{4{{{\unicode{230} }}_{R}}}}{{2 - {\unicode{230} }_{R}^{2}}}} \right)}^{{ - 1}}}$, ${{\unicode{230} }_{R}}$ = c_R/c₂, c_R – скорость поверхностных волн Рэлея.

Граничные условия на лицевой поверхности ${\varsigma } = - 1$ при ξ > 0 записываются в форме

$\frac{{{{\partial }^{2}}\Psi }}{{\partial {{\alpha }^{2}}}} - \frac{1}{{c_{R}^{2}}}\frac{{{{\partial }^{2}}\Psi }}{{\partial {{t}^{2}}}} + \frac{{{{k}_{c}}}}{{\unicode{230} _{R}^{2}}}\frac{{B{\kern 1pt} '}}{B}\frac{{\partial \Psi }}{{\partial \alpha }} = \frac{{{{B}_{\omega }}}}{{g{{\unicode{230} }_{R}}}}\frac{{\partial S}}{{\partial \alpha }}$

(4.3)

$\begin{gathered} \left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right)\frac{{{{\partial }^{2}}\varphi }}{{\partial {{\alpha }^{2}}}} - \frac{{\unicode{230} _{R}^{2}}}{{2c_{R}^{2}}}\frac{{{{\partial }^{2}}\varphi }}{{\partial {{t}^{2}}}} + \frac{{B{\kern 1pt} '}}{B}\frac{{\partial \varphi }}{{\partial \alpha }} + \left( {b + \frac{{\unicode{230} _{R}^{2}}}{{2b}}} \right)\frac{{{{\partial }^{2}}\psi }}{{\partial {{\alpha }^{2}}}} - \frac{{\unicode{230} _{R}^{2}}}{{2bc_{R}^{2}}}\frac{{{{\partial }^{2}}\psi }}{{\partial {{t}^{2}}}} + \left( {b + \frac{1}{{2b}}} \right)\frac{{B{\kern 1pt} '}}{B}\frac{{\partial \psi }}{{\partial \alpha }} = 0 \\ {{k}_{c}} = \left( {\frac{1}{{{{a}^{2}}}} + \frac{1}{{{{b}^{2}}}} + 1 - \frac{4}{g}} \right){\text{/}}\left( {\frac{{{{\unicode{230} }^{2}}}}{{{{a}^{2}}}} + \frac{1}{{{{b}^{2}}}} - \frac{2}{g}} \right) \\ \end{gathered} $

$\Psi = \frac{h}{b}\frac{{\partial \psi }}{{\partial z}},\quad S = I\left[ {\sqrt {\frac{{B(0)}}{B}} + \sum\limits_{n = 2}^\infty {(n{{F}_{n}} - F_{{n - 1}}^{'}){{{({{\tau }_{0}} - {{\xi }_{0}})}}^{{n - 1}}}} } \right]H({{\tau }_{0}} - {{\xi }_{0}})$

Аналогично записываются уравнения и для области ${\xi } < 0$. Однако, выражение для напряжения σ₁₃ в (4.2) не всегда является удобным. В частности, его сложно использовать при использовании преобразования Фурье по продольной координате. Поэтому найдена альтернативная форма:

(4.4)

$\begin{gathered} \frac{{\partial {{\sigma }_{{13}}}}}{{\partial \alpha }} = \frac{E}{{(1 + \nu )h}}\left( {\frac{{2 - {{\unicode{230} }^{2}}\unicode{230} _{R}^{2}}}{{2a}}\frac{{{{\partial }^{2}}\Phi }}{{\partial {{\alpha }^{2}}}} - \frac{{{{\unicode{230} }^{2}}\unicode{230} _{R}^{2}}}{{2a}}\frac{1}{{c_{R}^{2}}}\frac{{{{\partial }^{2}}\Phi }}{{\partial {{t}^{2}}}} + \frac{1}{{2a}}\frac{{B{\kern 1pt} '}}{B}\frac{{\partial \Phi }}{{\partial \alpha }} + \frac{{{{\partial }^{2}}\psi }}{{\partial {{\alpha }^{2}}}} - \frac{{\unicode{230} _{R}^{2}}}{2}\frac{1}{{c_{R}^{2}}}\frac{{{{\partial }^{2}}\Psi }}{{\partial {{t}^{2}}}} + \frac{{B{\kern 1pt} '}}{B}\frac{{\partial \Psi }}{{\partial \alpha }}} \right) \\ \Phi = \frac{h}{a}\frac{{\partial \varphi }}{{\partial z}} \\ \end{gathered} $

5. Решение задачи для цилиндрической оболочки. Рассмотрим задачу о распространении нестационарных волн в цилиндрической оболочке при граничных условиях (2.1). Получим решение для эквивалентной задачи. Рассматриваем только волну, инициируемую лицевой поверхностью z = –h. Разрешающие уравнения для потенциальных функций φ, ψ сохраняют вид (4.1), а граничные условия и выражения для напряжений и перемещений запишутся для всех значений ${\xi \;}( - \infty < \xi < \infty )$ в форме

(5.1)

$\begin{gathered} \unicode{230} _{R}^{2}\frac{{{{\partial }^{2}}\Psi }}{{\partial {{\xi }^{2}}}} - \frac{{{{\partial }^{2}}\Psi }}{{\partial {{\tau }^{2}}}} = \frac{{\unicode{230} _{R}^{{}}{{B}_{\omega }}}}{g}\frac{{\partial S}}{{\partial \xi }}\quad {\text{при}}\quad \varsigma = - 1 \\ \left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right)\frac{{{{\partial }^{2}}\varphi }}{{\partial {{\xi }^{2}}}} - \frac{1}{2}\frac{{{{\partial }^{2}}\varphi }}{{\partial {{\tau }^{2}}}} + \left( {b + \frac{{\unicode{230} _{R}^{2}}}{{2b}}} \right)\frac{{{{\partial }^{2}}\psi }}{{\partial {{\xi }^{2}}}} - \frac{1}{{2b}}\frac{{{{\partial }^{2}}\psi }}{{\partial {{\tau }^{2}}}} = 0\quad {\text{при}}\quad \varsigma = - 1 \\ \end{gathered} $

${{{v}}_{1}} = \frac{{\partial \varphi }}{{\partial \xi }} + b\frac{{\partial \psi }}{{\partial \xi }},\quad {{{v}}_{3}} = \frac{{\partial \varphi }}{{\partial \varsigma }} + \frac{1}{b}\frac{{\partial \psi }}{{\partial \varsigma }}$

(5.2)

$\begin{gathered} {{\sigma }_{{33}}} = - \frac{E}{{(1 + \nu )h}}\left( {g\frac{{{{\partial }^{2}}\varphi }}{{\partial {{\xi }^{2}}}} + b\frac{{{{\partial }^{2}}\psi }}{{\partial {{\xi }^{2}}}}} \right) \\ \frac{{\partial {{\sigma }_{{13}}}}}{{\partial \xi }} = \frac{E}{{(1 + \nu )h}}\left( {\frac{{2 - {{\unicode{230} }^{2}}\unicode{230} _{R}^{2}}}{{2a}}\frac{{{{\partial }^{2}}\Phi }}{{\partial {{\xi }^{2}}}} - \frac{{{{\unicode{230} }^{2}}}}{{2a}}\frac{{{{\partial }^{2}}\Phi }}{{\partial {{\tau }^{2}}}} + \frac{{{{\partial }^{2}}\Psi }}{{\partial {{\xi }^{2}}}} - \frac{1}{2}\frac{{{{\partial }^{2}}\Psi }}{{\partial {{\tau }^{2}}}}} \right) \\ \end{gathered} $

$\Phi = \frac{1}{a}\frac{{\partial \varphi }}{{\partial \varsigma }},\quad \Psi = \frac{1}{b}\frac{{\partial \psi }}{{\partial \varsigma }}$

При этом функция S записывается в виде

(5.3)

$S = IH(\tau - \xi )\quad {\text{при}}\quad \xi > 0\quad {\text{и}}\quad S = IH(\tau + \xi )\quad {\text{при}}\quad \xi < 0$

Для решения рассматриваемой задачи применим преобразование Лапласа по времени τ и преобразование Фурье по продольной координате ξ. Тогда граничные условия (5.1) и выражение для изображения касательного напряжения σ₁₃ примут вид:

(5.4)

$\begin{gathered} (\unicode{230} _{R}^{2}{{\chi }^{2}} + {{s}^{2}}){{\Psi }^{{LF}}} = - \sqrt {\frac{2}{\pi }} \frac{{\unicode{230} _{R}^{{}}{{B}_{\omega }}}}{g}\frac{{{{\chi }^{2}}}}{{s({{s}^{2}} + {{\chi }^{2}})}}\quad {\text{при}}\quad \varsigma = - 1 \\ \left[ {\left( {g + \frac{{\unicode{230} _{R}^{2}}}{2}} \right){{\chi }^{2}} + \frac{1}{2}{{s}^{2}}} \right]{{\varphi }^{{LF}}} + \left[ {\left( {b + \frac{{\unicode{230} _{R}^{2}}}{{2b}}} \right){{\chi }^{2}} + \frac{1}{{2b}}{{s}^{2}}} \right]{{\psi }^{{LF}}}\quad {\text{при}}\quad \varsigma = - 1 \\ \end{gathered} $

(5.5)

$\sigma _{{13}}^{{LF}} = i\frac{E}{{(1 + \nu )h}}\frac{1}{\chi }\left[ {\left( {\frac{{2 - \unicode{230} _{{}}^{2}\unicode{230} _{R}^{2}}}{{2a}}{{\chi }^{2}} + \frac{{\unicode{230} _{{}}^{2}}}{{2a}}{{s}^{2}}} \right){{\Phi }^{{LF}}} + \left( {{{\chi }^{2}} + \frac{1}{2}{{s}^{2}}} \right){{\Psi }^{{LF}}}} \right]$

где верхние индексы L и F обозначают интегральные преобразования Лапласа и Фурье, соответственно.

Решая систему дифференциальных уравнений по ${\varsigma }$ с граничными условиями (5.4), выпишем решение для изображения напряжения σ₁₃:

(5.6)

$\begin{gathered} \sigma _{{13}}^{{LF}} = - i\sqrt {\frac{2}{\pi }} I\frac{{\unicode{230} _{R}^{{}}{{B}_{\omega }}}}{g}\left[ {\left( {g\frac{{{{\chi }^{3}}}}{{s(\unicode{230} _{R}^{2}{{\chi }^{2}} + {{s}^{2}})({{s}^{2}} + {{\chi }^{2}})}} + \left( {\frac{{\unicode{230} _{{}}^{2}g}}{{2{{a}^{2}}}} + \frac{g}{{2{{b}^{2}}}} - \frac{1}{2}} \right)\frac{\chi }{{s({{s}^{2}} + {{\chi }^{2}})}}} \right)} \right.{{e}^{{ \mp a\chi (1 + \varsigma )}}}\,\,-- \\ \left. { - \,\,\left( {g\frac{{{{\chi }^{3}}}}{{S(\unicode{230} _{R}^{2}{{\chi }^{2}} + {{s}^{2}})({{s}^{2}} + {{\chi }^{2}})}} + \frac{1}{2}\frac{\chi }{{s({{s}^{2}} + {{\chi }^{2}})}}} \right){{e}^{{ \mp b\chi (1 + \varsigma )}}}} \right] \\ \end{gathered} $

где знаки $ \mp $ относятся к областям ${\xi } > 0~$ и ${\xi } < 0$, соответственно.

Обратим полученное изображение (5.6). Найдем сначала оригинал для преобразования Лапласа. Основываясь на следующем типовом преобразовании “изображение по Лапласу $ \Rightarrow $ оригинал”:

(5.7)

$\frac{\chi }{{s(\unicode{230} _{R}^{2}{{\chi }^{2}} + {{s}^{2}})}} \Rightarrow \frac{1}{{\unicode{230} _{R}^{2}\chi }}(1 - \cos \unicode{230} _{R}^{{}}\tau \chi )$

получаем формулу для одинарного преобразования искомого решения по Фурье:

(5.8)

$\begin{gathered} \sigma _{{13}}^{F} = - i\sqrt {\frac{2}{\pi }} I\frac{{\unicode{230} _{R}^{{}}{{B}_{\omega }}}}{g}\left[ {\left( {\frac{g}{{{{b}^{2}}\unicode{230} _{R}^{2}}}\frac{1}{\chi }(1 - \cos \unicode{230} _{R}^{{}}\tau \chi ) + \left( {\frac{{\unicode{230} _{{}}^{2}g}}{{2{{a}^{2}}}} - \frac{g}{{2{{b}^{2}}}} - \frac{1}{2}} \right)\frac{1}{\chi }(1 - \cos \tau \chi )} \right){{e}^{{ \mp a\chi (1 + \varsigma )}}}} \right.\,\,-- \\ \left. { - \,\,\left( {\frac{g}{{{{b}^{2}}\unicode{230} _{R}^{2}}}\frac{1}{\chi }(1 - \cos \unicode{230} _{R}^{{}}\tau \chi ) + \left( { - \frac{g}{{{{b}^{2}}}} + \frac{1}{2}} \right)\frac{1}{\chi }(1 - \cos \tau \chi )} \right){{e}^{{ \mp b\chi (1 + \varsigma )}}}} \right] \\ \end{gathered} $

Найдем теперь оригинал для преобразования Фурье. Основываясь на следующем типовом интеграле

(5.9)

$\int\limits_0^1 {\frac{{1 - \cos \tau \chi }}{\chi }{{e}^{{ - a\chi }}}\sin \xi \chi d\chi | = \arctan \left( {\frac{\xi }{a}} \right) - \frac{1}{2}\arctan \left( {\frac{{2\xi a}}{{{{a}^{2}} - {{\xi }^{2}} + {{\tau }^{2}}}}} \right)} $

получаем искомое выражение для напряжения σ₁₃:

$\begin{gathered} {{\sigma }_{{13}}} = \frac{2}{\pi }I\frac{{{{\unicode{230} }_{R}}{{B}_{\omega }}}}{g}\left[ {\left( {\frac{g}{{{{b}^{2}}\unicode{230} _{R}^{2}}} + \frac{{\unicode{230} _{{}}^{2}g}}{{2{{a}^{2}}}} - \frac{g}{{2{{b}^{2}}}} - \frac{1}{2}} \right){\text{arctg}}\left( {\frac{\xi }{{a(1 + \varsigma )}}} \right)} \right.\,\, + \\ + \,\,\left( { - \frac{g}{{{{b}^{2}}\unicode{230} _{R}^{2}}} + \frac{g}{{{{b}^{2}}}} - \frac{1}{2}} \right){\text{arctg}}\left( {\frac{\xi }{{b(1 + \varsigma )}}} \right)\,\,-- \\ \end{gathered} $

(5.10)

$\begin{gathered} - \,\,\frac{g}{{2{{b}^{2}}\unicode{230} _{R}^{2}}}{\text{arctg}}\left( {\frac{{2a\xi (1 + \varsigma )}}{{{{a}^{2}}{{{(1 + \varsigma )}}^{2}} - {{\xi }^{2}} + \unicode{230} _{R}^{2}{{\tau }^{2}}}}} \right)\,\,-- \\ - \,\,\frac{1}{2}\left( {\frac{{\unicode{230} _{{}}^{2}g}}{{2{{a}^{2}}}} - \frac{g}{{2{{b}^{2}}}} - \frac{1}{2}} \right){\text{arctg}}\left( {\frac{{2a\xi (1 + \varsigma )}}{{{{a}^{2}}{{{(1 + \varsigma )}}^{2}} - {{\xi }^{2}} + {{\tau }^{2}}}}} \right)\,\, + \\ \end{gathered} $

$\begin{gathered} + \,\,\frac{g}{{2{{b}^{2}}\unicode{230} _{R}^{2}}}{\text{arctg}}\left( {\frac{{2b\xi (1 + \varsigma )}}{{{{b}^{2}}{{{(1 + \varsigma )}}^{2}} - {{\xi }^{2}} + \unicode{230} _{R}^{2}{{\tau }^{2}}}}} \right)\,\, + \\ \left. { + \,\,\frac{1}{2}\left( { - \frac{g}{{{{b}^{2}}}} + \frac{1}{2}} \right){\text{arctg}}\left( {\frac{{2b\xi (1 + \varsigma )}}{{{{b}^{2}}{{{(1 + \varsigma )}}^{2}} - {{\xi }^{2}} + {{\tau }^{2}}}}} \right)} \right] \\ \end{gathered} $

Учитывая, что при ${\xi } \gg 1,{\tau } \gg 1$ и в рассматриваемой малой окрестности условного фронта ${\xi } = {{{\unicode{230} }}_{{\text{R}}}}{\tau }$ можно принять следующие оценки функций в (5.10):

(5.11)

$\begin{gathered} {\text{arctg}}\left( {\frac{\xi }{{a(1 + \varsigma )}}} \right) = \frac{\pi }{2},\quad {\text{arctg}}\left( {\frac{\xi }{{a(1 + \varsigma )}}} \right) = \frac{\pi }{2} \\ {\text{arctg}}\left( {\frac{{2a\xi (1 + \varsigma )}}{{{{a}^{2}}{{{(1 + \varsigma )}}^{2}} + {{\xi }^{2}} + {{\tau }^{2}}}}} \right) = 0,\quad {\text{arctg}}\left( {\frac{{2b\xi (1 + \varsigma )}}{{{{b}^{2}}{{{(1 + \varsigma )}}^{2}} - {{\xi }^{2}} + {{\tau }^{2}}}}} \right) = 0 \\ \end{gathered} $

окончательное выражение для напряжения σ₁₃ запишем в виде

(5.12)

$\begin{gathered} {{\sigma }_{{13}}} = I + I\frac{{{{B}_{\omega }}}}{{\pi {{\unicode{230} }_{R}}{{b}^{2}}}}\left[ { - {\text{arctg}}\left( {\frac{{2a\xi (1 + \varsigma )}}{{{{a}^{2}}{{{(1 + \varsigma )}}^{2}} - {{\xi }^{2}} + \unicode{230} _{R}^{2}{{\tau }^{2}}}}} \right)} \right.\,\, + \\ \left. {\, + {\text{arctg}}\left( {\frac{{2b\xi (1 + \varsigma )}}{{{{b}^{2}}{{{(1 + \varsigma )}}^{2}} - {{\xi }^{2}} + \unicode{230} _{R}^{2}{{\tau }^{2}}}}} \right)} \right] \\ \end{gathered} $

Рис. 2.

Список литературы

Кириллова И.В., Коссович Л.Ю. Уточненные уравнения эллиптического погранслоя в оболочках вращения при ударных поверхностных воздействиях нормального типа // Вестник С.-Петерб. ун-та. Математика. Механика. Астрономия. 2017. Вып. 1. С. 113–120.
Nigul U. Regions of effective application of the methods of three-dimensional and two-dimensional analysis of transient stress waves in shells and plates // Int. J. Solid and Structures. V. 5. № 6. 1969. P. 607–627.
Коссович Л.Ю., Кириллова И.В. Теория эллиптического погранслоя в оболочках вращения при ударных воздействиях нормального типа // XII Всероссийский съезд по фундаментальным проблемам теоретической и прикладной механики: сборник трудов в 4 томах. Т. 3: Механика деформируемого твердого тела. Уфа: РИЦ БашГУ. 2019. Т. 3. С. 484–486.
Лурье А.И. Пространственные задачи теории упругости. М.: Гостехиздат, 1955. 491 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал