Известия РАН. Механика твердого тела, 2020, № 4, стр. 43-49
ОПРЕДЕЛЕНИЕ НАГРУЗКИ, ВЫЗЫВАЮЩЕЙ ПОЯВЛЕНИЕ ПЛАСТИЧЕСКОЙ ДЕФОРМАЦИИ В РАСТЯГИВАЕМОЙ ПЛАСТИНЕ С ТРЕЩИНОЙ
В. В. Васильев a, *, С. А. Лурье a, b, В. А. Салов c
a Институт проблем механики РАН
Москва, Россия
b Институт прикладной механики РАН
Москва, Россия
c АО Центральный научно-исследовательский институт специального машиностроения
Москва, Россия
* E-mail: vvvas@dol.ru
Поступила в редакцию 16.01.2020
После доработки 04.04.2020
Принята к публикации 25.04.2020
Аннотация
Рассматривается задача о растяжении пластины с центральной или боковой трещиной. Полученное ранее решение, определяющее напряжения в пластине в окрестности центральной трещины, используется для предсказания нагрузки, при которой в пластине с боковой трещиной появляется пластическая деформация. В качестве критерия пластичности используется условие Мизеса. Результаты расчета сопоставляются с экспериментом, проведенном на пластинах из алюминиевого сплава, латуни и стали.
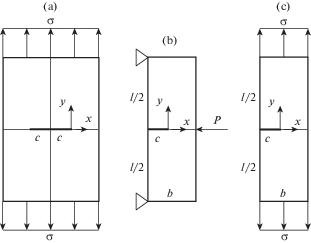
1. Введение. Напряженное состояние в растягиваемой упругой пластине в окрестности центральной трещины. В работе [1] получено решение плоской задачи теории упругости для растягиваемой пластины с центральной сквозной трещиной. Решение основано на обобщенном варианте теории упругости, уравнения которой основаны на рассмотрении малого, но конечного элемента среды [2]. В отличие от классического решения напряжения не являются сингулярными на концах трещины. В зависимости от относительной координаты $\bar {x} = x{\text{/}}c$, отсчитываемой от конца трещины (рис. 1a) и структурного параметра λ напряжения, действующие на оси x (y = 0), определяются следующими соотношениями:
(1.1)
$\begin{gathered} {{{{\bar {\sigma }}}}_{x}} = \frac{{{{{\sigma }}_{x}}}}{{\sigma }} = \left( {1 + \bar {x}} \right)\left[ {{{{\bar {x}}}^{2}}{{{\left( {2 + \bar {x}} \right)}}^{2}} + \frac{6}{{{{{\lambda }}^{2}}}}} \right]\frac{1}{{\sqrt {{{{\bar {x}}}^{5}}{{{\left( {2 + \bar {x}} \right)}}^{5}}} }} - \sqrt {\frac{{\bar {x}}}{{2 + \bar {x}}}} - \\ - \frac{1}{{2\sqrt {2\bar {x}} }}\left[ {\frac{3}{{{{{\lambda }}^{2}}{{{\bar {x}}}^{2}}}} + \frac{3}{{4{\lambda }\bar {x}}}\left( {\frac{1}{{\lambda }} - 4} \right) - \frac{1}{4}\left( {14 - \frac{3}{{\lambda }} - \frac{{15}}{{8{{{\lambda }}^{2}}}}} \right)} \right]{{e}^{{ - {\lambda }\bar {x}}}} \\ \end{gathered} $(1.2)
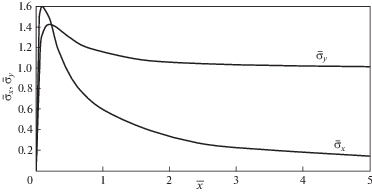
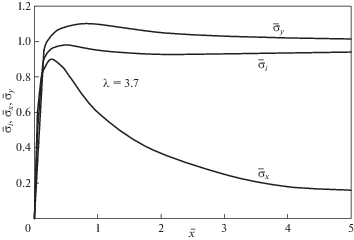
$\begin{gathered} {{{{\bar {\sigma }}}}_{y}} = \frac{{{{{\sigma }}_{y}}}}{{\sigma }} = \left( {1 + \bar {x}} \right)\left[ {{{{\bar {x}}}^{2}}{{{\left( {2 + \bar {x}} \right)}}^{2}} - \frac{6}{{{{{\lambda }}^{2}}}}} \right]\frac{1}{{\sqrt {{{{\bar {x}}}^{5}}{{{\left( {1 + \bar {x}} \right)}}^{5}}} }} + \\ + \;\frac{1}{{2\sqrt {2\bar {x}} }}\left[ {\frac{3}{{{{{\lambda }}^{2}}{{{\bar {x}}}^{2}}}} - \frac{3}{{4{\lambda }\bar {x}}}\left( {\frac{1}{{\lambda }} - 4} \right) - \frac{1}{4}\left( {2 + \frac{3}{{\lambda }} + \frac{{15}}{{8{{{\lambda }}^{2}}}}} \right)} \right]{{e}^{{ - {\lambda }\bar {x}}}} \\ \end{gathered} $Здесь λ = c/s, где c – размер трещины (рис. 1, a), а s – параметр, зависящий от материала пластины, определяемый экспериментально. Для случая ${\lambda } = 10$ зависимости ${{{\bar {\sigma }}}_{x}}(\bar {x})$ и ${{{\bar {\sigma }}}_{y}}(\bar {x})$, построенные с помощью равенств (1.1) и (1.2), показаны на рис. 2. Как следует из графиков, напряжения конечны и достигают максимальных значений в окрестности конца трещины (рис. 1a).
В работе [1] равенство (1.1) использовано для оценки прочности пластины из хрупкого материала
с центральной трещиной на основе критерия максимальных нормальных напряжений. Введен
коэффициент концентрации напряжений 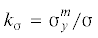 , представляющий собой отношение максимального напряжения отрыва к напряжению, прикладываемому
к пластине, предельное значение которого имеет вид ${\sigma } = {{{\sigma }}_{u}}{\text{/}}{{k}_{{\sigma }}}$, где ${{{\sigma }}_{u}}$ – предел прочности материала пластины.
, представляющий собой отношение максимального напряжения отрыва к напряжению, прикладываемому
к пластине, предельное значение которого имеет вид ${\sigma } = {{{\sigma }}_{u}}{\text{/}}{{k}_{{\sigma }}}$, где ${{{\sigma }}_{u}}$ – предел прочности материала пластины.
Расчетно-экспериментальный метод анализа прочности пластины заключается в следующем.
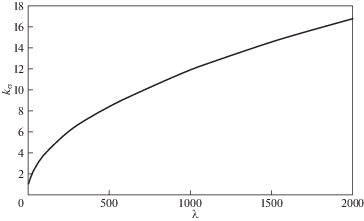
По формуле (1.2) строится зависимость коэффициента kσ от параметра λ, показанная на рис. 3. Проводится эксперимент по определению предельной нагрузки для пластины с трещиной
определенного размера c0, для которой находится разрушающее напряжение σ. По формуле 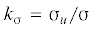 находится коэффициент концентрации напряжений в окрестности конца трещины, по графику
на рис. 3 определяется параметр λ и далее для экспериментальной пластины находится параметр
находится коэффициент концентрации напряжений в окрестности конца трещины, по графику
на рис. 3 определяется параметр λ и далее для экспериментальной пластины находится параметр
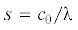 . Для пластины с центральной трещиной этот параметр считается константой, не зависящей
от длины трещины. Таким образом, для пластины с произвольным размером трещины c можно определить параметр ${\lambda } = с{\text{/}}s$, найти с помощью рис. 3 коэффициент kσ и установить разрушающую нагрузку ${\sigma } = {{{\sigma }}_{u}}{\text{/}}{{k}_{{\sigma }}}$. Экспериментальное исследование, проведенное на пластинах из полиметилметакрилата
с различными размерами трещины, подтвердило высокую точность метода [1].
. Для пластины с центральной трещиной этот параметр считается константой, не зависящей
от длины трещины. Таким образом, для пластины с произвольным размером трещины c можно определить параметр ${\lambda } = с{\text{/}}s$, найти с помощью рис. 3 коэффициент kσ и установить разрушающую нагрузку ${\sigma } = {{{\sigma }}_{u}}{\text{/}}{{k}_{{\sigma }}}$. Экспериментальное исследование, проведенное на пластинах из полиметилметакрилата
с различными размерами трещины, подтвердило высокую точность метода [1].
2. Хрупкое разрушение пластин с боковой трещиной. Рассмотрим изгибаемую пластину с боковой трещиной (рис. 1,b). Для того, чтобы распространить предлагаемый метод оценки прочности на такую пластину, введем следующую гипотезу. В связи с тем, что максимальные значения напряжений реализуются вблизи конца трещины (рис. 2), будем считать, что эти значения определяются равенствами (1.1) и (1.2) для любой трещины при условии, что σ является напряжением, действующим в сечении, где расположена трещина, в пластине без трещины. Тогда для пластины, показанной на рис. 1,b, имеем
где h – толщина пластины. Вводя коэффициент концентрации напряжений ${{k}_{{\sigma }}}$ = σu/σ, получим следующее выражение для разрушающей нагрузки:Для проверки метода были испытаны три пластины из полиметилметакрилата с пределом
прочности ${{{\sigma }}_{u}} = 83.3$ МПа. Длина пластин l = 180 мм. Первая пластина с параметрами b = 60.2 мм, $h = 2.96$ мм и $с = 17$ мм разрушилась при силе $Р = 230$ Н. Используя равенство (2.1), получим ${{k}_{{\sigma }}} = 14.5$. Согласно рис. 3 имеем ${\lambda } = 1470$ и 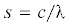 = = 0.0116 мм. Для второй пластины с параметрами $b = 60.4$ мм, $h = 2.97$ мм и c = 10 мм получим ${\lambda } = 860$ и при $s = 0.0116$ найдем ${\lambda } = 860$, ${{k}_{\sigma }} = 11.1$ и ${{P}_{u}} = 301$ Н, что на 3.8% отличается от экспериментального результата (313 Н). Для третьей пластины
с параметрами $b = 60.4$ мм, h = 2.96 мм и c = 22 мм при $s = 0.0116$ мм найдем ${\lambda } = 1900$, ${{k}_{{\sigma }}}$ = = 16.4 и ${{P}_{u}} = 203$ Н, что на 13.4% превышает экспериментальное значение (179 Н). Учитывая, что для третьей
пластины длина трещины превышает половину ее ширины, можно заключить, что метод позволяет
предсказать предельную нагрузку с удовлетворительной точностью.
= = 0.0116 мм. Для второй пластины с параметрами $b = 60.4$ мм, $h = 2.97$ мм и c = 10 мм получим ${\lambda } = 860$ и при $s = 0.0116$ найдем ${\lambda } = 860$, ${{k}_{\sigma }} = 11.1$ и ${{P}_{u}} = 301$ Н, что на 3.8% отличается от экспериментального результата (313 Н). Для третьей пластины
с параметрами $b = 60.4$ мм, h = 2.96 мм и c = 22 мм при $s = 0.0116$ мм найдем ${\lambda } = 1900$, ${{k}_{{\sigma }}}$ = = 16.4 и ${{P}_{u}} = 203$ Н, что на 13.4% превышает экспериментальное значение (179 Н). Учитывая, что для третьей
пластины длина трещины превышает половину ее ширины, можно заключить, что метод позволяет
предсказать предельную нагрузку с удовлетворительной точностью.
3. Упруго-пластическая деформация пластины с боковой трещиной. Соотношения (1.1) и (1.2) справедливы для линейно упругих пластин. Большинство металлов, для которых анализ прочности тонкостенных конструкций с трещинами представляет большой практический интерес, демонстрируют упруго-пластическое поведение. Для таких пластин обсуждаемый метод позволяет определить нагрузку, при превышении которой в металле появляется пластическая деформация. Как следует из рис. 2, в окрестности конца трещины максимальные значения нормальных напряжений являются соизмеримыми. Касательные напряжения при y = 0 отсутствуют по условию симметрии. Воспользуемся критерием пластичности Мизеса и запишем выражение для интенсивности напряжений
(3.1)
${{{\sigma }}_{i}} = \sqrt {{\sigma }_{x}^{2} + {\sigma }_{y}^{2} - {{{\sigma }}_{x}}{{{\sigma }}_{y}}} $Введем коэффициент концентрации напряжений 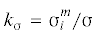 , где ${\sigma }_{i}^{m}$ – максимальное значение интенсивности напряжений, найденное с помощью равенств (1.1),
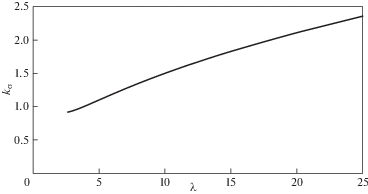
(1.2) и (3.1), а σ, как и ранее, напряжение, приложенное к пластине. Зависимость kσ от параметра λ представлена на рис. 4.
, где ${\sigma }_{i}^{m}$ – максимальное значение интенсивности напряжений, найденное с помощью равенств (1.1),
(1.2) и (3.1), а σ, как и ранее, напряжение, приложенное к пластине. Зависимость kσ от параметра λ представлена на рис. 4.
Расчетный предел пропорциональности для пластины с трещиной определяется, как и ранее, следующим образом: ${\sigma } = {{{\sigma }}_{u}}{\text{/}}{{k}_{{\sigma }}}$, где σu – предел пропорциональности для пластины без трещины. Экспериментальный предел пропорциональности определяется визуально как напряжение, при котором начинается отклонение экспериментальной диаграммы деформирования пластины от прямолинейной.
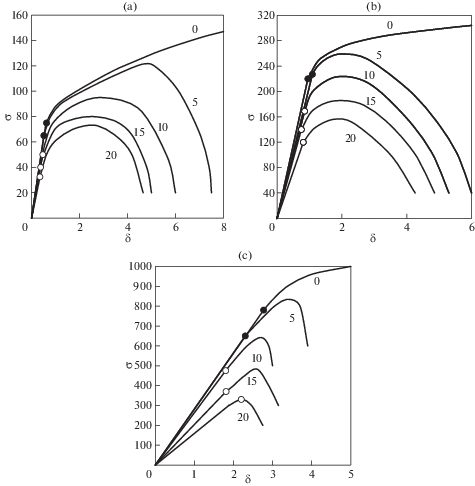
Экспериментальное исследование осуществлялось на пластинах из алюминиевого сплава, латуни и стали, которые нагружались по схеме, показанной на рис. 1с. Размеры пластин – b = 40 мм, l = 175 мм. Характеристики материалов представлены в таблице. Результаты представлены на рис. 5, где напряжение $\sigma $ измеряется в МПа, а перемещение ${\delta }$ в мм.
Результаты эксперимента и расчета для пластин из алюминиевого сплава представлены на рис. 5a. Номера кривых показывают длину трещины в мм.
Кривая “0” соответствует пластине без трещины. Параметр ${\delta }$ определяет взаимное смешение захватов испытательной машины и качественно характеризует
деформацию пластины. Темной точкой на кривой “0” показан предел пропорциональности
${{{\sigma }}_{u}} = 75$ МПа. Для пластины с трещиной длиной 5 мм (кривая “5”) экспериментально установленный
предел пропорциональности (темная точка на кривой) составляет ${\sigma } = 65$ МПа. Таким образом, коэффициент концентрации напряжений 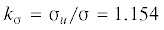 и согласно рис. 4 имеем ${\lambda } = 5.5$. Тогда
и согласно рис. 4 имеем ${\lambda } = 5.5$. Тогда 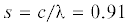 мм. Заметим, что для пластичного материала этот параметр примерно на порядок больше
значения, полученного выше для хрупкого материала (0.0116 мм). Как уже отмечалось,
будем считать, что полученный параметр s не зависит от длины трещины. Для пластины с трещиной длиной c = 10 мм (кривая “10” на рис. 5a) при $s = 0.91$ мм имеем ${\lambda } = 11$, kσ = 1.56 и предел пропорциональности ${\sigma } = 48.1$ МПа. При $с = 15$ мм (кривая “15”) получим ${\lambda } = 16.5$, kσ = 1.93 и ${\sigma } = 38.9$ МПа. И наконец, при $с = 20$ мм (кривая “20”) найдем ${\lambda } = 22$, kσ = 2.22 и ${\sigma } = 33.8$ МПа. Результаты расчета для пластин с трещинами длиной 10, 15 и 20 мм показаны светлыми
точками на соответствующих кривых.
мм. Заметим, что для пластичного материала этот параметр примерно на порядок больше
значения, полученного выше для хрупкого материала (0.0116 мм). Как уже отмечалось,
будем считать, что полученный параметр s не зависит от длины трещины. Для пластины с трещиной длиной c = 10 мм (кривая “10” на рис. 5a) при $s = 0.91$ мм имеем ${\lambda } = 11$, kσ = 1.56 и предел пропорциональности ${\sigma } = 48.1$ МПа. При $с = 15$ мм (кривая “15”) получим ${\lambda } = 16.5$, kσ = 1.93 и ${\sigma } = 38.9$ МПа. И наконец, при $с = 20$ мм (кривая “20”) найдем ${\lambda } = 22$, kσ = 2.22 и ${\sigma } = 33.8$ МПа. Результаты расчета для пластин с трещинами длиной 10, 15 и 20 мм показаны светлыми
точками на соответствующих кривых.
Экспериментальные и расчетные результаты для пластин из латуни представлены на рис. 5b. Кривая “0”, соответствующая пластине без трещины, позволяет заключить, что ${{{\sigma }}_{u}} = 220$ МПа (темная точка на этой кривой). Кривая “5”, соответствующая c = 5 мм, демонстрирует интересный эффект. Дело в том, что экспериментально определенный
предел пропорциональности ${\sigma } = 227$ МПа (темная точка на этой кривой) оказывается больше чем σu и получаемый коэффициент концентрации напряжений оказывается меньше единицы. Это
означает, что трещина повышает предел пропорциональности пластины. Это вывод подтверждается
расчетом. Как следует из рис. 4, ${{k}_{{\sigma }}} < 1$ при ${\lambda } < 4$. Предельным является значение ${{{\lambda }}_{0}} = 2.621$, при котором ${{k}_{{\sigma }}} = 0.919$. При ${\lambda } < {{{\lambda }}_{0}}$ максимальное значение σi не существует. Для рассматриваемой пластины при c = 5 мм имеем 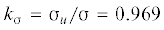 и согласно рис. 4 получаем ${\lambda } = 3.7$. Распределения напряжений в окрестности конца трещины для случая ${\lambda } = 3.7$ показаны на рис. 6.
и согласно рис. 4 получаем ${\lambda } = 3.7$. Распределения напряжений в окрестности конца трещины для случая ${\lambda } = 3.7$ показаны на рис. 6.
Как следует из графиков, максимальное значение напряжения ${{{\bar {\sigma }}}_{y}}$ превышает единицу, то есть имеет место концентрация этого напряжения в окрестности конца трещины. Однако максимальное значение интенсивности напряжения σi не достигает единицы и коэффициент концентрации этого напряжения оказывается меньшим единицы, что приводит к увеличению нагрузки, вызывающей появление пластической деформации в пластине с малой длиной трещины. Этот эффект, подтверждающийся как теоретически так и экспериментально, связан со структурой формулы (3.1) для интенсивности напряжений.
Продолжая анализ для пластины с трещиной с длиной c = 5 мм, найдем параметр 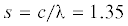 мм. Как и ранее, будем считать, что этот параметр является константой, не зависящей
от длины трещины. Для пластины с длиной трещины c = 10 мм имеем ${\lambda } = c{\text{/}}s$ = 7.4. Тогда из рис. 4 следует ${{k}_{{\sigma }}} = 1.3$ и ${\sigma } = {{{\sigma }}_{u}}{\text{/}}{{k}_{{\sigma }}} = 169$ МПа. Для пластины с длиной трещины c = 15 мм получим ${\lambda } = 11.1$, ${{k}_{{\sigma }}} = 1.57$ и ${\sigma } = 140$ МПа. Для пластины с длиной трещины c = 20 мм найдем ${\lambda } = 14.8$, ${\sigma } = 120$ МПа. Для пластин с трещинами длиной 10, 15 и 20 мм результаты расчета показаны светлыми
точками на соответствующих кривых на рис. 5b.
мм. Как и ранее, будем считать, что этот параметр является константой, не зависящей
от длины трещины. Для пластины с длиной трещины c = 10 мм имеем ${\lambda } = c{\text{/}}s$ = 7.4. Тогда из рис. 4 следует ${{k}_{{\sigma }}} = 1.3$ и ${\sigma } = {{{\sigma }}_{u}}{\text{/}}{{k}_{{\sigma }}} = 169$ МПа. Для пластины с длиной трещины c = 15 мм получим ${\lambda } = 11.1$, ${{k}_{{\sigma }}} = 1.57$ и ${\sigma } = 140$ МПа. Для пластины с длиной трещины c = 20 мм найдем ${\lambda } = 14.8$, ${\sigma } = 120$ МПа. Для пластин с трещинами длиной 10, 15 и 20 мм результаты расчета показаны светлыми
точками на соответствующих кривых на рис. 5b.
Результаты, полученные для пластин из стали, показаны на рис. 5,с. Кривая “0”, соответствующая пластине без трещины, позволяет заключить, что ${{{\sigma }}_{u}} = 780$ МПа (темная точка на кривой). Кривая с длиной трещины c = 5 мм дает ${\sigma } = 650$ МПа (темная точка на кривой). Таким образом, ${{k}_{{\sigma }}} = 1.2$, ${\lambda } = 6.2$ и $s = 0.8$ мм. При этом значении параметра $s$ и c = 10 мм получим ${\lambda } = 12.5$, ${{k}_{{\sigma }}} = 1.65$ и ${\sigma } = 470$ МПа. При c = 15 мм имеем ${\lambda } = 18.75$, ${{k}_{{\sigma }}} = 2.06$ и ${\sigma } = 379$ МПа. При c = 20 мм найдем ${\lambda } = 25$, ${{k}_{{\sigma }}} = 2.36$ и ${\sigma } = 330$ МПа. Для пластин с трещинами длиной 10, 15 и 20 мм результаты расчета показаны светлыми точками на соответствующих кривых на рис. 5с.
Таблица 1
| Характеристика | Алюминиевый сплав АД1 | Латунь Л68 | Сталь 1Х18Н10Т |
|---|---|---|---|
| Толщина, мм | 1.12 | 0.4 | 0.59 |
| Модуль упругости, ГПа | 71 | 110 | 220 |
| Предел прочности, МПа | 190 | 340 | 1100 |
| Предел пропорциональности, МПа | 75 | 220 | 780 |
Из рис. 5 можно заключить, что расчет предлагаемым методом удовлетворительно согласуется с результатами эксперимента.
3. Заключение. На основе обобщенного варианта теории упругости, позволяющего получать регулярные решения задач, являющихся в классической теории упругости сингулярными, предлагается метод определения предельной нагрузки, вызывающий появление пластической деформации в металлических пластинах с трещинами. Метод предполагает экспериментальное определение параметра среды, входящего в уравнения обобщенной теории, вычисление коэффициента концентрации напряжения в окрестности конца трещины и соответствующее снижение предела пропорциональности для пластины без трещины. Метод экспериментально подтвержден для пластин из алюминиевого сплава, латуни и стали.
Статья подготовлена по гранту РФФИ 19-01-00355.
Список литературы
Васильев В.В., Лурье С.А. Новый метод исследования прочности хрупких тел с трещинами // Деформация и разрушение материалов. 2019. № 9. С. 12–19.
Васильев В.В., Лурье С.А. Обобщенная теория упругости // Изв. РАН. МТТ. 2015. № 4. С. 16–27.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела