1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 4, 2020

Известия РАН. Механика твердого тела, 2020, № 4, стр. 96-114

АНАЛИЗ ТРЕЩИНОСТОЙКОСТИ СОЕДИНЕНИЙ МАТЕРИАЛОВ

М. Н. Перельмутер *

Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: perelm@ipmnet.ru

Поступила в редакцию 12.03.2020
После доработки 02.04.2020
Принята к публикации 15.04.2020

Полный текст (PDF)

Аннотация

Рассматривается модель разрушения соединения различных материалов при наличии участка ослабленных связей между материалами. Такой участок моделируется трещиной, между берегами которой действуют силы сцепления, зависящие от раскрытия трещины. Размер зоны взаимодействия берегов трещины (концевая область) может меняться в процессе роста трещины и не является малым по сравнению с размером трещины. Для анализа квазистатического роста трещины с концевой областью, заполненной связями, используется нелокальный критерий разрушения, учитывающий работу по деформированию связей в концевой области трещины. Состоянию предельного равновесия вершины трещины соответствует энергетическое условие – равенство скорости высвобождения энергии деформации в вершине трещины и скорости потребления энергии деформации связями в концевой области трещины (первое условие разрушения). Разрыв связей на краю концевой области определяется условием их предельной вытяжки (второе условие разрушения). Исходя из этих двух условий рассмотрены режимы докритического и квазистатического роста трещины и определяются два основных параметра разрушения – критическая внешняя нагрузка и размер концевой области трещины в состоянии предельного равновесия.

Ключевые слова: концевая область трещины, соединение материалов, нелокальный критерий разрушения

1. Введение. Выбор модели разрушения при анализе развития трещин по границе соединения материалов зависит от физико-механических свойств материалов и структуры адгезионного слоя. Если энергия, необходимая для образования единицы новой поверхности трещины, не зависит от характерного размера трещины, процесс разрушения локализован в малой области вблизи вершины трещины, и взаимодействием вновь образованных поверхностей трещины можно пренебречь, применяется критерий разрушения Гриффитса в энергетическом или силовом варианте. При малом размере зоны процесса разрушения нет также необходимости в ее явном моделировании при решении конкретных задач механики разрушения – в этом случае состояние предельного равновесия полностью определяется критическим коэффициентом интенсивности напряжений (или соответствующим энергетическим параметром). Границы соединения материалов не являются идеальными и, как правило, содержат зоны ослабленных или нарушенных связей, причем на части такой зоны связи могут отсутствовать. В таких соединениях в процесс разрушения вовлекается достаточно большая область вблизи вершины трещины; процесс разрушения определяется различными (как правило, нелинейными) механизмами, реализующимися на разных расстояниях от края трещины. Размер зоны процесса разрушения меняется при развитии трещины и не является малым в сравнении с характерным размером трещины. При этом трещиностойкость соединений материалов зависит от характерного размера трещины и возникает необходимость детального моделирования зоны процесса разрушения.

Одна из возможностей механико-математического моделирования зоны процесса разрушения на границе соединения материалов состоит в рассмотрении ее как части трещины и в явном приложении к поверхностям трещины в этой зоне сил сцепления, сдерживающих раскрытие трещины (модель концевой области трещины).

Модели трещины с силами сцепления в концевой области можно условно (так как физическая природа сил сцепления может быть одинакова в обоих случаях) разделить на два типа по форме представления напряжений в вершине трещины в состоянии предельного равновесия:

1) суммарный коэффициент интенсивности напряжений (КИН) от действия внешних нагрузок и сил сцепления в концевой области, определяющий сингулярную асимптотику напряжений в вершине модифицированной трещины, полагается равным нулю, следствием чего является ограниченность и непрерывность напряжений в вершине трещины;

2) суммарный КИН в вершине модифицированной трещины не равен нулю, т.е. предполагается сингулярное поле напряжений в вершине трещины.

Модели первого типа называют когезионными моделями концевой области трещины [1–3]. Эти модели применяются для однородных материалов, если процессы продвижения вершины трещины и формирования сил сцепления взаимосвязаны и определяются одним физическим механизмом. Следствием равенства нулю КИН в когезионной модели является также плавное смыкание берегов трещины в ее вершине. Отметим, что вершина трещины в этом случае совпадает с передним краем концевой области. Варианты когезионной модели получили широкое применение для решения различных задач механики разрушения без наложения ограничений на размер концевой области трещины после развития численных методов решения задач механики, в первую очередь, метода конечных элементов [4, 5]. При этом в качестве критерия разрушения используются два условия: условие критического раскрытия трещины на краю концевой области (или условие критической деформации) и условие достижения предельных напряжений в вершине трещины [5]. Выполнение критериальных условий для концевой области трещины достигается итерационным путем, причем, при численной реализации алгоритмов, условие плавного смыкания берегов трещины специально не накладывается [6].

Модели второго типа – это модели трещины со связями в концевой области – bridged crack models, см. [7]. Эти модели используются, если процессы деформирования и разрушения в концевой области включают в себя несколько физических механизмов, например, в адгезионных соединениях или композиционных материалах, где продвижение вершины трещины и формирование сил сцепления обусловлены различными механизмами. Материалы в этом случае рассматриваются как многофазные и многомасштабные, с учетом вклада каждой фазы и масштаба в трещиностойкость соединения.

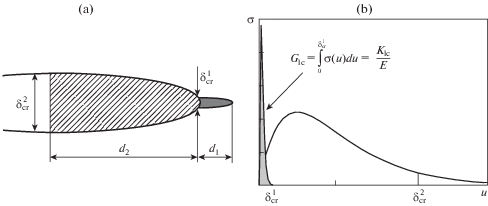
Основой для модели трещины со связями в концевой области является когезионная модель при многомасштабном взаимодействии между берегами трещины. Если, например, когезионная зона состоит из двух частей, соответствующих различным физическим механизмам ограничения раскрытия трещины, а когезионная кривая содержит, соответственно, два участка (см. рис. 1a,b), то условие конечности напряжений в вершине трещины можно представить в этом случае так:

(1.1)
${{K}_{\infty }} - K_{b}^{{(1)}} - K_{b}^{{(2)}} = 0$
где K∞ – КИН от действия внешних нагрузок, $K_{b}^{{(1)}}$ и $K_{b}^{{(2)}}$ – КИН, вызванные взаимодействием между берегами трещины в частях d1 и d2 когезионной зоны.

Во многих материалах часть когезионной зоны, примыкающая к вершине трещины, мала по сравнению с длиной трещины и размером второй части когезионной зоны $({{d}_{1}} \ll {{d}_{2}},{\kern 1pt} \;{{d}_{1}} \ll \ell )$, а величины критического раскрытия трещины на соответствующих частях зоны удовлетворяют условию $\delta _{{cr}}^{1} \ll \delta _{{cr}}^{2}$ (см. рис. 1a,b). В этом случае можно полагать, что первая часть когезионной зоны находится в состоянии предельного равновесия и, следовательно, вклад этой части когезионной зоны в трещиностойкость материала не зависит от длины трещины и является постоянной величиной

(1.2)
$K_{b}^{{(1)}} = {{K}_{{Ic}}} = \sqrt {E{{G}_{{Ic}}}} ,\quad {{G}_{{Ic}}} = \int\limits_0^{{\delta }_{{cr}}^{1}} {\sigma }\left( u \right)du$

С учетом этого предположения можно представить условие конечности напряжений (1.1) для когезионной зоны, состоящей из двух частей, как условие предельного равновесия в модели трещины со связями в концевой области, при допущении сингулярного поля напряжений вблизи вершины трещины (${{K}_{{Ic}}} \equiv K_{b}^{{(1)}}$, ${{K}_{b}} \equiv K_{b}^{{(2)}}$) [7]

(1.3)
${{K}_{\infty }} - {{K}_{b}} = {{K}_{{Ic}}}$

При таком описании концевой области трещины полагается (т.к. ${{d}_{1}} \ll {{d}_{2}}$ и ${\delta }_{{cr}}^{1} \ll {\delta }_{{cr}}^{2}$), что d1 = 0 и ${\delta }_{{cr}}^{1} = 0$ и рассматривается только часть кривой деформирования связей на участке от u = 0 до $u = {{{\delta }}_{{cr}}} \equiv {\delta }_{{cr}}^{2}$, а вклад части когезионной зоны, примыкающей к вершине трещины, принимается постоянным.

Таким образом, когезионная модель трещины является частным случаем модели трещины со связями в концевой области при ${{K}_{{Ic}}} = 0$ (рассмотрение когезионной кривой, соответствующей только одному масштабу взаимодействия между берегами трещины). Моделирование трещины с когезионной зоной, состоящей из нескольких частей, в рамках когезионной модели является достаточно трудоемким, требующим при численном решении дискретизации разного масштаба в когезионной зоне, тогда как модель трещины со связями в концевой области может быть успешно применена для решения таких задач. Преимуществом модели трещины со связями в концевой области при учете сингулярности поля напряжений в ее вершине является также возможность использования аппарата линейной механики разрушения и, соответственно, рассмотрения нелинейных процессов в концевой области трещины при решении задачи в линейной постановке.

Модель трещины со связями в концевой области применяется при оценке трещиностойкости различных видов композиционных материалов [8–12]. Развитие этой модели с учетом термофлуктуационного разрушения связей в концевой области трещины позволяет оценить время формирования дефектов на границе соединения материалов [13]. Задачи, связанные с восстановлением поврежденных конструкций, также приводят к рассмотрению модели трещины со связями в концевой области [14]. Новые направления в применении модели трещины со связями в концевой области возникают при анализе процесса самозалечивания трещин, который может рассматриваться как процесс восстановления связей между поверхностями трещины (формирования концевой области) [15].

Далее в работе для трещин, расположенных на границе соединения различных материалов, используется модель трещины со связями в концевой области. В рамках модели полагается, что

1) процесс разрушения локализован в концевой области трещины, которая является ее частью и может быть сравнима с размером всей трещины (в частности, связи могут полностью заполнять трещину);

2) к берегам трещины в концевой области приложены распределенные силы сцепления, зависящие от раскрытия трещины, в соответствии с законом деформирования связей, который определяется физической природой взаимодействия между берегами трещины и может изменяться при увеличении расстояния до ее вершины;

3) материал вне трещины полагается линейно-упругим, и деформация материала за вершиной трещины происходит совместно со слоем адгезива без нарушения его сплошности.

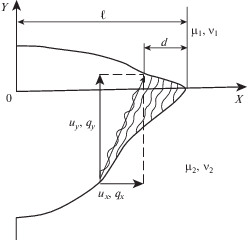
2. Модель концевой области трещины на границе соединения материалов. Рассмотрим трещину, расположенную на границе соединения материалов (см. рис. 2) и выделим часть трещины длины d, примыкающую к ее вершине (концевую область трещины), в которой поверхности трещины взаимодействуют, так что это взаимодействие сдерживает раскрытие трещины (${{{\mu }}_{{1,2}}}$ и ${{{\nu }}_{{1,2}}}$ – модули сдвига и коэффициенты Пуассона материалов подобластей 1 и 2, ${{u}_{{x,y}}}$ и ${{q}_{{x,y}}}$ – компоненты раскрытия трещины и усилий в связях в концевой области трещины). Опишем взаимодействие берегов трещины в рамках механической модели, не выделяя конкретных причин взаимодействия. Ввиду различия упругих свойств соединенных материалов в связях между берегами трещины, возникают, даже при одноосном растяжении, усилия Q(x), имеющие нормальную qy(x) и касательную qx(x), составляющие:

(2.1)
$Q(x) = {{q}_{y}}(x) - i{{q}_{x}}(x),\quad {{i}^{2}} = - 1$
Рис. 1

Рис. 2

К берегам трещины приложены нормальные и касательные напряжения численно равные qy(x) и qx(x), соответственно.

Компоненты раскрытия трещины, расположенной на границе между двумя различными материалами, $u(x,0) \equiv u(x)$, запишем по аналогии с выражением (2.1):

(2.2)
$u(x) = {{u}_{y}}(x) - i{{u}_{x}}(x)$
где ${{u}_{{y{\kern 1pt} ,x}}}(x)$ – проекции раскрытия трещины на оси координат $OX$ и $OY$ (рис. 2).

Соотношение, связывающее компоненты раскрытия трещины и усилия в связях (закон деформирования связей), представим, без потери общности, в форме квазилинейных зависимостей [16, 17]:

(2.3)
${{u}_{y}}(x) - i{{u}_{x}}(x) = {{c}_{y}}(x,{\sigma }){{q}_{y}}(x) - i{{c}_{x}}(x,{\sigma }){{q}_{x}}(x)$
где функции ${{c}_{{y,\;x}}}(x,{\sigma })$ – эффективные податливости связей, зависящие от положения связи вдоль концевой области, а модуль вектора усилий в связях σ(x) определяется как

(2.4)
${\sigma }(x) = \sqrt {q_{x}^{2} + q_{y}^{2}} $

Эффективные податливости связей в (2.3) определяются из соображений размерности так:

(2.5)
${{c}_{{y,x}}}(x,{\sigma }) = {{{\gamma }}_{{1{\kern 1pt} ,2}}}(x,{\sigma })\frac{H}{{{{E}_{b}}}}$
где ${{{\gamma }}_{{1{\kern 1pt} ,2}}}(x,{\sigma })$ – безразмерные функции, H – линейный размер, пропорциональный толщине зоны неоднородности на участке соединения материалов, ${{E}_{b}}$ – эффективный модуль упругости связей.

При постоянных значениях функций ${{{\gamma }}_{{1{\kern 1pt} ,2}}}(x,{\sigma })$, выражение (2.3) определяет линейно-упругий закон деформирования связей, одинаковый для всех точек концевой области трещины. Зависимость функций ${{{\gamma }}_{{1{\kern 1pt} ,2}}}(x,{\sigma })$ от координаты вдоль концевой области трещины соответствует переменной податливости связей. Зависимость этих функций от усилий в связях возникает также при рассмотрении нелинейных законов деформирования связей. Отметим, что рассмотрение различных моделей концевой области трещины приводит к необходимости введения, кроме длины концевой области, дополнительного линейного размера (H – в данном случае), характеризующего жесткость связей в концевой области трещины [18–20].

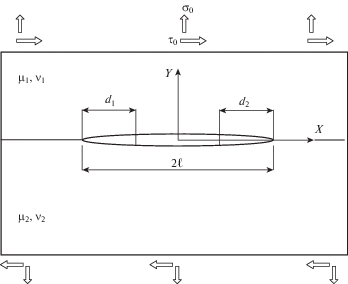
Рассмотрим прямолинейную трещину длины $2\ell $ с концевыми областями d1 и d2 (равными при одноосном растяжении), расположенную на границе соединения двух полуплоскостей из различных материалов, при действии внешних однородных нормальной ${{{\sigma }}_{0}}$ и сдвиговой ${{{\tau }}_{0}}$ нагрузок (рис. 3). При учете принципа суперпозиции, граничные условия на берегах трещины для плоской задачи теории упругости имеют вид

Рис. 3

1) при $ - \ell + {{d}_{2}} < x < \ell - {{d}_{1}}$

(2.6)
${{{\sigma }}_{{xy}}}(x,0) + i{{{\sigma }}_{{yy}}}(x,0) = - ({{{\tau }}_{0}} + i{{{\sigma }}_{0}})$

2) при $\ell - {{d}_{1}} \leqslant x \leqslant \ell ,\; - \ell \leqslant x \leqslant - \ell + {{d}_{2}}$

(2.7)
${{{\sigma }}_{{xy}}}(x,0) + i{{{\sigma }}_{{yy}}}(x,0) = ( - {{{\tau }}_{0}} + {{q}_{x}}(x)) + i( - {{{\sigma }}_{0}} + {{q}_{y}}(x))$

Усилия в связях ${{q}_{{x,y}}}(x)$ подлежат определению из решения задачи при внешних нагрузках ${{{\sigma }}_{0}},$ τ0 и известном законе деформирования связей. В рассматриваемой постановке задачи размеры концевых областей d1, 2 не предполагаются малыми по сравнению с длиной трещины, а усилия в связях зависят как от принятого закона деформирования связей, так и от размера концевой области.

Раскрытие (2.2) в концевой области трещины на границе между двумя различными материалами, $u\left( {x,0} \right) \equiv u(x)$, можно, ввиду линейности задачи теории упругости, представить так:

(2.8)
$u(x) = {{u}_{\infty }}(x) + {{u}_{Q}}(x)$
(2.9)
${{u}_{\infty }}(x) = {{u}_{{\infty y}}}(x) - i{{u}_{{\infty x}}}(x),\quad {{u}_{Q}}(x) = {{u}_{{Qy}}}(x) - i{{u}_{{Qx}}}(x)$
где ${{u}_{\infty }}(x)$ – раскрытие трещины от действия напряжений $ - {{{\sigma }}_{0}}$ и $ - {{{\tau }}_{0}}$ на берегах трещины без связей [21], ${{u}_{Q}}(x)$ – раскрытие трещины (сближение берегов трещины), обусловленное усилиями $ - {{q}_{{y,x}}}(x)$, возникающими в связях при действии внешних нагрузок и приложенными на берегах трещины в концевой области, компоненты с индексами $x,y$ в (2.9) – проекции соответствующих слагаемых раскрытия трещины на оси координат $OX$ и $OY$, (см. рис. 2).

Выражение (2.8) является исходным при получении системы сингулярных интегро-дифференциальных уравнений (СИДУ) для определения усилий в связях в концевой области трещины [16, 17]. Дифференцируя уравнение (2.8), имеем

(2.10)
$\frac{{\partial u(x)}}{{\partial x}} - \frac{{\partial {{u}_{Q}}(x)}}{{\partial x}} = \frac{{\partial {{u}_{\infty }}(x)}}{{\partial x}}$

В этом выражении производная раскрытия трещины в концевой области $\partial u(x){\text{/}}\partial x$ определяется дифференцированием выражения (2.3), производная раскрытия трещины от действия усилий ${{q}_{{x,y}}}(x)$, приложенных на берегах трещины, $\partial {{u}_{Q}}(x){\text{/}}\partial x$ может быть получена исходя из выражения для производных перемещений берегов трещины при действии произвольных нормальных и касательных усилий на берегах трещины, расположенной на границе соединения материалов [16], а производная раскрытия трещины без связей при действии однородных внешних напряжений определяется исходя из аналитического решения [21].

Используя соотношения (2.3) и (2.5) и переходя к безразмерным переменным (индекс ${\alpha }$ соответствует слагаемым раскрытия трещины в (2.8))

(2.11)
$s = \frac{x}{\ell },\quad {{u}_{{\alpha }}}(s) = \frac{{{{u}_{{\alpha }}}(x)}}{\ell },$
получим
(2.12)
${{c}_{0}}\frac{\partial }{{\partial s}}\left[ {{{{\gamma }}_{1}}(s,{\sigma }){{q}_{y}}(s) - i{{{\gamma }}_{2}}(s,{\sigma }){{q}_{x}}(s)} \right] - {{E}_{b}}\frac{{\partial {{u}_{Q}}(s)}}{{\partial s}} = {{E}_{b}}\frac{{\partial {{u}_{\infty }}(s)}}{{\partial s}}$
где параметр c0 (относительная податливость связей [16]) определяется как

(2.13)
${{c}_{0}} = \frac{H}{\ell }$

После подстановки представлений для производных, дифференцирования по переменной s в уравнении (2.12) и ряда алгебраических преобразований, получаем на промежутке $1 - d{\text{/}}\ell \leqslant s \leqslant 1$ нелинейную систему СИДУ относительно новых переменных задачи – функций ${{f}_{{1,2}}}(s)$

(2.14)
${{T}_{{ij}}}(s,{\sigma })\frac{{d{{f}_{j}}(s)}}{{ds}} + {{W}_{{ij}}}(s,{\sigma }){{f}_{j}}(s) + \Psi \int\limits_{1 - \frac{d}{\ell }}^1 {{G}_{{ij}}}(s,t){{f}_{j}}(t)dt = {{Z}_{i}}(s),\quad i,j = 1,2$
где усилия в концевой области трещины ${{q}_{{x,y}}}$ и функции f1, 2 связаны соотношением

(2.15)
${{q}_{y}}(s) - i{{q}_{x}}(s) = \sqrt {1 - s} \left( {{{f}_{2}}(s) - i{{f}_{1}}(s)} \right){{\left( {\frac{{1 - s}}{{1 + s}}} \right)}^{{ - i{\kern 1pt} {\beta }}}},\quad {\beta } = \frac{1}{{2\pi }}\ln \left( {\frac{{{{{\mu }}_{2}}{{k}_{1}} + {{{\mu }}_{1}}}}{{{{{\mu }}_{1}}{{k}_{2}} + {{{\mu }}_{2}}}}} \right),$

Здесь β – биупругая постоянная, определяющая степень различия механических свойств материалов подобластей, ${{k}_{{1,2}}} = 3 - 4{{{\nu }}_{{1,2}}}$ или ${{k}_{{1,2}}} = (3 - {{{\nu }}_{{1,2}}}){\text{/}}(1 + {{{\nu }}_{{1,2}}})$ для плоской деформации или плоского напряженного состояния, соответственно. Выражения для функций ${{T}_{{ij}}}(s,{\sigma })$, ${{W}_{{ij}}}(s,{\sigma })$, ${{G}_{{ij}}}(s,t)$ Zi(s) приведены в [16, 17].

Параметр Ψ в уравнении (2.14) характеризует относительную жесткость связей в концевой области трещины (отношение жесткости связей в концевой области трещины ${{E}_{b}}{\text{/}}H$ к жесткости участка соединения материалов без трещины)

(2.16)
$\Psi = \frac{{A{{E}_{b}}}}{{2{\pi }{{c}_{0}}}} = \frac{{{{E}_{b}}\ell }}{{2{\pi }H}}\left( {\frac{{{{k}_{1}} + 1}}{{{{{\mu }}_{{\text{1}}}}}} + \frac{{{{k}_{2}} + 1}}{{{{{\mu }}_{2}}}}} \right)$

3. Трещина с концевой областью на границе соединения материалов. Критерий разрушения. В работе для описания зоны процесса разрушения используется модель трещины со связями в концевой области без наложения ограничений на размер концевой области трещины. При использовании такой модели трещины необходим нелокальный критерий разрушения, позволяющий определять условия продвижения как края концевой области трещины, так и вершины трещины.

В качестве первого условия такого критерия разрушения обычно используется силовое условие (1.3) [7], где KIc – трещиностойкость материала, соответствующая механизму деформирования связей, находящихся в малой зоне вблизи вершины трещины. Другая возможность состоит, например, в использовании вместо условия (1.3) условия достижения критического напряжения в вершине трещины, при котором начинается рост трещины. При использовании критерия В.В. Новожилова [22] под напряжением в вершине трещины понимается среднее значение напряжения на некотором характерном участке вблизи ее вершины [23].

В качестве второго условия роста трещины с концевой областью возможен выбор условия критического раскрытия трещины на краю концевой области (условия предельной вытяжки связей) [7]:

(3.1)
$u({{{\sigma }}_{{cr}}},L,d) = {{{\delta }}_{{cr}}}$
где σcr – критическая внешняя нагрузка, при которой начинается разрыв связей на краю концевой области трещины, L и d – характерные линейные размеры трещины и ее концевой области, соответственно.

Заметим, что при использовании в критерии разрушения силовых условий вида (1.3) работа по деформированию связей в концевой области трещины, а также другие механизмы, связанные с потреблением энергии при росте трещины с концевой областью, оказываются вне рамок критерия разрушения.

В данной работе используется предложенный ранее [16, 17, 24] нелокальный критерий разрушения для трещин со связями в концевой области на границе соединения материалов. При использовании этого критерия состоянию предельного равновесия вершины трещины соответствует энергетическое условие – равенство скорости высвобождения энергии деформации в вершине трещины и скорости потребления энергии деформации связями в концевой области трещины (первое условие разрушения). Разрыв связей на краю концевой области определяется условием их предельной вытяжки (второе условие разрушения) (3.1). Комбинированный подход, основанный на энергетическом и силовом условиях разрушения используется также в моделях конечной механики разрушения [25].

Рассмотрим применение нелокального критерия разрушения для двумерной задачи об одноосном растяжении пластины с прямолинейной трещиной со связями в концевой области. Трещина расположена перпендикулярно направлению приложения нагрузки на прямолинейной границе соединения полуплоскостей из различных материалов.

Для прямолинейной трещины, расположенной на участке $\left| x \right| \leqslant \ell $, $y = 0$, с концевыми областями размера ${{d}_{1}} = {{d}_{2}} = d$ (рис. 3, ${{{\tau }}_{0}} = 0$), энергетическое условие, определяющее продвижение вершины трещины, запишется так [16, 17]:

(3.2)
$ - \frac{{\partial \Pi }}{{\partial \ell }} = \frac{{\partial U}}{{b\partial \ell }} + {{G}_{m}}$
где Π – потенциальная энергия тела с трещиной, U – потенциальная энергия деформации связей в концевой области трещины, b – толщина тела, Gm – энергетический параметр, определяющий трещиностойкость в малой зоне вблизи вершины трещины.

Введем обозначения

(3.3)
${{G}_{{{\text{tip}}}}}(d,\ell ) = - \frac{{\partial \Pi }}{{\partial \ell }},\quad {{G}_{{{\text{bond}}}}}(d,\ell ) = \frac{{\partial U}}{{b\partial \ell }} + {{G}_{m}}$
где ${{G}_{{{\text{tip}}}}}(d,\ell )$ – скорость высвобождения энергии деформации (поток энергии в вершину трещины [26]), ${{G}_{{{\text{bond}}}}}(d,\ell )$ – скорость потребления энергии деформации связями в концевой области трещины.

Выражение для скорости высвобождения энергии деформации для трещины, расположенной на границе соединения материалов, остается справедливым и при наличии связей в концевой области трещины, так как влияние связей выражается в приложении нагрузок к берегам трещины в ее концевой области. Таким образом, независимо от формы закона деформирования связей, скорость высвобождения энергии деформации определяется выражением [27]:

(3.4)
${{G}_{{{\text{tip}}}}}(d,\ell ) = \left( {\frac{{{{k}_{1}} + 1}}{{{{{\mu }}_{{\text{1}}}}}} + \frac{{{{k}_{2}} + 1}}{{{{{\mu }}_{{\text{2}}}}}}} \right)\frac{{K_{I}^{2} + K_{{II}}^{2}}}{{16c{{h}^{2}}({\pi \beta })}}$
где КИН KI и KII для трещины на границе соединения материалов определяются с учетом КИН от нагрузок на внешней поверхности тела (${{K}_{{{\text{I}},II,{\kern 1pt} \infty }}})$ и КИН от нагрузок в концевой области трещины (${{K}_{{{\text{I}},II,{\kern 1pt} {\text{b}}}}})$ [16, 17]

(3.5)
${{K}_{{\text{I}}}} + i{{K}_{{{\text{II}}}}} = ({{K}_{{{\text{I}},\infty }}} - {{K}_{{{\text{I}},b}}}) + i({{K}_{{{\text{I}}I,\infty }}} - {{K}_{{{\text{I}}I,b}}})$

Потенциальную энергию деформации связей в концевой области трещины определяем как:

(3.6)
$U = b\int\limits_{\ell - d}^\ell \Phi (u)dx,\quad \Phi (u) = \int\limits_0^{u(x)} {\sigma }(u)du,\quad u(x) = \sqrt {u_{x}^{2} + u_{y}^{2}} $
где Φ(u) – плотность потенциальной энергии деформации связей в концевой области трещины, ${{u}_{{x,y}}}(x)$ – компоненты раскрытия трещины в концевой области, σ(u) – модуль вектора усилий в связях.

Подставляя выражения (3.6) во второе равенство (3.3), получаем:

(3.7)
${{G}_{{{\text{bond}}}}}(d,\ell ) = \frac{{\partial U}}{{b\partial \ell }} + {{G}_{m}} = \frac{\partial }{{\partial \ell }}\int\limits_{\ell - d}^\ell \left( {\int\limits_0^{u(x)} {\sigma }(u)du} \right)dx\; + {{G}_{m}}$

Дифференцирование по верхнему и нижнему пределам интегрирования в выражении для скорости потребления энергии деформации связями (3.7) соответствует предположению об изменении размера концевой области трещины в результате разрыва связей на краю концевой области (при ${{x}_{0}} = \ell - d)$ и одновременном продвижении вершины трещины. В таком случае возможно выполнение условия автономности концевой области трещины.

Выполняя дифференцирование по верхнему и нижнему пределам в равенстве (3.7), получим:

(3.8)
${{G}_{{{\text{bond}}}}}(d,\ell ) = \int\limits_{\ell - d}^\ell \left( {\frac{{\partial {\kern 1pt} u(x)}}{{\partial {\kern 1pt} \ell }}{\sigma }(u)} \right)dx + {{G}_{m}} + {{G}_{c}} - {{G}_{b}}$
где введены обозначения
(3.9)
${{G}_{c}} = \int\limits_0^{u(\ell )} {\sigma }(u)du,\quad {{G}_{b}} = \int\limits_0^{u(\ell - d)} {\sigma }(u)du$
и в состоянии предельного равновесия трещины $u(\ell - d) = {{{\delta }}_{{{\text{cr}}}}}$ (согласно условию (3.1)).

Выбор модели трещины с ненулевым раскрытием в ее вершине ($u(\ell ) \ne 0$) предполагает, что концевая область состоит из двух частей, d и dc, на каждой из которых закон деформирования связей может быть различным, а параметр дифференцирования ($\ell )$ не является полной длиной трещины. При выборе такой модели концевой области трещины первый интеграл в (3.9) представляет собой плотность энергии деформации связей на участке dc концевой области трещины. В рассматриваемой здесь модели трещины полагаем, что ${{d}_{c}} \ll d$, толщина адгезионного слоя между областями из различных материалов мала по сравнению с длиной трещины ($H{\text{/}}\ell \to 0$) и $u(\ell ) = 0$. Тогда ${{G}_{c}} = 0$ и выражение (3.8) с учетом соотношений (2.3) можно записать так [24]:

(3.10)
${{G}_{{{\text{bond}}}}}(d,\ell ) = \int\limits_{\ell - d}^\ell \left( {\frac{{\partial {\kern 1pt} {{u}_{y}}(x)}}{{\partial {\kern 1pt} \ell }}{{q}_{y}}(u) + \frac{{\partial {\kern 1pt} {{u}_{x}}(x)}}{{\partial {\kern 1pt} \ell }}{{q}_{x}}(u)} \right)dx - {{G}_{b}} + {{G}_{m}}$

Величина Gb представляет собой плотность энергии деформации, выделяющейся при разрыве связей на краю концевой области ($x = \ell - d)$.

При рассмотрении адгезионных соединений с использованием нелокального критерия разрушения, основанного на условиях (3.3) и (3.1), параметр Gm определяем так [24]

(3.11)
${{G}_{m}} = {\eta }{{G}_{b}}$
где параметр ${\eta } \geqslant 0$ представляет собой относительную трещиностойкость соединения материалов.

Для однородного материала или адгезионного слоя, соединяющего разные материалы, полагаем, что законы деформирования связей в концевой области трещины и на ее продолжении одинаковы (η = 1), т.е.

(3.12)
${{G}_{m}} = {{G}_{b}} = \int\limits_0^{{{\delta }_{{{\text{cr}}}}}} {\sigma }(u)du$
и выражение (3.10) принимает вид:

(3.13)
${{G}_{{{\text{bond}}}}}(d,\ell ) = \int\limits_{\ell - d}^\ell \left( {\frac{{\partial {\kern 1pt} {{u}_{y}}(x)}}{{\partial {\kern 1pt} \ell }}{{q}_{y}}(u) + \frac{{\partial {\kern 1pt} {{u}_{x}}(x)}}{{\partial {\kern 1pt} \ell }}{{q}_{x}}(u)} \right)dx$

Случай η > 1 соответствует наличию дополнительных механизмов подкрепления в адгезионном слое за вершиной трещины, а случай $0 \leqslant {\eta } < 1$ соответствует “слабому” интерфейсу , причем η = 0 соответствует случаю “идеально слабого” интерфейса.

При рассмотрении адгезионного слоя, обладающего малой трещиностойкостью (сопротивление разрушению определяется только связями в концевой области), полагаем, что ${{G}_{b}} \gg {{G}_{m}}$ и η = 0. Для этого частного случая показано [28, 29], что ${{G}_{{{\text{bond}}}}}(d,\ell ) \to 0$, ${{G}_{{{\text{tip}}}}}(d,\ell ) \to 0$ при $(d{\text{/}}\ell ) \to 0$ и выражение (3.2) переходит условие конечности напряжений в вершине трещины в когезионной модели.

Для адгезионного слоя на границе соединения материалов (параметр ${{G}_{{{\text{bond}}}}}(d,\ell )$ определяется выражением (3.13)) состоянию предельного равновесия вершины трещины и края концевой области трещины соответствует выполнение необходимого условия

(3.14)
${{G}_{{{\text{tip}}}}}(d,\ell ) = {{G}_{{{\text{bond}}}}}(d,\ell )$
и достаточного условия (${{x}_{0}} = \ell - d$)

(3.15)
$u({{x}_{0}}) = [u_{x}^{2}({{x}_{0}}) + u_{y}^{2}({{x}_{0}}{{)]}^{{1/2}}} = {{{\delta }}_{{{\text{cr}}}}}$

Параметр ${{{\delta }}_{{{\text{cr}}}}}$ определяется свойствами связей в концевой области трещины, а также может зависеть от масштаба трещины (например, при изменении типа связей с ростом трещины).

Из совместного решения уравнений (3.14) и (3.15) можно определить размер концевой области ${{d}_{{{\text{cr}}}}}$ и критическое внешнее напряжение ${{{\sigma }}_{{{\text{cr}}}}}$ в состоянии предельного равновесия трещины. Скорость потребления энергии деформации ${{G}_{{{\text{bond}}}}}({{d}_{{{\text{cr}}}}},\ell )$, полученная из совместного решения этих уравнений, является энергетической характеристикой сопротивления адгезионному разрушению, ${{G}_{{{\text{cr}}}}} = {{G}_{{{\text{bond}}}}}({{d}_{{{\text{cr}}}}},\ell )$, причем величина ${{G}_{{{\text{cr}}}}}$ не остается постоянной при изменении длины трещины.

При монотонном нагружении тела, для заданных начальных размеров трещины и ее концевой области, можно выделить следующие режимы равновесия и квазистатического роста трещины [24]:

1. продвижение вершины трещины с одновременным возрастанием длины концевой области трещины без разрыва связей возможно при выполнении условий

(3.16)
${{G}_{{{\text{tip}}}}}(d,\ell ) \geqslant {{G}_{{{\text{bond}}}}}(d,\ell ),\quad u(\ell - d) < {{{\delta }}_{{cr}}}\;$

2. разрыв связей на краю концевой области трещины без продвижения вершины трещины происходит при выполнении условий

(3.17)
${{G}_{{{\text{tip}}}}}(d,\ell ) < {{G}_{{{\text{bond}}}}}(d,\ell ),\quad u(\ell - d) \geqslant {{{\delta }}_{{cr}}}$

Размер концевой области трещины в этом случае сокращается, стремясь к предельному значению для данного уровня нагрузки.

Указанные два этапа роста трещины можно рассматривать как процессы приспособляемости трещины к заданному уровню внешних нагрузок (докритический рост трещины);

3. продвижение вершины трещины с одновременным разрывом связей на краю концевой области происходит при одновременном выполнении условий (знаки равенства соответствуют квазистатическому росту трещины)

(3.18)
${{G}_{{{\text{tip}}}}}(d,\ell ) \geqslant {{G}_{{{\text{bond}}}}}(d,\ell ),\quad u(\ell - d) \geqslant {{{\delta }}_{{cr}}}$

В рамках рассматриваемой модели положение концевой области и вершины трещины не меняется при одновременном выполнении второго из условий (3.16) и первого условия (3.17).

Таким образом, величина внешней нагрузки и параметры связей определяют характер разрушения: продвижение вершины трещины с ростом концевой области; сокращение размера концевой области без продвижения вершины трещины; продвижение вершины трещины с одновременным разрывом связей на краю концевой области.

Заметим, что при рассмотрении адгезионного слоя с линейно-упругими связями [16, 17] выполнение условия (3.14) зависит только от относительных геометрических характеристик концевой области и трещины. Критическое значение размера концевой области, полученное из этого условия, может быть отнесено к трещине любой длины. Определение фактического размера трещины, соответствующего состоянию предельного равновесия, происходит при учете достаточного условия (3.15). Этот факт является очевидным подтверждением необходимости использования двухпараметрического критерия для полного описания предельного равновесия трещины с концевой областью.

4. Моделирование трещиностойкости соединений материалов. Выражения для энергетических характеристик трещины, а также зависимости критической внешней нагрузки и критического размера концевой области трещины от длины трещины могут быть получены аналитически, если усилия в связях не зависят от раскрытия трещины и являются постоянными (трещина в однородной плоскости с постоянными усилиями в связях) [28, 29].

При заданной кривой деформирования связей в концевой области трещины (усилия в связях зависят от раскрытия трещины) применение нелокального критерия разрушения (3.14)–(3.15) состоит из двух этапов:

1) определения усилий в связях и раскрытия в концевой области трещины на каждом шаге приращения длины трещины или ее концевой области (для прямолинейной трещины на границе соединения полуплоскостей – из решения уравнения (2.14) с учетом закона деформирования связей);

2) проверки выполнения условий (3.16)–(3.18) и определения режима развития трещины с приращением длины трещины и/или ее концевой области.

Исходные данные, необходимые на этих этапах, включают: 1) механические свойства материалов подобластей; 2) закон деформирования связей в концевой области трещины; 3) критическое раскрытие на краю концевой области трещины, ${{{\delta }}_{{cr}}}$; 4) плотность энергии деформации, выделяющейся при разрыве связей на краю концевой области, ${{G}_{b}}$; 5) трещиностойкость материала в малой зоне вблизи вершины трещины, ${{G}_{m}}$. Параметры 2)–5) являются масштабно-зависимыми и могут изменяться при росте трещины.

Рассмотрим этап проверки выполнения условий (3.16)–(3.18) и определения режима развития трещины. Начнем с анализа квазистатического режима роста трещины, который реализуется при выполнении условий (3.18) или эквивалентных им условий (3.14)–(3.15). Для трещины с адгезионным слоем на границе соединения материалов первое из уравнений в (3.18) принимает вид:

(4.1)
$\left( {\frac{{{{k}_{1}} + 1}}{{{{{\mu }}_{1}}}} + \frac{{{{k}_{2}} + 1}}{{{{{\mu }}_{2}}}}} \right)\frac{{K_{I}^{2} + K_{{II}}^{2}}}{{16c{{h}^{2}}({\pi \beta })}} = \int\limits_{\ell - d}^\ell \left( {\frac{{\partial {\kern 1pt} {{u}_{y}}(x)}}{{\partial {\kern 1pt} \ell }}{{q}_{y}}(u) + \frac{{\partial {\kern 1pt} {{u}_{x}}(x)}}{{\partial {\kern 1pt} \ell }}{{q}_{x}}(u)} \right)dx$

Для линейно-упругих связей в концевой области трещины решение системы уравнений (3.18) проводится в два этапа. На первом этапе выполняется совместное итерационное решение СИДУ (2.14) и интегрального уравнения (4.1). Из этого решения (если оно существует), определяется относительная критическая длина концевой области трещины в состоянии предельного равновесия ${{t}_{{cr}}} = d{\text{/}}\ell $ при заданных длине трещины, параметрах связей и материалов. Выполнение условия (4.1) для линейно-упругих связей в концевой области трещины зависит от параметра относительной жесткости связей Ψ (2.16), а при неизменных свойствах материалов и связей – от относительной податливости связей в концевой области трещины ${{c}_{0}} = H{\text{/}}\ell $ (2.13). Ввиду этого, относительное критическое значение длины концевой области, полученное из условия (4.1), может быть отнесено к трещине любого масштаба при допустимой внешней нагрузке. Критическая длина концевой области для заданной длины трещины определяется как ${{d}_{{cr}}} = \ell {{t}_{{cr}}}$. Критическую внешнюю нагрузку ${{{\sigma }}_{{cr}}}$, соответствующую решению ${{d}_{{cr}}}$ уравнения (4.1), находим из решения второго уравнения нелокального критерия разрушения (3.18) при заданных длине трещины и критическом раскрытии трещины на краю концевой области. Зависимости параметров разрушения от длины трещины, приведенные ниже, получаются в результате решения системы уравнений (2.14) и (3.18) для последовательности возрастающих длин трещин.

Для связей с нелинейной диаграммой деформирования необходимо выполнение итерационного решения системы уравнений (2.14) и (3.18) с изменением уровня внешней нагрузки и проверкой выполнения условия достижения предельного раскрытия ${{{\delta }}_{{cr}}}$ на краю концевой области. В качестве первого приближения принимается решение для линейно-упругих связей и определяется интервал поиска решения для внешней нагрузки $[{{c}_{1}}{{{\sigma }}_{{cr}}};{{c}_{2}}{{{\sigma }}_{{cr}}}]$ и концевой области $[{{w}_{1}}{{d}_{{cr}}};{{w}_{2}}{{d}_{{cr}}}]$, где ${{{\sigma }}_{{cr}}}$ – критическое внешнее напряжение и ${{d}_{{cr}}}$ – критическая длина концевой области для линейно-упругих связей, $0 < {{c}_{1}} < {{c}_{2}} < 1$ и ${{w}_{1}} < 1,$ ${\kern 1pt} {{w}_{2}} > 1$ – эмпирические постоянные, зависящие от формы кривой деформирования связей. Определяется размер шага по нагрузке Δσ = = ${{{\sigma }}_{{cr}}}({{c}_{2}} - {{c}_{1}}){\text{/}}N$, где N – число шагов. Для уровней внешней нагрузки вида σ0, i = = ${{c}_{2}}{{{\sigma }}_{{cr}}} - (i - 1)\Delta {\sigma }$, ($i = 1 \ldots N$) выполняется итерационное решение первого уравнения системы (3.18) с проверкой достижения критического раскрытия на краю концевой области.

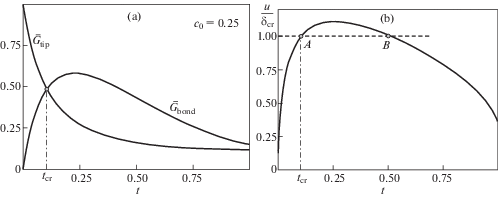
Графическая иллюстрация решения системы уравнений (2.14), (3.14) и (3.15) для линейно-упругих связей при постоянной вдоль концевой области трещины податливости связей (${{c}_{0}} = 0.25$, ${{E}_{1}} = 135{\kern 1pt} $ ГПа, ${{E}_{2}} = 25{\kern 1pt} $ ГПа, ${{E}_{b}} = {{E}_{2}}$ – модули упругости материалов и связей, ${{{\nu }}_{1}} = {{{\nu }}_{2}} = 0.35$) приведена на рис. 4a, b. Положение точки пересечения графиков ${{\bar {G}}_{{tip}}} = {{G}_{{tip}}}(d,\ell ){\text{/}}{{G}_{{tip}}}(0,\ell )$ и ${{\bar {G}}_{{bond}}} = {{G}_{{bond}}}\left( {d,\ell } \right){\text{/}}{{G}_{{tip}}}\left( {0,\ell } \right)$ на рис. 4a (здесь ${{G}_{{tip}}}(0,\ell )$ – поток энергии в вершину трещины при отсутствии связей) соответствует критическому значению относительной длины концевой области трещины tcr = = ${{d}_{{cr}}}{\text{/}}\ell \approx 0.105$, удовлетворяющему уравнению (3.14). Критическая внешняя нагрузка ${{{\sigma }}_{{cr}}}$, соответствующая найденному значению ${{t}_{{cr}}}$ и раскрытию на краю концевой области $u = {{{\delta }}_{{cr}}}$, определяется из решения уравнения (3.15). Это решение иллюстрируется на рис. 4b, где решению ${{t}_{{cr}}}$, удовлетворяющему обоим уравнениям системы (3.14) и (3.15), соответствует положение точки пересечения (точка A) прямой $u = {{{\delta }}_{{cr}}}$ и зависимости раскрытия трещины на краю концевой области (при $x = \ell - {{d}_{{cr}}}$) от длины концевой области при внешней нагрузке, равной критической (${{{\sigma }}_{0}} = {{{\sigma }}_{{cr}}}$). Второе решение уравнения (3.15) (точка B на рис. 4b) не согласуется с условием (3.14) и, следовательно, не определяет состояния предельного равновесия концевой области и вершины трещины.

Рис. 4

Рассмотрим режимы роста трещины с произвольным размером концевой области $0 < d \leqslant \ell $, полагая, что существует единственное решение уравнения (3.14). Пусть размер концевой области трещины принадлежит промежутку $0 < d < {{d}_{{cr}}}$. При монотонно возрастающей внешней нагрузке для трещины с такой концевой областью выполняется неравенство ${{G}_{{{\text{tip}}}}}(d,\ell ) > {{G}_{{{\text{bond}}}}}(d,\ell )$ и раскрытие трещины на краю концевой области не превышает критического значения ($u < {{{\delta }}_{{cr}}})$, что соответствует выполнению условий (3.16) (см. рис. 4a). В этом случае возможно увеличение длины трещины без разрыва связей на краю концевой области. При достижении критического размера концевой области и критической величины внешней нагрузки происходит переход к квазистатическому режиму разрушения, описываемому условиями (3.18). Если задан размер концевой области трещины d такой, что ${{d}_{{cr}}} < d < \ell $, то выполняются условия (3.17) , и при монотонном нагружении происходит разрыв связей на краю концевой области, размер концевой области трещины сокращается без продвижения вершины трещины, $d \to {{d}_{{cr}}}$. Переход к квазистатическому режиму разрушения происходит, так же, как и в первом случае, при достижении критического размера концевой области и критической величины внешней нагрузки.

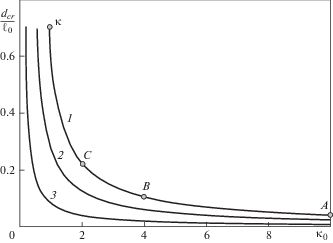
Для трещины фиксированной длины ($2{{\ell }_{0}}{{ = 10}^{{ - 3}}}$ м) рассмотрим зависимость параметров, определяемых из нелокального критерия разрушения при ${{{\delta }}_{{cr}}}$ = 2 × 10–7 м, от относительной жесткости связей в концевой области трещины ${{\kappa }_{0}} = {{\ell }_{0}}{\text{/}}H$ (${{\kappa }_{0}} = 1{\text{/}}{{c}_{0}}$, см. (2.13)) для трех наборов механических свойств материалов. Изменение относительной жесткости связей при постоянной длине трещины осуществляется за счет изменения параметра H. Зависимость относительной длины концевой области трещины в состоянии предельного равновесия ${{t}_{{cr}}} = {{d}_{{cr}}}{\text{/}}{{\ell }_{0}}$ от относительной жесткости связей κ0 приведена на рис. 5 для указанных выше параметров материала, использованных для формирования рис. 4 (кривая 1), а также для случаев ${{E}_{1}} = {{E}_{2}}$ (однородное тело, кривая 2) и ${{E}_{1}} = 0.2{{E}_{2}}$ (кривая 3). При выбранных параметрах материалов (для всех трех случаев полагалось ${{E}_{b}} = {{E}_{2}}$) состояние предельного равновесия трещины с концевой областью существует, если ${{\kappa }_{0}} \geqslant 0.944$ (кривая 1), ${{\kappa }_{0}} \geqslant 0.559$ (кривая 2), ${{\kappa }_{0}} \geqslant 0.186$ (кривая 3). Значительное изменение критического размера концевой области наблюдается для $0.186 \leqslant {{\kappa }_{0}} \leqslant 5$.

Рис. 5

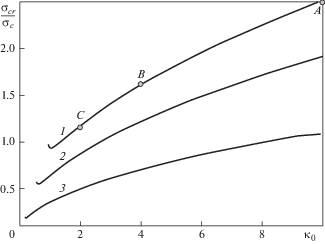
Для указанных выше трех наборов механических свойств материалов зависимость критической внешней нагрузки ${{{\sigma }}_{{cr}}}$, соответствующей началу квазистатического роста трещины (выполнение условий (3.18)), от относительной жесткости связей κ0, нормированная величиной

(4.2)
${{{\sigma }}_{c}} = \frac{{{{E}_{b}}}}{{{{\ell }_{0}}}}{{{\delta }}_{{cr}}}$
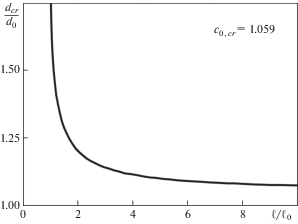
приведена на рис. 6. При увеличении относительной жесткости связей критический размер концевой области трещины уменьшается, а критическая внешняя нагрузка возрастает, ввиду того, что для достижения критического значения ${{{\delta }}_{{cr}}}$ при бо̀льшей жесткости связей необходима бо̀льшая нагрузка. При уменьшении относительной жесткости материалов ${{E}_{1}}{\text{/}}{{E}_{2}}$ (от кривой 1 к кривой 3) уровень критической внешней нагрузки снижается, ввиду увеличения коэффициента концентрации усилий на краю концевой области [16].

Рис. 6

При параметрах материалов, использованных для формирования кривой 1 (рис. 5), состояние предельного равновесия трещины с концевой областью существует, если ${{\kappa }_{0}} \geqslant {{\kappa }_{{0,cr}}} = 0.944$. Точка $\kappa $ на рис. 5 определяет критический размер концевой области трещины ${{d}_{{cr}}} = 0.702{{\ell }_{0}}$ при ${{\kappa }_{{0,cr}}} = 0.944$ (или ${{c}_{0}} \leqslant {{c}_{{0,cr}}} = 1.059$). Для данного значения относительной податливости связей получена зависимость критического размера концевой области трещины ${{d}_{{cr}}}$ от длины трещины $\ell $ для режима разрушения (3.18), см. рис. 7, где ${{\ell }_{0}}$ – начальная длина трещины, а нормировка размера концевой области трещины выполнена параметром

${{d}_{0}} = \frac{{{\pi }H}}{{{{E}_{b}}}}{{\left( {\frac{{{{k}_{1}} + 1}}{{{{{\mu }}_{1}}}} + \frac{{{{k}_{2}} + 1}}{{{{{\mu }}_{2}}}}} \right)}^{{ - 1}}},\quad H = {{c}_{{0,cr}}}{{\ell }_{0}}$
который зависит от механических свойств материалов и связей. Параметр d0 определен аналогично параметру, введенному ранее при анализе нелокального критерия разрушения для постоянных усилий в связях [28, 29]. При увеличении длины трещины критический размер концевой области трещины быстро стабилизируется, уже при $\ell = 5{{\ell }_{0}}$ имеем ${{d}_{{cr}}} \sim 1.1{{d}_{0}}$. Таким образом, при $\ell \gg {{\ell }_{0}}$ фактически выполняется условие автономности концевой области трещины.

Рис. 7

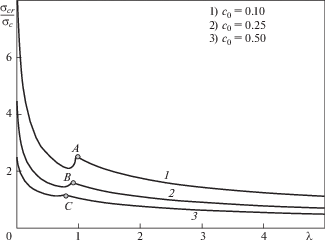
Рассмотрим далее процесс развития трех трещин равной длины $2{{\ell }_{0}}$, заполненных связями, при механических свойствах материалов, использованных для формирования кривой 1 (рис. 5) и различных начальных значениях относительной податливости связей (${{c}_{0}} = 0.1;0.25$; 0.5) из промежутка $0 < {{c}_{0}} < 1.059$ (промежуток существования решения системы уравнений (3.14) и (3.15) при заданных механических свойствах материалов и связей). При фиксированной длине трещины выбранным начальным значениям относительной податливости связей соответствуют значения параметров H = = $0.1{{\ell }_{0}};0.25{{\ell }_{0}};0.5{{\ell }_{0}}$, которые полагаются постоянными при росте каждой из трещин. Для рассматриваемых значений начальной относительной податливости связей процесс разрушения начинается с разрыва связей в центре трещины при выполнении условия (3.17) с последующим переходом к режиму квазистатического роста трещины. На рис. 8 приведены зависимости внешней нагрузки ${{{\sigma }}_{{cr}}}$ (нормированной величиной σc) от относительной длины части трещины, свободной от связей

(4.3)
${\lambda } = \frac{{\ell - d}}{{{{\ell }_{0}}}}$
где ${{\ell }_{0}}$ – начальная длина трещины, $\ell $ – текущая длина трещины, d – размер концевой области.

Рис. 8

Каждая из кривых на рис. 8 состоит из двух участков. Первый участок соответствует квазистатическому сокращению размера концевой области трещины (при выполнении условия (3.17)) от начальной величины $d = {{\ell }_{0}}$ (трещина заполнена связями, λ = 0) до $d = {{d}_{{cr}}}$ без изменения начальной длины трещины. Характер изменения внешней нагрузки ${{{\sigma }}_{{cr}}}$ определяется изменением раскрытия трещины на краю концевой области, см., например, рис. 4b для ${{c}_{0}} = 0.25$, где при $0.5 \leqslant t \leqslant 1$ (до точки $B$) внешняя нагрузка монотонно уменьшается при возрастании раскрытия трещины, на промежутке ${{t}_{{cr}}} \leqslant t \leqslant 0.5$ относительное раскрытие трещины превышает критическую величину и достигает максимума при определенном значении длины концевой области трещины, при котором величина внешней нагрузки будет минимальна. Начало второго участка каждой из кривых на рис. 8 отмечено точками A, B, C, которые определяют значения размера части трещины ${\lambda } = 1 - {{t}_{{cr}}}$, свободной от связей, и величины внешней нагрузки ${{{\sigma }}_{{cr}}}$, при которых происходит переход от режима разрыва связей на краю концевой области (без изменения длины трещины) к квазистатическому росту трещины при выполнении условия (3.18). Точки $A$, B и C на рис. 5 (кривая 1) при соответствующих значениях начальной относительной жесткости связей определяют относительные значения критического размера концевой области трещины, при которых происходит изменение режимов разрушения, показанное на рис. 8: ${{t}_{{cr}}} \approx 0.041\;{\kern 1pt} ({{\kappa }_{0}} = 10)$, ${{t}_{{cr}}} \approx 0.105$ (κ0 = 4), ${{t}_{{cr}}} \approx 0.225$ (κ0 = 2). Аналогично, на рис. 6 (кривая 1) точки A, B, C определяют величины внешней нагрузки, при которой происходит изменение режимов разрушения, показанное на рис. 8. При $2\ell {{ = 10}^{{ - 3}}}$ м, ${{{\delta }}_{{cr}}}$ = 2 × 10–7 м, ${{E}_{b}} = 25$ ГПа получаем ${{{\sigma }}_{c}} = 10$ МПа и переходу от режима разрыва связей к режиму квазистатического роста трещины соответствуют следующие значения внешней нагрузки: ${{{\sigma }}_{{cr}}} \approx 25.1$ МПа (κ0 = 10), ${{{\sigma }}_{{cr}}} \approx 16.1$ МПа (κ0 = 4), ${{{\sigma }}_{{cr}}} \approx 11.7$ МПа (κ0 = 2).

При росте трещины и H = const относительная податливость связей ${{c}_{0}} = H{\text{/}}\ell $ снижается. Происходит заметное уменьшение критической внешней нагрузки, но длина концевой области трещины в состоянии предельного равновесия изменяется незначительно (см. рис. 7). Например, для c0 = 0.5 размер концевой области изменяется как ${{d}_{{cr}}} \approx (0.225{\kern 1pt} - {\kern 1pt} 0.200){{\ell }_{0}}$ при изменении длины трещины, соответствующей рис. 8.

5. Заключение. Модель трещины на границе соединения материалов со связями между берегами дает возможность с единых позиций рассматривать процесс адгезионного разрушения, включая стадии формирования дефекта и роста микро- и макротрещины. Прочность бездефектного материала в рамках модели рассматривается как прочность связей в концевой области трещины. Использование нелокального критерия роста трещин со связями между берегами с кинематическим и энергетическим условиями разрушения позволяет выделить режимы докритического и квазистатического развития трещины, а также оценить предельный размер концевой области трещины, критическую внешнюю нагрузку и характеристики адгезионного сопротивления соединения материалов. Микромеханическое моделирование закона деформирования связей в концевой области трещины позволяет использовать модель также для решения задач оптимизации адгезионной трещиностойкости.

Модель трещины со связями в концевой области может быть использована при анализе процесса самозалечивания трещин, который рассматривается как процесс формирования концевой области трещины (восстановления адгезионных связей между поверхностями трещины). Эффективность процесса самозалечивания трещины определяется в этом случае по снижению КИН при формировании концевой области трещины за счет увеличения размера концевой области и возрастания жесткости связей. Изменение энергетических характеристик в процессе самозалечивания трещины позволяет оценить степень перехода трещины в состояние устойчивого равновесия при восстановлении адгезионных связей между поверхностями трещины.

Работа выполнена при финансовой поддержке Российского научного фонда (проект № 19-19-00616).

Список литературы

  1. Баренблатт Г.И. О равновесных трещинах, образующихся при хрупком разрушении. Общие представления и гипотезы. Осесимметричные трещины // Прикладная математика и механика. 1959. Т. 23. № 3. 434–444; Прямолинейные трещины в плоских пластинках № 4. С. 706–721. Связь с энергетическими теориями № 5. С. 893–900.

  2. Леонов М.Я., Панасюк В.В. Развитие мельчайших трещин в твердом теле // Прикл. механика. 1959. Т. 5. № 4. С. 391–401.

  3. Dugdale D.S. Yielding of steel sheets containing slits // Journal of the Mechanics and Physics of Solids . 1960. V. 8. № 2. P. 100–104.

  4. Elices M., Guinea G.V., Gomez J., Planas J. The cohesive zone model: advantages, limitations and challenges // Engineering Fracture Mechanics . 2002. V. 69. № 2. P. 137–163.

  5. Hillerborg A., Modeer M., Petersson P.-E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements // Cement and Concrete Research. 1976. V. 6. № 6. P. 773–781.

  6. Stang H., Olesen J.F., Poulsen P.N., Dick-Nielsen L. On the application of cohesive crack modeling in cementitious materials // Materials and Structures . 2007. V. 40. № 4. P. 365–374.

  7. Cox B.N., Marshall D.B. Concepts for bridged cracks in fracture and fatigue // Acta Metallurgica et Materialia. 1994. V. 42. № 2. P. 341–363.

  8. Ritchie R.O. Mechanisms of fatigue-crack propagation in ductile and brittle solids // International Journal of Fracture. 1999. V. 100. № 1. P. 55–83.

  9. Sorensen B.F., Gamstedt E.K., Ostergaard R.C., Goutianos S. Micromechanical model of cross-over fibre bridging – Prediction of mixed mode bridging laws // Mechanics of Materials. 2008. V. 40. № 4–5. P. 220–234.

  10. Nairn J.A. Analytical and numerical modeling of R curves for cracks with bridging zones // International Journal of Fracture. 2009. V. 155. P. 167–181.

  11. Гольдштейн Р.В., Перельмутер М.Н. Моделирование трещиностойкости композиционных материалов // Вычислительная механика сплошных сред. 2009. Т. 2. № 2. С. 22–39.

  12. Shao Y., Zhao H.P., Feng X.Q., Gao H. Discontinuous crack-bridging model for fracture toughness analysis of nacre // Journal of the Mechanics and Physics of Solids. 2012. V. 60. № 8. P. 1400–1419.

  13. Гольдштейн Р.В., Перельмутер М.Н. О кинетике формирования и роста трещин на границе соединения материалов // Изв. РАН. МТТ. 2012. № 4. С. 32–49.

  14. Wang C.H. Fatigue crack closure analysis of bridged cracks representing composite repairs // Fatigue & Fracture of Engineering Materials & Structures . 2000. V. 23. № 6. P. 477–488.

  15. Перельмутер М.Н. Моделирование кинетики самозалечивания трещин // Физическая мезомеханика. 2019. Т. 22. № 4. С. 47–55.

  16. Goldstein R., Perelmuter M. Modeling of bonding at an interface crack // International Journal of Fracture. 1999. V. 99. № 1–2. P. 53–79.

  17. Гольдштейн Р.В., Перельмутер M.Н. Трещина на границе соединения материалов со связями между берегами // Изв. РАН. МТТ. 2001. № 1. С. 94–112.

  18. Ентов В.М., Салганик Р.Л. К модели хрупкого разрушения Прандтля // Изв. АН СССР. МТТ. 1968. № 6. С. 87–99.

  19. Новожилов В. В. О необходимом и достаточном критерии хрупкой прочности // Прикладная математика и механика. 1969. Т. 33. № 2. С. 212–222.

  20. Rose L.R.F. Crack reinforcement by distributed springs // Journal of the Mechanics and Physics of Solids. 1987. V. 35. № 4. P. 383–405.

  21. Rice J.R., Sih G.C. Plane Problems of Cracks in Dissimilar Media // Journal of Applied Mechanics. 1965. V. 32. № 2. P. 418–423.

  22. Новожилов В.В. К основам теории равновесных трещин в хрупких телах // Прикладная математика и механика. 1969. Т. 33. № 5. С. 797–812.

  23. Греков М.А., Морозов Н.Ф. О равновесных трещинах в композитах, армированных однонаправленными волокнами // Прикладная математика и механика. 2006. Т. 70. № 6. С. 1063–1075.

  24. Перельмутер М.Н. Критерий роста трещин со связями в концевой области // Прикладная математика и механика. 2007. Т. 71. №1. С. 152–171.

  25. Cornetti P., Pugno N., Carpinteri A., Taylor D. Finite fracture mechanics: A coupled stress and energy failure criterion // Engineering Fracture Mechanics. 2006. V. 73. № 14. P. 2021–2033.

  26. Черепанов Г.П. Механика хрупкого разрушения. М.: Наука, 1974. 640 с.

  27. Салганик Р.Л. О хрупком разрушении склеенных тел // Прикладная математика и механика. 1963. Т. 27. № 5. С. 957–962.

  28. Perelmuter M. Nonlocal criterion of bridged cracks growth: Weak interface // Journal of the European Ceramic Society. 2014. V. 34. № 11. P. 2789–2798.

  29. Perelmuter M. Nonlocal criterion of bridged cracks growth: analytical analysis // Acta Mechanica. 2015. V. 226. № 2. P. 397–418.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал