Известия РАН. Механика твердого тела, 2020, № 4, стр. 50-70

1. Введение. Проблема идентификации трещин в стержнях по вибрационным характеристикам представляет значительный интерес как с теоретической, так и с прикладной точки зрения. В связи с этим, она изучалась в целом ряде публикаций [1–10]. При исследовании колебаний стержня с трещинами, как правило, используются упрощенные модели трещин. Одной из наиболее распространенных является модель, в которой трещины заменяются невесомыми пружинами, работающими, в случае продольных колебаний на растяжение – сжатие, а в случае поперечных колебаний – на поворот [1–8]. В рамках данной модели задачи идентификации трещин решались при различных, дополнительных, ограничительных предположениях. В частности, делались предположения о малости трещин [2–5, 7, 9] или предполагалось, что имеется ровно одна трещина [11, 12]. Были предложены также различные численные методы обнаружения и локализации дефектов [13–17]. Несмотря на приложенные значительные усилия, в задаче о поперечных колебаниях стержня остаются нерешенными наиболее существенные вопросы. Если не делать никаких дополнительных предположений о размерах и количестве трещин в стержне, то неизвестно сколько и отвечающих каким краевым условиям спектров достаточно знать для однозначного определения количества, расположения и размеров имеющихся трещин. В случае продольных колебаний стержня, ослабленного множественными трещинами, такая проблема была решена в [5, 18]. Было доказано, что количество, расположение и размеры трещин, соответствующие жесткости моделирующих их пружин, могут быть однозначно определены с помощью двух спектров, соответствующих свободным и жестко-свободным условиям на концах стержня. Кроме того, в [9] был разработан эффективный, численный алгоритм локализации трещиноподобных дефектов с помощью двух указанных спектров. Целью данной статьи является получение, для поперечных колебаний стержня, результатов, аналогичных тем, что были получены ранее в случае продольных колебаний. Ниже представлено решение следующих задач.

1. Доказано, что любое количество поперечных трещин в стержне может быть однозначно реконструировано по трем спектрам поперечных колебаний, отвечающих трем различным типам условий на концах стержня. Заметим, что трещины могут быть идентифицированы с помощью нескольких различных троек спектров.

2. Алгоритм локализации трещин, разработанный ранее для случая продольных колебаний [9], обобщен на случай поперечных колебаний.

3. С использованием разработанного алгоритма, проведено сравнение эффективности идентификации трещин с помощью различных, допустимых троек спектров.

2. Постановка задачи. Рассмотрим балку длины l, занимающую интервал $0 < x < l$. Площадь сечения S балки предполагается постоянной. Предполагается, что невесомые пружины, моделирующие поперечные трещины и работающие на поворот, расположены в точках ${{x}_{1}},{{x}_{2}}, \cdots ,{{x}_{n}}$, причем $0 = {{x}_{0}} < {{x}_{1}} < {{x}_{2}} < \cdots < {{x}_{n}} < {{x}_{{n + 1}}} = l$. Амплитуды поперечного перемещения оси балки при поперечных колебаниях на интервале ${{x}_{{j - 1}}} < x < {{x}_{j}}$ обозначим y_j(x), где $j = 1,2, \cdots ,n + 1$. Уравнение гармонических поперечных колебаний на интервале ${{x}_{{j - 1}}} < x < {{x}_{j}}$ имеет следующий вид

где E – модуль Юнга, I – момент инерции поперечного сечения, ${\rho }$ – плотность материала, ${\omega }$ – собственная частота, верхний индекс (4) обозначает производную четвертого порядка.

Перепишем уравнение (2.1) в виде

Условия сопряжения в местах расположения пружин имеют вид, см. [19]

где c_j – податливость  j-й пружины, определяемая длиной трещины и шириной балки.

Будем рассматривать краевые условия шести типов, в каждом из которых правый конец стержня предполагается свободным. Для случая жесткого закрепления левого конца краевые условия примут вид

Свободное опирание левого конца соответствует условиям

Несамосопряженные краевые условия имеют вид

Другой тип несамосопряженных условий имеет вид

В случае скользящих условий на левом конце имеем

Наконец, условия, когда оба конца балки свободны, записываются в виде

Собственные значения задачи (2.2), (2.3) с краевыми условиями (2.4), (2.5), (2.6), (2.7), (2.8) и (2.9) обозначим λ_i, μ_i, ν_i, ν_i, σ_i и ζ_i, соответственно. Следует отметить, что собственные значения задач (2.2), (2.3), (2.6) и (2.2), (2.3), (2.7) совпадают. Рассматриваемая задача заключается в восстановлении количества пружин $n$, их расположений x_j и податливостей c_j, $j = 1,2, \cdots ,n$, по трем спектрам.

3. Cведение поставленной задачи к обратной спектральной задаче для обыкновенного дифференциального уравнения четвертого порядка. Для того, чтобы свести рассматриваемую задачу к обратной спектральной задаче для обыкновенного дифференциального уравнения четвертого порядка на всем интервале $0 < x < l$, мы будем использовать подход, предложенный в [20], см. также [6]. Введем функцию y(x), определенную на всем интервале $0 < x < l$

Из уравнений. (2.2), (2.3) и (3.1) следует, что функция y(x) удовлетворяет уравнению

где δ(x) – дельта-функция Дирака.

Краевые условия для функции y(x) соответствуют краевым условиям (2.4)–(2.9).

Функция y(x) имеет разрывы в точках ${{x}_{1}},{{x}_{2}}, \cdots ,{{x}_{n}}$. Введем гладкую функцию y₀(x).

где T(x) определяется следующим образом

Производные от функции T(x) равны

где H(x) – функция Хевисайда.

Из уравнений (3.2), (3.3) и (3.5) следует

Краевые условия (2.4)–(2.9) переходят в краевые условия для функции y(x), которые, в свою очередь, совпадают с краевыми условиями для y₀(x)

Дифференцируя дважды уравнение (3.6), получим следующее уравнение

Из выражения для Δ_j (2.3) и равенства (3.3) следует, что уравнение (3.13) можно переписать в следующем виде

Согласно свойствам дельта-функции, справедливо следующее равенство

Из (3.14) и (3.15) получим

Введем функцию

Из (3.16) и (3.17) получим следующее соотношение

Из (3.6) и (3.17) следует, что краевые условия (3.7)–(3.12) преобразуются в следующие краевые условия для функции w(x)

Уравнение (3.18) имеет вид

где m(x) – неизвестная функция.

Таким образом, наша задача сведена к задаче восстановления неизвестной функции m(x) по трем спектрам, соответствующим трем из шести типов краевых условий (3.19)–(3.24). В [21–25] рассмотрен следующий класс уравнений

В этих работах доказано, что две неизвестные функции r(x) и m(x) могут быть восстановлены по трем спектрам. Кроме того, разработан алгоритм восстановления неизвестных функций, при этом предполагается, что r(x) и m(x) регулярные функции. Разработанный алгоритм использует приближение функций m(x) и $1{\text{/}}r\left( x \right)$ линейными комбинациями дельта-функций. По внешнему виду уравнение (3.25) является частным случаем уравнения (3.26) и кажется, что можно автоматически воспользоваться известными результатами, однако, ситуация оказывается несколько сложнее, поскольку в нашем случае функция m(x) выражается с помощью линейной комбинации дельта-функций. Тем не менее, можно показать, что доказательства, приведенные в [22–24], полностью проходят и в рассматриваемом случае.

4. Применение известных результатов к рассматриваемой задаче. Следуя [22], введем решения уравнения (3.25) со следующими данными Коши

Определим некоторые вспомогательные функции

Из данных Коши (4.1) следует, что введенные функции удовлетворяют следующим условиям на правом краю стержня

Из равенства ${\Theta '}\left( {x,{\lambda }} \right) = J{\text{'}}\left( {x,{\lambda }} \right)$ и условий на правом конце (4.3) следует равенство

Вычислим теперь значения введенных вспомогательных функций на левом краю балки. Пусть некоторая функция a(x, λ) есть решение уравнения (3.25). Рассмотрим следующий определитель

Можно видеть, что A(x, λ) удовлетворяет уравнению (3.25). Вычислим значения функции A(x, λ) и ее производных на краях балки

Рассмотрим краевые условия для функции A(x, λ) на левом краю балки для различных функций a(x, λ). Возьмем в качестве функции a(x, λ) решение уравнения (3.25) ${\varphi }(x,{\lambda })$, данные Коши для которого приведены в (4.1). Вторая и третья производные от функции A(x, λ) в этом случае имеют вид

Из (4.9) следует

Поскольку функция A(x, λ) является решением уравнения (3.25), из (4.6), (4.7) и (4.10) следует, что корни уравнения $A{\text{''}}\left( {0,\lambda } \right) = 0$ являются собственными значениями уравнения (3.25) с краевыми условиями (3.19), которые мы обозначили λ_i. Задачи на собственные значения, определяемые уравнением (3.25) с различными краевыми условиями, совпадают с задачами на собственные значения для колебаний балки Эйлера–Бернулли с расположенными внутри точечными массами. Такие задачи рассматривались в [26–29]. В этих работах было доказано, что собственные значения положительны, просты (по крайней мере, начиная с некоторого значения) и имеют асимптотику ${{{\lambda }}_{k}} = O({{k}^{4}})$, k → ∞. В указанных публикациях рассматривался один тип краевых условий. Для других краевых условий результаты получаются аналогично. Используя подход, развитый в [27–29] можно видеть, что функция $A{\text{''}}\left( {0,{\lambda }} \right)$ является целой функцией порядка 1/4. Следовательно, она представима в виде бесконечного произведения, см. [30]

где ${\text{const}} = A{\text{''}}\left( {0,0} \right)$.

Из уравнения (3.25) и краевых условий (4.1) следует

Учитывая (4.1) и (4.12) в выражении для $A{\text{''}}\left( {x,{\lambda }} \right)$ (4.8), получим

Из (4.2), (4.8) и (4.12), имеем

Из (4.11), (4.13) и (4.14) окончательно получим

Аналогичным образом, см. [22], получаются представления в виде бесконечных произведений остальных введенных функций на левом конце стержня

Рассмотрим решение уравнения (3.25), удовлетворяющее следующим граничным условиям: $w{\text{''}}\left( {0,{\lambda }} \right) = {{{\tau }}_{0}}$, $w{\text{'''}}\left( {0,{\lambda }} \right) = - {{\phi }_{0}}$, $w\left( {l,{\lambda }} \right) = 0$, $w{\text{'}}\left( {l,{\lambda }} \right) = 0$. Это решение может быть представлено в виде линейной комбинации функций $u\left( {x,{\lambda }} \right)$ и $v\left( {x,{\lambda }} \right)$, определенных в (4.1)

Подставляя краевые условия в уравнение (4.20) получим:

Решая уравнение (4.21) и учитывая (4.2), получим

Из (4.20), (4.22) и (4.2) следует

Равенства (4.23) аналогичны формулам, приведенным в [24]. Пусть χ(x) функция, удовлетворяющая на правом краю балки условиям: ${\chi }\left( l \right) = {\chi '}\left( l \right) = 0$. Аналогично [26], рассмотрим функционал $\int\limits_0^l {w{\text{''}}(x,{\lambda }){\chi ''}(x)dx} $. Интегрируя по частям и беря во внимание уравнение (3.18) и краевые условия, получим

Рассмотрим собственные функции уравнения (3.18), удовлетворяющие краевым условиям (3.19). Обозначим w_k(x) собственную функцию, соответствующую собственному значению λ_k. Из (4.24) следует

Из (4.25) следует ортогональность собственных функций, соответствующих различным собственным значениям

где ${{\left\| {{{w}_{k}}} \right\|}^{2}} = \int\limits_0^l {w_{k}^{2}\left( x \right)dx} + \sum\limits_{i = 1}^n {{{c}_{i}}w_{k}^{2}\left( {{{x}_{i}}} \right)} $.

Рассмотрим уравнение (4.24) с ${\chi }\left( x \right) = {{w}_{m}}\left( x \right)$.

Система собственных функций w_k(x) полна, в смысле введенной нормы, в пространстве функций, определенных в интервале (0, l) и равных нулю вместе с первой производной на правом конце интервала. Представим функцию $w\left( {x,{\lambda }} \right)$ в виде линейной комбинации функций w_k(x)

Из (4.26)–(4.28) получим

Подставляя выражение (4.29) в (4.28) и беря значение функции $w\left( {x,{\lambda }} \right)$ в точке x = 0, получим

Из (4.23) и (4.30), учитывая произвольность величин ${{{\tau }}_{0}}$ и ${{\phi }_{0}}$, имеем

Из (4.31), используя равенства (4.15), (4.17)–(4.19), получим

Формулы (4.32)–(4.34) аналогичны формулам, полученным в [23, 24], то есть, эти формулы справедливы и для функции m(x), имеющей вид $m\left( x \right) = 1 + \sum\limits_{i = 1}^n {{{c}_{i}}{\delta }\left( {x - {{x}_{i}}} \right)} $. Используя два равенства из (4.32)–(4.34) можно восстановить значения ${{w}_{m}}\left( 0 \right){{\left\| {{{w}_{m}}} \right\|}^{{ - 1}}}$ и $w_{m}^{'}\left( 0 \right){{\left\| {{{w}_{m}}} \right\|}^{{ - 1}}}$ по трем спектрам: $\left\{ {{{{\lambda }}_{i}}} \right\}$ и двум из трех спектров $\left\{ {{{{\mu }}_{i}}} \right\}$, $\left\{ {{{{\nu }}_{i}}} \right\}$ и $\left\{ {{{{\sigma }}_{i}}} \right\}$. Ниже мы рассмотрим восстановление неизвестной функции m(x) по спектру {λ_i} и величинам ${{w}_{m}}\left( 0 \right){{\left\| {{{w}_{m}}} \right\|}^{{ - 1}}}$ и $w_{m}^{'}\left( 0 \right){{\left\| {{{w}_{m}}} \right\|}^{{ - 1}}}$. Хотя наша неизвестная функция m(x) сингулярна, доказательство того, что она единственным образом восстанавливается по трем указанным множествам, полностью совпадает с доказательством из работ [23, 24]. Приведем для полноты изложения основные идеи этого доказательства. Согласно [23], можно заменить уравнение (3.18) системой уравнений

Дискретизируем систему уравнений (4.35). Представим коэффициент 1 из второго уравнения системы и m(x) из четвертого уравнения в виде линейной комбинации дельта-функций.

Используя аппроксимацию (4.36) в уравнении (4.35), получим

Решения уравнений (4.37) удовлетворяют следующим условиям: функции $w\left( {x,{\lambda }} \right)$ и τ(x, λ) непрерывны, функции θ(x, λ) и ϕ(x, λ) имеют разрывы в точках $x_{i}^{*}$. Пределы произвольной функции f(x) в точках $x_{k}^{*}$ слева и справа обозначим $f(x{{_{k}^{*}}^{ - }})$ and $f(x{{_{k}^{*}}^{ + }})$, соответственно. Обозначим

Из (4.37) и (4.38) получим

Краевые условия для закрепленного правого конца имеют вид

На левом конце, рассмотрим следующие краевые условия

Следуя [23, 24], введем обозначения

Здесь и далее верхний индекс T обозначает транспонирование матрицы.

Введем квадратные матрицы порядка N. Три из введенных матриц диагональные

где δ_ij – символ Кронекера. Четвертая матрица имеет вид

Введем также N-мерный вектор-столбец

Уравнения (4.39) с граничными условиями (4.40) и (4.41) можно переписать в матричном виде

Из уравнений (4.46) следует

где ${\mathbf{A}} = {{{\mathbf{E}}}^{T}}{{{\mathbf{L}}}^{{ - 1}}}{{{\mathbf{E}}}^{T}}{\mathbf{RE}}{{{\mathbf{L}}}^{{ - 1}}}{\mathbf{E}}$.

В случае свободного левого края $\left( {{{{\tau }}_{0}} = {{\phi }_{0}} = 0} \right)$ получим следующее уравнение на собственные значения

Матрицы M и A симметричные и положительно определенные, следовательно, собственные числа ${{{\lambda }}_{k}}$ действительные и положительные, а соответствующие собственные векторы ${{{\mathbf{u}}}^{{(k)}}} = (u_{0}^{{\left( k \right)}}, \cdots ,u_{{N - 1}}^{{\left( k \right)}})$ ортогональны ${{({{{\mathbf{u}}}^{{\left( p \right)}}})}^{T}}{\mathbf{M}}{{{\mathbf{u}}}^{{\left( k \right)}}} = {{M}_{p}}{{{\delta }}_{{pk}}}$ и формируют базис в N-мерном линейном пространстве. Величины $w_{k}^{2}\left( 0 \right){{\left\| {{{w}_{k}}} \right\|}^{{ - 2}}}$ и ${{w}_{k}}\left( 0 \right)w_{k}^{'}\left( 0 \right){{\left\| {{{w}_{k}}} \right\|}^{{ - 2}}}$, определенные в уравнениях (4.32)–(4.34), соответствуют величинам ${{(u_{0}^{{\left( k \right)}})}^{2}}M_{k}^{{ - 1}}$ и $u_{0}^{{\left( k \right)}}{\theta }_{0}^{{\left( k \right)}}M_{k}^{{ - 1}}$ в дискретной модели. Таким образом, мы предполагаем, что известны собственные значения ${{{\lambda }}_{k}}$, а также величины $\tilde {u}_{0}^{{\left( k \right)}} = u_{0}^{{\left( k \right)}}M_{k}^{{ - 1/2}}$ и ${\tilde {\theta }}_{0}^{{\left( k \right)}} = {\theta }_{0}^{{\left( k \right)}}M_{k}^{{ - 1/2}}$, необходимо найти величины ${{m}_{i}}$, f_i и l_i. Алгоритм восстановления величин ${{m}_{i}}$, f_i, и l_i разработанный в [23] и [24] может быть полностью перенесен на рассматриваемый нами случай. Дадим краткое описание этого алгоритма.

Введем следующие обозначения: $\tilde {u}_{i}^{{\left( k \right)}} = u_{i}^{{\left( k \right)}}M_{k}^{{ - 1/2}}$, ${\tilde {\theta }}_{i}^{{\left( k \right)}} = {\theta }_{i}^{{\left( k \right)}}M_{k}^{{ - 1/2}}$, ${\tilde {\tau }}_{i}^{{\left( k \right)}} = {\tau }_{i}^{{\left( k \right)}}M_{k}^{{ - 1/2}}$, $\tilde {\phi }_{i}^{{\left( k \right)}} = \phi _{i}^{{\left( k \right)}}M_{k}^{{ - 1/2}}$. В [23, 24] были получены важные равенства

Рассматриваемая задача состоит в следующем. Предполагается, что известны величины $\left\{ {{{{\lambda }}_{k}}} \right\}$, $\{ \tilde {u}_{0}^{{\left( k \right)}}\} $ и $\{ {\tilde {\theta }}_{0}^{{\left( k \right)}}\} $, $k = 1, \cdots ,N$. Заметим также, что $\{ {\tilde {\tau }}_{0}^{{\left( k \right)}} = 0\} $ и $\{ \tilde {\phi }_{0}^{{\left( k \right)}} = 0\} $, k = 1, ..., N. Требуется найти значения $\left\{ {{{m}_{i}}} \right\}$, $\left\{ {{{l}_{i}}} \right\}$, $i = 0, \cdots ,N - 1$ и $\left\{ {{{f}_{k}}} \right\}$, $k = 1, \cdots ,N$.

Следуя [23, 24], приведем алгоритм вычисления величин m_i, l_i, ${{f}_{{i + 1}}}$, $\tilde {u}_{{i + 1}}^{{\left( k \right)}}$, ${\tilde {\theta }}_{{i + 1}}^{{\left( k \right)}}$, ${\tilde {\tau }}_{{i + 1}}^{{\left( k \right)}}$ и $\tilde {\phi }_{{i + 1}}^{{\left( k \right)}}$ с помощью известных величин ${{{\lambda }}_{k}}$, $\tilde {u}_{i}^{{\left( k \right)}}$, ${\tilde {\theta }}_{i}^{{\left( k \right)}}$, ${\tilde {\tau }}_{i}^{{\left( k \right)}}$ и $\tilde {\phi }_{i}^{{\left( k \right)}}$. Рассматриваемый алгоритм состоит из семи шагов.

1. Вычисляется m_i по формуле (4.49).

2. Вычисляется l_i по формуле (4.50).

3. Вычисляется $\tilde {u}_{{i + 1}}^{{\left( k \right)}}$ по первому из уравнений (4.39)

4. Вычисляется $\tilde {\phi }_{{i + 1}}^{{\left( k \right)}}$ по четвертому из уравнений (4.39)

5. Вычисляется ${\tilde {\tau }}_{{i + 1}}^{{\left( k \right)}}$ по третьему из уравнений (4.39)

6. Вычисляется ${{f}_{{i + 1}}}$ по формуле (4.51)

7. Вычисляется ${\tilde {\theta }}_{{i + 1}}^{{\left( k \right)}}$ по второму из уравнений (4.39)

Следовательно, начиная с i = 0, можно последовательно определить все неизвестные величины.

В [23] вводятся последовательности функций

Доказывается, что из последовательностей $\{ {{P}^{{\left( N \right)}}}\left( x \right)\} $ и $\{ {{Q}^{{\left( N \right)}}}\left( x \right)\} $ можно выделить подпоследовательности, сходящиеся к функциям $P\left( x \right) = {{\left( {l - x} \right)}^{3}}{\text{/}}3$ и Q(x) = $\int\limits_x^\infty {P(t)dM(t)} $, соответственно, где $dM\left( x \right) = m(x)dx$. Следовательно, неизвестная функция m(x) может быть восстановлена.

Таким образом, неизвестные параметры из уравнения (3.18) восстанавливаются единственным образом по трем спектрам. Хотя представленный алгоритм очень важен с теоретической точки зрения, он не может быть использован на практике, поскольку он очень чувствителен к погрешностям в данных. В следующем разделе представлен устойчивый к погрешностям в исходных данных алгоритм, позволяющий с помощью трех спектров определить вносимые трещинами повреждения.

5. Алгоритм решения обратной задачи. Для того, чтобы построить устойчивый численный алгоритм в случае продольных колебаний стержня, содержащего множественные поперечные трещины, мы несколько переформулировали исходную постановку обратной задачи, сведя ее к последовательности оптимизационных задач [9]. Оптимизационные задачи часто используются для решения обратных задач [14–17], однако, для успешного применения такого подхода необходимо чтобы целевая функция была адекватна рассматриваемой задаче. В случае продольных колебаний стержня, ослабленного поперечными трещинами, предложенные в [9] целевые функции, учитывали отклонения двух вычисленных спектров от измеренных. Обобщая подход [9] на случай поперечных колебаний, выберем последовательность целевых функций, которые учитывают отклонение трех спектров. Обозначим собственные значения, соответствующие трем типам краевых условий, которые мы будем использовать для определения трещин ${\lambda }_{k}^{{\left( q \right)}}$, $q = 1,2,3$. В предложенном численном алгоритме мы используем конечно-элементную модель балки. В результате, прямая задача определения собственных частот сводится к системе уравнений

где K_q – матрица жесткости, M – матрица масс, d_q – собственный вектор.

Матрицы K_q содержат блоки, соответствующие конечным элементам. Каждый элемент обладает, вообще говоря, собственным модулем Юнга. Таким образом, собственные значения, определяемые уравнениями (5.1) зависят от модулей Юнга конечных элементов. Пусть нам известны собственные значения ${\lambda }_{k}^{{(q*)}}$, $k = 1, \ldots ,N$, $q = 1,2,3$, соответствующие трем типам краевых условий. Построим целевую функцию

Предположим, что трещины снижают жесткость, содержащих их элементов, но не влияют на плотность материала. Тогда, вместо уравнения (2.1), мы рассмотрим уравнение поперечных колебаний балки с переменным модулем Юнга

Слабая формулировка задачи, которая следует из уравнения (5.3), имеет вид

где $K\left( {u,v} \right) = \int\limits_0^l {p\left( x \right)u{\text{''}}\left( x \right)v{\text{''}}\left( x \right)dx} $, $p\left( x \right) = E{\text{*}}\left( x \right){\text{/}}E$, $M\left( {u,v} \right) = \int\limits_0^l {u\left( x \right)v\left( x \right)dx} $.

Собственные значения для различных краевых условий могу быть получены решением уравнения (5.4) в различных функциональных пространствах. Рассмотрим приближение функции$p\left( x \right)$ кусочно-постоянной функцией

Отметим, что интервалы $\left( {{{z}_{i}},{{z}_{{i + 1}}}} \right)$ могут включать несколько конечных элементов, используемых при разбиении. Для значений p_i справедливы неравенства: $0 < {{p}_{i}} \leqslant 1$. Если в интервале $\left( {{{z}_{i}},{{z}_{{i + 1}}}} \right)$ нет повреждений, то ${{p}_{i}} = 1$. Если p_i = 0, то это означает, что трещина полностью перерезает балку. Таким образом, в результате принятого приближения собственные значения ${\lambda }_{k}^{{\left( q \right)}}$ становятся функциями ${\mathbf{p}} = \left( {{{p}_{1}}, \cdots ,{{p}_{P}}} \right)$. Следовательно, функция F_N, введенная в (5.2), также является функцией от ${\mathbf{p}}$.

Алгоритм минимизации функции ${{F}_{N}}\left( {\mathbf{p}} \right)$ включает многократное решение прямой задачи нахождения собственных значений ${\lambda }_{k}^{{\left( q \right)}}\left( {\mathbf{p}} \right)$. В расчетах прямая задача решается методом конечных элементов с использованием кубических сплайнов. Функции ${{F}_{N}}({\mathbf{p}})$ представляют собой сумму квадратов. Для минимизации таких функций очень эффективен алгоритм Левенберга–Марквардта [31], использованный нами и в [9]. Применение этого алгоритма требует задание начального приближения для p. Кроме того, в процессе реализации алгоритма приходится вычислять производные от собственных значений $\partial {\lambda }_{k}^{{\left( q \right)}}\left( {\mathbf{p}} \right){\text{/}}\partial {{p}_{j}}$. В представленных ниже вычислениях, как и в [9], было выбрано начальное приближение ${{{\mathbf{p}}}^{0}} = \left( {1, \cdots ,1} \right)$. Такой выбор соответствует неповрежденной балке. В случае собственных значений ${{{\lambda }}_{k}}$, ${{{\mu }}_{k}}$, ${{{\sigma }}_{k}}$ и ${{{\zeta }}_{k}}$, соответствующих самосопряженным краевым условиям, производные от собственных значений выражаются через собственные векторы и производную от матрицы жесткости [32]

Здесь предполагается, что собственные векторы нормализованы $({\mathbf{Md}}_{k}^{{(q)}}({\mathbf{p}}),{\mathbf{d}}_{m}^{{(q)}}({\mathbf{p}}))$ = = δ_km.

В случае собственных значений ${{{\nu }}_{k}}$, соответствующих несамосопряженным краевым условиям, производные вычисляются по формуле [33]

где ${{{\mathbf{g}}}_{k}}\left( {\mathbf{p}} \right)$ – собственный вектор, отвечающий задаче на собственные значения $({{{\mathbf{K}}}^{T}}({\mathbf{p}}) - {{{\nu }}_{k}}{\mathbf{M}}){{{\mathbf{g}}}_{k}}({\mathbf{p}})$ = 0. Собственные векторы d_k(p) и g_m(p) удовлетворяют условиям $({\mathbf{M}}{{{\mathbf{d}}}_{k}}({\mathbf{p}}),{{{\mathbf{g}}}_{m}}({\mathbf{p}}))$ = δ_km.

Для того, чтобы уменьшить размерность подпространства, в котором ищется минимум функции ${{F}_{N}}\left( {\mathbf{p}} \right)$, решение задачи осуществляется в несколько этапов. Сперва балка разбивается на P одинаковых частей и минимизацией функции ${{F}_{N}}\left( {\mathbf{p}} \right)$ находятся значения $p_{i}^{*}$, соответствующие жесткостям той части балки, которая расположена в интервале$\left( {{{z}_{i}},{{z}_{{i + 1}}}} \right)$. В примерах ниже P = 11. Затем положения повреждений определяются более точно. Чтобы это сделать величина P удваивается. Поэтому каждый интервал $\left( {{{z}_{i}},{{z}_{{i + 1}}}} \right)$ делится на два одинаковых интервала, жесткость которых мы обозначаем ${{p}_{{i1}}}$ и ${{p}_{{i2}}}$. Если на первом этапе часть балки, расположенная в интервале $\left( {{{z}_{i}},{{z}_{{i + 1}}}} \right)$, оказалась неповрежденной ($p_{i}^{*} = 1$), то мы определяем ${{p}_{{i1}}} = 1$, ${{p}_{{i2}}} = 1$. Величины ${{p}_{{i1}}}$ и ${{p}_{{i2}}}$ мы рассматриваем в качестве переменных только если $p_{i}^{*} < 1$. После определения всех неизвестных ${{p}_{{i1}}}$, ${{p}_{{i2}}}$, процедура повторяется. В рассматриваемых ниже примерах количество элементов удваивалось трижды и, тем самым, доводилось до 88.

6. Численные примеры. Согласно представленным выше результатам, реконструкция дефектов может производиться с помощью следующих троек спектров: $\left\{ {{{{\lambda }}_{k}},{{{\mu }}_{k}},{{{\sigma }}_{k}}} \right\}$, $\left\{ {{{{\lambda }}_{k}},{{{\mu }}_{k}},{{{\nu }}_{k}}} \right\}$ и $\left\{ {{{{\lambda }}_{k}},{{{\sigma }}_{k}},{{{\nu }}_{k}}} \right\}$. Для сравнения эффективности идентификации с помощью указанных троек спектров рассмотрим несколько примеров. Во всех примерах рассматривается балка со следующими геометрическими и механическими параметрами: длина балки l = 1 м, балка имеет квадратное сечение с шириной $b = 0.02$ м и высотой $h = 0.02$ м, модуль Юнга материала $E = 2.1 \times {{10}^{{11}}}$ Н/м, плотность материала ${\rho }$ = 7800 кг/м³, коэффициент Пуассона $\nu = 0.3$. Собственные значения, которые являются входными данными для предложенного численного алгоритма, были получены численно, путем решения прямых задач. Подчеркнем, что прямые задачи были решены не методом конечных элементов, а решением задачи в исходной формулировке, представленной в разделе 2, с помощью метода, предложенного в [20].

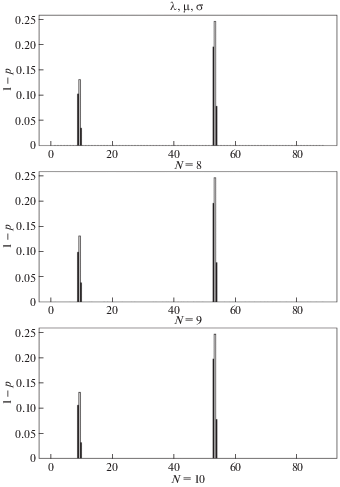
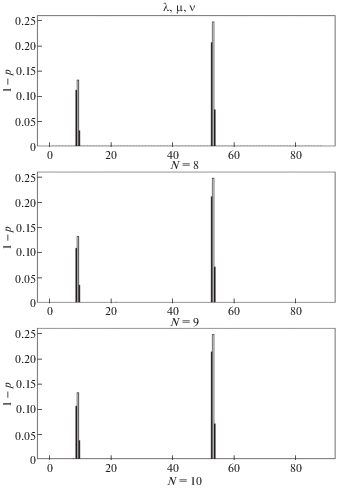
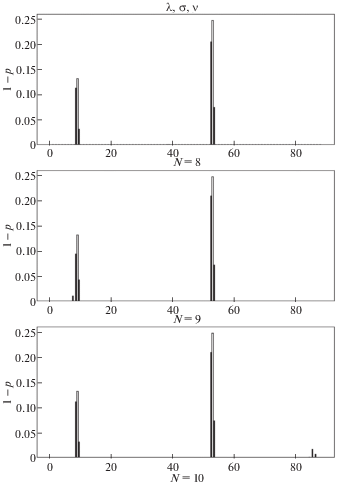
Сперва рассматривается задача идентификации двух односторонних трещин. Первая трещина расположена в точке ${{x}_{1}} = 0.1$ м и имеет относительную глубину ${{s}_{1}} = {{a}_{1}}{\text{/}}h$ = 0.1. Вторая трещина расположена в точке ${{x}_{2}} = 0.6$ м и имеет относительную глубину ${{s}_{2}} = {{a}_{2}}{\text{/}}h$ = 0.15. Здесь ${{a}_{i}}$ – размеры трещин. Соотношение между жесткостью элемента, содержащего трещину, и податливостью пружины c, моделирующей трещину, имеет вид

где Δl длина элемента. Податливость пружины выражается через длину односторонней трещины a [20]

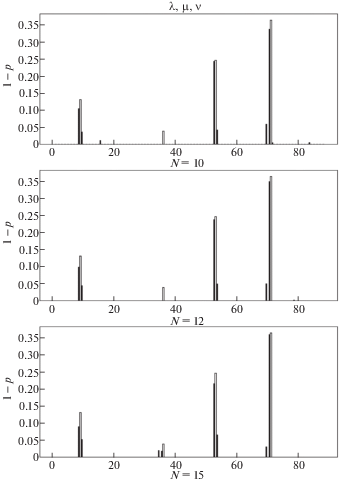
На рис. 1–3 представлены результаты восстановления податливостей элементов при использовании 8, 9 и 10 собственных значений из каждого спектра для спектров $\left\{ {{{{\lambda }}_{k}},{{{\mu }}_{k}},{{{\sigma }}_{k}}} \right\}$, $\left\{ {{{{\lambda }}_{k}},{{{\mu }}_{k}},{{{\nu }}_{k}}} \right\}$ и $\left\{ {{{{\lambda }}_{k}},{{{\sigma }}_{k}},{{{\nu }}_{k}}} \right\}$, соответственно. По оси $x$ отложены номера элементов, а по оси $y$ величины 1 – p, соответствующие податливостям элементов. Элементы занумерованы слева направо. Черные вертикальные полосы соответствуют полученным численным значениям податливостей элементов. Светлые вертикальные полосы соответствуют теоретическим значениям податливостей элементов, рассчитанным по формулам (6.1), (6.2). Как видно из рисунков, обе трещины обнаруживаются всеми тройками спектров. Результаты ведут себя устойчиво при увеличении количества используемых собственных значений. Рассматриваемые трещины находятся в 9 и 53 элементах, однако, поскольку они расположены весьма близко к границам 10 и 54 элементов, они обнаруживаются сразу в двух элементах. Результаты, полученные с помощью спектров $\left\{ {{{{\lambda }}_{k}},{{{\sigma }}_{k}},{{{\nu }}_{k}}} \right\}$, несколько хуже остальных. При N = 9 первая трещина немного хуже локализована, так как отражается в трех элементах, а при N = 10 появляется небольшое паразитное решение.

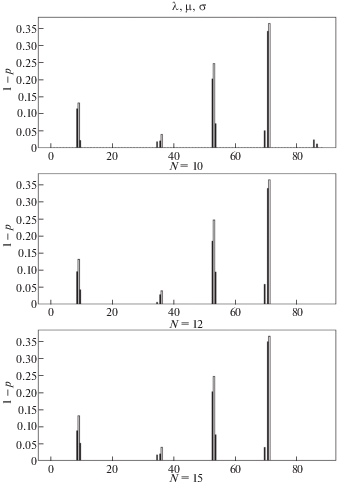
На рис. 4–6 представлены результаты идентификации четырех трещин. Здесь к двум трещинам, рассмотренным выше, добавлены трещины с параметрами: ${{x}_{3}} = 0.4$ м, ${{s}_{3}} = 0.05$, ${{x}_{4}} = 0.8$ м, ${{s}_{4}} = 0.2$. Таким образом, третья трещина расположена в элементе 36, а четвертая – в элементе 71. Чем больше трещин, тем большее количество собственных частот необходимо знать для их идентификации. Как видно из рис. 4, при использовании собственных значений $\left\{ {{{{\lambda }}_{k}},{{{\mu }}_{k}},{{{\sigma }}_{k}}} \right\}$ стабилизация результатов наступает с N = 12. В случае N = 10 имеется одно паразитное решение. Из рис. 5 видно, что при использовании собственных значений $\left\{ {{{{\lambda }}_{k}},{{{\mu }}_{k}},{{{\nu }}_{k}}} \right\}$ самая маленькая трещина начинает проявляться с N = 15. Наиболее плохие результаты получаются в случае идентификации с помощью спектров $\left\{ {{{{\lambda }}_{k}},{{{\sigma }}_{k}},{{{\nu }}_{k}}} \right\}$. Здесь появляется ряд паразитных решений. Достаточно устойчиво определяются только две трещины, имеющие наибольшие размеры, но и они локализуются недостаточно четко, затрагивая до четырех элементов.

7. Заключение. Рассмотрена задача идентификации конечного числа поперечных трещин в стержне по собственным частотам поперечных колебаний. Доказано, что любое число трещин может быть однозначно определено с помощью трех спектров, отвечающих различным краевым условиям. Определены три варианта троек спектров, с помощью которых возможна реконструкция дефектов. Разработан численный метод идентификации повреждений, соответствующих поперечным трещинам. Рассмотрены численные примеры, на которых сравнивалась эффективность идентификации трещин с помощью различных троек спектров.

Отметим, что доказательство того, что любое число трещин может быть идентифицировано с помощью трех спектров, опиралось на известные результаты по обратным спектральным задачам для обыкновенных дифференциальных уравнений четвертого порядка на отрезке. При этом, рассматриваемая обратная задача свелась к задаче восстановления одной, пусть и обобщенной функции, в то время как в классических результатах восстанавливается две регулярные функции. Это позволяет надеяться, хотя к настоящему времени такой строгий результат и отсутствует, что идентификация трещин возможна и с помощью двух спектров поперечных колебаний. Проверить это предположение, по меньшей мере численно, предполагается в дальнейших исследованиях.

Работа выполнена по теме государственного задания № госрегистрации AAAA-A20-120011690132-4 и при поддержке РФФИ (проект № 19-01-00100).