1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 4, 2020

Известия РАН. Механика твердого тела, 2020, № 4, стр. 7-24

АУКСЕТИКИ СРЕДИ МАТЕРИАЛОВ С КУБИЧЕСКОЙ АНИЗОТРОПИЕЙ

В. А. Городцов a, Д. С. Лисовенко a, *

a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: lisovenk@ipmnet.ru

Поступила в редакцию 12.02.2020
После доработки 28.02.2020
Принята к публикации 29.02.2020

Полный текст (PDF)

Аннотация

В статье приводится краткий обзор работ по кристаллическим материалам с отрицательным коэффициентом Пуассона (кристаллическим ауксетикам), обладающим кубической анизотропией. Продемонстрировано, что 1/4 всех кубических кристаллов обладают ауксетическими свойствами. Еще больше ауксетиков выявляется среди хиральным нано/микротрубок с кубической цилиндрической анизотропией. Установлено, что хиральные нано/микротрубки из кубических кристаллов проявляют при кручении линейный эффект Пойнтинга в отличие от известного нелинейного эффекта для изотропных материалов. В случае продольного растяжения двухслойных композитов показано, что происходит нарушение правила смесей Фойгта при наличии слоя из ауксетиков.

Ключевые слова: ауксетики, коэффициент Пуассона, кристаллы, нанотрубки, пластины, композиты

1. Введение. В механике долгое время принималось, что у реальных изотропных упругих материалов коэффициент Пуассона ν не бывает отрицательным [1], хотя термодинамическое ограничение в трехмерном случае

$ - 1 \leqslant \nu \leqslant 0.5$
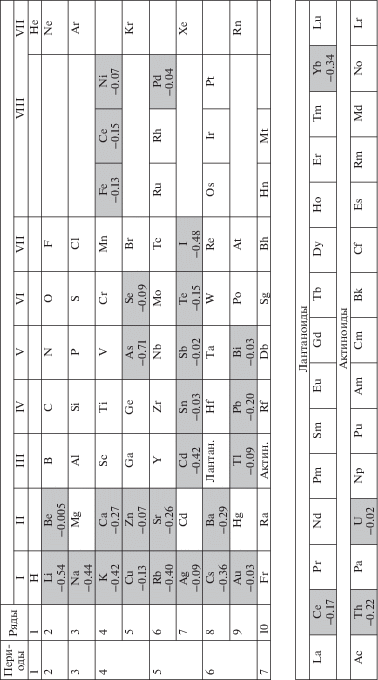
не требует этого. Не требует этого и ограничение
$ - 1 \leqslant \nu \leqslant \frac{1}{{D - 1}}$
при другой размерности изотропной среды D [2]. Материалам с отрицательным коэффициентом Пуассона было присвоено название ауксетики [3–5]. В анизотропной упругости положительная определенность энергии деформации не требует каких-либо общих теоретических ограничений на коэффициенты Пуассона упругих материалов в случае кристаллов триклинной, моноклинной, орторомбической, тетрагональной, ромбоэдрической, гексагональной и кубической систем [6].

Впервые о возможности отрицательного коэффициента Пуассона у реальных анизотропных материалов было сказано в известной монографии А. Лява [7], в которой говорилось о пирите FeS2 с отрицательным коэффициентом Пуассона –1/7. В 1962 году сообщалось об отрицательном коэффициенте Пуассона для кварца в интервале температур от 20 до 650°C [8]. Значение –0.6 достигалось при температуре близкой к 500°C. Позже отрицательность коэффициента Пуассона наблюдалась в ферромагнитных пленках (Fe, Ni, Co и пермаллое) [9], сплаве In-Tl [10], некоторых кубических кристаллах [11, 12], никелевом сплаве [13], цеолитах [14], металлических и полимерных пенах [15, 16]. На данный момент известно свыше 450 кристаллических материалов с отрицательным коэффициентом Пуассона [17–24]. Среди них наибольшее количество кристаллов с отрицательным коэффициентом Пуассона (более 300) обладают кубической анизотропией [18]. На рис. 1 представлена периодическая система элементов Д.И. Менделеева, на которой серым цветом указаны ауксетические элементы, составляющие 1/4 часть всех элементов. Указанные в периодической системе минимальные значения коэффициента Пуассона взяты из [17–23]. В [9] для ОЦК кристаллов, в [25] для $\alpha $-кристобалита, в [26] для черного фосфора и в [27] для бифталатов предлагались некоторые структурные модели, поясняющие ауксетическое поведение кристаллов.

Рис. 1

Описание поведения ауксетических анизотропных материалов базируется на анализе таких упругих характеристик, как коэффициенты Пуассона, модули Юнга и модули сдвига [19, 28, 29], и различных классификационных схемах [19, 30–32]. Ранняя общая классификация по коэффициенту Пуассона [30] опиралась на деление анизотропных материалов на полные ауксетики (материалы с отрицательными коэффициентами Пуассона при любых ориентациях), неауксетики (материалы с положительными коэффициентами Пуассона при любых ориентациях) и ауксетики, у которых знак коэффициента Пуассона может изменяться при изменении ориентации. В [31] последний тип ауксетиков предложено называть частичными ауксетиками.

2. Упругие свойства кубических кристаллов. Выражения для модуля Юнга $E$ и коэффициента Пуассона $\nu $ для кристаллов с кубической анизотропией можно записать в виде, предложенном в [18, 32],

$\frac{1}{e} = 1 - \frac{\delta }{2}M(\varphi ,\theta ),\quad \frac{\nu }{e} = - \frac{\delta }{2}[N(\varphi ,\theta ,\psi ) - \Pi ]$
(2.1)
$\begin{gathered} e = E{{s}_{{11}}},\quad \Pi \equiv - \frac{{2{{s}_{{12}}}}}{\Delta },\quad \delta \equiv \frac{\Delta }{{{{s}_{{11}}}}} \\ 0 \leqslant M\left( {\varphi ,\theta } \right) \equiv {{\sin }^{2}}2\theta + {{\sin }^{4}}\theta {{\sin }^{2}}2\varphi \leqslant \frac{4}{3} \\ \end{gathered} $
$0 \leqslant N\left( {\varphi ,\theta ,\psi } \right) \equiv 3{{\sin }^{2}}\theta {{\cos }^{2}}\theta {{\cos }^{2}}\psi + {{(\cos \theta \cos 2\varphi \cos \psi - \sin \psi )}^{2}}{{\sin }^{2}}\theta \leqslant 1$

Здесь безразмерный модуль Юнга e и коэффициент Пуассона ν зависят от двух безмерных параметров $\Pi $, δ и угловых переменных. Размерная комбинация коэффициентов податливости $\Delta \equiv {{s}_{{11}}} - {{s}_{{12}}} - 0.5{{s}_{{44}}}$ известна как параметр анизотропии для кубических кристаллов. Требование положительной определенности упругой энергии накладывает следующие ограничения на коэффициенты податливости

(2.2)
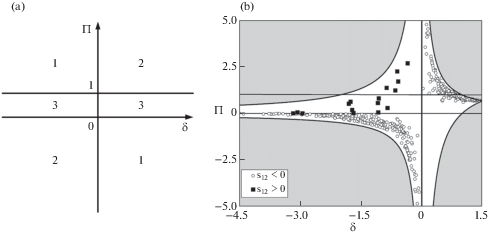
${{s}_{{11}}} > 0,\quad {{s}_{{44}}} > 0,\quad {{s}_{{11}}} > {{s}_{{12}}} > - 0.5{{s}_{{11}}}$
которые дают следующие ограничения безразмерных параметров в виде

(2.3)
$\Pi \delta > 2\delta - 2,\quad 1 > \Pi \delta > - 2,\quad \delta < 1.5$

Из (2.1)–(2.3) видно, что неауксетики характеризуются неравенствами $\Pi < 0$, δ < 0 или $\Pi > 1$, δ > 0. Это отражено на рис. 2a (области 2), на которой приведена классификационная схема для кубических кристаллов на основе двух параметров $\Pi $ и δ. На рис. 2b классификационная схема кубических кристаллов дополнена кривыми границ устойчивости (2.3). На этой схеме нанесены значения $\Pi $ и δ для более 1100 кубических кристаллов из [33]. Из этого рисунка видно, что около 3/4 кубических кристаллов являются неауксетиками.

Рис. 2

Для полных ауксетиков имеют место неравенства $\Pi < 0,\;\delta > 0$ или $\Pi > 1,\;\delta < 0$ (области 1 на рис. 2a). Таких ауксетических кристаллов известно не много: кристаллы Sm0.7Y0.3S, Sm0.75Y0.25S, Sm0.75La0.25S, Sm0.65La0.35S, Sm0.75Tm0.25S, Ba с положительным значением коэффициента податливости ${{s}_{{12}}} > 0$. Большинство кубических кристаллов имеют отрицательное значение коэффициента податливости ${{s}_{{12}}} < 0$. Кристаллы с ${{s}_{{12}}}$ > 0 (менее двух десятков) изображены на рис. 2b квадратами. Отметим еще, что согласно одним экспериментальным данным Sm0.7Y0.3S, Sm0.75Y0.25S, Ba – полные ауксетики, а согласно другим частичные ауксетики (см. [18]).

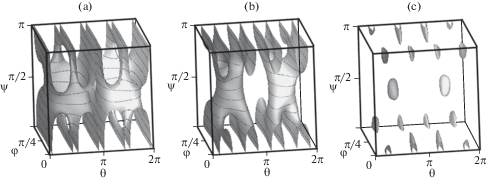
Частичные ауксетики характеризуются неравенством $0 \leqslant \Pi \leqslant 1$ (области 3 на рис. 2a), которое следует из (2.1). Численный анализ [18] показал, что большинство частичных ауксетиков имеют отрицательное значение коэффициента податливости ${{s}_{{12}}} < 0$ и $0 \leqslant \Pi \leqslant 1$, δ > 0. Полный список кубических ауксетиков представлен в таблицах 1–9 работы [18]. На рис. 3 изображено изменение формы поверхности ауксетичности $\nu (\varphi ,\theta ,\psi )$ = 0 в пространстве углов Эйлера при $\Pi = 0.1$ (a), $\Pi = 0.5$ (b) и $\Pi = 0.9$ (c). Как видно из этого рисунка по мере увеличения параметра $\Pi $ поверхность ауксетичности изменяется от “открытого типа” к “закрытому”. Такое топологическое изменение поверхности ауксетичности происходит при критическом значении безразмерного параметра ${{\Pi }_{c}} \approx 0.745$. Знак безразмерного параметра δ определяет по какую сторону от поверхности ауксетичности находится область с отрицательным коэффициентом Пуассона (при δ > 0 эта область располагается внутри).

Рис. 3

Максимальные и минимальные значения коэффициента Пуассона для кубических кристаллов выявляются среди следующих кристаллографических направлений

${{\nu }_{{[100],[001]}}} = \frac{{\Pi \delta }}{{\text{2}}},\quad {{\nu }_{{[001],[110]}}} = \frac{{\Pi \delta }}{{2 - \delta }}$
${{\nu }_{{[1\bar {1}0],[110]}}} = \frac{{\delta (\Pi - 1)}}{{2 - \delta }},\quad {{\nu }_{{(111),[111]}}} = \frac{{\delta (1.5\Pi - 1)}}{{3 - 2\delta }}$

Последние три индекса в квадратных скобках указывают направление растяжения, а первых три – поперечное направление. В круглых скобках будут указываться кристаллографические плоскости. Анализ этих формул с использованием термодинамических ограничений (2.3) показывает, что

$\Pi > 0,\quad 0 < \delta < 1.5{\kern 1pt} :\;\;{{\nu }_{{{\text{[}}001],[110]}}} > {{\nu }_{{[100],[001]}}} > {{\nu }_{{(111),[111]}}} > {{\nu }_{{[1\bar {1}0],[110]}}}$
$\Pi > 0,\quad \delta < 0{\kern 1pt} :\;\;{{\nu }_{{[1\bar {1}0],[110]}}} > {{\nu }_{{(111),[111]}}} > {{\nu }_{{[001],[110]}}} > {{\nu }_{{[100],[001]}}}$
$\Pi < 0,\quad \delta < 0{\kern 1pt} :\;\;{{\nu }_{{[1\bar {1}0],[110]}}} > {{\nu }_{{(111),[111]}}} > {{\nu }_{{[100],[001]}}} > {{\nu }_{{[001],[110]}}}$
$\Pi < 0,\quad 0 < \delta < 1.5{\kern 1pt} :\;\;{{\nu }_{{[100],[001]}}} > {{\nu }_{{[001],[110]}}} > {{\nu }_{{(111),[111]}}} > {{\nu }_{{[1\bar {1}0],[110]}}}$

Из этих неравенств видно, что для большинства частичных ауксетиков для которых справедливо $0 \leqslant \Pi \leqslant 1$ и δ > 0, минимальным значением коэффициента Пуассона будет ${{\nu }_{{[1\bar {1}0],[110]}}}$ и имеет место неравенство $\Delta > 2\left| {{{s}_{{12}}}} \right|$ [17]. Чтобы коэффициент Пуассона ${{\nu }_{{(111),[111]}}}$ был отрицательным должно выполняться неравенство $\Delta > 3\left| {{{s}_{{12}}}} \right|$ для кубических кристаллов, попадающих в $0 \leqslant \Pi \leqslant 1$ и δ > 0. Согласно экспериментальным данным для кубических кристаллов [33] был обнаружен один такой ауксетик – Mn85.3Ni8.8C5.9$(\Delta {\text{/|}}{{s}_{{12}}}{\text{|}} = 3.01)$ c ${{\nu }_{{(111),[111]}}} = - 0.01$.

В [28, 29] было показано, что кроме указанных ориентаций экстремальные значения коэффициента Пуассона могут наблюдаться при других ориентациях, например, при растяжении в направлении близком [111 ] . Это свойственно метастабильным кристаллам с эффектом памяти формы при мартенситной перестройке кристаллической решетки [29]. Для сплавов In-Tl (InTl (25at%Tl) ${{\nu }_{{\min }}} = - 1.079$; InTl (27at%Tl) ${{\nu }_{{\min }}}$ = = ‒1.079; InTl (27at%Tl, 200 K) ${{\nu }_{{\min }}} = - 1.079$) и Fe-Pd (FePd (28at%Pd) ${{\nu }_{{\min }}} = - 1.079$) значения экстремумов коэффициента Пуассона могут быть меньше –1 (предельного значения для изотропных материалов).

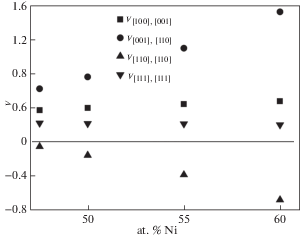
Экстремальные значения коэффициента Пуассона для сплавов могут сильно меняться при изменении от концентрации какого-либо из веществ. На рис. 4 приведены значения коэффициентов Пуассона для сплава AlNi в зависимости от атомного содержания никеля (at%Ni). На этом рисунке квадратами обозначены значения коэффициента Пуассона ${{\nu }_{{[100],[001]}}}$, кружками – ${{\nu }_{{{\text{[}}001],[110]}}}$, треугольниками с вершиной вверх – ${{\nu }_{{[1\bar {1}0],[110]}}}$, треугольниками с вершиной вниз – ${{\nu }_{{(111),[111]}}}$. Можно видеть, что коэффициенты ${{\nu }_{{[100],[001]}}}$ и ${{\nu }_{{(111),[111]}}}$ слабо зависят от концентрации никеля. Коэффициент Пуассона ${{\nu }_{{[1\bar {1}0],[110]}}}$ монотонно уменьшается с увеличением содержания никеля от –0.06 для AlNi (47.5at%Ni) до –0.74 для AlNi (60at%Ni). Сильное изменение ${{\nu }_{{[1\bar {1}0],[110]}}}$ выявляется у сплавов CuZn (латуни) и CuMn с изменением содержания цинка и марганца. В случае латуни коэффициент Пуассона меняется от ${{\nu }_{{[1\bar {1}0],[110]}}} = - 0.14$ для CuZn (4.1at%Zn) до ${{\nu }_{{[1\bar {1}0],[110]}}} = - 0.57$ для CuZn (47.8at%Zn). Для сплава CuMn коэффициент монотонно уменьшается от ${{\nu }_{{[1\bar {1}0],[110]}}} = - 0.14$ для CuMn (1.25at%Mn) до ${{\nu }_{{[1\bar {1}0],[110]}}} = - 0.61$ для CuMn (72at%Mn).

Рис. 4

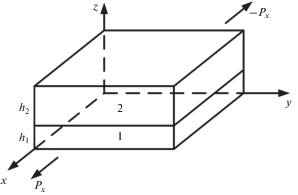
3. Продольное растяжение тонкой двухслойной пластины из кубических кристаллов. Рассмотрим продольное растяжение тонкой двухслойной пластины из кубических кристаллов, и обсудим особенности поведения эффективного модуля Юнга и эффективных коэффициентов Пуассона. Пластина из нижнего слоя 1 толщины h1 и верхнего слоя 2 толщины h2, заполненная одинаково ориентированными кубическими кристаллами, растягивается в продольном направлении вдоль оси x (рис. 5). Оси лабораторной системы координат $x,y,z$ совпадают с кристаллографическими осями [100 ] , [010], [001]. В предположении однородности деформаций слоев пластины в отсутствие сил на ее поверхностях и продольного кручения закон Гука определяет связи нормальных деформаций с нормальными напряжениями в слоях с k = 1 и k = 2

$\varepsilon _{x}^{k} = s_{{11}}^{k}\sigma _{x}^{k} + s_{{12}}^{k}\sigma _{y}^{k}$
$\varepsilon _{y}^{k} = s_{{12}}^{k}\sigma _{x}^{k} + s_{{11}}^{k}\sigma _{y}^{k}\quad (k = 1,2)$
$\varepsilon _{z}^{k} = s_{{12}}^{k}(\sigma _{x}^{k} + \sigma _{y}^{k})$
Рис. 5

Верхний индекс будет указывать номер слоя. Растяжение тонкой двухслойной пластины в направлении оси x удельной силой $P$ (при выборе единичной ширины пластины в направлении оси $y$) позволяет написать уравнения равновесия следующим образом

${{h}_{1}}\sigma _{x}^{1} + {{h}_{2}}\sigma _{x}^{2} = P,\quad {{h}_{1}}\sigma _{y}^{1} + {{h}_{2}}\sigma _{y}^{2} = 0$

Предположение жесткого контакта слоев тонкой двухслойной пластины дает равенство нормальных деформаций в плоскости пластины $\varepsilon _{x}^{1} = \varepsilon _{x}^{2}$, $\varepsilon _{y}^{1} = \varepsilon _{y}^{2}$. В итоге выражения эффективного модуля Юнга и эффективных коэффициентов Пуассона двухслойной пластины из кубических кристаллов принимают вид (см. подробнее [34, 35])

$E = \frac{1}{{{{h}_{1}} + {{h}_{2}}}}\frac{{2{{S}_{ + }}{{S}_{ - }}}}{{{{S}_{ + }} + {{S}_{ - }}}},\quad {{S}_{ \pm }} \equiv \sum\limits_{k = 1}^2 {\frac{{{{h}_{k}}}}{{s_{{11}}^{k} \pm s_{{12}}^{k}}}} $
$\nu _{{xy}}^{{}} \equiv \frac{{\varepsilon _{y}^{1}}}{{\varepsilon _{x}^{1}}} = - \frac{{\varepsilon _{y}^{2}}}{{\varepsilon _{x}^{1}}} = \frac{{{{S}_{ + }} - {{S}_{ - }}}}{{{{S}_{ + }} + {{S}_{ - }}}}$
$\nu _{{xz}}^{k} = - \frac{{\varepsilon _{z}^{k}}}{{\varepsilon _{x}^{1}}} = - \frac{{s_{{12}}^{k}}}{{s_{{11}}^{k} + s_{{12}}^{k}}}\frac{{2{{S}_{ - }}}}{{{{S}_{ + }} + {{S}_{ - }}}}$

Используя выражения для коэффициентов податливости слоев $s_{{11}}^{k} = 1{\text{/}}{{E}^{k}}$, $s_{{12}}^{k}$ = = ‒νk/Ek, перепишем формулы для E, νxy, $\nu _{{xz}}^{k}$ в виде

(3.1)
$E = \alpha \left\langle E \right\rangle ,\quad \left\langle E \right\rangle \equiv \frac{{{{h}_{1}}{{E}^{1}} + {{h}_{2}}{{E}^{2}}}}{{{{h}_{1}} + {{h}_{2}}}}$
(3.2)
$\alpha \equiv 1 + \frac{\lambda }{{1 + \lambda }}\frac{{{{{(\nu _{{}}^{1} - \nu _{{}}^{2})}}^{2}}}}{{\lambda [1 - {{{(\nu _{{}}^{2})}}^{2}}] + [1 - {{{(\nu _{{}}^{1})}}^{2}}]}},\quad \lambda \equiv \frac{{{{h}_{1}}{{E}^{1}}}}{{{{h}_{2}}{{E}^{2}}}}$
(3.3)
$\nu _{{xy}}^{{}} = \frac{{{{\nu }^{2}}[1 - {{{({{\nu }^{1}})}}^{2}}] + \lambda {{\nu }^{1}}[1 - {{{({{\nu }^{2}})}}^{2}}]}}{{1 - {{{({{\nu }^{1}})}}^{2}} + \lambda [1 - {{{({{\nu }^{2}})}}^{2}}]}}$
(3.4)
$\nu _{{xz}}^{1} = {{\nu }^{1}}(1 - {{\nu }^{2}})\frac{{1 + {{\nu }^{1}} + \lambda (1 + {{\nu }^{2}})}}{{1 - {{{({{\nu }^{1}})}}^{2}} + \lambda [1 - {{{({{\nu }^{2}})}}^{2}}]}}$
(3.5)
$\nu _{{xz}}^{2} = {{\nu }^{2}}(1 - {{\nu }^{1}})\frac{{1 + {{\nu }^{1}} + \lambda (1 + {{\nu }^{2}})}}{{1 - {{{({{\nu }^{1}})}}^{2}} + \lambda [1 - {{{({{\nu }^{2}})}}^{2}}]}}$

Согласно “правилу смесей Фойгта” для среднего значения модуля Юнга должно быть

(3.6)
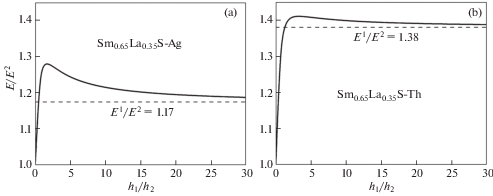
$\left\langle E \right\rangle = \frac{{{{E}^{1}}{{h}_{1}} + {{E}^{2}}{{h}_{2}}}}{{{{h}_{1}} + {{h}_{2}}}}$

Таким образом, формулы для эффективного модуля Юнга двухслойной пластины из кубических кристаллов (3.1), (3.2) вообще говоря, не следует правилу смесей (α ≠ 1). Используя ограничения (2.2), можно утверждать, что α > 1 (за исключением случая $\nu _{{}}^{1}$ = ν2). Из формулы (3.2) также можно видеть, что α возрастает с увеличением разности положительных коэффициентов Пуассона слоев для пары неауксетиков и для комбинации ауксетик-неауксетик. Однако при близких значениях модулей Юнга и коэффициентов Пуассона двух слоев точность предсказания эффективного модуля Юнга по правилу смесей Фойгта оказывается достаточно удовлетворительной. На рис. 6 представлены изменчивость эффективного модуля Юнга для пластин типа ауксетик-неауксетик Sm0.65La0.35S-Ag и Sm0.65La0.35S-Th в зависимости от отношения толщин слоев h1/h2. Для ауксетического кристалла Sm0.65La0.35S имеем ${{\nu }^{1}} = - 0.34$, ${{E}^{1}} = 50.8$ ГПа, а для кристаллов Ag и Th имеем упругие характеристики ${{\nu }^{2}} = 0.43$, ${{E}^{2}} = 43.5$ ГПа и ${{\nu }^{2}}$ = 0.39, ${{E}^{2}} = 43.5$ ГПа, соответственно. Можно видеть из рисунка, что правило смеси неприменимо для нахождения эффективного модуля Юнга двухслойной пластины с ауксетическим слоем. Наличие ауксетика приводит к тому, что эффективный модуль Юнга превосходит модули Юнга обоих исходных материалов E1 и E2 для любых толщин слоев.

Рис. 6

Анализ, проведенный в [34], показал, что эффективный коэффициент Пуассона также не следует правилу смесей для двухслойных пластин при наличии ауксетического слоя. В частности, было установлено, что эффективный продольный коэффициент Пуассона двухслойной пластины оказывается отрицательным при заполнении ауксетиком только одного слоя с достаточно большим параметром h1/h2 и отношением модулей Юнга. При малом отношении ${{h}_{1}}{{E}^{1}}{\text{/(}}{{h}_{2}}{{E}^{2}})$ эффективный продольный коэффициент Пуассона νxy оказывается положительным.

В [36] был проведен аналогичный анализ изменчивости эффективных характеристик двухслойных пластин из различно ориентированных кубических кристаллов при продольном растяжении. Установлено, что сильное различие зависимостей эффективных модулей Юнга и эффективных коэффициентов Пуассона таких двухслойных пластин от угла относительной ориентации и отношения толщин слоев имеет место при заполнении слоев одинаковыми кристаллами с положительными или отрицательными коэффициентами анизотропии δ. Например, в случае двухслойной пластины с кубическими кристаллами InTl (25at%Tl) и Li с δ > 0, эффективный модуль Юнга монотонно увеличивается и достигает максимального значения при угле ориентации 45°. Для двухслойной пластины из Sm0.75Tm0.25S с δ < 0 эффективный модуль Юнга монотонно уменьшается и при угле ориентации 45° достигает минимального значения. В [36] также было показано, что более полусотни кубических кристаллов с δ > 0 образовывали двухслойные пластины с эффективным модулем Юнга, который при некоторых значениях угла ориентации и толщин слоев превосходит оба модуля Юнга слоев, заполненных одинаковыми кристаллами. Тем самым, правило смесей по Фойгту не выполняется. Еще большее количество слоистых пластин с такими особенностями упругого поведения обнаружено, когда слои заполнялись различными неауксетиками и ауксетиками с положительными, отрицательными и очень малыми коэффициентами анизотропии.

В [37] проведено исследование эффективных свойств трехслойных пластин, состоящих из кубических кристаллов, при растяжении и изгибе. Эффективные модули Юнга слоистых пластин были во многих случаях больше, чем модули Юнга всех слоев, за исключением композитов с очень жесткими кристаллами. Эффективные продольные коэффициенты Пуассона при растяжении трехслойных пластин часто увеличивались с увеличением жесткости неауксетиков, изменяя отрицательный знак на положительный. Во многих случаях трехслойные пластины типа неауксетик-ауксетик-неауксетик характеризуются положительными эффективными поперечными коэффициентами Пуассона, тогда как оба эффективных (продольный и поперечный) коэффициента Пуассона могут быть отрицательными в трехслойных пластинах типа ауксетик-неауксетик-ауксетик. В случае изгиба симметричных пластин внешние слои оказывают более сильное влияние на эффективный продольный коэффициент Пуассона, чем при растяжении, что приводит к трем различным типам поведения [37]: (a) полной продольной ауксетичности (эффективные продольный и поперечный коэффициенты Пуассона принимают отрицательные значения), (b) полной продольной неауксетичности (эффективные продольный и поперечный коэффициенты Пуассона принимают положительные значения) и (c) сочетанию продольной ауксетичности и неауксетичности в зависимости от типа нагрузки (эффективные продольный и поперечный коэффициенты Пуассона с разными знаками).

Приведенные выше результаты для эффективных характеристик двухслойных и трехслойных пластин получены в рамках приближения сплошной среды. При рассмотрении растяжения слоистых пластин нужно учитывать особенности межмолекулярных связей между слоями. Для этого при описании в рамках сплошной среды вводят понятие поверхностной упругости [38].

4. Упругие свойства нано/микротрубок. Впервые нанотрубки были получены в 1952 г. [39]. Л.В. Радушкевич и В.М. Лукьянович сообщали об электронно-микроскопическом наблюдении полых волокон диаметром порядка 100 нм, полученных при термическом разложении окиси углерода на железном катализаторе. Широкое исследование углеродных нанотрубок началось с их наблюдения в 1991 г. [40] и неуглеродных нанотрубок в 1992 г. – WS2 нанотрубок [41], в 1993 г. – MoS2 нанотрубок [42], в 1995 г. – BN нанотрубок [43]. В настоящее время синтезировано большое количество неуглеродных нанотрубок. Среди них широко представлены нанотрубки из металлов, металл-дихалькогенидов, окислов металлов и др. [44]. Родственными нанотрубкам объектами являются микроусы и нанопроволки. Длинные тонкие нити исследовались еще до открытия нанотрубок. Трубки микронных толщин были получены также раньше 90-х годов [45, 46].

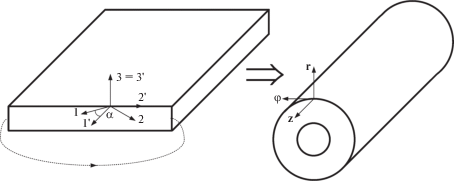
В [47] была предложена модель полого стержня, обладающего цилиндрической анизотропией, для описания механических свойств углеродных нано/микротрубок. В дальнейшем эта модель была применена для описания механических свойств неуглеродных нано/микротрубок с кубической, гексагональной, ромбоэдрической, тетрагональной, орторомбической и моноклинной цилиндрической анизотропией [18, 21, 22, 48–52]. В случае нано/микротрубок с кубической цилиндрической анизотропией [18] предполагалось, что трубки получались сворачиванием тонких пластин из кубических кристаллов с ориентацией (001) при различных углах хиральности $\alpha $ (рис. 7). При этом нормаль к плоскости пластины совпадает с осью 3, с кристаллографическим направлением [001]. Между исходным повернутым базисом прямоугольной пластины ${\mathbf{e}}_{1}^{'},{\mathbf{e}}_{2}^{'},{\mathbf{e}}_{3}^{'}$ и локальным ортогональным базисом свернутой цилиндрически анизотропной трубки ${{{\mathbf{e}}}_{r}},{{{\mathbf{e}}}_{\varphi }},{{{\mathbf{e}}}_{z}}$ имеет место соответствие ${\mathbf{e}}_{1}^{'} \to {{{\mathbf{e}}}_{z}}$, ${\mathbf{e}}_{2}^{'} \to - {{{\mathbf{e}}}_{\varphi }}$, ${\mathbf{e}}_{3}^{'} \to {{{\mathbf{e}}}_{r}}$. При рассмотрении задачи одноосного растяжения трубки (${{\sigma }_{{zz}}} = P$, ${{\sigma }_{{rr}}} = {{\sigma }_{{\varphi \varphi }}} = {{\sigma }_{{r\varphi }}} = {{\sigma }_{{rz}}} = {{\sigma }_{{\varphi z}}} = 0$) удельным усилием P было установлено, что оно возможно только при нулевом угле хиральности (при α = 0). В этом случае модуль Юнга E и угловой и радиальный коэффициенты Пуассона ${{\nu }_{{\varphi z}}}$ и ${{\nu }_{{rz}}}$ можно записать в виде

$E \equiv \frac{{{{\sigma }_{{zz}}}}}{{{{u}_{{zz}}}}} = \frac{1}{{{{s}_{{11}}}}},\quad {{\nu }_{{\varphi z}}} \equiv - \frac{{{{u}_{{\varphi \varphi }}}}}{{{{u}_{{zz}}}}} = {{\nu }_{{rz}}} \equiv - \frac{{{{u}_{{rr}}}}}{{{{u}_{{zz}}}}} = - \frac{{{{s}_{{12}}}}}{{{{s}_{{11}}}}}$
Рис. 7

Из формулы для коэффициентов Пуассона видно, что нано/микротрубки будут ауксетиками при ${{s}_{{12}}} > 0$. К таким материалам, например, относятся кристаллы Sm0.7Y0.3S, Sm0.75Y0.25S, Sm0.75La0.25S, Sm0.65La0.35S, Sm0.75Tm0.25S, TmSe.

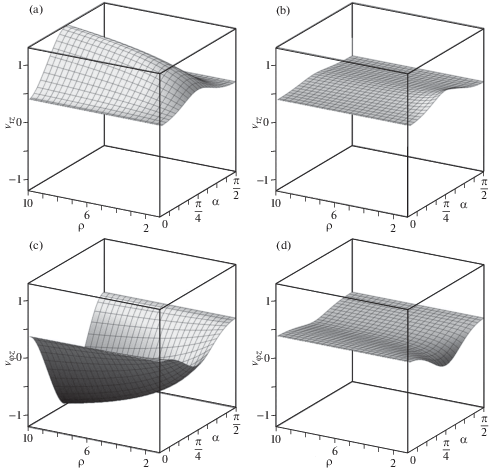
Решение задачи о продольном растяжении нано/микротрубки с цилиндрической кубической анизотропией и с ненулевым углом хиральности с помощью полуобратного метода Сен-Венана оказывается возможно при радиально неоднородных трех нормальных (${{\sigma }_{{rr}}}(r),{{\sigma }_{{\varphi \varphi }}}(r),{{\sigma }_{{zz}}}(r)$) и одном сдвиговом (${{\sigma }_{{\varphi z}}}(r)$) напряжениях. В результате были получены выражения для модуля Юнга и углового и радиального коэффициентов Пуассона ${{\nu }_{{\varphi z}}}$, ${{\nu }_{{rz}}}$, которые в этом случае отличны друг от друга. Эти выражения представлены в [15], и здесь не будут приводиться из-за громоздкости. Модуль Юнга зависит от коэффициентов податливости sij и параметра толщины трубки ρ =  ${{R}_{0}}{\text{/}}{{r}_{0}}$ (отношения внешнего радиуса к внутреннему), а коэффициенты Пуассона – от коэффициентов податливости, параметра толщины и радиальной координаты r. Численный анализ коэффициентов Пуассона нано/микротрубок из кубических кристаллов – неауксетиков, частичных и полных ауксетиков показал, что все эти трубки проявляют ауксетические свойства при различных углах хиральности. Например, у тонкой нано/микротрубки из железа (частичного ауксетика) отрицательный коэффициент Пуассона выявляется у ${{\nu }_{{\varphi z}}}$ на внутренней и внешней поверхности при углах хиральности близких к π/4 (рис. 8). На рис. 8 изображено изменение коэффициентов Пуассона ${{\nu }_{{rz}}}$ на внутренней (a) и внешней (b) поверхностях и ${{\nu }_{{\varphi z}}}$ на внутренней (c) и внешней (d) поверхностях железных нано/микротрубок. При углах хиральности близких к $\pi {\text{/}}4$ коэффициент Пуассона ${{\nu }_{{\varphi z}}}$ на внутренней поверхности монотонно уменьшается с увеличением параметра толщины ρ. Коэффициент ${{\nu }_{{\varphi z}}}$ на внешней поверхности при том же самом угле хиральности монотонно увеличивается и при $\rho $ = 1.21 меняет знак с отрицательного на положительный. В случае тонкой нано/микротрубки из алюминия (неауксетика) радиальный и окружной коэффициенты Пуассона имеют положительные значения. Отрицательным коэффициент Пуассона ${{\nu }_{{\varphi z}}}$ становится на внутренней поверхности при ρ = 10 и угле хиральности $\pi {\text{/}}4$. Для трубок из полного ауксетика Sm0.65La0.35S отрицательными оказывается как радиальный коэффициент Пуассона ${{\nu }_{{rz}}}$, так и окружной коэффициент ${{\nu }_{{\varphi z}}}$. Численный анализ, проведенный в [18], показал, что сильное изменение коэффициентов Пуассона наблюдается на внутренней поверхности нано/микротрубок.

Рис. 8

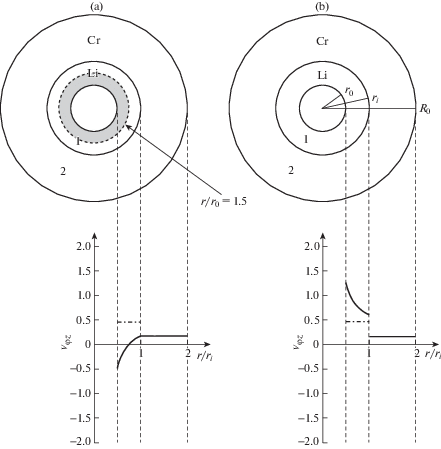
В [53] модель полого стержня, обладающего цилиндрической анизотропией, была применена для описания упругих свойств двухслойных нано/микротрубок из кубических кристаллов. Модуль Юнга такой нано/микротрубки зависит от коэффициентов податливости исходных материалов и отношения толщин слоев двухслойной трубки. Выражения для углового и радиального коэффициента Пуассона дополнительно зависят от радиальной координаты. Численный анализ показал, что в случае двухслойных трубок с одинаковыми объемами внутреннего и внешнего слоев модуль Юнга из ауксетика Sm0.75Tm0.25S ($\nu = - 0.46$, $E = 65.4$ ГПа) и неауксетиков Li, Ca, Th, Au, Al, Ge, Fe, SiC, W имеют место отклонения от правила смесей. Они быстро увеличиваются с увеличением модуля Юнга для неауксетика, заполняющего внутренний слой трубки. Для коэффициентов Пуассона правило смесей также не применимо из-за того, что деформационное влияние одного слоя двухслойных трубок на другой очень велико из-за жесткого сцепления слоев. Анализ упругих свойств двухслойной трубки, заполненной ауксетиком Sm0.75Tm0.25S во внешнем слое и неауксетиками во внутреннем слое, показал, что коэффициент Пуассона ${{\nu }_{{\varphi z}}}$ трубок с толщиной внешнего слоя, превосходящий толщину внутреннего слоя в два раза, проявляет отрицательные значения с относительно небольшими значениями модуля Юнга. При этом коэффициент ${{\nu }_{{\varphi z}}}$ внутреннего слоя может принимать значения, которые значительно ниже –1. В случае более жесткого неауксетика W во внутреннем слое его влияние превосходит влияние ауксетика, так что коэффициент Пуассона ${{\nu }_{{\varphi z}}}$ остается положительным во внутреннем слое и в части внешнего слоя. Радиальный коэффициент Пуассона ${{\nu }_{{rz}}}$ для обсуждаемых двухслойных трубок принимает отрицательные значения только во внешнем слое. В обратном случае, когда двухслойная нано/микротрубка заполнена ауксетиком Sm0.75Tm0.25S во внутреннем слое и неауксетиком во внешнем слое, окружной коэффициент Пуассона всегда положителен во внешней части двухслойных трубок, а зона отрицательного коэффициента уменьшается последовательно с увеличением модуля Юнга у неауксетиков. Более того, в случае жестких неауксетиков коэффициент Пуассона ${{\nu }_{{\varphi z}}}$ оказывается положительным во всем сечении двухслойной трубки несмотря на то, что внутренний слой первоначально заполнялся ауксетиком. Радиальный коэффициент Пуассона ${{\nu }_{{rz}}}$ принимает отрицательные значения во внутреннем слое и положительные значения во внешнем слое при заполнении его неауксетиками Ca, Al, Ge. В случае заполнения внешнего слоя более жестким неауксетиком W коэффициент ${{\nu }_{{rz}}}$ оказывается положительным в этом слое и меняет знак во внутреннем слое из-за сильного неауксетического влияния W. Отрицательный коэффициент Пуассона может получаться не только при заполнении двухслойной нано/микротрубки ауксетическим слоем, но и при двух неауксетических слоях! На рис. 9 изображено распределение коэффициентов Пуассона ${{\nu }_{{\varphi z}}}$ (a) и ${{\nu }_{{rz}}}$ (b) в ауксетическом двухслойном трубчатом композите Li-Cr, образованном парой неауксетиков (Li: $\nu = 0.46$, $E = 3.67$ ГПа; Cr: $\nu = 0.16$, $E = 32.8$ ГПа) при отношении толщин слоев равном 2. Как видно из рисунка коэффициент Пуассона ${{\nu }_{{\varphi z}}}$ меняет знак во внутреннем слое. Также ауксетические свойства были выявлены у двухслойных цилиндрических композитов из пар неауксетиков Ca-Eu0.2Ba0.8S, Ca-W, Ca-Mo.

Рис. 9

В [54, 55] с помощью методов молекулярной динамики исследованы механические свойства при растяжении (сжатии) хиральных металлических однослойных нанотрубок из кубических кристаллов меди, железа, алюминия и кобальта и дано сравнение с результатами, полученными в рамках теории упругости анизотропного тела [18]. Это сравнение показывает качественное соответствие результатов при существенном количественном различии. Было также установлено, что хиральные нанотрубки из меди, железа и кобальта проявляют ауксетические свойства при углах хиральности выше 39.8° при описании обоими методами.

В справочном энциклопедическом издании по экспериментальным упругим константам кристаллов Ландолт-Бернштайн [33] собрано около 1200 наборов по упругим константам кубических кристаллов. Анализ показал, что более 300 из них являются ауксетиками. В [18] установлено, что практически все нано/микротрубки из кубических кристаллов проявляют ауксетические свойства, т.е. изменение типа анизотропии (переход от прямолинейной анизотропии к криволинейной) приводит к ауксетичности объектов, обладающих цилиндрической анизотропией.

5. Линейный эффект Пойнтинга нано/микротрубок. Эффект Пойнтинга для изотропных материалов является эффектом второго порядка. Это впервые было установлено Дж.Г. Пойнтингом. Согласно его экспериментальным исследованиям длины различных проволок увеличиваются при их упругом кручении, и удлинение пропорционально квадрату угла кручения [56, 57]. В [58–60] было показано, что в рамках линейной анизотропной упругости возможен линейный эффект Пойнтинга у хиральных нано/микротрубок из кубических, тетрагональных и орторомбических кристаллов. Для анализа использовалась модель полого стержня, обладающего цилиндрической анизотропией. Нано/микротрубки получались сворачиванием тонких пластин из кубических кристаллов с ориентацией (001) при различных углах хиральности χ. В частном случае продольного растяжения нано/микротрубки с внутренним радиусов ${{r}_{0}}$ под действием удельной силы $P$ в отсутствие крутящего момента (M = 0) имеет место линейная связь угла кручения $\tau $ с продольной деформацией $\varepsilon $ [59]

(5.1)
$\tau {{r}_{0}} = \Lambda \varepsilon $

Коэффициент $\Lambda $ зависит от податливостей ${{s}_{{ij}}}$ и параметра толщины трубки $\rho $ (отношения внешнего радиуса к внутреннему). Анализ показывает, что в отсутствие крутящего момента растяжение нано/микротрубки из кубических кристаллов вызывает ее закручивание (обратный эффект Пойнтинга). В ситуации действия крутящего момента M в отсутствие растягивающего усилия (P = 0) происходит изменение длины нано/микротрубки (прямой эффект Пойнтинга), а имеет место при малых деформациях линейная связь угла кручения $\tau $ и продольной деформации $\varepsilon $ [59]

$\varepsilon = \Gamma \tau {{r}_{0}}$

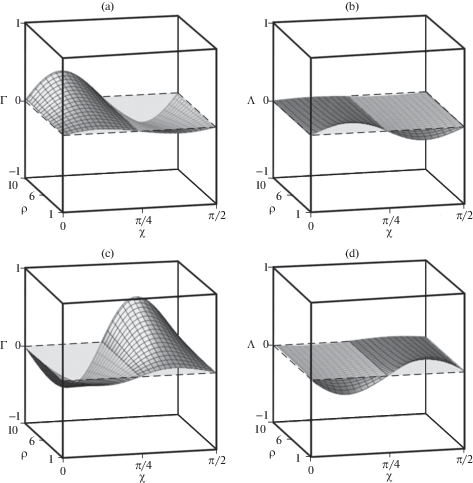
Коэффициент $\Gamma $ зависит от податливостей и параметра толщины. На рис. 10 показано изменение коэффициентов $\Gamma $ и $\Lambda $ с изменением угла хиральности χ и параметра толщины $\rho $ на примере нано/микротрубок из кристаллов Al и Cr с положительным и отрицательным коэффициентами анизотропии $\Delta = {{s}_{{11}}} - {{s}_{{12}}} - 0.5{{s}_{{44}}}$, соответственно. При фиксированном значении угла хиральности величина коэффициента $\left| \Lambda \right|$ монотонно падает с ростом параметра толщины трубки для всех кубических кристаллов, а коэффициент $\left| \Gamma \right|$ монотонно растет. Из рисунка также видно, что при углах хиральности 0 и π/4 эффект Пойнтинга исчезает. Изменения коэффициентов $\Gamma $ и $\Lambda $, отображенные на рис. 10a,b и рис. 10c,d, являются типичными для хиральных нано/микротрубок из кубических кристаллов с $\Delta > 0$ и $\Delta < 0$.

Рис. 10

В [54, 55] с помощью методов молекулярной динамики проанализирован эффект Пойнтинга для металлических нанотрубок из кубических кристаллов железа, кобальта, меди и алюминия при растяжении. Анализ показал, что для хиральных железных нанотрубок имеет место удовлетворительное качественное согласие между атомными расчетами и результатами в рамках теории анизотропной упругости. В случае нанотрубок из кобальта, меди и алюминия значения коэффициента $\Lambda $ с помощью атомистических расчетов значительно превышают оценки, полученные в рамках теории упругости анизотропного тела.

6. Заключение. Анализ показал, что среди 1100 кубических кристаллов из справочного издания Ландолт-Бернштайна более одной четверти материалов проявляет ауксетические свойства. Одна четверть элементов периодической системы элементов Д.И. Менделеева также являются ауксетиками. Среди них литий, калий, кальций, железо, никель, медь, золото, серебро, цинк, олово, свинец, кобальт. Свыше 450 кристаллов различных кристаллических систем являются ауксетиками. Для некоторых кубических ауксетиков минимальное значение коэффициента Пуассона может быть меньше –1 (меньше нижней границы для изотропных материалов). На основе двух безразмерных параметров для кубических кристаллов найдена удобная классификационная схема, разделяющая все материалы на полные ауксетики, частичные ауксетики и неауксетики. Для хиральных нано/микротрубок из кубических кристаллов продемонстрировано, что такие трубки проявляют ауксетические свойства, и характеризуются линейным эффектом Пойнтинга. При продольном растяжении двухслойных композитов из кубических кристаллов имеет место нарушение правила смесей Фойгта для различных комбинаций ауксетиков и неауксетиков.

Разнообразие механических эффектов, связанных с ауксетическими свойствами кубических кристаллов и конструкций из них, позволяют ожидать многих практических приложений.

Работа выполнена при поддержке гранта РНФ № 18-19-00736.

Список литературы

  1. Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 7. Теория упругости. М.: Наука, 1987. 248 с.

  2. Wojciehowski K.W. Negative Poisson ratios at negative pressures // Mol. Phys. Rep. 1995. V. 10. P. 129–136.

  3. Evans K.E., Nkansah M.A., Hutchinson I.J., Rogers S.C. Molecular network design // Nature. 1991. V. 353. № 6340. P. 124–125.

  4. Evans K.E. Auxetic polymers: a new range of materials // Endeavour. New series. 1991. V. 15. № 4. P. 170–174.

  5. Lim T.C. Auxetic Materials and Structures. Springer Singapore, 2015. 588 p.

  6. Ting T.C.T., Chen T. Poisson’s ratio for anisotropic elastic materials can have no bounds // Quart. J. Mech. Appl. Math. 2005. V. 58. № 1. P. 73–82.

  7. Love A.E.H. A treatise on the mathematical theory of elasticity. Cambridge: at the University Press. 1892. 369 p.

  8. Зубов В.Г., Фирсова М.М. Об особенностях упругого поведения кварца в области $\alpha $-$\beta $ перехода // Кристаллография. 1962. Т. 7. № 3. С. 469–471.

  9. Поперека М.Я., Балагуров В.Г. Ферромагнитные пленки с отрицательным коэффициентом Пуассона // ФТТ. 1969. Т. 11. № 12. С. 3507–3513.

  10. Gunton D.J., Saunders G.A. Stability limits on the Poisson ratio: application to a martensitic transformation // Proc. R. Soc. Lond. Ser. A. 1975. V. 343. № 1632. P. 63–83.

  11. Milstein F., Huang K. Existence of a negative Poisson ratio in fcc crystals // Phys. Rev. B. 1979. V. 19. № 4. P. 2030–2033.

  12. Baughman R.H., Shacklette J.M., Zakhidov A.A., Stafström S. Negative Poisson’s ratios as a common feature of cubic metals // Nature. 1998. V. 392. № 6674. P. 362–365.

  13. Светлов И.Л., Епишин А.И., Кривко А.И. Анизотропия коэффициента Пуассона монокристаллов никелевого сплава // ДАН СССР. 1988. Т. 302. № 2. С. 1372–1375.

  14. Grima J.N., Cassar R.N., Gatt R. On the effect of hydrostatic pressure on the auxetic character of NAT-type silicates // J. Non-Cryst. Solids. 2009. V. 355. № 24–27. P. 1307–1312.

  15. Lakes R.S. Foam structures with a negative Poisson’s ratio // Science. 1987. V. 235. № 4792. P. 1038–1040.

  16. Friis E.A., Lakes R.S., Park J.B. Negative Poisson’s ratio polymeric and metallic foams // J. Mater. Sci. 1988. V. 23. № 12. P. 4406–4414.

  17. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Ауксетическая механика кристаллических материалов // Изв. РАН. МТТ. 2010. № 4. С. 43–62.

  18. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С., Волков М.А. Отрицательный коэффициент Пуассона для кубических кристаллов и нано/микротрубок // Физ. Мезомех. 2013. Т. 16. № 6. С. 13–31. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S., Volkov M.A. Negative Poisson’s ratio for cubic crystals and nano/microtubes // Physical Mesomechanics. 2014. V. 17. № 2. P. 97–115.

  19. Gorodtsov V.A., Lisovenko D.S. Extreme values of  Young’s modulus and Poisson’s ratio of hexagonal crystals // Mechanics of Materials. 2019. V. 134. P. 1–8.

  20. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С., Волков М.А. Ауксетики среди 6-ти константных тетрагональных кристаллов // Письма о материалах. 2015. Т. 5. № 4. С. 409–413.

  21. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Модуль Юнга и коэффициент Пуассона для 7-ми константных тетрагональных кристаллов и нано/микротрубок из них // Физ. Мезомех. 2014. Т. 17. № 5. С. 5–14. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. Young’s modulus and Poisson`s ratio for seven-constant tetragonal crystals and nano/microtubes // Physical Mesomechanics. 2015. V. 18. № 3. P. 213–222.

  22. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С., Волков М.А. Механические характеристики 7-ми константных ромбоэдрических кристаллов и нано/микротрубок из них // Письма о материалах. 2016. Т. 6. № 2. С. 93–97.

  23. Волков М.А. Экстремальные значения коэффициента Пуассона триклинных и моноклинных кристаллов // Письма о материалах. 2014. Т. 4. В. 3. С. 167–170.

  24. Lethbridge Z.A.D., Walton R.I., Marmier A.S.H. et al. Elastic anisotropy and extreme Poisson’s ratios in single crystals // Acta Mater. 2010. V. 58. № 19. P. 6444–6451.

  25. Grima J.N., Gatt R., Alderson A., Evans K.E. On the origin of auxetic behaviour in the silicate $\alpha $‑cristobalite // J. Mater. Chem. 2005. V. 15. P. 4003–4005.

  26. Jiang J.W., Park H.S. Negative Poisson’s ratio in single-layer black phosphorus // Nat. Commun. 2014. V. 5. № 1. P. 4727.

  27. Новикова Н.Е., Лисовенко Д.С., Сизова Н.Л. Особенности структуры, упругие модули и картина деформации и разрушения по Кнупу монокристаллов гидрофталатов калия, рубидия, цезия и аммония // Кристаллография. 2018. Т. 63. № 3. С. 425–440.

  28. Norris A.N. Poisson’s ratio in cubic materials // Proc. Roy. Soc. A. 2006. V. 462. № 2075. P. 3385–3405.

  29. Епишин А.И., Лисовенко Д.С. Экстремальные значения коэффициента Пуассона кубических кристаллов // ЖТФ. 2016. Т. 86. № 10. С. 74–82.

  30. Ting T.C.T., Barnett D.M. Negative Poisson’s ratios in anisotropic linear elastic media // J. Appl. Mech. 2005. V. 72. № 6. P. 929–931.

  31. Branka A.C., Heyes D.M., Wojciechowski K.W. Auxeticity of cubic materials // Phys. Status Solidi B. 2009. V. 246. № 9. P. 2063–2071.

  32. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. Classification of cubic auxetics // Phys. Status Solidi B. 2013. V. 250. № 10. P. 2038–2043.

  33. Second and Higher Order Elastic Constants // Ed. by D.F. Nelson. Springer, 1992. V. 29a of Landolt-Börnstein – Group III Condensed Matter.

  34. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. Longitudinal elastic tension of two-layered plates from isotropic auxetics-nonauxetics and cubic crystals // Eur. J. Mech. A Solids. 2017. V. 63. P. 122–127.

  35. Gorodtsov V.A., Lisovenko D.S. Tension of thin two-layered plates of hexagonal crystals // Compos. Struct. 2019. V. 209. P. 453–459.

  36. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С., Волков М.А. Тонкие однородные двуслойные пластины из кубических кристаллов с различной ориентацией слоев // Физ. Мезомех. 2018. Т. 21. № 2. С. 5–13. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S., Volkov M.A. Thin homogeneous two-layered plates of cubic crystals with different layer orientation // Physical Mesomechanics. 2019. V. 22. № 4. P. 261–268.

  37. Gorodtsov V.A., Lisovenko D.S., Lim T.-C. Three-layered plate exhibiting auxeticity based on stretching and bending modes // Composite Structure. 2018. V. 194. P. 643–651.

  38. Городцов В.А., Лисовенко Д.С., Устинов К.Б. Шарообразное включение в упругой матрице при наличии собственных деформаций с учетом влияния свойств поверхности раздела, рассматриваемой как предел слоя конечной толщины // Изв. РАН. МТТ. 2019. № 3. С. 30–40.

  39. Радушкевич Л.В., Лукьянович В.М. О структуре углерода, образующегося при термическом разложении окиси углерода на железном контакте // ЖФХ. 1952. Т. 26. № 1. С. 88–95.

  40. Iijima S. Helical microtubules of graphitic carbon // Nature. 1991. V. 354. № 6348. P. 56–58.

  41. Tenne R., Margulis L., Genut M., Hodes G. Polyhedral and cylindrical structures of tungsten disulphide // Nature. 1992. V. 360. № 6403. P. 444–446.

  42. Margulis L., Salitra G., Tenne R., Talianker M. Nested fullerene-likestructures // Nature. 1993. V. 365. №. 6442. P. 113–114.

  43. Chopra N.G., Luyken R.J., Cherrey K. et al. Boron nitride nanotubes // Science. 1995. V. 269. № 5226. P. 966–967.

  44. Rao C.N.R., Govindaraj A. Nanotubes and nanowires. 2nd edition. Royal Society of Chemistry. 2011.

  45. Bacon R. Growth, structure, and properties of graphite whiskers // J. Appl. Phys. 1960. V. 31. № 2. P. 283–290.

  46. Tibbetts G.G. Why are carbon filaments tubular? // J. Crystal Growth. 1984. V. 66. № 3. P. 632–638.

  47. Городцов В.А., Лисовенко Д.С. Упругие свойства графитовых стержней и многослойных углеродных нанотрубок (растяжение и кручение) // Изв. РАН, МТТ. 2005. № 4. С. 42–56.

  48. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Мезомеханика многослойных углеродных нанотрубок и наноусов // Физ. Мезомех. 2008. Т. 11. № 6. С. 25–42. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. Mesomechanics of multiwall carbon nanotubes and nanowhiskers // Physical Mesomechanics. 2009. V. 12. № 1–2. P. 38–53.

  49. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. К описанию многослойных нанотрубок в рамках моделей цилиндрически анизотропной упругости // Физ. Мезомех. 2009. Т. 12. № 5. С. 5–14. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. To the description of multi-layered nanotubes in models of cylindrically anisotropic elasticity // Physical Mesomechanics. 2010. V. 13. № 1–2. P. 12–20.

  50. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Модули Юнга и коэффициенты Пуассона криволинейно анизотропных гексагональных и ромбоэдрических нанотрубок. Нанотрубки-ауксетики // ДАН. 2013. Т. 452. № 3. С. 279–283.

  51. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S., Volkov M.A. Negative Poisson’s ratio for six-constant tetragonal nano/microtubes // Phys. Status Solidi B. 2015. V. 252. № 7. P. 1580–1586.

  52. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S., Volkov M.A. Auxeticity in nano/microtubes produced from orthorhombic crystals // Smart Mater. Struct. 2016. V. 25. № 5. P. 054006.

  53. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S., Volkov M.A. Two-layered tubes from cubic crystals: Auxetic tubes // Physica Status Solidi B. V. 254. № 12. P. 1600815.

  54. Bryukhanov I.A., Gorodtsov V.A., Lisovenko D.S. Chiral Fe nanotubes with both negative Poisson’s ratio and Poynting’s effect. Atomistic simulation // Journal of Physics: Condensed Matter. 2019. V. 31. № 47. P. 475304.

  55. Брюханов И.А., Городцов В.А., Лисовенко Д.С. Атомистическое моделирование механических свойств хиральных металлических нанотрубок // Физ. Мезомех. 2019. Т. 22. № 6. С. 48–57.

  56. Poynting J.H. On pressure perpendicular to the shear planes in finite pure shears, and on the lengthening on loaded wires when twisted // Proc. Roy. Soc. London. A. 1909. V. 82. № 557. P. 546–559.

  57. Poynting J.H. On the changes in the dimensions of a steel wire when twisted, and on the pressure of distortional waves in steel // Proc. Roy. Soc. A. 1912. V. 86. № 590. P. 534–561.

  58. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Линейный эффект Пойнтинга при кручении и растяжении криволинейно-анизотропных трубок // ДАН. 2015. Т. 464. № 1. С. 35–38.

  59. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Эффект Пойнтинга для цилиндрически-анизотропных нано/микротрубок // Физ. Мезомех. 2016. Т. 19. № 1. С. 5–14. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. Poynting’s effect of cylindrically anisotropic nano/microtubes // Physical Mesomechanics. 2016. V. 19. № 3. P. 229–238.

  60. Гольдштейн Р.В., Городцов В.А., Лисовенко Д.С. Кручение цилиндрически анизотропных нано/микротрубок из 7-константных тетрагональных кристаллов. Эффект Пойнтинга // Физ. Мезомех. 2015. Т. 18. № 6. С. 5–11. Goldstein R.V., Gorodtsov V.A., Lisovenko D.S. Torsion of cylindrically anisotropic nano/microtubes from seven-constant tetragonal crystals. Poynting’s effect // Physical Mesomechanics. 2016. V. 19. № 4. P. 349–354.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал