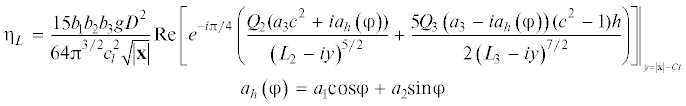Известия РАН. Механика твердого тела, 2020, № 4, стр. 126-139

ПРОСТЫЕ РЕШЕНИЯ ЛИНЕЙНОЙ ЗАДАЧИ О ВОЗБУЖДЕНИИ ДЛИННЫХ ВОЛН НА ПОВЕРХНОСТИ ЖИДКОСТИ ИСТОЧНИКОМ В УПРУГОМ ОСНОВАНИИ

С. Ю. Доброхотов^a, b, Х. Х. Ильясов^a, *, О. Л. Толстова^b, c

^a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

^b Московский физико-технический институт
Москва, Россия

^c Математический институт им. В.А. Стеклова РАН
Москва, Россия

^* E-mail: ilyasov@ipmnet.ru

Поступила в редакцию 12.01.2020
После доработки 15.01.2020
Принята к публикации 17.01.2020

DOI: 10.31857/S0572329920040030

Полный текст (PDF)

Аннотация

Рассматривается задача о возбуждении волн на поверхности слоя жидкости, лежащего на упругом полупространстве. Источник возбуждения располагается в упругой среде. Решается совместная система уравнений теории упругости в полупространстве и теории волн в жидкости. На основе полученных ранее упрощенного решения дисперсионного уравнения для водяной моды с учетом влияния упругого полупространства и интегрального представления перемещения поверхности жидкости, вызванных источником простого вида, строятся аналитические формулы для решения задачи в предположении длинных волн. Проводится сравнение результатов, полученных по аналитическим формулам и интегральным представлениям.

Ключевые слова: упругое полупространство, слой жидкости, поверхностные волны, задача Коши, возвышение свободной поверхности

1. Введение. Классическая модель, описывающая распространение длинных волн в океане основана на рассмотрении линеаризованных уравнений теории несжимаемой жидкости в предположении, что дно бассейна жесткое [1–4]. Однако предположение о жесткости дна не позволяет рассматривать процессы вне жидкого слоя, а следовательно, учитывать влияние на распространение волн очага землетрясения. Влияние очага описывают, как правило, начальные условия: обычно задается либо начальное возмущение в жидкости, либо начальное смещение дна. В такой классической постановке многие вопросы, связанные с распространением волн (в частности, волн цунами) остаются без ответа (например, какая часть энергии источника землетрясения переходит в энергию волны цунами, как влияют характеристики дна бассейна на скорость распространения волн в жидкости и т.д).

Существенно более сложная модель, основанная на совместном решении уравнений теории упругости в подстилающем полупространстве и теории волн в жидком слое, по-видимому, впервые была предложена Г.С. Подъяпольским и частично реализована им в [5]. Дальнейшее продолжение этот подход получил в работах [6–11].

Волновые процессы в системе упругое полупространство–слой несжимаемой жидкости можно представить [12, 13] как сумму распространяющихся с разными скоростями отдельных мод, которые в предельных случаях переходят в продольные, поперечные волны в упругом полупространстве, поверхностную волну Рэлея и волны возвышения на воде. При этом каждая из мод является “гибридной волной” в том смысле, что перемещения частиц как жидкости, так и упругой среды в ней отличны от нуля. В дальнейшем переходящую в предельном случае в волну возвышения в жидкости моду мы будем называть “водяной”. Значительное различие (более чем на порядок) в скоростях мод, переходящих в продольные, поперечные и рэлеевскую волны в упругой среде, по сравнению с “водяной” приводит к тому, что через сравнительно небольшое время с момента начального возмущения, возвышение свободной поверхности жидкости будет определяться только “водяной” модой. Этот факт позволяет построить решение задачи в виде относительно простой интегральной формулы [13].

В этой работе мы обсудим возможное влияние учета упругих свойств дна на некоторые характеристики распространяющихся волн в жидкости. Нас будут интересовать длинные волны. Мы хотим выяснить как повлияет отказ от жесткости дна и замена его на упругое основание на скорость распространения фронта длинной волны и ее профиль. При движении волны на большие расстояния возникают дисперсионные эффекты, которые могут приводить к изменению профиля и амплитуды волны. Учет дисперсионных эффектов важен с точки зрения определения размера источника.

2. Постановка задачи. 2.1. Система уравнений и граничных условий. Мы ограничимся здесь случаем постоянной глубины. Считаем, что идеальная незавихренная жидкость заполняет водоем, дно которого – упругое полупространство. Волновые движения жидкости описываются потенциалом перемещений ${\Psi }(x,z,t)$, деформации упругого полупространства – вектором смещений ${\mathbf{U}}(x,z,t) = ({{u}_{1}},{{u}_{2}},{{u}_{3}})$, где ${\mathbf{x}} \in {{R}^{2}}$ – горизонтальные координаты, z – вертикальная. Поверхность жидкости считаем свободной, невозмущенная поверхность жидкости задается уравнением z = 0, а граница раздела жидкого слоя и упругого полупространства – уравнением z = –D. Волны в упругом полупространстве описывают уравнения Ламэ

(2.1)

$c_{t}^{2}{{\nabla }^{2}}{\mathbf{U}} + (c_{l}^{2} - c_{t}^{2})\nabla {\text{div}}{\mathbf{U}} = {{{\mathbf{U}}}_{{tt}}},\quad z < - D$

Так как жидкость предполагается несжимаемой и безвихревой, в жидком слое имеем уравнение Лапласа для потенциала Ψ:

(2.2)

${{\nabla }^{2}}{\Psi } = 0,\quad - D < z < 0$

На невозмущенной поверхности жидкости выполняется кинематическое условие

(2.3)

$\frac{1}{g}{{{\Psi }}_{{tt}}} + {{{\Psi }}_{z}} = 0,\quad z = 0$

На границе раздела z = –D

(2.4)

$\frac{{\partial {{u}_{i}}}}{{\partial z}} + \frac{{\partial {{u}_{3}}}}{{\partial {{x}_{i}}}} = 0,\quad i = 1,2$

(2.5)

$(c_{l}^{2} - c_{t}^{2})\left( {\frac{{\partial {{u}_{1}}}}{{\partial {{x}_{1}}}} + \frac{{\partial {{u}_{2}}}}{{\partial {{x}_{2}}}} + \frac{{\partial {{u}_{3}}}}{{\partial z}}} \right) + 2c_{t}^{2}\frac{{\partial {{u}_{3}}}}{{\partial z}} = {\rho }\frac{{{{\partial }^{2}}{\Psi }}}{{\partial {{t}^{2}}}} + \left( {{\rho } - 1} \right){{u}_{3}}{\text{\;}}$

(2.6)

$\frac{{\partial {\Psi }}}{{\partial z}} = {{u}_{3}}$

и при $z \to \infty $ U → 0. Здесь c_l, c_t – скорости продольных и поперечных волн в упругой среде, ${\rho } = {{{\rho }}_{w}}{\text{/}}{{{\rho }}_{e}}$ – отношение плотностей жидкости и упругой среды. Приблизительные значения физических параметров задачи: $g \approx 0.01$ км/сек², ${{{\rho }}_{w}} \approx 1024$ кг/м³, ${{{\rho }}_{e}} \approx 3000$ кг/м³ для базальта и 2600 кг/м³ для гранита, ${{c}_{l}} \approx 22680$ км/ч (19800 км/ч), ${{c}_{t}} \approx 12600$ км/ч (10 080 км/ч) для базальта (гранита). Глубина бассейна D изменяется в пределах 2–5 км. Таким образом, можно считать, что ρ ≈ 1/3, $c = {{c}_{l}}{\text{/}}{{c}_{t}} \approx 1{\text{/}}\sqrt 3 $. Скорость распространения длинных волн ${v}$ в слое жидкости находится в пределах 700–720 км/ч, ${v}{\text{/}}{{c}_{l}} \approx 0.035$, ${v}{\text{/}}{{c}_{t}} \approx 0.063$. Параметры начальных возмущений и размеры области, в которой изучаются решения, мы обсудим позже.

Если решения U и Ψ системы (2.1)–(2.6) найдено, то превышение свободной поверхности жидкости η может быть восстановлено по формуле

(2.7)

${\eta } = - \frac{1}{g}{{\left. {\frac{{{{\partial }^{2}}{\Psi }}}{{\partial {{t}^{2}}}}} \right|}_{{z = 0}}} \equiv {{\left. {\frac{{\partial {\Psi }}}{{\partial z}}} \right|}_{{z = 0}}}$

2.2. Приведение задачи к стандартному виду. Поставленную задачу можно решать двумя способами. В некотором смысле задача является гиперболической, поэтому можно решать ее с помощью метода характеристик. Сначала решим задачу в упругом полупространстве, а когда возмущения доходят до поверхности, подключаем водяной слой. Второй способ основан на разложении решения в интеграл и ряд Фурье. При решении поставленной задачи мы использовали второй способ, который в этом случае кажется нам более эффективным и простым. Мы можем использовать общие результаты из теории операторов, если представим задачу в стандартном для теории операторов виде

(2.8)

${{{\mathbf{\Upsilon }}}_{{tt}}} = \hat {L}{\mathbf{\Upsilon }}$

где $\hat {L}$ – некоторый матричный дифференциальный оператор по переменным x и z. Для этого мы должны определить подходящим образом пространство, в котором заданы неизвестные функции. Нестандартность задачи обусловлена тем, что в системе (2.1)–(2.6) уравнение Лапласа не содержит производные по времени, но в некоторые граничные условия эти производные входят.

Наличие вариационного принципа, консервативность и физический смысл задачи показывают, что она должна быть самосопряженной, возможно, в пространстве со специальным скалярным произведением.

Для того чтобы представить задачу в стандартном виде (2.8), систему нужно преобразовать так, чтобы исключить уравнение Лапласа, а часть граничных условий будет играть роль уравнений.

Пусть R' – операция, сопоставляющая вектору ${\psi } = \left( {{{{\psi }}_{0}},{{{\psi }}_{D}}} \right)$, где ${{{\psi }}_{0}} = {\Psi }\left( {x,0,t} \right)$, ψ_D = ${\Psi }\left( {x, - D,t} \right)$, вектор $(R_{D}^{'}{\psi },R_{0}^{'}{\psi })$, составленный из нормальных производных решений задачи Дирихле

(2.9)

${{\nabla }^{2}}{\Psi } = 0,\quad - D < z < 0$

(2.10)

${\Psi }\left( {{\mathbf{x}},0,t} \right) = {{{\psi }}_{0}},\quad {\Psi }\left( {{\mathbf{x}}, - D,t} \right) = {{{\psi }}_{D}},\quad {\mathbf{x}} \in \left( { - \infty ,\infty } \right)$

Используя в качестве неизвестной вектор-функцию из пяти компонент (индекс T означает транспонирование)

${{{\mathbf{\Upsilon }}}^{T}} = {{({{u}_{1}}({\mathbf{x}},z,t),{{u}_{2}}({\mathbf{x}},z,t),{{u}_{3}}({\mathbf{x}},z,t),{{{\psi }}_{0}}({\mathbf{x}},t),{{{\psi }}_{D}}({\mathbf{x}},t))}^{T}}$

разрешая (2.5) относительно ${{\partial }^{2}}{\Psi /}\partial {{t}^{2}}$, получим для Y задачу вида (2.8) с начальными условиями

${{\left. {\mathbf{\Upsilon }} \right|}_{{t = 0}}} = {{{\mathbf{\Upsilon }}}^{0}},\quad {{\left. {{{{\mathbf{\Upsilon }}}_{t}}} \right|}_{{t = 0}}} = {{{\mathbf{\Upsilon }}}^{1}}$

В работе [9] была доказана теорема о существовании и единственности решения полученной задачи в более общем случае переменного дна. Отметим, что оператор $\hat {L}$ не является даже симметричным в пространстве с обычным скалярным произведением. Для доказательства “почти” симметричности скалярное произведение было введено особым образом и будет приведено позднее. Для доказательства самосопряженности оператора $\hat {L}$ было построено семейство самосопряженных операторов, приближающих $\hat {L}$. Стоит отметить работу [11], в которой для доказательства самосопряженности в подобной задаче были использованы в качестве неизвестных превышение свободной поверхности жидкости η и вектор смещений в упругой среде U.

3. Решение задачи в случае постоянного дна. 3.1. Метод Фурье и сведение задачи к одномерным операторным пучкам. Будем искать некоторые частные решения задачи в виде

${\mathbf{\Upsilon }} = {\mathbf{\hat {\Upsilon }}}{{e}^{{i{\omega }({\mathbf{p}},k)t + i{\mathbf{px}}}}}$

где ${\mathbf{p}} = ({{p}_{1}},{{p}_{2}})$ – двойственные по отношению к x₁, x₂ переменные. Решение задачи сводится к исследованию спектра оператора $\hat {L}({\mathbf{p}},\partial {\text{/}}\partial z)$, который действует на элементы ${\mathbf{\hat {\Upsilon }}} = {{({\mathbf{\hat {U}}}(z,{\mathbf{p}}),{{{\hat {\psi }}}_{0}}({\mathbf{p}}),{{{\hat {\psi }}}_{D}}({\mathbf{p}}))}^{T}}$. Опишем спектр этого оператора при каждом фиксированном p.

Очевидно, что функции ${\mathbf{\hat {U}}}$ вида ${\mathbf{\hat {U}}} = {\mathbf{\hat {U}}}({\mathbf{p}}){{e}^{{kz}}}$ являются решениями данной задачи. Подставив их в уравнения Ламэ, из условия существования ненулевого решения однородной системы уравнений получим уравнение для определения k, откуда находим

${{k}_{t}} = \sqrt {{{{\mathbf{p}}}^{2}} - {{{\omega }}^{2}}{\text{/}}c_{t}^{2}} ,\quad {{k}_{l}} = \sqrt {{{{\mathbf{p}}}^{2}} - {{{\omega }}^{2}}{\text{/}}c_{l}^{2}} $

где ${{{\mathbf{p}}}^{2}} = p_{1}^{2} + p_{2}^{2}$.

Используя (2.9), (2.10) и граничные условия, получаем выражения для ${{{\hat {\psi }}}_{0}}$, ${{{\hat {\psi }}}_{D}}$ через значение вертикальной составляющей потенциала перемещений упругой среды на границе раздела:

${{{\hat {\psi }}}_{0}} = \frac{g}{{{\text{ch}}(\left| {\mathbf{p}} \right|D)({{{\omega }}^{2}} - g\left| {\mathbf{p}} \right|{\text{th}}(\left| {\mathbf{p}} \right|D))}}{{\left. {{{{\hat {u}}}_{3}}} \right|}_{{z = - D}}}$

${{{\hat {\psi }}}_{D}} = \left| {\mathbf{p}} \right|\frac{{(g\left| {\mathbf{p}} \right| - {{{\omega }}^{2}}{\text{th}}\left( {{\mathbf{p}}D} \right))}}{{\left| {\mathbf{p}} \right|({{{\omega }}^{2}} - g\left| {\mathbf{p}} \right|{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right))}}{{\left. {{{{\hat {u}}}_{3}}} \right|}_{{z = - D}}}$

и уравнение, связывающее ω и p, называемое дисперсионным уравнением:

(3.1)

$\begin{gathered} \left( {{\lambda } - g\left| {\mathbf{p}} \right|{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)} \right)\left( { - 4{{{\mathbf{p}}}^{2}}{{k}_{t}}{{k}_{l}} + {{{(k_{t}^{2} + {{{\mathbf{p}}}^{2}})}}^{2}} - \frac{{{\lambda }g\left( {{\rho } - 1} \right){{k}_{l}}}}{{c_{t}^{4}}}} \right) \\ + \frac{{{{{\lambda }}^{2}}{\rho }{{k}_{l}}}}{{c_{t}^{4}}}\left( {g\left| {\mathbf{p}} \right| - {\lambda th}\left( {\left| {\mathbf{p}} \right|D} \right)} \right) = 0 \\ \end{gathered} $

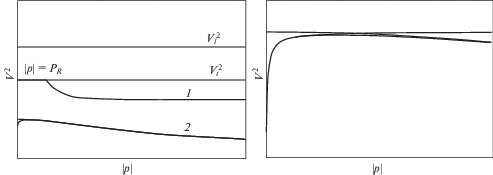
где λ = ω² соответствует второй производной по времени. Если ввести ${{{v}}^{2}} = {\lambda /}{{{\mathbf{p}}}^{2}}$ (фазовую скорость), то (3.1) примет вид

(3.2)

$\left( {{{{v}}^{2}} - \frac{g}{{\left| {\mathbf{p}} \right|}}{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)} \right)\left( { - 4{{{\tilde {k}}}_{t}}{{{\tilde {k}}}_{l}} + \left( {{{{(\tilde {k}_{t}^{2} + 1)}}^{2}} - \frac{g}{{\left| {\mathbf{p}} \right|}}\frac{{\left( {{\rho } - 1} \right){{{v}}^{2}}}}{{c_{t}^{4}}}\tilde {k}_{l}^{2}} \right) + {\rho }\frac{{{{{v}}^{4}}}}{{c_{t}^{4}}}\left( {\frac{g}{{\left| {\mathbf{p}} \right|}} - {{{v}}^{2}}{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)} \right)} \right) = 0$

${{\tilde {k}}_{t}} = \sqrt {1 - {{{v}}^{2}}{\text{/}}c_{t}^{2}} ,\quad {{\tilde {k}}_{l}} = \sqrt {1 - {{{v}}^{2}}{\text{/}}c_{l}^{2}} $

3.2. Спектр операторного пучка. Когда ${{{\omega }}^{2}} < {{{\mathbf{p}}}^{2}}c_{t}^{2}$, т.е. ${v} < {{c}_{t}}$ уравнение (3.1) имеет два действительных корня ${{{\lambda }}_{W}} = {{{\omega }}^{2}}\left( {\left| {\mathbf{p}} \right|} \right)$ и ${{{\lambda }}_{R}} = {\omega }_{R}^{2}\left( {\left| {\mathbf{p}} \right|} \right)$, соответственно уравнение (3.2) имеет корни ${{{v}}_{W}}$ и ${{{v}}_{K}}$, которые определяют две точки дискретного спектра, соответствующие поверхностным волнам в жидкости в предельном случае жесткого дна и волнам Рэлея в упругом полупространстве, когда слой жидкости отсутствует. Отвечающие им собственные функции обозначим соответственно ${{{\mathbf{\bar {\Upsilon }}}}_{W}}({\mathbf{p}},z)$ и ${{{\mathbf{\bar {\Upsilon }}}}_{R}}({\mathbf{p}},z)$.

Когда ${\lambda } \geqslant {{{\mathbf{p}}}^{2}}c_{t}^{2}$, спектр становится непрерывным, при ${{{\mathbf{p}}}^{2}}c_{t}^{2} \leqslant {\lambda } \leqslant {{{\mathbf{p}}}^{2}}c_{l}^{2}$ имеем двумерное подпространство собственных функций (${\mathbf{\bar {\Upsilon }}}_{t}^{{1,2}}({\mathbf{p}},z)$), которые отвечают поперечным волнам в упругой среде, а при ${\lambda } > {{{\mathbf{p}}}^{2}}c_{l}^{2}$ мы должны добавить решения, соответствующие продольным волнам в упругой среде (собственные функции ${{{\mathbf{\bar {\Upsilon }}}}_{l}}({\mathbf{p}},z)$).

Остановимся более подробно на исследовании точек дискретного спектра. Для корня уравнения (3.2), соответствующего поверхностным волнам в жидкости, мы можем считать значение отношения ${{{v}}^{2}}{\text{/}}c_{l}^{2}$ малой величиной, так как $Dg \leqslant 0.1$, c_l ~ 6, и тогда, считая ${{k}_{l}} \approx 1$, перепишем уравнение (3.2) в виде

${v}\left( {{{{v}}^{2}} - \frac{g}{{{\text{|}}{\mathbf{p}}{\text{|}}}}{\text{th}}\left( {{\text{|}}{\mathbf{p}}{\text{|}}D} \right)} \right)\left( { - 4{{{\tilde {k}}}_{t}} + \left( {{{{(\tilde {k}_{t}^{2} + 1)}}^{2}} - \frac{g}{{{\text{|}}{\mathbf{p}}{\text{|}}}}\frac{{\left( {{\rho } - 1} \right){{{v}}^{2}}}}{{c_{t}^{4}}}} \right) + {\rho }\frac{{{{{v}}^{4}}}}{{c_{t}^{4}}}\left( {\frac{g}{{{\text{|}}{\mathbf{p}}{\text{|}}}} - {{{v}}^{2}}{\text{th}}\left( {{\text{|}}{\mathbf{p}}{\text{|}}D} \right)} \right)} \right) = 0$

Воспользовавшись асимптотическим разложением для ${{k}_{t}} \approx 1 - {{{v}}^{2}}{\text{/}}(2c_{t}^{2})$, получим, вынося за скобки ${{{v}}^{2}}{\text{/}}c_{t}^{4}$:

$\frac{{{{v}^{2}}}}{{c_{t}^{4}}}\left( {\left( {{{v}^{2}} - \frac{g}{{\left| p \right|}}{\text{th}}\left( {\left| p \right|D} \right)} \right)\left( {\frac{{{{v}^{2}}}}{2} - \frac{g}{{\left| p \right|}}\left( {{\rho } - 1} \right)} \right) + {\rho }{{v}^{2}}\left( {\frac{g}{{\left| p \right|}} - {{v}^{2}}{\text{th}}\left( {\left| p \right|D} \right)} \right)} \right) = 0$

Корень ${{{v}}^{2}} = 0$ интереса не представляет. Для нахождения других корней мы имеем биквадратное уравнение, которое в области существования дискретного спектра имеет решение

(3.3)

${{{v}}^{2}} \approx g\left( {1 - \frac{{g{\rho }}}{{g + 2c_{t}^{2}\left| {\mathbf{p}} \right|}}} \right)\frac{{{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)}}{{\left| {\mathbf{p}} \right|}}$

При малых значениях $\left| {\mathbf{p}} \right|$ (для очень длинных волн) $\left| {\mathbf{p}} \right|D \leqslant 0.1$ и мы можем заменить ${\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)$ на $\left| {\mathbf{p}} \right|D$:

${{{v}}^{2}} \approx g\left( {1 - \frac{{g{\rho }}}{{g + 2c_{t}^{2}\left| {\mathbf{p}} \right|}}} \right)D$

или

(3.4)

${\lambda } \approx g\left( {1 - \frac{{g{\rho }}}{{g + 2c_{t}^{2}\left| {\mathbf{p}} \right|}}} \right)D{{{\mathbf{p}}}^{2}}$

откуда при |p| = 0 имеем ${{{v}}^{2}} \approx \left( {1 - {\rho }} \right)gD$.

Корень уравнения (3.2), соответствующий волнам Рэлея в упругом полупространстве, появляется при $\left| {\mathbf{p}} \right| = {{p}_{{cr}}}$, отщепляясь от прямой ${v} = {{c}_{t}}$, и при больших значениях |p| выходит на постоянное значение, соответствующее значению фазовой скорости волны Рэлея (при отсутствии слоя жидкости ${{{v}}_{R}} \approx 0.8{{c}_{t}}$. Учитывая значения c_t, c_l, D, g, можно при всех |p| отбросить члены с ${\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)$, которые описывают влияние слоя жидкости на Рэлеевскую составляющую решения. В результате получим уравнение

(3.5)

$ - 4c_{t}^{2}{{{v}}^{2}} + {{{v}}^{4}} - \frac{{g{{{\tilde {k}}}_{l}}}}{{\left| {\mathbf{p}} \right|}}{{{v}}^{2}} + c_{t}^{4}(4 - {{\tilde {k}}_{t}}{{\tilde {k}}_{l}}) = 0$

или

(3.6)

$\left| {\mathbf{p}} \right| = \frac{{g\widetilde {{{k}_{l}}}{{{v}}^{2}}}}{{4c_{t}^{4} - 4c_{t}^{2}{{{v}}^{2}} + {{{v}}^{4}} - 4c_{t}^{4}\widetilde {{{k}_{t}}}\widetilde {{{k}_{l}}}}}$

Полагая в (3.6) ${v} = {{c}_{t}}$, получаем, что

${{p}_{{cr}}} = \frac{g}{{c_{t}^{2}}}$

При $\left| {\mathbf{p}} \right| \to \infty $ получаем известное уравнение для фазовой скорости волны Рэлея.

Схематичное изображение спектра оператора показано на рис. 1 слева, цифрой 1 обозначена мода Рэлея, цифрой 2 – водяная мода. Горизонтальная прямая ${v} = {{c}_{t}}$ определяет нижнюю границу непрерывного спектра, а ${v} = {{c}_{l}}$ определяет границу, при переходе через которую двукратно вырожденный спектр становится трехкратно вырожденным. Справа на рисунке представлены дисперсионные кривые для водяной моды.

Рис. 1

3.3. Разложение решения по модам, интегральное представление решения и его упрощение для водяной моды. Рассмотрим следующую задачу Коши:

${{\left. U \right|}_{{t = 0}}} = {{U}^{0}}(x,z){\text{\;}}\quad {{\left. {\frac{{\partial U}}{{\partial t}}} \right|}_{{t = 0}}} = 0{\text{\;,}}\quad {{\left. {{{{\psi }}_{{W,D}}}} \right|}_{{t = 0}}} = {{\left. {\frac{{\partial {{{\psi }}_{{W,D}}}}}{{\partial t}}} \right|}_{{t = 0}}} = 0$

${{U}^{0}}(x,z)\quad (x = 0,{{z}_{0}}),\quad {{z}_{0}} < 0$

(3.7)

${{U}^{0}}(x,z) = a{\text{e}}(z)V(x){{e}^{{ - \frac{{{{{(z - {{z}_{0}})}}^{2}}}}{{2b_{3}^{2}}}}}},\quad V(x) = \frac{1}{{{{{(1 + {{{\left( {{{x}_{{\text{1}}}}{\text{/}}{{b}_{1}}} \right)}}^{2}} + {{{({{x}_{2}}{\text{/}}{{b}_{2}})}}^{2}})}}^{{3/2}}}}}$

Согласно общей теории решение задачи можно представить в виде разложения по собственным функциям оператора $\hat {L}$ (модам):

(3.8)

$\begin{gathered} {\Upsilon } = \mathop \sum \limits_ \pm \left\{ {\frac{1}{{2{\pi }}}\mathop \smallint \limits_{{{R}^{2}}} {{e}^{{ip,x}}}\left[ {{{e}^{{ \pm it{{{\omega }}_{W}}\left( {\left| {\mathbf{p}} \right|} \right)t}}}C_{W}^{ \pm }{{{{\tilde {\Upsilon }}}}_{W}}\left( {{\mathbf{p}},z} \right) + {{e}^{{ \pm it{{{\omega }}_{R}}\left( {\left| {\mathbf{p}} \right|} \right)t}}}C_{R}^{ \pm }{{{{\tilde {\Upsilon }}}}_{R}}{{{\left( {{\mathbf{p}},z} \right)}}_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}}}} \right.} \right. \\ + \left. {\left. {\mathop \smallint \limits_0^\infty \left( {{{e}^{{ \pm it{{{\omega }}_{t}}({\mathbf{p}},k)}}}\mathop \sum \limits_{m = 1}^2 C_{t}^{{ \pm ,m}}{\tilde {\Upsilon }}_{t}^{m}\left( {{\mathbf{p}},k,z} \right) + {{e}^{{ \pm it{{{\omega }}_{l}}\left( {{\mathbf{p}},k} \right)}}}C_{l}^{ \pm }{{{{\tilde {\Upsilon }}}}_{l}}\left( {{\mathbf{p}},k,z} \right)} \right)dk} \right]d{\mathbf{p}}} \right\} \\ \end{gathered} $

где $C_{W}^{ \pm }({\mathbf{p}}){\text{\;}}C_{R}^{ \pm }({\mathbf{p}}){\text{\;}}C_{t}^{{ \pm ,1}}({\mathbf{p}},k){\text{\;}}C_{t}^{{ \pm ,2}}({\mathbf{p}},k){\text{\;}}C_{l}^{ \pm }({\mathbf{p}},k)$ – коэффициенты Фурье разложения начальных данных.

Мы хотим определить, какой вклад в решение вносят слагаемые, соответствующие точке дискретного спектра, отвечающей водяной моде, так как при фиксированных x и достаточно больших временах в разложении решения по собственным функциям значимыми являются только слагаемые, соответствующие водяной моде. Нас интересует значение возвышения свободной поверхности η при временах, когда упругие моды уже не вносят существенный вклад в решение задачи. Это приводит к равенству

(3.9)

${\eta } = \mathop \sum \limits_ \pm \mathop \smallint \limits_{{{R}^{2}}} {{e}^{{i\left( {{\mathbf{px}} + {{{\omega }}_{W}}({\mathbf{p}})t} \right)}}}C_{W}^{ \pm }({\mathbf{p}}){{[{{{\bar {\Upsilon }}}_{W}}]}_{{\eta }}}({\mathbf{p}})d{\mathbf{p}}$

где ${{[{{{\bar {\Upsilon }}}_{W}}]}_{{\eta }}}({\mathbf{p}})$ – компонента вектора ${{\bar {T}}_{W}}$, соответствующая η,

${{{\tilde {\Upsilon }}}_{W}}({\mathbf{p}},z) = \left( {{\chi }({\mathbf{p}},z),{{{\zeta }}_{W}}({\mathbf{p}}),{{{\zeta }}_{D}}({\mathbf{p}})} \right)$

${\chi }({\mathbf{p}},z)$ соответствует $\tilde {U}$, а ${\zeta } = ({{{\zeta }}_{W}}({\mathbf{p}}),{{{\zeta }}_{D}}({\mathbf{p}}))$ соответствуют $\left( {{{{{\tilde {\psi }}}}_{W}},{{{{\tilde {\psi }}}}_{D}}} \right)$

${\chi } = A\left( {\left( \begin{gathered} {\mathbf{p}}{{k}_{t}} \\ - i{{{\mathbf{p}}}^{2}} \\ \end{gathered} \right){\text{\;}}{{e}^{{{{k}_{t}}\left( {z + D} \right)}}} + \frac{{k_{t}^{2} + {{p}^{2}}}}{{2{{k}_{l}}}}\left( {\begin{array}{*{20}{l}} { - {\mathbf{p}}} \\ {i{{k}_{l}}} \end{array}} \right){{e}^{{{{k}_{l}}\left( {z + D} \right)}}}} \right),\quad {\mathbf{p}} = \left( {\begin{array}{*{20}{l}} {{{p}_{1}}} \\ {{{p}_{2}}} \end{array}} \right)$

${{{\zeta }}_{W}} = \frac{{iAg{{{\lambda }}_{W}}}}{{2c_{t}^{2}{\text{ch}}\left( {\left| {\mathbf{p}} \right|D} \right)\left( {{{{\lambda }}_{W}} - g\left| {\mathbf{p}} \right|{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)} \right)}},\quad {{{\zeta }}_{D}} = {{{\zeta }}_{W}}\left( {1 - \frac{{{{{\lambda }}_{W}}{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)}}{{g\left| {\mathbf{p}} \right|}}} \right)$

Из условия нормировки

$\mathop \smallint \limits_{ - \infty }^{ - D} \langle {\bar {\chi }},{\chi }\rangle dz + \langle {\bar {\zeta }},R(p){\zeta }\rangle = 1,\quad {\text{где}}\quad R = \left( {\begin{array}{*{20}{l}} {\left| {\mathbf{p}} \right|{\text{cth}}\left( {\left| {\mathbf{p}} \right|D} \right)}&{ - \left| {\mathbf{p}} \right|{\text{/sh}}\left( {\left| {\mathbf{p}} \right|D} \right)} \\ {\left| {\mathbf{p}} \right|{\text{/sh}}\left( {\left| {\mathbf{p}} \right|D} \right)}&{ - \left| {\mathbf{p}} \right|{\text{cth}}\left( {\left| {\mathbf{p}} \right|D} \right)} \end{array}} \right)$

находим

(3.10)

$\begin{array}{*{20}{l}} {A = \left( {\frac{{{{{\mathbf{p}}}^{2}}(k_{t}^{2} + {{{\mathbf{p}}}^{2}})}}{{2{{k}_{t}}}}} \right. + \frac{{{{{(k_{t}^{2} + {{{\mathbf{p}}}^{2}})}}^{2}}(k_{l}^{2} + {{{\mathbf{p}}}^{2}})}}{{8k_{l}^{3}}} - \frac{{{{{\mathbf{p}}}^{2}}(k_{t}^{2} + {{{\mathbf{p}}}^{2}})}}{{{{k}_{l}}}}} \\ {{\text{\;}}{{{\left. { + \frac{{{\rho \lambda }_{W}^{2}\left| {\mathbf{p}} \right|{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)}}{{4c_{t}^{4}{{{\left( {{{{\lambda }}_{W}} - g\left| {\mathbf{p}} \right|{\text{th}}\left( {\left| p \right|D} \right)} \right)}}^{2}}}}\left( {{{g}^{2}} - 2g\frac{{{{{\lambda }}_{W}}}}{{\left| {\mathbf{p}} \right|}}{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right) + \frac{{{\lambda }_{W}^{2}}}{{{{{\mathbf{p}}}^{2}}}}} \right)} \right)}}^{{ - 1/2}}}} \end{array}$

Используя приведенные формулы, получаем

(3.11)

${\eta } = - \frac{1}{{4{\pi }}}\mathop \sum \limits_ \pm \mathop \smallint \limits_{\mathbb{R}_{p}^{2}} {{e}^{{i\left( {\langle {\mathbf{p}},{\mathbf{x}}\rangle \pm t{\omega }\left( {\left| {\mathbf{p}} \right|} \right)} \right)}}}\frac{{i{{{\omega }}^{4}}{{C}_{W}}\left( {\mathbf{p}} \right)A}}{{2c_{t}^{2}{\text{ch}}\left( {\left| {\mathbf{p}} \right|D} \right)\left( {{{{\lambda }}_{W}}\left( {\left| {\mathbf{p}} \right|} \right) - g\left| {\mathbf{p}} \right|{\text{th}}\left( {\left| {\mathbf{p}} \right|D} \right)} \right)}}d{\mathbf{p}}$

${{C}_{W}}({\mathbf{p}}) = \frac{1}{{2{\pi }}}\mathop \smallint \limits_{ - \infty }^{ - D} {\bar {\chi }}({\mathbf{p}},z)\left( {\mathop \smallint \limits_{\mathbb{R}_{x}^{2}} {{e}^{{ - i\langle {\mathbf{p}},{\mathbf{x}}\rangle }}}{{U}^{0}}\left( {{\mathbf{x}},z} \right)d{\mathbf{x}}} \right)dz$

Учитывая, что преобразование Фурье от функции V равно

$V = {{b}_{1}}{{b}_{2}}{{e}^{{ - \left| {\mathbf{p}} \right|\sqrt {b_{1}^{2}{\text{co}}{{{\text{s}}}^{2}}{\psi } + b_{2}^{2}{\text{si}}{{{\text{n}}}^{2}}{\psi }} }}}$

и учитывая выражение для собственных функций, получаем

(3.12)

${{C}_{W}} = - iA{{b}_{1}}{{b}_{2}}{{e}^{{ - \left| {\mathbf{p}} \right|b\left( {\psi } \right)}}}\left( {(i{{k}_{t}}\langle {\mathbf{p}},{\mathbf{a}}\rangle - {{{\mathbf{p}}}^{2}}{{a}_{3}}){{e}^{{{{k}_{t}}\left( {{{z}_{0}} + D} \right)}}}{{F}_{t}} + \frac{{k_{t}^{2} + {{p}^{2}}}}{{2{{k}_{l}}}}\left( { - i\langle {\mathbf{p}},{\mathbf{a}}\rangle + {{k}_{l}}{{a}_{3}}} \right){{e}^{{{{k}_{l}}\left( {{{z}_{0}} + D} \right)}}}{{F}_{l}}} \right)$

$b\left( {\psi } \right) = \sqrt {b_{1}^{2}{\text{co}}{{{\text{s}}}^{2}}{\psi } + b_{2}^{2}{\text{si}}{{{\text{n}}}^{2}}{\psi }} ,\quad \langle {\mathbf{p}},{\mathbf{a}}\rangle = {{p}_{1}}{{a}_{1}} + {{p}_{2}}{{a}_{2}}$

(3.13)

${{F}_{{t,l}}} = \mathop \smallint \limits_{ - \infty }^{ - D} {\text{e}}(z){{e}^{{{{k}_{{l,t}}}\left( {z - {{z}_{0}}} \right)}}}{{e}^{{\frac{{ - {{{(z - {{z}_{0}})}}^{2}}}}{{2b_{3}^{2}}}}}}dz$

Теперь попробуем упростить полученные формулы. Предполагая, что источник возбуждения расположен достаточно глубоко, его вертикальные размеры не велики, т.е. $\left| {{{z}_{0}}} \right| - D \gg {{b}_{3}}$, верхний предел в интегралах (3.13) можно заменить на ∞. Тогда получим, что

(3.14)

${{F}_{{t,l}}} \approx {{b}_{3}}\sqrt {2{\pi }} {{e}^{{\frac{{b_{3}^{2}k_{{t,l}}^{2}}}{2}}}}{\text{e}}({{z}_{0}} + b_{3}^{2}{{k}_{{t,l}}})$

Далее воспользуемся упрощенным выражением (3.3) для водяной моды (для λ_W), малостью величин $gD{\text{/}}c_{t}^{2}$, $gD{\text{/}}c_{l}^{2}$, заменим ${{k}_{t}} \approx \left| {\mathbf{p}} \right|(1 - {\lambda }2c_{t}^{2}{{p}^{2}})$, в результате получим

(3.15)

$\begin{gathered} \eta \approx - \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}g}}{{4\sqrt {2\pi } c_{t}^{2}}}\sum\limits_ \pm ^{} {\int\limits_{\mathbb{R}_{p}^{2}}^{} {{{e}^{{i(\langle {\mathbf{p}},{\mathbf{x}}\rangle \pm t\omega (|{\mathbf{p}}|))}}}} } \frac{{{{{\text{e}}}^{{ - |{\mathbf{p}}|\sqrt {b_{1}^{2}{{{\cos }}^{2}}\psi + b_{2}^{2}{{{\sin }}^{2}}\psi } }}}{{{\left( {1 - \rho + \frac{{2{\text{|}}{\mathbf{p}}{\text{|}}c_{t}^{2}}}{{\text{g}}}} \right)}}^{2}}{\text{sh}}({\text{|}}{\mathbf{p}}{\text{|}}D)}}{{{{{\mathbf{p}}}^{2}}\left( {1 + \frac{{2{\text{|}}{\mathbf{p}}{\text{|}}c_{t}^{2}}}{{\text{g}}}} \right)(\rho {\text{c}}{{{\text{h}}}^{2}}({\text{|}}{\mathbf{p}}{\text{|}}D) + {\text{th}}({\text{|}}{\mathbf{p}}{\text{|}}D))}} \\ \times \left( {(i{{k}_{t}}\langle {\mathbf{p}},{\mathbf{a}}\rangle - {{{\mathbf{p}}}^{2}}{{a}_{3}}){{e}^{{{{k}_{t}}({{z}_{0}} + D)}}}{{e}^{{\frac{{b_{3}^{2}k_{t}^{2}}}{2}}}} + \frac{{k_{t}^{2} + {{p}^{2}}}}{{2{{k}_{l}}}}( - i\langle {\mathbf{p}},{\mathbf{a}}\rangle + {{k}_{l}}{{a}_{3}}){{e}^{{{{k}_{l}}({{z}_{0}} + D)}}}{{e}^{{\frac{{b_{3}^{2}k_{l}^{2}}}{2}}}}} \right)d{\mathbf{p}} \\ \end{gathered} $

Обозначим φ – полярный угол вектора x, ψ – полярный угол вектора p, $\langle {\mathbf{p}},{\mathbf{x}}\rangle $ = = |x|rcos(ψ – φ), $r = \left| {\mathbf{p}} \right|$. В интеграле (3.15) перейдем к полярным координатам (r, ψ) и при этом будем предполагать, что точка x нодится достаточно далеко от начала координат. Применим метод стационарной фазы по углу ψ (см., например, [14]). Это даст дополнительные слагаемые с ${{e}^{{i\left( { \pm r\left| {\mathbf{x}} \right| \pm {\omega }t} \right)}}}$. Так как $\partial {\omega /}\partial r > 0$, то при t > 0 слагаемое с ${{e}^{{ \pm \left( {\left| {\mathbf{x}} \right|r + t{\omega }({\mathbf{p}})} \right)}}}$ вносит вклад в асимптотику меньше, чем слагаемые с ${{e}^{{ \pm \left( {\left| {\mathbf{x}} \right|r - t{\omega }({\mathbf{p}})} \right)}}}$ (в силу соображений, которые использовались при вычислении асимптотик быстроменяющихся интегралов) [15]. В результате получим

(3.16)

${{{\eta }}_{F}} \approx \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}{{g}^{2}}}}{{8{\pi }c_{t}^{2}c_{l}^{2}\sqrt {\left| {\mathbf{x}} \right|} }}{\text{Re}}\left[ {\mathop \smallint \limits_0^\infty {{e}^{{i\left( {\left| {\mathbf{x}} \right|r - t{\omega }\left( r \right) - {\pi }/4} \right)}}}\frac{{{{e}^{{ - r(b\left( {\psi } \right) - {{z}_{0}} - D)}}}{{{(1 - {\rho } + 2rc_{t}^{2}{\text{/}}g)}}^{3}}{\text{s}}{{{\text{h}}}^{2}}\left( {Dr} \right)}}{{\sqrt r {{{(1 + 2rc_{t}^{2}{\text{/}}g)}}^{2}}({\rho c}{{{\text{h}}}^{3}}\left( {Dr} \right) + {\text{sh}}\left( {Dr} \right))}}Qdr} \right]$

$Q = {{e}^{{\frac{{b_{3}^{2}{{r}^{2}}}}{2}}}}({{a}_{3}}({{c}^{2}} - R) + i{{a}_{h}}\left( {\varphi } \right)\left( {1 + R} \right)){\text{e}}({{z}_{0}} + b_{3}^{2}r)$

$R = ({{c}^{2}} - 1)r(D + b_{3}^{2}r + {{z}_{0}}),\quad c = {{c}_{l}}{\text{/}}{{c}_{t}},\quad {{a}_{h}}\left( {\varphi } \right) = {{a}_{1}}{\text{cos}}\left( {\varphi } \right) + {{a}_{2}}{\text{sin}}\left( {\varphi } \right)$

3.4. Длинноволновое приближение. Если рассматривать длинноволновое приближение, то $\left| {\mathbf{p}} \right|D$ можно считать достаточно малой величиной, а ${{b}_{j}} + \left| {{{z}_{0}}} \right| \gg D$, ${\text{sin}}(Dr) \approx Dr$, ${\text{ch}}\left( {Dr} \right) \approx 1$. В результате получим

(3.17)

${{\eta }_{L}} = \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}g}}{{4{\pi }c_{l}^{2}}}\frac{{{{D}^{2}}}}{{\sqrt {\left| {\mathbf{x}} \right|} }}{\text{Re}}\left[ {\mathop \smallint \limits_0^\infty {{r}^{{5/2}}}{{e}^{{i\left( {\left| {\mathbf{x}} \right|r - t{\tilde {\omega }}\left( r \right) - {\pi }/4} \right)}}}\frac{{{{e}^{{ - r\left( {b\left( {\psi } \right) - {{z}_{0}} - D} \right)}}}{{e}^{{b_{3}^{2}{{r}^{2}}/2}}}}}{{\left( {{\rho } + Dr} \right)}}Q{\text{e}}({{z}_{0}} + b_{3}^{2}r)dr} \right]$

где $Q = ({{a}_{3}}({{c}^{2}} - R) + i{{a}_{h}}({\varphi })(1 + R)),R = ({{c}^{2}} - 1)(D + b_{3}^{2}r + {{z}_{0}})r$

Дальнейшие упрощения связаны со следующими фактами. Во-первых, можно одновременно отбросить экспоненту ${{e}^{{b_{3}^{2}{{r}^{2}}/2}}}$, b₃r в множителе R, а также “срезающую” функцию. Кроме того, учитывая наличие в интеграле множителя r^5/2, быстрое стремление к 0 подынтегральной функции и существенное изменение подынтегральной функции лишь при очень малых r, частоту ${\tilde {\omega }}$ (дисперсионное соотношение) можно заменить на ${\tilde {\omega }} = \sqrt {gD} r = Cr$. В результате приходим к следующей формуле:

(3.18)

${{\eta }_{L}} = \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}g}}{{4{\pi }c_{l}^{2}}}\frac{{{{D}^{2}}}}{{\sqrt {\left| {\mathbf{x}} \right|} }}{\text{Re}}\left[ {\mathop \smallint \limits_0^\infty {{r}^{{5/2}}}{{e}^{{i\left( {\left( {\left| x \right| - tC} \right)r - {\pi }/4} \right)}}}\frac{{{{e}^{{ - r\left( {b\left( {\psi } \right) + h} \right)}}}}}{{\left( {{\rho } + Dr} \right)}}{\text{\;}}({{a}_{3}}({{c}^{2}} - R) + i{{a}_{h}}\left( {\varphi } \right)\left( {1 + R} \right))dr} \right]$

$R \approx - ({{c}^{2}} - 1)hr,\quad h = - {{z}_{0}} - D$

Величина h характеризует глубину залегания источника, считая от границы раздела вода–упругое основание.

Ясно, что последний интеграл сводится к вычислению двух интегралов

${{I}_{k}} = {{I}_{k}}\left( {y,L,{\gamma },D} \right) = \mathop \smallint \limits_0^\infty {{r}^{{k + 1/2}}}\frac{{{{e}^{{\left( {iy - L} \right){\text{\;}}r}}}}}{{{\gamma } + Dr}}dr = {{\left( { - i\frac{\partial }{{\partial y}}} \right)}^{k}}\mathop \smallint \limits_0^\infty \sqrt r \frac{{{{e}^{{\left( {iy - L} \right){\text{\;}}r}}}}}{{{\gamma } + Dr}}dr$

где $y = \left| {\mathbf{x}} \right| - Ct,{\text{\;}}L = b\left( {\psi } \right) + h,k = 2,3$. Тогда (3.18) примет вид

(3.19)

${{{\eta }}_{L}} = \frac{{{{b}_{1}}{{b}_{2}}{{b}_{3}}g}}{{4{\pi }c_{l}^{2}}}\frac{{{{D}^{2}}}}{{\sqrt {\left| {\mathbf{x}} \right|} }}{{\left. {{\text{Re}}[{{e}^{{ - i{\pi }/4}}}({{a}_{3}}({{c}^{2}} + i{{a}_{h}}\left( {\varphi } \right)){{I}_{2}} + \left( {{{a}_{3}} - i{{a}_{h}}\left( {\varphi } \right)} \right)({{c}^{2}} - 1)h{{I}_{3}})]} \right|}_{{y = \left| {\mathbf{x}} \right| - Ct}}}$

Интегралы I_2,3 вычисляются точно (см., например, [15]):

$\begin{gathered} {{I}_{2}} = \frac{{\sqrt {\pi } }}{{{{D}^{3}}}}\left[ {\frac{{3{{D}^{2}} - 2D{\gamma \xi } + 4{{{\left( {{\gamma \xi }} \right)}}^{2}}}}{{4{{{\xi }}^{{5/2}}}}} - \frac{{\sqrt {\pi } {{{\gamma }}^{{5/2}}}}}{{\sqrt D }}{{e}^{{{\gamma \xi }/D}}}{\text{erfc}}\left( {\sqrt {\frac{{{\gamma \xi }}}{D}} } \right)} \right] \\ {{I}_{3}} = \frac{{\sqrt {\pi } }}{{{{D}^{4}}}}\left[ {\frac{{15{{D}^{3}} - 6{{D}^{2}}{\gamma \xi } + 4D{{{\left( {{\gamma \xi }} \right)}}^{2}} - 8{{{\left( {{\gamma \xi }} \right)}}^{3}}}}{{8{{{\xi }}^{{7/2}}}}} + \frac{{\sqrt {\pi } {{{\gamma }}^{{7/2}}}}}{{\sqrt D }}{{e}^{{{\gamma \xi }/D}}}{\text{erfc}}\left( {\sqrt {\frac{{{\gamma \xi }}}{D}} } \right)} \right] \\ \end{gathered} $

где аргумент у ${\xi } = L - iy$ лежит на интервале $\left[ { - {\pi /}2,{\pi /}2} \right]$. При больших значениях вещественной части аргумента z функцию erfc(z) можно представить в виде асимптотического разложения:

${\text{erfc}}\left( z \right) = \frac{{{{e}^{{ - {{z}^{2}}}}}}}{{\sqrt \pi z}}\left( {1 + \mathop \sum \limits_{m = 1}^\infty {{{( - 1)}}^{m}}\frac{{1 \cdot 3 \ldots \left( {2m - 1} \right)}}{{{{{(2{{z}^{2}})}}^{m}}}}} \right)$

что дает

(3.20)

$\begin{gathered} {{I}_{2}} = \frac{{\sqrt \pi }}{{{{D}^{3}}}}\left[ {\frac{{3{{D}^{2}} - 2D\gamma \xi + 4{{{(\gamma \xi )}}^{2}}}}{{4{{\xi }^{{5/2}}}}} - \frac{{{{\gamma }^{2}}}}{{\sqrt \xi }}\left( {1 - \frac{D}{{2\gamma \xi }} + \frac{{3{{D}^{2}}}}{{4{{{(\gamma \xi )}}^{2}}}}...} \right)} \right] \\ \equiv - \frac{{\sqrt \pi {{\gamma }^{2}}}}{{\sqrt \xi }}\sum\limits_{m = 3}^\infty {{{{( - 1)}}^{m}}\frac{{(2m - 1)!{{D}^{{m - 3}}}}}{{{{2}^{{m - 1}}}(m - 1)!{{{(2\gamma \xi )}}^{m}}}}} \\ {{I}_{3}} = \frac{{\sqrt \pi }}{{{{D}^{4}}}}\left[ {\frac{{15{{D}^{3}} - 6{{D}^{2}}\gamma \xi + 4D{{{(\gamma \xi )}}^{2}} - 8{{{(\gamma \xi )}}^{3}}}}{{8{{\xi }^{{7/2}}}}} + \frac{{{{\gamma }^{3}}}}{{\sqrt \xi }}\left( {1 - \frac{D}{{2\gamma \xi }} + \frac{{3{{D}^{2}}}}{{4{{{(\gamma \xi )}}^{2}}}} - \frac{{15{{D}^{3}}}}{{8{{{(\gamma \xi )}}^{3}}}}...} \right)} \right] \\ \equiv \frac{{\sqrt \pi {{\gamma }^{3}}}}{{\sqrt \xi }}\sum\limits_{m = 4}^\infty {{{{( - 1)}}^{m}}\frac{{(2m - 1)!{{D}^{{m - 4}}}}}{{{{2}^{{m - 1}}}(m - 1)!{{{(2\gamma \xi )}}^{m}}}}} \\ \end{gathered} $

Можно воспользоваться другим способом вычисления интегралов I_2,3. Имеют место формулы

$\mathop \smallint \limits_0^\infty {{r}^{{k + 1/2}}}{{e}^{{ - {\xi }r}}}dr = {{\left( { - i\frac{\partial }{{\partial y}}} \right)}^{k}}\mathop \smallint \limits_0^\infty \sqrt r {{e}^{{ - {\xi }r}}}dr = {{\left( { - i\frac{\partial }{{\partial y}}} \right)}^{k}}\frac{{\sqrt {\pi } }}{{2{{{\xi }}^{{3/2}}}}} = \frac{{\sqrt {\pi } \left( {2k + 1} \right)!!}}{{{{2}^{{k + 1}}}{{\xi }^{{3/2 + k}}}}}$

Поэтому, если в формуле (3.18) подынтегральное выражение аппроксимировать функцией $Q{{r}^{{k + 1/2}}}{{e}^{{ - \tilde {L}r}}}$, подобрав параметры $\tilde {L}$ и Q так, чтобы у этой функции и функции ${{r}^{{k + 1/2}}}{\text{/}}({\gamma } + Dr){{e}^{{ - Lr}}}$, совпали точка r₀, в которой достигается максимум, и значение этого максимума, то мы получим явные приближенные выражения для решения.

Соответствующие вычисления, выполненные с помощью программы Mathematica [16], приводят к следующим формулам:

$\begin{gathered} \frac{{{{r}^{{\alpha }}}{{e}^{{ - Lr}}}}}{{{\gamma } + Dr}} \approx Q\left( {\alpha } \right){{r}^{{\alpha }}}{{e}^{{ - \tilde {L}\left( {\alpha } \right)r}}},\quad Q\left( {\alpha } \right) = (\tilde {L}\left( {\alpha } \right) - L){{e}^{{\left( {D\left( {1 + {\alpha }} \right) + L{\gamma } - w\left( {\alpha } \right)} \right)/\left( {2D} \right)}}} \\ \tilde {L}\left( {\alpha } \right) = \frac{{D\left( {1 - {\alpha }} \right) + L{\gamma } - w\left( {\alpha } \right)}}{{2{\gamma }}},\quad w\left( {\alpha } \right) = \sqrt {4{\alpha }DL{\gamma } + {{{((1 - {\alpha })D + L{\gamma })}}^{2}}} \\ \end{gathered} $

Выберем ${\alpha } = k + 1{\text{/}}2$ и положим

$\begin{gathered} {{w}_{k}} = w\left( {k + \frac{1}{2}} \right) \equiv \sqrt {4\left( {k + \frac{1}{2}} \right)DL{\gamma } + {{{\left( {\left( {\frac{1}{2} - k} \right)D + L{\gamma }} \right)}}^{2}}} \\ {{L}_{k}} = \tilde {L}\left( {k + \frac{1}{2}} \right) \equiv \frac{{\left( {1{\text{/}}2 - k} \right)D + L{\gamma } + {{w}_{k}}}}{{2{\gamma }}} \\ {{Q}_{k}} = Q\left( {k + \frac{1}{2}} \right) \equiv \left( {{{L}_{k}} - L} \right){{e}^{{\left( {\left( {k + 3/2} \right)D + L{\gamma } - {{w}_{k}}} \right)/\left( {2D} \right)}}} \\ \end{gathered} $

Напомним, что 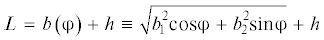; отсюда получим

${{I}_{k}} = \frac{{\sqrt {\pi } \left( {2k + 1} \right)!!{{Q}_{k}}}}{{{{2}^{{k + 1}}}{{{({{L}_{k}} - iy)}}^{{3/2 + k}}}}}$

и простые приближенные формулы для решения

(3.21)

где φ – полярный угол вектора $x$.

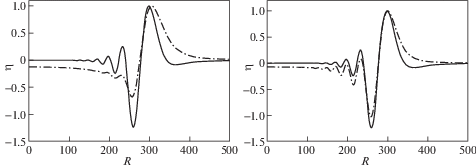
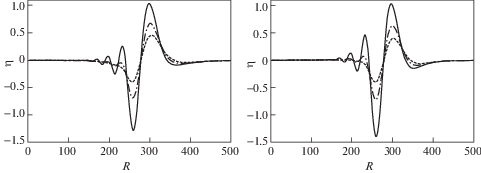
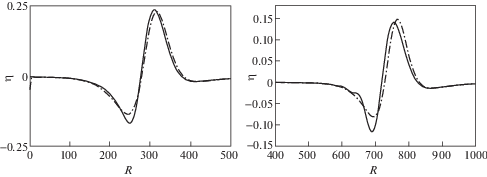
4. Результаты численных расчетов. Приведем некоторые расчеты для действующего в вертикальном направлении a₁ = a₂ = 0 осесимметричного источника c b₁ = b₂ = b₃ ≡ b. На рис. 2 показаны результаты расчетов возвышения поверхности жидкости в зависимости от расстояния от эпицентра в некоторый фиксированный момент времени (пространственные профили): полученные по формулам (3.11)–(3.13) – сплошная линия и по формулам из [12] – пунктирная линия. Амплитуда у источников задавалась таким образом, чтобы максимальное значение возвышения жидкости для обоих решений совпадали. Глубина залегания источника и его размер для расчетов по (3.11)–(3.13) задавались 43 км и 2 км, соответственно. Характеристический размер источника для вычислений по [12] на левом графике равен 5, на правом 3.5. Как видно из рисунка, несмотря на то, что множители ${{{\text{e}}}^{{ - \left( {b - {{z}_{0}}} \right)\left| {\mathbf{p}} \right|}}}$ в (3.11)–(3.13) и ${{{\text{e}}}^{{ - l\left| {\mathbf{p}} \right|}}}$ в [12] определяют размер источника, прямого соответствия между ними нет. Довольно хорошее согласие пространственных профилей достигается в том случае, когда характерный размер l почти в 3 раза меньше глубины залегания b – z₀ источника.

Рис. 2

Обратим внимание и на то, что в случае расположенного в упругом основании источника, головной гребень волны становится более крутым, а перед ним появляется характерное понижение уровня жидкости по отношению к невозмущенному состоянию. Как следует из расчетов, дисперсионные эффекты в волнах, порождаемых источником в упругой среде, выражены слабее, чем в волнах от источника на дне.

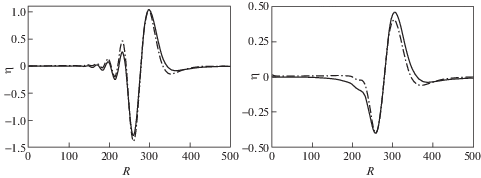
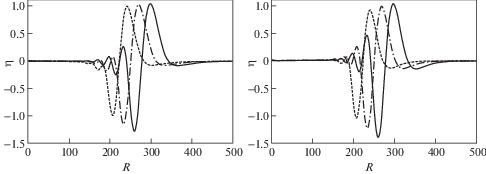
На рис. 3 показаны результаты расчетовЖ выполненных по (3.11)–(3.13) – сплошная линия в сравнении с длинноволновым приближением (3.18) – пунктирная линия. На графике слева глубина залегания источника составляет 43 км, на графике справа – 63 км, характерный размер источника равен 2 км, амплитуда источника для обоих графиков одинакова. Для профилей волн, полученных по длинноволновому приближению, передний фронт головного гребня круче, а впадина перед ним более заметна.

Рис. 3

Рис. 4 демонстрирует зависимость профиля волны от глубины залегания источника. Графики слева рассчитаны по (3.11)–(3.13), справа – по (3.18); параметры для расчета: b = 2. z₀ = –43 – сплошные, z₀ = –53 – штрихпунктирные, z₀ = –63 – пунктирные линии. С увеличением глубины источника на волновых профилях уменьшаются амплитуды “хвостовых” (следующих за головным) гребней, вплоть до их полного исчезновения. Волны становятся все более похожими на те, которые порождаются источником на дне [12] с большим значением характерного размера l, но при этом длина порождаемых волн меняется незначительно.

Рис. 4

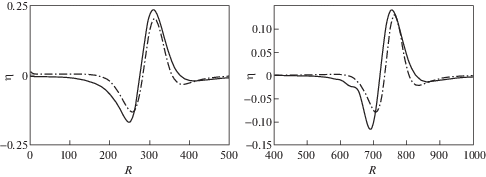
Поведение профилей волны в зависимости от толщины слоя жидкости показано на рис. 5; левый график рассчитан по (3.11)–(3.13), правый – по (3.18). Данные для расчетов: b = 2, z₀ = –43. Сплошные линии соответствуют толщине слоя D = 5, штрихпунктирные – D = 4.5, пунктирные – D = 4. Видно, что уменьшение толщины слоя приводит к снижению проявления “дисперсионных” эффектов в волнах: уменьшается количество хвостовых волн и их амплитуды. Из сравнения левого и правого графиков видно, что длинноволновая формула (3.18) дает большее изменение амплитуды волны в зависимости от толщины слоя.

Рис. 5

Уменьшение скорости поперечной волны в упругой среде, результаты расчетов приведены на рис. 6, приводит к незначительному увеличению амплитуд генерируемых волн, практически не влияя при этом на их длину. Длинноволновое приближение дает на 8–9% меньшие значения для головных впадин, при практически одинаковых амплитудах головного гребня. График слева построен по (3.11)–(3.13), справа – по (3.18). Скорости поперечных волн: c_t = 2900 – сплошные, c_t = 2800 – штрихпунктирные, c_t = 2700 – пунктирные линии. Остальные параметры: b = 2, z₀ = –43, D = 5.

Рис. 6

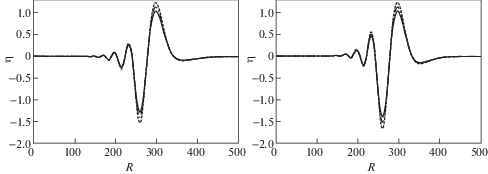
Результаты расчета волновых профилей для достаточно длинных волн, выполненные по точным формулам – сплошные линии и явным аналитическим зависимостям (3.19) – штрихпунктирные линии, представлены на рис. 7. Параметры для расчета взяты следующими: b = 2, z₀ = –83, D = 5, c_t = 2900. Сравнение показывает, что волновые профили полученные по явным формулам демонстрируют чуть меньшие амплитуды у головных гребня и впадины, а также более быстрый выход на стационарное значение. С увеличением расстояния (график справа) в волнах, полученных по точным зависимостям, начинают проявляться дисперсионные эффекты, отсутствующие в волнах, рассчитанных по (3.19).

Рис. 7

На рис. 8 приведено сравнение волновых профилей, рассчитанных по точным формулам – сплошные и аналитическим зависимостям (3.20) – штрихпунктирные линии, для тех же параметров, что и на предыдущем рисунке.

Рис. 8

Заключение. Получены простые формулы, позволяющие изучать влияние параметров источника и среды на распространение возбуждаемых этим источником длинных волн. Вывод этих формул опирается, в том числе, на предложенный способ упрощения подынтегральных выражений.

Работа выполнена при финансовой поддержке РФФИ (проект 17-01-00644 А).

Список литературы

Пелиновский Е.Н. Гидродинамика волн цунами. Нижний Новгород.: Институт прикладной физики РАН, 1996. 276 с.
Kanamori H. Mechanism of tsunami earthquakes // Phys. Earth Planet. Inter. 1972. № 6. P. 349–359.
Yamashita T., Sato R. Generation of tsunami by a fault model // J. Phys. Earth. 1974. № 22. P. 415–440.
Levin B.W., Nosov M.A. Physics of Tsunamis. Second Ed. Springer, 2016. 388 p.
Подъяпольский Г.С. Возбуждение цунами землетрясением // Методы расчета возникновения и распространения цунами. М.: Наука, 1978. С. 30–87.
Sabatier P.C. On water waves produced by ground motions // J. Fluid Mech. 1983. № 126. P. 27–58.
Гусяков В.К., Чубаров Л.Б. Численное моделирование возбуждения и распространения цунами в прибрежной зоне // Изв. РАН. Физика Земли. 1987. Вып. 11. С. 53–64.
Фрагела А. К. К задаче о движении идеальной жидкости в неограниченном упругом бассейне // Дифференц. уравнения. 1989. Т. 25. Вып. 8. С. 1417–1426.
Доброхотов С.Ю., Толстова О.Л., Чудинович И.Ю. Волны в жидкости на упругом основании. Теорема существования и точные решения // Матем. заметки, 1993. Т. 54. Вып. 3. С. 33–55.
Зволинский Н.В., Карпов И.И., Никитин И.С., Секерж-Зенькович С.Я. Возбуждение волн цунами и Рэлея гармоническим двумерным центром вращения // Изв. РАН. Физика Земли. 1994. Вып. 9. С. 29–33.
Гринив Р.О., Доброхотов С.Ю., Шкаликов А.А. Операторная модель задачи о колебаниях жидкости на упругом основании // Матем. заметки. 2000. Т. 68. Вып. 1. С. 57–70.
Dobrokhotov S.Yu, Tolstova O.L., Sekerzh-Zenkovich S.Ya, Vargas C.A. Influence of the elastic base of a basin on the propagation of waves on the water surface // Russ. J. Math. Physics. 2018. T. 25. № 4. P. 459–469.
Доброхотов С.Ю., Ильясов Х.Х., Секерж-Зенькович С.Я., Толстова О.Л. Простые решения задачи о волнах на поверхности жидкости в рамках линейной гидроупругой модели // ДАН. 2019. Т.18. № 4. С. 370–375.
Федорюк М.В. Асимптотика, интегралы и ряды. М.:Наука, 1987. 544 с.
Dobrokhotov S.Yu, Nazaikinskii V.E. Tirozzi, Asymptotic solutions of 2-D wave equations with variable velocity and localized right-hand side // Russian Journal of Mathematical Physics. 2010. V. 17. № 1. P. 66–76.
Wolfram Mathematica, www.wolfram.com/mathematica/

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал