Известия РАН. Механика твердого тела, 2020, № 3, стр. 92-103

ВЛИЯНИЕ УГЛЕРОДНЫХ ДОБАВОК НА МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭПОКСИДНОГО СВЯЗУЮЩЕГО

А. Н. Власов^a, *, Д. Б. Волков-Богородский^a, Ю. В. Корнев^a

^a Институт прикладной механики РАН
Москва, Россия

^* E-mail: bah1955@yandex.ru

Поступила в редакцию 24.12.2019
После доработки 12.01.2020
Принята к публикации 20.01.2020

DOI: 10.31857/S0572329920030198

Аннотация

В статье обосновывается выбор модификатора (наполнителя) эпоксидного связующего, а именно, углеродных нанотрубок. Полученный за счет модификации эпоксидный клей в твердом состоянии представляет собой 3-х фазный нанокомпозит, где матрица – это эпоксидная смола, наполнитель – нанотрубки, а контактный слой – это область эпоксидной смолы, молекулы которой подверглись конформации. Затем в эксперименте и теоретическими методами определялись его эффективные деформационные характеристики. Было показано, что метод асимптотического усреднения, единственный имеющий строгое математическое обоснование, дает сопоставимые результаты с экспериментальными определениями (расхождение ~3.4%).

Ключевые слова: эпоксидное связующее, матрица, включение, контактный слой, углеродные нанотрубки, эффективные деформационные характеристики, фрактальный метод оценки упругих свойств, метод Эшелби, метод асимптотического усреднения

1. Введение. Изделия из полимерных композитных материалов (ПКМ) широко используются в строительстве, авиационной и космической технике. Уникальный комплекс свойств (высокая удельная прочность, модуль упругости, термонапряженность) ПКМ достигается главным образом за счет повышения характеристик армирующих волокон. Однако, упруго-прочностные характеристики такого компонента композитов, как полимерной матрицы, на порядок уступают аналогичным показателям конструкционых волокон [1]. Вместе с тем матрица выполняет функцию сохранения в монослое композита достаточного уровня прочности при сжатии, межслоевом сдвиге, сопротивлении усталости, длительной прочности, деформационной теплостойкости, трещиностойкости и ряда других эксплуатационных характеристик.

Одним из направлений регулирования комплекса свойств ПКМ и изделий из них является введение добавок/наполнителей углеродных наноматериалов различного строения в состав полимерных матриц. В настоящее время углеродные нанонаполнители получили широкое применение, в том числе в качестве модификаторов для повышения механических характеристик исходных материалов. В частности, в работе [2] показано, что при диспергировании в полистироле 1% по массе многослойных углеродных нанотрубок, модуль упругости и прочность при разрушающих нагрузках увеличились более чем на 35%. Было зафиксировано увеличение жесткости до 3.5 раза эпоксидной матрицы при диспергировании 2% по масссе однослойных углеродных нанотрубок [3]. В результатах, полученных в работах других исследователей [4, 5], также отмечалось значительное уменьшение коэффициента трения и увеличение износостойкости в композитах гидроксиапатита с углеродными нанотрубками [6]. Нами исследовалось применение наномодифицированной клеевой композиции для повышения прочностных характеристик болтовых соединений в металло-композиционных конструкциях [7]. Конструкционные углепластики заняли прочное место в ряду материалов для авиционной и космической техники, где удельная масса составляет более 50%.

Для повышения эффективности механических характеристик (модуль упругости, прочность, вязкость) клеевой композиции выполнялась ее модификация углеродными наноматериалами. Модификация заключалась в добавлении малых концентраций наноматериалов в стандартную клеевую композицию, что теоретически за счет взаимодействия между нанонаполнителем и полимерной матрицей позволяет повысить ее прочность [8–11], а в перспективе и усталостную долговечность деталей, и конструкций из полимерных композиционных материалов.

2. Выбор наноматериалов для эффективной наномодифицированной клеевой композиции. Выбор оптимального типа наноматериалов для применения в клеевой композиции проводился путем компьютерного моделирования взаимодействия, широко применяемой в клеевых соединениях, эпоксидной смолы ЭД-20 с рядом потенциальных наполнителей – углеродных наноматериалов.

Исследовались механизмы взаимодействия эпоксидной матрицы с поверхностью частиц различных наполнителей (аморфного углерода (СН)170, фуллерена С240 и углеродных нанотрубок (УНТ) различного строения). Энергетические и прочностные характеристики межфазных слоев наполненных эпоксидных клеев исследовались в вычислительном эксперименте в рамках кластерного метода и подхода микроскопической координаты трения с использованием квантово-механического программного комплекса NDDO/sp-spd.

Для каждого рассмотренного адсорбционного комплекса (межфазного слоя с наполнителем) рассчитывалась энергия связывания E_b на одну мономерную единицу эпоксидного клея и максимальная сила сдвигового трения F_{sh_МАХ} как градиент полной энергии системы по выбранной координате трения. Результаты расчетов представлены в табл. 1.

Таблица 1

Адсорбционный комплекс	R, Å	Е_b, ккал/моль	F_{sh_MAX}, ккал/(моль ∙ Å)
ЭД-20 + углеродная частица CH170	2.7	–14.2	19.2
ЭД-20 + фуллерен С240	2.8	–13.8	18.8
ЭД-20 + углеродная трубка С288 (9,9) адсорбция по открытому концу	2.5	–23.5	26.8
ЭД-20 + углеродная трубка С288 (9,9) адсорбция по боковой стороне	2.7	–15.4	22.7
ЭД-20 + частица графена	2.8	–14.6	20.1
ЭД-20 + частица оксид графена	2.2	–33.2	37.5

Полученные результаты показывают, что наиболее подходящим наполнителем эпоксидных клеев являются нанотрубки. Далее будет рассматриваться именно этот наполнитель.

Материалы и методы. В работе были использованы углеродные нанотрубки марки “Таунит-М”, в качестве базовой клеевой композиции – эпоксидная смола ЭД-20. Характеристики углеродных нанотрубок типа “Таунит-М” представлены в табл. 2.

Таблица 2

Параметры	Значения
Наружный диаметр, нм	8÷15
Внутренний диаметр, нм	4÷8
Длина, мкм	2 и более
Общий объем примесей до очистки, %	до 5
после очистки, %	до 1
Насыпная плотность, г/см³	0.03÷0.05
Удельная геометрическая поверхность, м²/г	300÷320 и более
Термостабильность, °С	до 600

Порошок УНТ Таунит вводился в эпоксидную матрицу (смола ЭД-20) в количестве 0.01% по массе, типовой состав клеевой композиции представлен в табл. 3.

Таблица 3

№	Наименование ингредиентов	Массовые части (масс. ч.)
1	Смола ЭД-20	60.0
2	Отвердитель ПО-300	49.0
3	Пластификатор	12.0
4	Итого, масс. ч.	123.0

При введении УНТ в смолу ЭД-20 не использовались растворители. Смешение проводили по технологии ФГУП ЦАГИ. Добавки УНТ в смолу сначала вручную перемешивались в лабораторном стакане, а затем шток диспергатора помещали в данный стакан и озвучивали 3 цикла при максимальной мощности установки по 30 сек каждый с промежуточным охлаждением смолы до 30°С (технология ФГУП ЦАГИ).

Далее полученную смесь УНТ и смолы ЭД-20 смешивали с отвердителем и пластификатором в соответствии с рецептурой (см. табл. 3), и затем проводили процесс вакуумирования в вакуумном термошкафу Binder VD53 при температуре 60°С. Насосом Vacuumbrand GMBH ME-1 устанавливался вакуум на уровне 100 мБар, достижение вакуума происходило в течение 2 мин.

Эксперимент проводили для каждого образца в отдельности. Смешение компонентов клеевой композиции проводилось в течение 5 мин. Далее проводилось термостатирование образца 5 мин. при 60°С в термошкафу. Затем проводился процесс вакуумирования. Время вакуумирования для всех образцов составляло 30 мин.

Далее образцы клеевых композиций наносились на предметное стекло и выдерживались до их отверждения. После чего из экспериментов по наноиндентированию определялся их модуль упругости.

3. Механические характеристики эпоксидного связующего при ультразвуковом диспергировании и воздействии направленного волнового процесса. Для исследования свойств материалов методом наноиндентирования в настоящей работе применялся измерительный комплекс NanoTest 600 (Micro Materials Ltd.), позволяющий определять механические свойства широкого спектра материалов и покрытий в нано- и микромасштабе.

Суть метода наноиндентирования заключается во внедрении геометрически и физически аттестованной пирамиды (пирамида Берковича с углом при вершине 65.3° и радиусом закругления 200 нм) в материал и определении с высокой точностью зависимости нагрузка – глубина индентирования [12–14].

В работах [15–18] отмечается необходимость корректировки стандарнтных параметров эксперимента, для избежания проявления так называемого “nose effect”, когда на цикле разгрузки нагрузка уменьшается линейно, а внедрение продолжает расти. Данное поведение материала связано с проявлением его вязкоупругих свойств (с ползучестью) и приводит к характерному изгибу в зависимости нагрузка-внедрение на цикле разгрузки [15, 16]. В настоящей работе, для нивелирования возможного эффекта ползучести полимерной клеевой композиции в ходе эксперимента осуществлялась задержка при максимальной нагрузке в течение 100 с. Результаты экспериментов по наноиндентированию представлены в табл. 4.

Таблица 4

Образец	Образец 1 (ИСХ)		Образец 2 (УНТ)
Нагрузка	5 мН		5 мН
Параметр	Значение	разброс, %	Значение	разброс, %
Максимальная глубина индентирования (внедрение), нм	1189.4	2.6	1054.56	2.1
Пластическое внедрение, нм	1039.2	3.5	911.64	2.5
Приведенный модуль упругости, ГПа	2.8	8.16	3.2	8.5
Упругое восстановление	0.145	11	0.16	9.3

Полученные экспериментальные данные говорят о том, что введение углеродных нанотрубок в клеевые композиции в малых концентрациях (0.01% масс.) приводит к увеличению упругих свойств последних. В настоящем эксперименте был выбран сферо-конический индентор для уменьшения влияния микро шероховатости поверхности образца на результаты эксперимента, что существенно уменьшило разброс показателей, полученных при наноиндентировании, по сравнению с результатами предыдущих работ [7, 19].

4. Математическое моделирование по определению упругих свойств композитного клея. Для расчета упругого модуля клеевой композиции необходимо оценить размеры агрегатов, размеры межфазной области и их модули упругости. Для этого вначале необходимо определить объемное содержание модифицирующего наполнителя с помощью формулы [20]:

(4.1)

${{{\varphi }}_{f}} = \frac{{{{W}_{f}}}}{{{{{\rho }}_{f}}}}$

где W_f – массовое содержание нанонаполнителя, ρ_f – его плотность, кг/м³. Плотность наночастиц ρ_f определяется следующим образом [20]:

(4.2)

${{{\rho }}_{{\text{f}}}} = 188{{\left( {{{d}_{{{\text{CNT}}}}}} \right)}^{{1/3}}}$

где d_CNT – наружный диаметр углеродной нанотрубки, равный 8–15 нм (табл. 2).

Следовательно, средняя плотность углеродной нанотрубки будет равна ${{\rho }_{f}} = 424.35$ кг/м³. Таким образом, при содержании наполнителя равным 0.01% по массе массовое его содержание на 1 кг композита будет равно ${{W}_{f}} = 0.01$ кг, а объемное содержание равно ${{{\varphi }}_{{\text{f}}}} = 2.36 \times {{10}^{{--5}}}$.

Перейдем к оценке размеров агрегатов частиц. Макромолекулярные клубки создают максимально плотную структуру с максимальным предельным значением ее фрактальной размерности D_f ($D_{f}^{0}$), которая определяется согласно уравнению [21]:

(4.3)

$D_{f}^{0} = \frac{{4\left( {d + 1} \right)}}{7}$

где d – размерность евклидова пространства, в котором рассматривается фрактал; для d = 3 величина $D_{f}^{0}$ ≈ 2.29 (в нашем случае d = 3).

Далее для оценки величины D_f можно использовать модель необратимой агрегации, которая дает следующее соотношение для радиуса агрегата частиц R_agr [22]:

(4.4)

${{R}_{{{\text{agr}}}}}\sim c_{0}^{{--1/(d--{{D}_{f}})}}$

где с₀ – исходная концентрация агрегирующихся частиц.

Коэффициент в соотношении можно определить при следующих условиях: с₀ = φ_f и D_f = $D_{f}^{0}$. В случае углеродных нанотрубок соотношение принимает следующий вид [23]:

(4.5)

${{R}_{{{\text{agr}}}}} = 15{\varphi }_{f}^{{--1/\left( {d--{{D}_{f}}} \right)}}$

Далее оценим объемное содержание межфазной области, что вместе с размерами агрегатов частиц определяет размеры межфазной области.

“Открытая граница” фрактала или область его роста [24], представляет собой множество несвязанных между собой узлов роста N_g, которое определяется зависимостью как квадратный корень из объемного содержания нанонаполнителя ${\varphi }_{f}^{{1/2}}$ и выражается следующей зависимостью [20]:

(4.6)

${{N}_{g}} = 5.25 \times {{10}^{3}}{\varphi }_{f}^{{1/2}}$

Зависимость относительной доли межфазных областей φ_if от числа узлов кольцеобразных формирований углеродных нанотрубок, образующих “открытую границу” этих фрактальных объектов определяется следующим образом [20]:

(4.7)

${{{\varphi }}_{{if}}} = 1.10 \times {{10}^{{--2}}}N_{g}^{{1/2}}$

Следовательно, относительная доля межфазных областей будет равна

(4.8)

${{{\varphi }}_{{if}}} = 2.52 \times {{10}^{{--\frac{1}{2}}}}{\varphi }_{f}^{{1/4}} = 0.0555$

Авторы [25] предложили фрактальную модель упругости агрегатов дисперсного нанонаполнителя, в которой модуль упругости Е_agr указанных агрегатов определяется по формуле:

(4.9)

${{E}_{{{\text{agr}}}}} = {{E}_{{{\text{nf}}}}}{{\left( {\frac{a}{{{{R}_{{{\text{agr}}}}}}}} \right)}^{{d + 1.1}}}$

где Е_nf – модуль упругости нанонаполнителя, который для углеродных нанотрубок может достигать 2000 ГПа [26], 1000 ГПа [27], а – размер исходных частиц нанонаполнителя, R_agr – радиус их агрегатов.

Авторы [28] полагают, что для нанокомпозитов эпоксиполимер/УНТ величина Е_if в 3–4 раза превышает значение полимерной матрицы (в нашем случае Е_mx = 2.8 ГПа). Очевидно, что такое изменение свойств межфазных областей будет неизбежно сказываться на свойствах полимерной матрицы в общем, которая состоит из немодифицированной объемной матрицы и межфазных областей.

4.1. Фрактальные методы оценки упругих свойств. Реальный модуль упругости матрицы Е_m можно определить согласно правилу смесей, что предполагается и другими авторами [28, 29]:

(4.10)

${{E}_{m}} = {{{\varphi }}_{{{\text{if}}}}}{{E}_{{{\text{if}}}}} + \left( {1--{{{\varphi }}_{f}}--{{{\varphi }}_{{{\text{if}}}}}} \right){{E}_{m}}$

Таким образом, получаем реальный модуль упругости матрицы равный E_m = = 3.1885 ГПа.

Зависимость для определения модуля нанокомпозита по значениям реального модуля упругости матрицы Е_m и объемного содержания нанонаполнителя φ_f описывается следующим уравнением [30]:

(4.11)

${{E}_{n}} = \left( {1 + 5.6{{{\varphi }}_{f}}} \right){{E}_{m}}$

В результате получаем следующее значение модуля нанокомпозита наполненного углеродными нанотрубками: ${{E}_{f}} = 3.189$ ГПа.

4.2. Метод Эшелби по определению упругих свойств (4-х фазная модель). Наблюдаемые масштабные эффекты при сверхмалой концентрации частиц объясняются влиянием на характеристики композита большой удельной поверхности наночастиц. Поэтому в качестве модели композитного материала использовалась модель материала с межфазным слоем, характеристики которого определяются с помощью приведенных выше оценок.

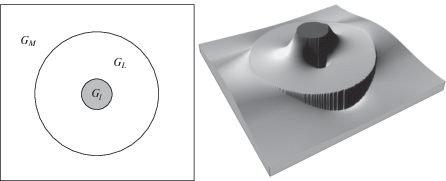
Определим эффективные деформационные характеристики эпоксидного связующего модифицированного нанотрубками, используя самосогласованный метод четырех сферических тел, позволяющий учитывать жесткость промежуточного межфазного слоя [31]. Этот метод предполагает нахождение аналитического решения задачи о деформировании составного сферического тела $G = {{G}_{I}} \cup {{G}_{L}} \cup {{G}_{M}}$, ${{G}_{I}} = \left\{ {r < {{r}_{0}}} \right\}$, G_L = $\{ {{r}_{0}} < r < {{r}_{1}}\} $, ${{G}_{M}} = \left\{ {{{r}_{1}} < r < {{r}_{2}}} \right\}$, погруженного в область ${{G}_{H}} = \left\{ {{{r}_{2}} < r} \right\}$ с эффективными характеристиками, при определенных условиях, заданных на бесконечности и соответствующих некоторому однородному напряженно-деформированному состоянию.

Для вычисления эффективного объемного модуля K_n область G_H, содержащая составное сферическое включение G подвергается всестороннему растяжению во всех направлениях, определяемому функцией перемещений на бесконечности $U_{0}^{{\left( H \right)}}$ = {x, y, z}. Для вычисления эффективного модуля сдвига μ_n область G_H с составным включением G подвергается однородной деформации чистого сдвига $U_{0}^{{\left( H \right)}} = \left\{ {x,--{\kern 1pt} y,0} \right\}$. Тогда эффективный модуль Юнга можно определить по формуле:

(4.12)

${{E}_{n}} = \frac{{9{{K}_{n}}{{\mu }_{n}}}}{{3{{K}_{n}} + {{\mu }_{n}}}}$

Эффективные характеристики окружающего многослойное включение материала определяются из энергетического принципа Эшелби, заключающегося в равенстве нулю приращения энергии при замене однородного тела с эффективными характеристиками на составное [31, 32], состоящее из многослойного включения сферической формы, погруженного в материал с эффективными характеристиками. При этом эффективные характеристики рассматриваются как дополнительные неизвестные переменные, а энергетический принцип – как дополнительное уравнение к системе линейных алгебраических уравнений. Во всех рассмотренных случаях энергетический принцип выражается правилом равенства нулю одного из коэффициентов в представлении аналитического решения в задаче Эшелби. Остальные коэффициенты, включая эффективный модуль K_n или μ_n, определяются из решения системы алгебраических уравнений.

Приведем вид этой системы для эффективного объемного модуля K_n:

(4.13)

${{A}_{0}} = {{A}_{1}} + {{B}_{1}},\quad {{A}_{0}}{{K}_{{\text{I}}}} = {{A}_{1}}{{K}_{L}}--{{B}_{1}}\frac{{4{{{\mu }}_{{\text{L}}}}}}{3},\quad {{A}_{1}} + {{c}_{1}}{{B}_{1}} = {{A}_{2}} + {{B}_{2}},\quad {{c}_{1}} = {{\left( {\frac{{{{r}_{0}}}}{{{{r}_{1}}}}} \right)}^{3}}$

(4.14)

${{A}_{1}}{{K}_{L}}--{{c}_{1}}{{B}_{1}}\frac{{4{{{\mu }}_{L}}}}{3} = {{A}_{2}}{{K}_{M}}--{{B}_{2}}\frac{{4{{{\mu }}_{M}}}}{3};\quad {{A}_{2}} + {{c}_{0}}{{B}_{2}} = 1$

(4.15)

${{A}_{2}}{{K}_{M}}--{{c}_{0}}{{B}_{2}}\frac{{4{{{\mu }}_{M}}}}{3} = {{K}_{{\text{н}}}},\quad {{c}_{0}} = {{\left( {\frac{{{{r}_{1}}}}{{{{r}_{2}}}}} \right)}^{3}}$

Шесть уравнений (4.13)–(4.15), где ${{A}_{0}},{{A}_{1}},{{A}_{2}},{{B}_{1}},{{B}_{2}},{{K}_{n}}$ неизвестные, определяются из контактных условий на межфазных границах (равенство перемещений и поверхностных сил). Разрешая эту систему линейных алгебраических уравнений, получаем зависимость для определения эффективного объемного модуля:

(4.16)

${{K}_{n}} = {{K}_{M}} + \frac{{{{c}_{0}}D}}{{1 + \frac{{\left( {1--{{c}_{0}}} \right)D}}{{\left( {{{K}_{M}} + \frac{4}{{3{{G}_{M}}}}} \right)}}}}$

(4.17)

$D = \frac{{{{K}_{{\text{I}}}}--{{K}_{M}}--\left( {1--{{c}_{1}}} \right)\left( {{{K}_{{\text{I}}}}--{{K}_{L}}} \right)\left( {1 + \frac{{\left( {{{K}_{M}}--{{K}_{L}}} \right)}}{{({{K}_{L}} + \frac{4}{{3{{G}_{L}})}}}}} \right)}}{{1 + \left( {1--{{c}_{1}}} \right)\frac{{\left( {{{K}_{{\text{I}}}}--{{K}_{L}}} \right)}}{{({{K}_{L}} + \frac{4}{{3{{G}_{L}})}}}}}}$

Приведем систему алгебраических уравнений для определения эффективного модуля сдвига μ_n:

(4.18)

${{A}_{0}}--9{{{\nu }}_{{\text{I}}}}{{D}_{0}} = {{A}_{1}} + \left( {1.25--{{{\nu }}_{{\text{L}}}}} \right){{B}_{1}} + 2.25{{C}_{1}}--9{{{\nu }}_{{\text{L}}}}{{D}_{1}}$

(4.19)

${{A}_{0}}--\left( {10.5--6{{\nu }_{I}}} \right){{D}_{0}} = {{A}_{1}} + \left( {0.5--{{\nu }_{L}}} \right){{B}_{1}}--1.5{{C}_{1}}--\left( {10.5--6{{\nu }_{L}}} \right){{D}_{1}}$

(4.20)

${{{\mu }}_{{\text{I}}}}{{A}_{0}} + 4.5{{{\mu }}_{{\text{I}}}}{{{\nu }}_{{\text{I}}}}{{D}_{0}} = {{{\mu }}_{{\text{L}}}}{{A}_{1}}--{{{\mu }}_{{\text{L}}}}\frac{{\left( {5--{{{\nu }}_{{\text{L}}}}} \right)}}{2}{{B}_{1}}--9{{{\mu }}_{{\text{L}}}}{{C}_{1}} + 4.5{{{\mu }}_{{\text{L}}}}{{{\nu }}_{{\text{L}}}}{{D}_{1}}$

(4.21)

${{{\mu }}_{{\text{I}}}}{{A}_{0}}--\left( {10.5 + 3{{{\nu }}_{{\text{I}}}}} \right){{{\mu }}_{{\text{I}}}}{{D}_{0}} = {{{\mu }}_{{\text{L}}}}{{A}_{1}} + {{{\mu }}_{{\text{L}}}}\frac{{\left( {1 + {{{\nu }}_{{\text{L}}}}} \right)}}{2}{{B}_{1}} + 6{{{\mu }}_{{\text{L}}}}{{C}_{1}}--{{{\mu }}_{{\text{L}}}}\left( {10.5 + 3{{{\nu }}_{{\text{L}}}}} \right){{D}_{1}}$

(4.22)

$\begin{gathered} {{A}_{1}} + {{c}_{1}}\left( {1.25--{{{\nu }}_{{\text{L}}}}} \right){{B}_{1}} + 2.25c_{1}^{{\frac{5}{3}}}{{C}_{1}}--9c_{1}^{{--\frac{2}{3}}}{{{\nu }}_{{\text{L}}}}{{D}_{1}} = \\ = {{A}_{2}} + \left( {1.25--{{{\nu }}_{{\text{M}}}}} \right){{B}_{2}} + 2.25{{C}_{2}}--9{{{\nu }}_{{\text{M}}}}{{D}_{2}} \\ \end{gathered} $

(4.23)

$\begin{gathered} {{A}_{1}} + {{c}_{1}}\left( {0.5--{{{\nu }}_{{\text{L}}}}} \right){{B}_{1}}--1.5c_{1}^{{\frac{5}{3}}}{{C}_{1}}--c_{1}^{{--\frac{2}{3}}}\left( {10.5--6{{{\nu }}_{{\text{L}}}}} \right){{D}_{1}} = \\ = {{A}_{2}} + \left( {0.5--{{{\nu }}_{{\text{M}}}}} \right){{B}_{2}}--1.5{{C}_{2}}--\left( {10.5--6{{{\nu }}_{{\text{M}}}}} \right){{D}_{2}} \\ \end{gathered} $

(4.24)

$\begin{gathered} {{{\mu }}_{{\text{L}}}}{{A}_{1}}--{{c}_{1}}{{{\mu }}_{{\text{L}}}}\frac{{\left( {5--{{{\nu }}_{{\text{L}}}}} \right)}}{2}{{B}_{1}}--9c_{1}^{{\frac{5}{3}}}{{{\mu }}_{{\text{L}}}}{{C}_{1}} + {{{\varepsilon }}_{0}}4.5c_{1}^{{--\frac{2}{3}}}{{{\mu }}_{{\text{L}}}}{{{\nu }}_{{\text{L}}}}{{D}_{1}} = \\ = {{{\mu }}_{{\text{M}}}}{{A}_{2}}--{{{\mu }}_{{\text{M}}}}\frac{{\left( {5--{{{\nu }}_{{\text{M}}}}} \right)}}{2}{{B}_{2}}--9{{{\mu }}_{{\text{M}}}}{{C}_{2}} + 4.5{{{\mu }}_{{\text{M}}}}{{{\nu }}_{{\text{M}}}}{{D}_{2}} \\ \end{gathered} $

(4.25)

$\begin{gathered} {{{\mu }}_{{\text{L}}}}{{A}_{1}} + {{c}_{1}}{{{\mu }}_{{\text{L}}}}\frac{{\left( {1 + {{{\nu }}_{{\text{L}}}}} \right)}}{2}{{B}_{1}} + 6{\text{c}}_{1}^{{\frac{5}{3}}}{{{\mu }}_{{\text{L}}}}{{C}_{1}}--c_{1}^{{--\frac{2}{3}}}{{{\mu }}_{{\text{L}}}}\left( {10.5 + 3{{{\nu }}_{{\text{L}}}}} \right){{D}_{1}} = \\ = {{{\mu }}_{{\text{M}}}}{{A}_{2}} + {{{\mu }}_{{\text{M}}}}\frac{{\left( {1 + {{{\nu }}_{{\text{M}}}}} \right)}}{2}{{B}_{2}} + 6{{{\mu }}_{{\text{M}}}}{{C}_{2}}--{{{\mu }}_{{\text{M}}}}\left( {10.5 + 3{{{\nu }}_{{\text{M}}}}} \right){{D}_{2}} \\ \end{gathered} $

(4.26)

${{A}_{2}} + {{c}_{0}}\left( {1.25--{{{\nu }}_{{\text{M}}}}} \right){{B}_{2}} + 2.25c_{0}^{{\frac{5}{3}}}{{C}_{2}}--9c_{0}^{{--\frac{2}{3}}}{{{\nu }}_{{\text{M}}}}{{D}_{2}} = 1 + 2.25{{C}_{3}}$

(4.27)

${{A}_{2}} + {{c}_{0}}\left( {0.5--{{{\nu }}_{{\text{M}}}}} \right){{B}_{2}}--1.5c_{0}^{{\frac{5}{3}}}{{C}_{2}}--c_{0}^{{--\frac{2}{3}}}\left( {10.5--6{{{\nu }}_{{\text{M}}}}} \right){{D}_{2}} = 1--1.5{{C}_{3}}$

(4.28)

${{{\mu }}_{{\text{M}}}}{{A}_{2}}--{{c}_{0}}{{{\mu }}_{{\text{M}}}}\frac{{\left( {5--{{{\nu }}_{{\text{M}}}}} \right)}}{2}{{B}_{2}}--9c_{0}^{{\frac{5}{3}}}{{{\mu }}_{{\text{M}}}}{{C}_{2}} + 4.5{\text{c}}_{0}^{{--\frac{2}{3}}}{{{\mu }}_{{\text{M}}}}{{{\nu }}_{{\text{M}}}}{{D}_{1}} = {{{\mu }}_{{\text{n}}}}--9{{{\mu }}_{{\text{n}}}}{{C}_{3}}$

(4.29)

${{{\mu }}_{{\text{M}}}}{{A}_{2}} + {{c}_{0}}{{{\mu }}_{{\text{M}}}}\frac{{\left( {1 + {{{\nu }}_{{\text{M}}}}} \right)}}{2}{{B}_{2}} + 6c_{0}^{{\frac{5}{3}}}{{{\mu }}_{{\text{M}}}}{{C}_{2}}--c_{0}^{{--\frac{2}{3}}}{{{\mu }}_{{\text{M}}}}\left( {10.5 + 3{{{\nu }}_{{\text{M}}}}} \right){{D}_{2}} = {{{\mu }}_{{\text{n}}}} + 6{{{\mu }}_{{\text{n}}}}{{C}_{3}}$

Двенадцать уравнений (4.18)–(4.29), где ${{A}_{0}},{{A}_{1}},{{A}_{2}},{{B}_{1}},{{B}_{2}},{{C}_{1}},{{C}_{2}},{{C}_{3}},{{D}_{0}},{{D}_{1}},{{D}_{2}},{{{\mu }}_{n}}$ неизвестные, соответствуют контактным условиям на межфазных границах (равенство нормальной и касательной составляющей перемещений и поверхностных сил). Разрешая эту систему линейных алгебраических уравнений, приходим к квадратному уравнению относительно модуля сдвига μ_n, положительный корень которого и определяет его значение.

4.3. Определение упругих характеристик методом асимптотического усреднения. Для определения эффективных характеристик композитного материала с учетом межфазного слоя воспользуемся также более точным и математически строго обоснованным методом асимптотического усреднения Бахвалова [33]. В этом методе формулируется полноценная задача теории упругости на параллелепипедной ячейке с включением с условиями проскальзывания на всех ее гранях рис. 1. Составленная таким образом композитная область подвергается одноосной деформации в рамках задачи линейной теории упругости:

(4.30)

$\frac{\partial }{{\partial {{{\xi }}_{i}}}}\left( {{{A}_{{ij}}}\left( {\xi } \right)\frac{{\partial u}}{{\partial {{{\xi }}_{j}}}}} \right) = 0,\quad \left[ u \right] = \left[ {{{A}_{{ij}}}\left( {\xi } \right)\frac{{\partial u}}{{\partial {{{\xi }}_{j}}}}{{n}_{i}}} \right] = 0,\quad p = {{A}_{{kj}}}\frac{{\partial u}}{{\partial {{{\xi }}_{j}}}}{{n}_{k}}$

(4.31)

${{\left. {{{u}_{1}}} \right|}_{{{\text{S}}_{1}^{ \pm }}}} = 0,\quad {{\left. {{{p}_{s}}} \right|}_{{{\text{S}}_{1}^{ \pm }}}} = 0,\quad {{\left. {{{u}_{2}}} \right|}_{{{\text{S}}_{2}^{ \pm }}}} = 0,\quad {{\left. {{{p}_{s}}} \right|}_{{{\text{S}}_{2}^{ \pm }}}} = 0,\quad {{\left. {{{u}_{3}}} \right|}_{{{\text{S}}_{3}^{ \pm }}}} = \pm 0.5{{L}_{3}},\quad {{\left. {{{p}_{s}}} \right|}_{{{\text{S}}_{3}^{ \pm }}}} = 0$

и производится расчет детальной картины напряженно-деформируемого состояния во всех элементах композитной области. Здесь $S_{k}^{ \pm }$ – грани, ортогональные направлению ξ_k, ${{p}_{s}}$ – вектор касательных сил на поверхности грани, ${{A}_{{ij}}}\left( {\xi } \right)$ – матрицы, характеризующие жесткостные параметры включений, матрицы и слоя, A_ij = $\{ {\mu }({{{\delta }}_{{ij}}}{{{\delta }}_{{kl}}} + {{{\delta }}_{{jk}}}{{{\delta }}_{{il}}}) + {\lambda }{{{\delta }}_{{ik}}}{{{\delta }}_{{jl}}}\} $.

Рис. 1

При сформулированных условиях средние деформации соответствуют одноосному деформированному состоянию $\langle {{{\varepsilon }}_{{11}}}\rangle = {{L}_{1}}$, $\langle {{{\varepsilon }}_{{ij}}}\rangle = 0$, $i,j \ne 1$. На этом основании эффективная жесткость рассчитывается как средние напряжения в ячейке, нормированные на среднюю деформацию растяжения:

(4.32)

${\text{C}}{\kern 1pt} \_{\kern 1pt} 11 = \langle {\sigma }{\kern 1pt} \_{\kern 1pt} 11{\text{\;}}\rangle {\text{/}}\langle {\varepsilon }{\kern 1pt} \_{\kern 1pt} 11{\text{\;}}\rangle ,\quad {\text{C}}{\kern 1pt} \_{\kern 1pt} 12 = \langle {\sigma }{\kern 1pt} \_{\kern 1pt} 22{\text{\;}}\rangle {\text{/}}\langle {\varepsilon }{\kern 1pt} \_{\kern 1pt} 11{\text{\;}}\rangle {\text{\;\;}}$

Модуль Юнга E_n отсюда рассчитывается по следующей формуле:

(4.33)

${{E}_{n}} = \frac{{\left( {{{C}_{{11}}}--{{C}_{{12}}}} \right)\left( {{{C}_{{11}}} + 2{{C}_{{12}}}} \right)}}{{{{C}_{{11}}} + {{C}_{{12}}}}}$

Эффективное решение задачи на ячейке достигается с помощью блочного аналитико-численного метода на системе функций, точно удовлетворяющих всем контактным условиям на межфазной границе [34].

4.4. Результаты расчетов. В табл. 5 представлены значения модулей деформации клеевой композиции, модифицированной УНТ, полученные в результате экспериментальных определений и полученных расчетным путем. Для их определения расчетным путем использовались 3-и метода: фрактальный, Эшелби–Кристенсена и асимптотического усреднения. Из таблицы видно хорошее соответствие значений модулей деформации, полученных экспериментально и вышеуказанными расчетными методами.

Таблица 5

Метод расчета	Образец 2 (УНТ)
Эксперимент	3.2
Фрактальный метод	3.19
Метод Эшелби–Кристенсена	3.06
Метод асимптотического усреднения	3.09

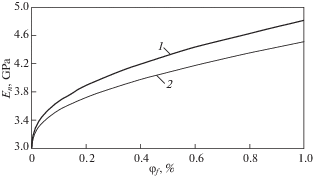
Зависимость эффективного модуля Юнга от объемной доли УНТ наполнителя в диапазоне от 0.00004% до 1%, посчитанные методом асимптотического усреднения (1) и методом Эшелби–Кристенсена (2), представлены на рис. 2.

Рис. 2

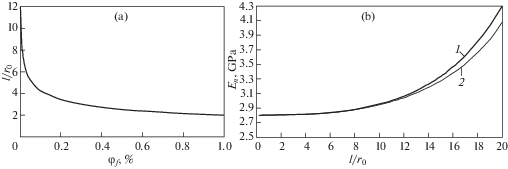
Величина межфазного слоя является основным фактором в данной модели композитного материала, объясняющим масштабный эффект усиления клеевой композиции. Зависимость относительной ширины межфазного слоя от объемной доли УНТ наполнителя в диапазоне от 0.00004% до 1% (по результатам фрактального анализа) и зависимость эффективного модуля Юнга от относительной ширины межфазной зоны при фиксированной объемной доле УНТ наполнителя ${{\varphi }_{н}} = 0.00236\% $, посчитанные методом асимптотического усреднения (1) и методом Эшелби–Кристенсена (2) представлены на рис. 3.

Рис. 3

5. Выводы. 1. Результаты компьютерного моделирования показали, что одной из наиболее эффективных добавок для повышения механических сдвиговых характеристик клеевой композиции на основе эпоксидной матрицы, являются открытые углеродные нанотрубки. Для них частицы наполнителя удерживаются фрагментами эпоксидных цепей как водородными, так и Ван-дер-Ваальсовыми силами.

2. Экспериментальным путем установлено, что при концентрации наномодифицирующих добавок в полимерном связующем 0.01% по массе, они являются достаточно эффективными.

3. Согласно результатам испытаний методом наноиндентирования введение углеродных нанотрубок (0.01% масс) в клеевые композиции приводит к увеличению их упругих свойств до 15%.

4. В ходе проведенных испытаний методом наноиндентирования установлено, что приведенный модуль упругости составляет 2.8 ГПа – для исходной композиции, 3.2 ГПа для композиции с углеродными нанотрубками.

5. Показано, что оценка модуля деформации клеевой композиции, модифицированной УНТ, методом асимптотического усреднения, единственным имеющим строгое математическое обоснование, дает сопоставимые результаты с экспериментальными определениями. Однако, для уверенного его применения необходимо проводить исследования по определению геометрических и механических свойств межфазного слоя и включений.

Работа выполнена в рамках государственного задания, номер государственной регистрации темы АААА-А19-119012290177-0.

Список литературы

Андриевский Р.А. Наноматериалы: концепции и современные проблемы // Рос. хим. ж. 2002. Т. XLVI. № 5. С. 50–56.
Qian D., Dickey E.C., Andrews R., Rantell T. Load transfer and deformation mechanisms in carbon nanotube-polystyrene composites //Appl. Phys. Lett. 2000. V. 76. P. 2868–2870.
Biercuk M.J., Llaguno M.C., Radosavljevic M., Hyun J.K., Johnson A.T., Fischer J.E. Carbon nanotubes composites for thermal management // Appl. Phys. Lett. 2002. V. 80. P. 2767.
Cadek M., Coleman J.N., Barron V., Hedicke K, Blau W.J. Morphological and mechanical properties of carbon-nanotube-reinforced semicrystalline and amorphous polymer composites // Appl. Phys. Lett., 2002. V. 81. P. 5123–5125.
Andrews R., Jacques D., Minot M., Rantell T. Fabrication of carbon multiwall nanotube/polymer composites by shear mixing // Macromol. Mater. Eng. 2002. V. 287. P. 395–403.
Mittal G., Dhand V., Rhee K.Y., Park S.-J., Lee W.R. A review on carbon nanotubes and graphene as fillers in reinforced polymer nanocomposites // J. Industrial Engineering Chemistry. 2015. V. 21. P. 11–25.
Вермель В.Д., Титов С.А., Корнев Ю.В., Никитина Е.А., Бойко О.В., Чиркунова С.В. Наномодифицированная клеевая композиция для повышения прочности узлов соединений авиационных конструкций на основе полимерных композиционных материалов // Сборник статей “Результаты фундаментальных исследований в прикладных задачах авиастроения”. Издательство “Наука”. 2016. С. 488–497.
Farzana Hussain, Mehdi Hojjati, Masami Okamoto and Russell E. Gorga Review article: Polymer-matrix Nanocomposites, Processing, Manufacturing, and Application // Journal of Composite Materials. 2006. V. 40. P. 1511.
Yanovsky Y.G., Yumashev O.B., Kornev Y.V., Karnet Y.N., Kozlov G.V. Some prospects for the use of carbon nanotubes as functional additives in elastomer composites // International Journal of Nanomechanics Science and Technology. 2011. T. 2. № 3. P. 185–203.
Kornev Y.V., Yanovskiy Y.G., Boiko O.V., Chirkunova S.V. Guseva M.A. The effect of carbon nanotubes on the properties of elastomeric materials filled with the mineral shungite // International Polymer Science and Technology. 2013. T. 40. № 2. P. 29–32.
Yanovsky Yu.G., Grigoryev F.V., Nikitina E.A., Vlasov A.N., Karnet Yu.N. Nanomechanical properties of polymer composite nanoclusters // Physical Mesomechanics. 2008. T. 11. № 5–6. P. 247–259.
Anthony C. Fisher-Cripps Nanoindentation. Springer-Verlag. New York. 2002. 197 p.
Oliver W. C., Pharr G. M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments // Journal of Materials Research. 1992. V. 7. № 6. P. 1564–1583.
Golovin Yu.I. Nanoindentation and mechanical properties of solids in submicrovolumes, thin near-surface layers and films: A Review // Physics of the solid state. 2008. V. 50. Issue 12. P. 2205–2236.
Tranchida D., Piccarolo S., Loos J., Alexeev A. Mechanical Characterization of polymers on a nanometer scale through nanoindentation. A study on pile-up and viscoelasticity // Macromolecules. 2007. V. 40. № 4. P. 1259–1267.
Tranchida D., Piccarolo S., Loos J., Alexeev A. Accurately evaluating Young’s modulus of polymers through nanoindentations: A phenomenological correction factor to the Oliver and Pharr procedure // Applied physics letters 2006. V. 89. Issue 17. Article 171905.
Oyen M.L., Cook R.F. Load-displacement behavior during sharp indentation of viscous-elastic-plastic materials // Journal of materials research. 2003. V. 18. № 1. P. 139–150.
Punich N., Sun Yong Improved method to determine the hardness and elastic moduli using nanoindentation // KMITL Sci. J. 2005. V. 5. № 2. P. 483–492.
Vermel V.D., Titov S.A., Kornev Y.V., Nikitina E.A., Boiko O.V. Nanomodified adhesive composition for aeronautical structures based on polymer composite material // American Journal of Applied Sciences. 2016. T. 13. № 3. P. 267–275.
Dolbin I.V., Kozlov G.V., Karnet Yu.N., Vlasov A.N. The mechanism of interphase regions growth in nanocomposites polymer/carbon nanotubes // Composites: Mechanics, Computations, Applications. An International Journal. 2019. V. 9. № 1. P. 213–220.
Family F. Fractal dimension and grand universality of critical phenomena // J. Stat. Phys. 1984, V. 36. № 5/6. P. 881–896.
Шогенов В.Н., Козлов Г.В. Фрактальные кластеры в физико-химии полимеров. – Нальчик: Полиграфсервис и Т. 2002, 268 с.
Kozlov G.V., Dolbin I.V. The simulation of carbon nanotubes as macromolecular coils: interfacial adhesion // Mater. Phys. Mech. 2017. V. 32. № 2. P. 103–107.
Rammal R., Toulouse G. Random walks on fractal structures and percolation clusters // J. Phys. Lett. 1983. V. 44. № 1. P. L13–L22.
Witten T.A., Rubinstein M., Colby R.H. Reinforcement of rubber by fractal aggregates // J. Phys. II France. 1993. V. 3. № 3. P. 367–383.
Schaefer D.W., Justice R.S. How are nanocomposites? // Macromolecules. 2007. V. 40. № 24. P. 8501–8517.
Moniruzzaman M. and Winey K.I. Polymer nanocomposites containing carbon nanotubes // Macromolecules. 2006. V. 39. № 16. P. 5194–5205.
Cadek M., Coleman J.N., Ryan K.P., Nicolosi V., Bister G., Fonsecca A. Reinforcement of polymers with carbon nanotubes: the role of nanotube surface area // Nano Lett. 2004. V. 4. № 2. P. 353–356.
Coleman J.N., Cadek M., Ryan K.P., Fonsecca A., Nady J.B., Blau W.J., Ferreira M.S. Reinforcement of polymers with carbon nanotubes. The role of an ordered polymer interfacial region. Experiment and modeling // Polymer. 2006. V. 47. № 23. P. 8556–8561.
Атлуханова Л.Б., Карнет Ю.Н., Козлов Г.В. Модуль упругости полимерной матрицы для нанокомпозитов полиуретан/углеродные нанотрубки // Механика композиционных материалов и конструкций. 2018. Т. 24. № 4. C. 634–643.
Кристенсен Р. Введение в механику композитов. М: Мир. 1982. 336 с.
Christensen R.M., Lo K.H. Solutions for effective shear properties in three phase sphere and cylinder models // J. Mech. Phys. Solids. 1979. V. 27. P. 315–330.
Бахвалов Н.С., Панасенко Г.П. Осреднение процессов в периодических средах. М.: Наука. Главная редакция физико-математической литературы. 1984. 352 с.
Волков-Богородский Д.Б. Метод радиальных множителей в задачах механики неоднородных сред с многослойными включениями // Механика композиционных материалов и конструкций. 2016. Т. 22. № 1. С. 19–39.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал