Известия РАН. Механика твердого тела, 2020, № 3, стр. 122-133

1. Введение. Решение новой задачи проектирования – проектирование под заданную стоимость – возможно при объединении моделей высокой точности с современными компьютерными технологиями и снижении объема экспериментов. Перспективное направление исследований – проектирование композитных конструкций с учетом технологии изготовления, когда технологический процесс принимается во внимание на этапе разработки изделия.

Рассматриваются задачи изгиба плоской прямоугольной многослойной панели, изготовленной из полимерных волокнистых композиционных материалов, с эксцентричным продольно-поперечным набором, с эксцентричным продольным набором и плоской прямоугольной композитной панели с несимметричной по толщине структурой пакета. Панели находятся под действием произвольным образом распределенной поперечной нагрузки q(x, y) в стационарном температурном поле интенсивности ΔT. Условия закрепления контура предполагаются достаточно общими.

Принимаются во внимание технологические факторы, имеющие место при изготовлении композитов: остаточные температурные напряжения, возникающие при охлаждении после завершения процесса отверждения, и технологическая операция предварительного натяжения армирующих волокон, осуществляемая в целях повышения несущей способности конструкции. Препреги при укладке слоев предварительно натянуты, после отверждения натяжение снято.

Исследование напряженно-деформированного состояния (НДС) плоских прямоугольных конструктивно-анизотропных композитных панелей является актуальным с точки зрения практики проектирования несущих поверхностей летательных аппаратов (ЛА). В публикациях последних двадцати лет при проведении теоретических исследований большинство авторов уделяет надлежащее внимание учету особенностей поведения композитных панелей. Представляют интерес классификация и анализ основных направлений развития теорий статических расчетов конструктивно-анизотропных композитных панелей и наиболее разработанные модели и уравнения. Ниже рассмотрены постановка статических задач, постановка задач при термомеханическом воздействии, постановка задач статики с учетом технологии изготовления, аналитические методы решения задач, численные методы решения задач, экспериментальные исследования.

Значительное число обзорных работ посвящено исследованиям в указанной области.

В [1] рассмотрены состояние и перспективы применения интегральных конструкций из композиционных материалов в авиационных конструкциях, а также вклад научной школы МАИ (НИУ) в создание научных основ механики проектирования и технологии изготовления композитных изделий авиационной и ракетно-космической техники.

В [2] приводится анализ современного состояния теорий пластин из композиционных материалов; в [3] дан обзор результатов при решении задач пространственного расчета НДС многослойных плит. В [4, 5] изложены результаты обширного обзора методов двумерного аналитического расчета многослойных систем и конструкций; в [6] представлен обзор работ, посвященных обоснованию использования гипотез Кирхгофа и оценке их погрешности применительно к двумерным моделям анизотропных слоистых пластин; в обзоре методов расчета [7] предложен список литературы по двумерным теориям высокого порядка с учетом деформации поперечного сдвига и строгим трехмерным решениям, особое внимание уделяется теориям Zig-Zag с кусочно-непрерывным полем перемещений по толщине пластины. В [8, 9] приведены обзоры методов статического расчета слоистых композитных пластин; в [10] проведен анализ современных тенденций и перспектив развития методов усреднения механики композитов.

Представлены результаты теоретических и численных исследований, выполненных авторами [11, 12] в области механики и вычислительной математики, а также неклассическая математическая модель деформирования тонкостенных многослойных композитных пластин; дана оценка влияния на характеристики НДС поперечных сдвиговых деформаций и обжатия нормали; проведены систематические сравнения полученных решений с решениями, найденными при использовании известных в литературе неклассических моделей, в том числе, – и в трехмерной постановке.

В [13] дан анализ литературы, посвященной разработке перспективных моделей деформирования упругих многослойных пластин, в которых не нарушаются условия непрерывности перемещений и поперечных напряжений на поверхности раздела слоев. В [12] исследованы проблемы деформирования упругих слоистых пластин на основе различных теорий; в [14] проведено сравнение точных решений с приближенными, построенными на основе гипотез Кирхгофа.

В монографии [15] анализируются подходы и аналитические методы расчета НДС элементов композитных конструкций ЛА в виде гладких пластин и подкрепленных панелей.

В рамках математического моделирования исследованы точные решения, полученные на основе уравнений теории упругости; представлено трехмерное решение задачи изгиба. Предложены уточненные математические модели НДС различной степени приближения, учитывающие деформации поперечного сдвига. Определяющие уравнения для слоистых ортотропных пластин и для композитных пластин с ребрами жесткости составлены на основе теории поперечных сдвиговых деформаций высокого порядка Reddy. Выполнен аксиоматический и асимптотический анализ уточненных “послойных” моделей композитных несимметричных пластин. При построении прикладной теории, основанной на гипотезе Кирхгофа–Лява, предлагается дополнительно учесть сжимаемость нормали. Применяется классическая теория слоистой конструкции в рамках гипотезы Кирхгофа; асимптотическим методом осуществляется оценка точности гипотез Кирхгофа в теории слоистых пластин. Рассматривается постановка краевых задач для разрешающих уравнений высоких порядков слоистых композитных пластин.

Для математического моделирования при термосиловом воздействии предложена теория термоупругости тонких многослойных анизотропных композитных пластин, которая построена из уравнений общей трехмерной теории термоупругости путем введения асимптотических разложений по малому параметру без введения гипотез относительно характера распределения перемещений и напряжений по толщине. Выполнена оценка теорий высокого порядка слоистых композитов при наличии градиента температурного поля. Представлен подход к решению задач об изгибе слоистых композитных термоупругих пластин на основе послойного моделирования.

Математическое моделирование с учетом технологии изготовления включает разработку методологии для прогнозирования перемещений из плоскости при искривлении плоских слоистых композитных панелей после охлаждения до комнатной температуры от повышенной температуры затвердевания при изготовлении; выявлено, что наличие искривлений в структуре материала пластин существенно изменяет картину распределения напряжений при статическом нагружении. Представлена математическая модель, с помощью которой оцениваются возникающие напряжения при отверждении пакета из композиционных материалов.

Аналитические методы решения задач статики содержат обобщенную версию теории многослойных пластин и методов расчета на основе схемы разложения компонент вектора перемещений каждого слоя в степенные ряды. В виде аналитических функций комплексных переменных строятся общие решения для анизотропных слоистых пластин со связью изгиб-растяжение в смешанной постановке задачи. Представлено в замкнутой форме аналитическое решение типа Навье; в задаче изгиба решение строится в одинарных тригонометрических рядах. Осуществлено приложение методологии метода Лурье–Воровича для исследования НДС трехмерных композитных пластин, разработан эффективный вариант метода однородных решений; в виде явных разложений по функциям Фадля–Папковича – однородным решениям – даются точные решения краевых задач подкрепленных панелей.

Численные методы решения статических задач предполагают разработку на основе полуаналитического МКЭ численной процедуры при использовании точных трехмерных уравнений механики сплошной среды. Предложен и реализован эффективный метод численного решения краевых задач неклассической теории, основанный на идеях инвариантного погружения. Разработана конечноэлементная модель с непрерывными напряжениями поперечного сдвига; построен сдвиговой элемент высокого порядка; разработан совместный на изгиб-растяжение конечный элемент; предложена версия МКЭ с элементом, учитывающим деформации растяжения–сжатия, изгиба и деформации поперечного сдвига первого порядка, разработан аналогичный конечный элемент для задач термоупругости. Рассмотрены и сопоставлены варианты конечноэлементного моделирования, применены модифицированные многослойные конечные элементы со ступенчато меняющимися перемещениями, учитывается несоблюдение гипотезы плоских сечений; выполнено математическое моделирование на основе МКЭ-деформирования панелей из ПКМ. МКЭ используется в рамках связанной задачи для анализа деформирования композитной подкрепленной панели при температурном нагружении.

В рамках экспериментальных исследований анализируется экспериментально поведение конструкции композитного кессона под действием нагрузок, вызывающих его изгиб и кручение; испытания кессона крыла из ПКМ являются частью экспериментальных работ по обеспечению прочности конструкции планера самолета МС-21. Выполнено экспериментальное исследование температурного поведения анизотропных композитных пластин. Осуществлена экспериментальная оценка перемещений подкрепленной композитной панели под силовой и тепловой нагрузкой.

Целью данной работы является исследование напряженно-деформированного состояния конструктивно-анизотропных композитных панелей в уточненной постановке с разрешающим дифференциальным уравнением восьмого порядка в рамках мультидисциплинарного подхода. Математическая модель и численная реализация решения представляют интерес с точки зрения практики проектирования панелей из современных композиционных материалов для перспективных изделий авиационной техники.

2. Математическая модель. Задачи решаются в перемещениях с использованием гипотез технической теории тонких пластин для обшивки и приводятся к нахождению смещений единой базисной поверхности приведения. В качестве расчетной модели предлагается схематизация панелей как конструктивно-анизотропных с осреднением жесткостей тонкостенных подкрепляющих элементов, которые находятся в условиях сложного сопротивления вследствие одностороннего контакта с обшивкой. Дальнейшее развитие теории тонкостенных упругих стержней применительно к общей контактной задаче для обшивки и ребра с уточнением модели последнего при закручивании составляет научную новизну работы.

Проблема определения НДС конструктивно-анизотропных панелей сведена к решению краевой задачи для уравнения восьмого порядка в частных производных в прямоугольной области. Данное решение в замкнутом виде построено в одинарных тригонометрических рядах для частного случая согласованных граничных условий по двум противоположным кромкам, а также методом однородных решений для произвольных несогласованных граничных условий на контуре [16]. Рассматриваются все возможные варианты закрепления граничных кромок в отношении связанных плоской задачи и задачи изгиба.

Согласно гипотезе Кирхгофа для компонент вектора перемещений k-го слоя обшивки

где u₀(x, y) и ${{{v}}_{0}}$(x, y) – перемещения u и ${v}$ при z = 0.

С использованием соотношений Коши, физических уравнений с учетом влияния температуры и предварительного натяжения волокон, а также формул преобразования напряжений при повороте осей координат компоненты тензора напряжений k‑го слоя панели определяются [17, 18] равенствами

где $\overline Q _{{i,j}}^{{\left( k \right)}}$, i, j = 1, 2, 6 – жесткости слоя, $\bar {\alpha }_{j}^{{\left( k \right)}}$,   j = 1, 2, 6 – коэффициенты температурного расширения слоя, $\bar {\varepsilon }_{{Нj}}^{{\left( k \right)}}$, j = 1, 2, 6 – деформация натяжения слоя, – приведенные к осям координат панели; ΔT – разность между комнатной температурой и температурой отверждения при расчете остаточных температурных напряжений, либо интенсивность внешнего температурного поля.

Уровень деформации предварительного натяжения слоя определяется допускаемой деформацией слоя с точностью до безразмерного коэффициента K_Нj,   j = 1, 2, 6, меняющегося от 0 до 1. При записи физических соотношений в виде (2.2) не принимается во внимание, что в препреге-слое предварительно натягиваются лишь волокна, в то время как после снятия натяжения слой деформируется полностью.

В силу совместной работы в одностороннем контакте с обшивкой элементы набора находятся в условиях косого изгиба и стесненного кручения. Для определения НДС ребер жесткости применяется предложенный В.З. Власовым вариационный метод расчета тонкостенных пространственных систем в перемещениях, дающий возможность построить теорию тонкостенных упругих стержней без введения гипотезы об отсутствии деформации сдвига срединной поверхности профиля. Перемещения и углы поворота панели и подкреплений по линиям контакта считаются равными.

Компоненты напряженно-деформированного состояния k-го слоя композитных стрингеров вычисляются по формулам [17, 18]

Здесь депланация поперечного сечения u₄(x) полагается свободной, $\omega _{1}^{{(k)}}\left( s \right)$ строится в соответствии с эпюрой секториальных площадей для открытых контуров. Учитывается деформация сдвига при кручении тонкостенного стержня, которая определяется его поворотом относительно выбранного полюса, а также относительно центра изгиба в рамках поправок по теории “чистого” кручения $\rho _{1}^{{(k)}}\left( s \right)$, $\rho _{{{{\omega }_{1}}}}^{{(k)}}\left( s \right)$ – длины перпендикуляров, опущенных на касательную к контуру в рассматриваемой точке из точки контакта стрингера с обшивкой и из центра изгиба, соответственно, $\rho _{1}^{0}\left( s \right)$ определяет дополнительный момент инерции продольного ребра при “чистом кручении”.

Аналогично (2.3), (2.4) строятся перемещения и напряжения ребер жесткости, расположенных по оси y.

Ниже рассматривается упрощенный вариант математической модели, соответствующий предположению о малости нормальных напряжений, обусловленных изгибом подкреплений в плоскости панели и депланацией их поперечных сечений. Используя асимптотические свойства и пренебрегая членами, соответствующими краевым эффектам, в выражениях (2.3), (2.4) будем считать, что стержни работают на растяжение–сжатие, изгиб из плоскости пластины и кручение. При этом задача сводится в дальнейшем к исследованию медленно меняющегося основного напряженного состояния в рамках разрешающего уравнения восьмого порядка в частных производных.

В статье [19] построена трехмерная теория прямоугольных пластин из композиционных материалов, свободная от гипотез Кирхгофа–Лява, выведены трехмерные уравнения для определения НДС типа “пограничный слой” в краевых зонах вблизи жестко защемленного края пластины. Методом асимптотического интегрирования дифференциальных уравнений трехмерной теории упругости строятся итерационные процессы для уточнения результатов классической теории во внутренних областях пластины и в узких краевых зонах. Решение задачи о краевой плоской деформации сводится к решению бигармонической задачи со специальными граничными условиями. Применяется вариационный метод, аналогичный методу Власова–Канторовича. Исследование сходимости полученного решения позволило построить аппроксимирующие функции по толщине пластинки в виде полиномов высокого порядка. Для учета реального характера закрепления панели в составе проектируемой конструкции выполнен анализ влияния упругости защемленного края путем решения контактной задачи о пластинке с упругим изотропным полупространством. Модифицированные граничные условия получены в рамках решения Флагмана–Буссинеска с использованием функций влияния и учетом дополнительной потенциальной энергии. Установлено, что влияние податливости закрепленного края ортотропной пластины из композиционных материалов приводит к некоторому снижению дополнительных напряжений краевой плоской деформации.

С математической точки зрения проблема исследования основного напряженно-деформированного состояния конструктивно-анизотропных панелей, трактуемых как ортотропные, сводится к решению краевой задачи в прямоугольной области для неоднородного линейного дифференциального уравнения восьмого порядка в частных производных относительно искомой потенциальной функции Ф(x, y) [17, 18]

Линейный дифференциальный оператор (2.5) содержит производные четной степени по каждой из координат

Линейные дифференциальные операторы связи кинематических и статических компонентов НДС с разрешающей потенциальной функцией Ф(x, y)

имеют вид L_Ny, L_Nyx, ${{L}_{{{{{\overline Q }}_{y}}}}}$, L_My, L_Hyx строятся аналогично L_Nx, L_Nxy, ${{L}_{{{{{\overline Q }}_{x}}}}}$, L_Mx, L_Hxy с заменой коэффициентов с индексом “x” на коэффициенты с индексом “y”; дифференциальные операторы L_Ny, L_Nyx, L_My, L_Hyx – шестого порядка, дифференциальный оператор ${{L}_{{{{{\overline Q }}_{y}}}}}$ – седьмого порядка; $N_{x}^{T}$, $N_{y}^{T}$, $N_{{xy}}^{T}$, $N_{{yx}}^{T}$, $M_{x}^{T}$, $M_{y}^{T}$, $H_{{xy}}^{T}$, $H_{{yx}}^{T}$ – температурные усилия и моменты, $N_{x}^{H}$, $N_{y}^{H}$, $N_{{xy}}^{H}$, $N_{{yx}}^{H}$, $M_{x}^{H}$, $M_{y}^{H}$, $H_{{xy}}^{H}$, $H_{{yx}}^{H}$ – усилия и моменты от натяжения.

Коэффициенты K_{8– i,i}, i = 0, 2, 4, 6, 8 в разрешающем уравнении (2.5) и коэффициенты R_{4 – i}, _i, i = 0, 2, 4, R_{5 – i,i}, i = 0, 2, 4, S_{5 – i,i}, i = 1, 3, 5 и т.д. в формулах связи (2.6) – постоянные величины, которые зависят от упругих свойств материала и геометрических параметров конструкции; x = x/a, y = y/b – безразмерные координаты, отнесенные к полудлине a и к ширине панели b, соответственно.

Линейные дифференциальные операторы связи (2.6) для симметричных компонентов НДС так же, как и линейный дифференциальный оператор разрешающего уравнения (2.5), содержат производные четной степени по каждой из координат. Косо-симметричные компоненты НДС определяются нечетными производными.

Краевая задача общего вида в прямоугольной области представлена условиями упругой заделки

коэффициенты γ_i, δ_i, α_i, β_i, i = 1, 2, 3, 4 меняются от 0 до 1.

Равенства (2.7), (2.8) позволяют рассмотреть все возможные варианты закрепления граничных кромок в отношении связанных плоской задачи и задачи изгиба: защемление, скользящую заделку, шарнирное закрепление, свободный край.

Влияние остаточных температурных напряжений, имеющих место при охлаждении после завершения процесса отверждения, а также предварительного натяжения армирующих волокон на несущую способность конструктивно-анизотропных панелей из композиционных материалов представляется возможным оценить в том случае, когда граничные условия являются несогласованными, а решение строится в одинарных тригонометрических рядах либо с использованием метода однородных решений.

Конкретные исследования связаны с условиями закрепления панелей в составе проектируемой конструкции.

Проанализируем НДС конструктивно-анизотропной композитной панели, шарнирно опертой по продольным и произвольным образом закрепленной по поперечным кромкам.

Решение краевых задач в прямоугольной области для уравнения (2.5) построено в замкнутом виде в одинарных тригонометрических рядах для частного случая граничных условий по двум противоположным кромкам

Эти условия принято называть согласованными: они соответствуют шарниру в отношении изгиба, а в отношении плоской задачи – скользящей заделке в тангенциальном направлении, когда часть контура панели нагружена потоками касательных сил. Панель по границе, перпендикулярной оси y, нагружена потоками касательных сил N_yx, которые уравновешиваются нормальными усилиями N_x на границе и площадках, перпендикулярных оси x.

Условия на торцах панели произвольны и могут быть условиями упругой заделки типа

в симметричной либо в несимметричной краевых задачах, соответственно; коэффициенты γ_i, δ_i, ε_i, ξ_i , i = 1, 2, 3, 4 меняются от 0 до 1.

3. Построение решения. Результаты численной реализации. Разрешающая функция – обобщенная функция перемещений, удовлетворяющая (2.5), (2.9) и затем – (2.10) либо (2.11), раскладывается в ряд по системе тригонометрических функций

то есть общее решение уравнения (2.5), удовлетворяющее граничным условиям, представим в одинарных тригонометрических рядах, где Ф_n(x) подлежит определению.

Исследуя далее задачу общего вида в смысле краевых условий по поперечным кромкам, в выражении (3.1) для Ф_n(x) оставим и четные, и нечетные функции, и с точностью до восьми произвольных постоянных запишем обобщенную функцию перемещений Ф(x, y)

Здесь Ф_n [P.I.] – частный интеграл обыкновенного неоднородного линейного дифференциального уравнения восьмого порядка для Ф_n(x), ${{\lambda }_{{nL}}} = {{z}_{L}}{{\lambda }_{{ny}}}а$, ${{\lambda }_{{ny}}} = \frac{{n\pi }}{b}$, z_L – корни соответствующего характеристического полинома, которые находятся численно с использованием встроенных функций операционной среды MATLAB.

В одинарные тригонометрические ряды с точностью до констант A_nL и B_nL (3.2) раскладываются компоненты вектора перемещений, деформации и кривизны поверхности приведения, углы поворота, внутренние силовые факторы. В одинарные тригонометрические ряды раскладывается внешняя нагрузка q(x, y), а также внутренние силовые факторы, связанные с температурой и натяжением.

Для окончательного определения компонентов НДС, то есть, по существу, системы неизвестных констант A_nL и B_nL (n = 1, 3, 5, …, L = 1, 2, 3, 4) необходимо удовлетворить граничным условиям на торцах конструкции при x = +1 и x = –1.

Если различным образом закреплены оба поперечных края панели, формируется и решается система восьми алгебраических уравнений. Когда строится решение симметричной краевой задачи, первые четыре уравнения будут реализовывать искомые произвольные постоянные B_nL (n = 1, 3, 5, …, L = 1, 2, 3, 4). При этом симметричные компоненты НДС зависят только от четных функций по координате x, косо-симметричные компоненты – от нечетных функций.

В соответствии с изложенным алгоритмом разработан пакет прикладных программ для PC на языке операционной среды MATLAB. Программы предназначены для исследования напряженно-деформированного состояния и компьютерной оптимизации процесса проектирования конструктивно-анизотропных панелей из композиционных материалов. В рамках связанных плоской задачи и задачи изгиба рассматриваются все возможные варианты закрепления кромок, вытекающие из условий упругой заделки.

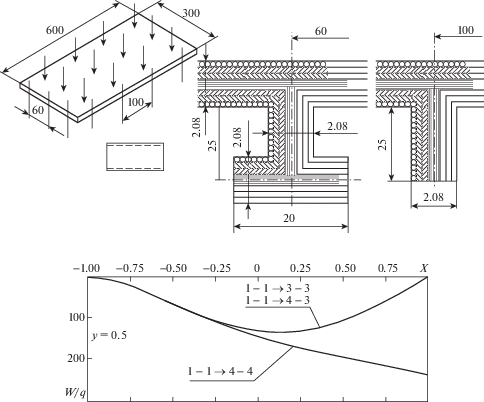
В качестве примера на рис. 1 представлены результаты определения перемещений в прямоугольных панелях из углепластика с эксцентричным продольно-поперечным набором, находящихся под действием постоянной погонной поперечной нагрузки q(x, y) = const. Граничные условия по координате x несимметричны. Один из краев x = –1 защемлен, на другом x = +1 рассмотрены три комбинации граничных условий в отношении плоской задачи и в отношении изгиба: шарнир либо свободный от усилий и моментов край. Проанализирована зависимость прогибов панели от типа граничных условий на торцах. Для граничных условий на рис. 1 введены обозначения: 1 – защемление, 2 – скользящая заделка, 3 – шарнир, 4 – свободный край.

Максимальные прогибы в центре панели отличаются на 12%. Прогибы вычисляются в долях нагрузки в мм³/кГ.

4. Верификация математической модели. Экспериментальные исследования устойчивости панелей. С целью оценки правомочности полученных теоретических зависимостей проведены серии испытаний экспериментальных моделей углепластиковых стрингерных панелей на равномерное сжатие в продольном направлении до потери устойчивости (рис. 2) [20].

Результаты натурных экспериментов и расчетные данные совпадают качественно по формам потери устойчивости и количественно с точностью до 12–13%, если не рассматривать переменное докритическое напряженное состояние. Учет неравномерности основного напряженного состояния приводит к увеличению точности до 8–10%. Критические напряжения определены в кГ/мм².

Проведены серии испытаний экспериментальных моделей подкрепленных панелей из изотропного материала на равномерное сжатие в продольном направлении до потери устойчивости (рис. 3). Полки стрингеров усилены жгутами из углепластика.

Результаты натурных экспериментов и расчетные данные совпадают качественно по формам потери устойчивости и количественно с точностью до 19–20%, если не рассматривать переменное докритическое напряженное состояние. Поперечное сечение стрингера экспериментальных панелей несимметрично, при численной реализации несимметрия не принималась во внимание.

5. Заключение. В операционной среде MATLAB разработаны программы и реализован процесс компьютерной многокритериальной оптимизации с учетом технологии изготовления конструктивно-анизотропных панелей из композиционных материалов, находящихся в условиях механического, внешнего температурного и технологического температурного воздействия.

Так как решение строится точными аналитическими методами, время расчета минимально, что представляет интерес с точки зрения практики проектирования с использованием параметрического анализа. Результаты расчетов дают возможность снижения и оптимизации весовых характеристик конструкции.