Известия РАН. Механика твердого тела, 2020, № 2, стр. 10-21

1. Введение. Исследование посвящено изучению процессов интенсивного деформирования материалов, когда накапливаемые ими необратимые деформации могут быть как деформациями ползучести, так и пластичности. Примером такого технологического процесса может служить холодная формовка [1], когда необратимые деформации накапливаются за счет медленного процесса ползучести, однако, это не исключает возникновение локальных областей пластического течения обычно в местах контакта деформируемого материала с оснасткой. Наличие таких областей приводит к значительному перераспределению полей напряжений и, следовательно, влияет на процесс ползучести. Таким образом, при моделировании таких процессов необходимо использовать теорию ползучести при одновременном учете возможностей возникновения и развития зон пластического течения. Учет же упругих деформаций позволяет при этом рассчитывать упругий отклик при разгрузке, в том числе остаточные напряжения и их релаксацию после полной разгрузки.

Учитывая, что в большинстве технологических процессов приобретаемые материалом деформации, как правило, большие, соответствующая модель должна быть моделью больших деформаций материалов с упругими, пластическими и вязкими свойствами.

Математических моделей больших упругопластических деформаций предложено достаточно много [2–13]. Здесь будем использовать математическую модель, в которой обратимые и необратимые деформации определяются дифференциальными уравнениями изменения [9, 12]. Обобщение модели на случай, когда большие необратимые деформации последовательно накапливаются сначала в условиях ползучести и потом пластического течения проведено недавно [14, 15]. Предложено разделять накапливаемые в материале необратимые деформации на деформации ползучести и пластического течения механизмом их производства. Таким образом, уравнение изменения необратимых деформаций является одним и тем же и для деформаций ползучести, и пластичности, различие заключается только в задании источника необратимых деформаций. Для деформаций ползучести источником являются скорости деформаций ползучести, а для пластических деформаций – скорости пластических деформаций. На упругопластических границах изменяется механизм накопления необратимых деформаций с вязкого на пластический и наоборот. Непрерывность в таком росте необратимых деформаций обеспечивается соответствующим заданием потенциалов ползучести и пластичности.

Первые решения краевых задач, учитывающих последовательное накопление необратимых деформаций ползучести и пластичности в рамках модели больших упруговязкопластических деформаций, получены в [15, 16], без учета вязкости при пластическом течении подобный подход в случае малых деформаций применялся в [17]. Здесь с использованием модели больших деформаций с последовательным изменением в механизме накопления необратимых деформаций приведем решение краевой задачи об антиплоском деформировании цилиндрического слоя в условиях ползучести с последующим пластическим течением.

2. Основные модельные соотношения. В прямоугольной системе пространственных декартовых координат Эйлера ${{x}_{i}}$ кинематика среды задается соотношениями [12]

Здесь ${{u}_{i}}$, ${{{v}}_{i}}$ – компоненты векторов перемещений и скорости точек среды; ${{d}_{{ij}}}$ – компоненты тензора деформаций Альманси; ${{e}_{{ij}}}$ и ${{p}_{{ij}}}$ – их обратимая и необратимая составляющие; ${D \mathord{\left/ {\vphantom {D {Dt}}} \right. \kern-0em} {Dt}}$ – оператор используемой объективной производной тензоров по времени, которая записана для произвольного тензора ${{n}_{{ij}}}$; ${{r}_{{ij}}}$ – компоненты тензора вращений. Источники ${{\gamma }_{{ij}}}$ и $\varepsilon _{{ij}}^{e} = {{\varepsilon }_{{ij}}} - {{\gamma }_{{ij}}}$ в уравнениях изменения обратимых и необратимых деформаций – скорости их накопления. При ${{\gamma }_{{ij}}} = 0$ компоненты тензора необратимых деформаций изменяются так же, как и при повороте системы координат или, как при движении среды без деформирования, т.е. ${{D{{p}_{{ij}}}} \mathord{\left/ {\vphantom {{D{{p}_{{ij}}}} {Dt}}} \right. \kern-0em} {Dt}} = 0$. Тензор вращений ${{r}_{{ij}}}$ отличается от классического тензора вихря скорости ${{w}_{{ij}}}$ наличием нелинейной части ${{z}_{{ij}}}$. Отметим, что при равенстве нулю составляющей ${{z}_{{ij}}}$ тензора вращений ${{r}_{{ij}}}$ производная в (2.1) переходит в производную Яумана.

Как и в работах [9, 12] полагаем, что используемый термодинамический потенциал (плотность распределения свободной энергии $\psi $) является изотропной функцией только обратимых деформаций. Тогда согласно закону сохранения энергии напряжения в среде полностью определяются обратимыми деформациями и связаны с ними формулой, аналогичной формуле Мурнагана в нелинейной теории упругости [18, 19]. Для несжимаемой среды данное соотношение примет вид

В соотношении (2.2) ${{\sigma }_{{ij}}}$ – компоненты тензора напряжений Эйлера–Коши, $p$ – неизвестная функция добавочного гидростатического давления. Для упругого потенциала $W = {{\rho }_{{\text{0}}}}\psi $ (${{\rho }_{{\text{0}}}}$ – плотность) принимаем его разложение в ряд Маклорена относительно свободного состояния

Здесь $\mu $ – модуль сдвига; $b$, $\chi $ – постоянные материала.

Диссипативный механизм необратимого деформирования связан с реологическими и пластическими свойствами материала. Будем считать далее, что необратимые деформации накапливаются с начала процесса деформирования и первоначально связаны с процессом ползучести материала.

В областях, где напряженное состояние еще не достигло поверхности текучести, или, где пластическое течение было, но прекратилось, соответствующий диссипативный механизм деформирования зададим в форме степенного закона ползучести Нортона [20], в котором полагаем скорости необратимых деформаций ${{\gamma }_{{ij}}}$ равными скоростям деформаций ползучести $\varepsilon _{{ij}}^{{v}}$

В зависимостях (2.4) $V\left( {{{\sigma }_{{ij}}}} \right)$ – термодинамический потенциал; ${{\sigma }_{1}}$, ${{\sigma }_{2}}$, ${{\sigma }_{3}}$ – главные значения тензора напряжений; $B$, $n$ – параметры ползучести материала.

С течением времени напряженное состояние достигает поверхности текучести, диссипативный механизм деформирования меняется и в материале начинается пластическое течение. В таком случае в области пластического течения полагаем ${{\gamma }_{{ij}}} = \varepsilon _{{ij}}^{p}$. Без разделения необратимых деформаций на составляющие будем считать, что накопленные к моменту начала пластического течения необратимые деформации ползучести (2.4) являются начальными значениями для накапливающихся далее в области течения пластических деформаций. В случае учета вязких свойств среды при пластическом течении также требуется совпадение скоростей необратимых деформаций при изменении механизма деформирования с вязкого на пластический.

Согласно принципу максимума Мизеса связь скоростей пластических деформаций $\varepsilon _{{ij}}^{p}$ с напряжениями устанавливается ассоциированным законом пластического течения

где $\varepsilon _{{ij}}^{{{{{v}}_{0}}}}$ – компоненты тензора скоростей деформаций ползучести в момент начала пластического течения.

В качестве пластического потенциала будем использовать условие текучести Треска, обобщенное на случай учета вязких свойств материала

в котором ${{\alpha }_{n}}$ – главные значения тензора ${{\alpha }_{{ij}}}$, k – предел текучести, $\eta $ – коэффициент вязкости.

3. Постановка и решение задачи до вязкопластического течения. Пусть слой несжимаемого материала расположен в зазоре между двумя жесткими коаксиальными цилиндрическими поверхностями радиусов ${{r}_{0}}$ и R $({{r}_{0}} < R)$. Рассмотрим процесс деформирования слоя при прямолинейном движении внутренней поверхности и неподвижности внешней поверхности. Считаем, что на цилиндрических стенках выполняются условия прилипания. Тогда в цилиндрической системе координат $r$, $\varphi $, $z$ граничные условия задачи примут вид

Здесь ${v} = {{{v}}_{z}}(r,t)$, $u = {{u}_{z}}\left( {r,t} \right)$ – единственные отличные от нуля компоненты векторов скорости и перемещения соответственно, ${{{v}}_{0}} = {{{v}}_{0}}(t)$, a₀ – задаваемые функция и постоянная. Из соотношений (2.1) в данном случае установим, что кинематика среды описывается зависимостями

В задачах данного класса диагональные компоненты тензоров деформаций являются малыми более высокого порядка по сравнению с недиагональными компонентами [21–24], поэтому в дальнейшем ограничимся слагаемыми первого порядка по диагональным компонентам и второго – по недиагональным. Принятое ограничение не является принципиальным для решения задачи и вводится с целью значительного упрощения вычислений. Из соотношений (2.2) и (2.3) в рассматриваемом случае найдем напряжения в среде

В рамках квазистатического приближения запишем уравнения равновесия для рассматриваемого случая

Проинтегрируем уравнения (3.4) в предположении, что напряжения конечны, т.е. ${{\partial P} \mathord{\left/ {\vphantom {{\partial P} {\partial z}}} \right. \kern-0em} {\partial z}}$ = 0:

Для компонент тензоров деформаций и скоростей деформаций из (2.1) справедливы соотношения

Считаем, что при увеличении скорости движения внутреннего цилиндра необратимые деформации первоначально накапливаются за счет медленного процесса ползучести.

Потенциал $V({{\sigma }_{{ij}}})$ в соотношении (2.4) в цилиндрической системе координат принимает форму

В данном потенциале ограничимся слагаемыми до порядка $n$ по напряжениям вследствие замечания, описанного перед зависимостями (3.3). Тогда для скоростей деформаций ползучести и компоненты ${{p}_{{rz}}}$ из формул (2.4), (3.3), (3.5) и (3.6) получим соотношения

Из зависимостей (3.2), (3.5)–(3.7) и условия прилипания (3.1) на поверхности $r = R$ следуют соотношения для скорости и перемещения

Здесь и далее точка сверху означает производную по времени.

С учетом граничных условий (3.1) на внутренней стенке $r = {{r}_{0}}$ из (3.8) получим обыкновенное дифференциальное уравнение для неизвестной функции ${{c}_{1}}\left( t \right)$

Дифференциальное уравнение (3.9) и система (3.6) решаются численно в пакете Wolfram Mathematica. Компонента напряжений ${{\sigma }_{{rr}}}$ находится из первого уравнения равновесия (3.4) с использованием краевого условия из (3.1). Далее из соотношений (3.3) определяются добавочное гидростатическое давление $P$ и компоненты тензора напряжений ${{\sigma }_{{\varphi \varphi }}}$ и ${{\sigma }_{{zz}}}$.

При возрастающей скорости движения внутреннего цилиндра ${{{v}}_{0}}$ полученное решение задачи будет справедливым до некоторого момента времени $t = {{t}_{0}}$, при котором в окрестности внутренней стенки $r = {{r}_{0}}$ выполнится условие пластичности (2.5), в нашем случае принимающее вид ${{\left. {{{\sigma }_{{rz}}}} \right|}_{{r = {{r}_{0}}}}} = - k$. Из первого соотношения (3.5) получим уравнение для определения момента времени t = t₀, в который начнется вязкопластическое течение: $c({{t}_{0}}) = - k{{r}_{0}}$.

4. Вязкопластическое течение. Развивающаяся с момента времени t = t₀ область вязкопластического течения ${{r}_{0}} \leqslant r \leqslant m(t)$ ограничена поверхностями r = r₀ и $r = m(t)$. В области $m(t) \leqslant r \leqslant R$ по-прежнему происходит вязкоупругое деформирование, то есть поверхность $r = m(t)$ является движущейся границей области вязкопластического течения.

В области $m(t) \leqslant r \leqslant R$ интегрированием уравнений равновесия (3.4) в условиях прилипания (3.1) на поверхности r = R установим, что продолжают выполняться зависимости (3.5) с неизвестной функцией интегрирования $c\left( t \right)$. Также в этой области остаются верными соотношения (3.7) и (3.8).

Интегрируя уравнения равновесия в области вязкопластического течения ${{r}_{0}} \leqslant r \leqslant m(t)$ и используя условие непрерывности компонент напряжений на упругопластической границе $r = m(t)$, получим, что в этой области также выполняются зависимости (3.5).

Пластический потенциал (2.5) в нашем случае запишется в следующей форме

Из соотношения (4.1) определим скорость пластических деформаций

Из условия совпадения скоростей необратимых деформаций на упругопластической границе $r = m(t)$ из (4.2) найдем

Из зависимостей (3.2), (3.5), (3.7), (4.2) и граничного условия для скорости на поверхности r = r₀ (3.1), найдем скорость в области вязкопластического течения

Положение упругопластической границы $r = m(t)$ в каждый момент времени задается обыкновенным дифференциальным уравнением, следующим из (3.8), (4.3) и условия непрерывности скоростей точек среды на этой границе

В области вязкоупругого деформирования $m(t) \leqslant r \leqslant R$ для необратимых и обратимых деформаций остаются справедливыми уравнения (3.6).

Интегрируя скорость пластических деформаций $\varepsilon _{{rz}}^{p}$ (4.2) по времени с учетом (3.5) и (3.7), найдем компоненту необратимых деформаций ${{p}_{{rz}}}$ в области течения ${{r}_{0}} \leqslant r \leqslant m(t)$

Здесь $g(r)$ – неизвестная функция интегрирования, которую найдем из условия непрерывности необратимых деформаций (3.7) и (4.5) на продвигающейся упругопластической границе:

в которой функция $\zeta = \zeta (r)$ определяется из обыкновенного дифференциального уравнения

Для компонент обратимых и необратимых деформаций в области вязкопластического течения ${{r}_{0}} \leqslant r \leqslant m(t)$ справедлива система (3.6).

Учитывая соотношения (3.2), (3.5), (3.6), (4.5) и условие непрерывности перемещений на упругопластической границе $r = m(t)$, найдем выражение для перемещений в области вязкопластического течения

При движении внутреннего цилиндра с постоянной скоростью с момента времени $t = {{t}_{1}} > {{t}_{0}}$ область вязкопластического течения продолжает развиваться согласно закону (4.4). Полученное выше решение остается верным как в области ${{r}_{0}} \leqslant r \leqslant m(t)$, так и в области $m(t) \leqslant r \leqslant R$. Изменение в краевом условии приведет только к изменению функции $\zeta (r)$: в области $m({{t}_{1}}) \leqslant r \leqslant m(t)$ она теперь определяется из дифференциального уравнения

в то время как в области ${{r}_{0}} \leqslant r \leqslant m({{t}_{1}})$ по-прежнему является решением уравнения (4.6)

5. Торможение вязкопластического течения и разгрузка среды. Не приводит к существенным изменениям в процессе деформирования и первоначальное уменьшение скорости движения внутренней поверхности, начиная с момента времени $t = {{t}_{2}} > {{t}_{1}}$. В отличие от случая, когда цилиндр движется с постоянной скоростью, функция $\zeta (r)$ в области ${{r}_{0}} \leqslant r \leqslant m({{t}_{1}})$ находится из уравнения (4.6), в области $m({{t}_{1}}) \leqslant r \leqslant m({{t}_{2}})$ – из (4.7), а в области $m({{t}_{2}}) \leqslant r \leqslant m(t)$ снова из (4.6) с граничным условием $\zeta \left( {m\left( {{{t}_{2}}} \right)} \right) = {{t}_{2}}$.

В расчетный момент времени $t = {{t}_{3}} > {{t}_{2}}$ рост области вязкопластического течения прекращается. Появляется новая граница $r = m(t)$, движущаяся от стационарной поверхности $r = m({{t}_{3}})$ к внутренней поверхности r = r₀ и отделяющая уменьшающуюся область течения ${{r}_{0}} \leqslant r \leqslant m(t)$ от области разгрузки $m(t) \leqslant r \leqslant m({{t}_{3}})$, в которой, как и в области $m({{t}_{3}}) \leqslant r \leqslant R$, теперь накапливаются необратимые деформации ползучести.

В области вязкоупругого деформирования $m({{t}_{3}}) \leqslant r \leqslant R$ и в области течения ${{r}_{0}} \leqslant r \leqslant m(t)$ остаются верными соотношения, справедливые в интервале времени ${{t}_{2}} \leqslant t \leqslant {{t}_{3}}$.

В области $m(t) \leqslant r \leqslant m({{t}_{3}})$ для компонент напряжений и скоростей необратимых деформаций выполняются соотношения (3.5) и (3.6).

Из (3.2), (3.5), (3.7) и условия непрерывности скорости на упругопластической границе $r = m({{t}_{3}})$ установим, что в области $m(t) \leqslant r \leqslant m({{t}_{3}})$ скорость вычисляется из первой зависимости (3.8).

Из условия непрерывности скоростей на упругопластической границе $r = m(t)$ получим уравнение ее изменения вида (4.4).

Интегрируя зависимость (3.7) по времени в области разгрузки $m(t) \leqslant r \leqslant m({{t}_{3}})$, получим соотношение для компоненты необратимых деформаций в этой области

В выражении (5.1) неизвестную функцию интегрирования ${{g}_{1}}(r)$ найдем из условия непрерывности необратимых деформаций на упругопластической границе $r = m(t)$

Здесь функция $\zeta = \zeta (r)$ удовлетворяет обыкновенному дифференциальному уравнению (4.6) с начальным условием $\zeta \left( {m\left( {{{t}_{3}}} \right)} \right) = {{t}_{3}}$.

Интегрируя второе уравнение (3.2) в области $m(t) \leqslant r \leqslant m({{t}_{3}})$ с учетом соотношений (3.5), (3.6), (5.1) и условия непрерывности перемещений на границе $r = m({{t}_{3}})$, найдем компоненту перемещений

В области ${{r}_{0}} \leqslant r \leqslant m(t)$ из второго уравнения (3.2) с учетом (3.5), (3.6), (4.5) и условия непрерывности перемещений на границе $r = m(t)$ найдем

В момент времени $t = {{t}_{4}} > {{t}_{3}}$ внутренний цилиндр остановится $({{{v}}_{0}}({{t}_{4}}) = 0)$. Скорость в области вязкопластического течения ${{r}_{0}} \leqslant r \leqslant m(t)$ будет вычисляться зависимостью

Уравнение для вычисления положения упругопластической границы $r = m(t)$ примет форму

В области $m({{t}_{3}}) \leqslant r \leqslant R$ компонента необратимых деформаций вычисляется из (4.5), в области $m(t) \leqslant r \leqslant m({{t}_{3}})$ – из (5.1). Функция ${{g}_{1}}(r)$имеет вид (5.2), в котором ζ = = $\zeta (r)$ в области $m({{t}_{k}}) \leqslant r \leqslant m({{t}_{3}})$ находится из уравнения (4.6) с начальным условием $\zeta (m({{t}_{2}}))$ = t₂, а в области $m(t) \leqslant r \leqslant m({{t}_{k}})$ вычисляется из уравнения

Для перемещений в областях $m(t) \leqslant r \leqslant m({{t}_{3}})$ и ${{r}_{0}} \leqslant r \leqslant m(t)$ продолжают выполняться зависимости (5.3) и (5.4).

В некоторый момент времени $t = {{t}_{5}}$ упругопластическая граница $r = m(t)$ совпадет с внутренней поверхностью $r = {{r}_{0}}$ и вязкопластическое течение в цилиндрическом слое прекратится. Для скорости во всем слое будет выполняться первое соотношение (3.8), в котором функция $c(t)$ примет вид

Перемещения в областях $m({{t}_{3}}) \leqslant r \leqslant R$ и ${{r}_{0}} \leqslant r \leqslant m({{t}_{3}})$ вычисляются соотношениями (3.8) и (5.3) соответственно.

Функция ${{{v}}_{0}}$ при расчетах была выбрана следующим образом:

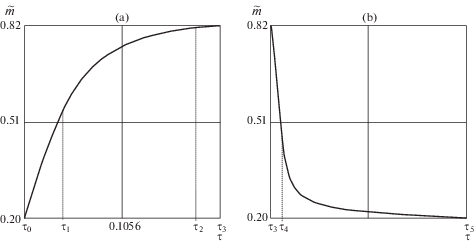
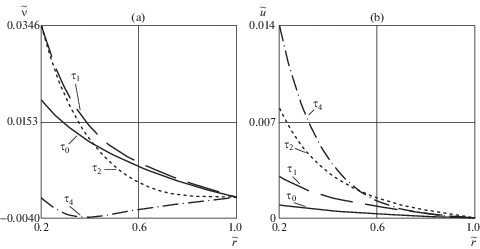
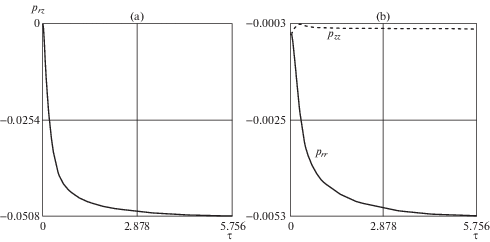
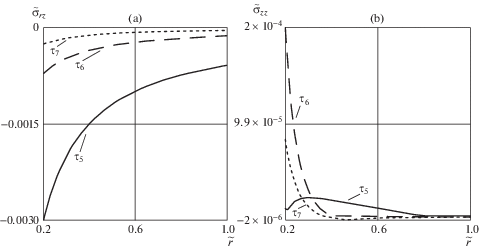
Расчеты проводились в безразмерных переменных $\tilde {r} = {r \mathord{\left/ {\vphantom {r R}} \right. \kern-0em} R}$, $\tau = {{{{\xi }_{1}}{{t}^{2}}} \mathord{\left/ {\vphantom {{{{\xi }_{1}}{{t}^{2}}} {{{r}_{0}}}}} \right. \kern-0em} {{{r}_{0}}}}$ при следующих значениях постоянных параметров ${k \mathord{\left/ {\vphantom {k {\mu = 0.003}}} \right. \kern-0em} {\mu = 0.003}}$, ${{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} R}} \right. \kern-0em} R} = 0.2$, $n = 3$, $B{{\mu }^{2}}\sqrt {{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {{{\xi }_{1}}}}} \right. \kern-0em} {{{\xi }_{1}}}}} = 3$, ${{{{\xi }_{2}}} \mathord{\left/ {\vphantom {{{{\xi }_{2}}} {{{\xi }_{1}}}}} \right. \kern-0em} {{{\xi }_{1}}}}$ = 0.5, $\left( {{\mu \mathord{\left/ {\vphantom {\mu \eta }} \right. \kern-0em} \eta }} \right)\sqrt {{{{{r}_{0}}} \mathord{\left/ {\vphantom {{{{r}_{0}}} {{{\xi }_{1}}}}} \right. \kern-0em} {{{\xi }_{1}}}}} = 10$, ${{a}_{0}} = {{10}^{{ - 6}}}$. График упругопластической границы $\tilde {m} = {m \mathord{\left/ {\vphantom {m R}} \right. \kern-0em} R}$ в интервале от ${{\tau }_{{\text{0}}}} = 0.0097$ до ${{\tau }_{{\text{3}}}} = 0.1121$ представлен на рис. 1a, в интервале от ${{\tau }_{{\text{3}}}}$ до ${{\tau }_{{\text{5}}}} = 5.756$ – на рис. 1b. Отметим, что ${{\tau }_{{\text{1}}}} = 0.03$, ${{\tau }_{{\text{2}}}} = 0.1$, ${{\tau }_{{\text{4}}}} = 0.4391$. Распределения скоростей и перемещений точек среды по слою в разные моменты времени показаны на рис. 2a и рис. 2b соответственно. Рисунок 3 иллюстрирует изменение необратимых деформаций в точках внутренней поверхности $r = {{r}_{0}}$ в интервале $0 \leqslant \tau \leqslant {{\tau }_{5}}$. Релаксация компонент напряжений ${{\sigma }_{{rz}}}$ и наибольшего из диагональных σ_zz показана на рис. 4a и рис. 4b соответственно (${{\tau }_{{\text{6}}}} = 1000$, ${{\tau }_{{\text{7}}}} = 10000$).

6. Заключение. Построено решение задачи о деформировании материала цилиндрического слоя, происходящем при прямолинейном равноускоренном движении внутреннего цилиндра, его последующем движении с постоянной скоростью и равнозамедленном движении до полной остановки, в то время как внешний цилиндр остается неподвижным. В условиях жесткого сцепления материала с граничными стенками рассмотрен случай, когда накапливаемые необратимые деформации являются и деформациями ползучести, и пластичности. Исследовано продвижение упругопластической границы, разделяющей области с разными действующими законами накопления необратимых деформаций, рассчитаны параметры напряженно-деформированного состояния среды, проведено наблюдение за релаксацией напряжений, происходящей после остановки цилиндра.

Работа выполнена при финансовой поддержке РФФИ (18-01-00038).