Известия РАН. Механика твердого тела, 2020, № 1, стр. 77-84

1. Введение. Нанокристаллические и ультрамелкозернистые материалы обладают уникальными механическими и физическими свойствами, такими как сверхвысокие значения прочности и твердости. Однако большинство наноструктурных материалов характеризуется крайне низкой пластичностью, что существенно сужает круг их практического применения [1–3]. В основном, низкая пластичность наноструктурных материалов связывается со значительным ограничением решеточного скольжения в связи с малым размером зерен и значительной объемной долей границ зерен. Отсутствие решеточного скольжения и связанных с ним эффектов в наноструктурных материалах во многих случаях проявляется в локализации пластической деформации, приводящей к шейкообразованию [2–5].

Вместе с тем, в последние годы активно развивается новый класс материалов с бимодальной структурой, которые представляют собой нанокристаллические или ультрамелкозернистые материалы с крупными зернами (микронного размера) внедренными в их структуру. Сочетание различных размеров микроструктуры в бимодальных материалах приводит к значительному улучшению пластических характеристик исходных наноматериалов. Согласно экспериментальным исследованиям [6–9] и компьютерному моделированию [10–13] бимодальные наноматериалы обладают одновременно высокой прочностью сравнимой с прочностными характеристиками их нанокристаллических аналогов и функциональной пластичностью значительно превосходящей пластичность обычных наноматериалов. Например, в экспериментальных работах [6, 7] была получена медь (Cu) с бимодальной структурой, предел текучести которой в несколько раз превосходил предел текучести крупнозернистой Cu, демонстрируя при этом значительно более высокую пластичность по сравнению с нанокристаллической Cu. Также, в работах [6, 7] отмечалось наличие решеточных дислокаций в больших (микронного размера) зернах. Предполагается, что именно в результате скольжения решеточных дислокаций образцы бимодальной Cu демонстрировали характерное для крупнозернистых материалов деформационное упрочнение, обеспечивающие им хорошую пластичность.

Известно, что графеновые включения даже при сравнительно малой их концентрации значительно улучшают прочность и теплопроводность основного материала. Вместе с тем, графеновые нанокомпозиты проявляют еще более низкую пластичность, чем исходные наноматериалы, так как графеновые включения дополнительно затрудняют реализацию не только решеточного скольжения, но также таких механизмов, как зернограничное скольжение, деформация двойникованием и миграция границ зерен, которые являются основными механизмами пластичности в нанокристаллических и ультрамелкозернистых материалах.

Однако, согласно последним экспериментальным исследованиям, сдвиг слоев графита относительно друг друга осуществляется при относительно низких значениях сдвигового напряжения, которое варьируется от 0.12 до 0.5 GPa [14]. Данный факт, позволяет предложить механизм зарождения частичных дислокаций (которые характеризуются более низким вектором Бюргерса, чем полные дислокации) способных скользить внутри нанозерен в результате сдвига слоев графена в графеновых включениях. При последовательном сдвиге параллельных слоев графена относительно друг друга происходит последовательное зарождение частичных дислокаций, в результате скольжения которых по параллельным плоскостям скольжения формируется нанодвойниковая прослойка. При этом, формирующиеся таким образом нанодвойники становятся концентраторами напряжений для зарождения новых частичных или полных дислокаций на соседних границах зерен.

Таким образом, основной целью данной работы является разработка теоретической модели, описывающей переход от деформации двойникованием, реализуемой за счет сдвигов слоев графена к решеточному скольжению внутри зерен микронного размера в графено-металлических композитах с бимодальной структурой.

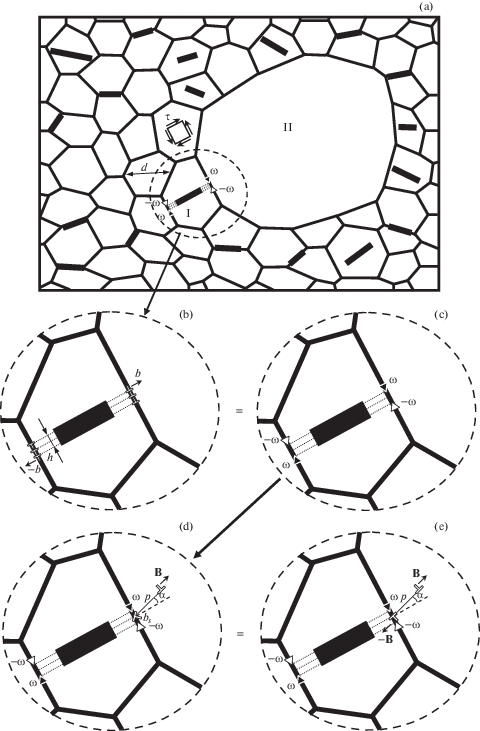
2. Модель. Рассмотрим двумерную модель бимодального материала со средним размером зерна ультрамелкозернистой матрицы d с графеновыми включениями, расположенными внутри зерен и по границам зерен матрицы, рис. 1a. Материал находится под действием внешней механической нагрузки $\sigma $, рис. 1a. В исходном состоянии имеются две нанодвойниковые прослойки шириной $h$, которые сформировались под действием внешнего сдвигового напряжения $\tau $ в результате последовательных сдвигов параллельных слоев графенового включения [14], рис. 1a и 1b.

Предполагается, что в результате сдвига одного слоя графена относительно другого происходит зарождение двух частичных дислокаций с векторами Бюргерса $ \pm {\mathbf{b}}$ ($ \pm {\mathbf{b}}$‑дислокации) на противоположных концах графенового включения, которые способны двигаться внутри зерна ультрамелкозернистой матрицы. Таким образом, последовательные сдвиги соседних параллельных графеновых слоев формируют две нанодвойниковые прослойки на концах графенового включения, которые упираются в противоположные границы зерен, формируя две стенки частичных $ \pm {\mathbf{b}}$-дислокаций, рис. 1a и 1b.

Согласно теории дислокаций в твердых телах стенка частичных дислокаций конечной длины может быть смоделирована диполем клиновых дисклинаций. Таким образом, две стенки частичных $ \pm {\mathbf{b}}$-дислокаций моделируются двумя диполями клиновых дисклинаций с мощностью $ \pm \omega $ ($ \pm \omega $-дисклинации), которые образуют квадруполь $ \pm \omega $-дисклинаций с плечами d и $h$, рис. 1c. Мощность дисклинаций может быть определена из выражения $\omega \approx b{\text{/}}\delta $, где $b = a{\text{/}}\sqrt 3 $ – модуль вектора Бюргерса частичных дислокаций, $\delta = a{\text{/}}\sqrt 3 $ – расстояние между соседними плоскостями скольжения частичных дислокаций, $a$ – параметр кристаллической решетки.

Далее рассмотрим процесс зарождения решеточной дислокации на одной из стенок частичных $ \pm {\mathbf{b}}$-дислокаций. В модели предполагается, что одна из границ зерен, к которой примыкает нанодвойниковая прослойка, является границей между маленьким зерном I ультрамелкозернистой матрицы и большим зерном II микронного размера, которые образуют бимодальную структуру, рис. 1a и 1b.

В суммарном поле внешнего сдвигового напряжения $\tau $ и напряжения квадруполя $ \pm \omega $-дисклинаций происходит испускание решеточной дислокации с вектором Бюргерса B (B-дислокации) из границы зерна в тело большого зерна II, рис. 1d. Эмиссия решеточной B-дислокации происходит в результате расщепления частичной b-дислокации стенки частичных $ \pm {\mathbf{b}}$-дислокаций на разностную дислокацию с вектором Бюргерса ${{{\mathbf{b}}}_{{\mathbf{s}}}} = {\mathbf{b}} - {\mathbf{B}}$, которая остается в границе зерна, и подвижную решеточную B-дислокацию, которая способна двигаться внутри большого зерна II, рис. 1d. В рамках используемого континуального подхода процесс эмиссии решеточной B-дислокации состоит в появлении диполя полных решеточных дислокаций с векторами Бюргерса $ \pm {\mathbf{B}}$ (диполь $ \pm {\mathbf{B}}$-дислокаций), рис. 1e. При этом одна решеточная дислокация (испущенная B-дислокации) скользит в теле большого зерна II, а вторая решеточная дислокация остается в границе зерна (неподвижная $ - {\mathbf{B}}$-дислокации), рис. 1d. Угол $\alpha $ задает ориентацию плоскостей скольжения решеточной дислокации, а параметр $p$ определяет расстояние пройденное решеточной B-дислокации в теле зерна, рис. 1d.

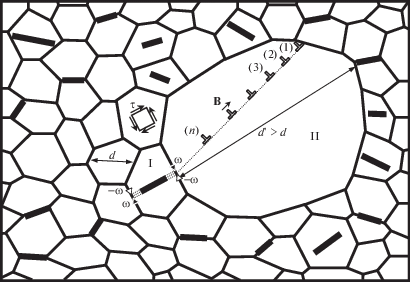
Эмиссия решеточной B-дислокации становится возможной при достижении внешним сдвиговым напряжением $\tau $ некоторой критической величины ${{\tau }_{{с1}}}$. При $\tau \geqslant {{\tau }_{{c1}}}$ решеточная B-дислокация испускается из границы зерна и скользит на расстояние $p$ в теле большого зерна II, рис. 1d. Далее возможно испускание второй решеточной дислокации, что требует повышения внешнего сдвигового напряжения $\tau $ до некоторого нового критического значения ${{\tau }_{{c2}}} > {{\tau }_{{с1}}}$, так как между первой и второй решеточными дислокациями действуют отталкивающие силы, затрудняющие эмиссию второй решеточной дислокации. Процесс испускания решеточных дислокаций из границы зерна, содержащей стенку частичных дислокаций, может многократно повторяться. При этом каждое новое испускание решеточной дислокации требует повышения внешнего сдвигового напряжения $\tau $ до нового критического значения ${{\tau }_{{с(n)}}} \geqslant {{\tau }_{{c(n - 1)}}}$. В результате такого последовательного испускания решеточных дислокаций из границы зерна формируется скопление решеточных дислокаций в теле большого зерна, рис. 2. В этом случае, скольжение решеточных дислокаций в теле большого зерна II обеспечивает дальнейшее развитие пластической деформации, заторможенное в ультрамелкозернистой матрице. Таким образом, осуществляется переход от деформации двойникованием, инициаторами которой являются графеновые включения внутри маленьких зерен I, к решеточному скольжению в больших зернах II, которое обеспечивает деформационное упрочнение бимодального материала характерное для крупнозернистых материалов, улучшая его пластические характеристики.

Далее рассмотрим энергетические характеристики и рассчитаем критические напряжения зарождения первой решеточной дислокации на границы зерна вблизи нанодвойниковой прослойки.

3. Энергетические характеристики и критические напряжения. Для расчета энергетических характеристик эмиссии решеточной дислокации из границы зерна, к которой примыкает нанодвойниковая прослойка, рис. 1d и 1e, исследуем переход дефектной системы из состояния с полной энергией ${{W}_{1}}$, характеризуемой квадруполем $ \pm \omega $-дисклинаций, рис. 1c, в состояние с полной энергией ${{W}_{2}}$, соответствующее испусканию первой решеточной ${\mathbf{B}}$-дислокации, рис. 1d и 1e. Такая трансформация дефектной системы энергетически выгодна при выполнении условия ${\Delta }W = {{W}_{2}} - {{W}_{1}} < 0$.

В нашем случае, разность энергий $\Delta W$ определяется выражением:

где ${{E}_{s}}$ – собственная энергия диполя решеточных $ \pm {\mathbf{B}}$-дислокаций; ${{E}_{i}}$ – энергия упругого взаимодействия между диполем $ \pm {\mathbf{B}}$-дислокаций и квадруполем $ \pm \omega $-дисклинаций; ${{E}_{t}}$ – энергия упругого взаимодействия внешнего сдвигового напряжения $\tau $ с диполем решеточных $ \pm {\mathbf{B}}$-дислокаций.

Собственная энергия ${{E}_{s}}$ диполя решеточных $ \pm {\mathbf{B}}$-дислокаций вычисляется с помощью известного выражения [14] следующим образом:

где $D = G{\text{/}}[2{\pi }(1 - {\nu })]$, G – модуль сдвига, $\nu $ – коэффициент Пуассона, p – расстояние, пройденное решеточной B-дислокацией, ${{r}_{c}} \approx B$ – радиус дислокационного ядра решеточных $ \pm {\mathbf{B}}$-дислокаций.

Энергия упругого взаимодействия ${{E}_{i}}$ между диполем $ \pm {\mathbf{B}}$-дислокаций и квадруполем $ \pm \omega $-дисклинаций вычисляется, как работа по зарождению дислокационного диполя в поле дисклинационного квадруполя. Окончательное выражение для энергии ${{E}_{i}}$ дается следующей формулой:

где ${{x}_{0}} = d$ и ${{y}_{0}} = h{\text{/}}2$ – координаты точки зарождения диполя решеточных $ \pm {\mathbf{B}}$-дислокаций.

Энергия взаимодействия ${{E}_{t}}$ внешнего сдвигового напряжения ${\tau }$ с диполем решеточных $ \pm {\mathbf{B}}$-дислокаций дается стандартным выражением:

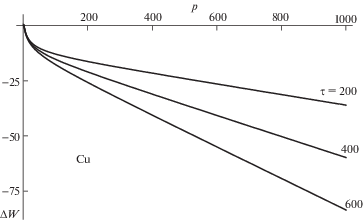
Используя формулы (3.1)–(3.4), составим выражение для разности энергий ${\Delta }W$. С помощью этого выражения построим зависимость разности энергий ${\Delta }W$ от расстояния $p$, пройденного решеточной дислокацией в теле большого зерна. Расчет зависимостей ${\Delta }W(p)$ проведем на примере бимодальной меди (Cu) с графеновыми включениями, используя следующие значения параметров материала: G = 44 ГПа, ${\nu } = 0.38$, $a = 0.358$ нм, $B = a\sqrt 2 {\text{/}}2$ [15]. Остальные параметры дефектной системы положим равными: $d = 100$ нм, $h = 5$ нм и ${\alpha } = 10$°.

На рис. 3 представлены расчеты зависимостей ${\Delta }W(p)$ (размерность разности энергий $\Delta W$ в Эв/нм, размерность расстояния p в нм) при различных значениях внешнего сдвигового напряжения ${\tau }$ (размерность в МПа). Как видно из рис. 3, при всех значениях напряжения ${\tau }$ зависимости ${\Delta }W(p)$ находятся в отрицательной области (${\Delta }W < 0$) и монотонно убывают с увеличением расстояния p, пройденного решеточной B-дислокацией. Это говорит о том, что процесс зарождения решеточной дислокации в поле напряжений квадруполя $ \pm {\omega }$-дисклинаций и ее последующего скольжения в теле большого зерна II является энергетически выгодным при данных параметрах дефектной системы.

Далее рассчитаем критическое напряжение ${{{\tau }}_{{c(n)}}}$, необходимое для эмиссии $n$-й решеточной дислокации из границы зерна. Для определения критического напряжения ${{{\tau }}_{{c(n)}}}$ требуется расчет разности энергий ${\Delta }{{W}_{n}}$, которая соответствует появлению $n$-й решеточной B-дислокации. Расчет разности энергий ${\Delta }{{W}_{n}}$ производится аналогично выше приведенному расчету разности энергий ${\Delta }W$, с дополнительным учетом энергии взаимодействия между испущенными решеточными дислокациями и определением точек устойчивого равновесия этих дислокаций в теле зерна.

Положения ${{p}_{{eq(n)}}}$ устойчивого равновесия испущенных решеточных B-дислокаций соответствуют точкам минимума на зависимостях ${\Delta }{{W}_{n}}({{p}_{n}})$ и могут быть найдены из решения уравнений ${\Delta }{{W}_{n}}{\text{/}}\partial {{p}_{n}} = 0$. Выполнение условий ${\Delta }{{W}_{n}}({{p}_{n}} = p{\text{'}}) = 0$ (где $p{\text{'}} = 1$ нм), ${{\left. {{\Delta }{{W}_{n}}} \right|}_{{{{p}_{n}} > p{\text{'}}}}} < 0$ и ${{\left. {\partial \Delta {{W}_{n}}{\text{/}}\partial {{p}_{n}}} \right|}_{{{{p}_{n}} > p{\text{'}}}}} \leqslant 0$ позволяют рассчитать величину критического сдвигового напряжения ${{{\tau }}_{{c(n)}}}$, то есть минимального сдвигового напряжения, при котором возможна эмиссия $n$-й решеточной дислокации из границы зерна.

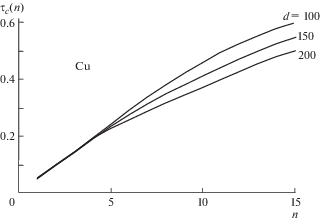
Расчет величины критического напряжения ${{{\tau }}_{{c(n)}}}$ произведем при тех же значениях параметров дефектной системы, выписанных выше. На рис. 4 приведена зависимость критического напряжения ${{{\tau }}_{{c(n)}}}$ (размерность критического напряжения в ГПа) от числа испущенных решеточных дислокаций $n$. Как видно из зависимостей ${{{\tau }}_{{c(n)}}}(n)$ на рис. 4 величина критического напряжения плавно нарастает с увеличением числа испущенных дислокаций, которые формируют скопление решеточных дислокаций в теле большого зерна II. Также из зависимостей ${{{\tau }}_{{с(n)}}}(n)$ видно, что увеличение размера зерна d (характеризующего средний размер зерен ультрамелкозернистой матрицы в нм) приводит к снижению величины критического напряжения ${{{\tau }}_{{c(n)}}}$, рис. 4.

4. Заключение. Таким образом, разработана теоретическая модель, описывающая смену механизма деформации в графено-металлическом композите с бимодальной структурой. В рамках модели осуществляется переход от деформации двойникованием, инициированной графеновыми включениями в ультрамелкозернистой матрице, к скольжению решеточных дислокаций, формирующих скопления в больших зернах микронного размера, которые вместе с ультрамелкозернистой матрицей образуют бимодальную структуру. Переход от деформации двойникованием, заторможенной в ультрамелкозернистой матрице, к решеточному скольжению позволяет существенно повысить пластические характеристики графено-металлических композитов с бимодальной структурой.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант 18-29-19086) и Министерства образования и науки (Задание 16.3483.2017/ПЧ).