Известия РАН. Механика твердого тела, 2019, № 6, стр. 136-147

1. Введение. Предполагается, что влияние поля температур на напряженно-деформированное состояние эластомеров проявляется двояко, через температурную зависимость модулей упругости и через механизм теплового расширения. Обычно при технических расчетах эластомеров температурной зависимостью модулей упругости пренебрегают, а тепловое расширение полагают подчиняющимся линейному закону λ = = $1 + \alpha \Delta T$, $\Delta T = T - {{T}_{0}}$, где $\alpha $ – линейный коэффициент теплового расширения, ${{T}_{0}}$ – начальная температура, $T$ – текущая температура, λ – кратность удлинения материального волокна [1, 2]. Такой подход приводит к тому, что для эластомеров с их низкими модулями упругости вклад теплового расширения в напряженное состояние становится пренебрежимо мал, и термомеханика применяется только для расчетов теплообразования при циклическом нагружении [3]. В работе [4] со ссылкой на эксперимент, и в работе [5] в результате теоретических рассуждений заявлено, что при конечных деформациях тепловое расширение эластомеров подчиняется экспоненциальному закону $\lambda = {{e}^{{\alpha \Delta T}}}$. Ниже продемонстрирована постановка задач статики нелинейной термоупругости с экспоненциальным законом зависимости теплового расширения от температуры. На примере цилиндрической деформации (комбинации плоской и антиплоской деформации) [6], позволяющей получить для потенциала энергии деформации Муни–Ривлина точные решения, показано существенное влияние температуры на напряженно-деформированное состояние эластомеров.

2. Общая постановка. В работе рассматривается вариант процесса термоупругой деформации как композиции деформирования под действием напряжений при неизменной температуре ${{T}_{0}}$ и свободного теплового расширения при неизменных напряжениях и изменении температуры от ${{T}_{0}}$ до T. Внутренняя диссипация отсутствует, поэтому деформация под действием напряжений не меняет температуру. Другой вариант композиции свободного теплового расширения с нулевыми напряжениями при изменении температуры от ${{T}_{0}}$ до T и деформирования под действием напряжений при неизменной температуре T рассмотрен в [4]. Последний вариант отличается от представленного тем, что тепловое расширение происходит при нулевых напряжениях и не дает вклада в энергию деформации. Поле температур считается однородным. Неискаженную конфигурацию при $T = {{T}_{0}}$, σ = 0 полагаем отсчетной. Здесь σ – обозначение для напряжения.

Соотношения между конфигурациями и векторы места точек в этих конфигурациях изображены на рис. 1. Введем следующие тензоры градиентов деформации:

Здесь F – тензор градиента изотермической деформации нелинейной теории упругости. Из (2.1) следует связь

При конечных деформациях термически изотропного материала тензор градиента деформации теплового расширения ${\mathbf{\bar {F}}}$ представляется в виде [4, 5]

Здесь E – единичный тензор, $\left\{ {{\mathbf{i}},{\mathbf{j}},{\mathbf{k}}} \right\}$ – базис декартовой системы координат. Два рядом стоящих вектора – диада. Таким образом,

Через тензор градиента деформации F* выражаются правый C* и левый B* тензоры деформации Коши–Грина (значок $Tr$ означает транспонирование, точка – скалярное произведение)

Их главные алгебраические инварианты имеют вид

Для изотермически несжимаемого материала ${{I}_{3}} = 1$.

Материал полагается механически и термически однородным и изотропным, а так же гиперупругим (отсутствует внутренняя диссипация). Это подразумевает существование потенциала энергии деформации, зависящего только от главных инвариантов правого или левого тензоров деформации Коши и температуры $W_{{}}^{*}(I_{1}^{*},I_{2}^{*},I_{3}^{*},T)$ такого, что:

Здесь D* тензор напряжений Пиолы [7] (по [8] – транспонированный первый тензор напряжений Пиолы–Кирхгофа).

Проведем стандартные преобразования [7] в выражении (2.5) с учетом теплового расширения для изотермически сжимаемого $\left( {{{I}_{3}} \ne 1} \right)$ материала

Была использована теорема Гамильтона–Келли $I_{1}^{*}{\mathbf{B}}_{{}}^{*} - {\mathbf{B}}_{{}}^{{*2}} = I_{2}^{*}{\mathbf{E}} - I_{3}^{*}{\mathbf{B}}_{{}}^{{* - 1}}$.

Для изотермически несжимаемого материала (${{I}_{3}} = 1$, $I_{3}^{*} = {{e}^{{6\alpha \Delta T}}}$) используя множитель Лагранжа h*, зависящий от координат точек и температуры, потенциал энергии деформации можно переписать в виде

Соотношение $I_{3}^{*}\partial W_{{}}^{*}{\text{/}}\partial I_{3}^{*} = {{I}_{3}}\partial W_{{}}^{*}{\text{/}}\partial {{I}_{3}}$, позволяет получить формулу

Введя обозначение $p_{{}}^{*} = 4(I_{2}^{*}\partial W_{{}}^{*}{\text{/}}\partial I_{2}^{*} + h_{{}}^{*}){\text{/}}\mu \left( T \right)$, получим

Здесь $\mu \left( T \right)$ – модуль сдвига линейной теории. Перепишем (2.6) в форме

Откуда, используя соотношение [7] ${\mathbf{D}}_{{}}^{*} = \sqrt {I_{3}^{*}} {\mathbf{F}}_{{}}^{{* - 1}} \cdot {\mathbf{S}}_{{}}^{*}$, где S* – тензор напряжений Коши, следует выражение для тензора напряжений Коши

В качестве потенциала энергии деформации возьмем вариант потенциала Муни–Ривлина в виде [9], то есть предполагается, что потенциал зависит от температуры неявно.

Здесь $\beta \in [ - 1,1]$ – безразмерный параметр. Это выражение позволяет записать S* форме

Используя соотношения (2.3), получим

В конфигурации I введем систему координат (${{q}^{1}},{{q}^{2}},{{q}^{3}}$), которые будем считать материальными, тогда базисные векторы этой системы в этой конфигурации примут вид (крестик означает векторное произведение)

Тензор градиента изотермической деформации связан с тензором градиента места соотношением

Здесь $\mathop \nabla \limits^0 = {{{\mathbf{R}}}^{k}}\partial {\text{/}}\partial {{q}^{k}}$ – оператор Гамильтона в базисе I конфигурации. ${{{\mathbf{\bar {r}}}}_{k}} = \partial {\mathbf{\bar {r}}}{\text{/}}\partial {{q}^{k}}$ – базис материальной системы координат в конфигурации II.

Уравнение равновесия, в отсутствии объемных внешних усилий, имеет вид

Здесь $\nabla _{{}}^{*} = {\mathbf{r}}_{{}}^{{*k}}\partial {\text{/}}\partial {{q}^{k}}$ – оператор Гамильтона в базисе III конфигурации, ${\mathbf{r}}_{{}}^{{*k}}$ – базис, взаимный с базисом ${\mathbf{r}}_{k}^{*}$ материальной системы координат в конфигурации III. Справедливо представление ${\mathbf{r}}_{k}^{*} = {\mathbf{F}}_{{}}^{*} \cdot {{{\mathbf{R}}}_{k}} = {{e}^{{\alpha \Delta T}}}{\mathbf{F}} \cdot {{{\mathbf{R}}}_{k}} = {{e}^{{\alpha \Delta T}}}{{{\mathbf{\bar {r}}}}_{k}}$ и $v_{{}}^{*} = {\mathbf{r}}_{1}^{*} \cdot {\mathbf{r}}_{2}^{*} \times {\mathbf{r}}_{3}^{*}$ = = ${{e}^{{3\alpha \Delta T}}}{{{\mathbf{\bar {r}}}}_{1}} \cdot {{{\mathbf{\bar {r}}}}_{2}} \times {{{\mathbf{\bar {r}}}}_{3}}$ = ${{e}^{{3\alpha \Delta T}}}\bar {v}$. Следовательно, ${\mathbf{r}}_{{}}^{{*k}} = {{e}^{{ - \alpha \Delta T}}}{{{\mathbf{\bar {r}}}}^{k}}$ и

Подставляя (2.7) в (2.8), получим

Исключая в (2.9) гидростатическую функцию, получим уравнение для нахождения деформации из конфигурации I в конфигурацию II.

Присутствие экспоненциальных множителей объясняется формулировкой уравнений равновесия в конфигурации III.

Силовые граничные условия можно записать в виде

Здесь n – единичный внешний нормальный вектор к граничной поверхности в конфигурации III, f* – плотность внешних поверхностных сил, приложенных к границе конфигурации III и рассчитанная на единицу поверхности в этой конфигурации.

3. Случай, когда изотермическая деформация является цилиндрической [6]. Рассматривается изотермическая деформация круглой цилиндрической втулки, подвергнутой на внутренней и внешней боковых поверхностях действию продольных сдвигающих сил ${\mathbf{Q}} = Q{\mathbf{k}}$ при температуре ${{T}_{0}}$. Через ${{R}_{1}}$ и ${{R}_{2}}$ обозначаются внутренний и внешний радиусы втулки, а через $H$ ее длина. Далее деформированная втулка помещается в однородное температурное поле $T$, в котором она свободно расширяется.

Решение проводится полуобратным методом. В качестве материальной системы координат выбрана цилиндрическая система ($R,\Phi ,Z$), причем ось $OZ$ совпадает с осью симметрии втулки. Втулка считается достаточно длинной, чтобы пренебречь торцевыми эффектами и считать напряженно-деформированное состояние независящим от $Z$. В этих условиях для описания цилиндрической деформации можно использовать кинематическую гипотезу коаксиальных сечений, то есть сечения цилиндрические и коаксиальные до деформации остаются таковыми и после деформации (ось единая для всех таких сечений совпадает с осью симметрии втулки). В цилиндрической системе координат в силу осевой симметрии вектор места в конфигурации II задается соотношением

Здесь $w(R)$ и $f(R)$ подлежащие определению функции, $\left\{ {{{{\mathbf{e}}}_{R}},\,\,{{{\mathbf{e}}}_{\Phi }},\,\,{\mathbf{k}}} \right\}$ – единичный базис цилиндрической системы координат с оператором Гамильтона

Тензор градиента места получается в виде

Так, что условие несжимаемости $(\det \mathop \nabla \limits^0 {\mathbf{\bar {r}}} = 1)$ принимает форму дифференциального уравнения $ff{\kern 1pt} ' = R$ (штрих означает производную по R), решение которого имеет вид $f\left( R \right) = \sqrt {{{R}^{2}} + R_{1}^{2}\eta } $. Здесь $\eta $ постоянная интегрирования, в дальнейшем играющая роль безразмерного параметра. Таким образом, имеем

Подставляя эти выражения в (2.7), получим

По (3.1) базисные векторы материальной системы координат в конфигурации II имеют вид ${{{\mathbf{\bar {r}}}}_{{\,1}}} = \xi (R){{{\mathbf{e}}}_{R}} + w{\kern 1pt} '(R){\mathbf{k}}$, ${{{\mathbf{\bar {r}}}}_{{\,2}}} = R{\text{/}}\xi (R){{{\mathbf{e}}}_{\Phi }}$, ${{{\mathbf{\bar {r}}}}_{{\,3}}} = {\mathbf{k}}$, по ним вычисляется сопряженный базис и оператор Гамильтона в базисе II конфигурации

Подставляя (3.2), (3.3) в (2.9), учитывая (3.5) и приравнивая к нулю компоненты полученного вектора, имеем уравнения равновесия

Уравнение (2.10) сводится к виду

и является следствием (3.6).

Из уравнения (3.6) следует, что

где $c$ – константа интегрирования.

Вектор единичной нормали ${\mathbf{n}}$ к любой цилиндрической поверхности $R = {\text{const}}$ внутри втулки в процессе термоупругой деформации не меняется и совпадает с ${{{\mathbf{e}}}_{R}}$. Будем считать, что внешняя нагрузка ${\mathbf{Q}} = Q{\mathbf{k}}$ “мертвая” и в процессе теплового расширения не меняется, поэтому ее можно вычислить до теплового расширения. Qk = = $\iint_{\bar {\Sigma }} {{\mathbf{n}} \cdot {\mathbf{\bar {S}}}d\bar {\sigma }}$. Здесь ${\mathbf{\bar {S}}} = {\mathbf{S}}*{{{\text{|}}}_{{\Delta T = 0}}}$, $d\bar {\sigma } = R{\text{/}}\xi \left( R \right)d\Phi dZ$. Далее

Использованы выражения (3.4) и (3.8) при $\Delta T = 0$. Из последнего соотношения получаем $c = Q{{\left( {\pi \mu \left( {{{T}_{0}}} \right)H} \right)}^{{ - 1}}}$, и из (3.4) следуют выражение для касательных напряжений

а так же уравнение для нахождения продольного сдвига

Из (3.10) следует, что при заданном Q температура влияет на продольное смещение только через тепловое расширение и параметр $\eta $, тогда как по (3.9) на распределение касательных напряжений она влияет еще и через зависимость $\mu \left( T \right)$.

Для нахождения параметра $\eta $ обратимся к плоской части цилиндрического напряженного состояния, порожденного конечным осевым сдвигом [6]. Уравнение (3.7) позволяет найти функцию гидростатического давления

Здесь $\xi (R)$ и $w{\kern 1pt} '(R)$ определяются формулами (3.1) и (3.10).

Из силовых граничных условий следует отсутствие нормальных напряжений на боковых поверхностях втулки $S_{{RR}}^{*}({{R}_{1}}) = S_{{RR}}^{*}({{R}_{2}}) = 0$. Получаем два уравнения для нахождения ${{p}_{0}}$ и $\eta $.

Перейдем к безразмерным переменным и параметрам

а так же введем плотность сдвигового усилия, отнесенную к площади внутренней боковой поверхности в отсчетной конфигурации I.

В новых переменных выражение для касательных напряжений и уравнение для нахождения продольного смещения примут вид

Для исключения продольного смещения втулки как жесткого целого потребуем, чтобы внутренняя обойма не смещалась, тогда выражение для продольного сдвига получится в форме

Из (3.13) получаем жесткостную характеристику втулки для продольного сдвига

Функция гидростатического давления примет вид

Здесь $\xi (t) = t({{t}^{2}} + \eta )$ и $\dot {v}(t)$ находится по (3.12).

Уравнения для нахождения ${{p}_{0}}$ и $\eta $ запишутся в форме

4. Решение поставленной задачи. Из первого уравнения в (3.16) и выражения для p* следует

Подставляя (4.1) в выражение для p*, а последнее во второе уравнение (3.16)

получим уравнение, связывающее $\eta $ и q (последнее входит в выражение для $\dot {v}$, а первое входит в выражения для $\xi $ и $\dot {v}$).

Вычисляя интегралы в (3.13), (3.14), (3.15) с учетом (4.1), имеем

Найденные выражения подставляются в (4.2), получаем уравнение для нахождения $\eta $, которое не приводится из-за громоздкости. Решая его для заданных $q,\;\alpha ,\;\beta ,\;\mu ({{T}_{0}})$, получим $\eta $. То есть на параметр $\eta $ температура влияет только через тепловое расширение. Далее по (3.11) вычисляется радиальное распределение сдвиговых касательных напряжений, а по (4.3) вычисляются жесткостные кривые продольного сдвига.

Зависимость $\mu (T)$ в области высокоэластичной деформации в [10] аппроксимируется выражением $\mu (T) = (273 + \Delta T){{\rho }_{m}}{{R}_{m}}{\text{/}}{{M}_{m}}$. Здесь ${{\rho }_{m}}$ – массовая плотность эластомера, ${{R}_{m}}$ – универсальная газовая постоянная, ${{M}_{m}}$ – средняя молекулярная масса эластомера. Таким образом, $\mu (T){\text{/}}\mu ({{T}_{0}}) = 1 + \Delta T{\text{/}}273$.

Отметим роль параметра $\beta \in [ - 1,1]$. При β = 1 потенциал Муни–Ривлина переходит в потенциал Трелоара, η = 0, напряжения и деформации в поперечной плоскости отсутствуют и напряженно-деформированное состояние становится антиплоским.

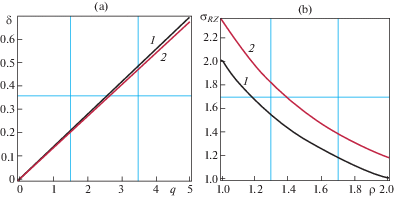
Из этих соотношений видно, что жесткость на сдвиг с ростом температуры растет, поведение распределения касательных напряжений определяется коэффициентом $kt = \left( {1 + \Delta T{\text{/}}273} \right){{e}^{{ - 3\alpha \Delta T}}}$. Для $\alpha = 0.0002$ [1] он больше единицы и растет с ростом температуры. На рис. 2 представлены жесткостные характеристики (а) и распределения касательных напряжений ${{\sigma }_{{RZ}}}$ (b) для (4.4) при температуре $\Delta T$ = 20° C (кривая 1) и $\Delta T$ = 60° C (кривая 2) для втулки с κ = 2. Здесь и ниже $\mu ({{T}_{0}}) = 5$ мПа, а распределения касательных напряжений вычисляются при $q = 2$ мПа.

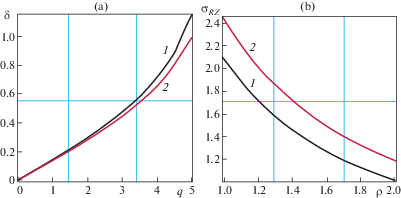
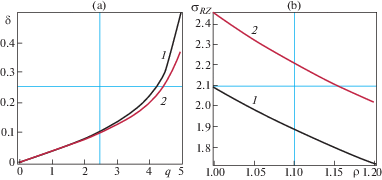
С убыванием $\beta $ от 1 до –1 увеличивается $\left| \eta \right|$ и возникает плоское напряженно-деформированное состояние в поперечной плоскости, причем ${{S}_{{RR}}} \ne 0$, ${{S}_{{\Phi \Phi }}} \ne 0$, ${{S}_{{R\Phi }}} = 0$. На рис. 3 и 4 представлены жесткостные характеристики (а) и распределения касательных напряжений ${{\sigma }_{{RZ}}}$ (b) при $\beta = - 1$.

Для возможности визуального сравнения на одной фигуре распределения касательных напряжений они приведены для поперечного сечения в недеформированной конфигурации. Рис. 3 соответствует κ = 2, а рис. 4 соответствует κ = 1.2. Кривые 1 отвечают температуре $\Delta T$ = 20° C, а кривые 2 отвечают температуре $\Delta T$ = 60° C. Повышение температуры увеличивает продольную жесткость втулки и сдвиговые касательные напряжения.

Толщина втулки практически не влияет на концентрацию напряжений (только через параметр η). Введем коэффициент концентрации касательных напряжений в виде $K[i] = \max {{\sigma }_{{RZ}}}[i]{\text{/}}q$ для $i$-й кривой. Тогда для втулки с κ = 2, $\kappa = 1.2$ K [1] = 1.05, K [2] = 1.23, так что коэффициент концентрации увеличивается в 1.17 раза. Сильнее толщина влияет на эффект увеличения жесткости втулки на сдвиг с ростом температуры. Так для κ = 2 максимальная разница между жесткостными кривыми 1 и 2 составляет 9%, а для $\kappa = 1.2{\kern 1pt} - {\kern 1pt} 13.3\% $. Эффект от повышения температуры является существенным как для концентрации касательных напряжений, так и для жесткостных кривых.

5. Заключение. Продемонстрирована постановка задач термоупругости, учитывающая нелинейную зависимость теплового расширения от температуры при конечных деформациях. В рамках этой постановки показано существенное влияние тепловых процессов на напряженно-деформированное состояние. Это два конкурирующих процесса – тепловое расширение эластомеров и увеличение модуля сдвига с ростом температуры. Первый снижает напряжения при “мертвой” нагрузке, а второй увеличивает. Для коэффициента теплового расширения $\alpha = 0.0002$ характерного для эластомеров и аппроксимации $\mu (T) = \left( {273 + \Delta T} \right){{\rho }_{m}}{{R}_{m}}{\text{/}}{{M}_{m}}$ в области высокоэластичной деформации второй процесс превалирует над первым.

В качестве примера рассмотрена изотермическая деформация круглой эластомерной цилиндрической втулки, подвергнутой на внутренней и внешней боковых поверхностях действию продольных сдвигающих сил с модулем $Q$ при температуре ${{T}_{0}}$. Далее, деформированная втулка помещается в однородное температурное поле $T$, в котором она свободно расширяется. Потенциал энергии деформации Муни–Ривлина взят в виде $W{\text{*}} = [(1 + \beta )(I_{q}^{*} - 3) + (1 - \beta )(I_{2}^{*} - 3)]\mu (T){\text{/}}4$, $\beta \in [ - 1,1]$. При β = 1 потенциал Муни–Ривлина переходит в потенциал Трелоара, напряжения и деформации в поперечной плоскости отсутствуют и напряженно-деформированное состояние становится антиплоским. С убыванием $\beta $ от 1 до –1 возникает плоская составляющая цилиндрического напряженно-деформированного состояния. Повышение температуры увеличивает продольную жесткость втулки и повышает сдвиговые касательные напряжения, увеличивая их концентрацию. Этот эффект не зависит от толщины втулки для распределения касательных напряжений и заметно зависит от нее для жесткостных кривых. Эффект от повышения температуры является существенным как для концентрации касательных напряжений, так и для жесткостных кривых.