Известия РАН. Механика твердого тела, 2019, № 6, стр. 85-97

Обобщение критерия мизеса на монокристаллы с гексагональной кристаллической решеткой

А. М. Власова^a, b, *, А. Г. Кесарев^a

^a Институт физики металлов УрО РАН
Екатеринбург, Россия

^b Уральский федеральный университет имени Первого Президента России Б.Н. Ельцина
Екатеринбург, Россия

^* E-mail: alisa@imp.uran.ru

Поступила в редакцию 24.01.2019
После доработки 20.02.2019
Принята к публикации 28.02.2019

DOI: 10.1134/S0572329919060126

Полный текст (PDF)

Аннотация

Получено естественное обобщение критерия текучести Мизеса с учетом анизотропии на монокристаллические материалы с гексагональной кристаллической решеткой. Поставлены краевые задачи для плоской деформации сжатием с противодавлением, для одноосного растяжения, сжатия и для чистого сдвига. Рассмотрен частный случай решения краевых задач для гексагонального магния чистотой 99.9% при комнатной температуре. Определены значения коэффициентов, входящих в функцию текучести и их погрешности. Сопоставлены расчетные и экспериментальные данные σ_0.2% для монокристаллов магния различных ориентировок.

Ключевые слова: магний, пластичность, предел текучести, поверхность текучести, критерий Мизеса, жесткопластическая модель

1. Введение. Для гексагональной плотноупакованной (ГПУ) кристаллической решетки характерны низкая симметрия, большое число деформационных мод, и недостаточность легких мод для обеспечения произвольной пластической деформации (которых требуется не меньше пяти [1]). Все это приводит к сильной зависимости механических свойств от образующейся в ходе пластической деформации текстуры, и резкому изменению механических свойств, в частности, к появлению анизотропии. Широко используемые в практических расчетах критерии текучести Треска и Мизеса [2] при упомянутых условиях становятся неприменимыми. Требуется обобщение данных критериев, с применением новых подходов.

Для описания механических свойств материалов, в настоящее время используются различные физические теории пластичности [3], зачастую приводящие к сложным компьютерным расчетам (кроме простейшей модели Закса) на основе трудоемких экспериментов. Кроме того, они приводят к негладкой поверхности текучести, что создает значительные математические трудности. Модели, опирающиеся на закон Шмида, не всегда выполняются для ГПУ кристаллов, ввиду того, что для них двойникование – действующий и подавляющий механизм пластической деформации при комнатной температуре [4].

Предлагается построение простой модели для описания механических свойств ГПУ металлов, состоящий из трех этапов: 1) нахождение простого феноменологического критерия текучести отдельного монокристалла, 2) использование подходящей процедуры усреднения по ориентировкам монокристаллов для описания свойств поликристалла с заданной текстурой, 3) описание эволюции текстуры.

Простота предложенной модели позволяет использовать для определения коэффициентов функции текучести меньшее число экспериментов, чем для моделей, основанных на законе Шмида и, в дальнейшем позволит построить простые модели поликристаллических ГПУ – материалов.

Целью данной работы явилось нахождение феноменологического критерия текучести гексагональных монокристаллов заданных ориентировок, позволяющего учесть анизотропию пределов текучести в различных направлениях, и при различных схемах нагружения. Постановка задачи и простейшие уравнения, описывающие частные случаи рассмотрены авторами ранее в [5]. Здесь поставлены краевые задачи для плоской деформации, одноосного растяжения и сжатия, чистого сдвига для ГПУ кристаллов, найдены их решения для монокристаллов магния при комнатной температуре. Определены коэффициенты, входящие в функцию текучести для магния при комнатной температуре, приводится оценка погрешностей коэффициентов и погрешностей аппроксимации. Результаты сопоставлены с экспериментальными данными.

2. Постановка задачи. Поскольку кристаллы с ГПУ решеткой относятся к классу симметрии 6/mmm [6], тогда естественным обобщением критерия Мизеса на данный случай является равенство нулю некоторого полинома f(p_{i, j}) зависящего от компонент тензора напряжений p_{i, j} и инвариантного относительно точечной группы 6/mmm. Полином выражается через скалярные инварианты первого и второго порядка симметрического тензора второго ранга, которые имеют вид [6]

(2.1)

${{p}_{{33}}},\quad {{p}_{{11}}} + {{p}_{{22}}},\quad 4{{p}_{{11}}}{{p}_{{22}}} - 4{{({{p}_{{12}}})}^{2}},\quad 4{{({{p}_{{23}}})}^{2}} + 4{{({{p}_{{13}}})}^{2}}$

Удобнее рассматривать эквивалентные инварианты

(2.2)

$\begin{gathered} {{I}_{p}} = {{p}_{{11}}} + {{p}_{{22}}} + {{p}_{{33}}},\quad {{I}_{1}} = {{\left( {{{p}_{{13}}}} \right)}^{2}} + {{\left( {{{p}_{{23}}}} \right)}^{2}},\quad {{I}_{2}} = {{p}_{{33}}} - \left( {{{p}_{{11}}} + {{p}_{{22}}}} \right){\text{/}}2 \\ {{I}_{3}} = {{\left( {{{p}_{{11}}} + {{p}_{{22}}}} \right)}^{2}} + 4[{{\left( {{{p}_{{12}}}} \right)}^{2}} - {{p}_{{11}}}{{p}_{{22}}}] = {{\left( {{{p}_{{11}}} - {{p}_{{22}}}} \right)}^{2}} + 4{{\left( {{{p}_{{12}}}} \right)}^{2}} \\ \end{gathered} $

Здесь p_{i, j} – компоненты тензора напряжений в системе координат кристалла. Ось 3 (OZ) нормальна к базисной плоскости (0001), а оси 1 (OX) и 2 (OY) лежат в базисной плоскости, ортогональны и соответствуют направлениям $[11\bar {2}0]$ и $[1\bar {1}00]$. Выражения (2.2) имеют простой физический смысл: I₁ – это квадрат максимального напряжения сдвига, приложенного к базисной плоскости, I₂ – движущая сила сжатия/растяжения кристалла вдоль кристаллографической оси [0001]; I₃ отвечает за максимальную разность напряжений растяжения–сжатия, действующих в базисной плоскости. Материал при пластической деформации несжимаем [2], а так как инвариант ${{I}_{p}}$ описывает гидростатическое давление, то он не может быть движущей силой пластической деформации и входить явно в f(p_i,_j). Искомый критерий текучести будем искать в виде

(2.3)

$f\left( {{{p}_{{ij}}}} \right) = a + k{{I}_{2}} + {{I}_{1}} + \alpha {{\left( {{{I}_{2}}} \right)}^{2}} + \beta {{I}_{3}} = 0$

где a, k, α, β – коэффициенты модели. В работе [7] для описания деформации анизотропного материала используют критерий Хилла [8]

(2.4)

$\begin{gathered} F{{\left( {{{p}_{{22}}} - {{p}_{{33}}}} \right)}^{2}} + G{{\left( {{{p}_{{33}}} - {{p}_{{11}}}} \right)}^{2}} + H{{\left( {{{p}_{{11}}} - {{p}_{{22}}}} \right)}^{2}} + \\ \, + 2L{{\left( {{{p}_{{23}}}} \right)}^{2}} + 2M{{\left( {{{p}_{{32}}}} \right)}^{2}} + 2N{{\left( {{{p}_{{12}}}} \right)}^{2}} = 1 \\ \end{gathered} $

от которого предлагаемый в данной работе критерий текучести отличается меньшим количеством независимых коэффициентов (благодаря учету группы симметрии) и наличием линейного члена, которого в критерии (2.4) нет, отражающего различие пределов текучести при сжатии и растяжении вдоль кристаллографической оси [0001], обусловленное работой различных деформационных механизмов для этих двух случаев [4, 9].

Выражение (2.3) инвариантно относительно общей группы вращений на произвольный угол вокруг оси Z, и не учитывает анизотропию свойств в базисной плоскости. Коэффициенты a, k, α, β в (2.3), вообще говоря, зависят от гидростатического давления, температуры и химического состава, но здесь данный вопрос не рассматривается. Физический смысл постоянной $a$ очевиден: положим в (2.3) критическое напряжение сдвига в базисной плоскости p₁₃= p_b, остальные p_ij = 0, тогда

(2.5)

${{\left( {{{p}_{{13}}}} \right)}^{2}} = {{\left( {{{p}_{b}}} \right)}^{2}} = - a$

Известно [2], что пластическое течение материала при медленном, квазиравновесном течении описывается уравнениями

(2.6)

${{\nabla }_{i}}{{P}_{{ij}}} = 0,\quad {{e}_{{ii}}} = 0,\quad f\left( {{{P}_{{ij}}}} \right) = 0,\quad {{e}_{{ij}}} = \dot {\theta }\left( t \right)\frac{{\partial f\left( {{{P}_{{ij}}}} \right)}}{{\partial {{P}_{{ij}}}}},\quad {{e}_{{ij}}} = 0.5\left( {{{\nabla }_{i}}{{v}_{j}} + {{\nabla }_{j}}{{v}_{i}}} \right)$

Здесь первое уравнение – условие равновесия, второе – условие несжимаемости, третье – равенство нулю функции текучести, описывающей поверхность текучести, четвертое – ассоциированный закон; ${{e}_{{ij}}}$ – тензор скоростей деформации, ${{v}_{i}}$ – скорость вещества в данной точке, $\theta \left( t \right)$ – произвольная функция времени.

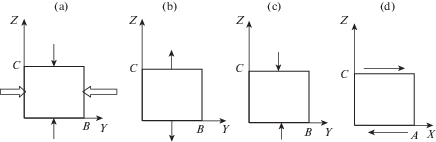
Для математического описания плоской деформации, осуществленной экспериментально в [4, 9–11], рассмотрим прямоугольный параллелепипед размерами $A \times B \times C$ с ребрами, параллельными осям лабораторной системы координат OX, OY и OZ, соответственно (рис. 1,a). Положим, что нормальная компонента скорости на верхней поверхности параллелепипеда направлена вниз, на нижней грани и двух боковых нормальные компоненты скорости равны нулю, силами трения пренебрегаем, и касательные компоненты равны нулю. На плоскостях, параллельных YOZ, напряжения равны нулю, накладываются следующие краевые условия

(2.7)

${{v}_{z}} = 0$, ${{P}_{{xz}}} = 0$, ${{P}_{{yz}}} = 0$ при $Z = 0$; ${{v}_{z}} = {{v}_{0}}$, ${{P}_{{xz}}} = {{P}_{{yz}}} = 0$, при $Z = C$

(2.8)

${{v}_{y}} = 0$, ${{P}_{{yx}}} = 0$, ${{P}_{{yz}}} = 0$ при $Y = 0$ и ${{{v}}_{y}} = 0$, ${{P}_{{yx}}} = 0$, ${{P}_{{yz}}} = 0$ при $Y = B$

(2.9)

${{P}_{{xi}}} = 0$, $i = x,y,z$ при $X = 0$ и $X = A$

Рис. 1

Краевая задача (2.2), (2.3), (2.6)–(2.9) описывает плоскую деформацию (рис. 1,a). Тонкой стрелкой на рис. 1 обозначены приложенные силы, а толстой – ограничения.

Большой научный и практический интерес представляет также свободное растяжение (рис. 1,b) и свободное сжатие (рис. 1,c) монокристаллов. Экспериментально проведены испытания [0001]-монокристаллов магния на сжатие [12, 13], $\left\langle {11\bar {2}0} \right\rangle $-мо-нокристаллов на растяжение [14], теоретически исследуется сжатие и растяжение [0001]-монокристаллов [15]. Свободному растяжению (рис. 1,b) и сжатию (рис. 1,c) соответствует краевая задача (2.2), (2.3), (2.6), (2.7), (2.9), (2.10).

(2.10)

${{P}_{{yi}}} = 0$, $i = x,y,z$, при $Y = 0$ и $Y = B$

Предполагая, что сдвиг происходит в направлении оси OX (рис. 1,d), находим условия

(2.11)

${{v}_{x}} = 0$, ${{P}_{{zz}}} = 0$, ${{P}_{{yz}}} = 0$, при $Z = 0$; ${{v}_{x}} = {{v}_{0}}$, ${{P}_{{zz}}} = {{P}_{{yz}}} = 0$, при $Z = C$

Краевая задача (2.2), (2.3), (2.6), (2.7), (2.9)–(2.11) искомая краевая задача для деформации сдвигом (рис. 1,d).

Для определения условий начала пластической деформации, ограничимся определением тензора напряжений, а тензор деформации вычислять не будем, поскольку для малых времен он не представляет большого интереса, а для больших – не имеет смысла в рамках данной модели из-за резкого изменения прочностных свойств магния при деформации. Краевые условия во всех рассматриваемых краевых задачах можно удовлетворить, полагая тензоры напряжений и деформаций не зависящими от координат

(2.12)

${{P}_{{ij}}}\left( {r,t} \right) = {{P}_{{ij}}},\quad {{e}_{{ij}}}\left( {r,t} \right) = {{e}_{{ij}}}$

3. Метод решения. 3.1. Краевая задача для плоской деформации гексагонального кристалла. Тензор напряжений ${\mathbf{p}}$ ищем в виде

(3.1)

${\mathbf{p}} = - R{{{\mathbf{e}}}_{2}} \otimes {{{\mathbf{e}}}_{2}} - P{{{\mathbf{e}}}_{3}} \otimes {{{\mathbf{e}}}_{3}}$

Краевые условия для касательных напряжений (2.9), (2.10) для (3.1), очевидно, выполняются, условия на скорость (2.11) могут быть удовлетворены выбором функции $\dot {\theta }\left( t \right)$. В силу краевых условий (2.8), (2.9), $\operatorname{R} $ – это напряжение реакции боковых стенок канала, $P$ – напряжение, приложенное к торцам ($Z = 0$, $Z = C$) соответственно (рис. 1,a).

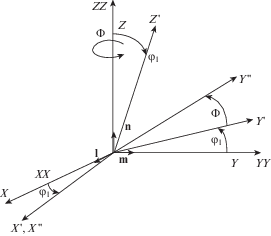
Ориентировка монокристалла относительно лабораторной системы координат описывается углами Эйлера. Пусть оси кристаллита X, Y, Z. Последовательно поворачивая его вокруг OZ на угол ${{\varphi }_{1}}$, вокруг оси X´ на угол $\Phi $, затем вокруг оси Z'' на угол ${{\varphi }_{2}}$ задаем новую ориентировку [16], оси которой мы обозначили выше индексами 1, 2 и 3 (рис. 2). Ввиду цилиндрической симметрии относительно оси 3, параллельной кристаллографическому направлению [0001], положение решетки в лабораторной системе координат описывается двумя углами (${{\varphi }_{1}}$, $\Phi $). В работе [5] использовались обозначения из [17]. Здесь, согласно [18], векторы ортогонального базиса системы координат, связанной с кристаллом, задаются через лабораторный базис в виде (l, m, n) = = $\left( {{{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}},{{{\mathbf{e}}}_{3}}} \right)T$, где матрица перехода от лабораторной системы к системе координат, связанной с кристаллом

(3.2)

$T = \left( {\begin{array}{*{20}{c}} {\cos {{\varphi }_{1}}}&{ - \sin {{\varphi }_{1}}\cos \Phi }&{ - \sin {{\varphi }_{1}}\sin \Phi } \\ {\sin {{\varphi }_{1}}}&{\cos {{\varphi }_{1}}\cos \Phi }&{\cos {{\varphi }_{1}}\sin \Phi } \\ 0&{ - \sin \Phi }&{\cos \Phi } \end{array}} \right)$

Рис. 2

Тогда векторы лабораторной системы координат выражаются через базис, связанный с кристаллом посредством $\left( {{{{\mathbf{e}}}_{1}},{{{\mathbf{e}}}_{2}},{{{\mathbf{e}}}_{3}}} \right) = \left( {{\mathbf{l}},{\mathbf{m}},{\mathbf{n}}} \right){{T}^{{ - 1}}}$, где ${{T}^{{ - 1}}} = {{T}^{T}}$ ввиду ортогональности преобразования. В развернутом виде компоненты тензора

(3.3)

$\begin{gathered} {{{\mathbf{e}}}_{1}} = \cos {{\varphi }_{1}}{\mathbf{l}} - \sin {{\varphi }_{1}}\cos \Phi {\mathbf{m}} - \sin {{\varphi }_{1}}\sin \Phi {\mathbf{n}} \\ {{{\mathbf{e}}}_{2}} = \sin {{\varphi }_{1}}{\mathbf{l}} + \cos {{\varphi }_{1}}\cos \Phi {\mathbf{m}} + \cos {{\varphi }_{1}}\sin \Phi {\mathbf{n}} \\ {{{\mathbf{e}}}_{3}} = - \sin \Phi {\mathbf{m}} + \cos \Phi {\mathbf{n}} \\ \end{gathered} $

Подставляя выражение (3.3) в (3.1), находим тензор напряжений в системе координат связанной с кристаллом

$\begin{gathered} {\mathbf{p}} = - R\left[ {\sin {{\varphi }_{1}}{\mathbf{l}} + \cos {{\varphi }_{1}}\cos \Phi {\mathbf{m}} + \cos {{\varphi }_{1}}\sin \Phi {\mathbf{n}}} \right] \otimes \\ \, \otimes \left[ {\sin {{\varphi }_{1}}{\mathbf{l}} + \cos {{\varphi }_{1}}\cos \Phi {\mathbf{m}} + \cos {{\varphi }_{1}}\sin \Phi {\mathbf{n}}} \right] - p\left[ { - \sin \Phi {\mathbf{m}} + \cos \Phi {\mathbf{n}}} \right] \otimes \\ \end{gathered} $

(3.4)

$\begin{gathered} \, \otimes \left[ { - {\text{sin}}\Phi {\mathbf{m}} + {\text{cos}}\Phi {\mathbf{n}}} \right] = - R{\text{si}}{{{\text{n}}}^{2}}{{\varphi }_{1}}{\mathbf{l}} \otimes {\mathbf{l}} - [R{\text{co}}{{{\text{s}}}^{2}}{{\varphi }_{1}}{\text{co}}{{{\text{s}}}^{2}}\Phi + p{\text{si}}{{{\text{n}}}^{2}}\Phi ]{\mathbf{m}} \otimes {\mathbf{m}} - \\ \, - [R{{\cos }^{2}}{{\varphi }_{1}}{{\sin }^{2}}\Phi + p{{\cos }^{2}}\Phi ]{\mathbf{n}} \otimes {\mathbf{n}} - 0.5R\sin 2{{\varphi }_{1}}\cos \Phi \left( {{\mathbf{l}} \otimes {\mathbf{m}} + {\mathbf{m}} \otimes {\mathbf{l}}} \right) - \\ \end{gathered} $

$\begin{gathered} \, - 0.5R\sin 2{{\varphi }_{1}}\sin \Phi \left( {{\mathbf{l}} \otimes {\mathbf{n}} + {\mathbf{n}} \otimes {\mathbf{l}}} \right) - \\ \, - 0.5[R{{\cos }^{2}}{{\varphi }_{1}}\sin 2\Phi - p\sin 2\Phi ]\left( {{\mathbf{n}} \otimes {\mathbf{m}} + {\mathbf{m}} \otimes {\mathbf{n}}} \right) \\ \end{gathered} $

Ограничение вдоль поперечного направления (2.11) приводит к условию

(3.5)

${{e}_{{22}}} = \theta (t)\frac{{\partial f}}{{\partial {{P}_{{22}}}}} = 0$

Частные производные функции текучести в системе координат, связанной с кристаллом имеют вид

(3.6)

$\begin{gathered} \frac{{\partial f}}{{\partial {{p}_{{11}}}}} = - \frac{k}{2} + \alpha \left[ {\frac{{{{p}_{{11}}} + {{p}_{{22}}}}}{2} - {{p}_{{33}}}} \right] + 2\beta \left( {{{p}_{{11}}} - {{p}_{{22}}}} \right),\quad \frac{{\partial f}}{{\partial {{p}_{{12}}}}} = 8\beta {{p}_{{12}}} \\ \frac{{\partial f}}{{\partial {{p}_{{13}}}}} = 2{{p}_{{13}}},\quad \frac{{\partial f}}{{\partial {{p}_{{23}}}}} = 2{{p}_{{23}}} \\ \frac{{\partial f}}{{\partial {{p}_{{33}}}}} = k + 2\alpha \left[ {{{p}_{{33}}} - \frac{{{{p}_{{11}}} + {{p}_{{22}}}}}{2}} \right] \\ \frac{{\partial f}}{{\partial {{p}_{{22}}}}} = - \frac{k}{2} + \alpha \left[ {\frac{{{{p}_{{11}}} + {{p}_{{22}}}}}{2} - {{p}_{{33}}}} \right] + 2\beta \left( {{{p}_{{22}}} - {{p}_{{11}}}} \right) \\ \end{gathered} $

Подставляя компоненты тензора (3.4) в критерий (2.3), получаем уравнение

(3.7)

$\begin{gathered} - \frac{1}{2}\{ k + \alpha [R(1 - 3{{\cos }^{2}}{{\varphi }_{1}}{{\sin }^{2}}\Phi ) + P(1 - 3{{\cos }^{2}}\Phi )]\} (1 - 3{{\cos }^{2}}{{\varphi }_{1}}{{\sin }^{2}}\Phi ) + \\ \, + 2\beta [P{{\sin }^{2}}\Phi - R{{\sin }^{2}}{{\varphi }_{1}} + R{{\cos }^{2}}{{\varphi }_{1}}{{\cos }^{2}}\Phi ]({{\sin }^{2}}{{\varphi }_{1}} - {{\cos }^{2}}{{\varphi }_{1}}{{\cos }^{2}}\Phi ) - \\ \, - 2\beta R{{\sin }^{2}}2{{\varphi }_{1}}{{\cos }^{2}}\Phi - 2{{\cos }^{2}}{{\varphi }_{1}}{{\sin }^{2}}\Phi [R(1 - {{\cos }^{2}}{{\varphi }_{1}}{{\sin }^{2}}\Phi ) - P{{\cos }^{2}}\Phi ] = 0 \\ \end{gathered} $

а из условия (3.5) с учетом (3.6) – уравнение

(3.8)

$\begin{gathered} a + k\left[ {\frac{R}{2}(1 - 3{{{\cos }}^{2}}{{\varphi }_{1}}{{{\sin }}^{2}}\Phi ) + \frac{P}{2}(1 - 3{{{\cos }}^{2}}\Phi )} \right] + \frac{1}{4}[{{R}^{2}}{{\sin }^{2}}2{{\varphi }_{1}}{{\sin }^{2}}\Phi + \\ \, + {{\sin }^{2}}2\Phi {{(R{{\cos }^{2}}{{\varphi }_{1}} - P)}^{2}}] + \alpha {{\left[ {\frac{R}{2}(1 - 3{{{\cos }}^{2}}{{\varphi }_{1}}{{{\sin }}^{2}}\Phi ) + \frac{P}{2}(1 - 3{{{\cos }}^{2}}\Phi )} \right]}^{2}} + \\ \, + \beta \{ {{[R({{\sin }^{2}}{{\varphi }_{1}} + {{\cos }^{2}}{{\varphi }_{1}}{{\cos }^{2}}\Phi ) + P{{\sin }^{2}}\Phi ]}^{2}} - 4PR{{\sin }^{2}}{{\varphi }_{1}}{{\sin }^{2}}\Phi \} = 0. \\ \end{gathered} $

Система уравнений (3.7), (3.8) позволяет определить критическое напряжение в задаче плоской деформации.

3.2. Краевая задача для одноосного растяжения и сжатия гексагонального кристалла. Примем за ${{p}_{c}}$ и ${{p}_{t}}$ критические сжимающие и растягивающие напряжения соответственно, тогда тензор напряжений $p$ будем искать в виде

(3.9)

${\mathbf{p}} = - {{p}_{c}}{{{\mathbf{e}}}_{3}} \otimes {{{\mathbf{e}}}_{3}}$ либо ${\mathbf{p}} = {{p}_{t}}{{{\mathbf{e}}}_{3}} \otimes {{{\mathbf{e}}}_{3}}$

Подставляя (3.3) в (3.9), а результат – в (2.2) и критерий текучести (2.3), аналогично задаче плоской деформации находим решение для одноосного сжатия (растяжения)

(3.10)

$\left[ {\beta {{{\sin }}^{4}}\Phi + 0.25{{{\sin }}^{2}}2\Phi + \frac{\alpha }{4}{{{(1 - 3{{{\cos }}^{2}}\Phi )}}^{2}}} \right]{{P}^{2}} + \frac{k}{2}(1 - 3{{\cos }^{2}}\Phi )P + a = 0$

при этом ${{p}_{t}} < 0$, ${{p}_{c}} > 0$. Уравнение (3.10) получается из (3.7) при $R = 0$.

3.3. Краевая задача для чистого сдвига гексагонального кристалла

(3.11)

${\mathbf{p}} = p\left( {{{{\mathbf{e}}}_{1}} \otimes {{{\mathbf{e}}}_{3}} + {{{\mathbf{e}}}_{3}} \otimes {{{\mathbf{e}}}_{1}}} \right)$

Подставляя выражения (3.3) в (3.10), находим

(3.12)

$\begin{gathered} f\left( {{{p}_{{ij}}}} \right) = a - \frac{{3p}}{2}\sin {{\varphi }_{1}}\sin 2\Phi + \frac{{9\alpha }}{4}{{p}^{2}}{{\sin }^{2}}{{\varphi }_{1}}{{\sin }^{2}}2\Phi + 4\beta {{p}^{2}}{{\sin }^{2}}\Phi \times \\ \, \times ({{\cos }^{2}}{{\varphi }_{1}} + {{\sin }^{2}}{{\varphi }_{1}}{{\cos }^{2}}\Phi ) + {{p}^{2}}({{\cos }^{2}}\Phi {{\cos }^{2}}{{\varphi }_{1}} + {{\sin }^{2}}{{\varphi }_{1}}{{\cos }^{2}}2\Phi ) = 0 \\ \end{gathered} $

3.4. Частные решения краевых задач в общем виде. Мы обозначаем деформационные схемы, так, как это принято в [9], где A и B – сжатие вдоль [0001] с противодавлением в направлении$\left\langle {10\bar {1}0} \right\rangle $ и $\left\langle {11\bar {2}0} \right\rangle $ соответственно, C и E – сжатие вдоль $\left\langle {10\bar {1}0} \right\rangle $ с противодавлением в направлении [0001] и $\left\langle {11\bar {2}0} \right\rangle $ соответственно, D и F – сжатие вдоль $\left\langle {11\bar {2}0} \right\rangle $ с противодавлением в направлении [0001] и $\left\langle {10\bar {1}0} \right\rangle $ соответственно, G – сжатие вдоль направления под углом Φ = π с OZ с противодавлением в направлении $\left\langle {10\bar {1}0} \right\rangle $. Одноосное растяжение в направлении $\left\langle {11\bar {2}0} \right\rangle $ обозначено в работе как схема tx, свободное одноосное сжатие и растяжение вдоль [0001] обозначается сz и tz соответственно. Статистическая обработка данных экспериментальных деформационных кривых из [9, 14, 19] проведена с доверительной вероятностью 0.95 и коэффициентом Стьюдента 2.8 и 3.2. Исходные эмпирические данные будут приведены в табл. 2 вместе с результатами расчетов согласно построенной модели.

Таблица 1

Коэфф.	$\lambda $	$\mu $	$\varepsilon $	$a$	$\alpha $	$\beta $	k
	1.32	4.94 × 10^–2	3.49 × 10^–5	–0.28	7.07 × 10^–4	5.36 × 10^–4	6.37 × 10^–2
$\delta $, %	12.3	25.9	20.5	20	46.4	58.7	48.6

Таблица 2

Схема нагру- жения, i	$p_{i}^{{э.}}$, МПа	$p_{i}^{{р.}}$, МПа	$\Delta p_{i}^{{э.}}$, МПа	$\Delta p_{i}^{{р.}}$, МПа	$\sum {\Delta p_{i}^{{э.}} + \Delta p_{i}^{{р.}}} $, МПа	${\text{\|}}p_{i}^{{р.}} - p_{i}^{{э.}}{\text{\|}}$, МПа
А	94.24 [9]	102.03	2.13	4.38	6.51	7.74
B	110.28 [9]	102.03	1.86	4.38	6.24	8.23
C	63.73 [9]	56.63	4.17	30.07	34.24	7.07
D	43.28 [9]	56.63	0.81	30.07	30.88	13.31
E	10.67 [9]	11.80	2.74	2.38	5.12	1.16
F	13.46 [9]	11.80	1.7	2.38	4.08	1.64
G	2.68 [9]	1.6	0.59	0.62	1.21	1.08
tx	91.66 [14]	52.28	1.54	6.48	8.02	39.38
bm	0.5 [19]	0.533	0.05	0.05	0.10	0.03
cz	110.3*	94.45	–	1.98	1.98	15.85
tz	15.5*	4.25	–	1.14	1.14	11.25

* – теоретичеcкие данные [15].

Ввиду цилиндрической симметрии критерия текучести, схемы A и B, C и D, E и F неразличимы, и в данной работе рассматриваются усредненные схемы AB , CD, EF. Пределы текучести для усредненных схем принимаются как среднее $\sigma _{{0.2}}^{{AB}}$ = p_AB = = $(\sigma _{{0.2}}^{A} + \sigma _{{0.2}}^{B}){\text{/}}2$, $\sigma _{{0.2}}^{{CD}} = {{p}_{{CD}}} = (\sigma _{{0.2}}^{C} + \sigma _{{0.2}}^{D}){\text{/}}2$, $\sigma _{{0.2}}^{{EF}} = {{p}_{{EF}}} = (\sigma _{{0.2}}^{E} + \sigma _{{0.2}}^{F}){\text{/}}2$.

Введем безразмерные переменные Q и коэффициенты µ, λ, ε для удобства решения и анализа

(3.13)

$Q = \frac{\alpha }{k}p,\quad \mu = \frac{\varepsilon }{\alpha },\quad \lambda = \frac{\alpha }{\beta },\quad \varepsilon = {{\left( {\frac{\alpha }{k}} \right)}^{2}} \cdot \left| a \right| \ll 1$

Решая систему уравнений (3.7), (3.8), при $\Phi = 0^\circ $, ${{\varphi }_{1}} = 0^\circ $, а также при $\Phi = 90^\circ $, ${{\varphi }_{1}} = 90^\circ $ находим, что критические напряжения Q для плоской деформации по усредненным схемам AB и EF описываются одним уравнением

(3.14)

${{Q}^{2}} - Q - \lambda {\text{/}}16 - \mu \lambda {\text{/}}4 - \mu = 0$

причем

(3.15)

${{Q}_{{AB}}} = \frac{{1 + \sqrt {1 + \lambda {\text{/}}4 + \mu \lambda + 4\mu } }}{2} > 0$

(3.16)

$ - {{Q}_{{EF}}} = \frac{{1 - \sqrt {1 + \lambda {\text{/}}4 + \mu \lambda + 4\mu } }}{2} < 0$

Решая систему уравнений (3.7), (3.8) при $\Phi = 90^\circ $, ${{\varphi }_{1}} = 0^\circ $ получаем решение ${{p}_{{CD}}}$ для краевой задачи плоской деформации по схеме CD

(3.17)

$p_{{CD}}^{2} = \frac{1}{\beta }\left( {\frac{{{{k}^{2}}}}{{4\alpha }} - a} \right)$

Или в безразмерной форме

(3.18)

${{Q}_{{CD}}} = \sqrt {\lambda \left( {0.25 + \mu } \right)} $

Решая уравнение (3.10) при $\Phi = 90^\circ $, ${{\varphi }_{1}} = 90^\circ $ получаем напряжение ${{Q}_{{tx}}}$ свободного растяжения вдоль OX

(3.19)

${{Q}_{{tx}}} = \frac{{1 + \sqrt {1 + 4\mu \left( {1 + 4{\text{/}}\lambda } \right)} }}{{1 + 4{\text{/}}\lambda }}$

Критические напряжения сжатия ${{p}_{{cz}}}$ и растяжения ${{p}_{{tz}}}$ вдоль Z находятся как абсолютная величина корней уравнения (3.10) при $\Phi = 0^\circ $ и любого ${{\varphi }_{1}}$

(3.20)

${{p}_{{cz}}} = \frac{k}{\alpha }{{Q}_{{cz}}},\quad {{p}_{{tz}}} = \frac{k}{\alpha }{{Q}_{{tz}}},\quad {{Q}_{{cz}}} = \frac{{1 + \sqrt {1 + 4\mu } }}{2},\quad {{Q}_{{tz}}} = \frac{{\sqrt {1 + 4\mu } - 1}}{2}$

Из (3.14) и формул Виета следует связь между ${{Q}_{{AB}}}$ и ${{Q}_{{EF}}}$

(3.21)

${{Q}_{{AB}}} - {{Q}_{{EF}}} = 1,\quad {{Q}_{{AB}}}{{Q}_{{EF}}} = \lambda {\text{/}}16 + \mu \lambda {\text{/}}4 + \mu $

Аналогично получаем взаимосвязь между ${{Q}_{{СZ}}}$ и ${{Q}_{{TZ}}}$

(3.22)

${{Q}_{{cz}}} - {{Q}_{{tz}}} = 1,\quad {{Q}_{{cz}}}{{Q}_{{tz}}} = \mu $

Из (3.21), (3.22) и (3.13) следует связь между напряжениями текучести для 4 схем в исходных переменных

(3.23)

${{p}_{{cz}}} - {{p}_{{tz}}} = {{p}_{{AB}}} - {{p}_{{EF}}} = k{\text{/}}\alpha = {{p}_{{ABEF}}}$

Кроме того, из формул (3.18), (3.21), (3.22) находим

(3.24)

${{Q}_{{AB}}}{{Q}_{{EF}}} - Q_{{CD}}^{2}{\text{/}}4 = {{Q}_{{cz}}}{{Q}_{{tz}}} = \mu ,\quad {{p}_{{AB}}}{{p}_{{EF}}} - p_{{CD}}^{2}{\text{/}}4 = {{p}_{{cz}}}{{p}_{{tz}}}$

Величины ${{p}_{{AB}}}$, ${{p}_{{EF}}}$, ${{p}_{{CD}}}$, ${{p}_{{cz}}}$, ${{p}_{{tz}}}$ выбраны положительными, ввиду физического смысла напряжений текучести. Нетрудно видеть, что неотрицательными являются ${{Q}_{i}}$ и коэффициенты $\mu $ и $\lambda $.

3.5. Оценки коэффициентов критерия текучести для чистого магния. Критическое напряжение сдвига в базисной плоскости ${{p}_{{bm}}}$ соответствует ориентировке с максимальным фактором Шмида. Тогда напряжение течения${{p}_{b}} = {{p}_{{bm}}}{\text{/cos}}\psi $, где $\psi $ – угол с ближайшим направлением базисного скольжения $\psi \in [0,30^\circ ]$, следовательно, максимальное p_bM критическое напряжение сдвига в базисной плоскости

(3.25)

${{p}_{{bM}}} = 2{{p}_{{bm}}}{\text{/}}\sqrt 3 $

Выберем ${{p}_{b}} = {{p}_{{bs}}}$, требуя минимума среднего квадрата относительной погрешности ${{p}_{b}}$

(3.26)

${{p}_{{bs}}} = {{\left( {\frac{{{{p}_{b}} - {{p}_{{bM}}}}}{{{{p}_{{bM}}}}}} \right)}^{2}} + {{\left( {\frac{{{{p}_{b}} - {{p}_{{bm}}}}}{{{{p}_{{bm}}}}}} \right)}^{2}} \to \min $

Дифференцируя (3.26) по ${{p}_{b}}$ и приравнивая производную к нулю, находим

(3.27)

${{p}_{{bs}}} = {{p}_{{bM}}}{{p}_{{bm}}}\frac{{{{p}_{{bM}}} + {{p}_{{bm}}}}}{{{{{\left( {{{p}_{{bM}}}} \right)}}^{2}} + {{{\left( {{{p}_{{bm}}}} \right)}}^{2}}}} = \frac{{1{\text{/}}{{p}_{{bM}}} + \sqrt 3 {\text{/}}\left( {2{{p}_{{bm}}}} \right)}}{{1{\text{/}}{{{\left( {{{p}_{{bm}}}} \right)}}^{2}} + 3{\text{/}}{{{\left( {2{{p}_{{bm}}}} \right)}}^{2}}}} = \frac{{4 + 2\sqrt 3 }}{7}{{p}_{m}}$

Поскольку анизотропия σ_0.2% для различных ориентировок различается на два порядка, то минимизация среднеквадратичной абсолютной погрешности не имеет смысла. Естественным путем нахождения коэффициентов $\lambda ,\;\mu $ будет минимизация среднего квадрата относительной погрешности целевой функции, что может рассматриваться разновидностью метода наименьших квадратов с введением весовых коэффициентов $1{\text{/}}{{p}_{i}}$, где $p_{i}^{{i \in \{ A,B,C,D,T,F,tx\} }}$ – измеренные значения соответствующих напряжений текучести.

Целевую функцию U запишем в виде

(3.28)

$U = \sum\limits_{i \in \left\{ {A,B,C,D,E,F,tx} \right\}} {{{{\left\{ {\left[ {{{Q}_{i}}\left( {\lambda ,\mu } \right) - {{Q}_{{i0}}}} \right]{\text{/}}{{Q}_{{i0}}}} \right\}}}^{2}}} $

что представляет собой средний квадрат относительной погрешности. Здесь ${{Q}_{{i0}}}$ – безразмерные пределы текучести, взятые из экспериментальных $\sigma _{{0.2}}^{{i \in \{ A,B,C,D,E,F,tx\} }}$, путем умножения на (3.23), а ${{Q}_{i}}\left( {\lambda ,\mu } \right)$ – соответствующие значения ${{Q}_{i}}$, вычисленные на основе выбранных значений параметров $\lambda ,\mu $ по формулам (3.15), (3.16), (3.18), (3.19). Минимизация целевой функции (3.28) с использованием функции fminsearch (Octave 4.0.0) дает хорошую сходимость. На рис. 3 приведены линии уровня целевой функции (3.28) в области$\mu \in \left[ {0,0.1} \right]$, $\lambda \in \left[ {0,3} \right]$.

Рис. 3

Исходя из значений ${{p}_{{bs}}}$, ${{p}_{{ABEF}}}$, $\lambda $, $\mu $ коэффициенты критерия определяются по формулам

(3.29)

$a = - {{({{p}_{{bs}}})}^{2}},\quad \varepsilon = \frac{{p_{b}^{2}}}{{p_{{ABEF}}^{2}}},\quad \alpha = \varepsilon {\text{/}}\mu ,\quad \beta = \varepsilon {\text{/(}}\mu \lambda {\text{)}},\quad k = \alpha {{p}_{{ABEF}}}$

Определение погрешностей коэффициентов $\lambda ,\mu $ проводилось путем [20] минимизации целевой функции (3.28) для 100 различных наборов исходных данных, на которые налагались возмущения, распределенные по нормальному закону с дисперсиями $D{{Q}_{i}}$, где $i \in \{ A,B,C,D,E,F,tx\} $. Дисперсии $D\lambda $ и $D\mu $ получены как квадрат стандарта выборки из 100 полученных таким образом $\lambda $ и $\mu $. Ввиду (3.29) $\varepsilon = f({{p}_{{bs}}},{{p}_{{ABEF}}})$, при этом ${{p}_{{ABEF}}}$ и ${{p}_{{bs}}}$ являются независимыми [21] (экспериментальные данные), поэтому погрешность δε равна

(3.30)

$\delta \varepsilon = 2\sqrt {{{{\left( {\delta {{p}_{{bm}}}} \right)}}^{2}} + {{{\left( {\delta {{p}_{{ABEF}}}} \right)}}^{2}}} $

(3.31)

${{\delta }^{2}}{{p}_{{ABEF}}} = \frac{{{{t}^{2}}({{s}^{2}}{{p}_{A}} + {{s}^{2}}{{p}_{B}} + {{s}^{2}}{{p}_{E}} + {{s}^{2}}{{p}_{F}})}}{{5{{{\left( {{{p}_{A}} + {{p}_{B}} - {{p}_{E}} - {{p}_{F}}} \right)}}^{2}}}}$

где ${{s}^{2}}{{p}_{i}}$ – квадрат стандарта соответствующей выборки, t – коэффициент Стьюдента.

Так как остальные коэффициенты (3.29) выражаются через $\varepsilon $, ${{p}_{{ABEF}}}$ и коэффициенты $\lambda ,\mu $ которые, в свою очередь сложным образом зависят от исходных данных, то относительные погрешности $\delta \alpha ,\;\delta \beta ,\;\delta k,\;\delta a$ других коэффициентов выражаются как

(3.32)

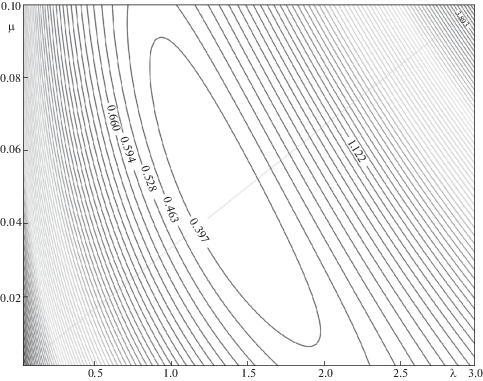
$\delta \alpha = \delta \varepsilon + \delta \mu ,\quad \delta \beta = \delta \varepsilon + \delta \mu + \delta \lambda ,\quad \delta k = \delta \varepsilon + \delta \mu + \delta {{p}_{{ABEF}}},\quad \delta a = 2\delta {{p}_{{bm}}}$

Значения коэффициентов $\mu ,\;\lambda ,\;\varepsilon ,\;a,\;\alpha ,\;\beta ,\;k$ и их погрешностей ${{\delta }_{i}}$ приводятся в табл. 1.

3.6. Верификация модели. По формулам (3.15)–(3.17), (3.19) рассчитаны значения напряжений текучести для схем, которые использовались при построении модели ${{p}_{{AB}}}$, ${{p}_{{CD}}}$, ${{p}_{{EF}}}$, ${{p}_{{tx}}}$, а также схем p_G, p_tz, p_cz.

Напряжения для сжатия с боковым противодавлением по схеме G равны и описываются уравнениями (3.7), (3.8), которые при $\Phi = \pi {\text{/}}3$, R = 0 дают

(3.33)

${{p}_{G}} = \sqrt {\frac{{{{k}^{2}}}}{{\alpha + 4\beta }} - 4a} $

Свободное сжатие (растяжение) вдоль [0001] описывается уравнением (3.10) при $\Phi = 0$, которое дает

(3.34)

$a - k{{p}_{{cz,tz}}} + \alpha p_{{cz,tz}}^{2} = 0$

Определим погрешности нахождения напряжений текучести для каждой из схем.

Так, дифференцируя уравнение (3.14), находим

(3.35)

$d{{Q}_{{AB,EF}}} = \frac{{\left( {1{\text{/}}16 + \mu {\text{/}}4} \right)d\lambda + \left( {\lambda {\text{/}}4 + 1} \right)d\mu }}{{\left| {2{{Q}_{{AB,EF}}} - 1} \right|}}$

откуда относительные погрешности $\delta {{Q}_{{AB,EF}}}$ выражаются как

(3.36)

$\delta {{Q}_{{AB,EF}}} = \frac{{\left( {1{\text{/}}16 + \mu {\text{/}}4} \right)\lambda \delta \lambda + \left( {\lambda {\text{/}}4 + 1} \right)\mu \delta \mu }}{{\left| {2{{Q}_{{AB}}} - 1} \right|{{Q}_{{AB,EF}}}}}$

Аналогично определяются относительные погрешности для других схем.

Выражения для относительной погрешности рассчитанных критических напряжений различных схем p_i имеют вид

(3.37)

$\delta {{p}_{i}} = \delta {{Q}_{i}} + \delta {{p}_{{ABEF}}}$

Введем абсолютные погрешности измерения $\Delta p_{i}^{{э.}}$, расчета $\Delta p_{i}^{{р.}}$, аппроксимации ${\text{|}}p_{i}^{{р.}} - p_{i}^{{э.}}{\text{|}}$, суммарную погрешность измерения и расчета $\sum {\Delta p_{i}^{{э.}} + \Delta p_{i}^{{р.}}} $ напряжений текучести для схем i, результаты расчетов $p_{i}^{{р.}}$ вместе с экспериментальными значениями напряжений $p_{i}^{{э.}}$приводятся в табл. 2.

Анализ результатов. Из пределов текучести σ_0.2% и σ_1% [11] приняты в качестве феноменологических значений, используемых при построении модели, σ_0.2 с минимальным значением остаточной пластической деформации, чтоб минимизировать упрочнение и исключить все моды, кроме включающейся сразу. Имеется значительный разброс (0.46–0.81 МПа) [19, 22, 23] для величины критического напряжение сдвига P_b в базисной плоскости, в данной работе используются только данные из [19].

При $\beta \to \infty $ и фиксированных остальных коэффициентах, из (3.13) следует, что $\lambda \to 0$, тогда, используя решения (3.15)–(3.17), (3.19) легко показать, что

(3.38)

${{p}_{{AB}}} \to {{p}_{{cz}}},\quad {{p}_{{EF}}} \to {{p}_{{tz}}},\quad {{p}_{{CD}}} \to 0,\quad {{p}_{{tx}}} \to 0$

При $\beta \to 0$ и фиксированных остальных параметрах, из (3.13) следует: $\lambda \to \infty $, из (3.15)–(3.17) следует, что ${{p}_{{AB}}}$, ${{p}_{{EF}}}$, ${{p}_{{CD}}}$ неограниченно возрастают, из (3.19) и (3.34) легко видеть, что при $\beta \to 0$

(3.39)

${{p}_{{tx}}} \to 2{{p}_{{cz}}}$

Таким образом, $\beta $ как коэффициент перед инвариантом I₃, характеризует способность системы совершать плоскую деформацию в базисной плоскости. При отсутствии вклада скольжения в базисной плоскости (β = 0) невозможны деформации по схемам AB , CD, EF, а свободное растяжение вдоль оси OX требует усилия вдвое большего, чем при свободном сжатии в перпендикулярном направлении, так как, по-видимому, в обоих случаях происходит сжатие вдоль оси OZ, но во втором случае растяжение идет одинаково в двух взаимно перпендикулярных направлениях (OX, OY), что легче, чем когда растяжение идет только в одном направлении.

Сравнение погрешностей аппроксимации с суммарной погрешностью (табл. 2) показывает, что для схем C, D погрешность аппроксимации значительно меньше суммарной; для схем A, B, E, F, G они одного порядка, и хуже всего аппроксимируется схемы tx. К сожалению, эмпирические данные для построения модели взяты из различных работ, состав размеры образцов, условия их получения и концентрация дефектов, внесенных при механической обработке для них различаются, что влечет изменение их механических свойств. Наличие между стенками канала и образцом силы трения при плоской деформации, сжатии и отсутствие ее при растяжении также является источником ошибок. С целью минимизации ошибок, обусловленных различием свойств, нужны, по-видимому, работы по проведению экспериментов над монокристаллами, выращенными в одинаковых условиях.

Теоретико-групповой подход показывает, что ограничиваясь полиномами второй степени улучшить данный критерий текучести нельзя. Такой критерий приводит к замене гексагональной системы цилиндрической, что не позволяет различить схемы нагружения A и B, C и D, E и F соответственно. Больше всего различаются критерии текучести для схем C и D . Наилучшее приближение этих значений одним (наименьшая относительная погрешность) находится из условия

(3.40)

$\frac{{{{p}_{C}} - p_{{CD}}^{'}}}{{{{p}_{C}}}} = \frac{{p_{{CD}}^{'} - {{p}_{D}}}}{{{{p}_{D}}}}$

где $p_{{CD}}^{'}$ – это значение напряжений, которое дает минимальную относительную погрешность. Из (3.40) следует

(3.41)

$p_{{CD}}^{'} = \frac{{2{{p}_{C}}{{p}_{D}}}}{{{{p}_{C}} + {{p}_{D}}}},\quad \delta p_{{CD}}^{'} = \frac{{{{p}_{C}} - {{p}_{D}}}}{{{{p}_{C}} + {{p}_{D}}}}$

И величина относительной погрешности $\delta p_{{CD}}^{'}$ составляет 19.1% , значит подход, основанный на полиномах второго порядка, не позволяет получить большую точность. В нашей предыдущей работе [5] была показана хорошая аппроксимация в области, где действующей модой является базисное скольжение, а в работе [24] показано, что при растяжении и сжатии эта область является преобладающей.

Благодаря сильной анизотропии пределов текучести монокристалов магния, поликристалл магния с хаотической ориентировкой зерен должен демонстрировать сложное композитоподобное поведение, которое объясняет многие его свойства, в частности, большое различие пределов текучести у литого (20 МПа), деформированного (186 МПа) и для отожженного (98 МПа) состояний. Предложенный критерий текучести можно применять к кристаллам любых гексагональных металлов, используя эмпирические данные для σ_0.2% требуемого металла, при этом коэффициенты модели будут отличаться от рассчитанных в данной работе. Используя усреднение по ориентировкам кристаллитов можно получить оценки для напряжений текучести текстурированных ГПУ металлов.

Заключение. Предложен наиболее общий критерий текучести, согласующийся с гексагональной симметрией. В отличие от критерия Хилла, предложенный критерий учитывает как основную анизотропию монокристалла магния, связанную с его ориентировкой, так и различие пределов текучести при сжатии и растяжении вдоль этой оси. Показано, что критерии, основанные на полиномах второго порядка, не позволяют учесть анизотропию, связанную с вращением вокруг гексагональной оси. На основе предложенной модели определены пределы текучести для ряда простых схем нагружения, встречающихся в экспериментальных работах, установлены связи между ними. На основе данных, имеющихся в литературе, найдены коэффициенты критерия для случая магния чистотой 99.9% при комнатной температуре, оценены их погрешности, полученные решения сопоставлены с экспериментальными данными. При помощи критерия, основанного на полиномах второго порядка погрешность, по-видимому, не может быть получена менее, чем 19%.

Работа выполнена в рамках государственного задания по теме “Давление” № АААА-А18-118020190104-3.

Список литературы

Полухин П.И., Горелик С.С., Воронцов В.К. Физические основы пластической деформации. М.: Металлургия, 1982. 584 с.
Седов Л.И. Механика сплошной среды, Т.2. М.: Наука, 1994. 560 с.
Трусов П.В., Волегов П.С., Кондратьев Н.С. Физические теории пластичности. Пермь: Издательство пермского национального исследовательского политехнического университета, 2013. 244 с.
Wonsiewicz B.C., Backofen W.A. Plasticity of magnesium crystals // Trans AIME. 1967. V. 239. P. 1422–1431.
Власова А. М., Кесарев А.Г. Модель деформации монокристаллического магния // Известия вузов. Физика. 2018. Т. 61. № 7. С. 68–78.
Теодосиу К. Упругие модели дефектов в кристаллах. М.: Мир, 1985. 352 с.
Loginov Yu.N., Solovei V.D., Kotov V.V. Transformation of the yielding condition during the deformation of HCP metallic materials // Russian metallurgy (Metally). 2010. V. 2010. № 3. P. 235–240.
Хилл Р. Математическая теория пластичности. М.: Гостехиздат, 1956. 408 с.
Kelly E.W., Hosford W.F. Plane-strain compression of magnesium and magnesium alloy crystals // Transactions of the metallurgical society of AIME. 1968. V. 242. P. 5–13.
Molodov K.D., Al-Samman T., Molodov D.A. On the diversity of the plastic response of magnesium in plane strain compression // Materials Science & Engineering A. 2016. V. 651. P. 63–68.
Chapius A., Driver J.H. Temperature dependency of slip and twinning in plane strain compressed magnesium single crystals // Acta Materialia. 2011. V. 59. P. 1986–1994.
Obara T., Yoshinaga H., Morozumy S. $\left\{ {11\bar {2}2} \right\}\left\langle {\bar {1}\bar {1}23} \right\rangle $ slip system in magnesium // Acta metallurgica. 1973. V. 21. P. 845–853.
Yoshinaga H., Horiuchi R. Deformation mechanisms in magnesium single crystals compressed in the direction parallel to hexagonal axis // Trans. JIM. 1963. V. 4. P. 1–8.
Tonda H., Ando S. Effect of Temperature and Shear Direction on Yield Stress by $\left\{ {11\bar {2}2} \right\}\left\langle {\bar {1}\bar {1}23} \right\rangle $ Silp in HCP Metals // Met. and Mater. Transactions A. 2002. V. 32 A. P. 831–836.
Zhang J., Joshi S.P. Phenomenological crystal plasticity modeling and detailed micromechanical investigations of pure magnesium // J. Mech. Phys. Solids. 2012. V. 60. P. 945–972.
Уманский Я.С., Скаков Ю.А., Иванов А.Н., Расторгуев Л.Н. Кристаллография, рентгенография и электронная микроскопия. М.:Металлургия, 1982. 631 с.
Курош А.Г. Курс высшей алгебры. М.: Государственное издательство физ.-мат. литературы, 1962. 431 с.
Федорчук В.В. Курс аналитической геометрии и линейной алгебры. М.: Издательство Московского Государственного Универститета, 1990. 328 с.
Shelly W. F., Nash R.R. Mechanical Properties of Magnesium Monocrystals // Transactions of the Metallurgical Society of AIME. 1960. V. 218. P. 416–423.
Калиткин Н.Н. Численные методы. СПб: БХВ – Петербург, 2011. 586 с.
Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Лаборатория Базовых Знаний, 2001. 632 с.
Hutchinson W.B., Barnett M.R. Effective values of critical resolved shear stress for slip in polycrystalline magnesium and other hcp metals // Scripta Materialia. 2010. V. 63. P. 737–740.
Yoshinaga H., Hotiuchi R. Work hardening characteristics of the basal slip of magnesium single crystals // Trans. JIM. 1962. V. 3. P. 220–226.
Kesarev A.G., Vlasova A.M. Modified Sachs’s model of deformation of polycrystalline magnesium // Russian Physics Journal. 2017. V. 60. № 5. P.890-899.
Севастьянов В.А. Курс теории вероятностей и математической статистики. М.: Наука, 1982. 256 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал