Известия РАН. Механика твердого тела, 2019, № 6, стр. 38-46

ОБ ОДНОМ ДИФФЕРЕНЦИАЛЬНОМ ОГРАНИЧЕНИИ В АСИММЕТРИЧНЫХ ТЕОРИЯХ МЕХАНИКИ РАСТУЩИХ ТЕЛ

Е. В. Мурашкин^a, *, Ю. Н. Радаев^a, **

^a Институт проблем маханики им. А.Ю. Ишлинского РАН
Москва, Россия

^* E-mail: murashkin@ipmnet.ru
^** E-mail: radayev@ipmnet.ru

Поступила в редакцию 09.05.2019
После доработки 20.05.2019
Принята к публикации 30.05.2019

DOI: 10.1134/S0572329919060102

Аннотация

В работе рассматривается проблема постановки граничных условий в асимметричных задачах механики растущих тел. Исследуются, прежде всего, условия на поверхности наращивания, которые являются важнейшими с точки зрения полноты теории. При выводе соотношений на поверхности наращивания используются результаты, известные из алгебры рациональных инвариантов. Получены геометрически и механически непротиворечивые дифференциальные ограничения на поверхности наращивания, справедливые для весьма широкого круга материалов и метаматериалов. Исследуются несколько вариантов определяющих соотношений на поверхности роста различных уровней сложности. Сформулированные дифференциальные ограничения подразумевают экспериментальную идентификацию нескольких определяющих функций. По этой причине полученные результаты могут служить общей основой в прикладных исследованиях по механике растущих тел с асимметричным тензором напряжений.

Ключевые слова: 3D-печать, поверхностный рост, напряжение, определяющее уравнение, рациональный инвариант

Введение. Традиционные методы изготовления изделий сложной формы подразумевают разнообразные технологические процессы обработки, как связанные со снятием материала, так и основанные на синтезе изделий путем последовательного нанесения материала на поверхность произвольной формы. Изготовление изделий путем добавления нового материала широко используется в современной инженерной практике [1]. К таким способам аддитивного производства относятся: лазерная стереолитография [2], селективное лазерное спекание, электронно-лучевая плавка, моделирование методом наплавления, метод многоструйного моделирования, изготовление объектов с использованием ламинирования, 3D-печать [3], компьютерная осевая литография, послойное бетонирование [4].

3D Printing (3DP) аналогичен технологии селективного лазерного спекания, только здесь не используется плавление: объект формируется из порошкового материала путем склеивания, с использованием струйной печати для нанесения жидкого клея. Технология 3D-печати позволяет производить цветное моделирование за счет добавления в клей красителей (непосредственно во время печати), или за счет использования нескольких печатающих головок с цветным клеем [3].

Послойное бетонирование конструкций также относится к методам аддитивных технологий [4]. Послойное бетонирование можно разделить на два вида, в зависимости от времени между заливками. В случае “горячего шва” перерыв между слоями меньше 12 часов. Второй тип послойной заливки – “холодный шов”. В этом случае необходимо дождаться полного затвердевания предыдущего слоя для исключения возможного растреcкивания не затвердевшей части под действием вновь добавленного материала.

Методы аддитивного производства, описанные выше, в основе своей используют хорошо известные природные процессы: аккреция космических объектов, формирование лавин и ледников, процессы роста кристаллов, рост атеросклеротических бляшек [5–7]. Для всех этих явлений характерен поверхностный рост. Рост атеросклеротической бляшки можно описать как процесс изначальной инфильтрации компонентов плазмы крови в тонкий приповерхностный слой внутренней стенки артерии. Рост зародыша кристалла происходит путем присоединения к его поверхности отдельных атомов или их групп.

Решение каждой конкретной задачи наращивания деформируемых тел представляет собой самостоятельную и трудоемкую проблему [8–14]. Существенной особенностью постановки краевых задач механики наращиваемых тел является постановка граничных условий на поверхности раздела исходного материала и наращиваемой части [15–17]. В настоящей работе будут рассматриваться несколько вариантов определяющих соотношений на поверхности наращивания, начиная от простейших соотношений (см. известную книгу Г.И. Быковцева: [17], С. 288–292) до некоторых существенных обобщений теории. При изложении будем придерживаться терминологии и обозначений, принятых в публикациях [17–21].

1. Основные соотношения в скоростях асимметричной механики растущих тел. Основные соотношения в механике растущих тел чаще всего удобно записывать в скоростях. В этом случае уравнения равновесия в произвольной пространственной системе криволинейных координат ${{x}^{k}}$ $(k = 1,2,3)$ для асимметричного тензора напряжений можно представить в операторной

(1.1)

$\nabla \cdot ({{\partial }_{ \cdot }}{\mathbf{\tau }}) + {{\partial }_{ \cdot }}{\mathbf{X}} = 0$

или координатной форме

(1.2)

${{\nabla }_{j}}({{\partial }_{ \cdot }}{{\tau }^{{ji}}}) + {{\partial }_{ \cdot }}{{X}^{i}} = 0$

где ${{\tau }^{{ij}}}$ – тензор напряжений Коши, ${{X}^{i}}$ – объемные силы, ${{\nabla }_{j}}$ – оператор ковариантного дифференцирования по пространственной метрике, ${{\partial }_{ \cdot }}$ – производная по времени при фиксированных координатах x^k. Мы подразумеваем асимметричность тензора напряжений ${{\tau }^{{ij}}}$:

(1.3)

${{\tau }^{{ij}}} \ne {{\tau }^{{ji}}}$

Для замыкания системы дифференциальных уравнений необходимо задать определяющие соотношения, связывающие скорости напряжений и деформаций по закону, характерному для того или иного тела/процесса. Модель деформирования растущего тела следует также дополнить граничными условиями на поверхности наращивания.

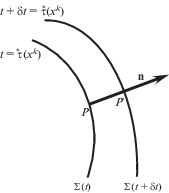
Зададим перемещающуюся в пространстве поверхность наращивания $\Sigma $ в неявном виде уравнением

(1.4)

$t = \mathop \tau \limits^* ({{x}^{i}})$

В этом случае единичная нормаль n к поверхности $\Sigma $, направленная в сторону ее распространения, вычисляется через вектор пространственного градиента от (1.4), т.е.

(1.5)

${{n}_{i}} = c{{\partial }_{i}}\mathop \tau \limits^* ,\quad c = {\text{|}}\nabla \mathop \tau \limits^* {{{\text{|}}}^{{ - 1}}}$

где c – линейная скорость поверхности наращивания в направлении нормали $n$, которая определяется согласно (рис. 1)

(1.6)

$c = \mathop {\lim }\limits_{\delta t \to 0} \frac{{{\text{|}}\overleftarrow {PP{\kern 1pt} '} {\text{|}}}}{{\delta t}}$

Рис. 1

Для восстановления напряжений по известным скоростям можно воспользоваться формулами, данными в [17]:

(1.7)

${{\tau }^{{ij}}} = \int\limits_{\mathop \tau \limits^* }^t \,[\partial \cdot {{\tau }^{{ij}}}({{x}^{k}},t{\kern 1pt} ')]dt{\kern 1pt} '\; + \mathop \tau \limits^* {{{\kern 1pt} }^{{ij}}}({{x}^{k}})$

где $\mathop \tau \limits^* {{{\kern 1pt} }^{{ij}}}({{x}^{k}}) = {{\tau }^{{ij}}}({{x}^{k}},t){{{\text{|}}}_{{t = \mathop \tau \limits^* ({{x}^{s}})}}}$ – напряжения в момент присоединения элементов к основному телу. Далее звездочкой сверху будем обозначать величины, вычисленные в момент присоединения элементов к основному телу.

Подставим актуальные напряжения (1.7) в уравнение равновесия

(1.8)

${{\nabla }_{j}}{{\tau }^{{ji}}} + {{X}^{i}} = 0$

В результате получим

(1.9)

${{\nabla }_{j}}\left\{ {\int\limits_{\mathop \tau \limits^* }^t \,[\partial \cdot {{\tau }^{{ji}}}({{x}^{k}},t{\kern 1pt} ')]dt{\kern 1pt} '\; + \mathop \tau \limits^* {{{\kern 1pt} }^{{ij}}}({{x}^{k}})} \right\} + {{X}^{i}} = 0$

Раскрывая скобки по правилу дифференцирования интеграла, зависящего от параметра¹ ¹, преобразуем соотношение (1.9) к виду

(1.10)

$\int\limits_{\mathop \tau \limits^* }^t \,{{\nabla }_{j}}[\partial \cdot {{\tau }^{{ji}}}({{x}^{k}},t{\kern 1pt} ')]dt{\kern 1pt} '\, - ({{\nabla }_{j}}\mathop \tau \limits^* ){{\left. {[\partial \cdot {{\tau }^{{ji}}}({{x}^{k}},t)]} \right|}_{{t = \mathop \tau \limits^* ({{x}^{s}})}}} + {{\nabla }_{j}}\mathop \tau \limits^* {{{\kern 1pt} }^{{ij}}}({{x}^{k}}) + {{X}^{i}} = 0$

Подставим формулу (1.5) в (1.10)

(1.11)

$\int\limits_{\mathop \tau \limits^* }^t \,{{\nabla }_{j}}[\partial \cdot {{\tau }^{{ji}}}({{x}^{k}},t{\kern 1pt} ')]dt{\kern 1pt} '\, - {{c}^{{ - 1}}}{{n}_{j}}{{\left. {[\partial \cdot {{\tau }^{{ji}}}({{x}^{k}},t)]} \right|}_{{t = \mathop \tau \limits^* ({{x}^{s}})}}} + {{\nabla }_{j}}\mathop \tau \limits^* {{{\kern 1pt} }^{{ij}}}({{x}^{k}}) + {{X}^{i}} = 0$

Меняя местами дифференцирования по пространственной и временной координате и вычисляя интеграл в (1.11) с учетом (1.8), получим

(1.12)

$ - {{X}^{i}} + {{\left. {{{X}^{i}}({{x}^{k}},t)} \right|}_{{t = \mathop \tau \limits^* ({{x}^{s}})}}} - {{c}^{{ - 1}}}{{\left. {{{n}_{j}}[\partial \cdot {{\tau }^{{ji}}}({{x}^{k}},t)]} \right|}_{{t = \mathop \tau \limits^* ({{x}^{k}})}}} + {{\nabla }_{j}}\mathop \tau \limits^* {{{\kern 1pt} }^{{ij}}}({{x}^{k}}) + {{X}^{i}} = 0$

Окончательно, группируя подобные слагаемые и умножая обе части равенства (1.12) на $c$, получим дифференциальное ограничение на поверхности наращивания в операторном виде

(1.13)

$c\left[ {\nabla \cdot \mathop \tau \limits^* ({{x}^{k}}) + {{{\left. {{{X}^{i}}({{x}^{k}},t)} \right|}}_{{t = \mathop \tau \limits^* ({{x}^{s}})}}}} \right] - {{\left. {n \cdot [\partial \cdot \tau ({{x}^{k}},t)]} \right|}_{{t = \mathop \tau \limits^* ({{x}^{s}})}}} = 0$

и координатной записи

(1.14)

$c\left[ {{{\nabla }_{j}}\mathop \tau \limits^* {{{\kern 1pt} }^{{ij}}}({{x}^{k}}) + {{{\left. {{{X}^{i}}({{x}^{k}},t)} \right|}}_{{t = \mathop \tau \limits^* ({{x}^{s}})}}}} \right] - {{n}_{j}}{{\left. {[\partial \cdot {{\tau }^{{ji}}}({{x}^{k}},t)]} \right|}_{{t = \mathop \tau \limits^* ({{x}^{s}})}}} = 0$

Условие (1.13) следует рассматривать как дифференциальное ограничение для напряжений на поверхности наращивания. Действительно, если удастся выразить напряжения $\mathop \tau \limits^* $ через актуальные напряжения $\tau $ на поверхности наращивания $\Sigma $, то из соотношения (1.13) можно получить дифференциальное уравнение для напряжений $\tau $. Альтернативные способы получения граничных условий на поверхности наращивания подробно обсуждались, например в [15, 16].

В общем случае напряжения $\mathop \tau \limits^* $ будут связаны с актуальными напряжениями на поверхности наращивания тензорно-функциональной зависимостью

(1.15)

$\mathop \tau \limits^* = {\mathbf{F}}(\tau ,{\mathbf{n}}, \ldots )$

Многоточие в соотношении (1.15) означает возможную зависимость функции F от дополнительных параметров, характеризующих процесс наращивания. В простейшей модели множество дополнительных параметров может быть пустым. В частности, функция F может зависеть от микроструктурных директоров и теплофизических переменных связанных с растущей поверхностью. Физический смысл дополнительных директоров [18–21] может быть связан с характерными направлениями выкладки волокон в тканных композитных материалах, арматуры в бетонных конструкциях, намотке нитей в катушке и т.д. Функция F, на самом деле, должна зависеть от таких комбинаций аргументов, которые инвариантны относительно поворотов вокруг оси, определяемой директором n.

2. Простейший вариант дифференциального ограничения на поверхности наращивания. Рассмотрим инвариантно-геометрическую интерпретацию случая, обсуждаемого в работе [17]. Пусть на поверхности наращивания $\tau $ известны поверхностные усилия ${\mathbf{t}}$:

(2.1)

${\mathbf{t = n}} \cdot {\mathbf{t}}$

В этом случае примем для сужения на двумерный плоский элемент $T$ тензора $\mathop \tau \limits^* $ обозначение $\mathop \tau \limits_{2d}^* $ и будем оперировать с простейшей зависимостью

(2.2)

$\mathop \tau \limits_{2d}^* = \mathop {\mathbf{F}}\limits_{2d} ({\mathbf{t,n}})$

В декартовой системе координат тензоры $\mathop \tau \limits_{2d}^* $ и $\mathop {\mathbf{F}}\limits_{2d} $ представляются в форме $2 \times 2$ матриц:

(2.3)

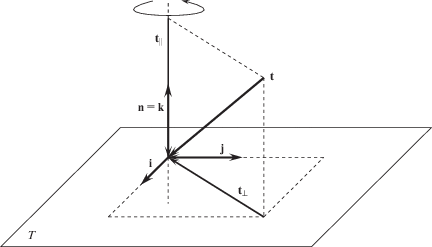
$\mathop \tau \limits_{2d}^* = \left( {\begin{array}{*{20}{c}} {{{\tau }_{{11}}}}&{{{\tau }_{{12}}}} \\ {{{\tau }_{{21}}}}&{{{\tau }_{{22}}}} \end{array}} \right),\quad \mathop {\mathbf{F}}\limits_{2d} = \left( {\begin{array}{*{20}{c}} {{{F}_{{11}}}}&{{{F}_{{12}}}} \\ {{{F}_{{21}}}}&{{{F}_{{22}}}} \end{array}} \right)$

В дальнейшем удобно воспользоваться разложением вектора поверхностных усилий (рис. 2) на сумму составляющих в виде

(2.4)

${\mathbf{t}} = {{{\mathbf{t}}}_{ \bot }} + {{{\mathbf{t}}}_{\parallel }}$

Рис. 2

Здесь ${{{\mathbf{t}}}_{ \bot }}$ – проекция вектора поверхностных усилий на касательную плоскость T к мгновенной поверхности наращивания $\Sigma $, ${{{\mathbf{t}}}_{\parallel }}$ – проекция на нормальное направление к поверхности наращивания.

В качестве аргументов тензорной функции F выберем совместные рациональные инварианты тензора второго ранга ${\mathbf{\tau }}$ и вектора n, неизменные при повороте координатного репера вокруг директора n. В таком случае, рационально независимую систему рациональных инвариантов [22] выпишем в следующем виде:

(2.5)

${\text{|}}{\mathbf{t}}{{{\text{|}}}^{2}} = {\mathbf{t}} \cdot {\mathbf{t}},\quad {\text{|}}{{{\mathbf{t}}}_{\parallel }}{\text{|}} = {\text{|}}{\mathbf{t}} \cdot {\mathbf{n}}{\text{|}},\quad {\text{|}}{{{\mathbf{t}}}_{ \bot }}{{{\text{|}}}^{2}}$

При этом, в системе инвариантов (2.5) существует очевидная сизигия

(2.6)

${\text{|}}{\mathbf{t}}{{{\text{|}}}^{2}} = {\text{|}}{{{\mathbf{t}}}_{\parallel }}{{{\text{|}}}^{2}} + \,{\text{|}}{{{\mathbf{t}}}_{ \bot }}{{{\text{|}}}^{2}}$

Поэтому, устраняя первый инвариант в списке (2.5), система независимых рациональных инвариантов примет вид

(2.7)

${\text{|}}{{{\mathbf{t}}}_{\parallel }}{\text{|}},\quad {\text{|}}{{{\mathbf{t}}}_{ \bot }}{{{\text{|}}}^{2}}$

Определяющее соотношение на поверхности наращивания $\tau $, с учетом (2.7), можно принять в форме

(2.8)

$\mathop \tau \limits_{2d}^* = \mathop {\mathbf{F}}\limits_{{\mathbf{2d}}} ({\text{|}}{{{\mathbf{t}}}_{\parallel }}{\text{|}},{\text{|}}{{{\mathbf{t}}}_{ \bot }}{{{\text{|}}}^{2}})$

Соотношение (2.8) имеет ясный механический смысл. Выберем декартову систему координат (рис. 2) таким образом, чтобы орт k был направлен вдоль нормали n к поверхности наращивания, а для проекции вектора поверхностных усилий ${\mathbf{t}}$ в касательной плоскости $T$ к поверхности наращивания справедливо следующее разложение

(2.9)

${\text{|}}{{{\mathbf{t}}}_{ \bot }}{{{\text{|}}}^{2}} = {\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {\mathbf{i}}{{{\text{|}}}^{2}} + \;{\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {\mathbf{j}}{{{\text{|}}}^{2}}$

Тогда проекции вектора ${\mathbf{t}}$ на орты выбранной системы координат можно выразить через актуальные напряжения

(2.10)

${\text{|}}{{{\mathbf{t}}}_{\parallel }}{\text{|}} = {\text{|}}{{\tau }_{{33}}}{\text{|}},\quad {\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {\mathbf{i}}{{{\text{|}}}^{2}} = \tau _{{31}}^{2},\quad {\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {\mathbf{j}}{{{\text{|}}}^{2}} = \tau _{{32}}^{2}$

В итоге, определяющее соотношение (2.8) запишем в форме

(2.11)

$\mathop {\mathbf{t}}\limits_{2d}^* = \mathop {\mathbf{F}}\limits_{2d} ({\text{|}}{{\tau }_{{33}}}{\text{|}},\tau _{{31}}^{2} + \tau _{{32}}^{2})$

Отметим, что соотношение (2.11) совпадает с аналогичным условием в работе [17]. Однако, в отличие от работы [17] тензор $\mathop {\mathbf{F}}\limits_{2d} $ не является шаровым, т.е. имеется четыре определяющих функции на поверхности наращивания² ².

Подставив условие (2.11) в уравнение (1.14), учитывая, что ${\mathbf{n = k}}$, получим дифференциальное ограничение для напряжений на поверхности наращивания в координатной форме

(2.12)

$c\left[ {{{\partial }_{j}}{{F}_{{ji}}} + {{{\left. {{{X}^{i}}({{x}^{k}},t)} \right|}}_{{t = \mathop \tau \limits^* ({{x}^{s}})}}}} \right] - {{\left. {\partial \cdot {{\tau }_{{3i}}}({{x}_{k}},t)} \right|}_{{t = \mathop \tau \limits^* ({{x}_{s}})}}} = 0\quad (i,j = 1,2,3)$

где ${{\partial }_{j}}$ – оператор дифференцирования по направлению:

(2.13)

${{\partial }_{3}} = {\mathbf{n}} \cdot \nabla ,\quad {{\partial }_{1}} = {\mathbf{i}} \cdot \nabla ,\quad {{\partial }_{2}} = {\mathbf{j}} \cdot \nabla $

т.е. в (2.13) индекс 3 соотвествует направлению нормали, а индексы 1 и 2 – касательным направлениям к поверхности наращивания.

Заметим, что система независимых совместных рациональных инвариантов (2.7) не является полной, в ней не учтены совместные инварианты, содержащие квадрат тензора напряжений t.

3. Инвариантно-полная формулировка дифференциального ограничения на поверхности наращивания. Полная система совместных инвариантов тензора второго ранга $\tau $ и вектора ${\mathbf{n}}$, кроме инвариантов (2.7), включает в себя дополнительные инварианты

(3.1)

${\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{\parallel }}{\text{|}} = {\text{|}}\mathop {\mathbf{t}}\limits_2 \; \cdot {\mathbf{n}}{\text{|}},\quad {\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}},\quad {\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}}$

В соотношении (3.1) вектор $\mathop {\mathbf{t}}\limits_2 $ вычисляется согласно

(3.2)

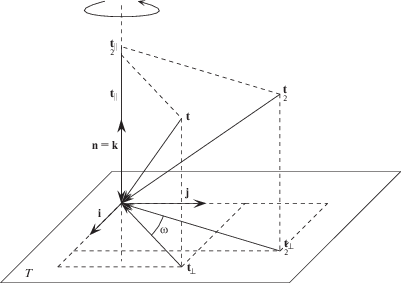
$\mathop {\mathbf{t}}\limits_2 = {\mathbf{n}} \cdot {{{\mathbf{t}}}^{2}},\quad {{\mathop {\mathbf{t}}\limits_2 }_{s}} = {{n}_{j}}{{\tau }^{{ji}}}{{\tau }_{{is}}} = {{t}^{i}}{{\tau }_{{is}}}$

Кроме того, следуя рассуждениям предыдущего раздела, для вектора $\mathop t\limits_2 $ в (3.1) (рис. 3) справедливо

(3.3)

$\mathop {\mathbf{t}}\limits_2 = {{\mathop {\mathbf{t}}\limits_2 }_{\parallel }} + {{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}$

Рис. 3

Вместо инварианта ${\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}}$ в (3.1) можно использовать ${{\cos }^{2}}\varpi $, в силу справедливости равенства

(3.4)

${\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}} = {\text{|}}{{{\mathbf{t}}}_{ \bot }}{{{\text{|}}}^{2}}{\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}}{{\cos }^{2}}\varpi $

Полная система совместных рациональных инвариантов тензора напряжений ${\mathbf{\tau }}$ и вектора ${\mathbf{n}}$ примет вид

(3.5)

${\text{|}}{{{\mathbf{t}}}_{\parallel }}{\text{|}},\quad {\text{|}}{{{\mathbf{t}}}_{ \bot }}{{{\text{|}}}^{2}},\quad {\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{\parallel }}{\text{|}},\quad {\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}},\quad {\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}}$

Тогда определяющее соотношение (1.15) на поверхности наращивания в терминах полной системы совместных инвариантов (3.5) асимметричного тензора второго ранга $\tau $ и вектора ${\mathbf{n}}$, для сужения на двумерный плоский элемент T тензора $\mathop \tau \limits^* $, примет вид

(3.6)

$\mathop {\mathop \tau \limits^* }\limits_{2d} = \mathop {\mathbf{F}}\limits_{2d} ({\text{|}}{{{\mathbf{t}}}_{\parallel }}{\text{|}},{\text{|}}{{{\mathbf{t}}}_{ \bot }}{{{\text{|}}}^{2}},{\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{\parallel }}{\text{|}},{\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}},{\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}})$

Выберем, как и в предыдущем случае, декартову прямоугольную систему координат (рис. 3) таким образом, чтобы орт k был направлен вдоль нормали ${\mathbf{n}}$ к поверхности наращивания. Для вектора проекции поверхностных усилий ${\mathbf{t}}$ в касательной плоскости T к поверхности наращивания примем (2.9), а для вектора ${{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}$ соответсвует очевидное равенство

(3.7)

${\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}} = {\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{ \bot }} \cdot {\mathbf{i}}{{{\text{|}}}^{2}} + \;{\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{ \bot }} \cdot {\mathbf{j}}{{{\text{|}}}^{2}}$

Инварианты (2.7) и (3.5) и длин проекций (2.9) и (3.7) вычисляются через актуальные напряжения ${\mathbf{\tau }}$ на поверхности наращивания согласно

$\begin{gathered} {\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {\mathbf{i}}{{{\text{|}}}^{2}} = \tau _{{31}}^{2},\quad {\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {\mathbf{j}}{{{\text{|}}}^{2}} = \tau _{{32}}^{2},\quad {\text{|}}{{{\mathbf{t}}}_{\parallel }}{\text{|}} = {\text{|}}{{{\mathbf{t}}}_{\parallel }} \cdot {\mathbf{n}}{\text{|}} = {\text{|}}{{\tau }_{{33}}}{\text{|}}, \\ {\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{ \bot }} \cdot {\mathbf{i}}{{{\text{|}}}^{2}} = {\text{|}}{{\tau }_{{3s}}}{{\tau }_{{s1}}}{{{\text{|}}}^{2}} = {\text{|}}{{\tau }_{{31}}}{{\tau }_{{11}}} + {{\tau }_{{32}}}{{\tau }_{{21}}} + {{\tau }_{{33}}}{{\tau }_{{31}}}{{{\text{|}}}^{2}} \\ \end{gathered} $

(3.8)

$\begin{gathered} {\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{ \bot }} \cdot {\mathbf{j}}{{{\text{|}}}^{2}} = {\text{|}}{{\tau }_{{3s}}}{{\tau }_{{s2}}}{{{\text{|}}}^{2}} = {\text{|}}{{\tau }_{{31}}}{{\tau }_{{12}}} + {{\tau }_{{32}}}{{\tau }_{{22}}} + {{\tau }_{{33}}}{{\tau }_{{32}}}{{{\text{|}}}^{2}}, \\ {\text{|}}{{\mathop {\mathbf{t}}\limits_2 }_{\parallel }} \cdot {\mathbf{n}}{\text{|}} = {\text{|}}{{\tau }_{{3s}}}{{\tau }_{{s3}}}{\text{|}} = {\text{|}}{{\tau }_{{31}}}{{\tau }_{{13}}} + {{\tau }_{{32}}}{{\tau }_{{23}}} + \tau _{{33}}^{2}{\text{|}} \\ \end{gathered} $

$\begin{gathered} {\text{|}}{{{\mathbf{t}}}_{ \bot }} \cdot {{\mathop {\mathbf{t}}\limits_2 }_{ \bot }}{{{\text{|}}}^{2}} = {\text{|}}{{\tau }_{{31}}}{{\tau }_{{3l}}}{{\tau }_{{l1}}} + {{\tau }_{{32}}}{{\tau }_{{3l}}}{{\tau }_{{l2}}}{{{\text{|}}}^{2}} = \\ \, = {\text{|}}\tau _{{31}}^{2}{{\tau }_{{11}}} + {{\tau }_{{31}}}{{\tau }_{{32}}}{{\tau }_{{21}}} + \tau _{{31}}^{2}{{\tau }_{{33}}} + {{\tau }_{{32}}}{{\tau }_{{31}}}{{\tau }_{{12}}} + \tau _{{32}}^{2}{{\tau }_{{22}}} + \tau _{{32}}^{2}{{\tau }_{{33}}}{{{\text{|}}}^{2}} \\ \end{gathered} $

Последнее из данных выше соотношений, содержащее кубические по напряжениям слагаемые, следует отнести к классу никогда не используемых в механике деформируемого твердого тела.

Определяющее соотношение на поверхности наращивания (3.6) с учетом выражений (3.8) можно выписать в форме

(3.9)

$\mathop {\mathop {\mathbf{t}}\limits^* }\limits_{2d} = \mathop {\mathbf{F}}\limits_{2d} ({\text{|}}{{\tau }_{{33}}}{\text{|}},\tau _{{31}}^{2} + \tau _{{32}}^{2},{\text{|}}{{\tau }_{{3s}}}{{\tau }_{{s3}}}{\text{|}},{\text{|}}{{\tau }_{{3s}}}{{\tau }_{{s1}}}{{{\text{|}}}^{2}} + \;{\text{|}}{{\tau }_{{3s}}}{{\tau }_{{s2}}}{{{\text{|}}}^{2}},{\text{|}}{{\tau }_{{31}}}{{\tau }_{{3l}}}{{\tau }_{{l1}}} + {{\tau }_{{32}}}{{\tau }_{{3l}}}{{\tau }_{{l2}}}{{{\text{|}}}^{2}})$

или в упрощенной форме

(3.10)

Граничные условия в форме дифференциальных ограничений на поверхности наращивания (1.13), (1.14), в случае, когда приращиваемый материал обладает микроструктурными особенностями, можно обобщить введением в аргументы функции (1.15) дополнительных микроструктурных директоров, связанных с характерными направлениями выкладки материала в процессах намотки нитей или производстве тканных композитов.

Заключение. 1. В работе выполнено исследование возможных, геометрически и механически непротиворечивых граничных условий на поверхности наращивания в форме дифференциальных ограничений.

2. Получена общая форма упомянутых ограничений для асимметричного тензора напряжений, справедливая для весьма широкого круга материалов и метаматериалов.

3. Аргументы определяющей тензорной функции на поверхности наращивания определяются набором инвариантов, неизменных по отношению к поворотам координатного репера.

4. Рассмотрена геометрическая интерпретация простейшего варианта дифференциального ограничения. Дана инвариантно–полная формулировка.

5. Развитый подход подразумевает экспериментальную идентификацию определяющих тензорных функций на поверхности наращивания.

6. Полученные результаты могут служить общей основой в прикладных исследованиях по механике растущих тел с асимметричным тензором напряжений.

Благодарности. Работа выполнена в рамках гранта Российского научного фонда (проект № 17–19–01257).

Список литературы

Berman B. 3-D printing: The new industrial revolution // Business horizons, 2012. V. 55. Iss. 2. P. 155–162.
Mankovich N.J., Cheeseman A.M., Stoker N.G. The display of three-dimensional anatomy with stereolithographic models // Journal of digital imaging. 1990. V. 3. № 3. P. 200–203.
Lipson H., Kurman M. Fabricated: The new world of 3D printing. John Wiley & Sons, 2013.
Panda B. et al. Additive manufacturing of geopolymer for sustainable built environment // Journal of cleaner production. 2017. V. 167. P. 281–288.
Stadnik N.E., Dats E.P. Continuum mathematical modelling of pathological growth of blood vessels // Journal of Physics: Conference Series. IOP Publishing, 2018. V. 991. № 1. P. 012075.
Stadnik N.E., Murashkin E.V., Dats E.P. Residual stresses computing in blood vessels in virtue of pathological growth processes. Proceedings of The World Congress on Engineering 2018, 4–6 July, 2018, London, U.K, Lecture Notes in Engineering and Computer Science, 2018. P. 618–622.
Stadnik N.E., Murashkin E.V., Dats E.P. Residual stresses in blood vessel wall during atherosclerosis // AIP Conference Proceedings, 2019. V. 2116. P. 380013. https://doi.org/10.1063/1.5114394
Southwell R.V. Introduction to the theory of elasticity, 2nd ed. Oxford Univ. Press. 1941.
Рашба Э.И. Определение напряжений в массивах от действия собственного веса с учетом порядка их возведения // Сб. тр. Ин-та строит. механики АН УССР. 1953. № 18. С. 23–27.
Харлаб В.Д. Линейная теория ползучести наращиваемого тела // Механика стержневых систем и сплошных сред: Тр. ЛИСП. Л.: ЛИСП. 1966. Вып. 49. С. 93–119.
Арутюнян Н.Х., Наумов В.Э., Радаев Ю.Н. Динамическое наращивание упругого слоя. Ч. 1. Движение потока осаждаемых частиц с переменной скоростью // Изв. АН СССР. МТТ. 1992. № 5. С. 6–24.
Арутюнян Н.Х., Наумов В.Э., Радаев Ю.Н. Динамическое наращивание упругого слоя. Ч. 2. Случай падения приращиваемых частиц с постоянной скоростью // Изв. АН СССР. МТТ. 1992. № 6. С. 99–112.
Наумов В.Э., Радаев Ю.Н. Термомеханическая модель наращиваемого тела: вариационная формулировка. Препринт / Ин-т проблем механики РАН. М., 1993. № 527. 39 с.
Дмитриева A.M., Наумов В.Э., Радаев Ю.Н. Наращивание термоупругого сферического слоя: применение вариационного подхода. Препринт / Ин-т проблем механики РАН. М., 1993. № 528. 64 с.
Арутюнян Н.Х., Наумов В.Э. Краевая задача теории вязкоупругопластических для растущего тела, подверженного // ПММ. 1984. Т.48. Вып. 1. С. 17–28.
Тринчер В.К. О постановке задачи определения напряжений в гравитационной состояния растущего тела // Изв. АН СССР. Механика твердого тела. 1984. № 2. С. 119–124.
Быковцев Г.И. Избранные проблемные вопросы механики деформируемых сред: Сборник статей. Владивосток: Дальнаука, 2002. 566 с.
Ковалев В.А., Радаев Ю.Н. Математические модели и современные физические теории поля // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2009. Т.9. №4(2). С. 41–94.
Ковалев В.А., Радаев Ю.Н. Волновые задачи теории поля и термомеханика. Саратов: Изд-во Саратов. ун-та, 2010. 328 с.
Ковалев В.А., Радаев Ю.Н. Точно сохраняющиеся инварианты связанного микрополярного термоупругого поля // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2012. Т. 12. № 4. С. 71–79.
Ковалев В.А., Радаев Ю.Н. Полевые уравнения и $d$-тензоры термоупругого континуума с “тонкой” микроструктурой // Изв. Сарат. ун-та. Нов. сер. Сер. Математика. Механика. Информатика. 2013. Т. 13 № 2 (1). С. 60–68.
Гуревич Г. Б. Основы теории алгебраических инвариантов. М., Л.: ОГИЗ, Государственное издательство технико-теоретической литературы, 1948. 408 с. [Eng. Trans. G.B. Gurevich, Foundations of the theory of algebraic invariants. Groningen, Noordhoff, 1964.]

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал