1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 6, 2019

Известия РАН. Механика твердого тела, 2019, № 6, стр. 98-107

ИДЕНТИФИКАЦИЯ ДЕФЕКТОВ ПОПЕРЕЧНОГО СЕЧЕНИЯ СТЕРЖНЯ ПО СОБСТВЕННЫМ ЧАСТОТАМ И ОСОБЕННОСТЯМ ФОРМЫ ПРОДОЛЬНЫХ КОЛЕБАНИЙ

Л. Д. Акуленко a, b, А. А. Гавриков a, *, С. В. Нестеров a

a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

b Московский государственный технический университет им. Н.Э. Баумана
Москва, Россия

* E-mail: gavrikov@ipmnet.ru

Поступила в редакцию 28.04.2019
После доработки 15.05.2019
Принята к публикации 03.06.2019

Полный текст (PDF)

Аннотация

Предложен метод решения обратных задач дефектоскопии для стержней, совершающих продольные колебания. Основываясь на моделировании дефекта сечения как известной функции, приближенно определяются основные параметры, его характеризующие, такие как местоположение и объем по двум низшим частотам колебаний свободного и консольно закрепленного стержней. С помощью численного моделирования показано, что для удовлетворительного определения свойств дефекта достаточно использовать несколько низших частот. Предложен также метод идентификации дефекта по одной низшей частоте свободного стержня при условии известного места нанесения дефекта, для чего требуется определять особенности форм колебаний. Приведены результаты экспериментального исследования.

Ключевые слова: задача Штурма–Лиувилля, обратная задача, дефекты, собственные колебания, продольные колебания

1. Введение. Решается задача идентификации дефектов поперечного сечения круглого стержня по измерениям собственных частот (СЧ) продольных колебаний и сравнению измеренных частот с СЧ эталонного стержня. В классической теории колебаний [1] обычно предполагается, что имеется достаточно полная информация о колебательной системе и основная трудность заключается в построении адекватной модели и решении соответствующих ей уравнений. При решении обратных задач, однако, также обычно вводятся некоторые априорные предположения относительно изучаемой системы, в данном случае – о типе дефекта. Например, в многочисленных публикациях дефекты поперечного сечения моделируются пружинами, работающими на растяжение–сжатие. Достаточно полные обзоры, посвященный этому подходу, даны в [2, 3]. Для решения обратной задачи здесь могут применяться как явные выражения [4], так и использоваться аналитические [4] и дифференциальные свойства собственных частот [5]. Отметим, что в последнем исследовании для определения местоположения дефекта введена схожая с используемой в излагаемой работе для решения прямой задачи величина производной собственного значения [6–8].

В настоящей статье используется аналитическая аппроксимация [9], моделирующая дефекты поперечного сечения стержня, позволяющая получить простые формулы для решения обратной задачи, т.е. определения дефектов и их размеров по измерениям продольных колебаний одного и того же стержня с дефектами при граничных условиях свободно-свободного и консольного закрепления. Дефекты предполагаются достаточно малыми, что вызывает малое изменение СЧ, однако приводящими к изменению как жесткости, так и плотности стержня, что существенно усложняет решение обратной задачи.

Анализ показывает, что консольное закрепление приводит к существенным технологическим трудностям, если оно осуществляется в физическом эксперименте. Поэтому для проведения экспериментальной идентификации дефектов предлагается использовать сравнение СЧ поврежденного и эталонного стержней, а также особенности форм продольных колебаний, для стержней со свободными концевыми условиями.

2. Постановка задачи. Пусть имеются два стержня круглого сечения единичной длины, одинакового почти везде диаметра, изготовленные из одного и того же материала. Один из стержней принят за эталон, а второй имеет дефект поперечного сечения, см. рис. 1. Дефект характеризуется отсчитываемым от левого конца расстоянием b и отношением площадей S1/S0, где S1 – наименьшая площадь сечения, S0 – площадь сечения эталона. Будем считать, что проводятся измерения СЧ продольных колебаний стержней в двух случаях.

Рис. 1

1) Оба стержня имеют свободные концы. Обозначим первую (низшую) СЧ эталона как ${{\omega }_{1}}$, а первую СЧ поврежденного (с дефектом) стержня как ${{\tilde {\omega }}_{1}}$.

2) Оба стержня жестко закреплены в левой граничной точке. Первую СЧ эталона обозначим ${{\Omega }_{1}}$, а первую СЧ поврежденного как ${{\tilde {\Omega }}_{1}}$.

Измерив четыре частоты ${{\omega }_{1}}{\text{,}}{{\tilde {\omega }}_{1}}{\text{,}}{{\Omega }_{1}}{\text{,}}{{\tilde {\Omega }}_{1}}{\text{,}}$ требуется определить положение дефекта b и его объем V. Первые СЧ эталона в обоих случаях хорошо известны [6]

${{\omega }_{1}} = \pi ,\quad {{\Omega }_{1}} = \frac{\pi }{2}$

Размерные частоты эталона вычисляются по формулам

${{f}_{1}} = \frac{1}{{2l}}\sqrt {\frac{E}{\rho }} \;{\text{Гц}},\quad {{F}_{1}} = \frac{1}{{4l}}\sqrt {\frac{E}{\rho }} \;{\text{Гц}}$
где $E$ и $\rho $ – модуль Юнга и плотность материала стержней соответственно, $l$ – их длина. Собственные функции также хорошо известны: ${{u}_{1}}(x) = cos\pi x$ в случае свободного стержня, ${{v}_{1}}(x) = sin\pi x{\text{/}}2$ в случае консольного (жесткого) закрепления левого конца стержня.

Перейдем к математической формулировке задачи. Наличие дефекта моделируется с помощью функции, выражающей площадь поперечного сечения в зависимости от координаты x

(2.1)
$S(x) = {{S}_{0}}\left( {1 - \frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}} \right)$

Величина параметра a характеризует малую ширину дефекта, c – его глубину, а b – место расположения дефекта. В дальнейшем примем, что $a = 5 \times {{10}^{{ - 4}}}$, т.е. имеет место весьма узкий разрез. Таким образом, по четырем СЧ требуется определить два параметра c и b. Для того, чтобы найти как связаны искомые параметры c и b с СЧ сформулируем две прямые задачи Штурма–Лиувилля: требуется найти первые СЧ краевых задач

(2.2)
$\frac{d}{{dx}}\left( {p(x)\frac{{du}}{{dx}}} \right) + \tilde {\lambda }r(x)u = 0,\quad u{\kern 1pt} '(0) = u{\kern 1pt} '(1) = 0$
(2.3)
$\frac{d}{{dx}}\left( {p(x)\frac{{dv}}{{dx}}} \right) + \tilde {\Lambda }r(x)v = 0,\quad v(0) = v{\kern 1pt} '(1) = 0$
где $p(x) = r(x) = S(x).$

3. Решение обратной задачи. Согласно принципу Релея [1, 6] имеет место равенство

(3.1)
${{\tilde {\lambda }}_{1}} = \frac{{\int\limits_0^1 {{{S}_{0}}\left( {1 - \frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}} \right){{{\left( {\frac{{d{{u}_{1}}}}{{dx}}} \right)}}^{2}}dx} }}{{\int\limits_0^1 {{{S}_{0}}\left( {1 - \frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}} \right)u_{1}^{2}dx} }}$

Подставим в (3.1) вместо ${{u}_{1}}$ собственную функцию неповрежденного стержня $u(x)$ = cosπx, тогда приближенно

(3.2)
${{\tilde {\lambda }}_{1}} \approx {{\pi }^{2}}\frac{{1 - 2\int\limits_0^1 {\frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}{{{\sin }}^{2}}\pi xdx} }}{{1 - 2\int\limits_0^1 {\frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}{{{\cos }}^{2}}\pi xdx} }}$

Заметим, что при $a \to 0$ справедливы равенства

(3.3)
$\begin{gathered} \mathop {lim}\limits_{a \to 0} \int\limits_0^1 {\frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}{{{\sin }}^{2}}\pi xdx} = \pi c\int\limits_0^1 {\delta (x - b){{{\sin }}^{2}}\pi xdx} = \pi c{{\sin }^{2}}\pi b \\ \mathop {lim}\limits_{a \to 0} \int\limits_0^1 {\frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}{{{\cos }}^{2}}\pi xdx} = \pi c\int\limits_0^1 {\delta (x - b){{{\cos }}^{2}}\pi xdx} = \pi c{{\cos }^{2}}\pi b \\ \end{gathered} $

Из равенств (3.2), (3.3) следует, что при $\pi c \ll 1$

(3.4)
$\sqrt {{{{\tilde {\lambda }}}_{1}}} = {{\tilde {\omega }}_{1}} = \pi \left( {1 + \pi ccos2\pi b} \right)$

Учитывая, что ${{\omega }_{1}} = \pi ,$ получаем уравнение, связывающее известные (измеренные) величины ${{\omega }_{1}},{{\tilde {\omega }}_{1}}$ и искомые параметры c, b

(3.5)
$\frac{{{{{\tilde {\omega }}}_{1}}}}{{{{\omega }_{1}}}} = 1 + \pi ccos2\pi b$

В случае консольного закрепления (задача (2.3)), используя функцию $v(x)$ = sinπx/2, принцип Релея приводит к равенству

(3.6)
$\sqrt {{{{\tilde {\Lambda }}}_{1}}} = {{\tilde {\Omega }}_{1}} \approx \frac{{{{\pi }^{2}}}}{4}\frac{{1 - 2\int\limits_0^1 {\frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}{{{\cos }}^{2}}\pi xdx} }}{{1 - 2\int\limits_0^1 {\frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}{{{\sin }}^{2}}\pi xdx} }}$

Из равенства (3.6) аналогично предыдущему находим (${{\Omega }_{1}} = \pi {\text{/}}2$):

(3.7)
$\frac{{{{{\tilde {\Omega }}}_{1}}}}{{{{\Omega }_{1}}}} = 1 - \pi ccos\pi b$

Из уравнений (3.5), (3.7) можно исключить параметр $c$ и получить независимое уравнение, определяющее положение дефекта $b$

(3.8)
$\left( {\frac{{{{{\tilde {\omega }}}_{1}}}}{{{{\omega }_{1}}}} - 1} \right)cos\pi b + \left( {\frac{{{{{\tilde {\Omega }}}_{1}}}}{{{{\Omega }_{1}}}} - 1} \right)cos2\pi b = 0$

Из численного эксперимента, который был проведен при $a = 5 \times {{10}^{{ - 4}}},$ $c{{ = 10}^{{ - 4}}}$ и различных значениях b, были найдены величины ${{\tilde {\omega }}_{1}},$ ${{\tilde {\Omega }}_{1}}$ с помощью решения прямых задач Штурма–Лиувилля (2.2), (2.3). Первые собственные числа ${{\tilde {\lambda }}_{1}},$ ${{\tilde {\Lambda }}_{1}}$ краевых задач находятся с помощью метода ускоренной сходимости [5] и по ним вычисляются СЧ ${{\tilde {\omega }}_{1}},$ ${{\tilde {\Omega }}_{1}}.$ Решая уравнение (3.8), находится положение дефекта $b,$ а решая (3.5) – параметр $c.$ В табл. 1 в первом столбце приведены результаты численного моделирования, во втором – использованные параметры, а в третьем – искомые параметры b и c, найденные согласно (3.5)–(3.8). Знаком * отмечены те случаи, когда уравнение (3.8) имеет два корня. Здесь следует выбирать тот корень, для которого величина c является положительной. Из табл. 1 видно, что при нахождении параметров b и c максимальная погрешность составляет 17%. По-видимому, причина такой большой погрешности заключается в предельном переходе $a \to 0$ при выводе формул (3.5)–(3.8) и аналогичным упрощениям.

Таблица 1
Вычисленные (измеренные) частоты для стержня с дефектом (${{\omega }_{1}} \approx 3.1416,$${{\Omega }_{1}} \approx 1.5708)$ Истинное значение параметров ($c{{ = 10}^{{ - 4}}},a = 5 \times {{10}^{{ - 4}}}$) Решение обратной задачи
${{\tilde {\omega }}_{1}} = 3.1424$, ${{\tilde {\Omega }}_{1}} = 1.5703$ $b = 0.1$ $b = 0.130$, $c = 1.16 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1421$, ${{\tilde {\Omega }}_{1}} = 1.5703$ $b = 0.15$ $b = 0.170$, $c = 1.16 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1419$, ${{\tilde {\Omega }}_{1}} = 1.5703$ $b = 0.2$ $b = 0.213$, $c = 1.17 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1415$, ${{\tilde {\Omega }}_{1}} = 1.5704$ $b = 0.25$ $b = 0.258$, $c = 1.17 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1407$, ${{\tilde {\Omega }}_{1}} = 1.5706$ $b = 0.4$ $b = 0.393$, $c = 1.17 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1405$, ${{\tilde {\Omega }}_{1}} = 1.5707$ $b = 0.45$ $b = 0.438$, $c = 1.15 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1405$, ${{\tilde {\Omega }}_{1}} = 1.5708$ $b = 0.55$ $b = 0.531$, $c = 1.08 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1407$, ${{\tilde {\Omega }}_{1}} = 1.5709$ $b = 0.6$ $b = 0.582$, $c = 1.05 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1415$, ${{\tilde {\Omega }}_{1}} = 1.5711$ $b = 0.75$ $b = 0.741$, $c = 1.00 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1419$, ${{\tilde {\Omega }}_{1}} = 1.5712$ $b = 0.8$ $b = 0.793$, $c = 1.00 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{1}} = 3.1421$, ${{\tilde {\Omega }}_{1}} = 1.5712$ $b = 0.85$ $b = 0.845$, $c = 9.99 \times {{10}^{{ - 5}}}$
${{\tilde {\omega }}_{1}} = 3.1424$, ${{\tilde {\Omega }}_{1}} = 1.5713$ $b = 0.9$ $b = 0.897$$c = 9.98 \times {{10}^{{ - 5}}}$

Для целей идентификации полученное значение параметра c может быть использовано следующим образом. Так как площадь поперечного сечения дефекта имеет вид

${{S}_{1}}(x) = {{S}_{0}}\frac{{ac}}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}$
то объем дефекта определяется как

${{V}_{{def}}} = \int\limits_0^1 {{{S}_{1}}(x)dx} = {{S}_{0}}c\int\limits_0^1 {\frac{a}{{{{a}^{2}} + {{{(x - b)}}^{2}}}}dx} $

Переходя к пределу при $a \to 0,$ получаем

(3.9)
${{V}_{{def}}} = {{S}_{0}}c\int\limits_0^1 {\pi \delta (x - b)dx} = {{S}_{0}}\pi c$

Таким образом, в результате применения изложенной процедуры имеем две величины, характеризующие дефектность стержня: b – место расположения дефекта и его объем ${{V}_{{def}}},$ который выражается через вычисленный параметр $c.$

4. Использование высших собственных частот. Если использовать две высших СЧ ${{\omega }_{n}} = \pi n$ и ${{\Omega }_{n}} = \pi (2n - 1){\text{/}}2,$ то можно показать, что приближенные формулы, связывающие искомые параметры дефекта и СЧ стержней с дефектами, принимают вид:

(4.1)
$\begin{array}{*{20}{c}} {\frac{{{{{\tilde {\omega }}}_{n}}}}{{{{\omega }_{n}}}} = 1 + \pi ccos2\pi nb} \\ {\frac{{{{{\tilde {\Omega }}}_{n}}}}{{{{\Omega }_{n}}}} = 1 - \pi ccos(2n - 1)\pi nb} \end{array}$
где $n = 1,2, \ldots .$ Исключая πc из системы (4.1), получим уравнение для нахождения положения дефекта

(4.2)
$\left( {\frac{{{{{\tilde {\omega }}}_{n}}}}{{{{\omega }_{n}}}} - 1} \right)cos(2n - 1)\pi b + \left( {\frac{{{{{\tilde {\Omega }}}_{n}}}}{{{{\Omega }_{n}}}} - 1} \right)cos2\pi nb = 0$

Уравнение (4.2) имеет лишние корни, но всегда среди них имеется корень, определяющий место положения дефекта.

В частности, для $b = 0.2,$ $c{{ = 10}^{{ - 4}}},$ $n = 2$ имеем

$\frac{{{{{\tilde {\omega }}}_{2}}}}{{{{\omega }_{2}}}} - 1 = - 2.859 \times {{10}^{{ - 4}}}\quad \frac{{{{{\tilde {\Omega }}}_{2}}}}{{{{\Omega }_{2}}}} - 1 = 0.832 \times {{10}^{{ - 4}}}$

Уравнение (4.2) имеет три корня ${{b}_{i}},$ проводящие к соответствующим значениям параметра c: ${{b}_{1}} = 0.19,$ ${{c}_{1}} = 1.25 \times {{10}^{{ - 4}}};$ ${{b}_{2}} = 0.53,$ ${{c}_{2}} = - 9.788 \times {{10}^{{ - 4}}};$ ${{b}_{3}}$ = 0.84, c3 = 2.197 × × ${{10}^{{ - 4}}}.$ Здесь второй корень следует отбросить, как дающий отрицательное значение параметра $c.$ Третий же корень весьма далек от положения дефекта, вычисленного по первой СЧ (см. табл. 1). Таким образом, остается принять значения, вычисленные с помощью первого корня. Аналогичным образом, для $b = 0.4$ имеем

$\frac{{{{{\tilde {\omega }}}_{2}}}}{{{{\omega }_{2}}}} - 1 = 0.8303 \times {{10}^{{ - 4}}}\quad \frac{{{{{\tilde {\Omega }}}_{2}}}}{{{{\Omega }_{2}}}} - 1 = 2.498 \times {{10}^{{ - 4}}}$

Здесь подходящий корень уравнения (4.2) равен ${{b}_{1}} = 0.397,$ ${{c}_{1}} = 0.97 \cdot {{10}^{{ - 4}}}$.

В табл. 2 приведены вычисления, аналогичные табл. 1, с использованием частот ${{\tilde {\omega }}_{n}},$ ${{\tilde {\Omega }}_{n}},$ $n = 2,3.$ Отметим, что в случае неоднозначного выбора корней уравнений (4.1), (4.2), выбираются корни, ближайшее к корням, найденным по низшим частотам.

Таблица 2
Вычисленные (измеренные) частоты для стержня с дефектом (${{\omega }_{2}} \approx 6.2832,{{\Omega }_{2}} \approx 4.7124)$ (${{\omega }_{3}} \approx 9.4248,{{\Omega }_{3}} \approx 7.8540)$ Истинное значение параметров (c = 10–4, $a = 5 \times {{10}^{{ - 4}}}$) Решение обратной задачи, $n = 2$ Решение обратной задачи, $n = 3$
${{\tilde {\omega }}_{2}} = 6.2814,{{\tilde {\omega }}_{3}} = 9.4221,$${{\tilde {\Omega }}_{2}} = 4.7128,{{\tilde {\Omega }}_{3}} = 7.8564$ $b = 0.2$ $b = 0.189$$c = 1.26 \times {{10}^{{ - 4}}}$ $b = 0.190$$c = 1.00 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{2}} = 6.2837,{{\tilde {\omega }}_{3}} = 9.4256,$${{\tilde {\Omega }}_{2}} = 4.7136,{{\tilde {\Omega }}_{3}} = 7.8512$ $b = 0.4$ $b = 0.397$$c = 9.64 \times {{10}^{{ - 5}}}$ $b = 0.404$$c = 1.11 \times {{10}^{{ - 4}}}$
${{\tilde {\omega }}_{2}} = 6.2837,{{\tilde {\omega }}_{3}} = 9.4256,$${{\tilde {\Omega }}_{2}} = 4.7110,{{\tilde {\Omega }}_{3}} = 7.8564$ $b = 0.6$ $b = 0.605$$c = 1.09 \times {{10}^{{ - 4}}}$ $b = 0.598$$c = 9.93 \times {{10}^{{ - 5}}}$
${{\tilde {\omega }}_{2}} = 6.2814,{{\tilde {\omega }}_{3}} = 9.4221,$${{\tilde {\Omega }}_{2}} = 4.7118,{{\tilde {\Omega }}_{3}} = 7.8512$ $b = 0.8$ $b = 0.794$$c = 1.07 \times {{10}^{{ - 4}}}$ $b = 0.801$$c = 1.11 \times {{10}^{{ - 4}}}$

Эти примеры показывают, что использование дополнительных высших собственных значений позволяет подтвердить наличие дефекта и уточнить его характеристики – положение и объем.

В приведенным выше расчетах размер дефекта предполагался относительно небольшим. Однако, предложенный подход может быть применен и для дефектов большего размера, хотя это может приводить к увеличению погрешности. В табл. 3 приведены результаты решения обратной задачи для параметров $a = 5 \times {{10}^{{ - 3}}},$ $c = 2.5 \times {{10}^{{ - 3}}}$ (таким образом, максимальное изменение площади сечения стержня достигает 50%).

Таблица 3
Вычисленные (измеренные) частоты для стержня с дефектом (${{\omega }_{1}} \approx 3.1416,{{\Omega }_{1}} \approx 1.5708)$ Истинное значение параметров ($c = 2.5 \times {{10}^{{ - 3}}},a = 5 \times {{10}^{{ - 3}}}$) Решение обратной задачи
${{\tilde {\omega }}_{1}} = 3.1455$, ${{\tilde {\Omega }}_{1}} = 1.5566$ $b = 0.2$ $b = 0.234$, $c = 3.87 \times {{10}^{{ - 3}}}$
${{\tilde {\omega }}_{1}} = 3.1132$, ${{\tilde {\Omega }}_{1}} = 1.5638$ $b = 0.4$ $b = 0.381$, $c = 3.91 \times {{10}^{{ - 3}}}$
${{\tilde {\omega }}_{1}} = 3.1132$, ${{\tilde {\Omega }}_{1}} = 1.5728$ $b = 0.6$ $b = 0.543$, $c = 1.99 \times {{10}^{{ - 3}}}$
${{\tilde {\omega }}_{1}} = 3.1455$, ${{\tilde {\Omega }}_{1}} = 1.5802$ $b = 0.8$ $b = 0.775$, $c = 2.50 \times {{10}^{{ - 3}}}$

5. Идентификация единичного дефекта поперечного сечения по собственным частотам и особенностям форм продольных колебаний. В предыдущих разделах для идентификации единичного дефекта использовались СЧ свободного и консольно закрепленных стержней. Здесь мы рассмотрим способ определения дефекта только с помощью СЧ свободного стержня в предположении, что площадь поперечного сечения стержня с дефектом по-прежнему задается функцией (2.1). Имея в виду в дальнейшем проведение физических экспериментов следует отметить, что стержни должны обладать высокой добротностью. При высокой добротности колебательной системы возможно выявить малое изменение СЧ, вызванное малыми дефектами. Краевые условия второго рода легко реализуются физически и обеспечивают максимальную добротность стержней.

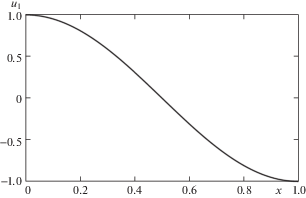
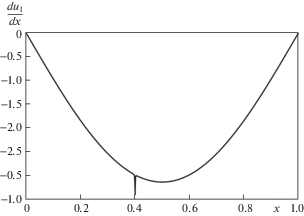
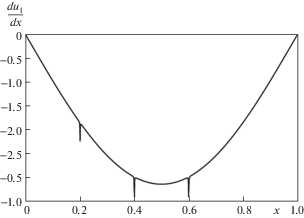
Как и выше, имеем уравнение (3.5), связывающее результаты измерений и величины искомых параметров, где ${{\omega }_{1}} = \pi ,$ СЧ поврежденного стержня ${{\tilde {\omega }}_{1}}$ определяется из физического или численного эксперимента. Таким образом, имеется только одно уравнение, связывающее параметры c и $b.$ Чтобы найти c нужно каким-то образом определить величину $b.$ Если стержень имеет дефект поперечного сечения, то первая собственная форма практически не отличается от косинусоиды (см. рис. 2, где для определенности полагается b = 0.4 длина стержня l = 1). Однако, ее первая производная, как показывают вычисления, имеет вид, представленный на рис. 3. Положение пика здесь совпадает с точкой $x = b.$ Графики ${{u}_{1}}(x)$ и $d{{u}_{1}}(x){\text{/}}dx$ здесь получены методом ускоренной сходимости при решении краевой задачи (2.2). Ниже будет показано, как можно в физическом эксперименте определить положение пика. Отметим, что при наличии нескольких (для определенности, трех) дефектов, моделируемых функцией

(5.1)
$S(x) = {{S}_{0}}\left( {1 - \frac{{a{{c}_{1}}}}{{{{a}^{2}} + {{{(x - {{b}_{1}})}}^{2}}}} - \frac{{a{{c}_{2}}}}{{{{a}^{2}} + {{{(x - {{b}_{2}})}}^{2}}}} - \frac{{a{{c}_{3}}}}{{{{a}^{2}} + {{{(x - {{b}_{3}})}}^{2}}}}} \right)$
производная первой формы также имеет ярко выраженные пики, см. рис. 4. Таким образом, график функции $d{{u}_{1}}(x){\text{/}}dx$ является весьма информативным, поскольку проявляются сразу все дефекты и места их расположения. Если использовать производные от собственных форм более высокого порядка, то при некоторых положениях дефекта пики на графиках либо пропадают совсем, либо выглядят плохо заметными. Наиболее полная информация о числе дефектов и местах их расположения извлекается из графика $d{{u}_{1}}(x){\text{/}}dx$.

Рис. 2
Рис. 3
Рис. 4

Пусть стержень без дефекта совершает продольные колебания по одной из форм

${{u}_{n}}(x) = Acos\frac{{\pi n}}{l}xcos{{\omega }_{n}}t$

При таких колебаниях поперечные сечения подвергаются либо сжатию, либо растяжению. Если радиус поперечного сечения $r,$ то в поперечном направлении к оси стержня его поверхность испытывает смещение

$\xi = \mu \frac{{d{{u}_{n}}(x)}}{{dx}} = - \mu r\frac{{\pi n}}{l}Asin\frac{{\pi n}}{l}xcos{{\omega }_{n}}t$
где $\mu $ – коэффициент Пуассона материала стержня. При n = 1 и n = 2 поверхности стержня изображены на рис. 5. Поскольку $\xi \approx d{{u}_{n}}(x){\text{/}}dx,$ то схематически поверхность стержня при наличии трех дефектов и колебаниях по первой форме принимает вид рис. 6.

Рис. 5
Рис. 6

Такого рода изменения поверхности стержня могут быть зафиксированы с помощью оптических средств измерения. Экспериментально определяя положение дефекта далее по формуле (3.5) находим величину параметра $c.$

6. Экспериментальные результаты. Для идентификации единичного дефекта поперечного сечения использовался резонансный метод определения СЧ, подробно описанный в [6]. Первоначально измерялись собственные частоты стержня без дефекта для стального стержня длиной $l = 60.2$ см, диаметром d = 1.62 см, скорость распространения продольных волн $\sqrt {E{\text{/}}\rho } = 5.19 \times {{10}^{5}}$ см/сек, коэффициент Пуассона μ = = $0.29 \pm 0.02.$ Были измерены 10 СЧ. Затем на стержне был нанесен дефект поперечного сечения (несимметричный пропил треугольным напильником) на расстоянии b = 24 см от нижнего конца стержня, где находился электромагнитный возбудитель колебаний, питаемый током генератора. Наглядно дефект представлен на рис. 7.

Рис. 7

Поскольку пропил был несимметричным, то нанесенный дефект не полностью соответствует принятой модели (2.1). Однако, исходя из равенства объемов нанесенного дефекта и описываемого функцией (2.1), параметры пропила были в безразмерном виде сопоставлены следующим значениям: $c = 1.8 \times {{10}^{{ - 3}}},$ $a = 6 \times {{10}^{{ - 3}}}$. После этого были измерены СЧ. Поскольку дефект был несимметричным, то наряду с продольными возбуждались поперечные и крутильные колебания, но их измеренные амплитуды оказались значительно меньше амплитуд продольных колебаний, за исключением 2-й частоты: здесь возникают дополнительные колебания на частоте 9.098 кГц с амплитудой, сравнимой с амплитудой продольных колебаний. Наиболее значимыми оказались 6 частот продольных колебаний, представленные в табл. 4 вместе с СЧ неповрежденного стержня. В крайнем правом столбце приведены значения параметра c, вычисленные по формуле (3.5) в предположении $b = 24{\text{/}}60.2.$ Если известно, что

${{c}_{n}} = \frac{{\frac{{{{{\tilde {f}}}_{n}}}}{{{{f}_{n}}}} - 1}}{{\pi cos(2\pi n \times 0.4)}}$
то, осредняя по всем частотам, получим

$c = \frac{1}{6}\sum\limits_{n = 1}^6 {{c}_{n}} = 1.2 \times {{10}^{{ - 3}}}$
Таблица 4
${{f}_{n}},$ кГц ${{\tilde {f}}_{n}},$ кГц cn
4.310 4.270 $3.65 \times {{10}^{{ - 3}}}$
8.620 8.577 $ - 5.1 \times {{10}^{{ - 4}}}$
12.930 12.918 $ - 9.56 \times {{10}^{{ - 4}}}$
17.240 17.151 $2.03 \times {{10}^{{ - 3}}}$
21.240 21.682 $6.6 \times {{10}^{{ - 3}}}$
25.760 25.683 $1.2 \times {{10}^{{ - 3}}}$

Если считать, что физически нанесенному дефекту соответствует $c = 1.8 \cdot {{10}^{{ - 3}}},$ то отличие составляет 33% Следует отметить, что простое сравнение двух спектров СЧ без дефекта и с дефектом обнаруживает следующие особенности спектра частот стержня с дефектом поперечного сечения:

1) Появляются низкочастотные колебания, частоты которых существенно ниже основной частоты продольных колебаний (в данном случае 4.310 кГц).

2) Появляются дублеты и триплеты, которые группируются около высокочастотных продольных колебаний.

Эти два обстоятельства позволяют сразу сделать вывод, что стержень, обладающий таким набором СЧ имеет дефект или несколько дефектов.

Работа выполнена по теме государственного задания (NN госрегистрации АААА-А17-117021310381-8, АААА-А17-117021310387-0) и частично поддержана грантом РФФИ № 18-01-00812 А.

Список литературы

  1. Журавлев В.Ф., Климов Д.М. Прикладные методы в теории колебаний. М.: Наука, 1988. 328 с.

  2. Morassi A. Damage Detection in Vibrating Beams // Morassi A., Vestroni F. (eds). Dynamic Methods for Damage Detection in Structures. CISM International Centre for Mechanical Sciences. V. 499. Vienna: Springer, 2008. P. 137–182.

  3. Шифрин Е.И. Обратная спектральная задача для упругого стержня, ослабленного поперечными трещинами // Черноусько Ф.Л. Актуальные проблемы механики. М.: Наука, 2015. С. 456–470.

  4. Shifrin E.I. Inverse spectral problem for a non-uniform rod with multiple // Mech. Syst. Signal Process. 2017. V. 96. P. 348–365.

  5. Rubio L., Fernández-Sáez J., Morassi A. Crack identification in non-uniform rods by two frequency data // Int. J. Solids Struct. 2015. V. 75–76. P. 61–80.

  6. Akulenko L.D., Nesterov S.V. High-Precision Methods in Eigenvalue Problems and Their Applications. Boca Raton: Chapman and Hall/CRC, 2005. 260 p.

  7. Акуленко Л.Д., Гавриков А.А., Нестеров С.В. Синтез неоднородной упругой системы с граничной нагрузкой // Вестн. МГУ. Матем. Механика. 2017. № 5. С. 36–42.

  8. Гавриков А.А. Решение краевых задач на собственные значения для линейных гамильтоновых систем с нелинейной зависимостью от спектрального параметра // ПММ. 2018. Т. 82. № 5. С. 605–621.

  9. Акуленко Л.Д., Нестеров С.В. Влияние дефекта массы на частоты и формы продольных колебаний стержня // Изв. РАН МТТ. 2014. № 1. С. 135–144.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал