Известия РАН. Механика твердого тела, 2019, № 6, стр. 3-11

О СМЕЩЕНИИ ПЕРИГЕЛИЯ ОРБИТЫ МЕРКУРИЯ

Н. И. Амелькин^*

Московский физико-технический институт
Москва, Россия

Поступила в редакцию 01.03.2019
После доработки 15.03.2019
Принята к публикации 21.03.2019

DOI: 10.1134/S0572329919050040

Аннотация

В рамках классической механики исследуется влияние планет Солнечной системы на прецессию орбиты Меркурия. Показано, что среднее смещение перигелия орбиты Меркурия, вычисленное в рамках плоской ограниченной задачи, составляет 556.5 угловых секунд за столетие и совпадает с наблюдаемым с относительной точностью 2.5%. Неполное совпадение между вычисленным средним смещением и данными наблюдений объясняется наличием в наблюдаемом смещении колебательных составляющих с суммарной амплитудой до 80 угловых секунд и периодами от нескольких лет до нескольких десятков лет.

Ключевые слова: Солнечная система, ограниченная круговая задача трех тел, смещение перигелия Меркурия

1. История вопроса. Многочисленные дискуссии о причинах “аномальной” прецессии орбиты Меркурия начались с середины девятнадцатого века после того, как французский астроном Урбен Леверье опубликовал результаты своих расчетов о движении Меркурия. По его расчетам [1, 2], где учитывалось влияние всех планет (табл. 1), перигелий Меркурия должен смещаться на 526.7 угловых секунд за столетие, а по данным 40-летних наблюдений Парижской обсерватории смещение составляло 565″ (по современным данным смещение равно 570″).

Таблица 1

Планета	Вклад в смещение перигелия Меркурия (за столетие в угловых секундах)
Венера	280.6
Земля	83.6
Марс	2.6
Юпитер	152.6
Сатурн	7.2
Уран	0.1
Σ	526.7

Разницу в 42.3″ пытались объяснить разными причинами, например, влиянием неизвестной планеты (Вулкана) между Солнцем и Меркурием или сплюснутостью Солнца за счет его вращения относительно инерциальной системы отсчета. Но никакой планеты внутри орбиты Меркурия обнаружено не было, а степень сплюснутости Солнца по современным оценкам явно недостаточна для эффекта в 42.3″. Были и другие попытки объяснения обнаруженной аномалии, в числе которых предложения о модификации ньютоновского закона всемирного тяготения (Ньюком С.).

В 1915 году Альберт Эйнштейн опубликовал окончательный вариант своей теории тяготения, получившей название “общая теория относительности” (ОТО) и рассчитал вытекающее из нее дополнительное смещение перигелия Меркурия [3]. Оно оказалось равным 43″ за столетие, т.е. с большой точностью совпало с упомянутой выше разницей в 42.3″. Многие из ученого сообщества приняли это совпадение, как доказательство адекватности ОТО. Но нашлись и критики, считающие совпадение случайным, или оспаривающие достоверность разницы в 42–43″ между рассчитанным методами классической механики смещением и наблюдениями [4]. Дискуссии по этому вопросу продолжаются до сих пор.

В данной работе расчет смещения перигелия Меркурия проводится в рамках классической механики. Показано, что разница между обусловленным влиянием планет средним значением смещения перигелия Меркурия и наблюдаемым значением (570″) существенно (в три раза) меньше 42″. Кроме того, установлено, что смещение перигелия не является равномерным. В нем присутствуют колебательные составляющие с амплитудами до 40″ и периодами от нескольких лет до нескольких десятков лет. Поэтому рассчитанная по данным наблюдений на интервалах времени в десятки и даже сотни лет скорость смещения перигелия Меркурия может существенно отличаться от истинной средней скорости, и этим обстоятельством можно объяснить неполное совпадение вычисленного аналитически среднего смещения перигелия с данными наблюдений.

2. Формулы для расчета влияния планет на смещение перигелия Меркурия. Учет влияния каждой планеты на движение Меркурия будем исследовать в рамках плоской ограниченной круговой задачи трех тел: Солнце–планета–Меркурий. Обозначим через $O{\mathbf{ij}}$ инерциальную систему отчета с началом в общем центре масс системы Солнце–планета, а через M и $m$ массу Солнца и массу планеты, соответственно. Солнце и планета движутся относительно инерциальной системы отсчета по закону

(2.1)

${{{\mathbf{R}}}_{M}} = \frac{{{\varepsilon }\operatorname{R} {\mathbf{e}}(t)}}{{1 + \varepsilon }},\quad {{{\mathbf{R}}}_{m}} = - \frac{{\operatorname{R} {\mathbf{e}}(t)}}{{1 + \varepsilon }},$ ${\mathbf{e}}(t) = {\mathbf{i}}\cos {\Omega }t + {\mathbf{j}}\sin {\Omega }t,\quad {\varepsilon } = m{\text{/}}M$

где $R$ – радиус орбиты планеты (расстояние между планетой и Солнцем), ${\Omega }$ – орбитальная угловая скорость планеты.

Положение Меркурия относительно инерциальной системы отсчета определяется радиус-вектором ${\mathbf{\rho + }}{{{\mathbf{R}}}_{M}}$, где через ${\mathbf{\rho }}$ обозначен вектор, соединяющий Солнце с Меркурием. Уравнение движения Меркурия относительно Солнца записывается в виде

(2.2)

${\mathbf{\ddot {\rho }}} = - \frac{{{\mu }{\mathbf{\rho }}}}{{{{{\rho }}^{3}}}}{\mathbf{ + }}\frac{{{\varepsilon }{{{\Omega }}^{2}}R{\mathbf{e}}(t)}}{{1 + \varepsilon }} - {\varepsilon \mu }\frac{{R{\mathbf{e}}(t) + {\mathbf{\rho }}}}{{{{{\left| {R{\mathbf{e}}(t) + {\mathbf{\rho }}} \right|}}^{3}}}};$ ${\mu } = {\gamma }M$

Перейдем к безразмерному времени ${\tau }$ и к безразмерной переменной ${\mathbf{r}}$ согласно формулам

(2.3)

${\tau } = {\Omega }t$, ${\mathbf{r}} = {{\mathbf{\rho }} \mathord{\left/ {\vphantom {{\mathbf{\rho }} R}} \right. \kern-0em} R}$

Тогда, учитывая соотношение

(2.4)

${\mu }(1 + {\varepsilon }) = {{{\Omega }}^{2}}{{R}^{3}}$

получим уравнение

(2.5)

$\frac{{{{d}^{2}}{\mathbf{r}}}}{{d{{{\tau }}^{2}}}} = - \frac{{\mathbf{r}}}{{{{r}^{3}}(1 + {\varepsilon })}}{\mathbf{ + }}\frac{{\varepsilon }}{{1 + {\varepsilon }}}\left( {{\mathbf{e}}({\tau }) - \frac{{{\mathbf{e}}({\tau }) + {\mathbf{r}}}}{{{{{\left| {{\mathbf{e}}({\tau }) + {\mathbf{r}}} \right|}}^{3}}}}} \right),$ ${\mathbf{e}}({\tau }) = {\mathbf{i}}\cos {\tau } + {\mathbf{j}}\sin {\tau }$

Второе слагаемое в правой части уравнения (2.5) представляет собой возмущающее ускорение. Ввиду того, что для всех планет параметр ${\varepsilon }$ не превышает значения 10^–3, для этого ускорения без ущерба для точности будем использовать выражение

(2.6)

${\mathbf{W}} = {\varepsilon }\left( {{\mathbf{e}}({\tau }) - \frac{{{\mathbf{e}}({\tau }) + {\mathbf{r}}}}{{{{{\left| {{\mathbf{e}}({\tau }) + {\mathbf{r}}} \right|}}^{3}}}}} \right)$

Обозначим через $x$ и $y$ компоненты вектора ${\mathbf{r}}$ в инерциальном базисе, т.е. r = ${\mathbf{i}}x + {\mathbf{j}}y$. Тогда для компонент возмущающего ускорения получим выражения

(2.7)

${{W}_{x}} = {\varepsilon }[\cos {\tau } - (\cos {\tau } + x){{Z}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}],\quad {{W}_{y}} = {\varepsilon }[\sin {\tau } - (\sin {\tau } + y){{Z}^{{{{ - 3} \mathord{\left/ {\vphantom {{ - 3} 2}} \right. \kern-0em} 2}}}}]$

$Z = 1 + z$; $z = {{r}^{2}} + 2(x\cos {\tau } + y\sin {\tau })$

Смещение перигелия орбиты Меркурия в рамках плоской задачи описывается формулой [5]

(2.8)

$\frac{{d{\omega }}}{{du}} = \frac{{{{r}^{2}}}}{e}\left( { - S\cos \vartheta + \left( {1 + \frac{r}{p}} \right)T\sin \vartheta } \right)$

Здесь $u$ – аргумент широты, $\vartheta $ – истинная аномалия, ${\omega }$ – угол между направлением на перигелий и осью $O{\mathbf{i}}$ инерциального базиса, e и p – эксцентриситет и параметр орбиты Меркурия, S и T – радиальная и трансверсальная компоненты возмущающего ускорения.

Считая, что ось $O{\mathbf{i}}$ инерциального базиса параллельна направлению от Солнца на точку перигелия орбиты Меркурия, будем иметь

$x = r\cos \vartheta ,\quad y = r\sin \vartheta $, $z = {{r}^{2}} + 2r\cos (\vartheta - {\tau })$

а радиальная и трансверсальная компоненты возмущающего ускорения запишутся в виде

(2.9)

$S = \frac{{x{{W}_{x}} + y{{W}_{y}}}}{r} = {\varepsilon }\cos (\vartheta - {\tau })\left( {1 - \frac{1}{{{{Z}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right) - {\varepsilon }\frac{r}{{{{Z}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}$

(2.10)

$T = \frac{{ - y{{W}_{x}} + x{{W}_{y}}}}{r} = {\varepsilon }\sin ({\tau } - \vartheta )\left( {1 - \frac{1}{{{{Z}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right)$

Раскладывая функцию ${{Z}^{{ - 3/2}}}$ в ряд Тейлора по степеням переменной $z$ и подставляя этот ряд в формулы (2.9) и (2.10), получим для компонент возмущающего ускорения после осреднения по времени ${\tau }$ следующие выражения:

(2.11)

$\bar {S} = {\varepsilon }r\left( {\frac{1}{2} + \frac{9}{{16}}{{r}^{2}} + \frac{{75}}{{128}}{{r}^{4}} + \frac{{1225}}{{2048}}{{r}^{6}} + \frac{{19845}}{{32768}}{{r}^{8}} + \ldots } \right)$

(2.12)

$\bar {T} = 0$

Таким образом, осредненное по времени ${\tau }$ возмущающее ускорение имеет только радиальную компоненту, причем этот факт не зависит от числа вычисленных членов разложения функции ${{Z}^{{ - 3/2}}}$.

Отметим, что ряд (2.11) можно выразить через полные эллиптические интегралы первого и второго рода, но такое представление не приводит к упрощению, поскольку указанные интегралы также записываются в виде рядов, а коэффициенты в этих рядах будут сложным образом зависеть от переменной $r$.

Для средней по времени скорости смещения перигелия Меркурия, учитывая соотношения (2.8)–(2.12), получим формулу

(2.13)

$\frac{{d{\omega }}}{{du}} = - \frac{{\varepsilon }}{e}\,\left( {\frac{1}{2}{{r}^{3}} + \frac{9}{{16}}{{r}^{5}} + \frac{{75}}{{128}}{{r}^{7}} + \frac{{1225}}{{2048}}{{r}^{9}} + \frac{{19845}}{{32768}}{{r}^{{11}}} + ...} \right)\cos \vartheta $

Далее в формуле (2.13) проведем осреднение по истинной аномалии $\vartheta $. Для этого необходимо вычислить средние значения функций

${{r}^{s}}\cos \vartheta = \frac{{{{p}^{s}}\cos \vartheta }}{{{{{(1 + e\cos \vartheta )}}^{s}}}}$

по истинной аномалии $\vartheta $. Обозначим среднее угловыми скобками и введем обозначение

(2.14)

${{f}_{s}} = - \frac{1}{e}\left\langle {\frac{{\cos \vartheta }}{{{{{(1 + e\cos \vartheta )}}^{s}}}}} \right\rangle $

Раскладывая функции ${1 \mathord{\left/ {\vphantom {1 {{{{(1 + e\cos \vartheta )}}^{s}}}}} \right. \kern-0em} {{{{(1 + e\cos \vartheta )}}^{s}}}}$ в ряд Тейлора по степеням $e\cos \vartheta $, получим

${{f}_{3}} = \frac{3}{2} + \frac{{15}}{4}{{e}^{2}} + \frac{{105}}{{16}}{{e}^{4}} + \frac{{315}}{{32}}{{e}^{6}} + \frac{{3465}}{{256}}{{e}^{8}} + \ldots $

${{f}_{5}} = \frac{5}{2} + \frac{{105}}{8}{{e}^{2}} + \frac{{315}}{8}{{e}^{4}} + \frac{{5775}}{{64}}{{e}^{6}} + \frac{{45045}}{{256}}{{e}^{8}} + \ldots $

(2.15)

${{f}_{7}} = \frac{7}{2} + \frac{{63}}{2}{{e}^{2}} + \frac{{1155}}{8}{{e}^{4}} + \frac{{15015}}{{32}}{{e}^{6}} + \frac{{315315}}{{256}}{{e}^{8}} + \ldots $

${{f}_{9}} = \frac{9}{2} + \frac{{495}}{8}{{e}^{2}} + \frac{{6435}}{{16}}{{e}^{4}} + \frac{{225225}}{{128}}{{e}^{6}} + \frac{{765765}}{{128}}{{e}^{8}} + \ldots $

${{f}_{{11}}} = \frac{{11}}{2} + \frac{{429}}{4}{{e}^{2}} + \frac{{15015}}{{16}}{{e}^{4}} + \frac{{85085}}{{16}}{{e}^{6}} + \frac{{2909907}}{{128}}{{e}^{8}} + \ldots $

…

В итоге для средней скорости смещения перигелия Меркурия получим формулу

(2.16)

$\left\langle {\frac{{d{\omega }}}{{du}}} \right\rangle = {\varepsilon }\left( {\frac{1}{2}{{p}^{3}}{{f}_{3}} + \frac{9}{{16}}{{p}^{5}}{{f}_{5}} + \frac{{75}}{{128}}{{p}^{7}}{{f}_{7}} + \frac{{1225}}{{2048}}{{p}^{9}}{{f}_{9}} + \frac{{19845}}{{32768}}{{p}^{{11}}}{{f}_{{11}}} + \ldots } \right)$

В приведенных формулах согласно (2.3) $p = {P \mathord{\left/ {\vphantom {P R}} \right. \kern-0em} R}$ – отношение параметра P орбиты Меркурия к расстоянию между возмущающей планетой и Солнцем. Поскольку орбиты планет не точно круговые, то указанное расстояние вычислялось в трех вариантах.

В первом варианте за среднее расстояние ${{R}_{k}}$ между k-ой планетой и Солнцем принимался параметр ${{P}_{k}}$ орбиты планеты. Во втором варианте за среднее расстояние принималось “среднее геометрическое”, определяемое из условия

$R_{k}^{2} = {{a}_{k}}{{b}_{k}} \Rightarrow {{R}_{k}} = {{P}_{k}}{{(1 - e_{k}^{2})}^{{ - {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4}}}}$

где ${{a}_{k}}$ и ${{b}_{k}}$ – большая и малая полуоси орбиты планеты, ${{e}_{k}}$ – эксцентриситет орбиты планеты. В третьем варианте за среднее расстояние принималось среднее по времени:

(2.17)

${{R}_{k}} = \frac{1}{T}\int\limits_0^T {{{R}_{k}}(t)dt} = \frac{{{{P}_{k}}}}{{2\pi }}(1 - e_{k}^{2})\int\limits_0^{2\pi } {\frac{{d{\theta }}}{{{{{(1 + {{e}_{k}}\cos {\theta })}}^{3}}}}} = {{P}_{k}}\left( {1 + \frac{1}{2}e_{k}^{2} + \ldots } \right)$

Но ввиду того, что орбиты всех планет (кроме Меркурия) близки к круговым, различие между этими тремя значениями оказывается незначительным и на конечный результат существенного влияния не оказывает (относительная разница в конечном результате составляет сотые доли процента). Ниже приводятся результаты расчетов, где расстояния ${{R}_{k}}$ вычислялись по третьему варианту, т.е. как средние по времени.

Их формулы (2.16) следует, что за счет возмущения от $k$-й планеты орбита Меркурия за один его оборот вокруг Солнца поворачивается на угол

(2.18)

$\begin{gathered} \Delta {{{\omega }}_{k}} = 2{\pi }{{{\varepsilon }}_{k}}\left( {\frac{1}{2}{{f}_{3}}p_{k}^{3} + \frac{9}{{16}}{{f}_{5}}p_{k}^{5} + \frac{{75}}{{128}}{{f}_{7}}p_{k}^{7} + \frac{{1225}}{{2048}}{{f}_{9}}p_{k}^{9} + \ldots } \right) \\ {{{\varepsilon }}_{k}} = {{{{m}_{k}}} \mathord{\left/ {\vphantom {{{{m}_{k}}} {M,\quad {{p}_{k}} = {P \mathord{\left/ {\vphantom {P {{{R}_{k}}}}} \right. \kern-0em} {{{R}_{k}}}}}}} \right. \kern-0em} {M,\quad {{p}_{k}} = {P \mathord{\left/ {\vphantom {P {{{R}_{k}}}}} \right. \kern-0em} {{{R}_{k}}}}}} \\ \end{gathered} $

За один земной год это смещение составит $\Delta {{{\omega }}_{k}}{{{{T}_{E}}} \mathord{\left/ {\vphantom {{{{T}_{E}}} {{{T}_{M}}}}} \right. \kern-0em} {{{T}_{M}}}}$, где ${{T}_{E}}$ и ${{T}_{M}}$ – периоды обращения Земли и Меркурия вокруг Солнца. Суммарное смещение перигелия Меркурия за один земной год, выраженное в угловых секундах, запишется в виде

(2.19)

$\Delta {\omega } = {{6}^{4}} \cdot {{10}^{3}}\frac{{{{T}_{E}}}}{{{{T}_{M}}}}\sum\limits_{k = 1}^N {{{{\varepsilon }}_{k}}\left( {\frac{1}{2}{{f}_{3}}p_{k}^{3} + \frac{9}{{16}}{{f}_{5}}p_{k}^{5} + \frac{{75}}{{128}}{{f}_{7}}p_{k}^{7} + \frac{{1225}}{{2048}}{{f}_{9}}p_{k}^{9} + \ldots } \right)} $

Для вычисления функций f_s и коэффициентов ${{{\varepsilon }}_{k}}$ и p_k использовались данные о массах планет и характеристиках их орбит (значениях больших полуосей и эксцентриситетов) из справочника [6]. Эти данные и вычисленные по ним значения коэффициентов p_k представлены в табл. 2. Здесь возмущающие планеты нумеруются в порядке их удаления от Солнца, ${{{\varepsilon }}_{k}}$ – отношение массы планеты к массе Солнца, a_k – отношение большой полуоси орбиты планеты к большой полуоси орбиты Земли. В значении массы для Земли учтена и масса Луны.

Таблица 2

Планета	$\varepsilon $	$a$	$e$	${{p}_{k}}$
Меркурий		$a = 0.3871$	$\,e = 0.2056$	$P = 0.37074$
Венера	${{{\varepsilon }}_{1}} = {1 \mathord{\left/ {\vphantom {1 {408524}}} \right. \kern-0em} {408524}}$	${{a}_{1}} = 0.7233$	${{e}_{1}} = 0.0068$	${{p}_{1}} = 0.51255$
Земля	${{{\varepsilon }}_{2}} = {1 \mathord{\left/ {\vphantom {1 {328900}}} \right. \kern-0em} {328900}}$	${{a}_{2}} = 1.0000$	${{e}_{2}} = 0.0167$	${{p}_{2}} = 0.37074$
Марс	${{{\varepsilon }}_{3}} = {1 \mathord{\left/ {\vphantom {1 {309870}}} \right. \kern-0em} {309870}}$	${{a}_{3}} = 1.5238$	${{e}_{3}} = 0.0933$	${{p}_{3}} = 0.24438$
Юпитер	${{{\varepsilon }}_{4}} = {1 \mathord{\left/ {\vphantom {1 {1047.35}}} \right. \kern-0em} {1047.35}}$	${{a}_{4}} = 5.2027$	${{e}_{4}} = 0.0489$	${{p}_{4}} = 0.07135$
Сатурн	${{{\varepsilon }}_{5}} = {1 \mathord{\left/ {\vphantom {1 {3501.47}}} \right. \kern-0em} {3501.47}}$	${{a}_{5}} = 9.5227$	${{e}_{5}} = 0.0535$	${{p}_{5}} = 0.03898$
Уран	${{{\varepsilon }}_{6}} = {1 \mathord{\left/ {\vphantom {1 {22945}}} \right. \kern-0em} {22945}}$00	0${{a}_{6}} = 19.1637$	${{e}_{6}} = 0.0462$	${{p}_{6}} = 0.01937$

Результаты расчетов смещения перигелия Меркурия по формуле (2.19) приведены в табл. 3. Здесь $n$ – число членов ряда, учитываемых в формулах (2.18) и (2.15). Из этой таблицы видно, что ряд, отвечающий возмущению от Венеры, сходится медленнее других. Объясняется этот факт тем, что для Венеры коэффициент ${{p}_{1}} = 0.51255$ имеет самое большое значение по сравнению с коэффициентами ${{p}_{k}}$ ($k = 2,3,\; \ldots $) для других планет.

Таблица 3

Планета	Вклад в среднее смещение перигелия Меркурия (за один год в угловых секундах)
Планета	$n = 4$	$n = 7$	$n = 9$
Венера	2.8235	2.9220	2.9276
Земля	0.9565	0.9594	0.9594
Марс	0.0241	0.0241	0.0241
Юпитер	1.5757	1.5758	1.5758
Сатурн	0.0763	0.0763	0.0763
Уран	0.0014	0.0014	0.0014
Σ	5.4575	5.5590	5.5646

Заметим, что по мере увеличения числа членов в рядах (2.18) и (2.15) величина $\Delta {\omega }$ увеличивается, поскольку все члены в этих рядах положительны. Но, как показали расчеты, дальнейшее увеличение числа $n$ ($n > 9$) не приводит к заметному изменению результата. Это позволяет констатировать, что значение $\Delta {\omega } = 5.565$ угловых секунды в год близко к среднему смещению перигелия Меркурия в рамках рассматриваемой модели.

Разница между вычисленным по формуле (2.19) значением $\Delta {\omega } = 5.565''$ и данными наблюдений (5.70″) составляет 0.135″ (относительная разница составляет 2.5%). Эта разница существенно (в три раза) отличается от величины 0.42″, которую приводят во многих источниках и трактуют как дополнительное (аномальное) смещение, необъяснимое с позиций классической механики, и относят к релятивистскому эффекту.

3. Колебательные составляющие в смещении перигелия Меркурия. При определении смещения перигелия Меркурия по данным наблюдений необходимо учитывать, что возмущающее ускорение помимо среднего (2.11) имеет зависящие от времени колебательные составляющие разной амплитуды, частоты и фазы. За счет них измеренное по наблюдениям смещение перигелия Меркурия может существенно отличаться от истинного среднего даже на интервалах наблюдений в сотни лет. Рассмотрим этот вопрос подробнее.

Поскольку направление на перицентр меняется очень медленно, то производную по аргументу широты без ущерба для точности можно заменить производной по истинной аномалии. Тогда на основании уравнения (2.8) при учете формул (2.9) и (2.10) получим уравнение

(3.1)

$\frac{{d{\omega }}}{{d\vartheta }} = \frac{{{\varepsilon }{{r}^{2}}}}{e}\left( { - \cos {\tau } + \frac{{r(\cos (2\vartheta - {\tau }) - \cos {\tau })}}{{2p}}} \right)\left( {1 - \frac{1}{{{{Z}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}} \right) + \frac{{{\varepsilon }{{r}^{3}}\cos \vartheta }}{{e{{Z}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}}}$

Из интеграла площадей для невозмущенного движения получим второе уравнение

(3.2)

$\frac{{d{\tau }}}{{d\vartheta }} = \frac{{{{r}^{2}}}}{{{{p}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$

Уравнения (3.1) и (3.2) в сочетании с уравнением конических сечений

(3.3)

$r = \frac{p}{{1 + e\cos \vartheta }}$

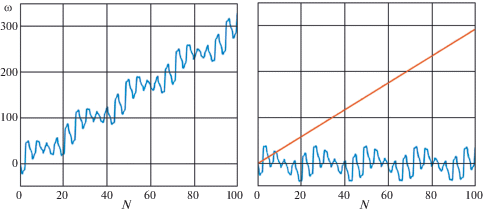
образуют замкнутую систему, в которой роль независимой переменной играет истинная аномалия. Численным интегрированием этой системы можно определить влияние возмущения от каждой планеты на поворот орбиты Меркурия (определить изменение угла ${\omega }$ в зависимости от числа оборотов Меркурия вокруг Солнца).

На рис. 1 слева представлено полученное численным интегрированием системы (3.1), (3.2) поведение ${\omega }$ за счет возмущения от Венеры. Здесь, как и всюду далее, $N$ – число земных лет, а ${\omega }$ вычисляется в угловых секундах. Полученный график свидетельствует о том, что величина ${\omega }$ меняется немонотонно. Если из этого графика “вычесть” вычисленное ранее среднее смещение (табл. 3), т.е. линейную функцию $N \cdot 2.9276$, то получится колебательная составляющая, изображенная на рис. 1 справа. Амплитуда этих колебаний достигает около сорока угловых секунд. Эта составляющая приближенно может быть описана в виде суммы двух колебаний с периодами ${{T}_{1}} \approx 5$ лет ${{T}_{2}} \approx 22$ года.

Рис. 1

Рис. 2

Рис. 3

Рис. 4

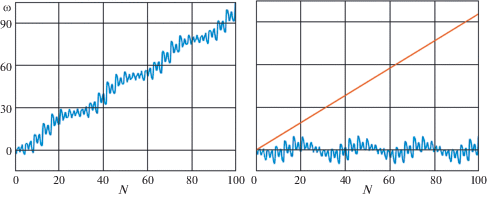
На рис. 2 приведен график поведения угла ${\omega }$ за счет возмущения от Земли. Здесь амплитуда колебательной составляющей достигает около десяти угловых секунд, а сама составляющая приближенно описывается суммой двух колебаний с периодами ${{T}_{1}} \approx 2$ года и ${{T}_{2}} \approx 28$ лет.

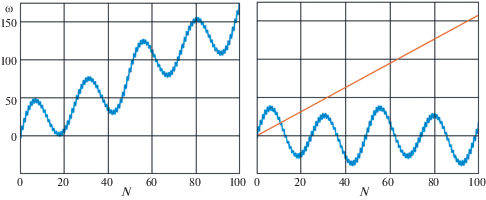
Влияние Юпитера на смещение перигелия Меркурия показано на рис. 3 . В этом случае, если не считать мелких осцилляций, колебательная составляющая близка к периодической функции с периодом около 50 лет, а ее амплитуда составляет около сорока угловых секунд.

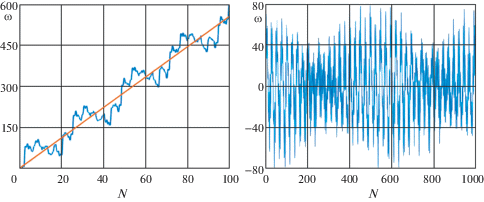
На рис. 4 слева показан график суммарного (при учете влияния всех планет) смещения перигелия Меркурия на интервале времени в сто лет, а справа – колебательная составляющая, вычисленная на интервале времени в одну тысячу лет.

Из представленных графиков следует, что в наблюдаемом смещении перигелия Меркурия помимо среднего имеются колебательные составляющие, суммарная амплитуда которых достигает 80 угловых секунд, с периодами от нескольких лет до нескольких десятков лет. Из-за наличия этих составляющих при вычислении среднего смещения по данным наблюдений на интервалах в десятки и даже сотни лет погрешность может существенно превышать указанные выше 2.5%, а для определения по данным наблюдений среднего смещения с относительной точностью до нескольких процентов потребное время наблюдений оценивается в тысячи лет. Поэтому утверждения о том, что наблюдаемое смещение перигелия орбиты Меркурия не объясняется полностью в рамках классической механики, нельзя признать строго обоснованными.

Автор выражает благодарность академику В.Ф. Журавлеву за обсуждение работы и замечания.

Список литературы

Le Verrier U. Théorie de mouvement de Mercure (фp.) // Ann. Observ. imp. 1859. V. 5. P. 1–96.
Le Verrier U. Lettre de M. Le Verrier à M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète (фp.) // Comptes rendus hebdomadaires des séances de l’Académie des sciences. 1859. V. 49. P. 379–383.
Эйнштейн А. Объяснение движения перигелия Меркурия в общей теории относительности // Собрание научных трудов в 4 томах. Т. I. С. 439–447.
Роузвер Н.Т. Перигелий Меркурия. От Леверье до Эйнштейна. Mercury’s perihelion. From Le Verrier to Einstein. М.: Мир, 1985. 244 с.
Дубошин Г.Н. Небесная механика. Основные задачи и методы. М.: Физматгиз, 1963. 588 с.
Справочное руководство по небесной механике и астродинамике. М.: Наука, 1976. 864 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал