1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 6, 2019

Известия РАН. Механика твердого тела, 2019, № 6, стр. 12-19

ВОЛНА РАЗГРУЗКИ В ЦИЛИНДРИЧЕСКОЙ СЕТИ

Дж. Г. Агаларов a, Т. Дж. Гасанова b, Г. А. Мамедова a, *

a Институт математики и механики Национальной академии наук Азербайджана
Баку, Азербайджан

b Азербайджанский архитектурно-строительный университет
Баку, Азербайджан

* E-mail: gular-gulshan@rambler.ru

Поступила в редакцию 02.02.2019
После доработки 16.02.2019
Принята к публикации 28.02.2019

Полный текст (PDF)

Аннотация

На основе уравнений движения сети в общем случае строятся уравнения движения цилиндрической сети.

Определяются варианты распространения волн в случае основы сети из упругих волокон. Решена задача о распространении волн разгрузки в предварительно натянутой сети. Задача решается методом характеристик. Задача иллюстрируется расчетами.

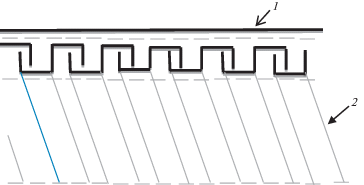
Ключевые слова: сеть, волна, скорость, деформация, радиус

Введение. В статьях [1–6] были исследованы волны в сетях в прямоугольной декартовой системе координат. Здесь исследуются волны в цилиндрической системе координат. Очевидно при растяжении цилиндрическая сеть будет сужаться; помещенная на жесткую трубу она при движении будет подвергаться действию сил трения между ней и трубой. Во избежание этого сеть помещается на винтовую трубу специального профиля, представляющую винтовой цилиндр с пористым наполнителем (Рудольф). На рис. 1 цифрой 1 – помечена сеть, 2 – пористый наполнитель. Такие трубы применяются, в частности при бурении и промывке скважин. Практически эти явления могут иметь место в гибких трубопроводах.

Рис. 1

Цель работы – состоит в исследовании волн в цилиндрических сетях. Учитывая множество вариантов распространения волн в цилиндрических сетях делается попытка решения задачи о непрерывных волнах.

1. Общие уравнения движения сети. Уравнение движения сети в пространстве, построенном на основе теории Рахматуллина Х.А., с учетом реакции поддерживающего тела и геометрические соотношения будут иметь вид, в отличие от [7, 8],

$\frac{\partial }{{\partial {{s}_{1}}}}\left( {{{\sigma }_{1}}{{{\bar {\tau }}}_{1}}} \right) + \frac{\partial }{{\partial {{s}_{2}}}}\left( {{{\sigma }_{2}}{{{\bar {\tau }}}_{2}}} \right) = 2\rho \frac{{{{\partial }^{2}}\bar {r}}}{{\partial {{\tau }^{2}}}} + p\bar {n}$
(1.1)
$\left( {1 + {{e}_{1}}} \right){{\bar {\tau }}_{1}} = \frac{{\partial{ \bar {r}}}}{{\partial {{s}_{1}}}};\quad \left( {1 + {{e}_{2}}} \right){{\bar {\tau }}_{2}} = \frac{{\partial{ \bar {r}}}}{{\partial {{s}_{2}}}}$
Здесь $\bar {r}$ – радиус вектор частицы сети, p – сила реакции опоры;

${{e}_{{\text{1}}}}$, ${{e}_{2}}$ – относительные удлинения соответствующих нитей;

${{{\text{s}}}_{{\text{1}}}}$, ${{s}_{2}}$ – Лагранжевы координаты частиц нитей;

${{\sigma }_{1}}$, ${{\sigma }_{2}}$ – условные напряжения, определяемые как сумма натяжений отдельных нитей одного семейства (пересекающих участок нити другого семейства), отнесение к первоначальной длине рассматриваемого элемента.

(Такое распределение массы и усилий допустимо при достаточно густой сети),

$\rho $ – масса сети, приходящая на единицу площади в начальном состоянии;

${{\bar {\tau }}_{1}}$ , ${{\bar {\tau }}_{2}}$ – единичные векторы, касательные к нитям;

$\bar {n}$ – нормаль к поверхности основания.

2. Координатная система. За базис цилиндрической системы принимаются: единичный вектор $\bar {i}$ – параллельный оси цилиндра, $\bar {j}$ – единичный вектор касательной к поперечному сечению цилиндра, $\bar {k}$ – единичный вектор, перпендикулярный к предыдущим.

Тогда

${{\bar {\tau }}_{1}} = {\text{cos}}{{\gamma }_{\iota }}\bar {\iota } + {\text{sin}}{{\gamma }_{1}}\bar {j};\quad {{\bar {\tau }}_{2}} = \cos {{\gamma }_{2}}\bar {\iota } + {\text{sin}}{{\gamma }_{2}}\bar {j}$
где ${{\gamma }_{{1,2}}}$ – углы нитей, образованные с осью цилиндра

Производные

$\frac{{\partial {{{\bar {\tau }}}_{1}}}}{{\partial {{s}_{1}}}} = \cos {{\gamma }_{1}}\frac{{\partial{ \bar {\iota }}}}{{\partial {{s}_{1}}}} + \bar {\iota }\frac{{\partial \left( {\cos {{\gamma }_{1}}} \right)}}{{\partial {{s}_{1}}}} + {\text{sin}}{{\gamma }_{1}}\frac{{\partial{ \bar {j}}}}{{\partial {{s}_{1}}}} + \bar {j}\frac{{\partial \left( {{\text{sin}}{{\gamma }_{1}}} \right)}}{{\partial {{s}_{1}}}}$
$\frac{{\partial {{{\bar {\tau }}}_{2}}}}{{\partial {{s}_{2}}}} = {\text{cos}}{{\gamma }_{2}}\frac{{\partial{ \bar {\iota }}}}{{\partial {{s}_{2}}}} + \bar {\iota }\frac{{\partial \left( {{\text{cos}}{{\gamma }_{2}}} \right)}}{{\partial {{s}_{2}}}} + {\text{sin}}{{\gamma }_{2}}\frac{{\partial{ \bar {j}}}}{{\partial {{s}_{2}}}} + \bar {j}\frac{{\partial \left( {{\text{sin}}{{\gamma }_{2}}} \right)}}{{\partial {{s}_{2}}}}$

Или учитывая

$\frac{{\partial{ \bar {\iota }}}}{{\partial {{s}_{1}}}} = \frac{{\partial{ \bar {\iota }}}}{{\partial {{s}_{2}}}} = 0;\quad \frac{{\partial{ \bar {j}}}}{{\partial {{s}_{1}}}} = - \frac{{{\text{sin}}{{\gamma }_{1}}}}{r}\bar {\kappa };\quad \frac{{\partial{ \bar {j}}}}{{\partial {{s}_{2}}}} = - \frac{{{\text{sin}}{{\gamma }_{2}}}}{r}\bar {\kappa }$

Получим

$\frac{{\partial {{{\bar {\tau }}}_{1}}}}{{\partial {{s}_{1}}}} = \frac{{\partial \left( {{\text{cos}}{{\gamma }_{1}}} \right)}}{{\partial {{s}_{1}}}}\bar {\iota } - \frac{{{{{\left( {{\text{sin}}{{\gamma }_{1}}} \right)}}^{2}}}}{r}\bar {\kappa } + \frac{{\partial \left( {{\text{sin}}{{\gamma }_{1}}} \right)}}{{\partial {{s}_{1}}}}\bar {j}$
(2.1)
$\frac{{\partial {{{\bar {\tau }}}_{2}}}}{{\partial {{\sigma }_{2}}}} = \frac{{\partial \left( {{\text{cos}}{{\gamma }_{2}}} \right)}}{{\partial {{s}_{2}}}}\bar {\iota } - \frac{{{{{\left( {{\text{sin}}{{\gamma }_{2}}} \right)}}^{2}}}}{r}\bar {\kappa } + \frac{{\partial \left( {{\text{sin}}{{\gamma }_{2}}} \right)}}{{\partial {{s}_{2}}}}\bar {j}$

Также учитывая $\vec {r} = x\vec {\iota } + r\vec {\kappa }$, имеем

$\frac{{\partial{ \vec {r}}}}{{\partial t}} = \frac{{\partial x}}{{\partial t}}\vec {\iota } + r\frac{{\partial{ \vec {\kappa }}}}{{\partial t}} = \frac{{\partial x}}{{\partial t}}\vec {\iota } + r\omega \vec {j}$
(2.2)
$\frac{{{{\partial }^{2}}\bar {r}}}{{\partial {{t}^{2}}}} = \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}\vec {\iota } + r\frac{{\partial \omega }}{{\partial t}}\vec {j} + r\omega \frac{{\partial{ \vec {j}}}}{{\partial t}}$ или $\frac{{{{\partial }^{2}}\bar {r}}}{{\partial {{t}^{2}}}} = \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}\vec {\iota } + r\varepsilon \vec {j} + r{{\omega }^{2}}\vec {\kappa }$
x – координата вдоль оси цилиндра, ω – угловая скорость, $\varepsilon {\text{*}}$ – угловое ускорение.

3. Уравнения движения цилиндрической сети. Подставив (2.1) и (2.2) в (1.1) получим

$\frac{\partial }{{\partial {{s}_{1}}}}\left( {{{\sigma }_{1}}{\text{cos}}{{\gamma }_{1}}} \right) + \frac{\partial }{{\partial {{s}_{2}}}}\left( {{{\sigma }_{2}}{\text{cos}}{{\gamma }_{2}}} \right) = 2\rho \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$
(3.1)
$\frac{\partial }{{\partial {{s}_{1}}}}\left( {{{\sigma }_{1}}{\text{sin}}{{\gamma }_{1}}} \right) + \frac{\partial }{{\partial {{s}_{2}}}}\left( {{{\sigma }_{2}}{\text{sin}}{{\gamma }_{2}}} \right) = r\varepsilon {\text{*}}$
$ - \frac{{{{\sigma }_{2}}}}{r}{\text{si}}{{{\text{n}}}^{2}}{{\gamma }_{2}} - \frac{{{{\sigma }_{2}}}}{r}{\text{si}}{{{\text{n}}}^{2}}{{\gamma }_{2}} = p + 2\rho r{{\omega }^{2}}$

Далее рассматривается симметричное расположение правых и левых волокон. Тогда уравнения (3.1), учитывая

${{\sigma }_{1}} = {{\sigma }_{2}} = \sigma ,\quad {{\gamma }_{1}} = - {{\gamma }_{2}} = \gamma ,\quad \omega = 0,\quad \varepsilon = 0$
примут вид

$\frac{\partial }{{\partial s}}\left( {\sigma {\text{cos}}\gamma } \right) = \rho \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$
(3.2)
$ - 2\sigma {\text{sin}}\gamma = p$

4. Геометрические соотношения. Определим производную радиуса-вектора $\vec {r}$ по $s$. Обозначив $\vec {r} = x\vec {i} + r\vec {k}$

$\frac{{\partial{ \bar {r}}}}{{\partial s}} = \frac{{\partial x}}{{\partial s}}\bar {\iota } + \frac{{\partial \kappa }}{{\partial s}}r = \frac{{\partial x}}{{\partial s}}\bar {\iota } + \frac{{\partial y}}{{\partial s}}\bar {j}$
$y$ – круговая координата, где согласно (1.1) и (2.1)

$\left( {1 + {{e}_{1}}} \right){\text{cos}}{{\gamma }_{1}}\vec {\iota } + \left( {1 + {{e}_{1}}} \right){\text{sin}}{{\gamma }_{1}}\vec {j} = \frac{{\partial r}}{{\partial {{s}_{1}}}}$
$\left( {1 + {{e}_{2}}} \right){\text{cos}}{{\gamma }_{2}}\vec {\iota } + \left( {1 + {{e}_{2}}} \right){\text{sin}}{{\gamma }_{2}}\vec {j} = \frac{{\partial r}}{{\partial {{s}_{2}}}}$
(4.1)
$\left( {1 + e} \right){\text{cos}}\gamma = \frac{{\partial x}}{{\partial s}}$
(4.2)
$\left( {1 + e} \right){\text{sin}}\gamma = \frac{{\partial y}}{{\partial s}}$

Поскольку сеть не вращается, то $y = {\text{const}}$ (по времени)

$\frac{{\partial \left( {\left( {1 + e} \right){\text{sin}}\gamma } \right)}}{{\partial t}} = 0$
или
(4.3)
$(1 + {{e}_{0}}){\text{sin}}{{\gamma }_{0}} = (1 + e)\sin \gamma $
где e0 и γ0 значения параметров в начальном состоянии.

Полагая материал сети линейно упругим, т.е. $\sigma = {\rm E} \cdot \varepsilon $, систему (3.2), (4.1) и (4.3) можно свести к одному квазилинейному уравнению второго порядка.

То есть из (3.2) следует

(4.4)
${\rm E} \cdot \frac{{\partial e}}{{\partial s}}{\text{cos}}\gamma + {\rm E} \cdot e \cdot \frac{\partial }{{\partial s}}{\text{cos}}\gamma = \rho \cdot \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$
или учитывая

(4.5)
$\frac{{\rm E}}{{1 + e}} \cdot \frac{{\partial e}}{{\partial s}}\frac{{\partial x}}{{\partial s}} + {\rm E} \cdot e \cdot \frac{\partial }{{\partial s}}\left( {\frac{1}{{1 + e}} \cdot \frac{{\partial x}}{{\partial s}}} \right) = \rho \cdot \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$

Или

(4.6)
$\frac{{\rm E}}{{1 + e}} \cdot \left( {1 - \frac{e}{{1 + e}}} \right) \cdot \frac{{\partial e}}{{\partial s}}\frac{{\partial x}}{{\partial s}} + \frac{{{\rm E} \cdot e}}{{1 + e}} \cdot \frac{{{{\partial }^{2}}x}}{{\partial {{s}^{2}}}} = \rho \cdot \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$

Из (4.3) и (4.1)

(4.7)
${{\left( {1 + e} \right)}^{2}} = {{\left( {\frac{{\partial x}}{{\partial s}}} \right)}^{2}} + {{(1 + {{e}_{0}})}^{2}}{\text{si}}{{{\text{n}}}^{2}}{{\gamma }_{0}}$

откуда

(4.8)
${{\left( {\frac{{\partial x}}{{\partial s}}} \right)}^{2}} = {{\left( {1 + e} \right)}^{2}} - {{(1 + {{e}_{0}})}^{2}}{\text{si}}{{{\text{n}}}^{2}}{{\gamma }_{0}}$
или

(4.9)
$\left( {1 + e} \right)\frac{{\partial e}}{{\partial s}} = \frac{{\partial x}}{{\partial s}}\frac{{{{\partial }^{2}}x}}{{\partial {{s}^{2}}}}$

Подставив (4.9) в (4.6), получим

$\frac{{\rm E}}{{1 + e}} \cdot \left( {1 - \frac{e}{{1 + e}}} \right) \cdot \frac{1}{{1 + e}}{{\left( {\frac{{\partial x}}{{\partial s}}} \right)}^{2}}\frac{{{{\partial }^{2}}x}}{{\partial s{}^{2}}} + \frac{{{\rm E} \cdot e}}{{1 + e}} \cdot \frac{{{{\partial }^{2}}x}}{{\partial {{s}^{2}}}} = \rho \cdot \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$
или
$\frac{{\rm E}}{{1 + e}} \cdot \left[ {\frac{{{{{\left( {\frac{{\partial x}}{{\partial s}}} \right)}}^{2}}}}{{{{{\left( {1 + e} \right)}}^{2}}}} + e} \right]\frac{{{{\partial }^{2}}x}}{{\partial {{s}^{2}}}} = \rho \cdot \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$
или

(4.10)
$\frac{{{{a}_{0}}^{2}}}{{1 + e}} \cdot \left[ {\frac{{{{{\left( {\frac{{\partial x}}{{\partial \sigma }}} \right)}}^{2}}}}{{{{{\left( {1 + e} \right)}}^{2}}}} + e} \right]\frac{{{{\partial }^{2}}x}}{{\partial {{s}^{2}}}} = \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$

Подставив (4.8) $\partial x{\text{/}}\partial s$ в (4.10), получим

(4.11)
$a_{0}^{2} \cdot \left[ {1 - \frac{{{{{(1 + {{e}_{0}})}}^{2}}{\text{si}}{{{\text{n}}}^{2}}{{\gamma }_{0}}}}{{{{{\left( {1 + e} \right)}}^{3}}}}} \right]\frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}} = \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$

Подставив (4.7) в (4.11), получим

(4.12)
$a_{0}^{2} \cdot \left[ {1 - \frac{{{{{(1 - {{e}_{0}})}}^{2}}{\text{si}}{{{\text{n}}}^{2}}{{\gamma }_{0}}}}{{{{{\left( {\sqrt {{{{\left( {\frac{{\partial x}}{{\partial s}}} \right)}}^{2}} + {{{(1 + {{e}_{0}})}}^{2}}{\text{si}}{{{\text{n}}}^{2}}{{\gamma }_{0}}} } \right)}}^{3}}}}} \right]\frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}} = \frac{{{{\partial }^{2}}x}}{{\partial {{t}^{2}}}}$

Последнее уравнение представляет собой квазилинейное уравнение в частных производных.

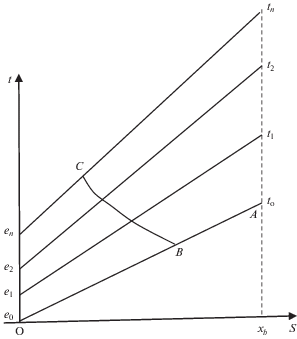
Коэффициент при $\frac{{{{\partial }^{2}}x}}{{\partial {{s}^{2}}}}$ в (4.11) с ростом $\frac{{\partial x}}{{\partial s}}$ растет, поэтому скорость волн с ростом деформации увеличивается, что ведет к образованию ударных волн [9]. Непрерывные волны будут возникать при разгрузке предварительно растянутого цилиндра. Рассмотрим этот случай (рис. 2). Здесь применяется метод характеристик.

Рис. 2

Из точки 0 волна распространяется с максимальной скоростью $a({{e}_{0}})$, поскольку волны с меньшей деформацией распространяются с меньшей скоростью и не будут влиять на состояние на фронте.

Пусть цилиндр находится в растянутом состоянии e0.

На границе цилиндр разгружается, т.е. конец его движется со скоростью $\vartheta $.

Характеристики уравнения (4.9) имеют вид, где

(4.13)
$ds = adt$
(4.14)
$ds = - adt$

Условия на характеристиках

(4.15)
$d{{x}_{t}} = ad{{x}_{s}}$ $\left( {\frac{{\partial x}}{{\partial s}} = {{x}_{s}},\,\,\,\frac{{\partial x}}{{\partial t}} = {{x}_{t}}} \right)$
и

(4.16)
$d{{x}_{t}} = - ad{{x}_{S}}$
$a = {{a}_{0}} \cdot \sqrt {1 - \frac{{{{{(1 - {{e}_{0}})}}^{2}}{\text{si}}{{{\text{n}}}^{2}}{{\gamma }_{0}}}}{{{{{\left( {\sqrt {{{{\left( {\frac{{\partial x}}{{\partial s}}} \right)}}^{2}} + {{{(1 + {{e}_{0}})}}^{2}}{\text{si}}{{{\text{n}}}^{2}}{{\gamma }_{0}}} } \right)}}^{3}}}}} $

Фронт волны разгрузки движется с скоростью $a({{e}_{0}})$. В области SОA (рис. 2) состояние покоя. Из условия на отрицательной характеристике BC следует ${{x}_{t}} = - \int_{x_{s}^{0}}^{{{x}_{s}}} {ad{{x}_{s}}} $; дифференцируя в направлении положительной характеристики имеем $d{{x}_{t}} = - ad{{x}_{s}}$.

Сравнивая с (4.15) получим ${{x}_{t}} = {\text{const}},{{x}_{s}} = {\text{const}}$ т.е. на положительных характеристиках ${{x}_{t}}$ и ${{x}_{s}}$ постоянны.

Из (4.13) имеем, учитываем постоянство xs на характеристике

(4.17)
$x = a(t - {{t}_{0}})$

На x = 0 выбираем ${{t}_{0}}$ и определяем ε.

Из (4.17)

${{t}_{0}} = t - \frac{x}{a}$
и соответственно

(4.18)
$\vartheta = {{\vartheta }_{0}}({{t}_{0}})$ или $\vartheta = {{\vartheta }_{0}}\left( {\tau - \frac{x}{a}} \right)$

Рассмотрим примеры: ${{\gamma }_{0}} = \frac{\pi }{4}$ и ${{\gamma }_{0}} = \frac{\pi }{6}$, ${{e}_{0}} = 0.1$, ${{a}_{0}} = 5000$ м/с.

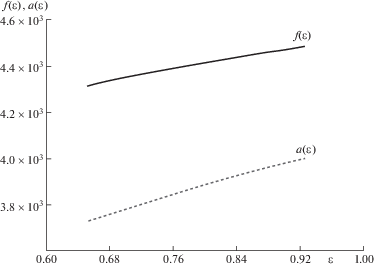
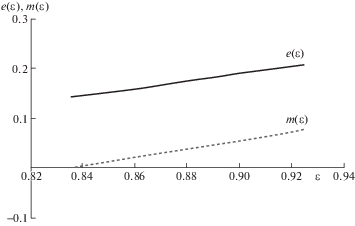
График $a({{x}_{s}}) = a(\varepsilon )$ (${{x}_{s}} = \varepsilon $), $f(\varepsilon )$ показан на рис. 3 и график e(ε), m(ε) показан на рис. 4.

Рис. 3
Рис. 4

Пусть на границе s = 0 цилиндр разгружается со скоростью $\vartheta (t)$.

На границе s = 0 также имеет место

Из (4.18),

(4.19)
$\vartheta (t) = - \int\limits_{{{\varepsilon }_{0}}}^\varepsilon {a({{x}_{s}})d{{x}_{s}}} $
где $\vartheta $ – функция верхнего предела интеграла.

Уравнение (4.19) является уравнением для определения осевой деформации сети ${{x}_{s}}$ = ε (в отличие от деформации волокон e), приближенно представив интеграл (4.12) в виде суммы имеем

(4.20)
$\vartheta = - \int\limits_{{{\varepsilon }_{0}}}^\varepsilon {a(\eta )d\eta } $
$\vartheta = \int\limits_\varepsilon ^{{{\varepsilon }_{0}}} {a(\eta )d\eta } $
$\begin{gathered} {{\vartheta }_{0}} = a({{\varepsilon }_{0}})\Delta \varepsilon \\ {{\vartheta }_{1}} = \left( {a({{\varepsilon }_{0}}) + a({{\varepsilon }_{1}})} \right) \cdot \Delta \varepsilon \\ {{\vartheta }_{2}} = \left( {a({{\varepsilon }_{0}}) + a({{\varepsilon }_{1}}) + a({{\varepsilon }_{2}})} \right) \cdot \Delta \varepsilon \\ ........................................... \\ {{\vartheta }_{n}} = \left( {a({{\varepsilon }_{0}}) + a({{\varepsilon }_{1}}) + \cdots + a({{\varepsilon }_{n}})} \right) \cdot \Delta \varepsilon \\ \end{gathered} $
или
$\vartheta = f(\varepsilon )$
т.е. обратную зависимость $\varepsilon \to \vartheta $ на границе. Поскольку положительные характеристики прямолинейны, можно определить ε во всей области движения. Функциональная зависимость скорости движения – скорость волны и деформация для данного примера представлена в табл. 1
(4.21)
${{\vartheta }_{n}} = f({{\varepsilon }_{0}} - \varepsilon )$
для ${{\gamma }_{0}} = \pi {\text{/}}4$ для ${{\gamma }_{0}} = \pi {\text{/}}6$.

Таблица 1
ε0 ε1 ε2 ε3 ε4 ε5 ε6 ε7 ε8 ε9 ε10 ε11
0.925 0.900 0.875 0.85 0.825 0.800 0.775 0.750 0.725 0.700 0.675 0.650
e(ε0) e(ε1) e(ε2) e(ε3) e(ε4) e(ε5) e(ε6) e(ε7) e(ε8) e(ε9) e(ε10) e(ε11)
0.209 0.190 0.171 0.152 0.134 0.116 0.098 0.081 0.063 0.046 0.030 0.014
${{\vartheta }_{0}}$ ${{\vartheta }_{1}}$ ${{\vartheta }_{2}}$ ${{\vartheta }_{3}}$ ${{\vartheta }_{4}}$ ${{\vartheta }_{5}}$ ${{\vartheta }_{6}}$ ${{\vartheta }_{7}}$ ${{\vartheta }_{8}}$ ${{\vartheta }_{9}}$ ${{\vartheta }_{{10}}}$ ${{\vartheta }_{{11}}}$
39.98 79.75 119.3 158.63 197.72 236.82 275.67 314.27 352.62 390.70 428.51 466.04
a(ε0) a(ε1) a(ε2) a(ε3) a(ε4) a(ε5) a(ε6) a(ε7) a(ε8) a(ε9) a(ε10) a(ε11)
3.998 × 103 3.977 × 103 3.955 × 103 3.933 × 103 3.909 × 103 3.885 × 103 3.860 × 103 3.835 × 103 3.808 × 103 3.781 × 103 3.753 × 103 3.724 × 103

Задавая на границе скорость движения конца сети как функцию времени можно определить деформацию как функцию времени на конце сети и вышеуказанным образом всюду в области $SOt$. Для примера возьмем $\vartheta = bt$ тогда $t = f(\varepsilon ){\text{/}}b$.

В зависимости от распределения скорости на границе определяется распределение деформации постоянной на характеристиках (рис. 3).

Таблица 2
ε0 ε1 ε2 ε3 ε4 ε5 ε6 ε7 ε8 ε9 ε10 ε11
0.925 0.92 0.915 0.910 0.905 0.900 0.895 0.890 0.885 0.880 0.875 0.870
e(ε0) e(ε1) e(ε2) e(ε3) e(ε4) e(ε5) e(ε6) e(ε7) e(ε8) e(ε9) e(ε10) e(ε11)
0.076 0.072 0.068 0.063 0.059 0.055 0.050 0.046 0.042 0.038 0.034 0.029
${{\vartheta }_{0}}$ ${{\vartheta }_{1}}$ ${{\vartheta }_{2}}$ ${{\vartheta }_{3}}$ ${{\vartheta }_{4}}$ ${{\vartheta }_{5}}$ ${{\vartheta }_{6}}$ ${{\vartheta }_{7}}$ ${{\vartheta }_{8}}$ ${{\vartheta }_{9}}$ ${{\vartheta }_{{10}}}$ ${{\vartheta }_{{11}}}$
44.81 89.59 134.5 179.09 223.8 268.49 313.15 357.79 402.4 446.98 491.54 536.07
a(ε0) a(ε1) a(ε2) a(ε3) a(ε4) a(ε5) a(ε6) a(ε7) a(ε8) a(ε9) a(ε10) a(ε11)
4.481 × 103 4.478 × 103 4.476 × 103 4.474 × 103 4.471 × 103 4.469 × 103 4.466 × 103 4.464 × 103 4.461 × 103 4.458 × 103 4.456 × 103 4.453 × 103

Список литературы

  1. Agalarov J.H., Gulieva M.A. Movement equation of a net in the plane // Изв. АН Азерб., сер. физ.-мат. наук, жур. “Математика и механика”. 1998. Т. XVIII. № 2. С. 103–105.

  2. Seyfullayev A.I., Gulieva M.A. To the solution of the equilibrium problem of the net // Proceedings of Institute of Mathematics and Mechanics of AS of Azerbaijan. Baku, 2000. V. XIII. P. 144–147.

  3. Агаларов Д.Г., Сейфуллаев А.И., Кулиева М.А. Численное решение одной плоской задачи равновесия сети // Механика, машиностроение. 2001. № 1. С. 3–4.

  4. Gulieva M.A. Tension of a rectangular net fastened from two adjacent sides // Proceedings of Institute of Mathematics and Mechanics of NAS of Azerbaijan, 2002. V. XVI (XXIV). P. 156–160.

  5. Agalarov J.H., Gulieva M.A. Waves of strong breaks in nets // Proceedings of Institute of Mathematics and Mechanics of NAS of Azerbaijan, 2002. V. XVII (XXV). P. 135–137.

  6. Агаларов Д.Г. Исследование движения сетей при ударе // Известия Академии Наук Азербайджанской ССР, Серия физико-технических и математических наук. 1982. № 6. С. 38–41.

  7. Рахматулин Х.А. Об ударе по гибкой нити // ПММ. 1947. Т. 10. № 3. С. 379–382.

  8. Agalarov J.H., Efendiev A.N. The propagation of nonlinear waves in a structure consisting of net system // Rakenteiden mekaniika seura RY Finish association for structural mechanics, 1988. V. 21. № 2. P. 3–10.

  9. Баренблат Г.И. О распространении мгновенных возмущений в среде с нелинейной зависимостью напряжений от деформаций // ПММ. 1953. Т. 17. № 4. С. 455–460.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал