Известия РАН. Механика твердого тела, 2019, № 5, стр. 45-58
ИЗГИБ И СТЕСНЕННОЕ КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ
В. Л. Присекин a, Г. И. Расторгуев a, *
a Новосибирский государственный технический университет
Новосибирск, Россия
* E-mail: rastorguev@adm.nstu.ru
Поступила в редакцию 05.10.2018
После доработки 05.10.2018
Принята к публикации 18.10.2018
Аннотация
Приведен вывод уравнений равновесия изгиба и кручения тонкостенного стержня с произвольным контуром поперечного сечения. Элементы конструкции стержня – пояса лонжеронов и стрингера – обладают жесткостью на растяжение–сжатие, а панели воспринимают только сдвиг. Панели соединяют пояса, что обеспечивает совместное деформирование всех элементов стержня. Перемещения поясов определяет гипотеза плоских сечений. При стесненном кручении перемещения поясов зависят от геометрических параметров и могут не совпадать с плоскостью поперечного сечения. Если на стержень действует только крутящий момент, то внутренние силы в поясах удовлетворяют уравнениям: сумма сил и суммы изгибающих моментов равны нулю. Ранг матрицы уравнений равен трем, поэтому в работе предложено образовать группы с разным числом поясов, и для каждой из них формировать уравнения равновесия стесненного кручения тонкостенного стержня. Это своеобразная форма уравнений равновесия поясов. Рассмотрены примеры кручения стержней.
1. Введение. Исследованию изгиба и кручения тонкостенного стержня с произвольным контуром поперечного сечения посвящено много работ [1–13]. В большинстве этих работ предполагается, что продольные силовые элементы работают на растяжение–сжатие, а обшивка и стенки лонжеронов – на сдвиг. Другой путь упрощения базируется на концепции замены стержня эквивалентным ортотропным стержнем (см., например, [14, 15]).
Наиболее полный учет дискретности подкрепляющего набора основывается на процедуре “склейки” решений для оболочки и набора по участкам [16–20] или с использованием дельта-функции Дирака для записи переменной жесткости тонкостенной подкрепленной конструкции [18, 20–22].
Несмотря на развитие вычислительных методов, в частности, МКЭ применительно к тонкостенным конструкциям [23–25], упрощенный подход при оценке прочности и жесткости авиационных конструкций достаточно широко применяется. В настоящей работе, как и в [1–12], предполагается, что элементы конструкции стержня – пояса лонжеронов и стрингера – обладают жесткостью на растяжение–сжатие, а панели представлены поясами и плоскими полосами жесткими только на сдвиг. Каждая панель или полоса соединяет два пояса, что обеспечивает совместное деформирование всех элементов стержня. Гипотеза плоских сечений определяет перемещения поясов стержня. При кручении стержня из-за формы контура поперечного сечения возникают внутренние силы в поясах Nj, которые удовлетворяют трем однородным уравнениям равновесия: $\sum {{{N}_{j}} = 0} $, $\sum {{{N}_{j}}{{y}_{j}} = 0} $, $ - \sum {{{N}_{j}}{{x}_{j}} = 0} $. Анализ уравнений приводит к выводу: все пояса следует разделить на группы численностью ${\text{ }}j = 4,5,\; \ldots ,\;n$. Тогда перемещения поясов каждой группы выразим вектором-столбцом ${{{\mathbf{\beta }}}^{{\text{т}}}}(z) = \left\{ {\begin{array}{*{20}{c}} {{{{\beta }}_{{4{\text{ }}}}}} \end{array}\begin{array}{*{20}{c}} {{{{\beta }}_{{5{\text{ }}}}}} \end{array} \ldots \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{{{\beta }}_{n}}} \end{array}} \end{array}} \right\}$, где ${{{\beta }}_{{j{\text{ }}}}}(z)$ – степень свободы поясов группы j из-за стеснения депланаций. В работе на основе принципа возможных перемещений получены дифференциальные уравнения равновесия изгиба и кручения тонкостенного стержня.
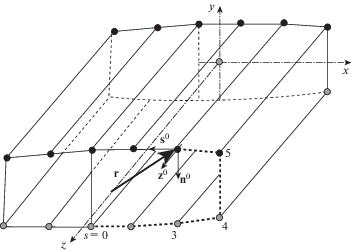
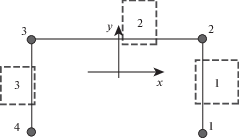
2. Постановка задач и основные уравнения. Крыло самолета большого удлинения представляет пример типичной конструкции тонкостенного стержня. Такая конструкция изображена на рис. 1. Поперечное сечение стержня представляет собой многосвязный замкнутый контур, образованный панелями крыла и стенками лонжеронов. Эти части конструкции соединяют пояса лонжеронов, и стрингеров. Для замкнутого контура количество панелей и стенок лонжеронов равно или больше числа поясов.
Примем, что оси x, y, z образуют правую ортогональную систему координат. Плоскости z = 0 и z = l определяют границы стержня. Начало осей координат расположено в центре тяжести поперечного сечения, а орты ${{{\mathbf{x}}}^{0}}$, ${{{\mathbf{y}}}^{0}}$ совпадают с осями главных моментов инерции стержня. Форма стержня – это линейчатая поверхность, образующие которой параллельны оси z. Для решения задачи изгиба и кручения стержня с произвольным контуром поперечного сечения примем допущение: панели, стенки лонжеронов представлены системой поясов, работающих на растяжение, и плоских полос, воспринимающих только сдвиг. На рис. 2 показана схема замены панели толщиной ${{h}_{0}}$ и поперечным размером ${{b}_{0}}$ на систему ${{k}_{0}}$ полос шириной ${{b}_{0}}{\text{/}}{{k}_{0}}$ с двумя поясами на границе площадью ${{b}_{0}} \cdot {{h}_{0}}{\text{/}}2{{k}_{0}}$ каждая. На границе соединения полос следует сложить площади поясов. Размеры полос по оси z и модуль сдвига материала соответствуют панели. Предложенная расчетная схема конструкции позволяет сформировать уравнения равновесия тонкостенного стержня, основанные на кинематических гипотезах. Отметим, что дальше полосы будем называть панелями.
В произвольном поперечном сечении положение точек панелей и поясов определено координатами $s$, $z$, где z – это расстояние от начала координат до плоскости сечения, а $s$ – длина контура поперечного сечения от начальной точки s = 0, при обходе контура в направлении против вращения часовой стрелки. Точку s = 0 совмещают с одним из поясов стержня. Введем номера поясов: номер 1 присвоим поясу с координатой s = 0. Затем, при обходе контура поперечного сечения стержня в направлении увеличения s, номера поясов представляют ряд натуральных чисел до значения $n$. На рис. 1 множество s изображено пунктирной линией, начиная c точки s = 0, и показана часть номеров поясов. Обозначим через ${{F}_{i}}$ площадь, ${{x}_{i}}$, ${{y}_{i}}$ – координаты центра тяжести пояса с номером $i$ ($i = 1,2, \ldots ,n$). Панелям так же присвоим номера $k = 1,2, \ldots ,m$. Следует отметить, что положение поясов определено в главной центральной системе координат $x$, $y$, $z$. Итог преобразований – это формирование таблицы поясов, их площадей, координат, и таблицы панелей, с указанием номеров примыкающих поясов.
Теория стесненного кручения была построена для расчета тонкостенного стержня, имеющего четыре пояса, что привело к понятию бимомента как системы уравновешенных сил. Здесь для расчета произвольного стержня применен принцип возможных перемещений, с помощью которого получены уравнения равновесия произвольного стержня, учитывающие изгиб и кручение конструкции.
Определение перемещений поясов и панелей выполним на основе двух допущений: гипотезы плоских сечений и гипотезы недеформируемости контура поперечного сечения. Пусть $U(z)$, $V(z)$, $W(z)$ – проекции перемещения поперечного сечения по направлению ортов ${{{\mathbf{x}}}^{0}}$, ${{{\mathbf{y}}}^{0}}$, ${{{\mathbf{z}}}^{0}}$, а ${\theta }(z)$ – угол поворота сечения в радианах относительно оси z. Введем координаты точек контура $x = {{x}_{0}}(s)$, $y = {{y}_{0}}(s)$, которые являются дифференцируемыми функциями переменной s. Обозначим символом ${\upsilon }(s,z)$ перемещение по направлению орта ${{{\mathbf{z}}}^{0}}$ точек панелей и поясов стержня. Тогда вектор ${\mathbf{\Delta }}$ полного перемещения точек стержня, с учетом поворота поперечного сечения на угол ${\theta }(z)$, в декартовой системе координат имеет вид:
(2.1)
${\mathbf{\Delta }} = (U - {{y}_{0}} \cdot {\theta }){{{\mathbf{x}}}^{0}} + (V + {{x}_{0}} \cdot {\theta }){{{\mathbf{y}}}^{0}} + {\upsilon }(s,z){{{\mathbf{z}}}^{0}}$Принято допущение ${\theta }(z) < 0.1$, поэтому $\sin {\theta } \approx {\theta }$, $\cos {\theta } \approx 1$. Перемещение ${\upsilon }$ образовано двумя компонентами ${\upsilon }\,(s,z) = w(s,z) + {\zeta }(s,z)$, где w(s, z) = W – ${{y}_{0}}dV{\text{/}}dz$ – ‒ x0dU/dz – перемещение, выраженное гипотезой плоских сечений, перемещение ${\zeta }(s,z)$ – это отклонение от плоскости (депланации). Отметим, что $w(s,z)$ определяет только деформацию удлинения, деформация сдвига панелей в соответствии с гипотезой плоских сечений, равна нулю. Для упрощения записи производные функций, зависящих от одной переменной, будем обозначать верхним символом “штрих” $dU{\text{/}}dz = U{\text{'}}$, $dx{\text{/}}ds = x{\text{'}}$, ${{d}^{2}}x{\text{/}}d{{s}^{2}} = x{\text{''}}$.
Локальную систему координат определим вектором ${\mathbf{r}} = {{x}_{0}}{{{\mathbf{x}}}^{0}} + {{y}_{0}}{{{\mathbf{y}}}^{0}}$, направленным из начала координат, в сечении $z$ до точки $s$ контура рис. 1. Перемещения и деформации элементов конструкции определим ортами правой системы координат ${{{\mathbf{s}}}^{0}}$, ${{{\mathbf{n}}}^{0}}$, ${{{\mathbf{z}}}^{0}}$:
(2.2)
${{{\mathbf{s}}}^{0}} = {\mathbf{r}}{\text{'}} = x_{0}^{'}{{{\mathbf{x}}}^{0}} + y_{0}^{'}{{{\mathbf{y}}}^{0}},$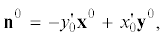 ${{{\mathbf{z}}}^{0}} = {{{\mathbf{s}}}^{0}} \cdot {{{\mathbf{n}}}^{0}}$
${{{\mathbf{z}}}^{0}} = {{{\mathbf{s}}}^{0}} \cdot {{{\mathbf{n}}}^{0}}$Орт ${{{\mathbf{s}}}^{0}}$ касается контура поперечного сечения в точке s и направлен против вращения часовой стрелки относительно оси z, как это показано на рис. 1. Орт n0 направлен по нормали к панели. Проекции вектора перемещений (2.1) на орты (2.2) определяют перемещения точек панелей в локальной системе координат: $u = {\mathbf{\Delta }}{{{\mathbf{s}}}^{0}}$, ${v} = {\mathbf{\Delta }}{{{\mathbf{n}}}^{0}}$, ${\upsilon }(s,z)\, = \,{\mathbf{\Delta }}{{{\mathbf{z}}}^{0}}$. Выразим перемещения точек панелей и поясов в поперечном сечении $z$:
(2.3)
$u = Ux_{0}^{'} + Vy_{0}^{'} + {\rho \theta ,}$ ${v} = - Uy_{0}^{'} + Vx_{0}^{'} + {\kappa \theta ,}$ ${\upsilon }(s,z) = w(s,z) + {\zeta }(s,z)$Здесь ${\rho } = {{x}_{0}}y_{0}^{'} - x_{0}^{'}{{y}_{0}}$ – это длина перпендикуляра из начала осей координат до линии касательной к контуру в точке s, ${\kappa } = {{x}_{0}}x_{0}^{'} + {{y}_{0}}y_{0}^{'}$. Перемещения (2.3) определяют деформации поясов ${{{\varepsilon }}_{z}}$ и сдвига панелей ${\gamma }$:
(2.4)
${\text{ }}{{{\varepsilon }}_{z}} = \partial w(s,z){\text{/}}\partial z + \partial {\zeta }(s,z){\text{/}}\partial z,\quad {{{\varepsilon }}_{s}} = \partial u{\text{/}}\partial s,\quad {\gamma } = \partial u{\text{/}}\partial z + \partial {\upsilon }(s,z){\text{/}}\partial s$Подставляя перемещения (2.1), (2.3) в определение ${\gamma }$ (2.4), получим выражение сдвига панели: ${\gamma } = {\rho \theta '} + \partial {\zeta }(s,z){\text{/}}\partial s$. Относительное удлинение панелей в направлении орта s0 равно нулю ${{{\varepsilon }}_{s}} = 0$, что соответствует гипотезе недеформируемости контура поперечного сечения. Гипотеза плоских сечений определяет напряжения, уравновешивающие внешние силы. В зонах ограничения перемещений ${\zeta }$ возникает дополнительное взаимно уравновешенное напряженное состояние.
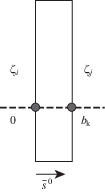
Деформацию сдвига ${{{\gamma }}_{k}}(z)$ панели k в сечении z определим как среднее значение ${\gamma }$ по координате $s$ (на рис. 3 линия интегрирования показана пунктиром):
Здесь ${{b}_{k}}$ – размер панели по направлению орта ${{{\mathbf{s}}}^{0}}$. Вычисленный интеграл определяет деформацию сдвига панели:
(2.5)
${{{\gamma }}_{k}} = b_{k}^{{ - 1}}({{{\zeta }}_{j}} - {{{\zeta }}_{i}} + {{{\omega }}_{k}}{\theta '})$Для плоской панели принято обозначение: ${{{\omega }}_{k}} = {{{\rho }}_{k}}{{b}_{k}}$. Деформацию сдвига всех панелей выразим вектором-столбцом:
Здесь введены векторы-столбцы: ${\mathbf{\zeta }}_{0}^{{\text{т}}} = ({{{\zeta }}_{1}},{{{\zeta }}_{2}},\; \ldots ,\;{{{\zeta }}_{n}})$ – депланации поясов ${{{\zeta }}_{i}}(z)$, i = = $1,2, \ldots ,n$; ${\mathbf{\gamma }}_{0}^{{\text{т}}} = ({{{\gamma }}_{1}},{{{\gamma }}_{2}},\; \ldots ,\;{{{\gamma }}_{m}})$ – сдвигов панелей ${{{\gamma }}_{i}}$ $i = 1,2,\; \ldots ,\;m$; ${{{\mathbf{\omega }}}^{{\text{т}}}} = ({{{\omega }}_{1}},{{{\omega }}_{2}},\; \ldots ,\;{{{\omega }}_{m}})$ – площадей ${{{\omega }}_{i}}$. Определены диагональная матрица ${{{\mathbf{D}}}_{{\mathbf{b}}}}$ с элементами на главной диагонали ${{b}_{j}}$, $j = 1,2,\; \ldots ,\;m$ и матрица S, размерностью $m$ строк (число панелей) и n столбцов (число поясов). Произведение ${\mathbf{S}}{{{\mathbf{\zeta }}}_{0}}$ выражает разность перемещения поясов в сечении z, соединяемых панелью. Число панелей, примыкающих к одному поясу, определено конструкцией стержня. Для каждой панели в строке k указывается номер i первого пояса при обходе контура поперечного сечения по направлению s0 и номер j второго. В эту строку $k$ матрицы S в столбец i заносится –1, а для столбца $j$ задается +1. Матрица S введена для формирования уравнений равновесия стержня. Программа расчета деформаций и внутренних сил основана на таблице соединения панелей и поясов. Образец такой таблицы приведен в первом примере (табл. 1).
Дальнейшие вычисления выполнены с учетом принятых допущений. Выразим напряжения в поясах и потоки касательных сил в панелях:
Здесь введены: E – модуль упругости, ${\nu }$ – коэффициент Пуассона, $G$ – модуль сдвига, ${{q}_{k}}{\text{ }}$– поток касательных сил в сечении панели $k$, ${{h}_{k}}$ – толщина панели. Напряжение σs не учитывают в уравнениях равновесия панелей, так как возможные деформации ${\delta }{{{\varepsilon }}_{s}} = 0$ и работа этих сил на возможных перемещениях равна нулю [26].
Формулы (2.1) определяют перемещения поясов ${{w}_{j}}(z)$ при условии, что центры тяжести поясов совпадают с контуром поперечного сечения: ${{x}_{j}} = {{x}_{0}}({{s}_{j}})$, ${{y}_{j}} = {{y}_{0}}({{s}_{j}})$. Перемещения поясов, определяемые гипотезой плоских сечений, имеют вид wj = = $\left\{ {\begin{array}{*{20}{c}} 1&{{{y}_{j}}}&{{{x}_{j}}} \end{array}} \right\}{\mathbf{f}}$. Здесь ${{{\mathbf{f}}}^{{\text{т}}}} = \left\{ {\begin{array}{*{20}{c}} W&{ - V{\text{'}}}&{ - U{\text{'}}} \end{array}} \right\}$ – это вектор-столбец перемещений и углов поворота поперечного сечения.
Для вывода уравнений равновесия тонкостенного стержня сформируем матрицы и вектора-столбцы, выражающие свойства поясов и панелей:
(2.6)
${{\Upsilon }_{{\mathbf{0}}}} = \left[ {\begin{array}{*{20}{c}} 1 \\ 1 \\ \ldots \\ 1 \end{array}\begin{array}{*{20}{c}} {{{y}_{1}}} \\ {{{y}_{2}}} \\ \ldots \\ {{{y}_{n}}} \end{array}\begin{array}{*{20}{c}} {{{x}_{1}}} \\ {{{x}_{2}}} \\ \cdots \\ {{{x}_{n}}} \end{array}} \right],$ ${{{\mathbf{w}}}_{{\mathbf{0}}}} = \left\{ {\begin{array}{*{20}{c}} {{{w}_{1}}} \\ {{{w}_{2}}} \\ {..} \\ {{{w}_{n}}} \end{array}} \right\},$ ${{{\mathbf{D}}}_{{\mathbf{F}}}} = \left[ {\begin{array}{*{20}{c}} {{{F}_{1}}} \\ 0 \\ {..} \\ 0 \end{array}\begin{array}{*{20}{c}} 0 \\ {{{F}_{2}}} \\ {..} \\ 0 \end{array}\begin{array}{*{20}{c}} {..} \\ {..} \\ {..} \\ {..} \end{array}\begin{array}{*{20}{c}} 0 \\ 0 \\ {..} \\ {{{F}_{n}}} \end{array}} \right],$ ${{{\mathbf{D}}}_{{\mathbf{h}}}} = \left[ {\begin{array}{*{20}{c}} {{{h}_{1}}} \\ 0 \\ {..} \\ 0 \end{array}\begin{array}{*{20}{c}} 0 \\ {{{h}_{2}}} \\ {..} \\ 0 \end{array}\begin{array}{*{20}{c}} {..} \\ {..} \\ {..} \\ {..} \end{array}\begin{array}{*{20}{c}} 0 \\ 0 \\ {..} \\ {{{h}_{m}}} \end{array}} \right]$.Перемещения поясов, относительные деформации и усилия определены гипотезой плоских сечений:
(2.7)
${\mathbf{w}} = {{\Upsilon }_{{\mathbf{0}}}}{\mathbf{f}},\quad {\mathbf{\varepsilon }} = {{\Upsilon }_{0}}{\mathbf{f}}{\text{'}},\quad {\mathbf{\sigma }} = [E{\text{/}}(1 - {{{\nu }}^{2}})]{{\Upsilon }_{0}}{\mathbf{f}}{\text{'}},\quad {\mathbf{N}} = {{{\mathbf{D}}}_{{\mathbf{E}}}}{{\Upsilon }_{0}}{\mathbf{f}}{\text{'}}$Здесь приняты обозначения: ${{{\mathbf{D}}}_{{\mathbf{E}}}} = [E{\text{/}}(1 - {{{\nu }}^{2}})]{{{\mathbf{D}}}_{{\mathbf{F}}}}$, ${\mathbf{N}}$ – вектор-столбец усилий в поясах. Учет поясов лонжеронов, как правило, приводит к расчёту конструкции стержня из разных материалов, что усложняет вычисления. Для решения упругих задач принципиальных сложностей не возникает. Отметим основное свойство матрицы ${{\Upsilon }_{0}}$. Введем вектор-столбец ${{{\mathbf{R}}}^{{\text{т}}}}\, = \,\left\{ {{{R}_{1}}{\text{,}}{{R}_{2}}, \ldots ,{{R}_{n}}} \right\}$ проекций произвольных сил на ось z, тогда произведение ${{{\mathbf{R}}}^{{\text{т}}}}{{\Upsilon }_{0}}$ = = $\left\{ {\sum {{{R}_{j}}} ,\sum {{{R}_{j}}{{y}_{j}}} , - \sum {{{R}_{j}}{{x}_{j}}} } \right\}$ определяет равнодействующую всех сил ${{R}_{j}}$ и их моменты относительно осей x, y. Если силы ${{R}_{j}}$ взаимно уравновешены, то для такой группы сил R имеем тождество:
(2.8)
${{{\mathbf{R}}}^{{\text{т}}}}{{\Upsilon }_{0}} = \left\{ {\begin{array}{*{20}{c}} {{\text{ }}0{\text{ }}} \end{array} \begin{array}{*{20}{c}} {0{\text{ }}} \end{array} \begin{array}{*{20}{c}} {{\text{ }}0{\text{ }}} \end{array} } \right\}$Тонкостенный стержень имеет $n$ степеней свободы перемещения поясов относительно оси z, что соответствует числу поясов. Три степени свободы представлены функциями $U(z)$, V(z), $W(z)$, которые выражают перемещения всех поясов. Оставшиеся $(n - 3)$ степени свободы перемещений поясов используем для формирования напряженного состояния, не учитываемого гипотезой плоских сечений. Описание стеснения депланации в поперечных сечениях стержня ранее было определено функциями ${\mathbf{\zeta }}_{0}^{{\text{т}}}(z) = \left\{ {\begin{array}{*{20}{c}} {{{{\zeta }}_{1}}{\text{(z) }}} \end{array}\begin{array}{*{20}{c}} {{{{\zeta }}_{2}}{\text{(z) }}} \end{array} \ldots {\text{ }}\begin{array}{*{20}{c}} {{{{\zeta }}_{n}}(z)} \end{array}} \right\}$. Однако, из этих $n$ функций лишь $(n - 3)$ могут быть произвольными, так как усилия в поясах должны удовлетворять условиям (2.8). Это вызывает сложности формирования и решения уравнений равновесия. Параметры ${{{\mathbf{\zeta }}}_{0}}(z)$ представим в виде произведения произвольных функций ${{{\beta }}_{j}}(z)$ на группу j перемещений поясов, удовлетворяющих условию (2.8). Число групп равно $(n - 3)$. Для их построения определим матрицу ${{{\mathbf{\lambda }}}_{0}} = {{{\mathbf{D}}}_{{\mathbf{F}}}}{{\Upsilon }_{0}}$. Преобразование ${{{\mathbf{\zeta }}}_{0}}(z)$ в линейно независимые группы выполним с помощью матрицы ${{{\mathbf{\lambda }}}_{1}}$ размерностью $n \cdot (n - 3)$:
(2.9)
${{{\mathbf{\lambda }}}_{0}} = \left[ {\begin{array}{*{20}{c}} {{{F}_{{1{\text{ }}}}}{\text{ }}} \\ {{{F}_{{2{\text{ }}}}}} \\ \ldots \\ {{{F}_{n}}{\text{ }}} \end{array}\begin{array}{*{20}{c}} {{{F}_{1}}{{y}_{{1{\text{ }}}}}} \\ {{{F}_{2}}{{y}_{{2{\text{ }}}}}} \\ \ldots \\ {{{F}_{n}}{{y}_{n}}{\text{ }}} \end{array}\begin{array}{*{20}{c}} {{{F}_{1}}{{x}_{1}}} \\ {{{F}_{2}}{{x}_{2}}} \\ \ldots \\ {{{F}_{n}}{{x}_{n}}} \end{array}} \right],$ ${\text{ }}{{{\mathbf{\lambda }}}_{1}} = \left[ {\begin{array}{*{20}{c}} {{{{\lambda }}_{{1,4}}}} \\ {{{{\lambda }}_{{2,4}}}} \\ \ldots \\ {{{{\lambda }}_{{n,4}}}} \end{array}\begin{array}{*{20}{c}} {{{{\lambda }}_{{1,5}}}} \\ {{{{\lambda }}_{{2,5}}}} \\ \ldots \\ {{{{\lambda }}_{{n,5}}}} \end{array}\begin{array}{*{20}{c}} {{{{\lambda }}_{{1,6}}}} \\ {{{{\lambda }}_{{2,6}}}} \\ \ldots \\ {{{{\lambda }}_{{n,6}}}} \end{array}\begin{array}{*{20}{c}} {...} \\ {...} \\ \ldots \\ \ldots \end{array}\begin{array}{*{20}{c}} {{{{\lambda }}_{{1,n}}}} \\ {{{{\lambda }}_{{2,n}}}} \\ \ldots \\ {{{{\lambda }}_{{n,n}}}} \end{array}} \right]$Элементы столбцов матрицы ${{{\mathbf{\lambda }}}_{1}} = \left[ {{{{\mathbf{c}}}_{4}}{\mathbf{, }}{{{\mathbf{c}}}_{5}},\; \ldots ,\;{{{\mathbf{c}}}_{{\mathbf{n}}}}} \right]$ – это неизвестные величины. Из формулы (2.8) следует, что минимальное число ненулевых сил равно 4. Номера столбцов матрицы ${{{\mathbf{\lambda }}}_{1}}$ начинаются с $j = 4$. Поэтому примем условие: число неизвестных элементов в столбце ${{{\mathbf{c}}}_{j}}$ равно номеру столбца j. Вычислим первые четыре элемента столбца ${{{\lambda }}_{{i,4}}}$, $i = 1, \ldots ,n$, а остальным элементам присвоим нулевые значения. Три уравнения для элементов столбца получим из условия ортогональности столбца ${{{\mathbf{c}}}_{4}}$ и матрицы ${{{\mathbf{\lambda }}}_{0}}$:
(2.10)
${\mathbf{c}}_{4}^{{\text{т}}}{{{\mathbf{\lambda }}}_{0}} = \left\{ {\begin{array}{*{20}{c}} {{\text{ }}0{\text{ }}} \end{array} \begin{array}{*{20}{c}} {0{\text{ }}} \end{array} \begin{array}{*{20}{c}} {0{\text{ }}} \end{array} } \right\}$Имеем три уравнения (2.10) для вычисления четырех неизвестных ${{\lambda }_{{i,4}}}$. Условие нормировки $\left| {{{{\lambda }}_{{i,4}}}} \right| \leqslant 1$ элементов столбца ${{{\mathbf{c}}}_{4}}$ дополняет эту систему уравнений. В результате задача сводится к решению системы уравнений с четырьмя неизвестными. На этом определение элементов столбца ${{{\mathbf{c}}}_{4}}$ матрицы ${{{\mathbf{\lambda }}}_{1}}$ завершено. Отметим, что после вычисления элементы строки ${\mathbf{c}}_{4}^{{\text{т}}}$ следует умножить на диагональную матрицу${{{\mathbf{D}}}_{{\mathbf{F}}}}$.
Как и в расчете ${{{\mathbf{c}}}_{4}}$, элементам ${{{\lambda }}_{{i,5}}}$ пятого столбца с индексом $i \geqslant 6$ присвоим нулевые значения. Для вычисления первых пяти элементов ${{\lambda }_{{i,5}}}$ столбца ${{{\mathbf{c}}}_{5}}$ к трем строкам ${\mathbf{\lambda }}_{0}^{{\text{т}}} = {{\left( {{{{\mathbf{D}}}_{{\mathbf{F}}}}{{\Upsilon }_{0}}} \right)}^{{\text{т}}}}$ добавим строку из вычисленных элементов столбца ${{{\mathbf{c}}}_{4}}$. Выполняя условие ортогональности ${{{\mathbf{c}}}_{5}}$ к четырем строкам ${\mathbf{\lambda }}_{0}^{{\text{т}}}$, сформируем четыре уравнения. Пятое уравнение – это условие нормировки $\left| {{{\lambda }_{{i,5}}}} \right| \leqslant 1$. После определения элементов ${\mathbf{c}}_{5}^{{\text{т}}}$ умножить на матрицу ${{{\mathbf{D}}}_{{\mathbf{F}}}}$. Процесс вычисления матрицы ${{{\mathbf{\lambda }}}_{1}}$ завершается определением элементов последнего столбца ${{{\mathbf{c}}}_{{\mathbf{n}}}}$.
Матрица ${{{\mathbf{\lambda }}}_{1}}$ образована столбцами:
(2.11)
${{{\mathbf{\lambda }}}_{1}} = \left[ {\begin{array}{*{20}{c}} {{{{\mathbf{c}}}_{4}}} \end{array}{{{\mathbf{c}}}_{5}} \ldots \begin{array}{*{20}{c}} {{{{\mathbf{c}}}_{{\mathbf{n}}}}} \end{array}} \right]$Условие ортогональности выполняется для каждого столбца, поэтому произведение матриц ${{\Upsilon }_{0}}$ и ${{{\mathbf{\lambda }}}_{1}}$ равно нулю и образует нулевую матрицу размерностью ${\text{3}} \cdot ({\text{n}} - {\text{3}})$:
(2.12)
$\Upsilon _{0}^{{\text{т}}}{{{\mathbf{\lambda }}}_{1}} = \left[ {\begin{array}{*{20}{c}} 0 \\ {{\text{0 }}} \\ 0 \end{array}{\text{ }}\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}{\text{ }}\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}{\text{ }}\begin{array}{*{20}{c}} {..} \\ {..} \\ {..} \end{array}{\text{ }}\begin{array}{*{20}{c}} 0 \\ 0 \\ 0 \end{array}} \right]$Отсюда следует, что любой столбец j матрицы ${{{\mathbf{\lambda }}}_{1}}$ с произвольным множителем скалярного типа $[E{\text{/}}(1 - {{{\nu }}^{2}})] \cdot {\beta }_{j}^{'}(z)$ определяет взаимно уравновешенную систему сил, удовлетворяющих тождеству (2.8). Для вывода уравнений равновесия тонкостенного стержня введем матрицу ${{\Upsilon }_{1}} = {\mathbf{D}}_{{\mathbf{F}}}^{{ - 1}} \cdot {{{\mathbf{\lambda }}}_{1}}$, элементы которой – безразмерные величины, а ${{\Upsilon }_{1}}$ представляет аналог матрицы ${{\Upsilon }_{0}}$, так как определяет перемещения и удлинения поясов, обусловленные стеснением депланации:
(2.13)
${{{\mathbf{\zeta }}}_{{\mathbf{\beta }}}} = {{\Upsilon }_{1}}{\mathbf{\beta }},$ ${{{\mathbf{\varepsilon }}}_{0}} = {{\Upsilon }_{1}}{\mathbf{\beta }}{\text{'}}$Здесь ${\mathbf{\beta }}(z)$ – вектор-столбец, компоненты которого являются функциями z ${\mathbf{\beta }}{{(z)}^{{\text{т}}}}\, = \,\left\{ {\begin{array}{*{20}{c}} {{{{\beta }}_{4}}(z)} \end{array},\begin{array}{*{20}{c}} {{{{\beta }}_{5}}(z)} \end{array}, \ldots \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {,{{{\beta }}_{n}}(z)} \end{array}} \end{array}} \right\}$. В развернутом виде имеем перемещения поясов ζβ = = $\sum\limits_{j = 4}^n {{{{\mathbf{c}}}_{{\mathbf{j}}}}{{{\beta }}_{j}}(z)} $ и деформацию ${{{\mathbf{\varepsilon }}}_{0}} = \sum\limits_{j = 4}^n {{{{\mathbf{c}}}_{{\mathbf{j}}}}{\beta }_{j}^{'}(z)} $. Выразим напряжения в поясах и усилия, из-за ограничения депланации:
(2.14)
${{{\mathbf{\sigma }}}_{0}} = [E{\text{/}}(1 - {{{\nu }}^{2}})]{{{\mathbf{\varepsilon }}}_{0}},\quad {{{\mathbf{N}}}_{0}} = {{{\mathbf{\Lambda }}}_{1}}{\mathbf{\beta }}{\text{'}},$ ${\text{ }}{{{\mathbf{\Lambda }}}_{1}} = {{{\mathbf{D}}}_{{\mathbf{E}}}}{{\Upsilon }_{1}}$Здесь через ${{{\mathbf{N}}}_{0}}$ обозначен вектор-столбец усилий в поясах, обусловленных депланацией. Представим матрицу ${{{\mathbf{\Lambda }}}_{1}}$ набором столбцов Λ1 = $[E{\text{/}}(1 - {{{\nu }}^{2}})]{{{\mathbf{\lambda }}}_{1}} = [E{\text{/}}(1 - {{{\nu }}^{2}})]$[c4, c5, ... cn], где ${{{\mathbf{c}}}_{{\mathbf{j}}}}$ определяют согласно (2.11) матрицу ${{{\mathbf{\lambda }}}_{1}}$. Тогда усилия в поясах стержня выразим суммой:
(2.15)
${{{\mathbf{N}}}_{0}} = [E{\text{/}}(1 - {{{\nu }}^{2}})]\sum\limits_{j = 4}^n {{{{\mathbf{c}}}_{{\mathbf{j}}}}{\beta }_{j}^{'}(z)} $Члены ряда (2.15) $[E{\text{/}}(1 - {{{\nu }}^{2}})]{{{\mathbf{c}}}_{{\mathbf{j}}}}{\beta }_{j}^{'}(z)$ сохраняют все установленные выше свойства для произвольного значения z. Например, из формулы (2.12) следует:
Для сходимости вычислений столбцов матрицы ${{{\mathbf{\lambda }}}_{1}}$ необходимо переномеровать пояса стержня, сохраняя их положение на контуре поперечного сечения. Номер 1 присвоить поясу с наибольшей площадью ${{F}_{{\max }}}$, расположенному на максимальном удалении от центра осей координат. Затем, при обходе контура в положительном направлении, присвоить номер $2$, ближайшему поясу с площадью ${{F}_{{\max }}}$, а наиболее удаленной группе поясов ${{F}_{{\max }}}$ – номера $3,{\text{ }}4$. Этот процесс напоминает сортировку поясов с убыванием площадей и расстояний от центра координат. Процесс замены номеров завершается на последней строке матрицы ${{\Upsilon }_{{\mathbf{0}}}}$. Необходимо стремится к равномерному заполнению контура новыми номерами поясов. Затем обновляются все таблицы и матрицы исходных данных.
Для вывода уравнений равновесия стержня, нагруженного распределенными силами и моментами, приведем формулы деформаций и напряжений в поясах и панелях:
(2.16)
${\mathbf{\varepsilon }} = {{\Upsilon }_{0}}{\mathbf{f}}{\text{'}} + {{\Upsilon }_{1}}{\mathbf{\beta }}{\text{'}},\quad {{{\mathbf{\gamma }}}_{0}} = {\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}({\mathbf{S}}{{\Upsilon }_{1}}{\mathbf{\beta }} + {\mathbf{\omega }}{\theta '}),\quad {\mathbf{\sigma }} = [E{\text{/}}(1 - {{{\nu }}^{2}})]{\mathbf{\varepsilon }},\quad {\mathbf{\tau }} = G{{{\mathbf{\gamma }}}_{0}}$Выразим так же силы в поясах и потоки касательных сил в панелях:
(2.17)
${{{\mathbf{N}}}_{{\mathbf{s}}}} = {\mathbf{N}} + {{{\mathbf{N}}}_{{\mathbf{0}}}} = {{{\mathbf{D}}}_{{\mathbf{E}}}}\left( {{{\Upsilon }_{0}}{\mathbf{f}}{\text{'}} + {{\Upsilon }_{1}}{\mathbf{\beta }}{\text{'}}} \right),\quad {\mathbf{q}} = {{{\mathbf{D}}}_{{\mathbf{G}}}}{\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}\left( {{\mathbf{S}}{{\Upsilon }_{1}}{\mathbf{\beta }} + {\mathbf{\omega }}{\theta '}} \right)$Отметим, что усилия в поясах Ns (2.17) определены гипотезой плоских сечений N и депланацией N0.
3. Уравнения равновесия тонкостенного стержня. Вывод уравнений равновесия тонкостенного стержня основан на принципе возможных перемещений [26]: если тело находится в состоянии равновесия, то разность работ внутренних сил δB и поверхностных δA на возможных перемещениях равна нулю: $\delta B - \delta A = 0$. В этой формулировке под поверхностными силами подразумеваются распределенные по оси z силы и моменты статически эквивалентные поверхностным силам:
Здесь Mz – внешний крутящий момент на конце стержня z = l; ${{p}_{x}}$, ${{p}_{y}}$, ${{p}_{z}}$ – распределенные по оси z силы, ${{{\mu }}_{z}}$ – распределенный крутящий момент.
Возможные перемещения ${{\Upsilon }_{0}}{\delta }{\mathbf{f}} + {{\Upsilon }_{1}}{\delta }{\mathbf{\beta }}$ и ${\delta \theta }$ определяют возможные деформации удлинения ${\delta }{\mathbf{\varepsilon }} = {{\Upsilon }_{{\mathbf{0}}}}{\delta }{\mathbf{f}}{\text{'}} + {{\Upsilon }_{{\mathbf{1}}}}{\delta }{\mathbf{\beta }}{\text{'}}$ и сдвига ${\delta }{\mathbf{\gamma }} = {\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}({\mathbf{S}}{{\Upsilon }_{{\mathbf{1}}}}{\delta }{\mathbf{\beta }} + {\mathbf{\omega }}{\delta \theta '})$, необходимые для вычисления работ внутренних сил. Преобразуем интегралы по объему поясов и панелей стержня. При вычислении интеграла по панелям контура следует, после перехода границы панели, заменить бесконечно малый элемент интеграла $h\,ds$ на площадь, примыкающего к панели пояса:
(3.1)
$\begin{gathered} {\text{ }}\int\limits_0^l {{\delta }{\mathbf{f}}{{{\text{'}}}^{{\text{т}}}}\Upsilon _{0}^{{\text{т}}}{{{\mathbf{D}}}_{{\mathbf{E}}}}{{\Upsilon }_{0}}{\mathbf{f}}{\text{'}}dz} + \int\limits_0^l {{\delta }{\mathbf{\beta }}{{{\text{'}}}^{{\text{т}}}}\Upsilon _{1}^{{\text{т}}}{{{\mathbf{D}}}_{{\mathbf{E}}}}{{\Upsilon }_{1}}{\mathbf{\beta }}{\text{'}}dz + } \\ + \;\int\limits_0^l {{\delta }{{{\mathbf{\beta }}}^{{\text{т}}}}\Upsilon _{1}^{{\text{т}}}{{{\mathbf{S}}}^{{\text{т}}}}{{{\mathbf{D}}}_{{\mathbf{G}}}}{\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}({\mathbf{S}}{{\Upsilon }_{{\mathbf{1}}}}{\mathbf{\beta }} + {\mathbf{\omega }}{\theta '})dz + } \int\limits_0^l {{\delta \theta '}{{{\mathbf{\omega }}}^{{\text{т}}}}{{{\mathbf{D}}}_{{\mathbf{G}}}}{\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}({\mathbf{S}}{{\Upsilon }_{{\mathbf{1}}}}{\mathbf{\beta }} + {\mathbf{\omega }}{\theta '})dz} - \\ - \;{{\left. {\int\limits_0^l {\left( {{\delta }W{{p}_{z}} + {\delta }V{{p}_{y}} + {\delta }U{{p}_{x}} + {\delta \theta }{{{\mu }}_{z}}} \right)} dz - {\delta \theta }{{M}_{z}}} \right|}_{{z = l}}} = 0 \\ \end{gathered} $Результат преобразования разности работ на возможных перемещениях в соответствии с положениями вариационного исчисления это дифференциальные уравнения равновесия и естественные граничные условия.
Приведем уравнения изгиба тонкостенного стержня:
Возможные варианты граничных условий определены заданием на расчет конструкции:
Для рассматриваемой задачи на границе z = 0 примем условие заделки стержня: W = 0, V = 0, $V{\text{'}} = 0$, U = 0, $U{\text{'}} = 0$. В сечении z = l выполним условие свободного конца стержня – внешние силы и изгибающие моменты равны нулю: $W{\text{'}} = 0$, $V{\text{''}} = 0$, $V{\text{'''}} = 0$, $U{\text{''}} = 0$, $U{\text{'''}} = 0$.
Дифференциальные уравнения равновесия для степеней свободы поясов разрешены относительно старших производных:
(3.2)
${{{\mathbf{J}}}_{{\mathbf{\beta }}}}{\mathbf{\beta }}{\text{''}} - {\mathbf{P\beta }} - {{{\mathbf{C}}}^{{\text{т}}}}{\theta '} = 0$Здесь ${\mathbf{\beta }}$ вектор-столбец функций порядка n – 3, ${{{\mathbf{J}}}_{{\mathbf{\beta }}}} = \Upsilon _{1}^{{\text{т}}}{{{\mathbf{D}}}_{{\mathbf{E}}}}{{\Upsilon }_{1}}$ диагональная матрица порядка $(n - 3)$, однако, из-за ошибок округления при вычислении матрицы ${{\Upsilon }_{1}}$, внедиагональные элементы по сравнению с диагональными представляют величины порядка $ \approx {\kern 1pt} {{10}^{{ - 15}}}$, ${\mathbf{C}} = {{{\mathbf{\omega }}}^{{\text{т}}}}{{{\mathbf{D}}}_{{\mathbf{G}}}}{\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}{\mathbf{S}}{{\Upsilon }_{1}}$ вектор-строка порядка n – 3, ${\mathbf{P}} = \Upsilon _{1}^{{\text{т}}}{{{\mathbf{S}}}^{{\text{т}}}}{{{\mathbf{D}}}_{{\mathbf{G}}}}{\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}{\mathbf{S}}{{\Upsilon }_{1}}$ матрица порядка $(n - 3) \cdot (n - 3)$, ${\theta '}$ – погонный угол кручения стержня. Преобразуем уравнение равновесия (3.2) к виду: $\Upsilon _{{\mathbf{1}}}^{{\text{т}}}({{{\mathbf{N'}}}_{0}} - {{{\mathbf{S}}}^{{\text{т}}}}{\mathbf{q}}) = 0$. Это уравнение показывает, что пояса нагружены потоками касательных сил панелей, формируемых матрицей ${{{\mathbf{S}}}^{{\text{т}}}}$. Решение системы уравнений (3.2) удовлетворяет граничным условиям:
(3.3)
$\delta {{{\mathbf{\beta }}}^{{\text{т}}}}\left. {({{{\mathbf{J}}}_{{\mathbf{\beta }}}}{\mathbf{\beta }}{\text{'}})} \right|_{0}^{l} = 0$Для задачи стесненного кручения стержня примем, что в сечении z = 0 степени свободы перемещений равны нулю ${\mathbf{\beta }} = 0$, а в сечении z = l отсутствуют внешние силы, приложенные к поясам: ${\mathbf{\beta }}{\text{'}} = 0$. На стержень в сечении z = l действует сосредоточенный крутящий момент Mz и распределенный крутящий момент ${{{\mu }}_{z}}$, определяющий изменение потока касательных сил в панелях:
Заменим в этом уравнении поток касательных сил ${\mathbf{q}}$, согласно формулам (2.17), и получим уравнение кручения стержня:
Здесь ${{J}_{\omega }} = {{{\mathbf{\omega }}}^{{\text{т}}}}{{{\mathbf{D}}}_{{\mathbf{G}}}}{\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}{\mathbf{\omega }}$ – скалярный параметр, ${\mathbf{C\beta }}{\text{'}}$ – произведение вектора-строки на вектор-столбец. Уравнение (3.4) определяет угол кручения стержня относительно оси z. Для однозначности решения дифференциального уравнения примем граничные условия: в сечении z = 0 угол кручения равен нулю ${\theta }(0) = 0$, а в сечении z = l, в соответствии с преобразованием разности работ (3.1), выполняется граничное условие:
(3.5)
${{J}_{\omega }}{\theta '}(l) + {{\left. {{\mathbf{C\beta }}(l) = {{M}_{z}}} \right|}_{{z = l}}}$Приведем вывод уравнений равновесия стержня, когда распределенный крутящий момент ${{{\mu }}_{z}} = 0$ и на стержень в сечении z = l действует только сосредоточенный крутящий момент Mz. В этом случае уравнение равновесия (3.4) можно интегрировать и получить решение ${{J}_{\omega }}{\theta '}(z) + {\mathbf{C\beta }}(z) = {\text{const}}$. Согласно граничному условию (3.5) значение ${\text{const}} = {{M}_{z}}$, поэтому в любой точке z осевой линии стержня выполняется уравнение:
Выразим погонный угол кручения:
Исключая угол ${\theta '}$ из уравнения (3.2) получим систему n – 3 дифференциальных уравнений для степеней свободы ${\mathbf{\beta }}(z)$:
(3.8)
${{{\mathbf{J}}}_{{\mathbf{\beta }}}}{\mathbf{\beta }}{\text{''}} - ({\mathbf{P}} - {{{\mathbf{C}}}^{{\text{т}}}}{\mathbf{C}}{\text{/}}{{J}_{\omega }}){\mathbf{\beta }} = {{{\mathbf{C}}}^{{\text{т}}}}{{M}_{z}}{\text{/}}{{J}_{\omega }}$Решение системы уравнений удовлетворяет граничным условиям (3.3): ${\mathbf{\beta }}(0) = 0$ и ${\mathbf{\beta }}{\text{'}}(l) = 0$. Эти условия определяют функции ${\mathbf{\beta }}{{(z)}^{{\text{т}}}} = \left\{ {\begin{array}{*{20}{c}} {{{{\beta }}_{4}}(z)} \end{array},\begin{array}{*{20}{c}} {{{{\beta }}_{5}}(z)} \end{array},\; \ldots \begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {,\;{{{\beta }}_{n}}(z)} \end{array}} \end{array}} \right\}$, затем по формуле (3.7) вычислим погонный гол ${\theta '}(z)$, и по формулам (2.17) найдем потоки касательных сил:
Здесь введены обозначения ${\mathbf{L}} = {{{\mathbf{D}}}_{{\mathbf{G}}}}{\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}{\mathbf{S}}{{\Upsilon }_{1}}$, ${\mathbf{g}} = {{{\mathbf{D}}}_{{\mathbf{G}}}}{\mathbf{D}}_{{\mathbf{b}}}^{{ - 1}}{\mathbf{\omega }}$
На основе полученных уравнений изучим частные случаи кручения тонкостенных стержней.
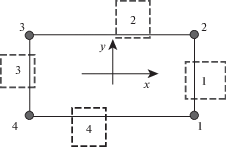
4. Численные результаты и их анализ. Пример 1. Кручение стержня с замкнутым контуром поперечного сечения. Стержень состоит из четырех поясов и четырех панелей. В $SI$ заданы следующие параметры: $E = 0.72 \times {{10}^{{11}}}$ Па, ${\text{ }}G = 0.27 \times {{10}^{{11}}}$ Па, ${\nu } = 0.3$, l = 1 м, ${{F}_{{1 - 4}}} = 2 \times {{10}^{{ - 4}}}$ м2, $b1 = b3 = 0.1$ м, $b2 = b4 = 0.3$ м, ${{M}_{z}} = 1.2 \times {{10}^{4}}$ Нм. Поперечное сечение стержня показано на рис. 4 с номерами поясов и панелей. Номера панелей обведены пунктирными квадратами. Последовательность соединения панелей и поясов приведена в табл. 1, которая является основой для формирования матрицы S. Поперечное сечение стержня имеет две оси симметрии. На стержень в сечении z = l действует только внешний крутящий момент Mz.
Матрицы ${{\Upsilon }_{0}}$ и ${{\Upsilon }_{1}}$ имеют вид:
(4.1)
${{\Upsilon }_{0}} = \left[ {\begin{array}{*{20}{c}} {1{\text{ }}} \\ {1{\text{ }}} \\ {1{\text{ }}} \\ {1{\text{ }}} \end{array}\begin{array}{*{20}{c}} { - 0.05} \\ {0.05} \\ {0.05} \\ { - 0.05} \end{array}\begin{array}{*{20}{c}} {0.15} \\ {0.15} \\ { - 0.15} \\ { - 0.15} \end{array}} \right]{\text{,}}\quad {{\Upsilon }_{1}} = \left[ {\begin{array}{*{20}{c}} {{\text{ }}1} \\ { - 1} \\ {{\text{ }}1} \\ { - 1} \end{array}} \right]$Степень свободы ${{{\beta }}_{4}}(z)$ представляет перемещения поясов вектора-столбца ${{\Upsilon }_{1}}$. Отметим, что параметры ${{J}_{\beta }}$, P, C для числа поясов n = 4 – скалярные величины. Матрица ${{\Upsilon }_{1}}$ состоит из одного столбца, у матрицы ${{\Upsilon }_{0}}$ второй и третий столбцы образованы координатами ${{y}_{j}}$, ${{x}_{l}}$ поясов стержня.
Уравнение равновесия поясов (3.8) имеет второй порядок относительно степени свободы ${{{\beta }}_{4}}$
(4.2)
${{J}_{{\beta }}}{\beta }_{4}^{{''}} - (P - {{C}^{2}}J_{{\omega }}^{{ - 1}}){{{\beta }}_{4}} = C{{M}_{z}}J_{{\omega }}^{{ - 1}}$Решение уравнения (4.2), удовлетворяющее граничным условиям ${{{\beta }}_{4}}(0) = 0$ и ${\beta }_{4}^{'}(l) = 0$, имеет вид:
(4.3)
${{{\beta }}_{4}}(z) = {\beta }0\left\{ {1 - {\text{ch}}({\lambda }(l - z)){\text{/ch}}({\lambda }l)} \right\}$Здесь приняты обозначения: ${\lambda } = \sqrt K $, $K = (P{{J}_{{\omega }}} - {{C}^{{\text{т}}}}C){{[{{J}_{{\omega }}}{{J}_{{\beta }}}]}^{{ - 1}}}$. Отметим, что параметр ${\beta }0 = ( - {{C}^{{\text{т}}}}{{M}_{z}}){{[P{{J}_{{\omega }}} - {{C}^{{\text{т}}}}C]}^{{ - 1}}}$ – это частное решение уравнения (4.2), оно определяет депланацию свободного стержня при кручении моментом. Приведем значения
параметров решения (4.3) ${\lambda } = 6.124$ и ${\beta }0 = 3.70 \times {{10}^{{ - 4}}}$. Матрица ${{\Upsilon }_{1}}$ состоит из одного столбца (4.1), поэтому перемещения поясов отличаются лишь знаком.
Степень свободы ${{{\beta }}_{4}}$ определяет перемещение поясов ${{{\mathbf{\zeta }}}_{{\mathbf{\beta }}}} = {{\Upsilon }_{1}}{{{\beta }}_{4}}(z)$. В сечении $z = l$ параметр β4(l) = $3.69 \times {{10}^{{ - 4}}}$, а в заделке равен нулю. Погонный угол кручения ${\theta '}$ имеет в заделке минимальное значение 0.0741, а в сечении z = l достигает величины 0.0987. Для свободного стержня, нагруженного крутящим моментом
Mz, погонный угол имеет величину 0.0988, что почти совпадает с полученным решением.
Погонный угол кручения ${\theta '}$ имеет в заделке минимальное значение 0.0741, а в сечении z = l достигает величины 0.0987. Для свободного стержня, нагруженного крутящим моментом
Mz, погонный угол имеет величину 0.0988, что почти совпадает с полученным решением.
Усилия в поясах образуют взаимно уравновешенные силы, называемые бимоментом, и определяются формулой ${{{\mathbf{N}}}_{0}} = {{{\mathbf{D}}}_{{\mathbf{E}}}}{{\Upsilon }_{1}}{\beta 0\lambda sh}({\lambda }(l - z)){\text{/ch}}({\lambda }l)$. Модуль сил имеет наибольшее значение в заделке $\left| {{{N}_{i}}} \right| = 3.27 \cdot {{10}^{4}}Н$, $i = 1,\; \ldots ,\;4$, на свободном конце z = l силы равны нулю ${{{\mathbf{N}}}_{0}} = 0$.
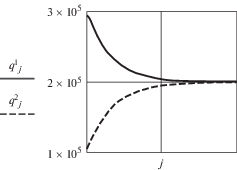
Формула (3.9) определяет поток касательных сил ${\mathbf{q}}$. Для изучаемого стержня ${\mathbf{q}}$ – это вектор-столбец четвертого порядка, элементы которого – потоки касательных сил в панелях стержня. На рис. 5 и далее в тексте заменены обозначения потоков касательных сил ${{q}_{i}}$, $i = 1,\; \ldots ,\;4$ на $q1,\; \ldots ,\;q4$. На конце стержня в сечении z = l потоки в панелях достигают значений $q1 = 2.004E5$, ${\text{ }}q2 = 1.996E5$. Эти величины почти не отличаются от потоков при кручении свободного стержня $q0 = {{M}_{z}}{\text{/}}2{\Omega }$ Н/м. Однако, в сечении z = 0 потоки определены гипотезой недеформируемости контура поперечного сечения. При повороте сечения вблизи плоскости $z = 0$ сдвиги панели 1 пропорциональны ${{{\rho }}_{1}} = {{x}_{2}}$ = 0.15, а панели 2 – ${{{\rho }}_{2}} = {{y}_{2}} = 0.05$, как это следует из матрицы ${{\Upsilon }_{0}}$ (4.1). Поэтому отношение потоков $q1 = 3E5$, $q2 = 1E5$ равно отношению ${{{\rho }}_{1}}{\text{/}}{{{\rho }}_{2}}$. Зависимость потоков касательных сил от переменной $z$ изображена на рис. 5.
Пример 2. Стержень с открытым контуром поперечного сечения. Контур стержня показан на рис. 6. Форма сечения – швеллер из четырех поясов и трех панелей. Поперечное сечение имеет одну ось симметрии, центр тяжести расположен вблизи стенки швеллера. Приведем параметры стержня: l = 1 м, ${{F}_{1}} = {{F}_{4}} = 6 \times {{10}^{{ - 4}}}$ м2, ${{F}_{2}} = {{F}_{3}} = 14 \times {{10}^{{ - 4}}}$ м2, $b1 = b3 = 0.1$ м, $b2 = 0.3$ м, ${{h}_{1}} = {{h}_{3}} = 0.011$ м, ${{h}_{2}} = 0.0065$ м, ${{M}_{z}} = 1.2 \times {{10}^{4}}$ Нм. Свойства материала стержня даны в первом примере. Для расчета перемещений поясов следует учесть толщины панелей, сформировать матрицы ${{{\mathbf{D}}}_{{\mathbf{G}}}},{\text{ }}{{{\mathbf{D}}}_{{\mathbf{b}}}}$ размерностью $3 \cdot 3$, матрицу ${\mathbf{S}}$ $3 \cdot 4$ и вектор-столбец ${\mathbf{\omega }}$ третьего порядка. Элементы матриц ${{\Upsilon }_{0}}$ и ${{\Upsilon }_{1}}$ отличаются от (4.1):
(4.4)
${{\Upsilon }_{0}} = \left[ {\begin{array}{*{20}{c}} {1{\text{ }}} \\ {1{\text{ }}} \\ {1{\text{ }}} \\ {1{\text{ }}} \end{array}\begin{array}{*{20}{c}} { - 0.07} \\ {0.03} \\ {0.03} \\ { - 0.07} \end{array}\begin{array}{*{20}{c}} {0.15} \\ {0.15} \\ { - 0.15} \\ { - 0.15} \end{array}} \right]{\text{,}}\quad {{\Upsilon }_{1}} = \left[ {\begin{array}{*{20}{c}} {{\text{ }}1} \\ { - 0.429} \\ {{\text{ }}0.429} \\ { - 1} \end{array}} \right]$Степень свободы ${{{\beta }}_{4}}(z)$ удовлетворяет уравнению (4.2), приведенному в примере 1. Эта функция определяет перемещения и усилия в поясах стержня.
Теперь перемещения поясов стержня выражены произведением ${{{\mathbf{\zeta }}}_{{\mathbf{\beta }}}}(z) = {{\Upsilon }_{1}}{{{\beta }}_{4}}(z)$. Усилия в поясах имеют вид 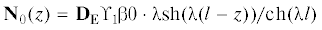 . В сечении z = 0 усилия ${{{\mathbf{N}}}_{0}}(0)$ принимают значения $ \pm {\text{1}}{\text{.015}} \times {{10}^{5}}$, а в сечении z = l – ${{{\mathbf{N}}}_{0}}(l) = 0$. Погонный угол кручения в точке z = 0 равен ${\theta '} = 8.67 \times {{10}^{{ - 3}}}$, затем этот параметр увеличивается и на конце стержня достигает значения ${\theta '} = 6.27 \times {{10}^{{ - 2}}}$. Полученные оценки свидетельствует о малой жесткости на кручение стержня с открытым
контуром поперечного сечения.
. В сечении z = 0 усилия ${{{\mathbf{N}}}_{0}}(0)$ принимают значения $ \pm {\text{1}}{\text{.015}} \times {{10}^{5}}$, а в сечении z = l – ${{{\mathbf{N}}}_{0}}(l) = 0$. Погонный угол кручения в точке z = 0 равен ${\theta '} = 8.67 \times {{10}^{{ - 3}}}$, затем этот параметр увеличивается и на конце стержня достигает значения ${\theta '} = 6.27 \times {{10}^{{ - 2}}}$. Полученные оценки свидетельствует о малой жесткости на кручение стержня с открытым
контуром поперечного сечения.
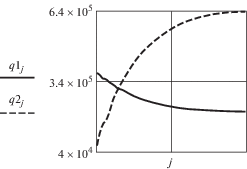
Изменение потоков касательных сил $q1$, $q1$, $q3$ в сечениях стержня показано на рис. 7. Отметим, что потоки в полках швеллера $q1 = q3$ всегда равны, но закон их изменения существенно отличается от потока $q2$ в стенке. Величины потоков приведены в табл. 2. Анализ данных показывает, что в сечении z = 0 поток в панели 2 почти на порядок меньше, чем в панелях 1 и 3. В окрестности сечения z = 0 деформация сдвига панелей пропорциональна произведению ${\rho } \cdot {\theta '}$. Для панелей 1 и 3 первый множитель равен ${{{\rho }}_{1}} = {{x}_{2}} = 0.15$, а для панели 2 равен ${{{\rho }}_{2}} = {{y}_{2}} = 0.03$. Эти координаты из матрицы ${{\Upsilon }_{0}}$ формул (4.6). Если учесть толщины панелей, то отношение потоков равно ${{{\rho }}_{1}}{{h}_{1}}{\text{/}}{{{\rho }}_{2}}{{h}_{2}}$ = = q1/q2 = 8.46, что подтверждает полученную оценку потоков касательных сил. С удалением от заделки поток $q2$ увеличивается, и в сечении z = l почти в три раза превосходит потоки в полках швеллера. Отметим, что момент потоков касательных сил в любом сечении стержня постоянный и удовлетворяет уравнению ${{{\mathbf{\omega }}}^{{\text{т}}}}{\mathbf{q}} = {{M}_{z}}$.
5. Заключение. Эта работа вызвана распространенным мнением о том, что не существует уравнений равновесия, описывающих депланацию произвольного тонкостенного стержня в задаче стесненного кручения [27]. По-видимому, в основе этого вывода сформировалось понятие бимомента как единственного представителя взаимно уравновешенного напряженного состояния поясов. Следует так же отметить и незавершенность исследований стесненного кручения тонкостенных стержней. В данной работе получены уравнения равновесия для изучения изгиба и кручения стержней с произвольным контуром поперечного сечения и на их основе получены численные результаты.
Список литературы
Уманский А.А. Кручение и изгиб тонкостенных авиаконструкций. М.: Оборонгиз, 1939. 112 с.
Ададуров Р.А. Определение касательных напряжений в тонкостенных конструкциях вблизи заделки // М.: Труды ЦАГИ. 1947. Вып. 615. 13 с.
Балабух Л.И. Расчет на прочность конических кессонов // М.: Труды ЦАГИ. 1947. Вып. 640. 54 с.
Феофанов А.Ф. Расчет тонкостенных конструкций. М.: Оборонгиз, 1958. 330 с.
Справочная книга по расчету самолета на прочность / Астахов М.Ф., Караваев А.В., Макаров С.Я. и др. М.: Гос. изд-во оборонной промышленности. 1954. 701 с.
Власов В.З. Тонкостенные упругие стержни. М.: Физматгиз, 1959. 574 с.
Образцов И.Ф. Методы расчета на прочность кессонных конструкций типа крыла. М.: Оборонгиз, 1960. 312 с.
Рабинович И.М. Основы строительной механики стержневых систем. М.: Гос. изд-во литературы по строительству, архитектуре и строит. материалам. 1960. 519 с.
Прочность, устойчивость, колебания. Справочник в трех томах / Под ред. Биргера И.А. и Пановко Я.Г. М.: Машиностроение, 1968. Т. 1. 831 с.
Кузьмин Н.А., Лукаш П.А., Милековский И.Е. Расчет конструкций из тонкостенных конструкций и оболочек. М.: Госсторойиздат, 1960. 264 с.
Джанелидзе Г.Ю. К теории тонких и тонкостенных стержней // Прикладная математика и механика. 1949. Вып. 6. Т. 13. С. 597–608.
Присекин В.Л., Галкина А.П. Расчет крыльев малого удлинения в условиях ползучести // Известия вузов. Авиационная техника. 1970. № 1. С. 76–78.
Лещенко А.П. Новые начала строительной механики тонкостенных конструкций. М.: Стройиздат, 1995. 719 с.
Жилин П.А. Линейная теория ребристых оболочек // Изв. АН СССР. МТТ. 1970. № 4. С. 150–162.
Yang B., Zhou J. Analysis of ring-stiffened cylindrical shells // Journal of Applied Mechanics. 1995. V. 62. P. 1005–1014.
Общая нелинейная теория упругих оболочек / Черных К.Ф. [и др.]. СПб.: Изд-во С.-Петерб. ун-та, 2002. 388 с.
Волчков Ю.М., Дергилева Л.А. Решение контактных задач на основе уточненной теории пластин и оболочек // ПМТФ. 2008. Т. 49. № 5. С. 169–176.
Семенов А.А. Алгоритмы исследования прочности и устойчивости подкрепленных ортотропных оболочек // Строительная механика инженерных конструкций и сооружений. 2014. № 1. С. 49–63.
Дудченко А.А. Прочность и проектирование авиационных конструкций из композиционного материала. М.: Изд-во МАИ, 2007. 199 с.
Образцов И.Ф., Онанов Г.Г. Строительная механика скошенных тонкостенных систем. М.: Машиностроение, 1973. 660 с.
Новицкий В.В. Дельта-функция и ее применение в строительной механике // Расчет пространственных конструкций. 1962. Вып. 8. С. 207–245.
Дудченко А.А., Сергеев В.Н. Нелинейные уравнения конической оболочки, подкрепленной дискретным набором шпангоутов // Вестник ПНИПУ. Механика. 2017. № 2. С. 78–98.
Martin G.V. Matrix load analysis method for flexible aircraft structures // SAE Techn. Pap. Ser. 1981. N 810610. 12 p.
Rajasekaran S. Finite element analysis of thin-walled for open cross sections // Structural Engineering Report / Department of Civil Engineering. University of Alberta. Edmonton. Canada. 1971. № 34. Sept. P. 144–160.
Серпик И.Н., Швыряев М.В. Конечно-элементное моделирование работы тонкостенных стержней открытого профиля для расчета пластинчато-стержневых систем // Известия вузов. Авиационная техника. № 1. С. 33–41.
Присекин В.Л., Расторгуев Г.И. Основы метода конечных элементов в механике деформируемых тел. Новосибирск: Изд-во Новосиб. гос. техн. ун-та, 2010. 237 с.
Ватин Н.И., Рыбаков В.А. Расчет металлоконструкций: седьмая степень свободы // Стройпрофиль. 2007. № 2 (56). С. 60–63.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела