Известия РАН. Механика твердого тела, 2019, № 5, стр. 37-44

Исследованию задачи о движении твердого тела на опорной поверхности посвящено достаточно большое число публикаций, подробный обзор которых можно найти в [1]. Качественный анализ динамически симметричного неоднородного шара на неподвижном основании проведен в работе [2]. Полагалось, что центр масс шара лежит на оси динамической симметрии и не совпадает с его геометрическим центром. Та же задача для тела состоящего из двух шаровых сегментов рассматривалась в [3]. Для технических приложений большой интерес представляет исследование динамики тел на вибрирующем основании, связанные с задачами вибротранспортировки [2] и сейсмоустойчивости [5–7].

1. Постановка задачи. Рассмотрим задачу о движении тяжелого неоднородного динамически симметричного шара радиуса R на вибрирующей в горизонтальном направлении абсолютно жесткой плоскости. Центр масс шара С лежит на оси динамической симметрии на расстоянии ${{c}_{0}}$ oт геометрического центра О. Введем подвижную систему координат Сx₁x₂x₃, так что ось Сx₃ проходит через точку О.

Из теорем об изменении количества движения и кинетического момента твердого тела получаем уравнения

Здесь m – масса тела, v и $\omega $ – векторы скорости центра масс и угловой скорости соответственно, g – ускорение свободного падения, N – нормальная составляющая реакции опорной плоскости, ${\mathbf{J}} = {\text{diag}}({{J}_{1}},{{J}_{1}},{{J}_{3}})$ – центральный тензор инерции шара, F⁰ – сила трения скольжения, M⁰ – момент трения верчения. Вектор восходящей вертикали $\gamma $ и радиус-вектор точки касания сферической поверхности с опорной плоскостью r, связаны соотношениями

Введем еще один вектор $\tau $, ортогональный вектору $\gamma $, вдоль которого происходит движение опорной плоскости. При рассмотрении более сложных законов движения основания, можно ввести еще один вектор ${\mathbf{n}} = \left[ {\gamma ,\tau } \right]$.

Условия постоянства векторов $\gamma $ и $\tau $ в системе координат Сx₁x₂x₃ имеют вид

В случае абсолютно жесткой опорной плоскости уравнение связи имеет вид

где ${\mathbf{u}} = {\mathbf{v}} + \left[ {\omega ,{\mathbf{r}}} \right] - {{V}_{1}} \cdot \tau - {{V}_{2}} \cdot {\mathbf{n}}$ – скорости точки контакта сферической поверхности тела с опорной плоскостью (скорость проскальзывания), ${{V}_{1}}(t) = {{Q}_{1}}\cos \left( {{{\theta }_{0}}t - {{\varphi }_{{01}}}} \right)$ – скорость опорной плоскости вдоль вектора τ, ${{V}_{2}}(t) = {{Q}_{2}}\cos \left( {{{\theta }_{0}}t - {{\varphi }_{{02}}}} \right)$ – скорость опорной плоскости вдоль вектора n, ${{Q}_{1}}$, ${{Q}_{2}}$, ${{\varphi }_{{01}}}$, ${{\varphi }_{{02}}}$ – амплитуды и фазы скоростей, ${{\theta }_{0}}$ – частота колебаний опорной плоскости.

При заданной модели трения система (1.1)–(1.5) замкнута относительно переменных ${\mathbf{v}}$, $\gamma $, $\omega $, τ и N. В отличии от случая движения тела на неподвижном основании [2], в систему уравнений входит вектор τ, задающий направление движения основания.

Введем безразмерное время ${{t}_{*}} = t{{\Omega }_{0}}$, где ${{\Omega }_{0}} = {{\left( {{{mg{{c}_{0}}} \mathord{\left/ {\vphantom {{mg{{c}_{0}}} {{{J}_{1}}}}} \right. \kern-0em} {{{J}_{1}}}}} \right)}^{{1/2}}}$ – собственная частота колебаний неоднородного шара на абсолютно гладком основании при отсутствии вращения вокруг оси Сx₃, а все линейные размеры отнесем к величине c₀ – расстоянию между центром масс и геометрическим центром сферической поверхности. Ограничимся рассмотрением малых амплитуд колебаний шара и будем полагать малыми величинами порядка $\varepsilon $ компоненты вектора нормали к опорной плоскости ${{\gamma }_{1}}$, ${{\gamma }_{2}}$, вектора направления движения основания ${{\tau }_{3}}$ и все компоненты вектора угловой скорости и скорости центра масс. Безразмерные силу трения и момент трения полагаем величинами порядка ε².

Из уравнения (1.5) можно выразить компоненту скорости центра масс ${{{v}}_{3}}$ и с помощью третьего уравнения (1.1) исключить из системы уравнений нормальную реакцию N. Из условия нормировки вектора $\gamma $ выражаем ${{\gamma }_{3}} = {{(1 - {{\varepsilon }^{2}}\gamma _{1}^{2} - {{\varepsilon }^{2}}\gamma _{2}^{2})}^{{1/2}}}$, а из условия ортогональности векторов $\gamma $ и $\tau $ находим ${{\tau }_{3}} = - \varepsilon \left( {{{\gamma }_{1}}{{\tau }_{1}} + {{\gamma }_{2}}{{\tau }_{2}}} \right){\text{/}}{{\gamma }_{3}}$.

В результате преобразований получаем систему девяти уравнений

В (1.6)–(1.10) i = 1, 2, введены следующие безразмерные параметры ${{\beta }_{1}} = {{mc_{0}^{2}} \mathord{\left/ {\vphantom {{mc_{0}^{2}} {{{J}_{1}}}}} \right. \kern-0em} {{{J}_{1}}}}$, β₂ = ${{{{J}_{3}}} \mathord{\left/ {\vphantom {{{{J}_{3}}} {{{J}_{1}}}}} \right. \kern-0em} {{{J}_{1}}}}$, $\delta = {{\left( {R - {{c}_{0}}} \right)} \mathord{\left/ {\vphantom {{\left( {R - {{c}_{0}}} \right)} {{{c}_{0}}}}} \right. \kern-0em} {{{c}_{0}}}}$, безразмерные силы и момент трения ${{f}_{i}} = {{\varepsilon }^{2}}m{{c}_{0}}\Omega _{0}^{2}f_{i}^{0}$, (i = 1, 2, 3), $M = {{\varepsilon }^{2}}mc_{0}^{2}\Omega _{0}^{2}{{M}^{0}}$, и оставлены слагаемые не выше второго порядка малости.

Полученные уравнения справедливы для любой модели трения. Для модели обобщенного вязкого трения [9] силы трения скольжения и момент трения верчения определяются следующими формулами

В безразмерном виде, с учетом введенных выше допущений и обозначений последние формулы принимают вид

В (1.11) оставлены слагаемые первого порядка малости и введены безразмерные коэффициенты трения ${{k}_{f}} = {{\varepsilon k_{f}^{0}} \mathord{\left/ {\vphantom {{\varepsilon k_{f}^{0}} {m{{\Omega }_{0}}}}} \right. \kern-0em} {m{{\Omega }_{0}}}}$, ${{k}_{m}} = \varepsilon {{k_{m}^{0}} \mathord{\left/ {\vphantom {{k_{m}^{0}} {m{{\Omega }_{0}}c_{0}^{2}}}} \right. \kern-0em} {m{{\Omega }_{0}}c_{0}^{2}}}$, которые полагаем малыми величинами порядка ε.

Система уравнений (1.6)–(1.10) с учетом принятой модели трения (1.11) образует замкнутую систему. Одно уравнение в данной системе является “лишним”, поскольку должно выполняться очевидное условие $\left( {\tau ,\tau } \right) = 1$. Так, например, при численном интегрировании системы уравнений последнее условие можно использовать для контроля точности получаемого решения.

2. Осредненные уравнения. При ε = 0 система (1.6)–(1.10) описывает движение неоднородного шара на абсолютно гладком основании. Порождающее решение имеет вид

Здесь ${{\psi }_{i}} = t + {{\varphi }_{i}}$, $i = 1,2$, при этом ${{{v}}_{1}}$, ${{{v}}_{2}}$ и ${{\omega }_{3}}$ – постоянные величины, в исходных уравнениях (1.6) и (1.8) они являются медленными функциями времени, причем скорость изменения ${{\omega }_{3}}$ имеет порядок ε².

В зависимости от значений амплитуд и фаз решение (2.1) соответствует либо плоскому движению тела, либо пространственному. Например, при ${{A}_{2}} = 0$ и ${{\psi }_{3}} = 0$ имеем колебания твердого тела в плоскости образованной векторами $\gamma $ и $\tau $, а при ${{A}_{2}} = {{A}_{1}}$, ${{\varphi }_{2}} = {{\varphi }_{1}} + \pi {\text{/}}2$ и ${{\psi }_{3}} = \varepsilon {{\omega }_{3}}t + {{\varphi }_{3}}$ получаем прецессию твердого тела на опорной плоскости.

При решении исходной системы уравнений (1.6)–(1.10) ограничимся рассмотрением главного резонанса. Введем малую частотную расстройку $\varepsilon \lambda = \theta - 1$, так что ψ_i(t) = = $(1 + \varepsilon \lambda )t + {{\varphi }_{i}}(t)$, $i = 1,2$, и малую частоту вращения εμ, так что ${{\psi }_{3}}(t) = \varepsilon \mu t + {{\varphi }_{3}}(t)$. Здесь $\theta = {{\theta }_{0}}{\text{/}}{{\Omega }_{0}}$ – безразмерная частота колебаний основания. Решение будем искать в виде (2.1), полагая амплитуды ${{A}_{2}}$, ${{A}_{1}}$, ${\rm T}$ и фазы колебаний ${{\varphi }_{1}}$, ${{\varphi }_{2}}$, ${{\varphi }_{3}}$ функциями времени. После подстановки в уравнения с учетом принятой модели трения (1.11) получаем систему уравнений в медленных переменных, которую не приводим, ввиду ее громоздкости.

После применения процедуры осреднения получаем следующую систему уравнений для медленных переменных ${{A}_{1}}$, ${{A}_{2}}$, ${\rm T}$, ${{\varphi }_{1}}$, ${{\varphi }_{2}}$, ${{\varphi }_{3}}$, ${{\omega }_{3}}$, ${{{v}}_{1}}$, ${{{v}}_{2}}$

Здесь введено обозначение ${{k}_{3}} = {{k}_{f}}\delta \left( {1 + \delta } \right) - {{k}_{m}}$.

Прежде всего, отметим, что скорость центра масс ${{{v}}_{1}}$, ${{{v}}_{2}}$ входит только в уравнения (2.7), так что эти две переменные можно исключить из рассмотрения.

Из уравнения (2.6) имеем ${\rm T} = const$. Как следует из (2.1), модуль единичного вектора $\tau $ определяется как ${{({{{\rm T}}^{2}} + {{\varepsilon }^{2}}\tau _{3}^{2})}^{{1/2}}}$. Учитывая, что в осредненных уравнениях (2.2)–(2.4) оставлены слагаемые не выше второго порядка малости, полагаем в дальнейшем T = 1. Из уравнения (2.5), в случае установившихся колебаний, следует формула для определения частоты

В первом приближении эта частота совпадает с частотой вращения тела вокруг оси Сx₃. Фаза ${{\varphi }_{3}}$ определяется точкой начала отсчета времени и выбором осей Сx₁ и Сx₂.

Для случая вибрации основания вдоль вектора $\tau $, решение системы уравнений (2.2)–(2.7) достаточно просто получается в предположении, что движение тела происходит в плоскости возбуждения колебаний. Полагая ${{Q}_{2}} = {{\varphi }_{{01}}} = {{A}_{2}} = {{\omega }_{3}} = {{{v}}_{2}} = 0$, T = 1 для установившихся колебаний, получаем систему нелинейных уравнений

Кроме того, из (2.5) следует μ = 0, из (2.7) – ${{{v}}_{1}} = 0$. Три уравнения в (2.8) обращаются в тождества при ${{\varphi }_{3}} = 0$, из первого и третьего уравнений получаем фазу и частотную расстройку, как функцию амплитуды колебаний

Равенство нулю фазы ${{\varphi }_{3}}$ означает, что в исходном положении ось Сx₁ подвижной системы координат совпадает с вектором τ. При произвольном положении твердого тела относительно неподвижной системы координат, получаем то же решение (2.9), но под ${{A}_{1}}$, ${{\varphi }_{1}}$ подразумеваем амплитуду и фазу колебаний проекции восходящей вертикали на ось твердого тела расположенную в плоскости векторов $\gamma $ и τ и ортогональную оси Сx₃.

Далее в уравнениях (2.2)–(2.4) полагаем ${{\varphi }_{3}} = 0$, после чего система несколько упрощается, и получаем систему пяти уравнений относительно${{A}_{1}}$, ${{A}_{2}}$, ${{\varphi }_{1}}$, ${{\varphi }_{2}}$, ${{\varphi }_{3}}$.

Скорость центра масс может быть получена из (2.7).

В общем случае не удается получить аналитического решения системы (2.10) при нулевой левой части, то есть для случая установившихся колебаний. Численное решение системы нелинейных алгебраических уравнений получено методом продолжения решения по параметру. Ранее этот метод успешно применялся к решению задач меньшей размерности [9, 10], подробное описание метода можно найти в [11].

Пусть для системы уравнений ${{U}_{i}}({\mathbf{r}},\lambda ) = 0$ при некотором значении ${{\lambda }^{k}}$ известно приближенное решение ${{{\mathbf{r}}}^{k}} = {{(A_{1}^{k},A_{2}^{k},\varphi _{1}^{k},\varphi _{2}^{k},\varphi _{3}^{k})}^{{\text{т}}}}$, тогда для значения ${{\lambda }^{{k + 1}}} = {{\lambda }^{k}} + \Delta \lambda $ приближенное решение представляется в виде ${{{\mathbf{r}}}^{{k + 1}}} = {{{\mathbf{r}}}^{k}} + \Delta {\mathbf{r}}$. Подставляя в систему (2.10) и линеаризуя полученные уравнения, определяем приращения неизвестных из системы

где ${{{\mathbf{R}}}^{k}}$ – вектор невязки на предыдущем шаге решения, элементы матрицы G имеют вид $g_{{ij}}^{{}} = {{d{{U}_{i}}} \mathord{\left/ {\vphantom {{d{{U}_{i}}} {d{{r}_{j}}}}} \right. \kern-0em} {d{{r}_{j}}}}$. Знак действительной части всех собственных значений матрицы G позволяет сделать вывод об устойчивости решения. Решение системы нелинейных уравнений (2.10) сводится к решению последовательности систем линейных уравнений (2.11). На каждом шаге вычислений контролируется величина невязки, и если относительная погрешность превышает заданную точность, то шаг варьируемой переменной уменьшается. В точках ветвления решений за независимый параметр принимается переменная, с наибольшим по модулю приращением на предыдущем шаге, что позволяет найти все существующие решения.

3. Результаты численного моделирования. В качестве примера рассмотрим шар со следующими безразмерными геометрическими характеристиками ${{\beta }_{1}} = 4$, ${{\beta }_{2}} = 1$, $\delta = 0.2$. Безразмерные амплитуды скорости движения основания полагаем ${{Q}_{1}} = 0.015\,$, ${{Q}_{2}} = {{10}^{{ - 8}}}$ и фазы ${{\varphi }_{{01}}} = 0$, ${{\varphi }_{{02}}} = \pi {\text{/}}2$.

Здесь вводится дополнительное предположение о наличии малой составляющей скорости основания в направлении n, поскольку на практике такая составляющая всегда существует. Коэффициент трения скольжения примем ${{k}_{f}} = 0.1$ и рассмотрим влияние коэффициента трения верчения на решение задачи.

При относительно больших значениях ${{k}_{m}} > 0.00041$ движение тела происходит исключительно в плоскости возбуждения колебаний и зависимость амплитуды ${{A}_{1}}$ от частотной расстройки $\lambda $ совпадает с (2.9), при этом ${{A}_{2}} \ll {{A}_{1}}$, ${{\omega }_{3}} = 0$. При меньших значениях ${{k}_{m}}$ происходит качественное изменение результатов решения.

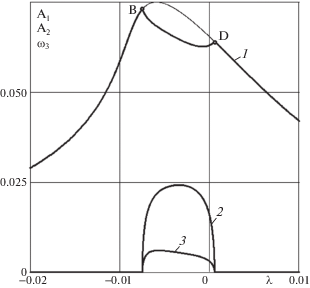
На рис. 1 приведены зависимости амплитуд колебаний твердого тела ${{A}_{1}}$, ${{A}_{2}}$ (кривые 1 и 2) и угловой скорости вращения ${{\omega }_{3}}$ (кривая 3) от частотной расстройки λ для ${{k}_{m}}$ = 0.00035. Устойчивые решения показаны жирной линией, неустойчивые – тонкой. Зависимость амплитуды колебаний в плоскости возбуждения ${{A}_{1}}$(λ) определяется формулой (2.9), но это решение на участке этой кривой между точками B и D является неустойчивым. Второе решение между точками B и D соответствует пространственному движению твердого тела. Тело вращается вокруг оси Cx₃ и в то же время точки этой оси движутся по эллипсам, большая ось которых несколько отклонена от вектора вдоль которого движется основание. Такое движение тела можно назвать псевдопрецессией.

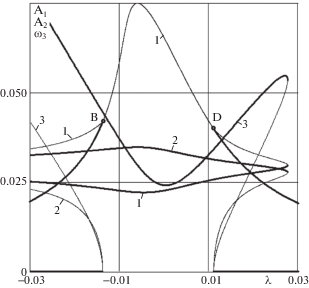
Уменьшение коэффициента трения верчения приводит к увеличению диапазона частотной расстройки, в которой происходит псевдопрецессия. При этом происходит еще одно качественное изменение полученных результатов. Те же зависимости амплитуд колебаний твердого тела (кривые 1 и 2) и угловой скорости вращения (кривая 3) от частотной расстройки для ${{k}_{m}} = 0.00012$ приведены на рис. 2. Кривые, соответствующие устойчивому пространственному движению тела, частично расположены правее точки D, так что в этом диапазоне частотной расстройки возможны как движения твердого тела в плоскости возбуждения колебаний, так и псевдопрецессия тела. При отсутствии трения верчения (k_m = 0) амплитуды колебаний и частота вращения неограниченно возрастают.

Сам факт существования пространственного движения неоднородного шара при вибрации опорной поверхности вдоль прямой не вызывает сомнений и наблюдается в простейшем натурном эксперименте. Количественные результаты требуют уточнения и экспериментальной проверки, в первую очередь из-за того, что коэффициенты трения могут быть заданы только очень приближенно. Неоднозначен и выбор модели трения. Рассмотренная в данной работе модель двухкомпонентного вязкого трения позволила получить относительно простое решение задачи.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (18-01-00335, 19-01-00140) и Программы № 29 Президиума РАН.