Известия РАН. Механика твердого тела, 2019, № 5, стр. 150-154
АНАЛИТИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ДЛИНЫ ДУГИ ЭЛЛИПТИЧЕСКОЙ КРИВОЙ
К. Н. Анахаев *
Институт прикладной математики и автоматизации
Кабардино-Балкарского научного центра Российской академии наук
Нальчик, Россия
* E-mail: anaha13@mail.ru
Поступила в редакцию 19.10.2018
После доработки 19.10.2018
Принята к публикации 22.02.2019
Аннотация
Эллиптические кривые широко распространены в очертаниях различных геофизических объектов, естественных и искусственных тел, траекториях движений планет, спутников, элементарных частиц и др. На их основе решаются многие теоретические и прикладные задачи, в том числе в области механики, геофизики и математической физики. Однако, до настоящего времени не в полной мере разработаны расчетные зависимости по нахождению длины отдельных участков (дуги) эллипса, востребованные в инженерной практике. В работе приведены аналитические зависимости для определения длины дуги и всего эллипса, полученные на основе представления неполного и полного эллиптических интегралов 2 рода в элементарных функциях и совпадающие с известными точными формулами для граничных очертаний эллипса – окружности и горизонтального отрезка прямой (тонкой плиты). Приведены также графики зависимости длины дуги эллипса от центрального угла и соотношения полуосей. Сравнение результатов решения тестовой задачи по предлагаемому методу с базовыми значениями численного расчета с использованием программы “Mathematic” показало достаточно близкое совпадение (≤0.5%).
Эллиптическая кривая
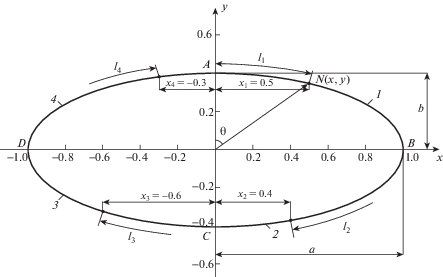
где x и y – текущие координаты по рис. 1; a и b – большая и малая полуоси эллипса, является одной из наиболее распространенных математических кривых 2-го порядка, на основе которой решаются многие теоретические и прикладные задачи механики, геофизики и математической физики, в том числе в области движения небесных тел, искусственных спутников и элементарных частиц. При этом длина эллиптической кривой ${{l}_{1}}$ (от оси 0y до рассматриваемой точки по часовой стрелке) на участке 1 (AB) (рис. 1) определяется зависимостью [1, 2](2)
${{l}_{1}} = a\int\limits_0^\varphi {\sqrt {1 - {{k}^{2}}{{{\sin }}^{2}}\varphi } } d\varphi = aE\left( {\varphi {\backslash }\alpha } \right)$Из равенства модуля $k = \sin \alpha $ выразим значение модулярного угла $\alpha $ через полуоси эллипса
В формуле (2) величина неполного эллиптического интеграла 2 рода $E\left( {\varphi {\backslash }\alpha } \right)$ не выражается через элементарные функции [2–4], а частные его значения аналитически рассчитываются либо медленно сходящимися рядами, либо путем трудоемкого перекрестного нелинейного интерполирования дискретных табличных данных. При этом для определения полной длины эллипса могут быть использованы также и приближенные формулы [5]. Отсутствие таковых для нахождения длины отдельных участков (дуги) эллипса вызывает неудобства и затруднения при решении различных задач механики и математической физики.
Для определения длины дуги эллипса от верхнего конца малой оси (точки A) до точки $N\left( {x,y} \right)$ на участке 1 (AB) l1 (рис. 1) преобразуем зависимость (2) с представлением неполного эллиптического интеграла 2 рода $E\left( {\varphi {\backslash }\alpha } \right)$ в элементарных функциях [6, 7] к виду
(6)
${{l}_{1}} = a\left\{ {\varphi - \left( {\varphi - \sin \varphi } \right)\frac{\alpha }{{90^\circ }} - \xi \left[ {\pi - \left( {\pi - 2} \right)\frac{\alpha }{{90^\circ }} - 2E\left( \alpha \right)} \right]\frac{{\varphi - \varphi {\text{*}}}}{{\pi - 2\varphi {\text{*}}}}} \right\}$(7)
$\varphi {\text{*}} = \frac{\pi }{4}\left( {1 + \frac{\alpha }{{65^\circ }}} \right)$, $\xi = \left\{ {\left. {\begin{array}{*{20}{c}} {0,}&{\varphi \leqslant \varphi {\text{*}}} \\ {1,}&{\varphi > \varphi {\text{*}}} \end{array}} \right\}} \right.$(8)
$E\left( \alpha \right) = \ln \sqrt {{{e}^{\pi }} - ({{e}^{\pi }} - {{e}^{2}}){{{\sin }}^{2}}\alpha } = \ln \sqrt {{{e}^{\pi }} - ({{e}^{\pi }} - {{e}^{2}})\left( {1 - \frac{{{{b}^{2}}}}{{{{a}^{2}}}}} \right)} $(9)
$E\left( \alpha \right) = \left[ {1 - \left( {1 - \frac{\pi }{4}} \right)\cos \alpha } \right](1 + \sqrt {{{{\cos }}^{3}}\alpha } ) = \left[ {1 - \left( {1 - \frac{\pi }{4}} \right)\frac{b}{a}} \right]\left[ {1 + {{{\left( {\frac{b}{a}} \right)}}^{{1,5}}}} \right]$Значения длин дуг эллипса ${{l}_{2}}$, ${{l}_{3}}$ и ${{l}_{4}}$ для участков 2(BC), 3(CD) и 4(DA) (от вертикальной оси 0y до рассматриваемых точек по часовой стрелке, рис. 1), соответственно, определяются формулами:
в которых величина ${{l}_{1}}$ находится по формуле (6) при значениях $\varphi $, подсчитанных по зависимости (4), соответственно, для абсцисс каждой из заданных точек.Для выражения зависимости длины дуги эллипса от центрального угла $\theta $ между вертикальной осью 0y и радиус-вектором 0N к рассматриваемой точке (рис. 1) амплитуду $\varphi $ для вышеприведенных формул следует определять по зависимости
(13)
$\varphi = \arcsin \left| {\frac{{b \cdot {\text{tg}}\theta }}{{\sqrt {{{a}^{2}} + {{b}^{2}}{\text{t}}{{{\text{g}}}^{2}}\theta } }}} \right|$При этом полная длина эллипса ${{L}_{э}}$ может быть определена по нижеследующим зависимостям (14) [6, 7] и (15)
(14)
${{L}_{э}} = 4a \cdot \ln \sqrt {{{e}^{\pi }} - ({{e}^{\pi }} - {{e}^{2}})\left( {1 - \frac{{{{b}^{2}}}}{{{{a}^{2}}}}} \right)} $(15)
${{L}_{э}} = 4a \cdot \left[ {1 - \left( {1 - \frac{\pi }{4}} \right)\frac{b}{a}} \right]\left[ {1 + {{{\left( {\frac{b}{a}} \right)}}^{{1,5}}}} \right]$Длина дуги между двумя произвольно расположенными точками эллипса находится как разность между значениями длин дуг от оси 0y, подсчитанных для каждой из этих точек в отдельности.
Для оценки точности полученных зависимостей по определению длин дуг эллипса в нижеследующей табл. 1 приводится сравнение их результатов с базовыми значениями, подсчитанными с использованием программных продуктов для тестовой задачи – эллипса с полуосями $a = 1.0$, $b = 0.4$.
Таблица 1
| Участки (по рис. 1) | Абсциссы заданных точек | Амплитуда $\varphi $ по (4) | Длина дуги эллипса | % | |
|---|---|---|---|---|---|
| базовое значение | по формулам автора (6)–(12) | ||||
| 1(AB) | ${{x}_{1}} = + 0.5$ | 0.52360 | 0.50392 | ${{l}_{1}} = 0.50618$ (0.50618) | +0.45 (+0.45) |
| 2(BC) | ${{x}_{2}} = + 0.4$ | 0.41152 | 1.89943 | ${{l}_{2}} = 1.89046$ (1.88783) | –0.47 (–0.61) |
| 3(CD) | ${{x}_{3}} = - 0.6$ | 0.64350 | 2.90868 | ${{l}_{3}} = 2.90487$ (2.90225) | –0.13 (–0.22) |
| 4(DA) | ${{x}_{4}} = - 0.3$ | 0.30469 | 4.30188 | ${{l}_{4}} = 4.28572$ (4.28047) | –0.38 (–0.50) |
| Полная длина эллипса ${{L}_{э}}$$(ABCDA)$ | 4.60264 | ${{L}_{э}} = 4.58695$ (4.58170) | –0.34 (–0.45) | ||
Как следует из таблицы, предлагаемые зависимости (6)–(12) для расчета длин дуг эллипса (выраженные в элементарных функциях) для рассмотренной тестовой задачи дают достаточно близкое приближение к базовым значениям (≤0.5%), причем для граничных очертаний эллипса – окружности и горизонтального отрезка прямой (тонкой плиты), указанные зависимости совпадают с известными точными формулами.
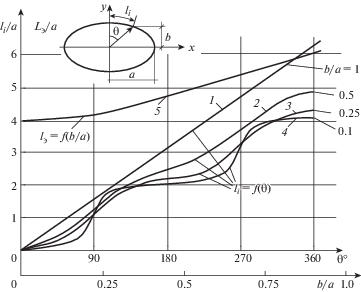
На рис. 2 приведены графики зависимостей длины дуги ${{l}_{i}} = f\left( \theta \right)$ и эллипса ${{L}_{э}} = f\left( {b{\text{/}}a} \right)$ от центрального угла $\theta $ и соотношений полуосей эллипса ($b{\text{/}}a$). Как видно из графиков, длина дуги li крайне неравномерно зависит от угла $\theta $, причем при увеличении значения $b{\text{/}}a > 0.5$ эта неравномерность “смягчается”, постепенно выпрямляясь для окружности. Длина эллипса ${{L}_{э}}$ для значений $0.4 \leqslant b{\text{/}}a \leqslant 1$ весьма близка к линейной зависимости и может быть описана простой формулой
которая рекомендуется для практического использования в указанном интервале.Заключение. В работе приведены аналитические зависимости для определения длины как отдельных участков (дуги), так и всего эллипса, полученные на основе представления неполного и полного эллиптических интегралов 2 рода в элементарных функциях. Для граничных очертаний эллипса – окружности и горизонтального отрезка прямой (тонкой плиты), предложенные зависимости совпадают с известными точными формулами. Приведены также графики зависимости длины дуги эллипса от центрального угла и соотношения полуосей. Сравнение результатов решения по предлагаемому методу для тестовой задачи – эллипса с полуосями a = 1.0, b = 0.4, с базовыми значениями численного расчета (программы “Mathematica”) показало достаточно близкое совпадение (≤0.5%).
Список литературы
Сикорский Ю.С. Элементы теории эллиптических функций с приложениями к механике. М.-Л., 1936. 365 с.
Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2. М.: Наука, 1969. 800 с.
Милн-Томсон Л. Эллиптические интегралы. В кн.: Справочник по специальным функциям. М.: Наука, 1979. С. 401–441.
Янке Е., Эмде Ф., Леш Ф. Специальные функции. М.: Наука, 1977. 342 с.
Бронштейн И.Н., Семендяев К.А. Справочник по математике М.: Наука, 1980. 975 с.
Анахаев К.Н. О методах расчета потенциальных (фильтрационных) потоков на основе эллиптических интегралов Якоби // Гидротехническое строительство. 2008. № 8. С. 7–9.
Anakhaev K.N. On methods of calculating potential (Seepage) flows on the basis of Jacobi elliptic integrals // Power Technology and Engineering. 2008. V. 42. № 5. P. 273–276.
Анахаев К.Н. О полных эллиптических интегралах 3-го рода в задачах механики // ДАН. 2017. Т. 473. № 2. С. 151–153.
Anakhaev K.N. Complete elliptic Jntegrals of the Third Kind in Problems of Mechanics // Doklady Physics. 2017. V. 62. № 3. P. 133–135.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела