Известия РАН. Механика твердого тела, 2019, № 5, стр. 142-149

Введение. Наряду с построением автономной модели расчета движения земного полюса, представляет интерес развитие и адаптивных моделей с учетом коррекции квазипостоянных коэффициентов модели (амплитуд основных гармоник), подверженных изменениям вследствие нестационарности возмущающих факторов, влияющих на движение земного полюса [1–5]. Такие модели не являются полностью автономными (их можно считать автономными на заданных требованиями задачи интервале времени), но имеют существенно большую точность прогнозирования. На практике выбор той или иной модели прогнозирования – результат компромиссного выбора между точностью прогноза, длительностью интервала прогнозирования (автономностью) и числом определяющих параметров, т.е. вычислительной сложностью модели.

В работах [3–5] исследуются точностные характеристики малопараметрических численно-аналитических моделей колебательного движения земного полюса в первом приближении. Модель движения земного полюса, рассмотренная в [6], представляет собой естественное уточнение ранее разработанной основной (двухчастотной) модели его колебаний и учитывает вариации амплитуд чандлеровской и годичной компонент, вызванные лунным возмущением.

В данной работе на основе численно-аналитического подхода предлагается модель колебаний полюса Земли, позволяющая улучшить точность прогноза его траектории во время нерегулярных эффектов, отмеченных ранее авторами [4, 5], вызванных изменчивостью амплитуд основных гармоник колебательного процесса. При изменении соотношения амплитуд основных компонент колебаний земного полюса, рассмотренных, например, в [6], его движение существенно отличается от движения “со средними параметрами”. Это приводит к необходимости модификации модели прогноза его движения для соответствующих интервалов времени.

1. Вариации тензора инерции свободного движения деформируемой Земли и постановка задачи. Для определения положения земного полюса на практике основополагающим является преобразование между двумя геоцентрическими системами координат – кёниговой системой ${{C}_{2}}{{{\xi }}_{1}}{{{\xi }}_{2}}{{{\xi }}_{3}}$ и связанной с Землей системой ${{C}_{2}}{{x}_{1}}{{x}_{2}}{{x}_{3}}$. Значения величин смещения полюса очень малы – они не превышают 0.5″ для годового его движения. Анализ данных наблюдений и измерений Международной службы вращения Земли (МСВЗ) [1] показывает, что влияние деформаций на вращение Земли вокруг центра масс оказывается весьма существенным. Таким образом, определение вариаций тензора инерции деформируемой Земли, а также вычисление вектора кинетического момента и его полной производной по времени, необходимо при исследовании как возмущенного, так и невозмущенного движения Земли относительно центра масс.

Вследствие предположения о малости деформаций среды мантии Земли будем рассматривать процесс деформирования в квазистатическом приближении, согласно линейной теории вязкоупругости [3, 7]. При сравнительно высокой частоте приливных колебаний мантия Земли ведет себя как упругое тело [8]. Влияние вязкости среды на коротких интервалах времени проявляется весьма слабо и в ряде случаев может быть опущено, например, при исследовании высокочастотных вариаций и краткосрочном прогнозировании движения земного полюса. Однако наличие в гидросфере мелко и крупномасштабных движений и турбулентных флуктуаций, что подтверждается геофизическими измерениями, может приводить к уменьшению кинетической энергии вращательного движения Земли и к затуханию чандлеровского колебательного процесса. В связи с этим является необходимым учет диссипативных свойств вязкоупругой мантии Земли. Эти допущения позволяют исследовать задачу в рамках методов механики и теории возмущений [8].

Оси системы координат ${{C}_{2}}{{x}_{1}}{{x}_{2}}{{x}_{3}}$, связанной с твердым ядром планеты в недеформированном ее состоянии, совместим с главными осями тензора инерции Земли. Для деформированного состояния обычно вводится система ${{C}_{2}}x_{1}^{'}x_{2}^{'}x_{3}^{'}$ путем переноса начала координат из точки C₂ в точку $C_{2}^{'}$ – центр масс с учетом малых деформаций – и параллельного переноса осей. Векторы перемещений u и ${\mathbf{w}}$, заданные в системах ${{C}_{2}}{{x}_{1}}{{x}_{2}}{{x}_{3}}$ и ${{C}_{2}}x_{1}^{'}x_{2}^{'}x_{3}^{'}$, связаны соотношением ${\mathbf{w}} = {\mathbf{u}} - {{{\mathbf{u}}}_{c}}$, где ${{{\mathbf{u}}}_{c}}$ – вектор перемещения центра масс Земли относительно твердого ядра. По данным наблюдений (например, спутниковой миссии GRACE – Gravity Recovery and Climate Experience [9]) перемещение центра масс крайне мало, поэтому в дальнейших выкладках им пренебрегается.

Предполагая, что мантия однородна и изотропна, вектор упругого перемещения u (в отсутствии диссипации) удовлетворяет уравнениям состояния Навье–Коши [10] и граничным условиям на поверхности Земли (P) и поверхности ядра (P₀):

Здесь ${\nu }$ – коэффициент Пуассона, ${\rho }$ – плотность, ${\mu }$ – модуль сдвига, $\nabla $ – оператор Гамильтона, $\Delta $ – оператор Лапласа, ${\mathbf{n}}$ – вектор нормали к P, ${{{\sigma }}_{n}}$ – тензор напряжений,

– массовая плотность сил инерции, ${\mathbf{\omega }} = {{\left( {{{{\omega }}_{{\text{1}}}}{\text{,}}{{{\omega }}_{{\text{2}}}}{\text{,}}{{{\omega }}_{{\text{3}}}}} \right)}^{{\text{т}}}}$ – вектор мгновенной угловой скорости вращения Земли, заданный своими компонентами для квазистационарной модели в системе координат ${{C}_{2}}{{x}_{1}}{{x}_{2}}{{x}_{3}}$, ${\mathbf{r}} = {{({{x}_{1}},{{x}_{2}},{{x}_{3}})}^{{\text{т}}}}$ – радиус-вектор, задающий положение точки планеты в недеформированном состоянии.

Вектор перемещения ${\mathbf{u}}$ можно представить в виде суммы ${\mathbf{u}} = {\mathbf{u}}({\mathbf{r}},{\mathbf{\omega }}) + {{{\mathbf{u}}}_{*}}({\mathbf{r}},t)$ векторов смещения в поле центробежных сил инерции ${\mathbf{u}}({\mathbf{r}},{\mathbf{\omega }})$ и смещения, вызванного гравитационными приливами от Луны и Солнца ${{{\mathbf{u}}}_{*}}({\mathbf{r}},t)$. Далее для построения модели невозмущенного движения полюса Земли на коротких интервалах времени определяются вариации тензора инерции ${\delta }J$ деформируемой Земли при ${\mathbf{u}} = {\mathbf{u}}({\mathbf{r}},{\mathbf{\omega }})$. Вектор ${\mathbf{u}}$ является решением краевой задачи (1.1), который может быть найден в виде разложения по степеням малого параметра 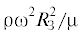(${{R}_{{\text{З}}}} \approx 6382$ км – радиус Земли).

При отсутствии внешних сил уравнения движения в связанной системе имеют вид:

Выпишем вектор ${\text{G}}$ кинетического момента Земли в деформированном состоянии:

Здесь ${\mathbf{u}}$ и ${\mathbf{\dot {u}}}$ – скорость и ускорение в связанной системе координат, $d{\mathbf{v}}$ – элемент объема. В выражениях ${\text{G}}$ и ${\dot {G}}$ можно пренебречь квадратичными членами по величине u. Тогда вектор ${\text{G}}$ представим в виде двух слагаемых главной части и малых вариаций, обусловленных смещениями u:

Вектор $\Delta {\text{G}}$ – дополнительный кинетический момент, возникающий вследствие деформаций планеты из-за центробежного потенциала, имеет вид:

Вследствие малости деформаций среда мантии описывается линейной теорией вязкоупругости, а процесс деформирования происходит квазистатически. В уравнениях задачи (1.1) будем пренебрегать малыми членами ${\mathbf{\ddot {u}}}$ и ${\mathbf{\omega }} \cdot {\mathbf{\dot {u}}}$. Также вследствие близости вектора ${\mathbf{\omega }}$ к главной оси инерции – оси фигуры Земли, можно пренебречь слагаемым ${\mathbf{\dot {\omega }}} \cdot {\mathbf{r}}$, а в (1.5) вторым слагаемым в сравнении с первым. В работах [3, 8] для описания деформированного состояния Земли применяется линейная теория вязкоупругости малых деформаций на основе модального подхода. Вектор перемещения u точек вязкоупругой среды может быть представлен в виде ряда по собственным формам задачи о свободных колебаниях упругой планеты. Предполагается, что характерное время T движения планеты (период собственного вращения) относительно центра масс существенно превосходит период свободных колебаний упругой части на собственной частоте, а также характерное время затухания свободных упругих колебаний на наинизшей собственной частоте много меньше T. Следуя [8] в первом приближении по ${\chi }$ (${\chi }$ – коэффициент, характеризующий вязкость), выражение для ${\mathbf{u}}$ имеет вид:

где u₀ – решение задачи в упругом приближении без учета вязкости.

Тогда вектор перемещений u можно найти в виде [8]:

где первое слагаемое – решение краевой задачи (1.1) при ${\mathbf{\Phi }} = - {\mathbf{\omega }} \cdot ({\mathbf{\omega }} \cdot {\mathbf{r}})$. Функции V_ij зависят от формы тела и параметров ${\rho }$, ${\mu }$, ${\nu }$ и являются решением уравнения: с соответствующими граничными условиями уравнения (1.1).

Далее, проецируя (1.5) и (1.6) на оси связанной системы, получим:

Тогда вариации компонент тензора инерции примут вид:

где δ_ij – символ Кронекера.

В результате вариации компонент тензора инерции Земли вследствие упругих деформаций (без учета вязкости) представляют собой переменную во времени квадратичную форму по компонентам вектора угловой скорости:

Здесь вводя стандартные обозначения $p = {{{\omega }}_{1}}$, $q = {{{\omega }}_{2}}$, $r = {{{\omega }}_{3}}$ и полагая ${{{\omega }}_{3}} \approx {{r}_{0}}$ (${{r}_{0}}$ – постоянное значение угловой скорости осевого вращения Земли) вследствие малости p, q ($p$, $q \ll r$), на начальном этапе пренебрежем квадратичными по p, q и их производным слагаемыми. Тогда получим выражения компонент тензора инерции Земли

линейные по p, q. Наибольшими по величине будут вариации $\delta {{J}_{{13}}}$, $\delta {{J}_{{23}}}$. Они имеют вид:

Таким образом, дифференциальные уравнения движения земного полюса будут содержать малые диссипативные слагаемые, определяемые полюсным приливом.

2. Прогноз движения земного полюса при нестационарных возмущениях. Из теории обработки временных рядов известно, что оптимальная оценка случайных измеряемых параметров – компромиссный выбор между динамической (точность модели) и стохастической (точность измерений) ошибками. Длительность интервала обработки наблюдений выбирается из условия минимума среднеквадратической ошибки при фиксированном наборе небольшого числа опорных функций. Уменьшение ошибки достигается повышением точности физической модели, что позволяет удлинить интервал обработки данных наблюдений и уменьшить дисперсии случайных составляющих оценок искомых параметров в определенных – не очень значительных пределах.

Рассмотренная в работах [6] модель движения земного полюса учитывает дополнительные слагаемые, основная частота которых соответствует или чандлеровской частоте, или годичной частоте в зависимости от соотношения амплитуд годичной и чандлеровской гармоник. При изменении амплитудного соотношения основная частота дополнительных слагаемых изменится достаточно быстро. Из обработки данных наблюдений и измерений МСВЗ [1] следует, что это явление нерегулярное. Оно приводит к динамическим эффектам, описанным в работе [6]. Такие изменения могут наблюдаться и в диссипативных системах не только при вариациях амплитуд основных гармоник, но и до наступления установившегося колебательного режима.

Рассмотрим модель движения земного полюса, учитывающую линейную диссипацию [11]. В качестве возмущений учтем годичное и чандлеровское возмущения с переменными амплитудами, близкими к наблюдаемым. Выпишем упрощенные уравнения для амплитуды и фазы движения полюса, которые имеют вид:

где ${{{\mu }}_{{ch/h}}} = {{{\mu }}_{{ch/h}}}(t)$, ${{{\nu }}_{h}}$, N – переменные амплитуды и частоты годичного и чандлеровского возмущений, приводящих к колебаниям земного полюса с параметрами, близкими к наблюдаемым; величины, ${{{\mu }}_{h}}\cos ({{{\nu }}_{h}}t)$, ${{{\mu }}_{h}}\sin ({{{\nu }}_{h}}t)$ имеют размерность удельного момента сил.

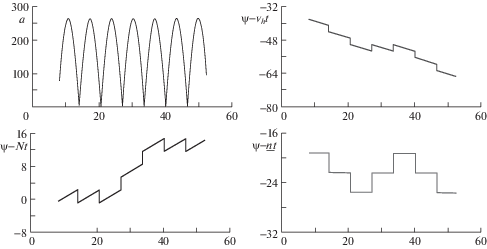
Интервалы времени, на которых ${{\dot {\psi }}^{{var}}} = \psi - N$ достаточно резко возрастает, соответствуют минимумам амплитуды колебательного процесса. Точнее, минимум амплитуды (биениям) приходится на максимум частоты $\dot {\psi }$. Для начального значения амплитуды, соответствующего минимальному ее значению, наблюдаемому в 2006 году (перед изменением амплитудного соотношения чандлеровской и годичной компонент), получим характерную картину переходного процесса при смене колебательного режима – вначале в одну сторону, затем в другую. На рис. 1 даны графики амплитуды и разностей $\psi - Nt$, $\psi - {{{\nu }}_{h}}t$, $\psi - (N + {{{\nu }}_{h}})t{\text{/}}2$, из которых видны значения частоты $\dot {\psi }$, соответствующие различным участкам колебательного процесса.

Для практических расчетов координат полюса Земли ${{x}_{p}} = p{\text{/}}r$, ${{y}_{p}} = - q{\text{/}}r$ рационально использовать двухчастотную модель [4] с годичной и чандлеровской составляющей:

Значение чандлеровской частоты N принимается постоянным и равным 0.843 цикла в год. Неизвестные коэффициенты ${{c}_{{x,y}}}$, $a_{{x,y}}^{{c,s}}$, $d_{{x,y}}^{{c,s}}$ – величины, подлежащие вычислению с помощью метода наименьших квадратов по измерениям МСВЗ. Здесь x_p и y_p формируются в угловых секундах.

Прогноз изменения средней частоты ${\dot {\psi }}$ и изменения амплитудного соотношения a_ch/a_h (соотношения амплитуд чандлеровского колебания a_ch и годичного колебания a_h) сделать весьма проблематично, а его точностные характеристики оценить сложно. Однако оценивать среднюю частоту можно в режиме адаптивного функционирования модели в реальном времени или с небольшим запаздыванием, не приводящим к ухудшению точности прогноза. Исключив тренд из данных x_p, y_p, получим значения угла $\psi $ и величины скорости $\dot {\psi }$ в интервале от начального до текущего момента времени. Например, для ситуации с близкими величинами амплитуд, отвечающими условиям a_ch > a_h, ${{\dot {a}}_{{ch}}} < 0$, ${{\dot {a}}_{h}} > 0$, шестилетний интервал модуляции можно разбить на два подинтервала – один короткий (в среднем 1.2 года) со значением средней частоты $\dot {\psi } < N$ (N – чандлеровская частота), и длительный интервал (в среднем 5.2 года), на котором среднее значение частоты близко к среднему арифметическому годичной и чандлеровской частот, т.е. $\dot {\psi } \cong \frac{{N + {{{\nu }}_{h}}}}{2}$ (${{\nu }_{h}}$ – частота годичной гармоники с периодом 1 год). Такая ситуация обнаруживается и после всплеска фазы 2006 года – средняя частота $\dot {\psi }$ близка к значению $(N + {{{\nu }}_{h}}){\text{/}}2$ в пределах погрешности вычисления.

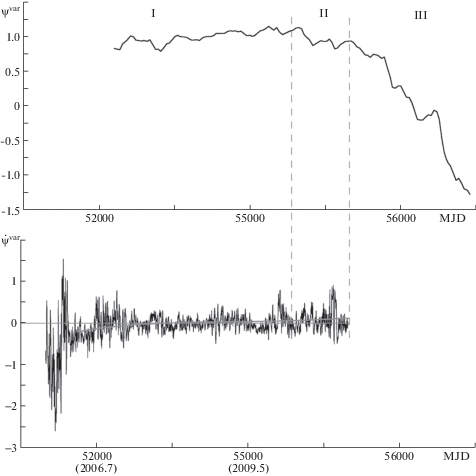
На рис. 2 даны графики вариаций ${{\psi }^{{var}}} = \psi - \bar {N}t$ и ${{\dot {\psi }}^{{var}}}$, измеряемых в радианах и в циклах/год соответственно, для шестилетнего интервала времени после 2006 года. При увеличении частоты до 1 цикла в год колебательный режим уже изменился. Можно сказать, что колебания перешли в другой режим несколько раньше – при частоте, большей $(N + {{{\nu }}_{h}}){\text{/}}2$. Первая область (I) соответствует средней частоте $(N + {{{\nu }}_{h}}){\text{/}}2$, средняя область (II) – линейному увеличению частоты ${{\dot {\psi }}^{{var}}}$, которой соответствует квадратичная зависимость в ${{\psi }^{{var}}}$, а третья область (III) – частоте годичного колебания уже после изменения колебательного режима.

Процедура фильтрации и настройка алгоритма может быть выполнена по методу “взвешенных” наименьших квадратов [12]. Средняя частота обращения земного полюса вокруг средней точки за один цикл перед переходным процессом близка к частоте 0.9225 циклa в год. Если колебательный режим будет изменен на годичный, то при минимуме амплитуды значение частоты станет больше 1 цикла в год, а если колебательный режим не изменится, то ее значение окажется меньше 0.843 цикла в год. Таким образом, упрощенное прогнозирование движения земного полюса при смене режимов колебаний заключается в использовании весовых коэффициентов метода наименьших квадратов на интервале одного обращения полюса вокруг среднего положения, непосредственно примыкающего к интервалу прогноза, а также в относительном их увеличении к концу в пределах этого интервала.

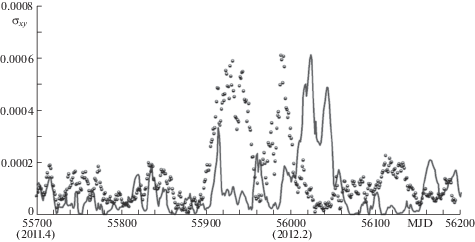
На рис. 3 даны среднеквадратические отклонения прогноза траектории движения полюса на 45 суток (сплошная линия) в сравнении с среднеквадратическими отклонениями прогнозов МСВЗ (дискретная линия – точки), публикуемых в Бюллетене А. На графиках среднеквадратические отклонения были отнесены к дате построения прогноза. Прогнозы рассчитывались с шагом, равным суткам. Средние значения отклонений прогнозов МСВЗ и разработанной модели от данных измерений составляют 12 и 10 угл. мс соответственно.

Заключение. Таким образом, разработанная численно-аналитическая модель колебаний полюса Земли позволяет улучшить точность прогноза его траектории во время нерегулярных эффектов, вызванных изменчивостью амплитуд основных гармоник колебательного процесса.

Работа выполнена в рамках реализации базовой части государственного задания Минобрнауки РФ (проект 9.7555.2017/БЧ).