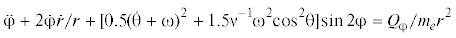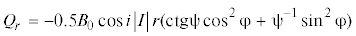Известия РАН. Механика твердого тела, 2019, № 4, стр. 48-62
О СТАБИЛИЗАЦИИ ДВИЖЕНИЯ ЭЛЕКТРОДИНАМИЧЕСКОЙ ТРОСОВОЙ СИСТЕМЫ НА ОКОЛОЗЕМНОЙ ОРБИТЕ
П. С. Воеводин a, Ю. М. Заболотнов a, *
a Самарский национальный исследовательский университет
Самара, Россия
* E-mail: yumz@yandex.ru
Поступила в редакцию 25.08.2018
После доработки 25.08.2018
Принята к публикации 19.12.2018
Аннотация
Анализируются алгоритмы стабилизации движения электродинамической тросовой системы на орбите спутника Земли. Рассматриваемая система состоит из двух малых космических аппаратов и соединяющего их троса. Тросовая система предназначена для изменения ее орбитальных параметров, при этом используется взаимодействие проводящего ток троса с магнитным полем Земли. Для описания движения системы используются несколько математических моделей, с различной степенью детализации описывающих ее движение. Предлагается алгоритм стабилизации движения тросовой системы в окрестности местной вертикали. Особенностью рассматриваемого алгоритма, основанного на принципе обратной связи, является стабилизация изгибных колебаний троса от действия распределенной нагрузки, действующей на проводящий ток трос в магнитном поле. Показывается, что неучет изгибных колебаний троса в алгоритмах стабилизации может привести не только к ухудшению качества стабилизации, но и к потере устойчивости движения системы (ее переходу во вращение).
1. Введение. Одно из направлений полезного применения космических тросовых систем это возможность изменения орбитальных параметров с помощью проводящих ток тросов [1]. Взаимодействие проводящих тросов с магнитным полем Земли (в перспективе с магнитными полями других планет) приводит к возникновению силы Ампера, которая, действуя на систему в целом, изменяет орбиту ее центра масс. Электродинамические тросовые системы (ЭДТС) могут функционировать в пассивном и активном режимах [1]. При движении в магнитном поле в проводнике (тросе) возникает электродвижущая сила (ЭДС) индукции, которая является причиной возникновения электрического тока определенного направления. Сила Ампера, действующая на элементарный участок троса, определяется известной формулой [1]
где I – величина тока, $B$ – вектор магнитной индукции, $\tau $ – единичный вектор, направленный по касательной к тросу.В пассивном режиме использование ЭДТС приводит к возникновению силы (1.1), тормозящей движение системы по орбите [1–4]. Активный режим функционирования ЭДТС соответствует случаю, когда наряду с ЭДС индукции имеется еще управляющая разность потенциалов [1], которая возникает за счет бортовых источников энергии концевых тел, и с помощью которой можно изменять величину и направление тока в тросе, а значит, и направление действия силы (1.1). Тем самым можно не только тормозить орбитальное движение, но и осуществлять стабилизацию орбитальных параметров или переводить систему на более высокую орбиту [5, 6]. Перспективность применения ЭДТС в космосе подтверждает тот факт, что до настоящего времени проведено уже более десятка реальных тросовых экспериментов с проводящими ток тросами на околоземных орбитах [3].
2. Постановка задачи. Известно, что положения равновесия ЭДТС, расположенные вблизи местной вертикали, так называемые “рабочие” положения равновесия системы, неустойчивы [1, 2, 7, 8]. Неустойчивость движения системы проявляется в возрастании ее маятниковых колебаний, что в конечном итоге (в зависимости от величины тока в тросе) ведет или к переходу системы во вращение, или к большой деформации троса, когда трос сминается и становится не натянутым. И в том, и в другом случае ЭДТС прекращает выполнять свои функции по целенаправленному изменению орбитальных параметров системы. Положение еще более усложняется для наклонных орбит с относительно большим эксцентриситетом, так как в этом случае всегда реализуется пространственный случай движения, при этом имеют место угловые маятниковые колебания системы как в плоскости, так вне плоскости орбиты [9]. Для наклонных эллиптических орбит на систему начинают действовать периодические возмущения, связанные с изменением аргумента широты и с угловыми маятниковыми колебаниями троса перпендикулярно плоскости орбиты. Это существенно усложняет решение задачи стабилизации движения ЭДТС в плоскости орбиты. Поэтому вопросам стабилизации движения ЭДТС в настоящее время уделяется большое внимание [10–13], при этом используются как пассивные [10], так и активные методы стабилизации [11–13]. При реализации активных методов чаще всего используются алгоритмы стабилизации, основанные на определении поправок к номинальным значениям тока [11–13], то есть $I = {{I}_{n}} + \Delta I$, где In – номинальная величина тока, ΔI – управляющие стабилизирующие воздействия, определяемые на основании принципа обратной связи. Поправки ΔI в известных работах строятся в зависимости от значений производных углов, определяющих положение троса относительно местной вертикали. Причем при построении алгоритмов стабилизации предполагается, что форма троса близка к прямой линии [11–13]. Однако, как известно, при действии распределенной нагрузки при движении ЭДТС по околоземной орбите имеют место изгибные колебания троса, причем, если масса троса много меньше массы концевых тел (то есть трос можно считать невесомым), то форма троса в любой момент времени представляют собой часть окружности некоторого радиуса [1], [14]. Почти периодические изменения радиуса этой окружности как раз и характеризуют его изгибные колебания. Взаимодействие изгибных колебаний троса с маятниковыми колебаниями системы имеет сложный характер, в частности, возможны случаи синхронизации изгибных и маятниковых колебаний в системе [14]. Неучет этих особенностей в движении ЭДТС, как показано ниже в представленной работе, может привести к потере устойчивости “рабочих” положений ЭДТС при использовании регуляторов, учитывающих только угловые скорости вращения системы относительно ее положений равновесия.
В настоящей работе предлагаются и исследуются алгоритмы стабилизации движения ЭДТС, в которых регулирование осуществляется не только по угловым скоростям вращения системы относительно вертикали, но и по скорости изменения расстояния между концевыми точками системы, то есть производной по времени хорды окружности, характеризующей изгибные колебания троса. На основании анализа предлагаемого подхода даются рекомендации по наиболее рациональному выбору параметров ЭДТС и ее режимов движения, обеспечивающих устойчивое движение системы на эллиптических и наклонных орбитах на больших интервалах времени. Сформулированные выводы подтверждаются результатами численного моделирования движения ЭДТС, состоящей из двух малых космических аппаратов и проводящего ток троса. Для оценки эффективности рассматриваемого подхода используются две математические модели, учитывающие изгибные колебания троса. Первая модель получена методом Лагранжа для невесомого троса в работе [14] с использованием методики, изложенной в [1]. В этой модели в отличие от [1] рассматривается случай произвольного соотношения масс концевых тел и наклонные эллиптические орбиты. Вторую модель движения ЭДТС можно назвать моделью с распределенными параметрами, так как в ней трос представляется совокупностью материальных точек. Эта модель учитывает распределение массы троса в гравитационном поле и изменение вектора магнитной индукции в пределах троса. Подобные модели использовались во многих работах для проведения поверочных расчетов при обосновании использования более простых моделей движения космических тросовых систем [15–18].
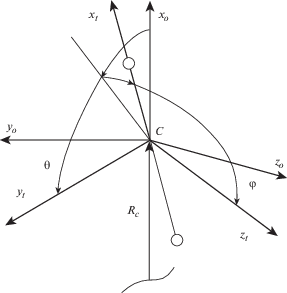
3. Уравнения движения системы относительно центра масс с невесомым тросом. Уравнения, описывающие колебания ЭДТС относительно центра масс, записываются в правой орбитальной прямоугольной системе координат $C{{x}_{o}}{{y}_{o}}{{z}_{o}}$ (рис. 1), начало которой совпадает с центром масс системы, ось $C{{x}_{o}}$ направлена по его радиус-вектору ${{R}_{c}}$, ось $C{{y}_{o}}$ – перпендикулярно ${{R}_{c}}$ и направлена в сторону орбитального движения. При записи уравнений используется предположение, что на трос действует постоянная распределенная нагрузка от сил Ампера (1.1), то есть изменением вектора магнитной индукции B вдоль троса пренебрегается. В этом случае форма невесомого троса в любой момент времени есть часть окружности некоторого радиуса [1]. Для этого случая в монографии [1] методом Лагранжа для экваториальной круговой орбиты в обобщенных координатах $r,{\theta ,}\,{\varphi }$, где $r$ – расстояние между концевыми точками (хорда окружности), ${\theta ,}\,{\varphi }$ – углы, определяющие положение хорды (или системы координат $C{{x}_{t}}{{y}_{t}}{{z}_{t}}$ с ней связанной, рис. 1) относительно системы координат $C{{x}_{o}}{{y}_{o}}{{z}_{o}}$ (рис. 1), получены соответствующие уравнения. Эти уравнения построены для случая, когда масса одного концевого тела много больше массы другого. В работе [14] проведено обобщение уравнений [1] на случай произвольного распределения масс концевых точек и на эллиптические наклонные орбиты. В этом случае имеем [14]
(3.1)
${\ddot {\theta }} + {\dot {\omega }} + {\text{2}}({\dot {\theta }} + {\omega })\left( {\dot {r}{\text{/}}r - {\dot {\varphi }tg\varphi }} \right) + 1.5{{{\nu }}^{{ - 1}}}{{{\omega }}^{{\text{2}}}}\sin 2{\theta } = {{Q}_{{\theta }}}{\text{/}}{{m}_{e}}{{r}^{2}}{{\cos }^{2}}{\varphi }$(3.2)
$\ddot {r} - r[{{{\dot {\varphi }}}^{2}} + {{({\dot {\theta }}\,{\text{ + }}\,{\omega })}^{2}}{\text{co}}{{{\text{s}}}^{2}}{\varphi } + {{{\nu }}^{{ - 1}}}{{{\omega }}^{2}}(3{{\cos }^{2}}{\theta co}{{{\text{s}}}^{{\text{2}}}}{\varphi } - 1)] = {{Q}_{r}}{\text{/}}{{m}_{e}}$Наряду с предположением о форме троса при выводе уравнений использовались следующие допущения: 1) гравитационное поле ньютоновское; 2) длина хорды много меньше расстояния до притягивающего центра $r \ll {{R}_{c}}$; 3) концевые тела – материальные точки; 4) орбита центра масс системы – невозмущенная. Если φ = 0, то движение системы происходит в плоскости орбиты.
Используется модель магнитного поля Земли – прямой диполь [1], поэтому
(3.4)
$B = {{B}_{0}}\left[ {{{e}_{z}} - 3\left( {{{e}_{z}} \cdot {{e}_{R}}} \right){{e}_{R}}} \right]$Обобщенные силы вычисляются из следующих выражений [14]
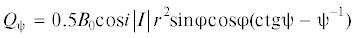 , $\Delta {{Q}_{{\theta }}}$ = 3B0IrΔsinicosθsinφsinu.
, $\Delta {{Q}_{{\theta }}}$ = 3B0IrΔsinicosθsinφsinu.
В отличие от [14], где использовалась более простая модель для магнитного поля $B = {{B}_{o}}{{e}_{z}}$, здесь приводятся обобщенные силы, которые соответствуют модели (3.4). Величина тока I считается положительной, если он направлен от точки ma к точке mb.
Угол ${\psi }$ определяется из геометрического соотношения [1]
(3.6)
$r = L{{{\gamma }}_{t}}{\text{/}}{{[{{\sin }^{2}}{\varphi } + {{\cos }^{2}}{\varphi }{{\left( {{\psi /sin\psi }} \right)}^{2}}]}^{{0.5}}}$Система (3.1–3.3) совместно с выражениями (3.4–3.6) описывает движение ЭДТС относительно своего центра масс с учетом изгибных колебаний троса. Изгиб троса характеризуется расстоянием между концевыми точками r и соответственно углом ${\psi }$ (3.6), значения которых определяют радиус части окружности ${{r}_{t}} = r{\text{/}}(2\sin {\psi )}$.
4. Положения относительного равновесия системы и анализ линеаризованных уравнений. Положения относительного равновесия можно определить только для экваториальной и круговой орбиты центра масс системы. Дело в том, что для наклонных и эллиптических орбит в системе существуют периодические возмущения, связанные с изменением аргумента широты $u$ и угла ${\varphi }$, что исключает возможность определения неизменных равновесных положений системы.
Для экваториальной круговой орбиты положения равновесия, близкие к вертикали, определяются из уравнений (3.1)–(3.2) и имеют вид $\left( {{\varphi } = {\dot {\varphi }} = 0} \right)$
(4.1)
${{{\theta }}_{1}} = \frac{1}{2}\arcsin \left( {\sigma } \right),\quad {{{\theta }}_{2}} = {{{\theta }}_{1}} + {\pi }$Остальные переменные системы (3.1–3.3) определяются из выражений
(4.2)
${{{\psi }}_{k}} = {\text{arctg}}\left( {\frac{{{{{\mu }}_{m}}\,\left| I \right|\,}}{{6{\mu }\,{{m}_{e}}{{{\cos }}^{2}}{{{\theta }}_{k}}}}} \right)$, ${{r}_{k}} = L\,{{{\gamma }}_{t}}\,\frac{{\sin {{{\psi }}_{k}}}}{{{{{\psi }}_{k}}}}$, ${{{\dot {\theta }}}_{k}} = {{\dot {r}}_{k}} = 0$; $k = 1,2$Положения равновесия (4.1–4.2) иногда называют “рабочими” положениями равновесия [1], так как с точки зрения использования ЭДТС для изменения орбитальных параметров системы они являются наиболее предпочтительными. Если ЭДТС совершает ограниченные колебания относительно положений равновесия (4.1–4.2), которые располагаются вблизи вертикали, то равнодействующая сил Ампера (1.1) почти параллельна вектору скорости центра масс системы и изменение высоты орбиты будут близки к максимальным. Очевидно, что условие существования положений равновесия (4.1–4.2) (условие статической устойчивости) будет иметь вид $\left| {\sigma } \right| < 1$.
Линеаризованная система относительно положений равновесия (4.1–4.2) имеет стандартную форму и приводится здесь в безразмерном виде
где $y = \left( {\Delta {\theta ,\theta }',\Delta r,r',{\varphi ,\varphi '}} \right)$ – вектор отклонений обобщенных координат и скоростей от положений равновесия, ${\tau } = \Omega \,t$ – безразмерное время, $\Omega $ – угловая скорость орбитального движения. При этом матрица $A$ частных производных имеет следующий вид(4.4)
$A = \left( {\begin{array}{*{20}{c}} 0&1&0&0&0&0 \\ {{{A}_{{21}}}}&0&0&{{{A}_{{24}}}}&0&0 \\ 0&0&0&1&0&0 \\ {{{A}_{{41}}}}&{{{A}_{{42}}}}&{{{A}_{{43}}}}&0&0&0 \\ 0&0&0&0&0&1 \\ 0&0&0&0&{{{A}_{{65}}}}&0 \end{array}} \right)$В безразмерных выражениях (4.3–4.4) сохранены те же обозначения, что и в исходных уравнениях (3.1–3.3), то есть, сделаны формальные замены $r \Rightarrow r{\text{/}}L$, ${{r}_{{1,2}}} \Rightarrow {{r}_{{1,2}}}{\text{/}}L$, $\Delta r \Rightarrow \Delta r{\text{/}}L$. В линеаризованной системе (4.3–4.4) уравнения для переменных ${\varphi ,}\Delta {\dot {\varphi }}$ отделяются и имеют всегда чисто мнимые корни. Остальные собственные числа матрицы (4.4) определяются из следующего характеристического уравнения
где ${{p}_{2}} = - \left( {{{A}_{{21}}} + {{A}_{{43}}} + {{A}_{{24}}}{{A}_{{42}}}} \right)$, ${{p}_{1}} = - {{A}_{{24}}}{{A}_{{41}}}$, ${{p}_{0}} = {{A}_{{21}}}{{A}_{{43}}}$Если ${{p}_{1}} = 2I{{B}_{o}}\left( {{{m}_{a}} - {{m}_{b}}} \right){\text{/}}({{m}_{a}}{{m}_{b}}{{{\omega }}^{2}}) = 0$, то есть когда массы концевых точек одинаковы и момент от сил Ампера отсутствует, то остальные уравнения также имеют чисто мнимые корни. Если ${{p}_{1}} \ne 0$, то решения уравнений (4.3) всегда неустойчивы, что также было отмечено в монографии [1] для частного случая ${{m}_{b}} \gg {{m}_{a}}$.
Для анализа эволюционных движений ЭДТС при постоянном токе первые четыре уравнения системы (4.3) приводятся к двум уравнениям второго порядка
В нормальных координатах система (4.6) принимает
(4.7)
$E\frac{{{{d}^{2}}{\xi }}}{{d{{{\tau }}^{2}}}} + D{\xi } = {{b}_{n}}\frac{{d{\xi }}}{{d{\tau }}}$Здесь необходимо отметить, что при малых изгибах троса, когда ${{{\psi }}_{{1,2}}} \to 0$ (${{{\psi }}_{{1,2}}} > 0$), имеем ${{{\omega }}_{2}} \gg {{{\omega }}_{1}}$, так как ${{A}_{{43}}} \to \infty $ (см. (4.4)). Кроме того, первая нормальная координата совпадает с исходной переменной ${{{\xi }}_{1}} = \Delta {\theta }$, а вторая координата ${{{\xi }}_{2}} = {\delta }\Delta {\theta + }\Delta r$.
Представление системы (4.6) в виде (4.7) позволяет выделить в явном виде слагаемые, непосредственно влияющие на неустойчивость движения системы (4.4). Это компоненты $ - {\delta }{{A}_{{24}}}$ и ${\delta }{{A}_{{24}}}$ матрицы ${{b}_{n}}$ (4.7), причем эти слагаемые пропорциональны малому параметру δ, так как ${\delta } \to 0$ при ${{{\psi }}_{{1,2}}} \to 0$.
В связи с этим применим к системе (4.7) стандартный метод медленно изменяющихся амплитуд [19], применяя замену переменных
(4.8)
${{{\xi }}_{{1,2}}} = {{K}_{{1,2}}}\cos {{{\gamma }}_{{1,2}}}$, $d{{{\xi }}_{{1,2}}}{\text{/}}d{\tau } = - {{K}_{{1,2}}}{{{\omega }}_{{1,2}}}\sin {{{\gamma }}_{{1,2}}}$После усреднения по фазам нетрудно получить
(4.9)
$d{{K}_{{1,2}}}{\text{/}}d{\tau } = \pm \frac{{3\sin 2{{{\theta }}_{k}}}}{{{\omega }_{2}^{2} - {\omega }_{1}^{2}}}{{K}_{{1,2}}} = \pm {\eta }{{K}_{{1,2}}}$, ${\eta } = \frac{{{{{\mu }}_{m}}I\left( {{{m}_{b}} - {{m}_{a}}} \right)}}{{{\mu }\,{{m}_{a}}{{m}_{b}}({\omega }_{2}^{2} - {\omega }_{1}^{2})}}$В усредненных уравнениях для простоты сохранены те же обозначения для амплитуд колебаний ${{K}_{{1,2}}}$, что и для исходных не усредненных переменных (4.8). Величина коэффициента ${\eta }$, определяющая скорость возрастания амплитуд колебаний, есть приближенная оценка модулей вещественных частей собственных значений матрицы A. Так, например, для исходных данных, приведенных в таблице 1, для круговой (e = 0) и экваториальной (i = 0) орбиты имеем ${\eta } = 3.66 \times {{10}^{{ - 3}}}$ и $\left| {\operatorname{Re} ({{\lambda }_{{1,2,3,4}}})} \right| = 3.58 \times {{10}^{{ - 3}}}$, при этом ω1 = 1.71, ω2 = 13.62, δ = 3.63 × 10–3. Частота колебаний по углу ${\varphi }$ равна 1.415.
Таблица 1.
| ${{m}_{a}},\,{\text{кг}}$ | 2 |
| ${{m}_{b}},\,{\text{кг}}$ | 6 |
| $L,\,{\text{км}}$ | 1 |
| ${{I}_{n}},\,{\text{A}}$ | ±0.1 |
| ${{E}_{t}},\,{\text{Н}}$ | 7070 |
| $H,\,{\text{км}}$ | 1000 |
| $e$ | 0, 0.01 |
| $i$ | 0, π/3 |
| ${{{\varphi }}_{0}},\,{{{\dot {\varphi }}}_{0}}$ | 0 |
| ${{{\theta }}_{0}}$ | 0 |
Таким образом, если концевое тело (mb) смещается противоположно направлению орбитального движения $\sin 2{{{\theta }}_{k}} > 0$, то неустойчивость движения системы обусловлена возрастанием амплитуд маятниковых колебаний в плоскости орбиты (по углу $\Delta {\theta }$). Если же $\sin 2{{{\theta }}_{k}} < 0$, то неустойчивость движения проявляется в возрастании амплитуд продольных (или изгибных) колебаний троса $\Delta r = {{{\xi }}_{2}} - {\delta }\Delta {\theta }$, так как ${\delta }$ – малый параметр. Причем, как следует из (4.9), знак и величина $\sin 2{{{\theta }}_{k}}$ определяется величиной тока и соотношением масс концевых тел, то есть от знака и величины момента равнодействующей сил Ампера.
5. Синтез приближенно оптимального регулятора для экваториальной орбиты. Для синтеза приближенно оптимального регулятора воспользуемся принципом динамического программирования Беллмана [20] в сочетании с методом усреднения. Метод усреднения использовался во многих работах для решения различных задач построения приближенно оптимальных управлений, например, в [21–24]. Здесь применяется процедура синтеза линейного регулятора, аналогичная алгоритму синтеза при решении задачи стабилизации движения твердого тела вокруг неподвижной точки [25] для случая, близкого к движению волчка Лагранжа. Рассматриваемый алгоритм, как показано ниже, позволит для частного случая круговой орбиты получить уравнения для регулятора в аналитической форме.
Для решения задачи синтеза регулятора рассматривается система (4.7) с управлением и малым параметром ${\varepsilon }$
(5.1)
$E\frac{{{{d}^{2}}{\xi }}}{{d{{{\tau }}^{2}}}} + D{\xi } = {\varepsilon }\left( {{{b}_{n}}\frac{{d{\xi }}}{{d{\tau }}} + {{V}^{{ - 1}}}M\Delta u} \right)$Введение малого параметра ${\varepsilon }$ в систему (5.1) является формальным (масштабный коэффициент), то есть предполагается, что движение системы (5.1) слабо отличается от гармонических колебаний в нормальных координатах. Причем управление также ищется в классе малых управляющих воздействий, сопоставимых по порядку с возмущениями.
При синтезе регулятора используется квадратичный критерий оптимальности следующего вида
где $P\left( {{{K}_{1}},{{K}_{2}},\Delta u} \right) = {{s}_{1}}K_{1}^{2} + {{s}_{2}}K_{2}^{2} + {{s}_{3}}\Delta {{u}^{2}}$, ${{s}_{{1,2,3}}}$ – положительные безразмерные весовые коэффициенты, причем полагается, что $\sum {{{s}_{k}} = 1} $.Движение системы (5.1) рассматривается на асимптотически большом интервале времени
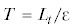 , где ${{L}_{t}} < \infty $ – некоторая константа. В этом случае функционал изменяется на величину порядка O(1).
, где ${{L}_{t}} < \infty $ – некоторая константа. В этом случае функционал изменяется на величину порядка O(1).
В соответствии с принципом динамического программирования, оптимальное управление определяется из условия [20], [25]
(5.3)
$\mathop {\min }\limits_u \left( {\frac{{\partial W}}{{\partial K}} \cdot \frac{{dK}}{{d{\tau }}} + \frac{{\partial W}}{{\partial {\gamma }}} \cdot \frac{{d{\gamma }}}{{d{\tau }}} + {\varepsilon }P\left( {K,\Delta u} \right)} \right) = 0$Дифференциальные уравнения для переменных ${\text{K,}}\,{\gamma }$ в соответствии с методом медленно изменяющихся амплитуд [19] имеют вид
(5.4)
$d{{K}_{{1,2}}}{\text{/}}d{\tau } = - \frac{{\varepsilon }}{{{{{\omega }}_{{1,2}}}}}{{f}_{{1,2}}}\sin {{{\gamma }}_{{1,2}}}$(5.5)
$d{{{\gamma }}_{{1,2}}}{\text{/}}d{\tau } = {{{\omega }}_{{1,2}}} - \frac{{\varepsilon }}{{{{{\text{K}}}_{{1,2}}}{{{\omega }}_{{1,2}}}}}{{f}_{{1,2}}}{\text{cos}}{{{\gamma }}_{{1,2}}}$С учетом вида правых частей уравнения (5.4–5.5) и функции $P$ выражение, стоящее под знаком минимума (5.3), представляет собой квадратичный степенной полином по управлению $u$. Поэтому из условия минимума этого полинома оптимальное управление определяется в виде
(5.6)
$\begin{gathered} \Delta {{u}^{o}}\left( W \right) = \frac{1}{{2{{s}_{3}}}}\sum\limits_{k = 1}^2 {\frac{{{{N}_{k}}}}{{{{{\omega }}_{k}}}}{{F}_{k}}\left( W \right)} \hfill \\ {{F}_{k}}\left( W \right) = \frac{{\partial W}}{{\partial {{K}_{k}}}}\cos {{{\gamma }}_{k}} - \frac{1}{{{{K}_{k}}}}\frac{{\partial W}}{{\partial {{{\gamma }}_{k}}}}\sin {{{\gamma }}_{k}} \hfill \\ \end{gathered} $Подставив управление (5.6) в выражение (5.3), получаем уравнение в частных производных для определения функции $W$
(5.7)
${\varepsilon }\sum\limits_{k = 1}^2 {\left( {{{s}_{k}}K_{k}^{2} - \frac{{{{f}_{k}}}}{{{{{\omega }}_{k}}}}{{F}_{k}}\left( W \right)} \right)} + \sum\limits_{k = 1}^2 {\frac{{\partial W}}{{\partial {{{\gamma }}_{k}}}}{{{\omega }}_{k}}} - {\varepsilon }{{s}_{3}}\Delta {{u}^{o}}{{\left( W \right)}^{2}} = 0$Уравнение (5.7) решается приближенно методом усреднения. В соответствии с этим решения для уравнений (5.4–5.5), (5.7) ищутся в виде асимптотических рядов
(5.8)
$\begin{gathered} K = {{K}_{{av}}}v + {\varepsilon }{{\nu }_{1}}\left( {{{K}_{{av}}},{{{\gamma }}_{{av}}}} \right) + {{{\varepsilon }}^{2}}... \\ {\gamma } = {{{\gamma }}_{{av}}} + {\varepsilon }{{{\mu }}_{1}}\left( {{{K}_{{av}}},{{{\gamma }}_{{av}}}} \right) + {{{\varepsilon }}^{2}}... \\ W\left( {{{K}_{{av}}},{{{\gamma }}_{{av}}}} \right) = {{W}_{0}}\left( {{{K}_{{av}}}} \right) + {\varepsilon }{{W}_{1}}\left( {{{K}_{{av}}},{{{\gamma }}_{{av}}}} \right) + {{{\varepsilon }}^{2}}... \\ \end{gathered} $Подставляя (5.8) в уравнение (5.7) и усредняя по фазам, получим
(5.9)
${\varepsilon }\sum\limits_{k = 1}^2 {\left( {{{s}_{k}}K_{k}^{2} - \frac{1}{{{{{\omega }}_{k}}}}\left\langle {{{f}_{k}}{{F}_{k}}\left( {{{W}_{0}}} \right)} \right\rangle } \right)} - {\varepsilon }{{s}_{3}}\left\langle {\Delta {{u}^{o}}{{{\left( {{{W}_{0}}} \right)}}^{2}}} \right\rangle + O({{{\varepsilon }}^{2}}) = 0$При записи усредненного уравнения (5.9) для упрощения обозначений индекс $(a{v})$ для новых переменных опущен. При усреднении также учитывалось, что $\left\langle {\sum\limits_{k = 1}^2 {{{\partial {{W}_{1}}} \mathord{\left/ {\vphantom {{\partial {{W}_{1}}} {\partial {{{\gamma }}_{k}}{{{\omega }}_{k}}}}} \right. \kern-0em} {\partial {{{\gamma }}_{k}}{{{\omega }}_{k}}}}} } \right\rangle $ = 0.
Функция ${{W}_{0}}\left( {{{K}_{1}},{{K}_{2}}} \right)$, соответствующая первому приближению метода усреднения (5.9), ищется в виде положительно определенной квадратичной формы
(5.10)
${{W}_{0}}\left( {{{K}_{1}},{{K}_{2}}} \right){\text{ = }}{{a}_{{11}}}K_{1}^{2} + {{a}_{{22}}}K_{2}^{2} + 2{{a}_{{12}}}{{K}_{1}}{{K}_{2}}$Подставляя (5.10) в уравнение первого приближения (5.9), нетрудно найти
(5.11)
${{a}_{{kk}}}{\text{ = 2}}{{s}_{3}}\frac{{{{{\omega }}_{k}}}}{{{{N}_{k}}}}\left[ {{{{\left( { - 1} \right)}}^{{k + 1}}}{\eta }\frac{{{{{\omega }}_{k}}}}{{{{N}_{k}}}} + {{{\left( {{{{\eta }}^{2}}\frac{{{\omega }_{k}^{2}}}{{N_{k}^{2}}} + \frac{{{{s}_{k}}}}{{2{{s}_{3}}}}} \right)}}^{{0.5}}}} \right]$, $k = 1,2$Полная производная функции ${{W}_{0}}$ по времени, определенная в силу уравнений первого приближения, будет иметь вид
где $\langle P({{K}_{1}},{{K}_{2}},\Delta {{u}^{o}})\rangle $ – знакоопределенная по ${{K}_{{1,2}}}$ и положительная функция, определенная на решениях усредненной системы первого приближения.Положительно определенная функция ${{W}_{0}}$ в соответствии с уравнением (5.12) монотонное убывает. Отсюда следует монотонное убыванию амплитуд колебаний ${{K}_{{1,2}}}$. Соответствие свойств устойчивости усредненной и исходной систем уравнений рассмотрено, например, в монографии [26] и обеспечивается общими теоремами метода усреднения.
Подставляя функцию (5.10) в выражение для оптимального управления (5.6), переходя к исходным переменным (учитывая (4.8) и ${\xi } = {{V}^{{ - 1}}}x$), получим уравнение регулятора в виде
После подстановки (5.13) в уравнения (5.4–5.5) и проведения процедуры усреднения, усредненная система с управлением будет иметь вид
(5.14)
$d{{K}_{k}}{\text{/}}d{\tau } = {{{\eta }}_{k}}{{K}_{k}}$, ${{{\eta }}_{k}} = - \frac{1}{{{{{\omega }}_{k}}}}{{\left( {{\omega }_{k}^{2}{{{\eta }}^{2}} + \frac{{{{s}_{k}}}}{{2{{s}_{3}}}}N_{k}^{2}} \right)}^{{0.5}}}$, $k = 1,2$При постоянных коэффициентах ${{{\eta }}_{k}}$ уравнения (5.14) нетрудно проинтегрировать и получить аналитическое решение
(5.15)
${{K}_{k}}\left( {\tau } \right) = {{K}_{k}}\left( 0 \right){{e}^{{{{{\eta }}_{k}}{\tau }}}},\quad k = 1,2$Для исходных данных, приведенных в таблице (при $e = i = 0$, ${{I}_{n}} = 0.1\,A$), и при равных весовых коэффициентах ${{s}_{{1,2,3}}} = 1{\text{/}}3$, имеем ${{k}_{{\theta }}} = - 8.30$, ${{k}_{r}} = - 1.03$, ${{{\eta }}_{1}} = - 1.38$, ${{{\eta }}_{2}}$ = –0.35.
Применение метода усреднения позволяет определить аналитические соотношения между параметрами ЭДТС, весовыми коэффициентами критерия оптимальности (5.2), коэффициентами регулятора и получающимися характеристиками переходного процесса в системе регулирования.
Если рассматривать движение усредненных систем на фазовой плоскости (K1, K2), то очевидно особая точка “седло” при введении управления превращается в особую точку “устойчивый узел”. Изменяя соотношения между весовыми коэффициентами ${{s}_{{1,2,3}}}$ всегда можно обеспечить требуемые характеристики переходных процессов в системе.
6. Математическая модель движения системы с распределенными параметрами. При построении математической модели движения ЭДТС (3.1–3.3) было принято ряд допущений. Здесь можно отметить: 1) невесомость троса; 2) форма троса – часть окружности; 3) неизменность вектора магнитной индукции B в пределах длины троса; 4) постоянство орбитальных параметров центра масс системы. Поэтому для сравнительного анализа здесь также используется более сложная модель движения, в которой трос представляется дискретной совокупностью материальных точек, связанных между собой упругими односторонними механическими связями. Подобные модели использовались во многих работах, например, в [15–18]. Особенностью данной модели является учет распределенных нагрузок от сил Ампера.
После дискретизации троса уравнения ЭДТС записываются в виде
(6.1)
${{m}_{k}}\frac{{{{d}^{2}}{{r}_{k}}}}{{d{{t}^{2}}}} = {{G}_{k}} + {{F}_{k}} + {{T}_{k}} - {{T}_{{k + 1}}},\quad k = 1,2,\;...\;n$Для определения ${{F}_{k}}$ сначала вычисляются силы Ампера, действующие на k-й участок троса
(6.2)
$\Delta {{F}_{k}} = I\left| {{{r}_{{k + 1}}} - {{r}_{k}}} \right|\left( {{{\tau }_{k}} \times {{B}_{k}}} \right),\quad k = 1,2,\;...\;n - 1$Распределение сил ${{S}_{k}}$ по материальным точкам ЭДТС осуществляется следующим образом
(6.3)
${{F}_{1}} = \frac{{\Delta {{F}_{1}}}}{2},\quad {{F}_{n}} = \frac{{\Delta {{F}_{{n - 1}}}}}{2},\quad {{{\mathbf{F}}}_{k}} = \frac{1}{2}\left( {\Delta {{F}_{{k - 1}}} + \Delta {{F}_{k}}} \right),\quad k = 2,3,\;...\;n - 1$При использовании системы (6.1) гравитационные силы Gk (центральное ньютоновское поле) и силы натяжения троса Tk определяются так же, как в работе [18], где при растяжении применялся закон Гука, и рассматривалась односторонняя механическая связь между точками.
7. Численные результаты. Сравнение результатов моделирования управляемого движения ЭДТС по различным моделям проводилось для экваториальных и наклонных, круговых и эллиптических орбит. Для уменьшения уровня управляющего воздействия $\Delta I$ и для обеспечения приблизительно равной длительности переходных процессов по различным координатам были выбраны не равные весовые коэффициенты в критерии оптимальности (5.2), удовлетворяющие следующим соотношениям: ${{s}_{1}}{\text{/}}{{s}_{3}} = 0.01$, ${{s}_{2}}{\text{/}}{{s}_{3}} = 0.1$. При этом имеем ${{k}_{{\theta }}} = - 0.85$, ${{k}_{r}} = - 0.32$, ${{{\eta }}_{1}} = - 0.14$, ${{{\eta }}_{2}} = - 0.11$. Исходные данные соответствуют таблице ($i = 0,\,\,e = 0,\,\,I = 0.1\,{\text{A}}$). Изменение направления тока ($I = - 0.1\,{\text{A}}$) практически не влияет на полученный результат.
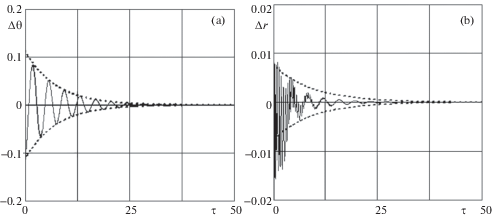
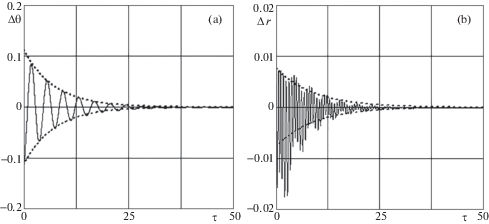
Если рассматривать линеаризованные не усредненные уравнения (4.3), то совпадение результатов с аналитическим решением (5.15) почти идеальное по обеим координатам ($\Delta {\theta },\,\,\Delta r$). Сравнение аналитического решения (5.15) с нелинейными моделями (3.1–3.3) и (6.1) показывает, что малая погрешность определения амплитуд колебаний сохраняется по переменной $\Delta {\theta }$, а по переменной $\Delta r$ имеет место совпадение результатов по времени переходного процесса. Данный вывод иллюстрируется рис. 2, 3, где рис. 2 соответствует модели (3.1–3.3), а рис. 3 – модели (6.1). Результаты, приведенные на рис. 2, 3, соответствуют случаю, когда в начальном положении ЭДТС расположена на вертикали и по тросу начинают пропускать ток. При реализации управляемого движения начальные малые возмущения по углу ${\varphi }$, по которому система не управляема, например, ${{{\varphi }}_{0}} < 1$, в соответствии с нелинейными моделями (3.1–3.3) и (6.1) остаются ограниченными, причем их амплитуды колебаний немного уменьшаются. При использовании модели (6.1) количество материальных точек, моделирующих распределенную массу троса, была равной шести. Дальнейшее увеличение дискретизации троса, даже в два раза, практически не изменяло полученных результатов. Учет массы троса в модели (6.1) немного изменяло положение равновесие системы, однако из-за сравнительно ее малой величины (для таблицы масса троса $0.2\,{\text{кг}}$) это изменение было не значительным (0.001 по углу ${\theta }$ и 0.005 по переменной r).
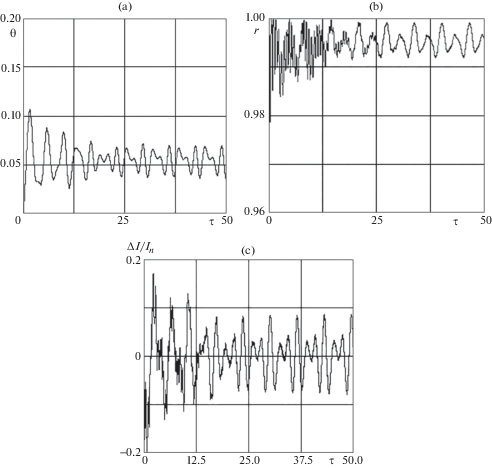
Использование полученного управления при тех же исходных данных для эллиптических и наклонных орбит также возможно, однако приводит к периодическим возмущениям, связанным с изменением аргумента широты (3.5) и колебаниями по углу ${\varphi }$. Причем в соответствии с уравнениями (3.1–3.3) возмущения по углу ${\varphi }$ имеют место, если даже в начальном состоянии ЭДТС находится в плоскости орбиты. В этом случае в окрестности положений равновесия (4.1–4.2) системы возникают ограниченные колебания, близкие к периодическим. На рис. 4 приводятся зависимости, полученные по модели (6.1), и иллюстрирующие действие указанных периодических возмущений, когда $e = 0.01$ и $i = {\pi /}3$.
Изменение параметров орбитального движения (центра масс системы) за время реализации переходного процесса практически не влияет на результаты приведенных расчетов. В данных примерах почти круговых орбит изменение большой полуоси орбиты на отрезке ${\tau } \in \left[ {0,50} \right]$ была равна соответственно –24.16 км и –11.80 км, что подтверждает известный факт снижения эффективности использования ЭДТС на наклонных орбитах (приблизительно в $1{\text{/cos}}i$ раза). Орбиты, близкие к полярным, требуют отдельного рассмотрения.
Дискретность управления (обновление значения управляющего воздействия) в соответствии с (5.13) для приведенных результатов была равна $20\,{\text{с}}$, увеличении времени до 100 c не сказывалось на качестве переходных процессов в системе. Другие особенности реальных систем регулирования, например, случайный характер измерений, запаздывание, не учитывались.
Здесь необходимо отметить, что все приведенные результаты справедливы при достаточно малой величине тока In. Во-первых, должно выполняться условие статической устойчивости вертикальных положений равновесия $\sigma < 1$ (4.1), критическая величина тока в приведенном примере для экваториальной орбиты – $0.45\,{\text{A}}$; во-вторых, в соответствии с величиной тока In должна быть выбрана величина весового коэффициента ${{s}_{3}}$ (5.2), определяющая уровень управляющего воздействия.
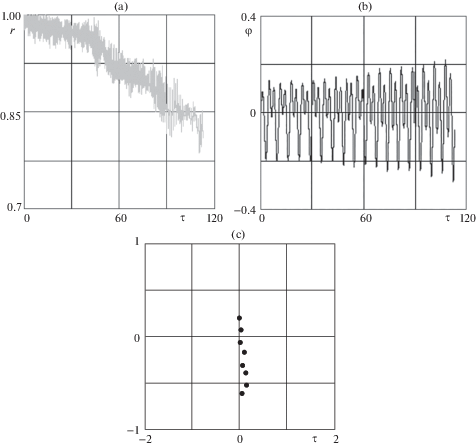
При использовании управления без обратной связи по отклонению $r'$ (5.13), то есть при ${{k}_{r}} = 0$, система теряет устойчивость, как на экваториальных, так и на наклонных орбитах. На рис. 5 приводятся результаты моделирования, показывающие поведение системы при отсутствии регулирования по отклонению $r'$ для случая, когда $e = 0.01$ и $i = {\pi /}3$. Используются те же исходные данные, что и для рис. 4. Здесь имеет место постепенное увеличение деформации троса, что проявляется в уменьшении расстояния между концевыми точками рис. 5,a. Увеличение деформации троса сопровождается увеличением амплитуд колебаний троса по углу ${\varphi }$ вне плоскости орбиты рис. 5,b. В конечном итоге трос сминается, так как не воспринимает сжимающих усилий, и имеет сложную форму рис. 5,с. Результаты, приведенные на рис. 5, получены по математической модели (6.1). Естественно математическая модель (3.1–3.3), в которой используется предположение о форме троса в виде дуги окружности, такие эволюционные движения системы полностью описать не может.
7. Заключение. В работе рассмотрены некоторые особенности стабилизации движения ЭДТС на околоземной орбите. Предложена аналитическая процедура расчета приближенно оптимального регулятора для данной задачи, основанная на совместном применении принципа динамического программирования Беллмана и метода усреднения. Показано, что при наличии малых начальных возмущений с помощью предлагаемого подхода удается обеспечить устойчивость переходных процессов для экваториальных и наклонных орбит. Данный вывод подтверждается результатами математического моделирования по модели с распределенными параметрами, учитывающей растяжимость и массу троса. Предлагаемый приближенно оптимальный регулятор обеспечивает уменьшение амплитуд маятниковых и продольных (изгибных) колебаний ЭДТС. Приводится пример потери устойчивости движения ЭДТС при отсутствии контроля над изгибными колебаниями троса.
Работа поддержана грантом РФФИ РФ 16-41-630637.
Список литературы
Белецкий В.В., Левин Е.М. Динамика космических тросовых систем. М.: Наука, 1990. 336 с.
Levin E.M. Dynamic analysis of space tether missions. San Diego: American Astronautical Society, 2007. 453 p.
Zhong R., Zhu Z.H. Dynamics of Nanosatellite Deorbit by Bare Electrodynamic Tether in Low Earth Orbit // J. of Spacecraft and Rockets. 2013. V. 50. № 3. P. 691–700.
Chen X., Sanmartín J.R. Bare-tether cathodic contact through thermionic emission by low-work-function materials // Physics of Plasmas. 2012. V. 19. P. 1–8.
Zhong R., Zhu Z.H. Optimal Control of Nanosatellite Fast Deorbit Using Electrodynamic Tether // J. of Guidance, Control, and Dynamics. 2014. V. 37. № 4. P. 1182–1194.
Fuhrhop K.R. Theory and Experimental Evaluation of Electrodynamic Tether Systems and Related Technologies // PhD Dissertation. University of Michigan. 2007. 307 p.
Левин Е.М. Устойчивость стационарных положений равновесия электродинамических тросовых систем на орбите // Космические исследования. 1987. Т. 25. № 4. С. 491–501.
Pelaez J., Lorenzini T.C., Lopez-Rebollal O., Ruiz M. A new kind of dynamic instability in electrodynamic tethers // Journal of the Astronautical Sciences. 2000. V. 48(4). P. 449–476.
Kojima H., Sugimoto T. Stability analysis of in-plane and out-of-plane periodic motions of electrodynamic tether system in inclined elliptic orbit // Acta Astronautica. 2009. V. 65. P. 477–488.
Mantellato R., Pertile M., Colombatti G., Lorenzini E.C. Analysis of Passive System to Damp the Libration of Electrodynamic Tethers for Deorbiting // AIAA SPACE 2013 Conference and Exposition, San Diego. AIAA 2013–5390. P. 1–9.
Iñarrea M., Lanchares V., Pascual A.I., Salas J.P. Attitude stabilization of electrodynamic tethers in elliptic orbits by time-delay feedback control // Acta Astronautica. 2014. V. 96. P. 280–295.
Zhou X., Li J, Baoyin H., Zakirov V. Equilibrium control of electrodynamic tethered satellite systems in inclined orbits // J. of Guidance, Control, and Dynamics. 2006. V. 29(6). P. 1451–1454.
Corsi J., Iess L. Stability and control of electrodynamic tethers for de-orbiting applications // Acta Astronautica. 2001. V. 48. Iss. 5–12. P. 491–501.
Воеводин П.С., Заболотнов Ю.М. Моделирование и анализ колебаний электродинамической тросовой системы на орбите спутника Земли // Математическое моделирование. 2017. Т. 29. № 6. С. 21–34.
Дигнат Ф., Шилен В. Управление колебаниями орбитальной тросовой системы // Прикладная математика и механика. 2000. Т. 64. Вып. 5. С. 747–754.
Заболотнов Ю.М., Фефелов Д.И. Динамика движения капсулы с тросом на внеатмосферном участке спуска с орбиты // Известия СНЦ РАН. 2006. Т. 8. № 3. С. 841–848.
Zhong R., Zhu Z.H. Dynamic Analysis of Deployment and Retrieval of Tethered Satellites using a Hybrid Hinged-Rod Tether Model // International J. of Aerospace and Lightweight Structures (IJALS). 2015. V. 5(1). PP. 1–21.
Заболотнов Ю.М. Управление развертыванием орбитальной тросовой системы, состоящей из двух малых космических аппаратов // Космические исследования. 2017. Т. 55. № 3. С. 236–246.
Боголюбов H.H., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. М.: Наука, 1981. 496 с.
Беллман Р. Динамическое программирование. М.: Изд-во иностр. лит., 1960. 400 с.
Черноусько Ф.Л., Акуленко Л.Д., Соколов Б.Н. Управление колебаниями. М.: Наука, 1980. 384 с.
Моисеев Н.Н. Асимптотические методы нелинейной механики. М.: Наука, 1986. 378 с.
Салмин В.В., Ишков С.А., Старинова О.Л. Методы решения вариационных задач механики космического полета с малой тягой. Самара: Изд-во СНЦ РАН, 2006. 162 с.
Акуленко Л.Д. Асимптотические методы оптимального управления М.: Наука, 1987. 365 с.
Заболотнов Ю.М., Лобанков А.А. Синтез регулятора для стабилизации движения твердого тела вокруг неподвижной точки // Изв. РАН. МТТ. 2017. № 3. С. 59–71.
Хапаев М.М. Усреднение в теории устойчивости. М.: Наука, 1986. 192 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела