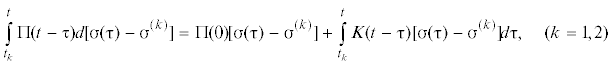Известия РАН. Механика твердого тела, 2019, № 4, стр. 27-38

1. Введение. Основной целью работы является формулировка, краткий анализ и обсуждение некоторых особенностей применения наследственных соотношений общего вида. Наибольший интерес в таких случаях вызывает явление ползучести, связанное с развитием обратимых деформаций в областях линейного и нелинейного вязкоупругого поведения и необратимых – в области вязкопластического поведения материала.

Основы теории ползучести лежат в реологии, в которой процессы ползучести в деформируемых телах моделируются при помощи упругого элемента Гука, вязкого элемента Ньютона и жесткопластического элемента Сен-Венана [1].

Наиболее простые модели реономных деформируемых тел – Максвелла и Фойгта, каждая из которых состоит из одного упругого и одного вязкого элементов способны приближенно отразить лишь некоторые черты поведения таких материалов при их деформировании. Более успешно справляются с этой задачей многоэлементные модели. Однако “…использование сложных многоэлементных моделей приводит к громоздким математическим выражениям и, все-таки, не позволяет удовлетворительно описать деформирование реальных материалов во времени” [2, с. 376]. Таким образом, продолжающиеся и в настоящее время попытки обобщения моделей деформирования путем увеличения числа указанных элементарных моделей не имеют никакой перспективы, да и в этом нет никакой необходимости, поскольку дифференциальные зависимости деформаций от напряжений, получаемые из рассмотрения различных многоэлементных моделей, при их достаточно высоком порядке, эквивалентны, как это следует из курса теории интегральных уравнений, интегральному соотношению Вольтерра – наиболее общей линейной форме определяющего соотношения. В одномерном случае это соотношение имеет вид [3]:

где $t$ – время, ${\varepsilon }$ – деформация, ${\sigma }$ – напряжение, $E$ – модуль Юнга, $K(t,{\tau })$ – ядро интегрального оператора. Указанные соотношения, в силу своей линейности, не могут быть применены при исследовании нелинейных процессов деформирования реономных тел. Это обстоятельство послужило основой развития альтернативного подхода, связанного с использованием нелинейных упругих и вязких элементов, в результате чего в качестве основного упрощенного закона нелинейного деформирования была предложена “псевдолинейная” зависимость вида [3]: где ${{\Phi }_{1}}({\sigma },{\varepsilon })$ и ${{\Phi }_{2}}({\sigma },{\varepsilon })$ – нелинейные функции двух переменных ${\sigma }$ и ${\varepsilon }$. На соотношении (1.2) основано также применение в теории ползучести эмпирических зависимостей, в которых скорость деформации представляется функцией времени, напряжений и некоторых других параметров. Недостатки такого подхода очевидны: в рассматриваемом случае скорость деформации представляет собой лишь частную производную, наличия которой недостаточно для определения полного приращения деформаций, что, в свою очередь, не позволяет точно определять изменение размеров деформируемых тел; понятно, что применительно к дискам или лопаткам турбин такие неточности могут привести к катастрофическим последствиям. Эмпирические зависимости, кроме того, иногда плохо обусловлены; некоторые примеры этого приведены, например, в работе [4].

По-видимому, разработка соотношений вида (1.2) и их широкое применение определялись практической необходимостью и отсутствием альтернативы, поскольку далее в работе [3, с. 301] утверждается: “Нелинейные дифференциальные уравнения первого порядка, естественно, не могут полностью описать все явления деформирования материала во времени. Это было выявлено нами ранее в отношении линейного деформирования. Повышение порядка дифференциальных зависимостей приводит к более громоздким формулам и решениям, поэтому желательно и для нелинейно деформируемых материалов иметь интегральные соотношения между напряжениями и деформациями наследственного типа”. Подобное мнение высказывается также в работах [5, 6].

Решение этой проблемы связано с применением кратно-интегрального ряда Вольтерра [3, 5], который, следуя [3], в частном случае представим в виде:

Нетрудно заметить, что первые два слагаемых правой части этого соотношения тождественно совпадают с общим линейным законом деформирования (1.1), а последующие слагаемые могут быть использованы для описания процессов нелинейного деформирования. Соотношение (1.3) достаточно сложно и не всегда адекватно [7], поскольку содержит больше неизвестных функций, чем можно определить экспериментально; кроме того, без специальных предположений о ядрах многократных интегралов в (1.3), из него не могут быть получены некоторые частные законы нелинейной вязкоупругости, используемые на практике [3].

Для преодоления этих трудностей разными авторами предлагались чрезвычайно большое число различных нелинейных теорий вязкоупругости: квазилинейных, главных нелинейных и пр., полный анализ которых чрезвычайно затруднителен, да к тому же в этом, как будет показано ниже, нет необходимости. Основная причина состоит в том, что рассматриваемые здесь функционалы являются аналитическими; в противном случае соотношение (1.3) не имело бы места [8]. Это означает, что все упомянутые выше многочисленные теории вязкоупругости, построенные на основе соотношения (1.3), являются аналитическими, в силу чего они не могут быть использованы для описания процессов деформирования, происходящих с нарушением непрерывности входящих в них функций или их производных, характерных для пластических деформаций; их применение ограничено лишь областями линейного и нелинейного вязкоупругого (но не вязкопластического) поведения.

Предлагаемые здесь формы определяющих соотношений, помимо основных, используемых для описания линейных и нелинейных вязкоупругих деформаций, содержат также дополнительные слагаемые, предназначенные для учета вязкопластических деформаций.

2. Новая форма определяющих соотношений нелинейной теории вязкоупругости. Определение функций ползучести и предела линейности. Используя выражение аналитического нелинейного функционала, представленного рядом Фантапье, при помощи двух линейных [9], в работе [10] вводится определяющее соотношение

Исходя из тех же предпосылок, предложим другую форму определяющего соотношения, содержащую, в отличие от соотношения (2.1), предельный параметр, в данном случае – предел линейности. Предлагаемую форму такого соотношения в случае одноосного напряженного состояния для стабильного материала, представим в виде:

где ${\Pi }$ и ${{{\Pi }}_{1}}$ – функции ползучести, ${\sigma *}$ – предел линейности, т.е. значение напряжения, при достижении которого происходит нарушение линейности определяющего соотношения, ${{t}_{1}}$ – момент времени, при котором это происходит; он определяется из уравнения ${\sigma }({{t}_{1}}) = s{\text{*}}$, где величина $s{\text{*}}$ представляет собой константу, устанавливаемую, как правило, экспериментально. Далее выражения вида (2.2) будем называть компакт-формой.

Соотношения вида (2.2), несмотря на свой исключительно простой вид, не получили большого распространения, поскольку возобладало превратное мнение о больших трудностях их применения и невозможности определения входящих в эти соотношения материальных функций и параметров. Однако это не так, что нетрудно продемонстрировать на конкретном примере. С этой целью применим соотношение (2.2) к исследованию процесса ползучести при одноосном растяжении. При реализации нагружения в виде ${\sigma }(t) = {{{\sigma }}_{0}}h(t)$, где $h(t)$ – функция Хевисайда, в линейной области поведения материала соотношение (2.2) примет вид ${{{\varepsilon }}_{0}}(t) = {\Pi }(t){{{\sigma }}_{0}}$. Отсюда определяем линейную функцию ползучести $\Pi (t) = {{{\varepsilon }}_{0}}(t){\text{/}}{{{\sigma }}_{0}}$. Предел линейности ${\sigma *}$ определяется по нарушению условий аддитивности и однородности; он совпадает с тем значением напряжения, при котором происходит нарушение аддитивности (однородности) линейного функционала. В нелинейной области поведения вязкоупругого материала соотношение (2.2) при тех же условиях нагружения, при ${{{\sigma }}_{1}} > {\sigma *}$ (в рассматриваемом случае t₁ = 0) приводится к виду:

Отсюда легко находим:

При мгновенно-линейно-упругом поведении материала ${{{\varepsilon }}_{1}}(0){\text{/}}{{{\sigma }}_{1}} = {\Pi }(0)$; при этом ${{{\Pi }}_{1}}(0)$ = 0.

В случае затруднений при определении предела линейности σ* по нарушению условий аддитивности и однородности, предлагается использовать другую методику определения значения σ* и функции ползучести ${{{\Pi }}_{1}}(t)$. Именно, допустим, что вид линейной функции ползучести ${\Pi }(t)$ известен. Затем, при помощи двух диаграмм ползучести, полученных заведомо в нелинейной области (это легко устанавливается по нарушению, например, условия однородности) при ${\sigma }(t) = {{{\sigma }}_{1}}h(t)$ и ${\sigma }(t) = {{{\sigma }}_{2}}h(t)$, используя соотношение (2.3), имеем:

Разделив первое из уравнений на второе, находим:

Функция ${{{\Pi }}_{1}}(t)$ определяется при помощи любого из уравнений системы (2.4).

3. Применение новых форм определяющих соотношений вязкопластичности. Упомянутый выше предел линейности, связывая области линейного и нелинейного поведения вязкоупругого деформируемого материала, “привязан” скорее к используемой математической модели, хотя и, несомненно, отражает некоторые особенности его поведения, скорее всего, на микро- и/или мезо-уровне. По структуре определяющих соотношений вязкоупругости видно, что взаимосвязь различных областей поведения вязкоупругого материала при деформировании осуществляется непрерывным образом, как для деформации, так и для ее производных различного порядка, за счет чего и обеспечиваются непрерывное изменение характера деформирования и обратимость этого процесса. Последнее означает, что рассматриваемая выше математическая модель деформирования вязкоупругих материалов дает возможность описывать процесс разгрузки по нелинейному закону, на необходимость чего указывается, например, в работе [11]. При этом в цитируемой работе отмечается, что несовпадение диаграмм нагрузки и разгрузки не означает появления остаточных деформаций.

Таким образом, вопрос о возможности описания процессов необратимого деформирования в рамках регулярной теории вязкоупругости решить невозможно. Первый шаг на пути решения этой проблемы связан с установлением причин возникновения пластических деформаций. В последнее время во многих исследованиях одной из таких причин указывается движение дислокаций, т.е. совершенно другой, отличный от конформационного, сохраняющего относительные положения частей тела, деформирования, механизм. Будем считать кардинальное изменение механизма деформирования или добавление нового общим правилом, определяющим возникновение необратимых деформаций.

Определяющие соотношения для описания процессов необратимого деформирования должны содержать, дополнительно к соотношениям вязкоупругости, слагаемые, описывающие этот процесс. Наиболее простой путь решения этой проблемы состоит в присоединении к общему соотношению для вязкоупругого материала дополнительного слагаемого. В одномерном случае (рассматриваемом здесь для упрощения) получаемое соотношение примет вид [12, 13]:

где первое слагаемое в правой части полностью тождественно соотношению (2.2), ${{t}_{{n1}}}$ – момент возникновения причины, ведущей к образованию необратимых деформаций. Применительно именно к соотношению вида (3.1) эта величина выбирается как момент времени, при котором напряжение (в данном случае – при одноосном напряженном состоянии) достигает предела текучести. Условно предел текучести $\vartheta $ определяется как значение напряжения, которое при мгновенном нагружении и последующей разгрузке обеспечивает возникновение остаточной деформации, равной 0.002. Остальные символы в (3.1) имеют аналогичный смысл с величинами, присутствующими в пояснении к соотношению (2.2). Предусматривается, что верхний предел интегрирования во внешнем интеграле во втором слагаемом фиксируется в момент начала разгрузки или в какое-либо другое, специально выбранное время, что позволяет зафиксировать значение второго интеграла в (3.1) на постоянном уровне; в этом случае его значение определяет остаточную деформацию. Поскольку оба слагаемые в соотношении (3.1) представляют собой аналитические функционалы, соотношения вида (3.1) получили название кусочно-аналитических [12]. При наличии двух или большего числа не связанных между собой причин возникновения необратимых деформаций (особенно, если они возникают в разное время), процесс обобщения соотношения (3.1) производится путем добавления дополнительных слагаемых такой же структуры, как и второе слагаемое правой части соотношения (3.1). При этом предельные параметры в таких дополнительных слагаемых в общем случае не совпадают с пределом текучести $\vartheta $, определенным указанным выше способом.

Наиболее важным моментом выбора приемлемой формы определяющего соотношения является, несомненно, адекватность такого соотношения, связанная с возможностью определения входящих в него материальных функций и параметров. Покажем на примере соотношения (3.1), что, как и выше, эта процедура предельно проста.

Допустим, что функции ползучести и предел линейности в первом слагаемом правой части соотношения (3.1) найдены. При определении материальных функций и предельных параметров, входящих во второе слагаемое соотношения (3.1) обратим внимание, прежде всего, на то, что верхний предел внешних интегралов в обоих слагаемых один и тот же. Это означает, что при ${\sigma } > \vartheta $ полная деформация является суммой деформаций, определяемых как первым, так и вторым слагаемым правой части соотношения (3.1), в силу чего при определении конкретного вида второго слагаемого этого соотношения будем исходить из равенства

в котором ${\varepsilon }(t)$ представляет собой диаграмму ползучести, полученную при выполнении условия ${\sigma } > {\sigma **}$; здесь σ** имеет смысл предела текучести, независимо от того, совпадает ли его значение с величиной $\vartheta $ или нет. В любом случае значение ${{t}_{{n1}}}$ и предельный параметр σ** определяются по начальному моменту нарушения возможности применения первого слагаемого в соотношении (3.1).

Интеграл в правой части соотношения (3.2) легко вычисляется при помощи полученных на предыдущем этапе функций ползучести и предела линейности. Алгоритм определения функций ползучести ${{\Pi }_{2}}$, ${{\Pi }_{3}}$ и параметра σ*** аналогичен алгоритму, примененному при определении $\Pi $, ${{\Pi }_{1}}$ и σ*. При необходимости введения дополнительного третьего и последующих слагаемых такой же структуры, как и второе, они определяются аналогично.

Первое слагаемое в соотношении (3.1) будем считать базовым элементом, а последующие, при их наличии, – дополнительными элементами. Такое многоэлементное определяющее соотношение имеет наиболее общую форму, из которой нетрудно вывести все известные формы определяющих соотношений связи между напряжениями и деформациями в механике деформируемого твердого тела, вплоть до закона Гука.

Известны также и некоторые другие формы определяющих соотношений типа (3.1) и его обобщений. Так, в работе [12] предложена несколько более простая форма определяющего соотношения, которая также может быть достаточно просто использована при необходимости учета остаточных деформаций:

Это соотношение, как и рассматриваемые выше кусочно-аналитические формы определяющих соотношений, допускает описание мгновенных упругих и мгновенных пластических деформаций; при этом ${{\Pi }_{1}}(0) = 0$ (см. пояснение к формуле (2.3)), в то время, как значение функции ползучести ${{\Pi }_{2}}(t)$ при t = 0 может быть как равным нулю, так и отличаться от него. Определение материальных функций и параметров в (3.3) производится по такому же алгоритму, как и выше. В первую очередь определяем эти величины в первом слагаемом правой части (3.3). Для определения величины σ**, входящей во второе слагаемое правой части (3.3) можно также использовать уже известную нам методику. С этой целью воспользуемся диаграммами ползучести, полученными для тех значений напряжений, для которых расчет при помощи первого слагаемого правой части (3.3) дает существенно заниженные результаты. Выберем две такие, различающиеся между собой диаграммы, полученные при ${\sigma }(t) = {{{\sigma }}_{1}}h(t)$ и σ(t) = = ${{{\sigma }}_{2}}h(t)$. Введем величины

В результате, при помощи соотношения (3.3) получим систему двух уравнений:

Разделив первое из уравнений на второе, находим:

После этого функция ползучести ${{\Pi }_{2}}(t)$ определяется при помощи любого из уравнений системы (3.4):

Необходимо также обратить внимание на то, что в некоторых случаях [12, 13] функция ползучести ${{\Pi }_{1}}(t)$ в соотношении (3.1) тождественно равна нулю, в силу чего первое слагаемое в этом соотношении представляет собой линейный функционал. Очевидно, что имеются самые различные сочетания линейных и компактных форм нелинейных функционалов. Особый интерес, однако, представляет кусочно-линейная форма определяющих соотношений, полученная ранее [14] совсем из других соображений. Она имеет вид:

где ${{{\sigma }}^{{(1)}}}$, …, ${{{\sigma }}^{{(n)}}}$ – предельные параметры, имеющие смысл пределов линейности, текучести и т.п. или отражающие наличие какого-либо явления, влияющего на математическую форму или физическое содержание определяющего соотношения, ${{t}_{1}}, \ldots ,{{t}_{n}}$ – моменты времени, при которых эти явления возникают. Определение входящих в соотношение (3.5) функций ползучести и предельных параметров производится при помощи диаграмм ползучести, получаемых при постепенно возрастающих значениях, задаваемого с использованием функции Хевисайда при $t = 0$, напряжения по подробно описанной выше методике, что очень важно для обеспечения адекватности предлагаемых форм соотношений [7].

Функция ползучести $\Pi (t)$ в соотношении (3.5) определяется в области линейного поведения материала. Для определения функции ползучести ${{\Pi }_{1}}(t)$ и первого предельного параметра σ⁽¹⁾ необходимо иметь, по крайней мере, две диаграммы ползучести, полученные при двух различных значениях напряжений ${{{\sigma }}_{1}} > {{{\sigma }}^{{(1)}}}$ и ${{{\sigma }}_{2}} > {{{\sigma }}^{{(1)}}}$, обеспечивающих нелинейное поведение деформируемого материала, что легко определяется по признаку невозможности описания поведения материала при помощи только первого слагаемого правой части соотношения (3.5). Принимая во внимание в этом случае только два первых слагаемых соотношения (3.5), имеем:

Точно так же, как и выше, отсюда находим предельный параметр σ⁽¹⁾ и функцию ползучести ${{\Pi }_{1}}(t)$.

В дальнейшем, только нарушение возможности описания поведения материала при использовании n первых слагаемых соотношения (3.5) служит признаком введения в это соотношение n + 1-го слагаемого; при этом определяются функция ползучести ${{\Pi }_{n}}(t)$ и предельный параметр σ⁽ⁿ⁾. Нижние пределы интегрирования – моменты времени ${{t}_{1}}, \ldots ,{{t}_{n}}$ для заданных условий нагружения ${\sigma } = {\sigma }(t)$ устанавливаются путем решения уравнений вида: ${\sigma }({{t}_{i}}) = {{{\sigma }}^{{(i)}}},i = 1,...,n$.

В заключение обратим внимание на то, что функции ползучести и предельные параметры устанавливаются непосредственно по диаграммам ползучести. Это обстоятельство дает дополнительную возможность оценить справедливость некоторых используемых в механике реономных материалов гипотез, например, совпадут ли пределы текучести, определенные по остаточной деформации 0.002 с одной стороны и путем расчетов по диаграммам ползучести – с другой.

4. Исследование механических свойств алюминиевого сплава Д16. Применим представленные выше соотношения связи между напряжениями и деформациями для определения материальных характеристик деформируемого материала – функций ползучести и предельных параметров, используя экспериментальные данные по мгновенному растяжению и кратковременной ползучести алюминиевого сплава Д16 при температурах Т, равных 20°С, 100°С, 200°С, 300°С и 350°С [15]. При Т = 20°С и Т = = 100°С ползучесть не наблюдалась.

При помощи диаграмм мгновенного деформирования находим значения пределов текучести $\vartheta \equiv {{\vartheta }_{{0.2}}}$, т.е. значений напряжений, обеспечивающих возникновение остаточной деформации 0.002 при различных температурах. Установлено, что для указанного ряда температур они равны 108; 104; 98; 65 и 44 МПа соответственно. Обнаружено, что на графике зависимости $\vartheta $ от T значение предела текучести, равное 98 МПа при температуре 200°С, приводит к возникновению угловой точки, исчезающей, если считать $\vartheta $ = 92 МПа; именно последнее значение будет получено ниже путем расчета по диаграммам ползучести.

Предел текучести в представленных выше определяющих соотношениях разграничивает области линейного и нелинейного вязкоупругого поведения с одной стороны и вязкопластического – с другой. Заметим, что с точки зрения практических приложений обе области представляют значительный интерес: первая – для оценки работоспособности длительно работающих при высоких температурах конструкций, вторая – при изучении вопросов, связанных с накоплением необратимых деформаций и разрушением. В первом случае можно ограничиться исследованиями при значениях напряжений, не превосходящих предела текучести; во втором – необходимы исследования при постепенно возрастающих напряжениях, в областях, как ниже, так и выше предела текучести.

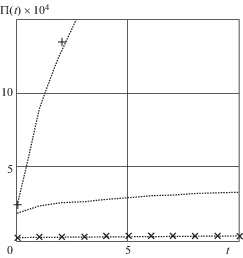
4.1. Механические характеристики сплава Д16 при температуре Т = 200°С. Диаграммы ползучести представлены для пяти уровней напряжения: 85.54; 103.44; 121.35 и 139.26 МПа – (от 0 до 10 мин, через 1 мин) и при 159.15 МПа – для значений времени 0, 1 и 2 мин. Предел текучести сплава Д16 для этой температуры равен 98 МПа (его альтернативное значение – 92 МПа). В силу того, что только один эксперимент производился при напряжении, не превосходящем значения предела текучести (при любом его выборе), для исследования линейного и нелинейного вязкоупругого деформирования практически никакой, необходимой для детального исследования этой области, информации нет. Тем не менее, допустим, что диаграмма ползучести, полученная при 85.54 МПа, определяет линейную функцию ползучести (достаточной экспериментальной информации для проверки этого предположения, к сожалению, нет). В этом случае приводимые несколько других диаграмм ползучести при более высоких уровнях напряжения позволяют применить кусочно-линейную теорию вязкопластичности. Это возможно в том случае, когда пределы линейности и аналитичности совпадают, что обнаружено для некоторых материалов [12–14]. Будем считать, что это условие выполняется и в данном случае. Тогда область нелинейного вязкоупругого поведения исключается, как и необходимость определения соответствующих ей механических характеристик деформируемого материала. Исходя из этого, в данном случае используем определяющие соотношения в виде (3.5); определение первого предельного параметра σ⁽¹⁾ и функции ползучести ${{\Pi }_{1}}{\text{(}}t{\text{)}}$ производим при помощи системы уравнений (3.6), используя диаграммы ползучести, полученные при постоянных напряжениях 103.4 и 121.35 МПа. Отдельные значения линейной функции ползучести $\Pi (t)$ отмечены крестиками на рис. 1 . Расчетное (по диаграммам ползучести) среднее значение предельного параметра σ⁽¹⁾ равно 92 МПа. Функция ползучести ${{\Pi }_{1}}(t)$, определенная при помощи уравнений (3.6), отмечена кружками на рис. 1 .

Расчетами также установлено, что первые два члена определяющего соотношения (3.5) не позволяют описать процесс деформирования при значении постоянного напряжения, равного 139.25 МПа. Исходя из этого, добавим третье слагаемое в правой части соотношения (3.5). Для определения предельного параметра σ⁽²⁾ и функции ползучести ${{\Pi }_{2}}(t)$ используем две последующие диаграммы ползучести, полученные при 139.25 МПа и 159.15 МПа. Поскольку вторая из этих диаграмм получена в укороченном виде, механические характеристики получены только для трех первых моментов времени. Так же, как и выше, были определены механические характеристики деформируемого материала, входящие в третье слагаемое соотношения (3.5). Расчетное значение второго предельного параметра σ⁽²⁾ = 130 МПа. Определенная затем функция ползучести ${{\Pi }_{2}}(t)$ отмечена знаками “+” на рис. 1 .

Таким образом, у нас имеется полный набор механических характеристик сплава Д16 для указанной температуры: предельные параметры и функции ползучести, необходимый для применения кусочно-линейной формы определяющего соотношения. Используем его для расчета диаграммы деформирования сплава Д16 при температуре Т = 200°С при одноосном напряженном состоянии с постоянной скоростью нагружения:

т.е. по закону, не использованному в тарировочных экспериментах. Входящие в (3.5) отдельные интегралы удобно преобразовать к виду [5]: где $K(t) = \dot {\Pi }(t)$. С целью упрощения расчетов будем использовать простейшие аппроксимации входящих в соотношение (3.5) функций ползучести:

Аппроксимирующие кривые, расположенные в непосредственной близости к соответствующим экспериментально определенным функциям ползучести, представлены на рис. 1 пунктирными линиями.

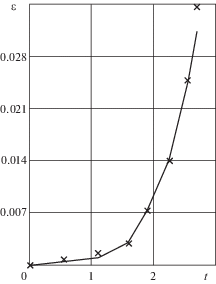
Результаты расчетов приведены на рис. 2 . На нем экспериментально определенная зависимость ${\varepsilon } = {\varepsilon }(t)$ представлена сплошной кривой. Расчетные значения деформаций указаны в отдельных точках, обозначенных крестиками.

Таким образом, можно заключить, что удовлетворительное совпадение расчетных значений деформаций с соответствующей экспериментальной зависимостью, свидетельствует как о справедливости использованных предположений, так и о перспективных возможностях применения кусочно-линейной формы определяющих соотношений при описании высокотемпературной ползучести металлов.

4.2. Механические характеристики сплава Д16 при температуре Т = 300°С. Диаграммы ползучести в этом случае представлены для восьми уровней постоянного напряжения: 35.81; 39.79; 42.57; 45.36; 47.75; 55.71; 67.73 и 77.58 МПа – все, кроме двух последних, диаграммы получены в интервале времени от 0 до 10 мин, через 1 мин. Предел текучести сплава Д16 для этой температуры, определенный выше при помощи соответствующей диаграммы мгновенного деформирования, равен 65 МПа.

Предварительный анализ упомянутых здесь диаграмм ползучести с точки зрения приращения их значений для фиксированных моментов времени привел к отбраковке трех последних диаграмм. Таким образом, диаграммы ползучести, полученные при значениях постоянного напряжения, не превышающего в таком случае предела текучести, позволяют определить механические характеристики сплава Д16 только в области линейной и нелинейной вязкоупругости. Определим характеристики сплава Д16 при заданной температуре, применяя как кусочно-линейную, так и компакт-форму определяющих соотношений.

Три первые диаграммы ползучести удовлетворяют условиям однородности; именно они были использованы для определения линейной функции ползучести $\Pi (t) \times {{10}^{5}}$, одной и той же, как для компакт-формы (2.2), так и для кусочно-линейной формы определяющих соотношений (3.5). Ее значения (в 1/МПа) приведены во втором столбце табл. 1; в первом столбце этой таблицы даны значения времени t (в мин.). Понятно, что общим у этих форм соотношений должен быть и предел линейности – первый предельный параметр. Для его определения в обоих случаях используются диаграммы ползучести, полученные при постоянных напряжениях 45.36 и 47.75 МПа. Их значения (в МПа) для компакт-формы приведены в третьем, а для кусочно-линейной формы – в пятом столбцах табл. 1. Функция ползучести $\Pi _{1}^{{cf}}{\text{(}}t{\text{)}}$, входящая в выражение компакт-формы, приведена (в 1/МПа) в четвертом столбце табл. 1, функция $\Pi _{1}^{{pl}}(t)$, фигурирующая в кусочно-линейной форме определяющих соотношений приведена в виде $\Pi _{1}^{{pl}}(t) \times {{10}^{5}}$ (в 1/МПа) в шестом столбце этой же таблицы.

Таким образом, в рассматриваемом здесь случае экспериментальные данные дают возможность определения механических характеристик деформируемого материала лишь в области линейного и нелинейного вязкоупругого поведения сплава Д16 при Т = 300°С. Показано, что для описания процесса ползучести существует возможность применения как компакт-формы, так и кусочно-линейной формы определяющих соотношений при тождественном совпадении линейной функции ползучести и пределов линейности, вычисляемых при помощи соотношений разной формы.

4.3. Механические характеристики сплава Д16 при температуре Т = 350°С. Диаграммы ползучести в этом случае представлены для семи уровней постоянного напряжения: 35.81; 39.79; 42.57; 45.36; 47.75; 55.71 и 61.67 МПа. Все диаграммы ползучести, кроме последней, получены в интервале времени от 0 до 10 мин, через 1 мин. Предел текучести сплава Д16 для температуры Т = 350°С равен 44 МПа. Нетрудно установить, что первые три диаграммы ползучести, полученные при напряжениях, не превышающих этого значения, не удовлетворяют условиям однородности; это свидетельствует о нелинейности поведения деформируемого материала. Использование первой из них для нахождения линейной функции ползучести не привело к положительному результату. Таким образом, в данном случае имеется только возможность ограниченного применения кусочно-линейной формы определяющего соотношения

преобразуя его при задании напряжения при помощи функции Хевисайда при t = 0 к виду:

Видно, что выражение (4.2) позволяет частично определить механические характеристики материала, именно, сумму функций ползучести $[\Pi (t) + {{\Pi }_{1}}(t)]$, произведение ${{\Pi }_{1}}(t){{{\sigma }}^{{(1)}}}$, ${{{\sigma }}^{{(2)}}}$ и ${{\Pi }_{2}}(t)$. Эти величины в виде $(\Pi + {{\Pi }_{1}}) \times {{10}^{4}}$(в 1/МПа), ${{\Pi }_{1}}{{{\sigma }}^{{(1)}}} \times {{10}^{5}}$, ${{{\sigma }}^{{(2)}}}$ (в МПа) и ${{\Pi }_{2}} \times {{10}^{3}}$ (в 1/МПа) представлены соответственно во 2–5 столбцах табл. 2; в первом столбце этой таблицы приведены значения времени (в мин). Обратим особое внимание на точное совпадение второго предельного параметра с определенным при помощи диаграммы мгновенного деформирования пределом текучести, равном 44 МПа и на частичную возможность использования соотношения (4.2) при ступенчатом задании напряжения в начальный момент времени.

Таким образом, можно заключить, что выделение в этом случае линейной и нелинейной вязкоупругих областей (при напряжениях ${\sigma }$, меньших предела текучести) и вязкопластической области (при напряжениях ${\sigma }$, больших предела текучести), при введении необходимого набора механических характеристик, приводит к адекватной кусочно-линейной форме определяющих соотношений, пригодной для описания процессов ползучести.

5. Заключение. Предлагаемые формы определяющих соотношений удовлетворительно описывают процессы деформирования реономных материалов в линейной и нелинейной вязкоупругих и вязкопластических областях, учитывая при этом нарушение аналитического характера процессов. Соотношения весьма удобны с точки зрения определения входящих в них функций ползучести и предельных параметров, разграничивающих разные области поведения деформируемого материала. Используемые для этого экспериментальные данные желательно получать при постепенно возрастающих нагрузках, ориентируясь, в первую очередь, на предел текучести. При этом определенный смысл имеет получение диаграмм ползучести не по результатам 3–5 экспериментов, проведенных при одинаковых напряжениях, а для их различных значений; усреднение может быть проведено и по итоговым характеристикам. В таком случае общее число экспериментов не увеличится, однако при этом появляются дополнительные возможности контроля эксперимента.

Экспериментальные исследования процессов деформирования металлов и сплавов в условиях кратковременной ползучести, подобные тем, что были использованы в настоящей работе, имеют, тем не менее, большое значение. Такой подход существенно сокращает затраты, позволяя на основе результатов предварительных краткосрочных экспериментов определять оптимальные условия проведения длительных экспериментов.

Работа выполнена при частичной поддержке РФФИ (проект № 17-08-00210).