Известия РАН. Механика твердого тела, 2019, № 4, стр. 8-26
РЕШЕНИЕ ОБРАТНОЙ СПЕКТРАЛЬНОЙ ЗАДАЧИ ДЛЯ СТЕРЖНЯ, ОСЛАБЛЕННОГО ПОПЕРЕЧНЫМИ ТРЕЩИНАМИ, С ПОМОЩЬЮ ОПТИМИЗАЦИОННОГО АЛГОРИТМА ЛЕВЕНБЕРГА–МАРКВАРДТА
И. М. Лебедев a, Е. И. Шифрин a, *
a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия
* E-mail: shifrin@ipmnet.ru
Поступила в редакцию 14.01.2019
После доработки 14.01.2019
Принята к публикации 30.01.2019
Аннотация
Рассматриваются продольные колебания стержня, ослабленного поперечными трещинами. Трещины предполагаются открытыми и моделируются пружинами, работающими на растяжение–сжатие. Жесткости пружин соответствуют размерам трещин. Разработан метод идентификации числа и положения поперечных трещин, а также жесткости соответствующих им пружин по двум спектрам, отвечающим двум типам условий на концах стержня: свободный – свободный и закрепленный – свободный. Разработанный метод основан на минимизации целевой функции, характеризующей отличие между заданными (измеренными) и вычисляемыми в ходе реализации алгоритма собственными частотами. Минимизация целевой функции осуществляется с помощью алгоритма Левенберга–Марквардта. Рассмотрены численные примеры. Исследована устойчивость получаемых результатов по отношению к шуму в исходных данных.
1. Введение. Проблеме идентификации трещин и других локализованных дефектов в стержнях и балках с помощью собственных частот посвящено значительное количество публикаций. В большинстве публикаций, в целях сохранения одномерности задачи, трещины моделируются пружинами. В случае продольных колебаний предполагается, что соответствующая трещине пружина работает на растяжение – сжатие, а в случае поперечных колебаний – на поворот. Среди публикаций, в которых в случае продольных колебаний трещины заменялись пружинами, работающими на растяжение – сжатие, можно отметить обзор [1] и статьи [2–8]. Связь между длиной трещины и жесткостью соответствующей пружины изучалась в [6]. Другие модели повреждений рассматривались в [9–12]. Известно несколько различных подходов к решению задачи идентификации трещин. В большинстве работ задача решалась в предположении малости трещин, что отвечает малости податливости соответствующих им пружин. Такое предположение существенно упрощает задачу, поскольку она становится линейной по отношению к неизвестным податливостям пружин. Проблема идентификации одиночной трещины рассматривалась в публикациях [2, 5, 7]. Задача идентификации двух малых трещин решалась в [13–15]. Различные способы идентификации произвольного числа малых трещин предложены в [16, 17].
Для решения рассматриваемых задач также широко применялись численные методы. Прямая задача определения собственных частот может быть сведена к нахождению нулей детерминантного уравнения, зависящего от параметров имеющихся трещин. Если некоторые собственные частоты известны, то эти же уравнения можно рассматривать как нелинейные уравнения относительно параметров трещин. В [18] задача идентификации как одиночной, так и множественных трещин решалась путем численного решения указанной системы уравнений методом Ньютона. В [19, 20] прямая задача решалась как методом конечных, так и граничных элементов. Идентификация трещин также осуществлялась путем решения соответствующей системы нелинейных уравнений методом Ньютона. В значительном числе публикаций трещины в балках и балочных конструкциях искались с помощью сведения исходной задачи к задаче минимизации целевой функции и дальнейшего поиска минимума одним из вариантов генетического алгоритма или методом на основе роя частиц [21–24]. Во всех указанных публикациях не исследовался вопрос о том, каковы должны быть исходные данные для того, чтобы обеспечить однозначное определение трещин. Во многих случаях предполагалось, что количество трещин известно заранее. Кроме того, сами применяемые методы не могут гарантировать нахождение решения.
Строгий алгоритм идентификации одиночной трещины произвольного размера предложен в [25] и [26] для случаев продольных и поперечных колебаний стержня, соответственно.
Достаточно общий результат был получен в [27]. В этой статье доказано, что любое количество трещин произвольного размера в стержне постоянного сечения однозначно восстанавливается по двум спектрам, соответствующим двум типам условий на концах: свободный – свободный и закрепленный – свободный. Результат был получен сведением исходной задачи к обратной задаче Штурма–Лиувилля. Кроме того, в статье представлен алгоритм восстановления повреждений по $N$ собственным частотам, отвечающим каждому из краевых условий, и показано, что при $N \to \infty $ получаемые решения стремятся к точному решению обратной задачи. Представленный алгоритм основан на методе М.Г. Крейна. Отметим, что аналогичные результаты для стержня переменного сечения получены в [28].
Несмотря на то, что предложенный в [27, 28] алгоритм строго обоснован, расчеты показали, что он недостаточно устойчив по отношению к погрешностям в исходных данных и к количеству используемых собственных частот $N$.
В данной статье рассматривается та же, корректная постановка задачи, что и в [27]. Повреждения восстанавливаются по одинаковому количеству собственных частот $N$, отвечающих условиям на концах стержня: свободный – свободный и закрепленный – свободный. При этом предлагается иной, более устойчивый к шуму в исходных данных алгоритм.
Предлагаемый алгоритм состоит из следующих элементов. Сперва строится конечно-элементная модель стержня. Повреждения учитываются изменением модуля Юнга в локальных матрицах жесткости. Затем строится целевая функция, зависящая от модулей Юнга в локальных матрицах жесткости. Целевая функция характеризует отклонение вычисляемых для рассматриваемой матрицы жесткости собственных частот колебаний стержня от заданных (измеренных). Минимизация целевой функции осуществляется с помощью алгоритма Левенберга–Марквардта.
Статья организована следующим образом. В разделе 2 дается постановка задачи. В разделе 3 представлена конечно-элементная модель стержня. В разделе 4 дано описание алгоритма Левенберга–Марквардта. Реализация алгоритма требует вычисления производных от собственных частот по параметрам, характеризующим жесткости элементов стержня. Метод вычисления таких производных представлен в разделе 5. В разделе 6 рассмотрены численные примеры. Выводы представлены в разделе 7.
2. Постановка задачи. Пусть упругий стержень имеет длину l и постоянную площадь поперечного сечения A. Предположим, что стержень занимает интервал $0 < x < l$ и содержит $n$ трещин, моделируемых пружинами, работающими на растяжение–сжатие. Обозначим координаты расположения трещин ${{x}_{1}},{{x}_{2}},\; \ldots ,\;{{x}_{n}}$, где 0 = ${{x}_{0}} < {{x}_{1}} < {{x}_{2}} < \cdots $ < < xn < xn + 1 = l. Обозначим ${{u}_{j}}\left( x \right)$ амплитуды перемещений стержня при продольных гармонических колебаниях в интервале ${{x}_{{j - 1}}} < x < {{x}_{j}}$. Здесь $j = 1,2,\; \ldots ,\;n + 1$. Уравнение продольных гармонических колебаний стержня имеет вид [4, 6]
(2.1)
$u_{j}^{{''}}\left( x \right) + {\lambda }{{u}_{j}}\left( x \right) = 0,\quad j = 1,2,\; \ldots ,\;n + 1,\quad {{x}_{{j - 1}}} < x < {{x}_{j}}$Условия сопряжения в местах расположения трещин (пружин) имеют вид [4, 6]
(2.2)
$u_{j}^{'}\left( {{{x}_{j}}} \right) = u_{{j + 1}}^{'}\left( {{{x}_{j}}} \right),\quad {{u}_{{j + 1}}}\left( {{{x}_{j}}} \right) - {{u}_{j}}\left( {{{x}_{j}}} \right) = {{{\Delta }}_{j}} = EA{{c}_{j}}u_{j}^{'}\left( {{{x}_{j}}} \right),\quad j = 1,2,\; \ldots ,\;n$Рассматривается два типа условий на концах стержня. В случае, когда концы стержня свободны от усилий, краевые условия имеют вид
Случай, когда один конец стержня закреплен, а другой свободен, приводит к следующим краевым условиям
Обозначим отличные от нуля собственные числа задачи (2.1), (2.2), (2.3) ${{{\lambda }}_{1}},{{{\lambda }}_{2}},{{{\lambda }}_{3}},\; \ldots $. Собственные числа задачи (2.1), (2.2), (2.4) обозначим ${{{\mu }}_{1}},{{{\mu }}_{2}},{{{\mu }}_{3}},\; \ldots $.
В [27] было доказано, что любое количество трещин произвольного размера однозначно восстанавливается по двум указанным выше спектрам. Кроме того, была предложена конструктивная процедура реконструкции трещин по усеченным данным, использующим конечное число N собственных чисел из каждого спектра. При этом, в случае $N \to \infty $, получаемые по усеченным данным приближенные решения стремятся к точному.
Здесь предлагается другая, менее чувствительная к погрешностям в заданных собственных числах, процедура идентификации трещин. В предлагаемом численном методе используется конечно-элементная аппроксимация. В результате задача на собственные значения сводится к виду
Здесь ${{{\mathbf{K}}}_{i}}$ – матрицы жесткости, отвечающие при i = 1 и i = 2 краевым условиям (2.3) и (2.4) соответственно, ${\mathbf{M}}$ – матрица масс, d – собственный вектор.
Матрицы ${{{\mathbf{K}}}_{i}}$ состоят из блоков, отвечающих конечным элементам. Каждый элемент имеет, вообще говоря, свою жесткость. Таким образом, собственные числа, определяемые уравнением (2.5), зависят от жесткостей конечных элементов. Предположим, что нам известны (измерены) собственные числа ${\lambda }_{1}^{*},{\lambda }_{2}^{*},\; \ldots ,\;{\lambda }_{N}^{*}$ и ${\mu }_{1}^{*},{\mu }_{2}^{*},\; \ldots ,\;{\mu }_{N}^{*}$, отвечающие краевым условиям (2.3) и (2.4). Построим целевую функцию
(2.6)
$F = \sum\limits_{k = 1}^N {\left[ {{{{\left( {\frac{{{{{\lambda }}_{k}} - {\lambda }_{k}^{*}}}{{{\lambda }_{k}^{*}}}} \right)}}^{2}} + {{{\left( {\frac{{{{{\mu }}_{k}} - {\mu }_{k}^{*}}}{{{\mu }_{k}^{*}}}} \right)}}^{2}}} \right]} $Здесь ${{{\lambda }}_{k}}$ и ${{{\mu }}_{k}}$ – собственные числа, определяемые уравнением (2.5) при i = 1 и i = 2, соответственно.
Необходимо найти такое распределение жесткостей конечных элементов, которое доставляет минимум функционалу (2.6). Поскольку при решении обратной задачи путем минимизации целевой функции необходимо много раз решать прямую задачу, успешность метода во многом зависит от эффективности алгоритма решения прямой задачи. Используемый в статье алгоритм представлен в следующем разделе. Эффективность решения обратной задачи также решающим образом зависит от выбора и реализации метода поиска экстремума, адекватного имеющейся целевой функции. Алгоритм минимизации представлен в разделе 4.
3. Конечно-элементная модель стержня. При построении конечно-элементной модели стержня с трещинами предполагается, что трещины влияют на локальную жесткость стержня, но не влияют на его плотность. В связи с этим, уравнение продольных гармонических колебаний стержня имеет вид
(3.1)
$\left( {E{\text{*}}\left( x \right)u{\text{'}}\left( x \right)} \right){\text{'}} + {\rho }{{{\omega }}^{2}}u\left( x \right) = 0,\quad 0 < x < l$Умножая уравнение (3.1) на функцию ${v}\left( x \right)$, удовлетворяющую соответствующим краевым условиям, интегрируя и деля на E, получаем слабую формулировку задачи
Здесь $K\left( {u,{v}} \right) = \int\limits_0^l {p\left( x \right)} u{\text{'}}\left( x \right){v}{\text{'}}\left( x \right)dx$, $M\left( {u,{v}} \right) = \int\limits_0^l {u(x)} {v}\left( x \right)dx$, $p(x) = E{\text{*}}\left( x \right){\text{/}}E$.
Функция $u(x) \in {{H}^{1}}\left( {\Omega } \right)$, где Ω – отрезок [0, 1], удовлетворяющая (3.2) $\forall \;{\text{v}}\left( x \right) \in {{H}^{1}}\left( {\Omega } \right)$, является решением уравнения (3.1), удовлетворяющим краевым условиям (2.3).
Обозначим ${{H}^{{1*}}}\left( {\Omega } \right)$ подпространство пространства H1(Ω), являющееся пополнением в норме H1(Ω) непрерывно дифференцируемых функций, обращающихся в ноль в какой-либо окрестности точки 0. Функция $u(x) \in {{H}^{{1*}}}\left( {\Omega } \right)$, удовлетворяющая (3.2) $\forall {v}\left( x \right) \in {{H}^{{1*}}}\left( {\Omega } \right)$, является решением уравнения (3.1), удовлетворяющим краевым условиям (2.4).
В выражении для $K(u,{v})$ будем полагать, что p(x) кусочно-постоянная функция
(3.3)
$p\left( x \right) = {{p}_{i}},\quad {{z}_{i}} < x < {{z}_{{i + 1}}},\quad i = 1,2, \ldots ,\;P,\quad {{z}_{i}} = (i - 1) \cdot l{\text{/}}P$Обозначим $h = l{\text{/}}P = {{z}_{{i + 1}}} - {{z}_{i}}$, $i = 1,\; \ldots ,\;P$.
Заметим, что справедливы неравенства $0 < {{p}_{i}} \leqslant 1$. Случай ${{p}_{i}} = 1$ соответствует целому элементу, расположенному в интервале ${{z}_{i}} < x < {{z}_{{i + 1}}}$, а ${{p}_{i}} = 0$ – полностью разрушенному.
При задании конкретных значений pi собственные значения уравнения (3.2) могут быть найдены с помощью метода конечных элементов. Пусть аппроксимация собственной функции ищется в L-мерном пространстве и ${{{\varphi }}_{1}}\left( x \right),\; \ldots ,\;{{{\varphi }}_{L}}\left( x \right)$ – некоторый базис в этом пространстве. Обозначим ${{u}_{{FEM}}}\left( x \right)$ аппроксимацию u(x) в данном пространстве.
(3.4)
${{u}_{{FEM}}}\left( x \right) = \sum\limits_{k = 1}^L {{{{\alpha }}_{k}}{{{\varphi }}_{k}}\left( x \right)} $Из (3.2), (3.3) и (3.4) получаем
(3.5)
$\sum\limits_{k = 1}^L {\left( {\sum\limits_{i = 1}^P {{{p}_{i}}} \int\limits_{{{z}_{i}}}^{{{z}_{{i + 1}}}} {{\varphi }_{k}^{'}\left( x \right){\varphi }_{j}^{'}\left( x \right)dx - {\lambda }\int\limits_0^l {{{{\varphi }}_{k}}\left( x \right){{{\varphi }}_{j}}\left( x \right)dx} } } \right)} {{{\alpha }}_{k}} = 0$Стандартный метод конечных элементов (МКЭ) использует полиномиальные функции формы, то есть кусочно-полиномиальные функции φk(x). Определение собственных значений (3.5) с помощью МКЭ приводит к хорошим результатам только в случае низких частот. В случае вычисления более высоких собственных частот для достижения удовлетворительной точности требуются большие вычислительные затраты. Неэффективность МКЭ в данном случае связана с тем, что при высоких частотах собственные функции становятся быстро осциллирующими. Одним из методов, позволяющих повысить точность вычисления более высоких собственных частот при более низких вычислительных затратах, является обобщенный метод конечных элементов, основные идеи которого были заложены в публикациях [29, 30]. Суть рассматриваемого метода состоит в построении конечномерного пространства функций, локально отражающих доступную информацию о неизвестном решении краевой задачи. В рассматриваемой задаче целесообразно дополнить множество стандартных функций формы функциями, учитывающими осцилляцию решения. В данной статье при решении прямой задачи определения собственных значений был использован вариант обобщенного метода конечных элементов, предложенный в [31] для решения задачи о продольных колебаниях стержня переменного сечения. В [31] в качестве стандартных базисных функций были взяты кусочно-линейные функции.
(3.6)
${{{\varphi }}_{i}}\left( x \right) = \left\{ \begin{gathered} 1 + \frac{{x - {{z}_{i}}}}{h},\quad x \in \left( {{{z}_{{i - 1}}},{{z}_{i}}} \right) \hfill \\ 1 - \frac{{x - {{z}_{i}}}}{h},\quad x \in \left( {{{z}_{i}},{{z}_{{i + 1}}}} \right) \hfill \\ 0,\quad x \notin \left( {{{z}_{{i - 1}}},{{z}_{{i + 1}}}} \right) \hfill \\ \end{gathered} \right.$Эти функции дополнены функциями вида ${{{\varphi }}_{i}}\left( x \right){{{\gamma }}_{{j1}}}\left( {x,{\lambda }} \right)$ и ${{{\varphi }}_{i}}\left( x \right){{{\gamma }}_{{j2}}}\left( {x,{\lambda }} \right)$, где функции ${{{\gamma }}_{{j1}}}\left( {x,{\lambda }} \right)$ и ${{{\gamma }}_{{j2}}}\left( {x,{\lambda }} \right)$ определяются следующим образом
(3.7)
$\begin{gathered} {{{\gamma }}_{{j1}}}\left( {x,{\lambda }} \right) = \left\{ \begin{gathered} \sin \left( {\sqrt {\lambda } \left( {x - {{z}_{{j - 1}}}} \right)} \right),\quad x \in \left( {{{z}_{{j - 1}}},{{z}_{j}}} \right) \hfill \\ \sin \left( {\sqrt {\lambda } \left( {{{z}_{{j + 1}}} - x} \right)} \right),\quad x \in \left( {{{z}_{j}},{{z}_{{j + 1}}}} \right) \hfill \\ 0,\quad x \notin \left( {{{z}_{{j - 1}}},{{z}_{{j + 1}}}} \right) \hfill \\ \end{gathered} \right. \hfill \\ {{{\gamma }}_{{j2}}}\left( {x,\lambda } \right) = \left\{ \begin{gathered} \cos \left( {\sqrt {\lambda } \left( {x - {{z}_{{j - 1}}}} \right)} \right) - 1,\quad x \in \left( {{{z}_{{j - 1}}},{{z}_{j}}} \right) \hfill \\ \cos \left( {\sqrt {\lambda } \left( {{{z}_{{j + 1}}} - x} \right)} \right) - 1,\quad x \in \left( {{{z}_{j}},{{z}_{{j + 1}}}} \right) \hfill \\ 0,\quad x \notin \left( {{{z}_{{j - 1}}},{{z}_{{j + 1}}}} \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $Собственные значения определяются итерационным методом. В качестве нулевого приближения n-го собственного значения ${\lambda }_{n}^{0}$ берется собственное значение, получаемое стандартным МКЭ с использованием базиса φi. Затем это значение уточняется с помощью итерационной процедуры. На каждом шаге аппроксимация собственной функции ищется в виде
С помощью этой аппроксимации находится следующее приближение собственного значения
${\lambda }_{n}^{{i + 1}}$. Итерационная процедура продолжается до достижения заданной точности ${\varepsilon }$, 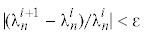 . Расчеты показали, что алгоритм сходится достаточно быстро.
. Расчеты показали, что алгоритм сходится достаточно быстро.
4. Алгоритм оптимизации. Рассматриваемая обратная задача свелась к поиску минимума функции, задаваемой уравнением (2.6). Из уравнений (3.2), (3.3) и (3.5) следует, что собственные значения ${{{\lambda }}_{k}}$, ${{{\mu }}_{k}}$, а следовательно и целевая функция F зависят от параметров ${\mathbf{p}} = \left( {{{p}_{1}},\; \ldots ,\;{{p}_{P}}} \right)$. Функция F(p) представляет собой сумму квадратов. Для минимизации такой функции весьма эффективен метод, предложенный в статьях Левенберга [32] и Марквардта [33]. Возможности и варианты алгоритма Левенберга–Марквардта, а также его применение к решению разнообразных обратных задач обсуждаются в ряде статей, см., например, [34–37].
Напомним коротко основные идеи алгоритма Левенберга–Марквардта. Рассматривается задача минимизации функции
(4.1)
$F\left( {\mathbf{p}} \right) = \sum\limits_{k = 1}^K {{{{\left( {{{f}_{k}}\left( {\mathbf{p}} \right) - {{g}_{k}}} \right)}}^{2}}} $Здесь ${\mathbf{p}} = \left( {{{p}_{1}},\; \ldots ,\;{{p}_{P}}} \right)$, gk – заданные величины, ${{f}_{k}}\left( {\mathbf{p}} \right)$ – известные функции.
Требуется найти вектор p*, доставляющий минимум функции F(p). Алгоритм поиска p* представляет собой итерационную процедуру. Введем обозначения: g = = $({{g}_{1}}, \ldots ,{{g}_{K}})$T, ${\mathbf{f}}({\mathbf{p}}) = {{({{f}_{1}}({\mathbf{p}}), \ldots ,{{f}_{K}}({\mathbf{p}}))}^{{\text{T}}}}$. Здесь и далее верхний индекс “T” означает транспонирование матрицы. Пусть в качестве начального приближения выбраны параметры ${{{\mathbf{p}}}^{0}} = (p_{1}^{0},\; \ldots ,\;p_{P}^{0})$. Далее выбирается шаг ${\Delta }{\mathbf{p}} = \left( {{\Delta }{{p}_{1}},\; \ldots ,\;{\Delta }{{p}_{P}}} \right)$ для приближения к решению задачи. В разложении функций ${{f}_{k}}\left( {\mathbf{p}} \right)$ по формуле Тейлора ограничимся линейными слагаемыми
(4.2)
${\mathbf{f}}({{{\mathbf{p}}}^{0}} + {\Delta }{\mathbf{p}}) \approx {\mathbf{f}}({{{\mathbf{p}}}^{0}}) + {\mathbf{J}}{\Delta }{\mathbf{p}}$Здесь ${\mathbf{J}}$ – матрица Якоби, ${\mathbf{J}} = \left( {\partial {{f}_{k}}{\text{/}}\partial {{p}_{m}}} \right)$.
Из (4.1) и (4.2) следует
(4.3)
$F({{{\mathbf{p}}}^{0}} + {\Delta }{\mathbf{p}}) \approx \left( {{\mathbf{d}} + {\mathbf{J}}{\Delta }{\mathbf{p}},\;{\mathbf{d}} + {\mathbf{J}}{\Delta }{\mathbf{p}}} \right)$Минимизация многочлена второго порядка по Δp в уравнении (4.3) приводит к равенству
(4.4)
${{{\mathbf{J}}}^{{\text{T}}}}{\mathbf{J}}{\Delta }{\mathbf{p}} = - {{{\mathbf{J}}}^{{\text{T}}}}{\mathbf{d}}$Определение шага ${\Delta }{\mathbf{p}}$ из системы уравнений (4.4) соответствует алгоритму Гаусса–Ньютона. Заметим, что для однозначной разрешимости уравнений (4.4) необходимо выполнение условия $K \geqslant P$, так как в противном случае матрица ${{{\mathbf{J}}}^{{\text{T}}}}{\mathbf{J}}$ не имеет обратной. В ряде случаев матрица ${{{\mathbf{J}}}^{{\text{T}}}}{\mathbf{J}}$ плохо обусловлена и итерационный процесс, задаваемый уравнением (4.4) не сходится.
В алгоритме Левенберга–Марквардта уравнение (4.4) заменяется регуляризованным уравнением
(4.5)
$({{{\mathbf{J}}}^{{\text{T}}}}{\mathbf{J}} + {\kappa }{\mathbf{I}}){\Delta }{\mathbf{p}} = - {{{\mathbf{J}}}^{{\text{T}}}}{\mathbf{d}}$Здесь I – единичная матрица, ${\kappa } > 0$ – параметр регуляризации, который пересчитывается на каждом шаге.
Поскольку матрица ${{{\mathbf{J}}}^{{\text{T}}}}{\mathbf{J}}$ положительно определена уравнение (4.5) однозначно разрешимо. Если оказывается, что $F({{{\mathbf{p}}}^{0}} + {\Delta }{\mathbf{p}}) < F({{{\mathbf{p}}}^{0}})$, то p0 заменяется на ${{{\mathbf{p}}}^{0}} + {\Delta }{\mathbf{p}}$, а при поиске следующего шага в уравнении (4.5) параметр ${\kappa }$ заменяется на ${\alpha \kappa }$, где $0 < {\alpha } < 1$. В случае $F({{{\mathbf{p}}}^{0}} + {\Delta }{\mathbf{p}}) > F({{{\mathbf{p}}}^{0}})$ параметр p0 сохраняется и шаг ищется заново путем решения уравнения (4.5), в котором ${\kappa }$ заменяется на ${\beta \kappa }$, где ${\beta } > 1$. Таким образом, когда мы находимся вдали от решения и функция F(p) быстро убывает, алгоритм приводит к увеличению шага ${\Delta }{\mathbf{p}}$ для ускорения процесса сходимости. Если же мы подошли близко к решению, то шаг убывает. При больших значениях параметра ${\kappa }$ алгоритм Левенберга–Марквардта приближается к алгоритму градиентного спуска, а при малых ${\kappa }$ к алгоритму Гаусса–Ньютона. Как видно из представленного описания, алгоритм содержит несколько параметров: начальное значение параметра ${\kappa }$, обозначим его ${{{\kappa }}_{0}}$, а также значения величин ${\alpha }$ и ${\beta }$. Расчеты показывают [34, 35], что выбор величины ${{{\kappa }}_{0}}$ не имеет особого значения, поскольку величина ${\kappa }$ корректируется на каждом шаге. В [35] указано, что часто ${{{\kappa }}_{0}}$ выбирается в виде ${{{\kappa }}_{0}} = {\tau } \cdot \max {{({{{\mathbf{J}}}^{{\text{T}}}}{\mathbf{J}})}_{{ii}}}$, где ${\tau } = {{10}^{{ - 3}}}$. Тестовые примеры, рассмотренные в [34], показали, что можно варьировать параметры ${\alpha }$ и ${\beta }$ в достаточно широких пределах, не влияя существенно на эффективность алгоритма. Согласно представленным в [34] результатам, алгоритм наиболее эффективен, когда эти параметры принадлежат областям: $0.1 \leqslant {\alpha } \leqslant 0.5$, $1.2 \leqslant {\beta } \leqslant 2$. Еще одним важным параметром алгоритма является начальное приближение ${{{\mathbf{p}}}^{0}}$. Для задачи, рассматриваемой в статье, естественным выбором начального приближения является ${{{\mathbf{p}}}^{0}} = \left( {1,1,\; \ldots ,\;1} \right)$, то есть в качестве начального приближения берется неповрежденный стержень.
Остановка алгоритма осуществляется при достижении одного из следующих условий: 1) ${\text{|}}{{{\mathbf{J}}}^{{\text{T}}}}{\mathbf{d}}{\text{|}} < {{{\varepsilon }}_{1}}$, 2) $\left| {\Delta {\mathbf{p}}} \right| < {{{\varepsilon }}_{2}}$, 3) $F\left( {\mathbf{p}} \right) < {{{\varepsilon }}_{3}}$, 4) число итераций достигает некоторого предельного значения ${{N}_{{\max }}}$. В [34, 35] предельные значения ${{{\varepsilon }}_{i}}$ выбираются в диапазоне $1 \times {{10}^{{ - 15}}}{\kern 1pt} - {\kern 1pt} 1 \times {{10}^{{ - 12}}}$, а величина ${{N}_{{\max }}}$ в пределах 102–104.
Отметим, что алгоритм Левенберга–Марквардта может быть применен как к задачам без ограничений, так и с ограничениями. В рассматриваемой задаче параметры находятся внутри параллелепипеда $0 \leqslant {{p}_{i}} \leqslant 1$.
Для реализации алгоритма необходимо вычислять матрицу Якоби J, то есть вычислять производные от собственных значений ${\lambda }$ и ${\mu }$ по параметрам pi. Поскольку сами собственные значения, как указывалось выше, определяются численно с помощью метода конечных элементов, то вычисление производных становится непростой задачей. Численное дифференцирование, как известно, является некорректной задачей, в том смысле что малые возмущения функции могут приводить к большим ошибкам в вычисленных производных. Метод вычисления производных, позволяющий избежать указанные трудности, представлен в следующем разделе.
5. Метод вычисления производных от собственных значений. Пусть, для определенности, мы ищем производные $\partial {{{\lambda }}_{m}}{\text{/}}\partial {{p}_{j}}$. Соответствующую задачу на собственные значения (2.5) можно переписать в виде
(5.1)
$\left( {{\mathbf{K}}\left( {\mathbf{p}} \right) - {\lambda }\left( {\mathbf{p}} \right){\mathbf{M}}} \right){\mathbf{d}}({\mathbf{p}}) = 0$В этом случае все собственные числа простые и положительные. Способ вычисления производных представлен в [38]. Различные обобщения можно найти в [39, 40] и имеющихся там ссылках. Идея метода [38] заключается в следующем. Пусть ${{{\lambda }}_{m}}\left( {\mathbf{p}} \right)$ – собственное число и ${{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right)$ – соответствующий ему собственный вектор, нормированный следующим образом
(5.2)
$\left( {{\mathbf{M}}{{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right),\;{{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right)} \right) = 1$Умножая (5.1) скалярно на ${{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right)$, получим равенство
(5.3)
$\left( {\left( {{\mathbf{K}}\left( {\mathbf{p}} \right) - {{{\lambda }}_{m}}\left( {\mathbf{p}} \right){\mathbf{M}}} \right){{{\mathbf{d}}}_{m}}({\mathbf{p}}),\;{{{\mathbf{d}}}_{m}}({\mathbf{p}})} \right) = 0$Продифференцируем равенство (5.3) по ${{p}_{j}}$. В результате получим
(5.4)
$\begin{gathered} \left( {\left( {\frac{{\partial {\mathbf{K}}({\mathbf{p}})}}{{\partial {{p}_{j}}}} - \frac{{\partial {{{\lambda }}_{m}}({\mathbf{p}})}}{{\partial {{p}_{j}}}}{\mathbf{M}}} \right){{{\mathbf{d}}}_{m}}({\mathbf{p}}),{{{\mathbf{d}}}_{m}}({\mathbf{p}})} \right) + \left( {\left( {{\mathbf{K}}({\mathbf{p}}) - {{{\lambda }}_{m}}({\mathbf{p}}){\mathbf{M}}} \right)\frac{{\partial {{{\mathbf{d}}}_{m}}({\mathbf{p}})}}{{\partial {{p}_{j}}}},\,\,{{{\mathbf{d}}}_{m}}({\mathbf{p}})} \right) + \\ + \;\left( {\left( {{\mathbf{K}}({\mathbf{p}}) - {{{\lambda }}_{m}}({\mathbf{p}}){\mathbf{M}}} \right){{{\mathbf{d}}}_{m}}({\mathbf{p}}),\frac{{\partial {{{\mathbf{d}}}_{m}}({\mathbf{p}})}}{{\partial {{p}_{j}}}}} \right) = 0 \\ \end{gathered} $Третье слагаемое в (5.4) равно нулю в силу равенства (5.1). Второе слагаемое в (5.4) также равно нулю в силу симметрии матриц ${\mathbf{K}}\left( {\mathbf{p}} \right)$, ${\mathbf{M}}$ и равенства (5.1). Таким образом, равенство (5.4) приводится к виду
(5.5)
$\left( {\frac{{\partial {\mathbf{K}}\left( {\mathbf{p}} \right)}}{{\partial {{p}_{j}}}}{{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right),{{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right)} \right) - \frac{{\partial {{{\lambda }}_{m}}\left( {\mathbf{p}} \right)}}{{\partial {{p}_{j}}}}\left( {{\mathbf{M}}{{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right),\,\,{{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right)} \right) = 0$Из (5.5) и условия нормировки (5.2) окончательно имеем
(5.6)
$\frac{{\partial {{{\lambda }}_{m}}\left( {\mathbf{p}} \right)}}{{\partial {{p}_{j}}}} = \left( {\frac{{\partial {\mathbf{K}}\left( {\mathbf{p}} \right)}}{{\partial {{p}_{j}}}}{{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right),{{{\mathbf{d}}}_{m}}\left( {\mathbf{p}} \right)} \right)$Таким образом, производные от собственных чисел выражаются через производные от матрицы жесткости и собственные векторы.
6. Численные примеры. Заметим, что представленный метод позволяет определять жесткости поврежденных элементов, но не размеры соответствующих им трещин. Вместе с тем, при определенных предположениях о типе повреждения оказывается возможным также оценить и размеры трещин. Предположим, что стержень имеет прямоугольное сечение. Рассмотрим элемент стержня длины ${\Delta }l$. Напряжение в этом элементе обозначим ${\sigma }$. Энергия деформации неповрежденного элемента стержня равна
Если элемент содержит одну пружину, податливость которой равна c, то энергия деформации элемента увеличится на величину ${\Delta }W$
Следовательно, энергия деформации элемента стержня с пружиной равна
Если поврежденность моделируется изменением модуля Юнга элемента, то энергия деформации неповрежденного элемента с модулем Юнга $E{\text{*}}$ будет иметь вид аналогичный (6.1)
Из равенств (6.3) и (6.4) имеем
Из (6.5), с учетом равенства $E{\text{*/}}E = p$, получим
В случае, когда пружиной моделируется двусторонняя краевая трещина длины $a$, податливость пружины выражается через длину трещины следующим образом [6]
где ${\nu }$ – коэффициент Пуассона, $s = a{\text{/}}{{h}_{0}}$, ${{h}_{0}}$ – высота стержня.Формулы (6.6) и (6.7) позволяют связать модуль Юнга поврежденного элемента с длиной находящейся в нем трещины:
Во всех рассмотренных ниже примерах приняты следующие параметры стержня: длина l = 1 м, прямоугольное поперечное сечение высоты ${{h}_{0}} = 0.02$ м и ширины b = 0.02 м, модуль Юнга $E = 2.1 \times {{10}^{{11}}}$ Н/м2, коэффициент Пуассона ${\nu } = 0.3$, плотность ${\rho } = 7800$ кг/м3.
Собственные значения ${{{\lambda }}_{1}},\; \ldots ,\;{{{\lambda }}_{N}}$ и ${{{\mu }}_{1}},\; \ldots ,\;{{{\mu }}_{N}}$, являющиеся входными данными для решения обратной задачи, получены численно путем решения прямой задачи. Подчеркнем, что прямая задача решалась не методом конечных элементов, а с помощью решения задачи в исходной постановке, представленной в разделе 2, методом, предложенным в [41] для решения прямой задачи о поперечных колебаниях стержня с трещинами и примененным к задаче о продольных колебаниях в [6]. Независимое от техники решения обратной задачи получение исходных данных в какой-то мере моделирует использование входных данных, полученных экспериментально. Отметим, что большее количество собственных значений позволяет использовать более мелкую конечно-элементную сетку, что приводит к более точной идентификации ослабленных участков рассматриваемого стержня. В представленных ниже примерах в алгоритме Левенберга–Марквардта были взяты следующие значения введенных выше параметров: ${\alpha } = 1{\text{/}}3$, β = 2.
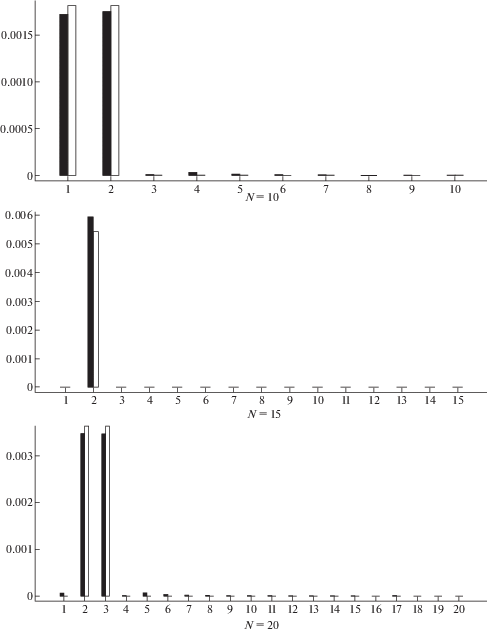
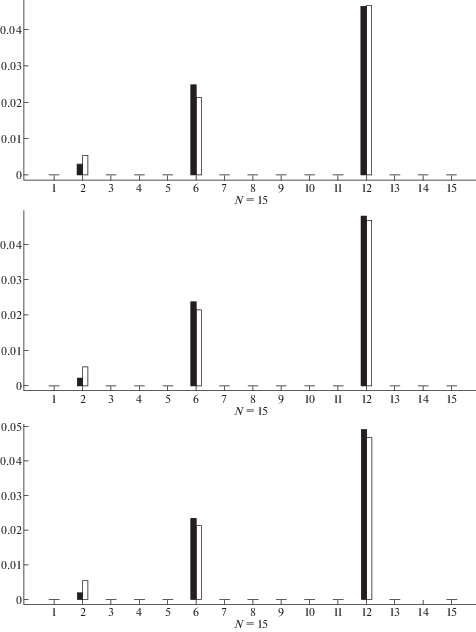
Пример 1. Рассмотрим стержень с одиночной трещиной, расположенной в точке ${{x}_{1}} = 0.1$ и имеющей относительную длину ${{s}_{1}} = 0.1$. Результаты восстановления жесткостей элементов по N = 10, 15 и 20 собственным числам ${{{\lambda }}_{i}}$ и ${{{\mu }}_{i}}$ представлены на рис. 1. Отметим, что в представленных результатах количество элементов, на которое разбит стержень было взято соответствующим количеству собственных чисел N. Элементы занумерованы слева направо. По оси x отложены номера элементов, а по оси y величины 1 – p, соответствующие податливостям элементов. Черные и белые вертикальные полосы соответствуют численным и ожидаемым результатам, соответственно. Заметим, что в случае N = 10 трещина попадает в узел, принадлежащий элементам 1 и 2. При N = 15 трещина находится внутри элемента 2. При N = 20 трещина снова попадает в узел, который принадлежит элементам 2 и 3. Все это хорошо видно из рис. 1.
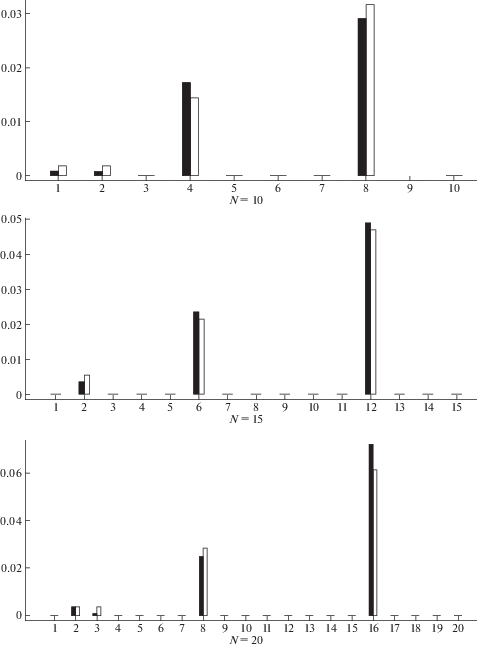
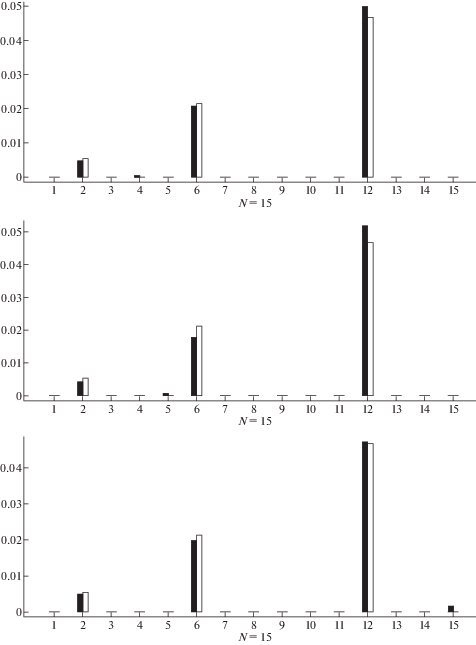
Пример 2. Рассмотрим стержень, содержащий три трещины. Здесь к трещине, рассмотренной в примере 1, добавлены две трещины с параметрами: ${{x}_{2}} = 0.36$, ${{s}_{2}} = 0.2$, ${{x}_{3}} = 0.78$, ${{s}_{3}} = 0.3$. Расположения второй и третьей трещин выбраны так, чтобы не попадать в узлы рассматриваемых разбиений. Результаты идентификации повреждений представлены на рис. 2. Из рис. 2 видно, что предлагаемый алгоритм позволил обнаружить все трещины, однако, поскольку длины трещин отличаются значительно, податливость элемента, содержащего самую маленькую трещину определяется недостаточно точно.
В таблице 1 представлены восстановленные по податливостям элементов, согласно формулам (6.6), (6.7), длины трещин. В первом столбце даны номера трещин $i$, отсчитываемых слева направо. Во втором столбце приведено количество собственных значений N, использованных для восстановления податливостей элементов. В третьем столбце даны относительные длины трещин ${{s}_{i}}$. В четвертом столбце представлены восстановленные значения относительных длин трещин ${{r}_{i}}$. В последнем столбце приведена относительная погрешность восстановления длины трещин в процентах ${{{\delta }}_{i}}$.
Таблица 1
| i | N | ${{s}_{i}}$ | ${{r}_{i}}$ | ${{{\delta }}_{i}}$ |
|---|---|---|---|---|
| 1 | 10 | 0.1 | 0.0469 | 53 |
| 15 | 0.0720 | 28 | ||
| 20 | 0.0231 | 77 | ||
| 2 | 10 | 0.2 | 0.2189 | 9 |
| 15 | 0.2062 | 3 | ||
| 20 | 0.1860 | 7 | ||
| 3 | 10 | 0.3 | 0.2874 | 4 |
| 15 | 0.3051 | 2 | ||
| 20 | 0.3262 | 9 |
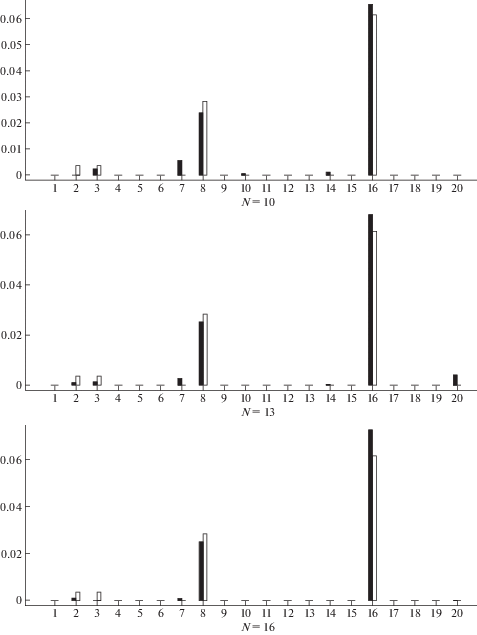
Пример 3. В случае наличия $n$ трещин имеется $2n$ неизвестных, представляющих собой координаты трещин и податливости, соответствующих им пружин. Когда исходная задача заменяется конечно-элементной моделью с n элементами, то аналогами упомянутых неизвестных являются номера поврежденных элементов и их жесткости. В силу этого, может показаться, что для их идентификации достаточно использовать n собственных значений, отвечающих каждому из краевых условий. Данный пример имеет своей целью подчеркнуть, что целесообразно рассматривать результаты идентификации повреждений с помощью различного количества собственных значений не только потому, что количество трещин априори неизвестно, но и потому, что зачастую, для качественного определения повреждений нужна некоторая переопределенность исходных данных. В данном примере рассматривается стержень с теми же тремя трещинами, что и в примере 2. Стержень разбит на 20 элементов. На рис. 3 представлены результаты идентификации повреждений по N = 10, 13 и 16 собственным частотам, отвечающим каждому из краевых условий. Из рис. 3 видно, что имеющиеся повреждения обнаруживаются при всех рассмотренных значениях N. При N = 10 и N = 13 появляются некоторые паразитные решения. Отметим, что паразитное повреждение в элементе 7 обнаруживается еще и потому, что хотя трещина находится в элементе 8, но весьма близко к правому концу элемента 7. Обнаруженное при N = 13 повреждение в элементе 20 является паразитным и может быть исключено при рассмотрении совокупности решений при разных $N$.
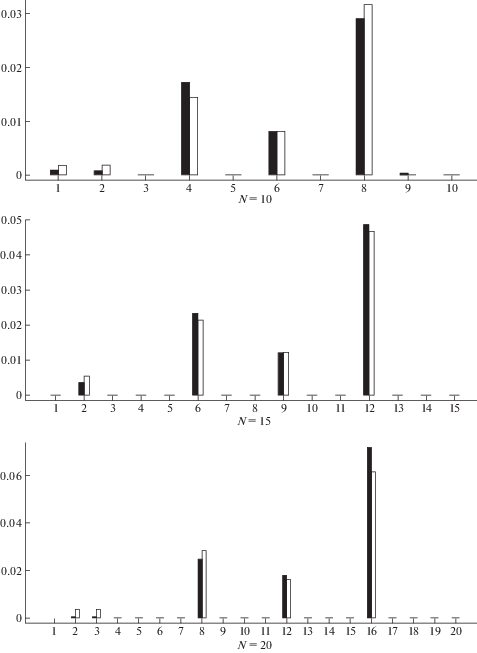
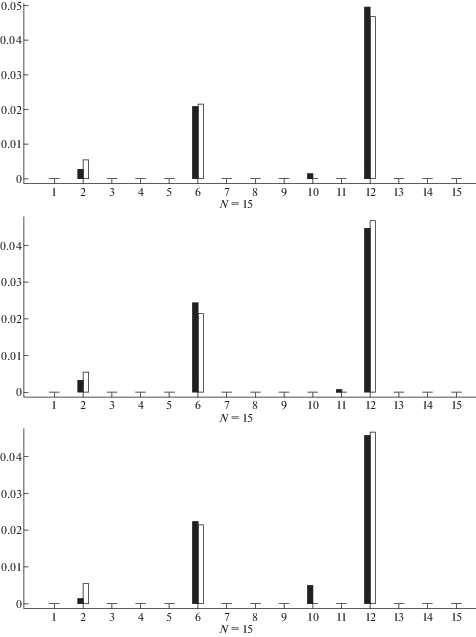
Пример 4. Идентификация четырех трещин. Здесь к трем трещинам, рассмотренным в примере 2, добавлена трещина с параметрами ${{x}_{4}} = 0.57$, ${{s}_{4}} = 0.15$. Результаты реконструкции податливостей элементов представлены на рис. 4. Из рис. 4 видно, что в отличие от первой трещины, четвертая трещина идентифицируется достаточно четко, поскольку ее размер меньше размера самой большой трещины лишь в два раза.
В представленных выше результатах исходные данные (собственные значения) были получены численно путем решения прямой задачи и, следовательно, содержали только погрешности, связанные с погрешностями численного счета. В реальном эксперименте погрешности могут быть больше, поэтому важно оценить насколько предлагаемый алгоритм чувствителен к погрешностям в исходных данных. Для оценки чувствительности алгоритма внесем шум в полученные численно данные. Поскольку величины ${{{\mu }}_{i}}$ и ${{{\lambda }}_{i}}$ должны чередоваться, интенсивность шума целесообразно оценивать в долях их разности. Вместо полученных численно величин ${{{\lambda }}_{i}}$ и ${{{\mu }}_{i}}$ для решения обратной задачи будем брать величины
(6.9)
$\begin{gathered} {\lambda }_{i}^{{{\text{noise}}}} = {{{\lambda }}_{i}} + \left( {{{{\lambda }}_{i}} - {{{\mu }}_{i}}} \right){\eta }\sqrt 3 {{U}_{i}} \\ {\mu }_{j}^{{{\text{noise}}}} = {{{\mu }}_{j}} + \left( {{{{\lambda }}_{j}} - {{{\mu }}_{j}}} \right){\eta }\sqrt 3 {{U}_{j}} \\ \end{gathered} $Здесь Ui и Uj – различные реализации случайной величины, равномерно распределенной в интервале (–1, 1).
Из (6.9) следует, что ${\lambda }_{i}^{{{\text{noise}}}}$, ${\mu }_{i}^{{{\text{noise}}}}$ – случайные величины с математическим ожиданием $M[{\lambda }_{i}^{{{\text{noise}}}}] = {{{\lambda }}_{i}}$, $M[{\mu }_{i}^{{{\text{noise}}}}] = {{{\mu }}_{i}}$ и средним квадратическим отклонением ${\sigma }[{\lambda }_{i}^{{{\text{noise}}}}]$ = = ${\sigma }[{\mu }_{i}^{{{\text{noise}}}}]$ = (λi – μi)η. Величина ${\eta }$ характеризует уровень шума.
На рис. 5–7 представлены результаты решения задачи для стержня с тремя трещинами, рассмотренными в примере 2, с уровнем шума в данных ${\eta } = 0.05$, ${\eta } = 0.08$ и ${\eta } = 0.1$, соответственно. Стержень разбит на 15 элементов. Количество использованных для решения обратной задачи собственных значений, отвечающих каждому из краевых условий N = 15. Поскольку результаты зависят от реализации случайных величин, для каждого уровня шума представлены результаты трех различных реализаций.
Из рис. 5–7 видно, что дефекты достаточно хорошо определяются при всех рассмотренных уровнях шума. Для уровней шума ${\eta } = 0.08$ и ${\eta } = 0.1$ в некоторых реализациях появляются малые паразитные повреждения.
7. Заключение. На основании анализа полученных численных результатов можно сделать следующие выводы.
1. Предложенный метод позволяет обнаруживать и идентифицировать множественные трещины в стержне с хорошей точностью.
2. Для более качественной идентификации повреждений следует сравнить результаты идентификации, полученные с помощью различного количества собственных значений в качестве исходных данных.
3. Метод достаточно устойчив к шуму в исходных данных.
4. В случае, когда имеются трещины, размеры которых сильно отличаются, самые маленькие трещины могут недостаточно хорошо идентифицироваться.
Работа выполнена по теме государственного задания № госрегистрации AAAA-A17-117021310386-3 и при поддержке РФФИ (проект № 19-01-00100).
Список литературы
Dimarogonas A.D. Vibration of cracked structures: a state of the art review // Engineering Fracture Mechanics. 1996. V. 55. P. 831–857.
Narkis Y. Identification of crack location in vibrating simply supported beams // J. Sound and Vibration. 1994. V. 172. № 4. P. 549–558.
Morassi A. A uniqueness result on crack location in vibrating rods // Inverse Problems in Engineering. 1997. V. 4. P. 231–254.
Biscontin G., Morassi A., Wendel P. Asymptotic separation of the spectrum in notched rods // J. Vibration and Control. 1998. V. 4. P. 237–251.
Morassi A. Identification of a crack in a rod based on changes in a pair of natural frequencies // J. Sound and Vibration. 2001. V. 242. P. 577–596.
Ruotolo R., Surace C. Natural frequencies of a bar with multiple cracks // J. Sound and Vibration. 2004. V. 272. P. 301–316.
Dilena M., Morassi A. The use of antiresonances for crack detection in beams // J. Sound and Vibration. 2004. V. 276. P. 195–214.
Singh K.V. Transcendental inverse eigenvalue problems in damage parameter estimation // Mechanical Systems and Signal Processing. 2009. V. 23. P. 1870–1883.
Ахтямов А.М., Ильгамов М.А. Модель изгиба балки с надрезом: прямая и обратная задачи // Прикладная механика и техническая физика. 2013. Т. 54. № 1. С. 152–162.
Акуленко Л.Д., Нестеров С.В. Влияние дефекта массы на частоты и формы продольных колебаний стержня // Изв. РАН. МТТ. 2014. № 1. С. 135–144.
Ильгамов М.А. Продольные колебания стержня с зарождающимися поперечными трещинами // Изв. РАН. МТТ. 2017. № 1. С. 23–31.
Акуленко Л.Д., Байдулов В.Г., Георгиевский Д.В., Нестеров С.В. Эволюция собственных частот продольных колебаний стержня при увеличения дефекта поперечного сечения // Изв. РАН. МТТ. 2017. № 6. С. 136–144.
Morassi A., Rollo M. Identification of two cracks in a simply supported beam from minimal frequency measurements // J. Vibration and Control. 2001. V. 7. P. 729–739.
Rubio L., Fernandez-Saez J., Morassi A. Identification of two cracks in a rod by minimal resonant and antiresonant frequency data // Mechanical Systems and Signal Processing. 2015. V. 60–61. P. 1–13.
Rubio L., Fernandez-Saez J., Morassi A. Identification of two cracks with different severity in beams and rods from minimal frequency data // J. Vibration and Control. 2016. V. 22. № 13. P. 3102–3117.
Khiem N.T., Toan L.K. A novel method for crack detection in beam-like structures by measurements of natural frequencies // J. Sound and Vibration. 2014. V. 333. P. 4084–4103.
Shifrin E.I. Identification of a finite number of small cracks in a rod using natural frequencies // Mechanical Systems and Signal Processing. 2016. V. 70–71. P. 613–624.
Singh K.V. Transcendental inverse eigenvalue problems in damage parameter estimation // Mechanical Systems and Signal Processing. 2009. V. 23. P. 1870–1883.
Lee J. Identification of multiple cracks in a beam using natural frequencies // J. Sound and Vibration. 2009. V. 320. P. 482–490.
Lee J. Identification of a crack in a beam by the boundary element method // J. Mechanical Science and Technology. 2010. V. 24. № 3. P. 801–804.
Casciati S. Stiffness identification and damage localization via differential evolution algorithms // Structural Control and Health Monitoring. 2008. V. 15. P. 436–449.
Khaji N., Mehrjoo M. Crack detection in a beam with an arbitrary number of transverse cracks using genetic algorithms // J. Mechanical Science and Technology. 2014. V. 28. № 3. P. 823–836.
Eroglu U., Tufekci E. Exact solution based finite element formulation of cracked beams for crack detection // Int. J. Solids and Structures. 2016. V. 96. P. 240–253.
Sandesh S., Shankar K. Application of a hybrid of particle swarm and genetic algorithm for structural damage detection // Inverse Problems in Science and Engineering. 2010. V. 18. № 7. P. 997–1021.
Rubio L., Fernandez-Saez J., Morassi A. The full nonlinear crack detection problem in uniform vibrating rods // J. Sound and Vibration. 2015. V. 339. P. 99–111.
Fernandez-Saez J., Morassi A., Pressacco M., Rubio L. Unique determination of a single crack in a uniform simply supported beam in bending vibration // J. Sound and Vibration. 2016. V. 371. P. 94–109.
Shifrin E.I. Inverse spectral problem for a rod with multiple cracks // Mechanical Systems and Signal Processing. 2015. V. 56–57. P. 181–196.
Shifrin E.I. Inverse spectral problem for a non-uniform rod with multiple cracks // Mechanical Systems and Signal Processing. 2017. V. 96. P. 348–365.
Melenk J.M., Babuska I. The partition of unity finite element method: Basic theory and applications // Computer methods in applied mechanics and engineering. 1996. V. 139. P. 289–314.
Babuska I., Melenk J.M. The partition of unity method // Int. J. Numerical Methods in Engineering. 1997. V. 40. P. 727–758.
Arndt M., Machado R.D., Scremin A. An adaptive generalized finite element method applied to free vibration analysis of straight bars and trusses // J. Sound and Vibration. 2010. V. 329. P. 659–672.
Levenberg K. A method for the solution of certain non-linear problems in least squares // Quarterly of Applied Mathematics. 1944. V. 2. № 2. P. 164–168.
Marquardt D.W. An algorithm for the least-squares estimation of nonlinear parameters // SIAM J. Applied Mathematics. 1963. V. 11. № 2. P. 431–441.
Lampton M. Damping-undamping strategies for Levenberg–Marquardt nonlinear least-squares method // Computers in Physics. 1997. V. 11. № 1. P. 110–115.
Lourakis M.I.A. A brief description of the Levenberg- Marquardt algorithm implemented by levmar // Foundation of Research and Technology. 2005. V. 4. № 1. P. 1–6.
Pujol J. The solution of nonlinear inverse problems and the Levenberg-Marquardt method // Geophysics. 2007. V. 72. № 4. P. W1–W16.
Sarvi F., Shojaee S., Torkzadeh P. Damage identification of trusses by finite element model updating using an enhanced Levenberg–Marquardt algorithm // Int. J. Optimization in Civil Engineering. 2014. V. 4. № 2. P. 207–231.
Fox R.L., Kapoor M.P. Rates of change eigenvalues and eigenvectors // AIAA J. 1968. V. 6. № 12. P. 2426–2429.
Nelson R.B. Simplified calculation of eigenvector derivatives // AIAA J. 1976. V. 14. № 9. P. 1201–1205.
Van Der Aa N.P., Ter Morsche H.G., Mattheij R.R.M. Computation of eigenvalue and eigenvector derivatives for a general complex-valued eigensystem // Electron. J. Linear Algebra. 2007. V. 16. № 1. article 26. P. 300–314.
Shifrin E.I., Ruotolo R. Natural frequencies of a beam with an arbitrary number of cracks // J. Sound and Vibration. 1999. V. 222. № 3. P. 409–423.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела