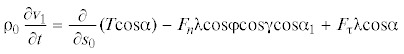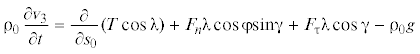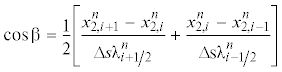Известия РАН. Механика твердого тела, 2019, № 4, стр. 63-75
ДИНАМИКА ДЕФОРМИРОВАНИЯ ПРОВОДА ЭЛЕКТРОПЕРЕДАЧИ
Р. Ш. Гимадиев *
Казанский государственный энергетический университет
Казань, Россия
* E-mail: gimadievr@mail.ru
Поступила в редакцию 12.09.2018
После доработки 12.09.2018
Принята к публикации 18.09.2018
Аннотация
Разработана математическая модель динамики деформирования провода воздушной линии электропередачи в пространственной постановке, уравнения решаются на основе метода конечных разностей по явной схеме. В отдельных случаях точность вычислений сравнивается с полученными аналитическими решениями. Проведено численное исследование нагружения линии электропередачи под совместным воздействием ветровой и весовой нагрузки. Предложен численный метод расчета обрыва проводов и движение частей после обрыва. Выявлен механизм появления колебательного движения типа “пляски проводов” при действии переменной ветровой нагрузки. Исследуется процесс теплопроводности и динамики деформирования линии при растапливании обледенения провода нагревом, изучаются переходные процессы деформирования линии электропередачи.
Введение. В связи с относительной дешевизной воздушных линий электропередач по сравнению с кабельными и учитывая большие расстояния воздушные линии (ВЛ) находят широкое применение. Провода ВЛ подвергаются значительным механическим нагрузкам. Они постоянно нагружены собственным весом. Среди причин дополнительных механических нагрузок можно выделить действие ветровых нагрузок и гололедно-изморозевые отложения. Эти причины увеличивают нагрузки на провода, а также могут обуславливать такие опасные формы динамических колебательных процессов, как вибрация и пляска проводов. Пляска проводов вызывается сочетанием весовых и ветровых нагрузок особого профиля. Механические нагрузки могут вызывать повреждения линий электропередач, что уменьшает надежность электроснабжения и требует затрат на восстановление ВЛ.
Для повышения надежности воздушных ВЛ используются типовые технические решения, а также предлагаются новые технические решения для изучения явления гололеда и пляски проводов и борьбы с ними [1–4, 14–16].
Проблема изучения механических повреждений проводов ВЛ, как с применением экспериментальных, так и теоретических подходов моделирования процессов нагружения, и нахождения методов повышения надежности является весьма актуальной.
Теоретическому изучению механических нагрузок на ВЛ посвящен ряд работ [5–10], использующих различные подходы к моделированию формы и натяжений в проводах, их можно условно разбить на две группы: 1) на основе конечных формул, как без учета, так и с учетом растяжимости проводов; 2) базирующиеся на численном интегрировании уравнений движения.
К первой группе относятся традиционные подходы, полученные в предположении статического нагружения. Нагрузка, обусловленная собственным весом провода считается равномерно распределенной. Так в [4, 5] полагают, что провод нерастяжим и имеет форму параболы (при длине пролета до 800 м) или форму цепной линии (при длине пролета более 800 м. В работе [7] получены конечные формулы для расчета статического напряженно-деформированного состояния ВЛ с учетом ее растяжения. Преимуществом этих подходов, является простота их использования. Однако они не позволяют исследовать динамику нагружения проводов ВЛ.
Вторая группа подходов к расчету механического нагружения ВЛ позволяет исследовать динамику нагружения ВЛ. Эти подходы основаны на математическом моделировании движения проводов ВЛ под действием нагрузок с использованием уравнений движения абсолютно гибкой системы [5–10]. Уравнения движения представляют собой нелинейные уравнения в частных производных, которые дополняются начальными и граничными условиями. Этот подход связан составлением математической модели, ее программированием и проведением численных экспериментов. Он является существенно более трудоемким, чем первый подход. В качестве тестирования программ могут служить разработки первой группы.
Представляет практический интерес, на основе разработанных моделей исследовать динамическое поведение провода при воздействии совместно весовой и ветровой нагрузки, деформирование провода при растапливании обледенения нагревом и поведение ВЛ в режиме “пляски провода”.
Низкочастотные колебания ВЛ электропередачи рассматривались в работах [3, 14–16].
1. Постановка задачи. Моделирование динамики ВЛ электропередачи проводится по модели абсолютно гибкой системы. Под абсолютно гибкими системами мы будем понимать физические объекты, которые пренебрежимо слабо воспринимают изгибные напряжения, т.е. работают только на растяжение и сжатие. К ним можно отнести: протяженные линии передачи энергий, линии оптико-волоконной связи, тросы находящиеся в потоке жидкости [12] и т.д. Опоры ВЛ принимаются абсолютно жесткими.
Абсолютно гибкая система в поле силы тяжести с линейной плотностью ${{{\rho }}_{0}}(s)$, перемещается в пространстве под действием распределенной погонной нормальной нагрузки ${{{\mathbf{F}}}_{n}}$ и распределенной погонной касательной нагрузки ${{{\mathbf{F}}}_{\tau }}$. Деформация гибкой системы характеризуется степенью удлинения ${\lambda } = ds{\text{/}}d{{s}_{0}} = 1 + e$, где $d{{s}_{0}}$ и $ds$ – длины элементов гибкой системы в недеформированном и деформированном состоянии, $e$ – относительное удлинение. Для элемента гибкой системы c массой $dm$ в соответствии с законом сохранения массы имеем $dm = {{{\rho }}_{0}}d{{s}_{0}} = {\rho }ds$.
2. Метод и построение решения. Векторное уравнение, описывающее движение упругой весомой гибкой системы под действием погонных нагрузок ${{{\mathbf{F}}}_{{\text{n}}}}$, ${{{\mathbf{F}}}_{{\tau }}}$, натяжением ${\mathbf{T}}$, в поле силы тяжести с ускорением свободного падения ${\mathbf{g}}$ имеет вид
(2.1)
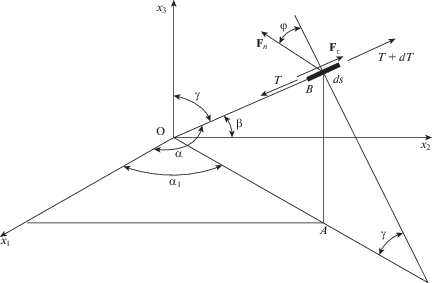
${{{{{\rho }}_{0}}{{\partial }^{2}}{\mathbf{r}}} \mathord{\left/ {\vphantom {{{{{\rho }}_{0}}{{\partial }^{2}}{\mathbf{r}}} {\partial {{t}^{2}}}}} \right. \kern-0em} {\partial {{t}^{2}}}} = {{\partial {\mathbf{T}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{T}}} {\partial {{s}_{0}}}}} \right. \kern-0em} {\partial {{s}_{0}}}} + {{{\mathbf{F}}}_{n}} + {{{\mathbf{F}}}_{{\tau }}} + {\mathbf{g}}{{{\rho }}_{0}}$Рассмотрим векторное уравнение движения в проекциях на оси декартовой системы координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$, ускорение ${\mathbf{g}}$ направлено вниз вдоль оси $O{{x}_{3}}$, рис. 1.
Пусть угол между элементом $ds$ гибкой системы и осями координат $O{{x}_{1}}$, $O{{x}_{2}}$, $O{{x}_{3}}$ составляет соответственно α, ${\beta }$, ${\gamma }$.
Распределенная касательная нагрузка с интенсивностью ${{{\mathbf{F}}}_{{\tau }}}$ действует вдоль элемента ds гибкой системы. Действующий вектор нормальной нагрузки с интенсивностью Fn составляет угол $\varphi $ к плоскости OAB. Дополнительно введем угол ${{{\alpha }}_{1}}$ – между осью $O{{x}_{1}}$ и плоскостью OAB. Учитывая, что
Так как ${{(\partial {{x}_{1}})}^{2}} + {{(\partial {{x}_{2}})}^{2}} + {{(\partial {{x}_{3}})}^{2}} = {{({\lambda }\partial {{s}_{0}})}^{2}}$, то
В дальнейшем индекс нуль в координате s0 будем опускать и будем понимать s как лагранжеву координату (т.е. связанную с гибкой системой).
Учитывая
(2.2)
${{{\rho }}_{0}}\frac{{\partial {{{v}}_{3}}}}{{\partial t}} = \frac{\partial }{{{\text{ }}\partial s}}\left( {\frac{T}{{\lambda }}\frac{{\partial {{x}_{3}}}}{{\partial s}}} \right) + {{F}_{n}}{\lambda }\cos \varphi \sin {\gamma } + {{F}_{{\tau }}}\frac{{\partial {{x}_{3}}}}{{\partial s}} - {{{\rho }}_{0}}g$Уравнения движения в вертикальной плоскости $O{{x}_{1}}{{x}_{2}}$, ось $O{{x}_{2}}$ направлена вертикально. В этом случае для (2.2) надо положить
(2.3)
${{{\rho }}_{0}}\frac{{\partial {{{v}}_{2}}}}{{\partial t}} = \frac{\partial }{{{\text{ }}\partial s}}\left( {\frac{T}{{\lambda }}\frac{{\partial {{x}_{2}}}}{{\partial s}}} \right) + {{F}_{n}}\frac{{\partial {{x}_{1}}}}{{\partial s}} + {{F}_{{\tau }}}\frac{{\partial {{x}_{2}}}}{{\partial s}} - {{{\rho }}_{0}}g$Уравнения движения (2.3) можно записать и в компактной форме
(2.4)
${{{\rho }}_{{\text{l}}}}\frac{{{\text{ }}\partial {{{v}}_{k}}}}{{\partial t}} = \frac{\partial }{{\partial s}}\left( {\frac{T}{{\lambda }}\frac{{\partial {\text{ }}{{x}_{k}}}}{{\partial s}}} \right) + {{( - 1)}^{k}}{{F}_{n}}\frac{{\partial {{x}_{{3 - k}}}}}{{\partial s}} + {{F}_{{\tau }}}\frac{{\partial {{x}_{k}}}}{{\partial s}} - {{{\rho }}_{{\text{l}}}}g(k - 1)$Составляющие аэродинамических сил, действующих на гибкую систему определяются по формулам [12]
(2.5)
${{F}_{n}} = \frac{{{\rho }U_{\infty }^{2}}}{2}d({{c}_{n}}{{\sin }^{2}}{\alpha } + {{c}_{{\tau }}}\sin {\alpha }),$ ${{F}_{{\tau }}} = \frac{{{\rho }U_{\infty }^{2}}}{2}d{{c}_{{\tau }}}{{\cos }^{2}}{\alpha }$Поперечные колебания гибких систем влияют на нормальные составляющие погонных усилий Fn: при движении элемента гибкой системы против потока эта составляющая увеличивается, а по потоку – уменьшается. С учетом этого пересчет можно вести по формуле [13]
(2.6)
${{F}_{n}}(s,t) = F_{n}^{0}(s,t){{[1 - {\mu }{{V}_{n}}{\text{/}}{{U}_{\infty }}]}^{2}}{\text{sign}}\left[ {1 - {\mu }{{V}_{n}}{\text{/}}{{U}_{\infty }}} \right]$Уравнения движения (2.2) решаются в безразмерном виде, введя следующие безразмерные параметры:
Уравнения дополняются физическими соотношениями $T = T(e)$, $e \geqslant 0$ при растяжении и e < 0 при сжатии (в частности при линейном законе $T = Ee$), кинематическими соотношениями
(2.7)
${{\partial {{x}_{k}}} \mathord{\left/ {\vphantom {{\partial {{x}_{k}}} {\partial {\tau }}}} \right. \kern-0em} {\partial {\tau }}} = {{{v}}_{k}}$(2.8)
${{({{\partial {{x}_{1}}} \mathord{\left/ {\vphantom {{\partial {{x}_{1}}} {\partial s}}} \right. \kern-0em} {\partial s}})}^{2}} + {{({{\partial {{x}_{2}}} \mathord{\left/ {\vphantom {{\partial {{x}_{2}}} {\partial s}}} \right. \kern-0em} {\partial s}})}^{2}} + {{({{\partial {{x}_{3}}} \mathord{\left/ {\vphantom {{\partial {{x}_{3}}} {\partial s}}} \right. \kern-0em} {\partial s}})}^{2}} = {{{\lambda }}^{2}},$ ${\lambda } = 1 + e$Начальные и граничные условия для провода запишутся в виде
(2.9)
${{x}_{k}}({\tau },{{s}_{{\text{l}}}}) = f_{k}^{s}(\tau ),$ ${{{v}}_{k}}({\tau },{{s}_{{\text{l}}}}) = \varphi _{k}^{s}({\tau }),$ $k = 1,2,3$3. Разностная схема решения задачи. Система уравнений (2.2), (2.5)–(2.9) решается методом конечных разностей, в рассмотрение вводится дискретная область
Используя для аппроксимации производных центральные разности на сдвинутой на полшага сетке и явную конечно-разностную схему, уравнения (2.2) в безразмерном виде представим как
(3.1)
$\begin{gathered} {v}_{{3,i}}^{{n + 1/2}} = {v}_{{3,i}}^{{n - 1/2}} + \;\frac{{\Delta \tau {{A}_{N}}}}{{{{\rho }_{0}}\Delta s}}\left\{ {\left[ {T_{{i + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{n}\frac{{x_{{3,i + 1}}^{n} - x_{{3,i}}^{n}}}{{\Delta s\lambda _{{i + 1/2}}^{n}}} - T_{{i - 1/2}}^{n}\frac{{x_{{3,1}}^{n} - x_{{3,i - 1}}^{n}}}{{\Delta s\lambda _{{i - 1/2}}^{n}}}} \right]} \right. \hfill \\ + \,\,\frac{1}{2}[\lambda _{{i + 1/2}}^{n}\left( {{{f}_{n}}} \right)_{{i + 1/2}}^{{n - 1/2}} + \lambda _{{i - 1/2}}^{n}\left( {{{f}_{n}}} \right)_{{i - 1/2}}^{{n - 1/2}}]{\text{cos}}\varphi {\text{sin}}\gamma \hfill \\ \left. {_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}}}}}}}}}}}}} + \;\frac{1}{{2\Delta s}}[\left( {{{f}_{\tau }}} \right)_{{i + 1/2}}^{{n - 1/2}}(x_{{3,i + 1}}^{n} - x_{{3,i}}^{n}) + \left( {{{f}_{\tau }}} \right)_{{i - 1/2}}^{{n - 1/2}}(x_{{3,i}}^{n} - x_{{3,i - 1}}^{n})]} \right\} - \Delta \tau \cdot g \hfill \\ \end{gathered} $Результаты решения задачи на шаге интегрирования n служат в качестве начальных и граничных условий для следующего шага интегрирования.
Явная расчетная схема наряду с достоинством имеет и недостаток: появляются высокочастотные осцилляции решения за фронтом волн. Для сглаживания решений используется корректировка скоростей элементов:
(3.2)
${{{{{{\bar {v}}}}_{k}} = {{{v}}_{k}} + {\beta }{{\partial }^{2}}{{{v}}_{k}}} \mathord{\left/ {\vphantom {{{{{{\bar {v}}}}_{k}} = {{{v}}_{k}} + {\beta }{{\partial }^{2}}{{{v}}_{k}}} {\partial {{s}^{2}}}}} \right. \kern-0em} {\partial {{s}^{2}}}}$В разностном представлении корректировка (3.2) имеет вид
(3.3)
${{{\bar {v}}_{{k,i}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} = {v}_{{k,i}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} + {\beta }({v}_{{k,i + 1}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} - 2{v}_{{k,i}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} + {v}_{{k,i - 1}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}})} \mathord{\left/ {\vphantom {{{\bar {v}}_{{k,i}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} = {v}_{{k,i}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} + {\beta }({v}_{{k,i + 1}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} - 2{v}_{{k,i}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} + {v}_{{k,i - 1}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}})} {\Delta {{s}^{2}}}}} \right. \kern-0em} {\Delta {{s}^{2}}}}$Физическое соотношение принимается в виде формулы Кельвина–Фойгта
где $\dot {e}$ – скорость деформации, ${\eta }$ – коэффициент внутреннего трения в материале.Разрыв линии ВЛ происходит, когда натяжение в элементе i в момент времени ${{{\tau }}_{n}}$ превышает допускаемое натяжение разрыва в материале $T_{i}^{n} \geqslant \left[ T \right]$, или разрыв происходит в результате механического повреждения. Пусть разрыв линии произошел в элементе между узлами ${{i}_{l}}$ и ${{i}_{r}} = {{i}_{l}} + 1$, и натяжение между этими узлами мгновенно принимает нулевое значение $T({{i}_{l}}) = 0$. Для расчета по формуле (3.1) добавляем расширенную сетку для левого пролета ${{i}_{{l + 1}}}$ и для правого пролета ${{i}_{{r - 1}}}$ соответственно
(3.5)
${v}_{{k,{{i}_{{l + 1}}}}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} = {v}_{{k,{{i}_{l}}}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}$ ${v}_{{k,{{i}_{{r - 1}}}}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}} = {v}_{{k,{{i}_{r}}}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}$Таким образом получаем гладкие решения вторых производных для узлов (3.1) с i = 2 по $i = {{i}_{l}}$ для левого пролета и с $i = {{i}_{r}}$ по $i = \operatorname{int} \left( {s{\text{/}}\Delta s} \right)$ для правого пролета.
Координаты узловых точек разностной сетки, или кинематические соотношения записываются в виде
(3.6)
$x_{{k,{\text{ }}i}}^{{n + 1}} = x_{{k,{\text{ }}i}}^{n} + \Delta {\tau }{\bar {v}}_{{k,{\text{ }}i}}^{{n + {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}$Необходимым условием сходимости численного решения по явной схеме к решению дифференциального уравнения является условие Куранта–Фридрихса–Леви. Для материала с линейной характеристикой упругости E это условие запишется в виде $\Delta {\tau } \leqslant \Delta s\sqrt {{{{\rho }}_{0}}{\text{/}}E} $, или
где ${{{\alpha }}_{k}}$ – коэффициент Куранта.И так сквозные расчеты проводятся по формулам (3.1)–(3.7). В алгоритме динамической задачи шаг интегрирования (3.7) обеспечивают устойчивость решения. Аэродинамическое демпфирование среды (2.6) и внутреннее трение в материале (3.4) улучшают устойчивость численного алгоритма.
Равновесное состояние гибкой системы получается как предельное решение динамической задачи. Выбор коэффициента корректировки скоростей и коэффициента устойчивости численного решения осуществляется путем проведения численных экспериментов на модельных задачах. Для численных расчетов динамики ВЛ можно использовать результаты моделирования динамики ленточных парашютов в потоке [13, с. 52–61]: коэффициент ${\mu }$ в формуле (2.6) выбирается в диапазоне 0.1–0.2; а β = = $(0.015{\kern 1pt} --{\kern 1pt} 0.03)\Delta {{s}^{2}}$ в формуле (3.3) и ${{{\alpha }}_{k}} = (0.5{\kern 1pt} \div {\kern 1pt} 1)$ в формуле (3.7).
4. Результаты тестовых исследований. Рассмотрим по отдельности действие ветровой нагрузки и силы веса.
4.1. Влияние ветровой нагрузки. Ветровая нагрузка интенсивностью p действует в горизонтальной плоскости $O{{x}_{1}}{{x}_{2}}$. Перепад давления, возникающий за счет ветра, действует по нормали к деформируемой линии и распределяется равномерно. При этом деформированное состояния линии с двумя закрепленными концами определяется следующими приближенными формулами [11]
(4.1)
$T = pr,$ ${{x}_{1}} = r[1 - \sqrt {1 - {{{\left( {{l \mathord{\left/ {\vphantom {l {\left( {2r} \right)}}} \right. \kern-0em} {\left( {2r} \right)}}} \right)}}^{2}}} ],$Относительная погрешность приближенного решения (4.1) составляет:
Решение (4.1) используем для тестовой отработки влияния ветровой нагрузки в численных расчетах.
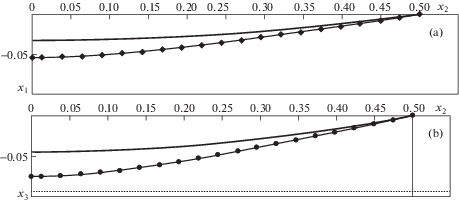
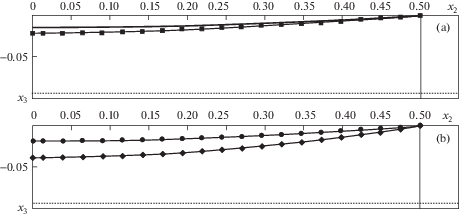
Расчеты по (4.1): пусть линейная плотность электрических проводов равна $\rho = 0.5$ [кг/м], а плотность обледенения ${{\rho }_{{\text{о}}}} = \rho $. Общая плотность составляет $\rho = 1.0$ [кг/м]; l = 160 [м]; $E = 80734 \cdot g$ [H] – модуль упругости; диаметр провода $d = 0.01553$ [м]; скорость ветра ${{V}_{\infty }} = 20$ м/с; погонная ветровая нагрузка $p = {{{\rho }}_{a}}V_{\infty }^{2}d{\text{/}}2$ [Н/м]. Расчеты по (4.1) дают: $\varphi = 0.132$; $r = {\text{3}}{\text{.793}}$, ${{x}_{1}} = {\text{0}}{\text{.03309375}}$, а численные расчеты по (3.1)–(3.7) при ${\tau } = 24.7$ дают ${{x}_{1}} = 0.03310$, фиг. 2a. Относительная погрешность составляет менее ${\theta } = 0.007$%. При этом погрешность самого приближенного решения не превышает величины δ = 0.004 × 10–2%. Максимальный прогиб ${{x}_{1}} = 0.0543$ при ${\tau } = 0.29$.
4.2. Влияние веса. А для анализа точности численных расчетов влияния веса, который действует вдоль оси $O{{x}_{3}}$ в плоскости $O{{x}_{2}}{{x}_{3}}$ можно использовать решение [7]. Уравнение деформированной цепной линии определяется по
(4.2)
${{x}_{3}} = {{{\rho }}_{0}}g\left[ {{{\left( {1 + {\varepsilon }} \right)} \mathord{\left/ {\vphantom {{\left( {1 + {\varepsilon }} \right)} {\left( {E{\varepsilon }} \right)}}} \right. \kern-0em} {\left( {E{\varepsilon }} \right)}}} \right](x_{2}^{2} - l{{x}_{2}}){\text{/}}2$Максимальный прогиб в середине пролета составляет
(4.3)
${{x}_{3}} = - {{l}^{2}}{{{\rho }}_{0}}g\left[ {{{\left( {1 + {\varepsilon }} \right)} \mathord{\left/ {\vphantom {{\left( {1 + {\varepsilon }} \right)} {\left( {E{\varepsilon }} \right)}}} \right. \kern-0em} {\left( {E{\varepsilon }} \right)}}} \right]{\text{/}}8$(4.4)
${\varepsilon } = \sqrt[3]{{{{\gamma } \mathord{\left/ {\vphantom {{\gamma } 2}} \right. \kern-0em} 2} + {{{[{{{\left( {{{\gamma } \mathord{\left/ {\vphantom {{\gamma } 2}} \right. \kern-0em} 2}} \right)}}^{2}} - {{{\left( {{{\gamma } \mathord{\left/ {\vphantom {{\gamma } 3}} \right. \kern-0em} 3}} \right)}}^{3}}]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}} + \sqrt[3]{{{{\gamma } \mathord{\left/ {\vphantom {{\gamma } 2}} \right. \kern-0em} 2} - {{{[{{{\left( {{{\gamma } \mathord{\left/ {\vphantom {{\gamma } 2}} \right. \kern-0em} 2}} \right)}}^{2}} - {{{\left( {{{\gamma } \mathord{\left/ {\vphantom {{\gamma } 3}} \right. \kern-0em} 3}} \right)}}^{3}}]}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}$Расчеты по (4.3), (4.4) дают ${\gamma } = 0.16365 \times {{10}^{{ - 6}}}$ и ${\varepsilon } = 0.0054798{\text{ }}$ и ${{x}_{3}} = - 0.04546$.
На фиг. 2б расчеты по (3.1)–(3.7) ${{x}_{3}} = - 0.04540$ при времени τ = 32.6. При этом относительная погрешность ошибки по сравнению с точным решением составляет $\theta \approx 0.12$%. Максимальный прогиб ${{x}_{3}} = 0.0753$ реализуется в момент времени τ = 0.21.
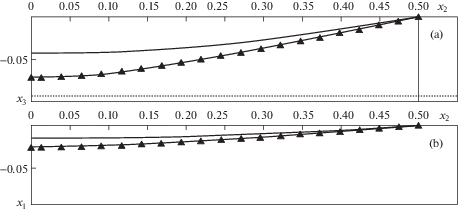
4.3. Расчет пространственной формы ВЛ под воздействием совместной ветровой и весовой нагрузки. Начальное состояние гибкой системы в момент времени τ = 0 примем в виде прямой линии (что приближает к оптимальному весу ВЛ). Из этого состояния система деформируется до значения максимальных прогибов в вертикальной плоскости ${{x}_{3}} = - 0.0717$ (рис. 3,a) и ${{x}_{1}} = - 0.0279$ в горизонтальной плоскости (рис. 3,b) при времени τ = 0.204. По истечении времени $\tau = 40.75$ система выходит на равновесное состояние и максимальные прогибы составляют ${{x}_{3}} = - 0.0433$ и ${{x}_{1}} = - 0.0169$, рис. 3a, 3,b.
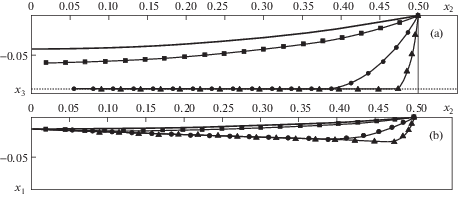
4.4. Движения ВЛ после разрыва в середине пролета. В алгоритме расчета движения ВЛ после разрыва используются следующие допущения: а) при установившемся режиме воздействия ветровой и весовой нагрузки обрыв провода для примера происходит по середине пролета; б) в момент падения на землю воздействие ветровой нагрузки на провод прекращается; в) при падении на землю происходит частично упругий удар и в расчетах принято, что кинетическая энергия отскока составляет 36% от энергии вертикального удара. На рис. 4а, 4,b приводятся результаты расчета движения после разрыва провода по середине пролета в моменты времени τ = 40.85; 41.87; 50.93.
4.5. Влияние порыва ветра. Низкочастотные колебания ВЛ электропередачи (частоты порядка 1 Гц) происходят из-за порыва ветра. Колебания могут проявляться с амплитудой выше метра [14–16]. В этих работах отмечается, что механизм появления колебаний не всегда ясен.
Рассмотрим порыв ветра, который действует в горизонтальной плоскости $O{{x}_{1}}{{x}_{2}}$ с синусоидальным законом изменения
(4.5)
$p\left( \tau \right) = {{q}_{0}}d\left| {{\text{sin}}\left( {\pi {\text{n/}}\delta } \right)} \right|$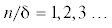 – точки нули синусоиды.
– точки нули синусоиды.
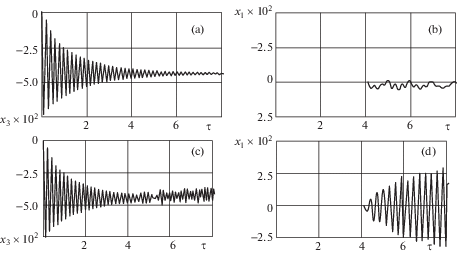
На рис. 5a, 5b, 5,d приводятся результаты расчета движения средней точки пролета в соответствии с алгоритмом (3.1)–(3.7). Начальное состояние пролета при времени τ = 0 принята в виде прямой линии. Из этого состояния под действием силы веса провода реализуется переходный процесс до формы равновесного состояния (рис. 5,a). Максимальный прогиб равен ${{x}_{3}} = - 4.54$ × 10–2. При времени ${\tau } = 4$ действует порыв ветра в соответствии (4.5). Колебания средней точки провода приводится в горизонтальной плоскости, рис. 5,b.
Рассмотрим следующий вариант, давление ветра меняется по закону (4.5) при времени ${\tau } \geqslant 4$ и совпадает с движением при скорости элементов провода ${{\nu }_{{{{x}_{{1i}}}}}} \leqslant 0$, а при движении элемента провода ${{\nu }_{{{{x}_{{1i}}}}}} > 0$ равен нулю. То есть порыв ветра способствует раскачиванию провода в горизонтальной плоскости $O{{x}_{1}}{{x}_{2}}$. Эти результаты расчета приводятся на рис. 5,d. Амплитуда колебаний в плоскости $O{{x}_{1}}{{x}_{2}}$ возрастает. Эти колебания отражаются на колебаниях провода в вертикальной плоскости $O{{x}_{2}}{{x}_{3}}$ и способствуют возникновению колебаний типа “пляски проводов”.
5. Термоупругая задача ВЛ. В осенне-зимне-весенний период создаются благоприятные условия для образования гололедных отложений на линиях электропередачи. Для борьбы с этим опасным явлением разрабатываются и используются различные технологии, в том числе основанные на нагревании проводов с целью плавки гололеда [1, 2].
При образовании гололеда масса провода увеличивается и система переходит в новое равновесное деформированное состояние. При включении нагрева провод еще больше провисает за счет температурного удлинения. После прогрева обледенение сбрасывается, температура спадает до температуры окружающей среды, и форма провода переходит снова в равновесное состояние, которое соответствует нагружению только весом самого провода.
5.1. Безразмерное уравнение теплопроводности для линейного элемента имеет вид
где $0 < s < 1$, ${\text{0}} < {\text{t}} < {{{\text{t}}}_{k}}$, $f$ – плотность тепловых источников.5.2. Уравнение теплопроводности в разностном представлении
Пусть $\varphi _{i}^{j} = f_{i}^{j}$, ${{s}_{i}} = i \cdot h$, $i = 0,1,2,\; \ldots ,\;.N$, $h = {\text{ }}{{\text{1}} \mathord{\left/ {\vphantom {{\text{1}} N}} \right. \kern-0em} N}$ – шаг разбиения по лагранжевой координате, N – число разбиений пролета, ${{t}_{i}} = j \cdot {\tau }$, $j = 0,1,2,\; \ldots ,\;L$, ${\tau } = {{{{t}_{k}}} \mathord{\left/ {\vphantom {{{{t}_{k}}} L}} \right. \kern-0em} L}$ – шаг интегрирования по времени, L – число разбиений временного интервала. Для (5.1) имеем
(5.2)
$u_{i}^{{j + 1}} = \left( {1 - 2\frac{\tau }{{{{h}^{2}}}}} \right)u_{i}^{j} + \frac{\tau }{{{{h}^{2}}}}(u_{{i + 1}}^{j} + u_{{i - 1}}^{j}) + \tau \varphi _{i}^{j}$Устойчивость схемы в сеточной норме для шага интегрирования требует выполнения условия ${\tau } = {\alpha }{{{{h}^{2}}} \mathord{\left/ {\vphantom {{{{h}^{2}}} 2}} \right. \kern-0em} 2}$, ${\text{0}} < {\alpha } \leqslant {\text{1}}$.
5.3. Аппроксимация граничных условий. Аппроксимацию можно проводить двумя способами. Вариант 1. Для аппроксимации граничных условий воспользуемся квадратичным полиномом Лагранжа по трем точкам отрезка. Для первых производных по времени на концах отрезка имеем
а для вторых производных по координате на границах имеем
Тогда для границ на шаге интегрирования $(j + 1)$ имеем
(5.3)
$u_{N}^{{j + 1}} = \frac{{2{\tau }}}{{3{{h}^{2}}}}u_{N}^{j} + \frac{4}{3}\left( {1 - \frac{{\tau }}{{{{h}^{2}}}}} \right)u_{{N - 1}}^{j} - \frac{1}{3}\left( {1 - 2\frac{{\tau }}{{{{h}^{2}}}}} \right)u_{{N - 2}}^{j} + 2{\tau }\varphi _{i}^{j}$Вариант 2. Для границ воспользуемся линейной аппроксимацией
(5.4)
$u_{N}^{{j + 1}} = \left( {1 + 2\frac{{\tau }}{{{{h}^{2}}}}} \right)u_{N}^{j} + \frac{{\tau }}{{{{h}^{2}}}}(u_{{N - 2}}^{j} - 2u_{{N - 1}}^{j}) + {\tau }\varphi _{N}^{j}$5.4. Тестовые расчеты теплопроводности по двум вариантам. Для расчетов примем следующие исходные данные: начальная длина провода $l = 160$ [м]; коэффициент линейного расширения алюминиевого провода составляет ${{{\alpha }}_{t}} = 23.8 \times {{10}^{{ - 6}}}$ [1/K]; модуль упругости $E = 6.25 \times {{10}^{{10}}}$ [Н/м2] [4]; диаметр провода $d = 0.0147$ [м]; плотность материала провода ρ = 2700 [кг/м3]; теплоемкость единицы массы c = 0.9 [кДж/(кг ⋅ K)]; коэффициент теплопроводности k = 209 [Вт/(м ⋅ K)]; K – температура Кельвина. Количество элементов N = 50.
Теплоизолированный провод разделен на две части. Мгновенно левый пролет нагрет до 200°C (473.15 K), а правый имеет температуру окружающей среды минус 5°C. В безразмерном виде эти температуры составят 1.7322 и 0.9817. Перераспределение температуры по длине и по времени происходит без потери тепла и процесс продолжается до температуры выравнивания до величины $\left( {1.7322 + 0.9817} \right) \times 0.5$ = 1.35695, что соответствует 370.65089 K.
Расчеты теплопроводности проводим по (5.2) при аппроксимации граничных условий по варианту 1 и варианту 2 и сравниваем с точным значением 1.35695.
По варианту 1 (аппроксимация граничных условий квадратичным полиномом Лагранжа) численный расчет дает температуру выравнивания 1.36058 за 2.3 с.
По варианту 2 (линейная аппроксимация граничных условий) расчет дает 1.35689. Вариант 2 дает наилучшую сходимость.
5.5. Линейное тепловое расширение. Относительное температурное расширение составляет
(5.5)
${{{{{\varepsilon }}_{t}} = \left( {{{l}_{2}} - {{l}_{1}}} \right)} \mathord{\left/ {\vphantom {{{{{\varepsilon }}_{t}} = \left( {{{l}_{2}} - {{l}_{1}}} \right)} {{{l}_{1}}}}} \right. \kern-0em} {{{l}_{1}}}} = {{{\alpha }}_{t}}\Delta u$(5.6)
$T = E{{{\varepsilon }}_{t}}{{\pi {{d}^{2}}} \mathord{\left/ {\vphantom {{\pi {{d}^{2}}} 4}} \right. \kern-0em} 4}$Расчеты по выше принятым исходным данным дают: относительное температурное удлинение ${{\varepsilon }_{t}} = 24.4 \times {{10}^{{ - 4}}}$, усилие, возникающее в проводе за счет температурного удлинения соответственно T = 25.9 кН.
5.6. Динамика ВЛ с учетом веса провода, веса обледенения и теплопроводности. Для примера пусть плотность обледенения равна плотности самого провода ${{\rho }_{{\text{о}}}} = \rho $, на практике может превышать в несколько раз. В соответствии с решением уравнения движения провод под действием только собственного веса при времени $t = 2.7$ с перемещается до максимального прогиба ${{x}_{3}} = 3.4$ м (рис. 6,a – линия –◼–, ${{x}_{3}} = 0.021253$), при этом натяжение составляет $T = 12$ кН, затем в результате переходного процесса по истечении времени около 30 с самоустанавливается до формы равновесного состояния с максимальным прогибом x3 = 2.3 м (${{x}_{3}} = 0.01438$) м. На эту форму равновесного состояния накладывается равномерная по длине масса обледенения. Система снова выходит на равновесное состояние с массой провода и обледенения, это состояние в момент времени $t = 51$ с приводится на рис. 6,b (линия –⚫–). При этом максимальный прогиб составляет ${{x}_{3}} = 2.95$ м (${{x}_{3}} = 0.01844$) и натяжение $T = 9.8$ кН. Считается, что в момент времени $t = 51$ с 1/10 часть пролета мгновенно нагрета до температуры 150°С, и эта температура держится неизменной на этой части и нагревает остальную часть пролета за счет теплопроводности в течение 5 с. В течение этого времени эта температура успевает распространиться и выровняться до 150°С по всей длине. При этом происходит удлинение за счет теплового расширения, рис. 6,b (линия –◆–). В конце нагрева прогиб достигает величины ${{x}_{3}} = 6.20$ м (${{x}_{3}} = 0.03875$), и температурное натяжение в проводе составляет величину 38 кН.
После этого масса обледенения считается сброшенной мгновенно и в течение одной секунды температура выравнивается с температурой окружающей среды, равной минус 5°С. Рассчитывается дальнейшее движение, система переходит в новое равновесное состояние с максимальным прогибом ${{x}_{3}} = 2.3$ м (${{x}_{3}} = 0.01438$) и натяжением в проводе 6.2 кН (это равновесное состояние приведено на рис. 6a сплошной линией).
Отметим, что изменение температуры по времени связано со скоростью изменения температуры, а изменение движение элементов провода связано с ускорением. Поэтому в конце нагрева провода температура по длине провода распределяется почти равномерно, а упругие относительные удлинения по длине имеют неустановившийся характер, упругие натяжения только со временем выравниваются. Поэтому в конце нагрева более точно можно оценить только температурное натяжение.
6. Заключение. Получено уравнение движения деформируемой линии электропередачи в пространственной постановке. Разработан метод расчета динамики линии электропередачи в пространственной постановке. Проведены численные исследования нагружения ВЛ весовой, ветровой и нагрузкой обледенения. Предложен метод расчета обрыва провода и движение частей после обрыва. Разработан метод расчета термоупругой задачи при обледенении и растапливании ВЛ. Выявлен механизм появления колебательного движения типа “пляски проводов” при действии переменной ветровой нагрузки. Достоверность численных расчетов для частных случаев проверяется полученными аналитическими решениями.
Список литературы
Минуллин Р.Г., Фардиев И.Ш. Локационная диагностика воздушных линий электропередачи: монография. Казань: Казан. гос. энерг. ун-т, 2008. 203 с.
Угаров Г.Г., Колесников А.А., Башкевич В.Я. Синтез системы управления плавкой отложений на воздушных линиях электропередач, оборудованных информационно-измерительной системой // Вест. Сарат. гос. техн. ун-т. 2008. Т. 3. № 1. С. 120–128.
Шевченко Е.В., Удод Т.Е. Разработка методов борьбы с пляской проводов ВЛ для Украины // Металлические конструкции. 2006. Т. 12. № 4. С. 239–247.
Бацева Н.Л. Специальные вопросы проектирования электроэнергетических систем и сетей: учебное пособие // Томск: Изд-во Томск. политехн. ун-т, 2008. 254 с.
Шевченко Е.В., Митраков В.А., Танасогло А.В. Определение редуцированного натяжения при обрыве провода // Металлические конструкции. 2010. Т. 16. № 3. С. 189–198.
Соколов А.И. Нелинейные колебания абсолютно гибкого провода в потоке воздуха // Наука и образование: электронное научно-техническое издание. 2008. № 4-1. 5 с.
Гимадиев Р.Ш., Динмухаметов Ф.Ф., Галимуллин Н.Р. Расчет пространственной динамики ВЛ при совместном воздействии ветровой и весовой нагрузки // Изв. вузов. Проблемы энергетики. 2010. № 3–4. С. 28–37.
Гимадиев Р.Ш., Динмухаметов Ф.Ф. Моделирование разрыва линий передачи энергий // Изв. вузов. Проблемы энергетики. 2008. № 7–8. С. 137–143.
Гимадиев Р.Ш., Гимадиева Т.З. Математическое моделирование деформирования линии электропередачи с учетом теплопроводности // Изв. вузов. Проблемы энергетики. 2011. № 9. С. 51–59.
Гимадиев Р.Ш. Задача термоупругости линий электропередач // Тез. докл 8-й Межд. науч-техн. конф. “Инновационные машиностроительные технологии, оборудование и материалы–2017” (МНТК “ИМТОМ-2017” Часть 2, 6–8 декабря 2017, г. Казань. С. 141–145.
Гимадиев Р.Ш., Ильгамов М.А. Статическое взаимодействие профиля мягкого крыла с потоком несжимаемой жидкости // Изв. вузов. Авиационная техника. 1998. № 1. С. 43–48.
Девнин С.И. Гидроупругость конструкций при отрывном обтекании. Л.: Судостроение, 1975. 192 с.
Гимадиев Р.Ш. Динамика мягких оболочек парашютного типа. Казань: Казан. гос. энерг. ун-т, 2006. 208 с.
McCombe John, Haigh F.R. Overhead Line Practice. 3rd ed. Macdonald, 1966. P. 216–219.
Ryan Hugh. High Voltage Engineering and Testing. IET, 2001, p. 192, ISBN 0-85296-775-6.
Pansini A.J. Power Transmission and Distribution. Fairmont Press, 2004. P. 204–205. ISBN 0-88173-503-5.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела