Известия РАН. Механика твердого тела, 2019, № 4, стр. 39-47

1. Введение. В настоящее время обязательным требованием при проектировании атомных станций (АС) является проведение прогнозных расчетов при возникновении нештатных ситуаций, например падение самолета на реактор АС. Защитная оболочка реактора АС представляет собой геометрически сложную железобетонную конструкцию. При проектировании подобных конструкций, помимо анализа поведения отдельных элементов при различных видах воздействия, необходим также анализ поведения конструкции в целом. Существующие инженерные методики, основанные на упрощенных подходах, не позволяют проследить за динамикой разрушения материалов и влияния на этот процесс волновых явлений, эволюция которых при ударном воздействии является одним из определяющих факторов.

Проведение с этой целью натурных экспериментов сопряжено, как правило, с большими материальными затратами и не всегда возможно, к тому же в эксперименте не всегда удается получить полную картину, особенно это касается динамических процессов, когда необходима информация об интересующих параметрах в различные моменты времени. Поэтому существует потребность в моделях и методах, позволяющих проводить анализ и предсказывать поведение конструкций при различных видах эксплуатационных нагрузок и возможных нештатных ситуациях. Для адекватного описания поведения конструкций необходимо учитывать пространственный характер реализующегося в них напряженно-деформированного состояния (НДС), обусловленный несколькими факторами:

– конструкционные особенности, приводящие к геометрической несимметричности;

– учет реальных условий нагружения – как правило, они не симметричны;

– анизотропия физико-механических свойств материалов элементов конструкций.

Наличие хотя бы одного из вышеперечисленных факторов делает необходимым проведение анализа в трехмерной постановке, что является весьма сложной и трудоемкой задачей, так как в этом случае помимо создания адекватной модели поведения материалов необходимо учитывать реальную геометрию и пространственное расположение различных элементов конструкции.

В работе численно моделируется взаимодействие падающего самолета Boeing 747–400 с защитной оболочкой атомной станции. Контактное воздействие самолета на оболочку заменено импульсным воздействием с параметрами, приведенными в [1]. Оболочка имеет сложную многослойную сотовую структуру, состоящую из слоев бетона и фибробетона, скрепленных со стальными фермами. Численное моделирование проводится методом конечных элементов [2] в трехмерной динамической постановке, с использованием авторского высокопроизводительного алгоритма и программного комплекса [3], в котором реализован алгоритм построения сетки сложных геометрических объектов.

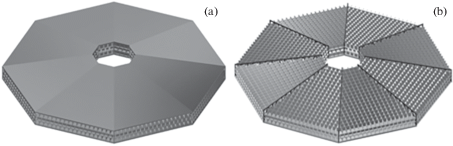
2. Постановка задачи. Общий вид защитной оболочки представлен на рис. 1 ,а. Верхняя и нижняя крышки оболочки представляют собой трехслойную конструкцию. Материал верхнего слоя – фибробетон (толщина – 0.05 м), материал среднего слоя железобетон (толщина 0.2 м), материал нижнего слоя – фибробетон (толщина – 0.05 м). Фибробетон – бетон, в который в качестве армирующего материала добавляется тонкая фибра. В данном случае использовалась углеродная фибра. Объем углеродной фибры составлял 0.2%. Между верхней и нижней крышками оболочки располагается трехслойная сотовая конструкция. На рис. 1 ,b приведена структура сотовой конструкции оболочки. Слои смещены на 0.5 м относительно друг друга. Размер сот – 1 м, толщина стенок – 0.05 м, материал стенок – фибробетон. В целом оболочка состоит из восьми сегментов, скрепленных между собой стальными фермами, изготовленными из стали А400. Общая толщина защитной оболочки составляет 3.6 м, диаметр – 52 м. Из-за сложной геометрии конструкции, стальные армирующие элементы в слое бетона явно не выделялись, их наличие учитывалось через эффективные модули, свойства усреднялись по объему. Следует отметить, что весьма серьезной проблемой при расчете конструкций, содержащих большое количество различных элементов, является создание трехмерной конечно-элементной сетки. По сути это отдельная задача, от решения которой зависит и точность вычислений и временные затраты на решение задачи. Конечно-элементная модель защитной оболочки содержала 100 млн тетраэдрических конечных элементов.

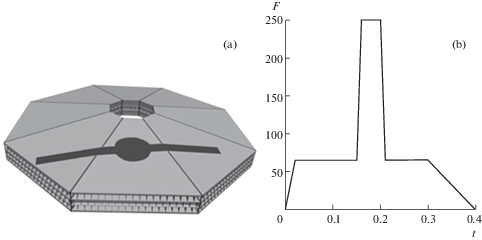
Воздействие падающего самолета на защитную конструкцию при численном моделировании заменялось импульсом, параметры которого приведены в [1]. Направление импульса соответствовало падению самолета под углом 10 градусов к горизонту. Область приложения импульса и кривая изменения величины импульса (в МН) во времени (в секундах) приведена на рис. 2 ,а и 2,b, соответственно. Темным цветом обозначены зоны приложения нагрузки от фюзеляжа (круговая область) и крыльев (прямоугольная область). До 0.15 с импульс прикладывается в зоне контакта конструкции с фюзеляжем, затем в контакт вступают крылья, в этот момент достигается максимальное значение импульса – 250 МН.

3. Основные уравнения математической модели. Система уравнений, описывающих нестационарные адиабатные движения сжимаемой среды в произвольной системе координат ($i = 1,2,3$), включает следующие уравнения – неразрывности, движения и энергии соответственно

где ${{a}^{k}} = \frac{{\partial {{{\upsilon }}^{k}}}}{{\partial t}} + {{{\upsilon }}^{i}}{{\nabla }_{i}}{{{\upsilon }}^{k}}$, ${{\nabla }_{i}}{{\sigma }^{{ik}}} = {\sigma }_{{,i}}^{{ik}} + {\Gamma }_{{im}}^{k}{{{\sigma }}^{{im}}} + \Gamma _{{im}}^{m}{{{\sigma }}^{{ik}}}$

Здесь F^k – компоненты вектора массовых сил; $\Gamma _{{ij}}^{k}$ – символы Кристоффеля; ${{{\sigma }}^{{ij}}}$ – контравариантные компоненты симметричного тензора напряжений; E _– удельная внутренняя энергия; ${\rho }$ – плотность среды; ${{{\upsilon }}^{i}}$ – компоненты вектора скорости; ${{e}_{{ij}}}$ – компоненты симметричного тензора скоростей деформаций:

Поведение исследуемых материалов, как металлических, так и бетона, описывалось упругопластической моделью. Тензор напряжений представляется в виде суммы девиаторной ${{S}^{{ki}}}$ и шаровой части P:

где g^ij – метрический тензор.

Давление в материалах рассчитывалось по уравнению Ми-Грюнайзена как функция удельной внутренней энергии E и плотности $\rho $:

где K₀, K₁, K₂, K₃ – константы материала, V₀ – начальный удельный объем, $V$ – текущий удельный объем.

Предполагая, что для среды справедлив принцип минимума работы истинных напряжений на приращениях пластических деформаций, запишем связь компонент тензора скоростей деформаций и девиатора напряжений в виде:

Здесь производные по времени от компонент тензора напряжений приняты в формулировке Яуманна:

где ${{\omega }_{{ij}}} = {{\left( {{{\nabla }_{i}}{{\upsilon }_{j}} - {{\nabla }_{j}}{{\upsilon }_{i}}} \right)} \mathord{\left/ {\vphantom {{\left( {{{\nabla }_{i}}{{\upsilon }_{j}} - {{\nabla }_{j}}{{\upsilon }_{i}}} \right)} 2}} \right. \kern-0em} 2}$, G – модуль сдвига.

Материал ведет себя упруго (λ = 0), если выполняется условие Мизеса:

и пластически (λ > 0), если оно нарушается. Здесь ${{\sigma }_{d}}$ – динамический предел текучести, который может быть, в общем случае, функцией скоростей деформаций, давления и температуры. Для бетона учитывалась зависимость предела текучести от давления [4]:

Если условие (3.1) нарушается, то для вычисления компонент девиатора напряжений применяется процедура приведения к кругу текучести. Для этого компоненты ${{S}^{{ij}}}$ умножаются на нормирующий множитель, что равносильно описанию поведения среды в пластической области уравнениями теории Прандтля-Рейса.

В качестве локального критерия сдвигового разрушения для материала ферм принимается предельная величина интенсивности пластических деформаций:

где T₁, T₂ – первый и второй инварианты тензора деформаций.

При описании разрушения бетона используется критерий Хоффмана [5]. Этот критерий учитывает различие в пределах прочности на сжатие и растяжение, анизотропию прочностных свойств:

где ${{C}_{i}}$ определяется из следующих соотношений: где ${{X}_{t}}$, ${{X}_{c}}$, ${{Y}_{t}}$, ${{Y}_{c}}$, ${{Z}_{t}}$, ${{Z}_{c}}$ – пределы прочности по осям $X$, $Y$, $Z$ на растяжение и сжатие соответственно, а S_xy, S_yx, S_zx – пределы прочности на сдвиг по соответствующим осям. В случае изотропного материала ${{X}_{t}} = {{Y}_{t}} = {{Z}_{t}} = {{R}_{t}}$, ${{X}_{c}} = {{Y}_{c}} = {{Z}_{c}} = {{R}_{c}}$, S_xy = S_yz = = S_zx = ${{R}_{{sh}}}$.

Предполагается, что разрушение бетона в условиях интенсивных динамических нагрузок происходит следующим образом [6]:

– если критерий прочности (3.2) нарушается в условиях сжатия (${{e}_{{kk}}} \leqslant 0$), то дальнейшее поведение материала описывается гидродинамической моделью ${{\sigma }_{{ij}}} = - P$;

– если критерий (3.2) нарушается в условиях растяжения (${{e}_{{kk}}} > 0$), то материал считается полностью разрушенным, и компоненты тензора напряжений полагаются равными нулю.

В экспериментах показано, что при динамических нагрузках происходит увеличение прочностных характеристик бетона [7]. Причем зависимость пределов прочности на сжатие и растяжение от скорости деформаций отличаются. Связь пределов прочности статических с динамическими выражена через коэффициент динамичности: ${{K}_{d}}$ = = R_d/R_s, где R_d – динамическая прочность, R_s – статическая прочность.

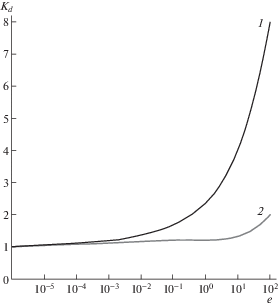
На основе экспериментальных данных [7] были получены аппроксимационные зависимости для коэффициентов динамичности бетона при сжатии (3.3) и растяжении (3.4). Соответствующие графики зависимости K_d от скорости деформаций (в с^–1) приведены на рис. 3 , где кривая 1 описывает зависимость коэффициента динамичности при растяжении, кривая 2 – при сжатии.

Предел прочности бетона на сдвиг определяется из значений пределов прочности на сжатие и растяжение [4] ${{R}_{{sh}}} = 0.55\sqrt {{{R}_{c}}{{R}_{t}}} $.

Описанная модель поведения материалов и численный алгоритм были протестирован в ходе согласованных экспериментальных и численных исследований по ударному нагружению железобетонных балок [6]. Исследуемая железобетонная балка имела такую же структуру, как верхняя и нижняя крышки защитной оболочки. В ходе тестовых исследований было получено хорошее согласование экспериментальных и численных результатов, подтвердившее адекватность модели и численного алгоритма.

Основные характеристики материалов имели следующие значения: бетон – ${\rho } = $ 2450 кг/м³, коэффициент Пуассона $\nu = 0.2$, ${{R}_{t}} = 1.75$ МПа, ${{R}_{c}} = 22$ МПа, $G = 10.8$ МПа, ${{\sigma }_{s}}$ = 7.7 МПа; фибробетон – ${\rho } = 2450$ кг/м³, коэффициент Пуассона $\nu = 0.2$, ${{R}_{t}} = 3.4$ МПа, прочность на сжатие ${{R}_{c}} = 41$ МПа, $G = 17.1$ МПа, ${{\sigma }_{s}} = 7.7$ МПа; сталь – ${\rho } = 7850$ кг/м³, коэффициент Пуассона $\nu = 0.3$, $G = 78.5$ МПа, ${{\sigma }_{d}} = 390$ МПа.

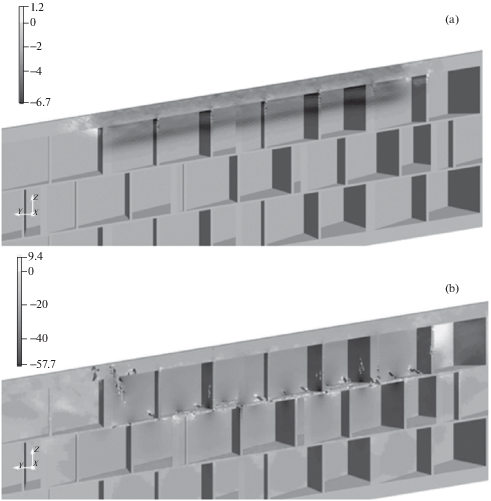
4. Обсуждение результатов. В рамках поставленной задачи были проведены численные исследования динамики напряженно-деформированного состояния и разрушения защитной оболочки при импульсном воздействии. На рис. 3, а и 3,b представлено распределение значений (в МПа) компоненты тензора напряжений σ_zz в радиальном сечении оболочки, проходящем через центральную точку приложения нагрузки в моменты времени 0.2 и 0.8 мс, соответственно. Графики иллюстрируют распространение волны сжатия (отрицательные значения напряжений) по толщине оболочки и формирование растягивающих напряжений (положительные значения) по периметру зоны приложения импульса и внутри оболочки на свободных поверхностях сотовой структуры. К моменту времени 0.8 мс (рис. 3 ,b) в результате действия растягивающих напряжений уже наблюдаются разрушения сотовой структуры. Растягивающие напряжения возникают в результате выхода волны сжатия на свободные поверхности сот, от которых они отражаются волнами разгрузки. Наличие свободных поверхностей внутри оболочки с одной стороны понижает уровень сжимающих напряжений, но с другой стороны приводит к формированию областей растяжений, в которых инициируется разрушение сотовой структуры, зарождаются трещины.

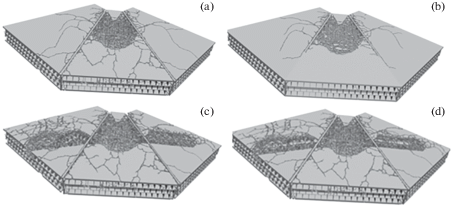
Динамику развития разрушения оболочки можно проследить на рис. 5,a –5,d, где представлена лицевая поверхность оболочки в моменты времени 12, 100, 160 и 300 мс, соответственно. Разрушения возникают непосредственно в области приложения импульса, и, в результате действия растягивающих напряжений, возникают трещины по периметру приложения нагрузки, которые с течением времени распространяются по поверхности оболочки. Стальные фермы деформируются, но разрушений в них нет, так же следует отметить, что фермы являются концентраторами напряжений за счет существенного различия в упругих и прочностных свойствах стали и фибробетона. К моменту времени 160 мс (рис. 5 ,с) добавляется воздействие от крыльев самолета и можно наблюдать увеличение объема разрушений в оболочке.

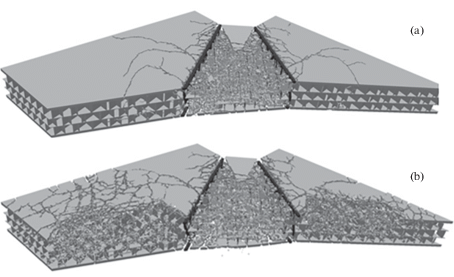
На рис. 6 ,а, 6,b представлена тыльная поверхность конструкции в моменты времени 20 и 300 мс. Как видно из рисунков на тыльной поверхности оболочки, непосредственно под зоной приложения нагрузки, образуются трещины, которые с течением времени распространяются в радиальном направлении. Эти трещины возникают в результате действия растягивающих напряжений, которые возникают в момент выхода волны сжатия на тыльную поверхность и затем развиваются в течение времени нагрузки.

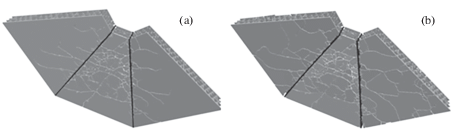
Разрушение оболочки по толщине иллюстрируют рис. 7, а и 7,b, где в последовательные моменты времени 20 и 300 мс приведено поперечное сечение оболочки по срединной поверхности, проходящей через зоны приложения импульса. Вначале наблюдается разрушение в круговой зоне приложения импульса от фюзеляжа самолета, а затем в областях приложения импульсов от крыльев. Как видно из рисунков бетонная конструкция полностью разрушается по толщине.

5. Заключение. В рамках феноменологического подхода механики сплошной среды предложена модель и создана методика расчета оболочечных конструкций со сложной внутренней структурой при интенсивных динамических нагрузках. Методика реализована в полной трехмерной постановке на базе модифицированного метода конечных элементов. На основе разработанной методики, можно проводить широкопараметрические численные эксперименты по выбору оптимальных конструктивных решений.

Численно исследована динамика напряженно-деформированного состояния и разрушения защитной оболочки АС с сотовой внутренней структурой при импульсном воздействии. Установлено, что разрушение сотовой структуры инициируется в областях действия растягивающих напряжений, которые возникают в момент выходы волны сжатия на свободные поверхности сот. С течением времени происходит дальнейшее развитие возникших разрушений в результате действия импульсной нагрузки.

Работа выполнена при поддержке Российского фонда фундаментальных исследований, проекты № 18-41-703003 и № 18-48-700035, Национального фонда естественных наук Китая, проект № 11672048 и Чанъаньского университета, проект № 310825153510.