Известия РАН. Механика твердого тела, 2019, № 3, стр. 118-123

1. Возмущенное движение земного полюса на частоте прецессии орбиты Луны. Фундаментальная астрометрическая задача построения прогноза колебательного движения земного полюса связана с разработкой высокоточной динамической модели вращательно-колебательного движения Земли и идентификацией ее параметров на основе данных Международной службы вращения Земли (МСВЗ) [1]. Надежный прогноз весьма важен для решения задач навигации космических аппаратов и при исследовании ряда астрометрических, геодинамических и геофизических проблем. Представляет научный и практический интерес разработка модели прогноза движения земного полюса как в автономном, так и в адаптивном режимах.

Известно [1–4], что в каждый момент времени движение относительно центра масс трехосной Земли с переменным тензором инерции представляет собой мгновенный поворот вокруг некоторой оси под действием возмущающих гироскопических, гравитационных и приливных моментов сил. Этот вектор наклонен под различными переменными углами как к оси фигуры Земли, так и к вектору кинетического момента, модели которых строятся независимо и описывают движение земного полюса в системе ITRS и небесного полюса в небесной системе GCRS (Geocentric Celestial Reference System) соответственно. Последняя представляет собой Кенигову систему координат, полученную параллельным переносом небесной системы ICRS (International Celestial Reference System), которую в пределах доступной точности измерений можно считать инерциальной системой. Движение небесного полюса представляет собой прецессию и нутацию оси вращения Земли, теория которых хорошо разработана и содержится в рекомендациях Международного астрономического Союза [1].

Ориентацию связанной с Землей системы координат ITRS относительно небесной системы GCRS удобно представить в канонических переменных Андуайе, которые обозначим L, G, ${{G}_{{{{{\xi }}_{3}}}}}$ для моментов импульсов и ${{{\varphi }}_{1}}$, ${{{\varphi }}_{2}}$, ${{{\varphi }}_{3}}$ для угловых переменных. Переход от связанной системы к небесной осуществляется путем пяти последовательных поворотов на углы ${{{\varphi }}_{1}}$, ${{{\delta }}_{2}}$, ${{{\varphi }}_{2}}$, ${{{\delta }}_{1}}$, ${{{\varphi }}_{3}}$, где углы ${{{\delta }}_{1}}$, ${{{\delta }}_{2}}$ определяются соотношениями

Динамика возмущенного движения земного полюса обусловлена, в частности, изменением угла ${{{\delta }}_{2}}$, который определяет изменение амплитуды колебаний.

Функционал Рауса R движения Земли относительно центра масс в рассматриваемых переменных имеет вид

Здесь A, B, C – главные центральные моменты инерции “замороженной” фигуры Земли с учетом экваториального выступа; ${\delta }C$ – малые вариации осевого момента инерции; величины ${{J}_{{pr}}}$, ${{J}_{{qr}}}$ – центробежные моменты инерции, содержащие наблюдаемые возмущения с годичной и близкой к чандлеровской частотам.

Приливной потенциал ${{U}_{{M2}}}$, приводящий к вариациям тензора инерции Земли, выражается суммой гармонических слагаемых с комбинационными частотами [1, 3]:

Здесь t – гринвичское среднее солнечное время. Величины ν_i = ${{a}_{i}}{{\dot {l}}_{M}} + {{b}_{i}}{{\dot {l}}_{S}} + {{c}_{i}}{{\dot {p}}_{M}}$ + + ${{d}_{i}}{{\dot {p}}_{S}}$ + ${{e}_{i}}{{{\dot {\Omega }}}_{M}}$ суть линейные комбинации с целочисленными коэффициентами производных угловых параметров ${{l}_{{M,S}}}$, ${{p}_{{M,S}}}$, ${{{\Omega }}_{M}}$. Параметры ${{l}_{M}}$ и ${{l}_{S}}$ суть средние долготы Луны и Солнца соответственно с периодами 27.55 и 365.25 звездных суток. Величина p_M есть средняя долгота перигея Луны, изменяющаяся с периодом 8.85 года, а p_S – средняя долгота перигея Солнца, изменяющаяся с периодом 25700 лет. Параметр ${{{\Omega }}_{M}}$ определяет долготу восходящего узла Луны: он изменяется с периодом 18.61 года.

Фигура Земли вследствие возмущения приливного потенциала создает дополнительный возмущающий потенциал ${\delta }W(t)$, зависящий от времени. Наибольшим по величине слагаемым из разложения потенциала δW является возмущение от второй гармоники ${\delta }{{W}_{2}}$:

Изменение сферической функции в (1.4) $\Delta {{Y}_{2}}({\theta },{\varphi })$ выражается через коэффициенты второго порядка разложения геопотенциала:

Вариации коэффициентов геопотенциала получаются из (1.3) и имеют вид:

${{\Theta }_{{ij}}}$ – линейные комбинации углов ${{{\tau }}_{0}}$, ${{l}_{{M,S}}}$, ${{p}_{{M,S}}}$, ${{{\Omega }}_{M}}$. Величина ${{{\tau }}_{0}} = t - {{l}_{M}} - {{l}_{S}}$ есть гринвичское среднее лунное время; h – отношение вертикального приливного смещения земной поверхности к смещению эквипотенциальной поверхности приливообразующего потенциала; коэффициент $\chi $ имеет значение 1 для однородной модели Земли и 0.843 для реальной Земли.

Вариации коэффициентов второй зональной гармоники геопотенциала могут быть выражены через вариации компонентов тензора инерции

следующим образом:

2. Уравнения возмущенного движения земного полюса. Для описания вариаций элементов тензора инерции и коэффициентов геопотенциала удобно принять следующие обозначения в разложении тензора инерции $\delta {{J}_{{ij}}}$:

${\delta }{{J}_{{ij}}}(t)$ – внутригодовые и межгодовые вариации; ${\delta }J_{{ij}}^{{({\varphi })}}$, ${\delta }J_{{ij}}^{{(2{\varphi })}}$ – суточные и полусуточные вариации.

Внутрисуточные вариации ${\delta }J_{{ij}}^{{({\varphi })}}$, ${\delta }J_{{ij}}^{{(2{\varphi })}}$ содержат составляющие колебаний с комбинационными частотами ${{{\nu }}_{i}}$ пространственного варианта задачи деформируемая Земля–Луна в поле притяжения Солнца.

В рамках статической теории приливов Земли [2] для вариаций осевых моментов инерции выполняются приближенные равенства:

Здесь k – коэффициент пропорциональности. Наличие же в океане приливов с измененными фазами основных гармоник приливного потенциала приводит к появлению дополнительных слагаемых в $\delta C$ с суточными и полусуточными периодами:

Наибольшим по амплитуде слагаемым, содержащимся в (2.1), оказывается гармоника с периодом 18.61 лет.

Согласно [4, 5] модель движения полюса Земли можно описать упрощенными дифференциальными уравнениями, полученными из классических динамических уравнений Эйлера-Лиувилля

Здесь ${{x}_{p}}$, ${{y}_{p}}$ – координаты движения полюса Земли в связанной системе, ${{\sigma }_{{x,y}}} = \sigma $ – коэффициент суммарной диссипации, ${{N}_{{x,y}}}\, = \,N$ – чандлеровская частота (${{N}_{{x,y}}}\, \approx \,0.84{\kern 1pt} - {\kern 1pt} 0.85$ циклов в год), ${{{\mu }}_{{x,y}}}$ определяют возмущающие моменты сил в колебательном процессе земного полюса.

Математическая модель колебаний полюса Земли содержит две основные составляющие – чандлеровское колебание с периодом около 433 зв. сут. и амплитудой, достигающей 0.2′′–0.25′′, и годичное колебание с периодом, приблизительно равным одному году, и амплитудой 0.07′′–0.08′′. Координаты полюса (x_p, y_p), согласно данной модели, описываются выражениями

Здесь $\tau $ – время, измеряемое стандартными годами; N – чандлеровская частота (выбирается на основе спектрального анализа длительного ряда наблюдений); величины ${{c}_{x}}({\tau })$, ${{c}_{y}}({\tau })$ представляют собой координаты точки среднего полюса. Оптимальные значения коэффициентов модели (1.2) находятся с помощью метода наименьших квадратов на основе статистической обработки астрометрических данных высокоточных измерений угловых параметров движения Земли. При этом выполняются приближенные равенства

отражающие структурные свойства модели.

Можно показать, что с помощью преобразования [6]

удается проиллюстрировать синхронные колебание полюса Земли и прецессионное движение лунной орбиты. В (2.4) введены обозначения: α, β – постоянные фазы, зависящие от начального отсчета времени; ${{a}_{0}}$ – среднее значение амплитуды колебаний полюса; c_x, c_y – величины, содержащие константы, вековые слагаемые и вариации с периодами больше шести лет; ${{{\nu }}_{T}}$ – частота шестилетней амплитудной модуляции колебательного движения полюса.

Во вращающейся относительно исходной системы координат ITRS (International Terrestrial Reference System), в которой наблюдается движение земного полюса, фаза его движения согласно двухчастотной модели чандлеровских и годичных колебаний с постоянными коэффициентами будет совершать мелкомасштабные колебания с периодами, не превышающими период их модуляции. Однако наблюдаемый полюс в этой системе совершает в несколько раз большее по амплитуде циклическое обратное движение вокруг среднего положения с частотой прецессии орбиты Луны, то есть в том же направлении, в каком двигаются узлы лунной орбиты.

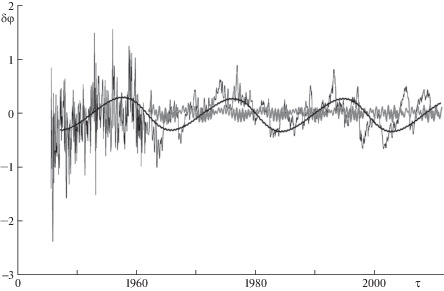
Обозначив через ${\delta \varphi }$ полярный угол в новой системе (${{{\xi }}_{p}}$, ${{{\eta }}_{p}}$), можно проиллюстрировать синфазность движения полюса и прецессии орбиты Луны.

На фиг. 1 на график фазы колебательного движения земного полюса (измеряемой в радианах), полученной согласно двухчастотной модели движения полюса с постоянными коэффициентами (черная зигзагообразная линия) и согласно наблюдениям МСВЗ (полужирная серая линия) в новой системе координат, наложен график отклонения точки пересечения земного экватора и лунной орбиты от точки весеннего равноденствия (полужирная черная линия) в зависимости от времени, измеряемого в годах. Периодическое отклонение точки пересечения земного экватора и лунной орбиты от точки весеннего равноденствия происходит вследствие прецессии орбиты Луны с периодом 18.61 лет. В новой системе координат график фазы движения земного полюса иллюстрирует вариации в шестилетней модуляции чандлеровской и годичной компонент. Отметим, что сильные флуктуации, присутствующие на графике до 1962 года, обусловлены большей ошибкой измерений положения земного полюса.

Определив регулярную составляющую вариации фазы и выполнив обратное преобразование (к исходной системе ITRS), можно получить дополнительные слагаемые к основной двухчастотной модели (2.3) колебательного процесса земного полюса.

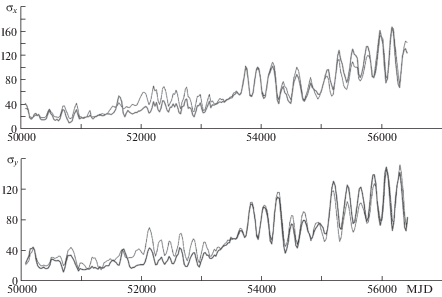
На фиг. 2 даны среднеквадратические отклонения двухлетней экстраполяции координат полюса, измеряемые в угловых миллисекундах, согласно двухчастотной модели в автономном режиме без учета (тонкая линия) и с учетом (полужирная линия) дополнительных слагаемых модели. По оси абсцисс отложено время MJD (Modified Julian Date) [1]. Коэффициенты основной двухчастотной модели регулярного движения земного полюса определены на длительном интервале интерполяции, непосредственно предшествующем интервалу верификации модели. Исходя из результатов проведенного численного моделирования и верификации модели при различных интервалах времени можно сделать вывод о том, что дополнительные слагаемые модели в среднем позволяют повысить точность определения положения земного полюса на 5‒7 см при прогнозе на 2–8 лет.

Заключение. На основе небесномеханической модели и анализа астрометрических данных наблюдений получены дополнительные слагаемые долгопериордического движения земного полюса, учитывающие возмущения от Солнца и Луны. С помощью численно-аналитического моделирования показано, что дополнительные слагаемые приводят к значимому уточнению прогноза полюса на интервалы времени от 2 до 8 лет.