Известия РАН. Механика твердого тела, 2019, № 3, стр. 147-154

1. Введение. Системы с запаздыванием широко распространены в радиотехнике, устройствах автоматического управления, электронике и др. Обусловленные запаздыванием колебательные явления возникают в вибрационных машинах, регуляторах, транспортных системах (ленточные транспортеры и др.), электро- и пневмосистемах, прокатных станах, следящих системах и т.д. Эти колебания могут быть как вредными, так и полезными. В последнем случае запаздывание вводится специально, например, в системе ультразвукового станка.

Для математического описания систем с запаздыванием используются, чаще всего, нелинейные дифференциальные уравнения с отклоняющимся аргументом. Так как решение таких уравнений сопряжено большими трудностями, то при этом выделяется класс квазилинейных систем, изучение которых проводится с помощью приближенных методов. Среди них широко используется математически хорошо обоснованный асимптотический метод теории нелинейных колебаний [1, 2].

Изучению колебательных систем с запаздыванием и идеальным источником энергии посвящено достаточно много работ, чего нельзя сказать о случае систем с неидеальным источником или ограниченным возбуждением. Систематическая теория систем с неидеальными источниками энергии изложена впервые в работе В.О. Кононенко [3]. Дальнейшее развитие эта теория получила в целом ряде работ, отраженных, в частности, в [4, 5]. Системы с запаздыванием и неидеальным источником энергии рассматривались в небольшом числе работ [4–10] и др. В одних работах из приведенного списка запаздывание присутствует в силе упругости, а в других – зависящей от скорости силе трения. Действие вызывающей автоколебания силы трения на динамику систем рассмотрены в достаточно большом числе работ, в том числе в [3–18]. Изученная в [3–5, 10–15] модель фрикционной автоколебательной системы, взаимодействующей с источником энергии ограниченной мощности, положена в основу работ [7–9], в которых запаздывание присутствует в силе трения, вызывающей автоколебания. В этих работах, в случае запаздывающей силы трения и ограниченной мощности источника энергии рассмотрены, помимо автоколебаний, по отмеченной в [4, 5] классификации типов и смешанных колебаний взаимодействие “вынужденных колебаний и автоколебаний”, “параметрических колебаний и автоколебаний”. В продолжение [7–9] ниже рассмотрим более сложный случай, т.е. смешанные вынужденные, параметрические и автоколебания.

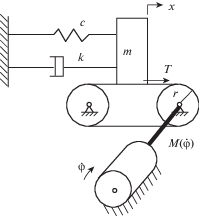
2. Модель системы. Примем, что возбуждающая автоколебания сила трения зависит от запаздывания постоянной величины. А также автоколебания возможны в случае отсутствия последнего. Динамическая модель такой автоколебательной системы с ограниченным возбуждением от двигателя с суммарной (включающей движущий момент и момент сил сопротивления) моментной характеристикой $M({\dot {\varphi }})$, представлена на фиг. 1, где ${\dot {\varphi }}$ – скорость вращения ротора двигателя.

Уравнения движения системы с учетом внешних воздействий (вынуждающего λsinνt и параметрического $(c + b\cos pt)x$) имеют вид

Здесь m, c, b, p, λ, ${\nu }$, V, k , I, r – постоянные величины, а сила трения T(U_τ) зависит от относительной скорости ${{U}_{{\tau }}} = V - {{\dot {x}}_{{\tau }}}$, ${{\dot {x}}_{{\tau }}} = \dot {x}(t - {\tau })$, где τ – постоянный временной фактор запаздывания, $V = r{\dot {\varphi }}$, $f(x)$ – нелинейная часть силы упругости.

Выражение силы трения имеет вид

Здесь q, α₁, α₃ – положительные постоянные, $sgn{{U}_{{\tau }}} = 1$ при $V > {{\dot {x}}_{{\tau }}}$ и $sgn{{U}_{{\tau }}} = - 1$ при $V < {{\dot {x}}_{{\tau }}}$. Следует отметить, что представление силы трения в таком виде отражает наиболее распространенную падающую характеристику коэффициента трения от скорости скольжения, которая наблюдалась также при рассмотрении проблемы измерения сил трения в условиях космического эксперимента на орбите [18].

Прежде чем перейти к построению решений (2.1) отметим следующее. Как показано в [4, 5], в случае, когда система находится под внешним и параметрическим воздействием, в ней могут возникнуть много сложных процессов. Для отражения резонансных (захватываемых) колебаний, обусловленных одновременным выполнением определенных соотношений между частотой автоколебаний и частотами обоих воздействий, в [4, 5] обоснованно введено “условие синхронности резонансных частот внешнего и параметрического воздействий” или кратко “условие синхронности”. В соответствии с этим условием ${\nu } = jp$, где $j = {{{{s}_{1}}{{n}_{2}}} \mathord{\left/ {\vphantom {{{{s}_{1}}{{n}_{2}}} {{{s}_{2}}{{n}_{1}}}}} \right. \kern-0em} {{{s}_{2}}{{n}_{1}}}}$, s₁, s₂, n₁, n₂ – взаимно простые, целые (небольшие) числа. Поскольку на практике главный интерес представляют основные резонансы (${\omega } \approx {p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0em} 2}$, ${\omega } \approx {\nu }$) от влияния обоих воздействий, то примем условие синхронности  j = 1/2.

3. Решения уравнений. Для построения решений (2.1) используем метод усреднения нелинейной механики [2]. С этой целью примем следующие предположения: силы в правой части (2.1) и запаздывание малы; скорость двигателя изменяется мало за период колебаний. На этой основе вводим в уравнения (2.1) малый параметр ε, который впоследствии примем равным единице, и имеем

Искомые решения (3.1) представим в виде

где a, ξ и Ω – медленно изменяющиеся амплитуда, фаза и скорость.

Введя переменную $u = r\Omega $, рассмотрим два принципиально различных случая: $u \geqslant a{\omega }$ и $u < a{\omega }$. С учетом того, что в области резонанса ${\omega } \approx 0.5p$ (расстройка частот мала) получим из (3.1) на основе (3.2) усредненные уравнения нестационарных движений:

а) $u \geqslant a{\omega }$

б) $u < a{\omega }$

где ${{{\psi }}_{ * }} = 2{\pi } - \arcsin ({u \mathord{\left/ {\vphantom {u {a{\omega })}}} \right. \kern-0em} {a{\omega })}}$, $G(a,u) = \frac{{3{{{\alpha }}_{3}}q}}{4}[{{a}^{2}}{{{\omega }}^{2}} - H(u)]$, $H(u) = 4(u_{0}^{2} - {{u}^{2}})$,

В ряде практических случаев часто представляет интерес смещение центра колебаний x₀, с учетом которого имеем $x = {{x}_{0}} + a\cos {\psi }$. Это смещение определяется из выражения

где ${{G}_{0}}(a) = \frac{1}{{2{\pi }}}\int\limits_0^{2{\pi }} {f(a\cos {\psi })} d{\psi }$

Из выражений ${\beta }(a)$ и ${{G}_{0}}(a)$ видно влияние силы упругости f(x) на них: при четной функции $f(x)$ имеем ${\beta }(a) \equiv 0$, ${{G}_{0}}(a) \ne 0$, а нечетной – ${\beta }(a) \ne 0$, ${{G}_{0}}(a) \equiv 0$. Если, например, $f(x) = {{{\gamma }}_{3}}{{x}^{3}} + {{{\gamma }}_{5}}{{x}^{5}}$, то ${\beta }(a) = \frac{{{{a}^{3}}}}{8}\left( {3{{{\gamma }}_{3}} + \frac{{5{{{\gamma }}_{5}}{{a}^{2}}}}{2}} \right)$, ${{G}_{0}}(a) \equiv 0$.

Из уравнений (3.3) и (3.4) при условиях $\dot {a} = 0$, ${\dot {\xi }} = 0$, $\dot {u} = 0$ получим уравнения стационарных движений. Решения этих уравнений позволяют найти для стационарных движений амплитуду a и скорость u, которые являются наиболее важными на практике (фаза колебаний в большинстве случаев не представляет интереса).

При $u \geqslant a{\omega }$ для определения амплитуды и фазы имеем выражения

где ${{B}_{1}} = {{B}_{1}}(a,u,{\tau }) = \frac{a}{{2m}}[G(a,u){cos\omega \tau } + k]$, ${{B}_{2}} = {{B}_{2}}(p) = \frac{{2{\lambda }}}{{m(p + 2{\omega })}}$, ${{B}_{3}} = {{B}_{3}}(p) = \frac{b}{{2mp}}$, B₄ = ${{B}_{4}}(p,a,u,{\tau }) = {\omega } - \frac{p}{2} + \frac{{{\beta }(a)}}{{{\omega }ma}} + \frac{1}{{2m}}G(a,u)sin{\omega \tau }$, $R = \frac{{{{B}_{2}} \pm \sqrt {B_{2}^{2} + 8{{a}^{2}}{{B}_{3}}({{B}_{3}} + {{B}_{4}})} }}{{4a{{B}_{3}}}}$.

В случае $u < a{\omega }$ амплитуда стационарных колебаний практически не зависит от частоты и определяется приближенным выражением aω ≈ u. Зависимость амплитуды колебаний от скорости источника энергии и частоты внешних воздействий представляет собою поверхность. Сечения этой поверхности $a(u,p)$ показаны, в частности, ниже в п. 5.

Из условия $\dot {u} = 0$ имеем для $u \geqslant a{\omega }$ и $u < a{\omega }$ уравнение общего вида

в котором

а) $u \geqslant a{\omega }$, ${{S}_{ + }}(u,{{p}_{{\text{ф }}}}) = rT(u) + \frac{3}{2}r{{{\alpha }}_{3}}qu{{{\omega }}^{2}}{{a}^{2}}$;

б) $u < a{\omega }$, ${{S}_{ - }}(u,{{p}_{{\text{ф }}}}) = rT(u) + \frac{3}{2}r{{{\alpha }}_{3}}qu{{{\omega }}^{2}}{{a}^{2}} + \frac{{rq}}{{\pi }}(3{\pi } - 2{{{\psi }}_{ * }})$.

В случае $u < a\omega $, с учетом приближенного равенства aω ≈ u для стационарной амплитуды, выражение $S(u,{{p}_{{\text{ф }}}})$ принимает простую, зависящую только от u, форму

Функция $S(u,{{p}_{{\text{ф }}}})$ представляет нагрузку на источник энергии и пересечение ее кривой с кривой $M({u \mathord{\left/ {\vphantom {u r}} \right. \kern-0em} r})$ определяет стационарные значения скорости u. График кривой $S(u,{{p}_{{\text{ф }}}})$ строится на основе вычисленных стационарных значений амплитуды. Необходимо теперь определить условия устойчивости стационарных движений.

4. Устойчивость стационарных решений. Для определения устойчивости стационарных движений составляем уравнения в вариациях и пользуемся критериями Рауса–Гурвица. Полученные таким путем критерии устойчивости имеют вид:

Коэффициенты ${{b}_{{is}}}$ (i, s = 1, 2, 3) определяются при $u \geqslant a{\omega }$ выражениями

Если, например, $f(x) = {{{\gamma }}_{3}}{{x}^{3}} + {{{\gamma }}_{5}}{{x}^{5}}$, то ${\beta '}(a) = \frac{{{{a}^{2}}}}{8}\left( {9{{{\gamma }}_{3}} + \frac{{25}}{2}{{{\gamma }}_{5}}{{a}^{2}}} \right)$.

В случае $u < a{\omega }$ изменяются лишь коэффициенты

а другие остаются в прежнем виде (как в случае $u \geqslant a{\omega }$).

С учетом того, что в области резонанса разность $p - 2{\omega }\sim {\varepsilon }$, можно принять приближенно $p + 2{\omega } \approx 4{\omega }$, вследствие чего уравнения и выражения коэффициентов ${{b}_{{is}}}$ упрощаются.

Как показано в [3–5], критерию ${{D}_{3}} > 0$ можно придать эквивалентную наглядную форму

позволяющую судить об устойчивости непосредственно по виду кривой.

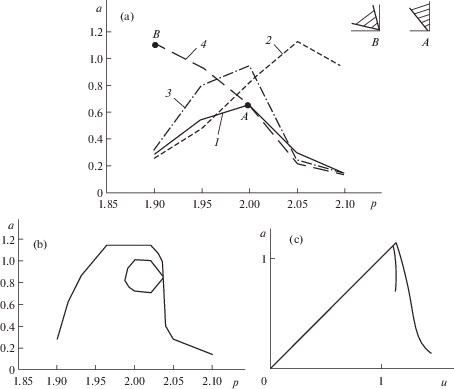
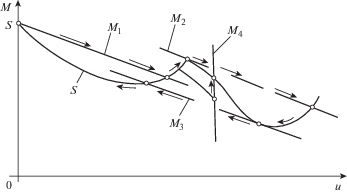
5. Результаты расчетов. Приведенные выражения достаточно сложные и не позволяют без численных расчетов получить информацию о влиянии запаздывания в силе трения на динамику системы. Чтобы получить информацию о влиянии запаздывания на амплитудно-частотно-скоростную зависимость $a(u,p)$ и устойчивость стационарных режимов были выполнены расчеты при следующих параметрах: ${\omega } = 1{{c}^{{ - 1}}}$, $m = 1$ кгс ⋅ с² ⋅ см^–1, $b = 0.07$ кгс ⋅ см^–1, ${\lambda } = 0.02$ кгс, $k = 0.02$ кгс ⋅ с ⋅ см^–1, $q = 0.5$ кгс, ${{{\alpha }}_{1}} = 0.84$ c · см^–1, ${{{\alpha }}_{3}} = 0.18$ с³ ⋅ см^–3, r = 1 см, I = 1 кгс ⋅ с ⋅ см². Показанные на фиг. 2 и фиг. 3 зависимости получены при $f(x) \equiv 0$. На фиг. 2,а представлены зависимости амплитуды колебаний от частоты при u = 1.26 и различных значениях запаздывания: кривая 1 (τ = 0), кривая 2 (τ = π/2), кривая 3 (τ = π), кривая 4 (τ = 3π /2). Графики представлены в виде кусочно-линейных из-за небольшого числа расчетных точек, обусловленных большой трудоемкостью расчета выражений, хотя должны быть на самом деле гладкими. Показанный на фиг. 2,b график имеет место для u = 1.14, τ = 0, а фиг. 2,с отражает зависимость амплитуды от скорости u при p = 2, τ = 0. Фиг. 2,b показывает интересный, многозначный в узкой области частот вид амплитудной кривой. Устойчивость колебаний с какой-либо амплитудой в указанных на графиках диапазонах частот зависит от крутизны характеристики источника энергии, выраженной величиной N. Колебания устойчивы в пределах заштрихованных секторов для N (точка А относится к кривой 1), хотя эти секторы должны быть указаны на самом деле на кривой нагрузки $S(u,{{p}_{{\text{ф }}}})$. Поскольку нагрузка $S(u,{{p}_{{\text{ф }}}})$ зависит от амплитуды колебаний, то ее форма зависит от формы амплитудной кривой. Представленная на фиг. 3 кривая $S(u,{{p}_{{\text{ф }}}})$ соответствует амплитудной кривой, показанной на фиг. 2,с. При изменении скорости (увеличении, уменьшении) источника энергии u посредством перемещения характеристики $M({u \mathord{\left/ {\vphantom {u r}} \right. \kern-0em} r})$ в системе проявляются различного характера переходы из одного состояния в другое, показанные стрелками. Такого рода переходы при отсутствии запаздывания в силе трения подробно описаны в [4, 5] и имеют место также при его наличии. Поэтому их описание здесь не приводится во избежание повторения.

В заключение отметим, что здесь представлены не все результаты проведенных расчетов и анализа. Они показывают многообразие явлений, которые могут быть обусловлены взаимодействием сил в источнике энергии и сил трения с запаздыванием.