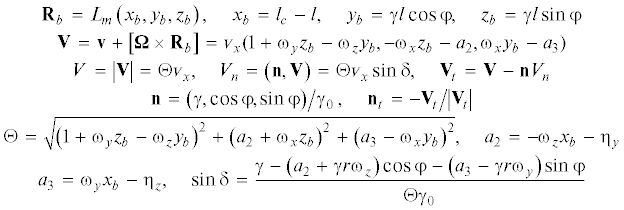1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 2, 2019

Известия РАН. Механика твердого тела, 2019, № 2, стр. 85-92

УСТОЙЧИВОСТЬ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ КОНУСА, ВРАЩАЮЩЕГОСЯ ВОКРУГ ОСИ СИММЕТРИИ

К. Ю. Осипенко *

Институт проблем механики им. А.Ю. Ишлинского РАН, Национальный исследовательский Московский государственный строительный университет
Москва, Россия

* E-mail: kirill-o@mail.ru

Поступила в редакцию 12.10.2017
После доработки 12.10.2017
Принята к публикации 08.11.2017

Полный текст (PDF)

Аннотация

Изучается влияние постоянного трения на устойчивость прямолинейного движения конуса, вращающегося вокруг оси симметрии. Предполагается, что боковая поверхность конуса обтекается безотрывно и на этой поверхности действуют нормальные напряжения и трение, которые определяются по методу локального взаимодействия. Нормальные контактные напряжения принимаются пропорциональными квадрату нормальной составляющей скорости, а трение считается постоянным по модулю и действующим в направлении обратном проекции вектора скорости на касательную плоскость. При замороженных скорости движения центра масс и угловой скорости вращения вокруг оси симметрии получены критерии асимптотической устойчивости в виде системы двух неравенств, не содержащей интегралов. Подробно изучено влияние трения на устойчивость прямолинейного движения однородного конуса.

Ключевые слова: проникание, траектория, вращение вокруг оси симметрии, устойчивость

1. Введение. В ряде работ [1–3] авторы изучали влияние вращения вокруг оси симметрии на глубину проникания осесимметричного тела в упругопластическую среду, а также оптимизацию формы вращающегося тела. Контактные напряжения в этих работах определялись на основе метода локального взаимодействия, а изменение глубины проникания происходит за счет того, что трение на боковой поверхности тела изменяет свое направление из-за вращения и его проекция на ось симметрии уменьшается. Однако эти результаты справедливы только при условии, что прямолинейное движение вращающегося тела является устойчивым, поэтому изучение влияния вращения на устойчивость при действии на боковой поверхности тела нормальных напряжений и трения является важным для практических приложений.

В общем виде эта задача рассматривалась в работах [4–8]. Исследовалась асимптотическая устойчивость прямолинейного движения с постоянной скоростью тела при отсутствии его вращения вокруг оси симметрии [4–7] и получены критерии асимптотической устойчивости тела, вращающегося вокруг оси симметрии [8]. Для вращающегося тела были получены критерии устойчивости, зависящие от интегралов по длине тела. В случае однородного конуса, на поверхности которого действуют только нормальные напряжения, зависящие от квадрата нормальной составляющей скорости (инерционное сопротивление), а трение отсутствует, критерии асимптотической устойчивости удалось свести к двум алгебраическим неравенствам и подробно исследовать его устойчивость [8]. Оказалось, что в этом случае вращение повышает устойчивость прямолинейного движения конуса. Однако влияние трения на устойчивость вращающегося тела в этих работах исследовано не было.

В данной работе изучается влияние трения на устойчивость прямолинейного движения с постоянной скоростью конуса при действии на его поверхности инерционных нормальных напряжений и постоянного (пластического) трения. В этом случае удалось свести критерии асимптотической устойчивости к системе, не содержащей интегралов. Для случая однородного конуса был проведен расчет областей параметров, при которых его прямолинейное движение будет устойчиво. Расчеты показали, что при наличии трения вращение конуса вокруг оси симметрии может приводить к потере его устойчивости. Дальнейшее увеличение угловой скорости вращения вновь повышает устойчивость конуса, однако придание быстрого вращения не всегда технически осуществимо.

2. Постановка задачи. Круговой конус массы m, длины ${{L}_{m}}$ и тангенса угла полураствора $\gamma $ движется по инерции в безграничной среде. Главный момент инерции конуса при поперечном вращении ${{I}_{2}}$, а моментом инерции относительно оси симметрии ${{I}_{1}}$. Центр масс конуса расположен на оси его симметрии на расстоянии ${{L}_{c}}$ от вершины.

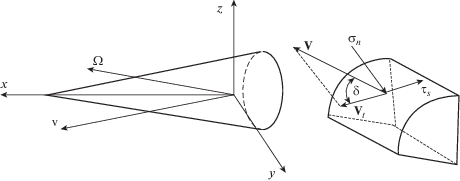
Введем системы координат $\left\{ {R\varphi L} \right\}$ и $\left\{ {xyz} \right\}$, связанные с конусом. В цилиндрической системе координат $\left\{ {R\varphi L} \right\}$ боковая поверхность конуса задается выражениями ${{R}_{b}} = \gamma L,0 \leqslant \varphi \leqslant 2\pi ,0 \leqslant L \leqslant {{L}_{m}}$. Начало прямоугольной системы координат $\left\{ {xyz} \right\}$ поместим в центр масс конуса: $x{{L}_{m}} = {{L}_{c}} - L$, $y{{L}_{m}} = R\cos \varphi $, $z{{L}_{m}} = R\sin \varphi $. Движение конуса в системе координат $\left\{ {xyz} \right\}$ определяется вектором скорости ${\mathbf{v}} = \left( {{{v}_{x}},{{v}_{y}},{{v}_{z}}} \right)$ центра масс и вектором угловой скорости вращения относительно центра масс Ω = = $({{\Omega }_{x}},{{\Omega }_{y}},{{\Omega }_{z}})$ (фиг. 1).

Фиг. 1

Введем безразмерные величины

$\begin{gathered} r = \gamma l,\quad l = \frac{L}{{{{L}_{m}}}},\quad {{l}_{c}} = \frac{{{{L}_{c}}}}{{{{L}_{m}}}},\quad {{\gamma }_{0}} = \sqrt {1 + {{\gamma }^{2}}} ,\quad {{\eta }_{y}} = \frac{{{{v}_{y}}}}{{{{v}_{x}}}},\quad {{\eta }_{z}} = \frac{{{{v}_{z}}}}{{{{v}_{x}}}} \\ {{\omega }_{x}} = \frac{{{{L}_{m}}{{\Omega }_{x}}}}{{{{v}_{x}}}},\quad {{\omega }_{y}} = \frac{{{{L}_{m}}{{\Omega }_{y}}}}{{{{v}_{x}}}},\quad {{\omega }_{z}} = \frac{{{{L}_{m}}{{\Omega }_{z}}}}{{{{v}_{x}}}} \\ \end{gathered} $

Выражения для внешней нормали, проекций вектора скорости ${\mathbf{V}}$ произвольной точки на поверхности тела на нормаль и на касательную плоскость в системе координат $\left\{ {xyz} \right\}$ даются формулами

Вектор напряжений на боковой поверхности конуса зададим в виде суммы касательных и нормальных напряжений: ${\mathbf{\Sigma }} = {{\tau }_{s}}{{{\mathbf{n}}}_{t}} - {{\sigma }_{n}}{\mathbf{n}}$, где ${{\tau }_{s}}$ – постоянное по модулю касательное напряжение (пластическое трение), ${{{\mathbf{n}}}_{t}}$ – единичный касательный вектор в направлении скольжения; ${{\sigma }_{n}}$ – контактное давление

(2.1)
${{\tau }_{s}} = {\text{const}},\quad {{\sigma }_{n}} = \frac{{{{\rho }_{0}}{{C}_{f}}V_{n}^{2}}}{2} = \frac{{mv_{x}^{2}\sigma }}{{L_{m}^{3}}},\quad \sigma = \frac{{L_{m}^{3}{{\rho }_{0}}{{C}_{f}}}}{{2m}}{{\Theta }^{2}}{{\sin }^{2}}\delta $

Здесь ${{\rho }_{0}}$ – плотность среды, ${{С }_{f}} = {\text{const}}$. На основании конуса напряжения отсутствуют. Запишем выражения для результирующей силы и момента, действующих на конус в системе координат $\left\{ {xyz} \right\}$:

$\begin{gathered} {\mathbf{F}} = \left( {{{F}_{x}},{{F}_{y}},{{F}_{z}}} \right) = L_{m}^{2}\gamma {{\gamma }_{0}}\int\limits_0^1 {\int\limits_0^{2\pi } {l{\mathbf{\Sigma }}d\varphi dl} } \\ {\mathbf{M}} = \left( {{{M}_{x}},{{M}_{y}},{{M}_{z}}} \right) = L_{m}^{2}\gamma {{\gamma }_{0}}\int\limits_0^1 {\int\limits_0^{2\pi } {\left[ {{{{\mathbf{R}}}_{b}} \times {\mathbf{\Sigma }}} \right]ld\varphi dl} } \\ \end{gathered} $

Система дифференциальных уравнений движения жесткого тела вращения в системе координат $\left\{ {xyz} \right\}$ записывается в следующем виде [8, 9]:

(2.2)
$\begin{gathered} m({{{\dot {v}}}_{x}} + {{\Omega }_{y}}{{v}_{z}} - {{\Omega }_{z}}{{v}_{y}}) = {{F}_{x}},\quad m({{{\dot {v}}}_{y}} + {{\Omega }_{z}}{{v}_{x}} - {{\Omega }_{x}}{{v}_{z}}) = {{F}_{y}} \\ m\left( {{{{\dot {v}}}_{z}} + {{\Omega }_{x}}{{v}_{y}} - {{\Omega }_{y}}{{v}_{x}}} \right) = {{F}_{z}},\quad {{I}_{1}}{{{\dot {\Omega }}}_{x}} = {{M}_{x}},\quad {{I}_{2}}{{{\dot {\Omega }}}_{y}} + \left( {{{I}_{1}} - {{I}_{2}}} \right){{\Omega }_{z}}{{\Omega }_{x}} = {{M}_{y}} \\ {{I}_{2}}{{{\dot {\Omega }}}_{z}} + \left( {{{I}_{1}} - {{I}_{2}}} \right){{\Omega }_{x}}{{\Omega }_{y}} = {{M}_{z}},\quad \left( {{\mathbf{v}},{\mathbf{W}}} \right) = \left( {{{{\mathbf{v}}}_{{\mathbf{0}}}},{{{\mathbf{W}}}_{{\mathbf{0}}}}} \right)\quad {\text{п р и }}\quad t = 0,\quad {{(}^{\centerdot }}) = {d \mathord{\left/ {\vphantom {d {dt}}} \right. \kern-0em} {dt}} \\ \end{gathered} $

В случае малых возмущений относительно прямолинейного движения $({{\eta }_{y}} \ll 1,$ ${{\eta }_{z}} \ll 1,{{\omega }_{y}} \ll 1,{{\omega }_{z}} \ll 1)$, замороженных скорости движения центра масс и угловой скорости вращения вокруг оси симметрии, систему дифференциальных уравнений (2.2) можно линеаризовать и получить критерии асимптотической устойчивости прямолинейного движения. Для тела вращения эти критерии имеют следующий вид [8]:

(2.3)
${{D}_{1}} > 0,\quad {{D}_{1}}{{D}_{2}} - {{D}_{3}} > 0,\quad \left( {{{D}_{1}}{{D}_{2}} - {{D}_{3}}} \right){{D}_{3}} - D_{1}^{2}{{D}_{4}} > 0$
где

(2.4)
$\begin{gathered} {{D}_{1}} = - 2\left( {{{B}_{1}} + {{B}_{7}}} \right) \\ {{D}_{2}} = B_{1}^{2} + B_{2}^{2} + B_{7}^{2} + B_{8}^{2} + 4{{B}_{1}}{{B}_{7}} - 2{{B}_{4}}{{B}_{6}} - 2{{B}_{3}}{{B}_{5}} \\ {{D}_{3}} = 2[\left( {{{B}_{1}}{{B}_{3}} - {{B}_{2}}{{B}_{4}}} \right){{B}_{5}} - {{B}_{1}}(B_{7}^{2} + B_{8}^{2}) - (B_{1}^{2} + B_{2}^{2}){{B}_{7}} - \\ - \;{{B}_{4}}\left( {{{B}_{5}}{{B}_{8}} - {{B}_{6}}{{B}_{7}}} \right) + \left. {\left( {{{B}_{1}}{{B}_{4}} + {{B}_{2}}{{B}_{3}}} \right){{B}_{6}} + {{B}_{3}}\left( {{{B}_{6}}{{B}_{8}} + {{B}_{5}}{{B}_{7}}} \right)} \right] \\ {{D}_{4}} = {{\left( {{{B}_{1}}{{B}_{7}} - {{B}_{4}}{{B}_{6}} - {{B}_{2}}{{B}_{8}} - {{B}_{3}}{{B}_{5}}} \right)}^{2}} + {{\left( {{{B}_{1}}{{B}_{8}} + {{B}_{2}}{{B}_{7}} - {{B}_{3}}{{B}_{6}} + {{B}_{4}}{{B}_{5}}} \right)}^{2}} \\ \end{gathered} $

Выражения для ${{B}_{1}},{{B}_{2}},\; \ldots ,\;{{B}_{8}}$ в общем случае тела вращения, на боковой поверхности которого действует трение и нормальные напряжения, задаваемые по методу локального взаимодействия, приведены в [8] и имеют громоздкий вид. Однако в случае конуса, пластического трения и зависимости $\sigma $ от $\Theta ,\delta $, задаваемой (2.1), эти выражения могут быть существенно упрощены и приведены к следующему виду

(2.5)
$\begin{gathered} {{B}_{1}} = - \pi \kappa \gamma \gamma _{0}^{2}({{J}_{1}} + \omega _{x}^{2}{{\gamma }^{4}}{{J}_{3}}) - \frac{{\pi G}}{{\gamma _{0}^{2}}},\quad {{B}_{2}} = {{\omega }_{x}},\quad {{B}_{3}} = - \pi \kappa {{\omega }_{x}}{{\gamma }^{3}}\gamma _{0}^{2}{{J}_{3}}, \\ {{B}_{4}} = \pi \kappa \gamma \gamma _{0}^{2}({{l}_{c}}{{J}_{1}} - {{J}_{2}} + \omega _{x}^{2}{{\gamma }^{4}}{{l}_{c}}{{J}_{3}}) + \frac{{\pi G}}{{3\gamma _{0}^{2}}}[3{{l}_{c}} - 2\gamma _{0}^{2}] + 1, \\ {{B}_{5}} = - \pi {{j}_{2}}\kappa {{\omega }_{x}}{{\gamma }^{3}}\gamma _{0}^{2}{{J}_{3}}, \\ {{B}_{6}} = \pi {{j}_{2}}\kappa \gamma \gamma _{0}^{2}[{{l}_{c}}{{J}_{1}} - {{J}_{2}} + \omega _{x}^{2}{{\gamma }^{4}}{{l}_{c}}{{J}_{3}}] + \frac{{\pi {{j}_{2}}G}}{{3\gamma _{0}^{2}}}[3{{l}_{c}} - 2\gamma _{0}^{2}], \\ {{B}_{7}} = - \pi {{j}_{2}}\kappa \gamma \gamma _{0}^{2}[l_{c}^{2}{{J}_{1}} - 2{{l}_{c}}{{J}_{2}} + (1 + \omega _{x}^{2}{{\gamma }^{4}}l_{c}^{2}){{J}_{3}}] - \frac{{\pi {{j}_{2}}G}}{{6\gamma _{0}^{2}}}[6l_{c}^{2} - 8\gamma _{0}^{2}{{l}_{c}} + 3\gamma _{0}^{4}] \\ {{B}_{8}} = \left( {1 - \frac{{{{j}_{2}}}}{{{{j}_{1}}}}} \right){{\omega }_{x}} \\ \end{gathered} $

Здесь введены безразмерные величины

$\kappa = \frac{{L_{m}^{3}{{\tau }_{s}}}}{{mv_{x}^{2}}},\quad {{j}_{1}} = \frac{{L_{m}^{2}m}}{{{{I}_{1}}}},\quad {{j}_{2}} = \frac{{L_{m}^{2}m}}{{{{I}_{2}}}},\quad G = \frac{{{{C}_{f}}L_{m}^{3}{{\rho }_{0}}{{\gamma }^{2}}}}{{2m}}$
$\begin{gathered} {{J}_{0}} = \int\limits_0^1 {\frac{{dl}}{{{{{(1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}{{l}^{2}})}}^{{\frac{3}{2}}}}}}} ,\quad {{J}_{1}} = \int\limits_0^1 {\frac{{ldl}}{{{{{(1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}{{l}^{2}})}}^{{\frac{3}{2}}}}}}} , \\ {{J}_{2}} = \int\limits_0^1 {\frac{{{{l}^{2}}dl}}{{{{{(1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}{{l}^{2}})}}^{{\frac{3}{2}}}}}}} ,\quad {{J}_{3}} = \int\limits_0^1 {\frac{{{{l}^{3}}dl}}{{{{{(1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}{{l}^{2}})}}^{{\frac{3}{2}}}}}}} \\ \end{gathered} $

Интегралы ${{J}_{1}}$ и ${{J}_{2}}$ больше нуля, поэтому ${{B}_{1}} < 0$. Подставив интегралы ${{J}_{1}}$, ${{J}_{2}}$, ${{J}_{3}}$ в выражение для ${{B}_{7}}$, получим

$\begin{gathered} {{B}_{7}} = - \pi {{j}_{2}}\kappa \gamma \gamma _{0}^{2}\left[ {\int\limits_0^1 {\frac{{{{{(l_{c}^{2} - l)}}^{2}}ldl}}{{{{{(1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}{{l}^{2}})}}^{{\frac{3}{2}}}}}}} + \omega _{x}^{2}{{\gamma }^{4}}l_{c}^{2}\int\limits_0^1 {\frac{{{{l}^{3}}dl}}{{{{{(1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}{{l}^{2}})}}^{{\frac{3}{2}}}}}}} } \right] - \\ - \;\frac{{\pi {{j}_{2}}G}}{{2\gamma _{0}^{2}}}\left[ {{{{(\sqrt 2 {{l}_{с }} - \gamma _{0}^{2})}}^{2}} + \left( {2\sqrt 2 - \frac{8}{3}} \right)\gamma _{0}^{2}{{l}_{c}}} \right] \\ \end{gathered} $

Из последней формулы видно, что ${{B}_{7}} < 0$. Следовательно, первое неравенство в (2.3) выполняется всегда и критерии асимптотической устойчивости прямолинейного движения конуса сводятся к двум неравенствам

(2.6)
${{D}_{1}}{{D}_{2}} - {{D}_{3}} > 0,\quad \left( {{{D}_{1}}{{D}_{2}} - {{D}_{3}}} \right){{D}_{3}} - D_{1}^{2}{{D}_{4}} > 0$

Интегралы ${{J}_{0}},{{J}_{1}},{{J}_{2}},{{J}_{3}}$ вычисляются аналитически

(2.7)
$\begin{gathered} {{J}_{0}} = \frac{1}{{\sqrt {1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}} }},\quad {{J}_{1}} = \frac{{ - 1}}{{\omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}\sqrt {1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}} }} + \frac{1}{{\omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}}} \\ {{J}_{2}} = \frac{{ - 1}}{{\omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}\sqrt {1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}} }} + \frac{1}{{\omega _{x}^{3}{{\gamma }^{3}}\gamma _{0}^{3}}}\ln [\sqrt {1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}} + \gamma {{\gamma }_{0}}\sqrt {\omega _{x}^{2}} ] \\ {{J}_{3}} = \frac{{ - 1}}{{\omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}\sqrt {1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}} }} + \frac{{2\sqrt {1 + \omega _{x}^{2}{{\gamma }^{2}}\gamma _{0}^{2}} }}{{\omega _{x}^{4}{{\gamma }^{4}}\gamma _{0}^{4}}} - \frac{2}{{\omega _{x}^{4}{{\gamma }^{4}}\gamma _{0}^{4}}} \\ \end{gathered} $

Таким образом, в случае конуса, инерционных нормальных напряжениях и пластическом трении критерии асимптотической устойчивости сводятся к системе двух неравенств (2.6), не содержащей интегралов.

3. Области устойчивого движения. Рассмотрим подробнее случай однородного конуса

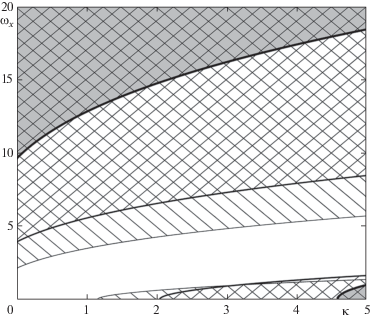
${{l}_{c}} = {3 \mathord{\left/ {\vphantom {3 4}} \right. \kern-0em} 4},\quad {{j}_{1}} = \frac{{10}}{{3{{\gamma }^{2}}}},\quad {{j}_{2}} = \frac{{80}}{{(1 + 4{{\gamma }^{2}})}}$

Расчет областей параметров $\gamma ,G,\kappa ,{{\omega }_{x}}$, в которых прямолинейное движение однородного конуса при замороженной скорости движения центра масс будет асимптотически устойчивым, проводился по формулам (2.4)–(2.7) в системе компьютерной математики GNU Octave. Для случая, когда на боковой поверхности конуса действуют только касательные напряжения, а нормальные напряжения отсутствуют $({{\sigma }_{n}} = G$ = 0), на фиг. 2 показаны области параметров $\kappa ,{{\omega }_{x}}$, при которых движение конуса будет асимптотически устойчивым. Области устойчивости для конусов $\gamma = 0.2,0.4$, 0.6 показаны на фиг. 2 затемнением, правой штриховкой (линии штриховки нанесены с наклоном вправо под углом 45°) и левой штриховкой (линии штриховки нанесены с наклоном влево под углом 45°) соответственно. Из фиг. 2 видно, что вращение конуса вокруг оси симметрии может приводить к потере его устойчивости. Однако дальнейшее увеличение ${{\omega }_{x}}$ снова делает его устойчивым. Если $G = 0$ и вращающийся конус движется устойчиво, то увеличивая $\kappa $ (увеличивая ${{\tau }_{s}}$ или уменьшая скорость) его можно сделать неустойчивым. Из фиг. 2 видно, что верхняя граница области неустойчивости при $G = 0$, $\kappa \to 0$ стремится к конечному значению ${{\omega }_{x}}$. Этот результат оказался неожиданным, так как в [8] показано, что при $\kappa = 0$ $G \to 0$ верхняя граница области неустойчивости стремится к значению ${{\omega }_{x}} = 0$.

Фиг. 2

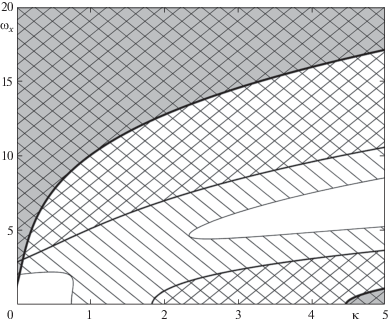
На фиг. 3 показаны области параметров $\kappa ,{{\omega }_{x}}$, при которых движение однородного конуса $\gamma = 0.2$ будет устойчивым при действии на боковой поверхности трения и нормальных напряжений. Области устойчивости для случаев $G = 0.01,0.2,0.27$ показаны на фиг. 3 затемнением, правой штриховкой и левой штриховкой соответственно. Из фиг. 3 видно, что с ростом $G$ (с увеличением нормальных напряжений или уменьшением плотности конуса) диапазон значений ${{\omega }_{x}}$, при которых конус движется устойчиво, в большинстве случаев увеличивается, однако при малом $\kappa $ увеличение $G$ может приводить к потере устойчивости. При $G \ne 0$ сделать устойчивый вращающийся конус неустойчивым путем увеличения $\kappa $ возможно уже не всегда, а только при достаточно больших ${{\omega }_{x}}$.

Фиг. 3

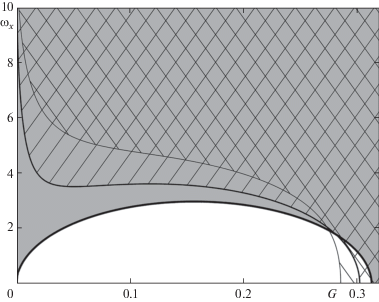
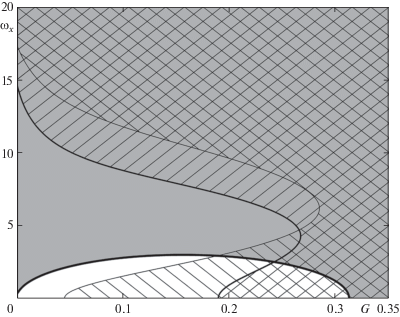
На фиг. 4, 5 показаны области параметров $G,{{\omega }_{x}}$ при которых движение однородного конуса $\gamma = 0.2$ будет устойчивым. Области устойчивости для случаев $\kappa = 0,0.2,0.5$ показаны на фиг. 4 затемнением, правой штриховкой и левой штриховкой соответственно. Области устойчивости для случаев $\kappa = 0,2,4$ показаны на фиг. 5 затемнением, правой штриховкой и левой штриховкой соответственно. Из фиг 4, 5 видно, что при малом $G$ области устойчивости для случаев $\kappa = 0$ и $\kappa \ne 0$ различаются очень сильно. При малом $G$ появление даже небольших $\kappa $ (малое трение или большая скорость) приводит к существенному уменьшению области параметров, при которых прямолинейное движение конуса при замороженной скорости центра масс является устойчивым.

Фиг. 4
Фиг. 5

4. Заключение. При замороженных скорости движения центра масс и угловой скорости вращения вокруг оси симметрии влияние пластического трения на асимптотическую устойчивость прямолинейного движения однородного конуса является неоднозначным. При отсутствии вращения вокруг оси симметрии рост трения приводит к увеличению области параметров, при которых движение конуса является устойчивым, а в случае вращения вокруг оси симметрии появление трения может приводить к потере устойчивости.

Работа выполнена по теме Госзадания (номер госрегистрации АААА-А17-117021310380-1) и при частичной финансовой поддержке Российским фондом фундаментальных исследований (проект № 17-08-00775a).

Список литературы

  1. Симонов И.В. О качественных особенностях движения осесимметричного твердого тела с вращением в упругопластической среде // Докл. АН. 2006. Т. 411. № 4. С. 480–484.

  2. Баничук Н.В., Иванова С.Ю. О поступательном движении с вращением жестких осесимметричных тел в упругопластических средах. Актуальные проблемы механики. 50 лет Институту проблем механики им. А.Ю. Ишлинского РАН. М: Наука 2015 г. С. 393–405.

  3. Баничук Н.В., Иванова С.Ю. Оптимизация формы затупленных осесимметричных тел, движущихся поступательно с вращением в упругопластической среде // Проблемы прочности и пластичности. 2015. Т. 77. № 4. С. 367–378.

  4. Симонов И.В. Об устойчивости движения удлиненного тела вращения в упругопластической среде при отрыве потока // ПММ. 2000. Т. 64. Вып. 2. С. 313–322.

  5. Осипенко К.Ю. Об устойчивости пространственного движения тела вращения в упругопластической среде // Изв. РАН. МТТ. 2012. № 2. С. 68–77.

  6. Якунина Г.Е. Особенности высокоскоростного движения тел в плотных средах // ПММ. 2012. Т. 76. Вып. 3. С. 429–449.

  7. Митенков Ф.М., Баженов В.Г., Котов В.Л., Тарасова А.А. Численно-аналитический метод исследования устойчивости осесимметричного движения тел вращения в грунтовых средах // Докл. АН. 2016. Т. 470. № 5. С. 531–535.

  8. Осипенко К.Ю. Устойчивость пространственного движения тела при учете отрыва потока и вращения вокруг оси симметрии // Изв. РАН МТТ № 4. 2016. С. 153–165.

  9. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Т. 2. М.: Наука, 1983. 640 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал