Известия РАН. Механика твердого тела, 2019, № 2, стр. 63-71
К ТЕОРИИ ЗВУКОВЫХ БАРЬЕРОВ: ДИФРАКЦИЯ ПЛОСКИХ, ЦИЛИНДРИЧЕСКИХ И СФЕРИЧЕСКИХ ВОЛН НА “ТВЕРДО-МЯГКОЙ” ПОЛУПЛОСКОСТИ
М. Ш. Исраилов *
Комплексный научно-исследовательский институт РАН
Грозный, Россия
* E-mail: israiler@hotmail.com
Поступила в редакцию 28.09.2017
После доработки 28.09.2017
Принята к публикации 18.10.2017
Аннотация
При проектировании звуковых барьеров важное значение имеет выяснение вопросов о целесообразности частичного или полного покрытия поверхности барьера абсорбентом или конструирования барьеров с рассеивающими звук поверхностями. Исследование указанных прикладных проблем для плоских барьеров приводит к необходимости постановки и решения задач дифракции звуковых волн на полуплоскости с разнотипными (неодинаковыми) граничными условиями на сторонах полуплоскости. Решение таких задач традиционными методами существенно усложняется в сравнении с рассмотрениями аналогичных задач для однотипных краевых условий на всей границе рассеивающего тела и приводит зачастую к труднообозримым результатам.
В работе предложены простые способы решения задач дифракции акустических волн на полуплоскости с краевыми условиями Неймана на одной стороне полуплоскости и Дирихле – на другой. Для плоских падающих волн способ основан на применении метода разделения переменных с последующим суммированием рядов Фурье–Бесселя. В случае цилиндрических и сферических волн способ решения состоит в использовании полученных результатов для плоских волн в сочетании с методом геометрической теории дифракции Келлера.
Получены новые аналитические решения задач дифракции плоских, цилиндрических и сферических волн на твердо-мягкой полуплоскости, справедливые во всей области дифракции или в дальней зоне, на больших расстояниях от ребра барьера. Эти решения той же “простоты”, что и соответствующие решения для однотипных краевых условий, что делает их удобными при сравнительном анализе в приложениях к звуковым барьерам.
1. Дифракция плоских звуковых волн. Впервые задача дифракции плоских звуковых волн на полуплоскости при разных краевых условиях на ее сторонах (Неймана на одной стороне полуплоскости и Дирихле – на другой) рассмотрена А.Д. Роулинзом [1], который использовал для ее решения метод Винера–Хопфа (традиционно применяемый в задачах рассеяния волн на плоских препятствиях). Однако, в отличие от случаев с однотипными (одинаковыми) краевыми условиями на сторонах полуплоскости, здесь метод приводит не к одному, а к системе (двух) функциональных уравнений и к необходимости факторизации матрицы 2 × 2 с элементами в виде аналитических функций, что сильно усложняет реализацию метода. В результате, в обозримом виде удалось получить только асимптотическое представление решения в дальней зоне, справедливое на расстояниях от ребра полуплоскости, значительно превышающих длину звуковой волны.
В работе [2] нами предложен существенно более простой метод решения этой задачи, приводящий к аналитическому решению одинаково эффективному во всей области дифракции – как в ближней зоне (на конечных расстояниях и вблизи ребра), так и на больших (в сравнении с длиной волны) расстояниях от полуплоскости. Начав с постановки задачи, изложим вкратце суть метода и приведем некоторые новые решения, относящиеся к случаю плоских падающих волн. Эти результаты необходимы в последующих пунктах для построения решений задач дифракции цилиндрических и сферических волн на полуплоскости в аналогичной постановке.
Избыточное давление p в газе (воздухе) или идеальной сжимаемой жидкости, возникающее из-за возмущений в дополнение к давлению в среде в состоянии покоя, удовлетворяет в линейном (акустическом) приближении волновому уравнению или следующему уравнению Гельмгольца
в случае стационарных движений с гармоническим законом изменения по времени t: $p = P(x,y,z)\exp ( - i{\omega }t)$. В уравнении (1.1) $\Delta $ есть оператор Лапласа, а волновое число k связано с частотой $\omega $ соотношением $k = \omega {\text{/}}c$, в котором $c$ – скорость звука в газе.Тому же уравнению (1.1) удовлетворяет и потенциал скоростей частиц среды Φ = = $ - iP{\text{/}}(\omega {{\rho }_{0}})$; ${{\rho }_{0}}$ – плотность среды в состоянии покоя.
Пусть полуплоскость, вставленная в среду (барьер), является частью координатной плоскости и описывается в декартовой системе координат соотношениями $y = 0,$ x > 0, $ - \infty < z < + \infty $. На полуплоскость набегает плоская звуковая волна pi = = ${{P}^{i}}(x,y){\text{exp}}( - i\omega t)$, в которой компонента скорости $\text{v}_{z}^{i} = 0$ и плоскость равной фазы параллельна ребру барьера. Тогда движение в среде является плоским (${{\text{v}}_{z}} \equiv 0$) и давление P, а также потенциал скоростей $\Phi $ зависят только от координат $(x,y)$ или $(r,\theta )$, если в плоскости $z = {\text{const}}$ введены полярные координаты.
В соответствии со сказанным, падающая волна может быть задана в виде
и есть плоская волна, образующая угол ${{\theta }_{0}}$ с барьером.Предположим, что сторона барьера θ = 0 является идеально отражающей звук (акустически “твердой”), а сторона $\theta = 2\pi $ – полностью поглощающей звук (акустически “мягкой”). Эти условия сводятся, соответственно, к однородным условиям Неймана и Дирихле для полного давления P на сторонах полуплоскости, т.е. к условиям
(1.3)
$\partial P{\text{/}}\partial \theta = 0\quad {\text{п р и }}\quad \theta = 0\quad {\text{и }}\quad P = 0\quad {\text{п р и }}\quad \theta = 2\pi $Поскольку рассеивающее падающую волну тело (полуплоскость) имеет угловую точку, то для обеспечения единственности решения необходимо выполнение “условий на ребре”; вывод их для акустической среды дан, например, в монографии [3]. Полученные в [3] условия (формулы 5.2.3) могут быть в случае стационарной задачи записаны в следующей эквивалентной форме: единственность решения обеспечивается когда
где C – константа.Наконец, решение стационарной динамической задачи должно удовлетворять условию излучения на бесконечности. Чтобы правильно сформулировать это условие в случае наличия границ, простирающихся до бесконечности, нужно выделить из решения падающую волну и все отраженные волны, которые не обязаны удовлетворять условию излучения. Представим $P$ в виде суммы падающей $({{P}^{i}})$, отраженной $({{P}^{r}})$ и дифрагированной $({{P}^{d}})$ волн, то есть в виде
Тогда для обеспечения единственности решения функция ${{P}^{d}}$ должна удовлетворять в рассматриваемом двумерном случае следующему условию излучения на бесконечности
(1.6)
$\mathop {\lim }\limits_{r \to \infty } {{r}^{{1/2}}}(\partial {{P}^{d}}{\text{/}}\partial r - ik{{P}^{d}}) = 0$Пусть в уравнении плоской волны (1.2) $0 < {{\theta }_{0}} \leqslant \pi $. Это означает, в соответствии с граничными условиями (1.3), что освещенная сторона $\theta = 0$ барьера является акустически “твердой”. Поскольку отраженная волна от стороны полуплоскости (на которой должно выполняться однородное краевое условие Неймана) элементарно определяется, то для суммы падающей и отраженной волн ${{P}_{0}} \equiv {{P}^{i}} + {{P}^{r}}$ имеем (эта часть решения называется “решением геометрической оптики”).
(1.7)
${{P}_{0}} = \left\{ {\begin{array}{*{20}{l}} {\exp \left[ { - ikr\cos (\theta - {{\theta }_{0}})} \right] + \exp \left[ { - ikr\cos (\theta + {{\theta }_{0}})} \right],\quad 0 < \theta < \pi - {{\theta }_{0}}} \\ {\exp \left[ { - ikr\cos (\theta - {{\theta }_{0}})} \right],\quad \pi - {{\theta }_{0}} < \theta < \pi + {{\theta }_{0}}} \\ {0,\quad \pi + {{\theta }_{0}} < \theta < 2\pi } \end{array}} \right.$Видно, что решение геометрической оптики (1.7) имеет разрывы на линиях, разделяющих области: теневую, освещенную одной падающей волной и освещенную падающей и отраженной волнами. Таким образом, задача сводится к нахождению дифрагированной волны ${{P}^{d}}$, компенсирующей эти разрывы. Простой путь построения решения задачи (1.1)–(1.6), предложенный в [2], состоит в использовании метода Фурье. Легко показывается, что ряд
(1.8)
$P(r,\theta ) \equiv {{P}_{0}} + {{P}^{d}} = \frac{1}{\pi }\sum\limits_{n = 0}^\infty {{{a}_{n}}{{J}_{{l(n)/2}}}(kr)\cos \frac{{l(n)\theta }}{2}} $(1.9)
$P(r,\theta ) = 2\sum\limits_{n = 0}^\infty {\exp \left( { - il(n)\pi {\text{/}}4} \right)} {{J}_{{l(n)/2}}}(kr)\cos \left[ {l(n){{\theta }_{0}}{\text{/}}2} \right]\cos \left[ {l(n)\theta {\text{/}}2} \right]$Ряд (1.9) удобен для вычисления поля при конечных kr, в частности, для исследования поведения поля вблизи ребра барьера. Но он может быть и просуммирован по способу, развитому в [2] и использующему известное представление бесселевой функции в виде интеграла по петлеобразному контуру, обходящему начало координат (точку r = 0). Тогда решение (1.9) приобретает конечную аналитическую форму, выражаясь через сумму двух интегралов:
Сумма внеинтегральных членов в (1.10) совпадает с функцией ${{P}_{0}}$ в представлении (1.5), определяемой формулой (1.7). Следовательно, сумма двух интегральных членов для $\alpha = {{\alpha }_{1}}$ и $\alpha = {{\alpha }_{2}}$ дает дифракционное поле ${{P}^{d}}(r,\theta )$.
При $kr \to \infty $, т.е. на больших расстояниях от ребра полуплоскости в сравнении с длиной звуковой волны, основной вклад в значения интегралов $I(r,\theta - {{\theta }_{0}})$ и $I(\theta + {{\theta }_{0}})$ в (1.10) дает окрестность точки $\lambda = 0$. Разлагая подынтегральные функции в названных интегралах в ряды в окрестности $\lambda = 0$ и интегрируя их в [2] получено следующее асимптотическое представление дифракционного поля в дальней зоне
(1.11)
$P_{{hs}}^{d} = {{P}_{{hs}}} - {{P}_{0}}\sim {{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} }_{{hs}}} = - \frac{{{{e}^{{i(kr + {\pi \mathord{\left/ {\vphantom {\pi 4}} \right. \kern-0em} 4})}}}}}{{2\sqrt {\pi kr} }}\left\{ {\frac{{\cos \left[ {1{\text{/}}4(\theta - {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta - {{\theta }_{0}})} \right]}} + \frac{{\cos \left[ {1{\text{/}}4(\theta + {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta + {{\theta }_{0}})} \right]}}} \right\}$Полученные решения и их асимптотики помечены индексами “hs” (hard-soft) чтобы подчеркнуть, что результат относится к дифракции на “твердо-мягкой” полуплоскости, у которой освещенная сторона является идеально отражающей. Формула (1.11) справедлива вне малых окрестностей особых лучей ${{\alpha }_{{1,2}}} \equiv \theta \mp {{\theta }_{0}} = \pi $, разделяющих теневую область и области, в которых существует только падающая волна и падающая и отраженная волны (точнее при $\left| {\left( {\theta \mp {{\theta }_{0}}} \right) - \pi } \right| > \delta > 0$, где $\delta $ – число более высокого порядка малости чем ${{(kr)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$).
Можно показать, что вне указанных окрестностей асимптотическое решение А.Д. Роулинза [1, формулы (31)] совпадает с (1.11), однако решение (1.11) значительно проще, что важно для вывода простых закономерностей гашения звука барьерами.
На практике защищаемый от звука объект или его часть могут попадать в окрестность границы раздела теневой и освещенной областей, где решение (1.11) не справедливо. Поэтому представляет интерес получение равномерной асимптотики решения в дальней зоне, имеющее смысл для всех углов $\theta $. Для вывода последней достаточно заметить, что интеграл по действительной оси, входящий в выражение $I(r,\alpha )$ из (1.10) (обозначим его через $I{\text{'}}$), асимптотически (при $kr \to \infty $) эквивалентен интегралу, преобразующемуся в интеграл Френеля. А именно, имеют место равенства
(1.12)
$\begin{gathered} I'\sim \frac{1}{{{{2}^{{1/4}}}{{e}^{{i\pi /8}}}}}\int\limits_{ - \infty }^{ + \infty } {\frac{{{{e}^{{ - kr{{\lambda }^{2}}}}}d\lambda }}{{\lambda - \sqrt 2 {{e}^{{i\pi /4}}}\cos ({\alpha \mathord{\left/ {\vphantom {\alpha {2)}}} \right. \kern-0em} {2)}}}}} = \\ = \;{{2}^{{3/4}}}{{e}^{{i\pi /8}}}\eta \int\limits_0^\infty {\frac{{{{e}^{{ - kr{{\lambda }^{2}}}}}d\lambda }}{{{{\lambda }^{2}} - i{{\eta }^{2}}}}} = \pm \sqrt \pi {{2}^{{3/4}}}{{e}^{{i\pi /8 - ikr{{\eta }^{2}}}}}F\{ \left| \eta \right|\sqrt {kr} \} \\ \end{gathered} $Здесь использованы обозначения: $\eta \equiv \sqrt 2 \cos (\alpha {\text{/}}2)$ и $F(z) \equiv \int_z^\infty {\exp (i{{\mu }^{2}})d\mu } $ (интеграл Френеля); при этом, верхний знак берется при $\eta > 0$, а нижний – при $\eta < 0$.
С учетом результата (1.12), получаем из (1.10) равномерную асимптотику дифрагированного поля в дальней зоне в виде (${{Q}_{ \pm }} \equiv \sqrt {2kr} \cos \left[ {1{\text{/}}2(\theta \pm {{\theta }_{0}})} \right]$):
(1.13)
$\begin{gathered} P_{{hs}}^{d}\sim \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{{hs}}^{1} = - \frac{{{{e}^{{ - i\pi /4}}}}}{{\sqrt {\pi kr} }}\left\{ {{{e}^{{ - ikr\cos (\theta - {{\theta }_{0}})}}}\frac{{\cos \left[ {1{\text{/}}4(\theta - {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta - {{\theta }_{0}})} \right]}}\left| {{{Q}_{ - }}} \right|F\left( {\left| {{{Q}_{ - }}} \right|} \right)} \right. + \\ + \;\left. {{{e}^{{ - ikr\cos (\theta + {{\theta }_{0}})}}}\frac{{\cos \left[ {1{\text{/}}4(\theta + {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta + {{\theta }_{0}})} \right]}}\left| {{{Q}_{ + }}} \right|F\left( {\left| {{{Q}_{ + }}} \right|} \right)} \right\} \\ \end{gathered} $Вне малых окрестностей особых лучей ${{\alpha }_{{1,2}}} \equiv \theta \mp {{\theta }_{0}} = \pi $ можно в формуле (1.13) $\left| {{{Q}_{ \pm }}} \right|F\left( {\left| {{{Q}_{ \pm }}} \right|} \right)$ при $kr \to \infty $ заменить на $i\exp (iQ_{ \pm }^{2}){\text{/}}2$ в силу асимптотики интеграла Френеля $F(z)\sim i{{(2z)}^{{ - 1}}}\exp (i{{z}^{2}}) + O({{z}^{{ - 3}}})$ для больших положительных z, получаемой методом интегрирования по частям (см., например, [5], с. 569). Следовательно, вне указанных окрестностей асимптотика (1.13) приводится к виду (1.11).
Решение для случая, когда освещенная сторона полуплоскости является акустически “мягкой” может быть получено, полагая в (1.2) угол падения большим $\pi $ ($\pi < {{\theta }_{0}}$ < 2π). Тогда освещенной будет сторона полуплоскости $\theta = 2\pi $, являющаяся, согласно краевым условиям (1.3), поглощающей звук. В этом случае очевидно “решение геометрической оптики” (типа (1.7)) и асимптотика решения в дальней зоне дается теми же функциями (1.11), (1.13), в которых необходимо только сделать замену аргументов: ${{\theta }_{0}} \to 2\pi - {{\theta }_{0}}$, $\theta \to 2\pi - \theta $ (и отсчитывать углы от акустически “мягкой” стороны полуплоскости в противоположном направлении). Таким образом, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} {}_{{sh}}(r,\theta ,{{\theta }_{0}})$ = = ${{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} }_{{hs}}}(r,2\pi - \theta ,2\pi - {{\theta }_{0}})$, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{{sh}}^{1}(r,\theta ,{{\theta }_{0}}) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{{hs}}^{1}(r,2\pi - \theta ,2\pi - {{\theta }_{0}})$ и, следовательно, выражения для $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} {}_{{sh}}$ и $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{P} _{{sh}}^{1}$ совпадают с (1.11), (1.13), если в последних изменить знаки перед вторыми слагаемыми.
2. Дифракция цилиндрических волн. Автомобили на автостраде производят звук в области частот от 10 до 2000 Гц. При этом, пик интенсивности (в децибелах) достигается для колебаний частоты, равной примерно 500 Гц [6]. Шум от качения колес железнодорожного состава по рельсу состоит из колебаний с частотами от 50 до 4000 Гц с пиковым значением интенсивности для колебаний частоты ≈1600 Гц [7]. Таким образом, при скорости звука в воздухе равной 330 м/с основной вклад в создаваемый шум вносят звуковые колебания с длинами волн равными ≈66 см в первом случае и ≈21 см – во втором. Шумозащищающие барьеры и щиты (экраны), расположенные вдоль автострад и железных дорог, находятся от источников звука на расстояниях, сравнимых или одного порядка с названными длинами волн. Поэтому, для оценки эффективности барьеров необходимо иметь решения задач дифракции волн от источника (линейного или точечного), когда приближение плоской падающей волны может оказаться слишком грубым и неприемлемым. Однако, расстояния от барьеров до защищаемых от шума зданий или других объектов даже в черте города значительно (на порядок или несколько порядков) превышают указанные длины волн. Следовательно, достаточно получить асимптотические решения рассматриваемых задач в дальней зоне (вдали от ребра барьера). Последнее обстоятельство важно, поскольку далеко не всегда существуют в удобном аналитическом виде решения возникающих здесь задач дифракции и, сверх того, если даже точное решение найдено, удобнее воспользоваться асимптотическим решением для вывода в наиболее простой и наглядной форме характеристик гашения волн экранами.
Поток машин на автостраде и длинный железнодорожный состав можно рассматривать как линейно распределенные источники звука, возбуждающие цилиндрические волны. Когда источники звука распределены на прямой, параллельной ребру полуплоскости, возникает плоская задача дифракции, сформулированная в п. 1, в которой плоскую падающую волну (1.2) необходимо заменить на цилиндрическую волну
(2.1)
${{P}^{i}}(r,\theta ;{{r}_{0}},{{\theta }_{0}}) = H_{0}^{{(1)}}(kR),\quad R \equiv \sqrt {{{r}^{2}} + r_{0}^{2} - 2r{{r}_{0}}\cos (\theta - {{\theta }_{0}})} $В (2.1) R есть расстояние от точки $({{r}_{0}},{{\theta }_{0}}$), в которой сосредоточен источник, до произвольной точки наблюдения $(r,\theta )$, а $H_{0}^{{(1)}}(z)$ – функция Ханкеля первого рода. Выбор этой функции из двух линейно независимых решений $H_{0}^{{(1)}}(kR)$ и $H_{0}^{{(2)}}(kR)$ плоского уравнения Гельмгольца (1.1) объясняется тем, что в силу известных асимптотических свойств функций Ханкеля $H_{0}^{{(1,2)}}(kR)\sim \sqrt {2{\text{/}}(\pi kR)} \cdot \exp \left[ { \pm i(kR - \pi {\text{/}}4)} \right]$ при $kR \gg 1$ (знак “+” относится к функции первого рода), только волна (2.1) является уходящей на бесконечность и удовлетворяющей условию излучения (1.6) (при выбранном временном множителе $\exp ( - i\omega t)$).
Как и в п. 1, предположим, что $0 < {{\theta }_{0}} \leqslant \pi $; тогда освещенная сторона полуплоскости $\theta = 0$ является в соответствии с граничным условием (1.3) акустически “твердой”.
Поскольку, как отмечено выше, для приложений к звуковым барьерам достаточно получения асимптотического решения в дальней зоне, используем для его получения в случае цилиндрической падающей волны метод геометрической теории дифракции Келлера, наиболее подробно изложенный в работе [8]. Согласно этой теории дифрагированная от ребра полуплоскости цилиндрическая волна представляется в виде
в котором амплитуда $A = a(\theta ;{{\theta }_{0}},{{r}_{0}},k){\text{/}}\sqrt r $ удовлетворяет закону сохранения энергии в лучевой трубке. Функция $a(\theta ;{{\theta }_{0}},{{r}_{0}},k)$ определяется из решения эталонной задачи о дифракции плоской волны на полуплоскости, а именно, той плоской волны, в которую переходит цилиндрическая падающая волна (2.1) при удалении источника в бесконечность вдоль луча $\theta = {{\theta }_{0}}$. Тогда, при ${{r}_{0}} \to \infty $ (а, следовательно, и $kR \to \infty $) волна от источника (2.1) переходит в плоскую волну(2.3)
${{P}^{{i0}}} = {{m}_{C}}({{r}_{0}},k){{e}^{{ - ikr\cos (\theta - {{\theta }_{0}})}}},\quad {{m}_{C}}({{r}_{0}},k) \equiv \sqrt {\frac{2}{{\pi k{{r}_{0}}}}} {{e}^{{ik{{r}_{0}} - i\pi /4}}}$Следовательно, решение задачи дифракции плоской волны (2.3) на “твердо-мягкой” полуплоскости совпадает с решением (1.11), помноженным на множитель (амплитуду падающей волны) ${{m}_{C}}$, т.е. оно равно
(2.4)
$P_{{hs}}^{{d0}} = - \frac{{{{e}^{{ik({{r}_{0}} + r)}}}}}{{\sqrt 2 \pi k\sqrt {{{r}_{0}}r} }}\left\{ {\frac{{\cos \left[ {1{\text{/}}4(\theta - {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta - {{\theta }_{0}})} \right]}} + \frac{{\cos \left[ {1{\text{/}}4(\theta + {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta + {{\theta }_{0}})} \right]}}} \right\}$Сравнивая (2.4) с (2.2) получаем значение функции $a(\theta ;{{\theta }_{0}},{{r}_{0}},k)$ и дифракционную волну $P_{C}^{d}$. Выражение для $P_{C}^{d}$, которое в данном случае (дифракции цилиндрической волны) совпадает с (2.4), перепишем в виде
(2.5)
$P_{C}^{d} = P_{{hs}}^{{d0}} = - \frac{{{{e}^{{ik({{r}_{0}} + r)}}}}}{{2\pi k\sqrt {{{r}_{0}}r} }}{{D}_{{hs}}}(\theta ,{{\theta }_{0}})$(2.6)
$D{}_{{hs}}(\theta ,{{\theta }_{0}}) = \sqrt 2 \left\{ {\frac{{\cos \left[ {1{\text{/}}4(\theta - {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta - {{\theta }_{0}})} \right]}} + \frac{{\cos \left[ {1{\text{/}}4(\theta + {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta + {{\theta }_{0}})} \right]}}} \right\}$Выбор коэффициента дифракции (2.6) со множителем $\sqrt 2 $ продиктован тем, чтобы сделать запись решения в форме (2.5) универсальной, в которой при других граничных условиях (например, однотипных) заменяется только коэффициент дифракции.
Чтобы получить полное решение задачи нужно к полю дифракции (2.5), (2.6) добавить в соответствующих областях падающую (2.1) и отраженную от стороны полуплоскости цилиндрические волны, т.е. добавить “решение геометрической оптики”, аналогичное (1.7), которое и в данном случае легко выписывается. Полученная асимптотика непригодна при $\theta \approx \pi \pm {{\theta }_{0}}$, т.е. в окрестности границ по разному освещенных областей, из-за того, что выражение (2.6) не справедливо в этих окрестностях. Однако, в рассматриваемой задаче может быть получена и равномерная асимптотика, компенсирующая (сглаживающая) разрывы на линиях $\theta = \pi \pm {{\theta }_{0}}$ части решения типа (1.7), если принять во внимание, что асимптотики дифракционных полей для цилиндрической (2.5) и плоской волн (1.11) связаны между собой через множитель (константу) ${{m}_{C}}({{r}_{0}},k) \equiv \sqrt {2{\text{/}}(\pi k{{r}_{0}})} {{e}^{{ik{{r}_{0}} - i\pi /4}}}$ (через тот же, что связывает волну от источника (2.1) и плоскую волну (2.3)). Следовательно, указанная равномерная асимптотика дается равенством
3. Дифракция сферических волн на твердо-мягкой полуплоскости. Сферическая волна от точечного источника в точке $A({{r}_{0}},\theta {}_{0},{{z}_{0}})$задается в виде
(3.1)
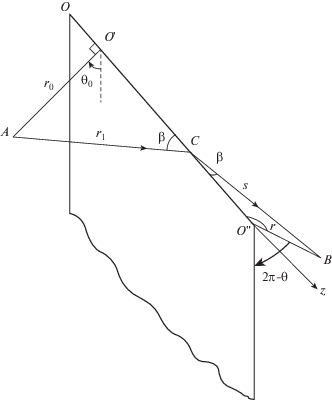
${{P}^{i}} = {{e}^{{ik{{R}_{1}}}}}{\text{/}}{{R}_{1}},\quad {{R}_{1}} \equiv \sqrt {{{r}^{2}} + r_{0}^{2} - 2r{{r}_{0}}\cos (\theta - \theta {}_{0}) + {{{(z - {{z}_{0}})}}^{2}}} $Считаем угол ${{\theta }_{0}}$, отсчитываемый по часовой стрелке от акустически твердой стороны полуплоскости (фиг. 1) меньшим π; тогда эта сторона будет освещенной. Поле (давление) в произвольной точке $B(r,\theta ,z)$, вызванное дифракцией волны (3.1) на ребре $OO{\text{''}}$ полуплоскости будем также искать, используя геометрическую теорию дифракции Дж.Б. Келлера [8]. Согласно этой теории в пространственном случае каждый луч $AC$, попавший в точку С ребра, возбуждает бесконечное множество дифрагированных лучей, образующих в однородной среде (с одинаковой скоростью звука во всех направлениях) круговой конус с осью, совпадающей с ребром полуплоскости. Тогда из принципа Ферма для однородной среды следует, что дифракционный луч, попавший в точку наблюдения В исходит из той точки С ребра, для которой расстояние вдоль лучей $AC + CB$ является кратчайшим. Последнее имеет место, когда угол полураствора конуса дифрагированных лучей совпадает с углом, образуемым падающим лучом AC с ребром барьера (на фигуре этот угол обозначен через $\beta $).
Амплитуда поля в точке В выписывается из условия сохранения энергии в лучевой трубке, включающей в себя малый элемент ребра вблизи точки С (в нашем случае прямолинейный элемент радиуса кривизны $\rho = \infty $), что приводит к результату (см. [8], §§ 4–6, где приняты несколько иные обозначения)
(3.2)
$P_{S}^{d} = {{a}_{0}}a(\theta ,{{\theta }_{0}},k,\beta ){{[s(1 + r_{1}^{{ - 1}}s)]}^{{ - 1/2}}}{{e}^{{ik({{r}_{1}} + s)}}}$В формуле (3.2) ${{r}_{1}} = \left| {AC} \right|$, $s = \left| {CB} \right|$ и ${{a}_{0}}$ есть амплитуда сферической волны (3.1) в точке С, т.е. ${{a}_{0}} = 1{\text{/}}{{r}_{1}}$.
Как и в предыдущем пункте, функция $a(\theta ,{{\theta }_{0}},k,\beta )$ определяется из решения эталонной задачи о дифракции плоской волны на полуплоскости, но уже пространственной, в которой луч, перпендикулярный плоскости фронта и попадающий в точку С ребра образует угол $\beta $ с ребром полуплоскости (иначе говоря, фронт плоской волны перпендикулярен лучу AC). Точное асимптотическое решение этой пространственной задачи с граничными условиями (1.3) так же, как и в случае однотипных граничных условий, легко получить из соответствующей точной асимптотики (1.11) двумерной задачи заменой в последней k на $k\sin \beta $ и умножением выражения (1.11) на множитель $\exp (ikz\cos \beta )$. С другой стороны, асимптотическое представление этого решения, полученное по методу геометрической теории дифракции в [8] содержит неопределенную функцию $a(\theta ,{{\theta }_{0}},k,\beta )$ пространственной задачи (заметим, что форма асимптотики в геометрической теории дифракции не зависит от типа краевых условий, от краевых условий зависит вид функции $a(\theta ,{{\theta }_{0}},k,\beta )$). Сравнивая указанные асимптотические решения, имеем
(3.3)
$a(\theta ,{{\theta }_{0}},k,\beta ) = - \frac{{{{e}^{{i\pi /4}}}}}{{2\sqrt {\pi k} \sin \beta }}\left\{ {\frac{{\cos \left[ {1{\text{/}}4(\theta - {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta - {{\theta }_{0}})} \right]}} + \frac{{\cos \left[ {1{\text{/}}4(\theta + {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta + {{\theta }_{0}})} \right]}}} \right\}$Подставляя теперь (3.3) в (3.2), получаем асимптотику решения в дальней зоне для задачи дифракции сферической волны на твердо-мягкой полуплоскости в виде
(3.4)
$\begin{gathered} P_{S}^{d} = - \frac{{{{e}^{{ik({{r}_{1}} + s) + i\pi /4}}}}}{{2\sqrt {\pi k} \sqrt {r{}_{1}s({{r}_{1}} + s)} \sin \beta }}\left\{ {\frac{{\cos \left[ {1{\text{/}}4(\theta - {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta - {{\theta }_{0}})} \right]}} + \frac{{\cos \left[ {1{\text{/}}4(\theta + {{\theta }_{0}})} \right]}}{{\cos \left[ {1{\text{/}}2(\theta + {{\theta }_{0}})} \right]}}} \right\} = \\ = \; - \frac{{{{e}^{{ikL}}}}}{{2\sqrt {2\pi kL} }}\frac{{{{e}^{{i\pi /4}}}}}{{\sqrt {{{r}_{0}}r} }}{{D}_{{hs}}}(\theta ,{{\theta }_{0}}) \\ \end{gathered} $В (3.4) введены обозначения (фиг. 1): $L = {{r}_{1}} + s = \left| {AC} \right| + \left| {CB} \right|$, ${{r}_{0}} = r{}_{1}\sin \beta $, r = ssinβ.
4. Заключение. Полезно дать сводку полученных решений в виде таблицы, в которой (при разнотипных краевых условиях) коэффициент дифракции D следует положить равным ${{D}_{{hs}}}$, если освещенная сторона полуплоскости является акустически твердой, и равным ${{D}_{{sh}}}$, если освещенная сторона является акустически мягкой. Эти коэффициенты, в соответствии с полученными в работе решениями, даются соотношениями (верхний знак относится к ${{D}_{{hs}}}$)
Таблица 1 дает также асимптотические решения задач дифракции на полуплоскости и для однотипных краевых условий, если для коэффициента дифракции принять одно из следующих выражений
При этом, Dh (с верхним знаком в приведенной формуле) соответствует краевым условиям Неймана на сторонах полуплоскости, а Ds – условиям Дирихле на них. Асимптотические решения для однотипных краевых условий известны и выписаны, например, в [9] (следует иметь в виду, что в этой работе коэффициенты дифракции Dh и Ds приведены с ошибочным множителем 1/2; можно этот множитель ввести в выражения для $D{}_{h}$ и ${{D}_{s}}$, но тогда следует изменить коэффициенты при $D(\theta ,{{\theta }_{0}})$ в приведенных в [9] асимптотических решениях для всех трех типов падающих волн).
Работа выполнена при финансовой поддержке РФФИ (грант № 17-08-00066).
Таблица 1
| Падающая волна | Дифрагированная волна в дальней зоне ($kr \gg 1$, $kL \gg 1$) |
|---|---|
| Плоская | ${{P}^{d}} = - \frac{1}{{2\sqrt {2\pi kr} }}{{e}^{{ikr + i\pi /4}}}D(\theta ,{{\theta }_{0}})$ |
| Цилиндрическая | $P_{C}^{d} = - \frac{{{{e}^{{ikr}}}}}{{\sqrt {2\pi kr} }}\frac{{{{e}^{{ik{{r}_{0}}}}}}}{{\sqrt {2\pi k{{r}_{0}}} }}D(\theta ,{{\theta }_{0}})$ |
| Сферическая | $P_{S}^{d} = - \frac{{{{e}^{{ikL}}}}}{{2\sqrt {2\pi kL} }}\frac{{{{e}^{{i\pi /4}}}}}{{\sqrt {{{r}_{0}}r} }}D(\theta ,{{\theta }_{0}})$ |
Список литературы
Rawlins A.D. The solution of a mixed boundary value problem in the theory of diffraction by a semi- infinite plane // Proc. Roy. Soc. L. 1975. A346. № 1647. P. 469–484.
Исраилов М.Ш. Дифракция акустических и упругих волн на полуплоскости при разнотипных граничных условиях // Изв. РАН. МТТ. 2013. № 3. С. 121–134.
Friedlender F.G. Sound pulses. Cambridge: Univ. Press, 1958. Фридлендер Ф. Звуковые импульсы. М.: Изд-во иностр. лит., 1962. 232 с.
Holmes M.H. Introduction to Perturbation Methods. N.Y. ets.: Springer, 1995. 338 p.
Born M., Wolf E. Principles of optics. London: Pergamon Press, 1959. Борн М., Вольф Э. Основы оптики. М.: Наука, 1970. 856 с.
Klinger R.E., McNerney M.T., Busch-Vishniac I. Design Guide for Highway Noise Barriers // Res. Rep. U.S. Department of Transportation. Washington, 2003. 81 p.
Hohenwarter D. Railway Noise Propagation Models // J. Sound and Vibration. 1990. V. 141. № 3. P. 17–41.
Keller J.B. Diffraction by an aperture. I // New York Univ., Inst. Math. Sci., Tech. Rep. № EM-92. N.Y., 1956. 61 p.
Menounou P., Busch-Vishniac I.J., Blackstock D.T. Directive line source model: A new model for sound diffraction by half-planes and wedges // J. Acoust. Soc. Am. 2000. V. 107. № 6. P. 2973–2986.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела