Известия РАН. Механика твердого тела, 2019, № 2, стр. 111-125
Послойный анализ напряженно-деформированного состояния трехслойных оболочек с вырезами
a Институт прикладной механики РАН
Москва, Россия
b Московский авиационный институт (национальный исследовательский университет)
Москва, Россия
* E-mail: vbak@yandex.ru
Поступила в редакцию 05.11.2017
После доработки 05.11.2017
Принята к публикации 28.02.2018
Аннотация
Напряженно-деформированное состояние (НДС) трехслойных оболочек с вырезами недостаточно исследовано, что является одной из причин, ограничивающих их применение в современных конструкциях. На основе блочного конечно-элементного подхода разработана уточненная модель послойного анализа НДС нерегулярных трехслойных оболочек. Рассмотренный подход позволяет достаточно точно моделировать неоднородность пакета слоев и слоя заполнителя, условия закрепления слоев и приложения к ним нагрузок, применять различные модели для исследования несущих слоев и заполнителя. С использованием аппроксимаций конечных элементов (КЭ) несущих слоев построены аппроксимирующие функции перемещений трехмерного КЭ заполнителя и на их основе создана модель для уточненного расчета НДС, позволяющая учесть изменение характеристик материала и напряженного состояния, в том числе по радиальной координате в слое заполнителя. Проведено в уточненной постановке исследование напряженно-деформированного состояния в слоях трехслойных оболочек с вырезами, в т.ч. несквозными. Выявлено значительное снижение и сглаживание напряжений краевого эффекта в слоях трехслойных оболочек с несквозными вырезами по сравнению со сквозными вырезами вследствие перераспределения нагрузки, так как значительную ее часть берут на себя слои с ненарушенной сплошностью.
1. Введение. В современной технике большое применение находят элементы конструкций оболочечного типа. Интерес к трехслойным оболочкам объясняется высокими показателями весовой эффективности, удельной прочности и жесткости, тепло-, звуко-, виброизоляционных свойств. При проектировании конструкций нередко приходится нарушать сплошность оболочек отверстиями, приводящими к появлению зон повышенных напряжений, причем наибольшие из них могут в несколько раз превышать напряжения вдали от таких зон. Недостаточное знание истинной картины напряженно-деформированного состояния (НДС) может привести к разрушению конструкции или к увеличению ее веса. Слабое развитие моделей, которые должны позволять с высокой точностью и степенью детализации провести расчет НДС трехслойных, в общем случае нерегулярных оболочек, сдерживает их широкое использование в современной технике [1, 2]. Поэтому создание новых и развитие существующих моделей и применение их для уточненного расчета трехслойных нерегулярных оболочек является важной научно-технической задачей [3–6].
Исследованию НДС элементов конструкций с вырезами уделяется большое внимание. Этим вопросом занимались Г.А. Ванин, А.Н. Гузь, А.С. Космодамианский, А.И. Лурье, И.М. Пирогов, И.Н. Преображенский, Н.Т. Савин, Н. Рао и многие другие. Обзоры работ по расчету оболочек с вырезами приведены в [7–10] и др. Анализ этих работ показывает, что решение подобных задач аналитическими методами сталкивается с большими трудностями математического характера, особенно для оболочек с прямоугольными вырезами. Вследствие этого для исследования оболочечных элементов тонкостенных конструкций с вырезами применяются численные методы [11–15] и др.
В подавляющем большинстве работ исследуются изотропные оболочки. Значительно меньше работ по исследованию композитных оболочек с вырезами [16–21].
Вопросы расчета трехслойных сферических оболочек с малыми круговыми, эллиптическими и криволинейными отверстиями рассматривались в работах [22–25]. Это в основном работы Ванина Г.А. и его соавторов.
Концентрация напряжений около отверстий в трансверсально-изотропных оболочках рассматривалась в книге [26]. В ней отмечается, что получены точные решения задач о концентрации напряжений около кругового отверстия, либо около жесткого включения в сферической оболочке, то есть задач, для которых переменные разделяются. В этой работе также сказано, что для отверстий другой формы получить точные решения в рамках теории трансверсально-изотропных оболочек не представляется возможным.
Вопросы, связанные с расчетом трехслойных цилиндрических оболочек с прямоугольными вырезами (распространенной формой вырезов в конструкторской практике), рассматривались в работах [27–29]. Однако в уточненной постановке достоверных решений задач о распределении напряжений около прямоугольных отверстий в трехслойных оболочках неизвестно. Недостаточная изученность этой проблемы связана с большими сложностями получения решения. Это приводит к необходимости привлечения к решению проблемы численных методов. Наиболее подходящим для решения указанных задач является метод конечных элементов (МКЭ), позволяющий проводить с необходимой точностью и степенью детализации построение моделей и расчет исследуемых конструкций.
Модели и расчет слоистых оболочек методом конечных элементов рассматривались в монографиях [30–36].
В данной работе рассматривается подход послойного анализа [37–39], при котором можно создавать и применять разные модели для расчета слоев. В соответствие с этим подходом модели строятся отдельно для несущих слоев и заполнителя трехслойных оболочек. При необходимости заполнитель разбивается по толщине на дополнительные слои. Затем все слои собираются в блоки, с помощью которых проводится моделирование НДС трехслойных оболочек.
2. Постановка задачи. Рассмотрим построение блочной конечно-элементной модели (БКЭМ) трехслойных оболочек, позволяющей достаточно точно учесть неоднородность оболочки, в том числе на уровне слоя заполнителя, наличие сквозных и несквозных вырезов, конкретные условия приложения нагрузок к слоям и различные условия их закрепления, моментное состояние несущих слоев, трехмерное напряженное состояние в слое заполнителя. Построенные модели позволяют исследовать НДС трехслойных оболочек с переменными толщиной и физико-механическими свойствами слоев, изменение НДС по координатам, в том числе по толщине заполнителя, провести учет которых при обычно применяемых подходах, как правило, не удается.
Наиболее распространенными аппроксимациями для КЭ при расчете слоистых оболочек, как правило, являются полиномы первого и второго порядка. Однако еще в статье [40] отмечается, что с помощью одних только полиномиальных функций нельзя учесть всех форм перемещений искривленных элементов как жесткого тела и что если добиваться учета перемещения как жесткого тела путем уменьшения шага расчетной сетки, то сходимость к точному решению, как правило, имеет место, но оказывается очень медленной. Это же показано в работах [31, 38, 41–45]. В большинстве работ для слоистых оболочек в отличие от однородных оболочек, учет перемещений как жесткого тела при построении искривленных элементов не проведен, что приводит к необходимости значительно измельчать сетку разбиений на КЭ, а это в свою очередь приводит к большим порядкам систем уравнений. То есть удовлетворительная точность достигается для довольно громоздких конечно-элементных моделей (КЭМ).
В работах [31, 41, 43–50] разработан ряд КЭ для расчета напряженно-деформированного состояния трехслойных и многослойных оболочек, имеющих достаточно эффективные аппроксимации. Эффективная (позволяющая повысить скорость сходимости численных результатов, а следовательно, уменьшить порядок систем уравнений, что особенно актуально при послойном анализе) модель получена для осесимметричных цилиндрических трехслойных оболочек [46–49], благодаря использованию точных аналитических решений в качестве аппроксимирующих функций перемещений несущих слоев. Для неосесимметричных круговых цилиндрических слоисто-неоднородных оболочек эффективные модели для уточненного анализа напряженно-деформированного состояния представлены в работах [31, 38, 41, 43–45, 50] и др. публикациях автора рассматриваемой статьи. Эти модели строятся с помощью функций формы для КЭ несущих слоев, основанных на аппроксимации обобщенных деформаций с последующим удовлетворением уравнениям совместности деформаций [31, 38, 41, 43–45]. Применение для расчета конечных элементов с такими эффективными функциями формы позволяет значительно увеличить скорость сходимости получаемых результатов [31, 38, 41, 43–45, 50], а, следовательно, приводит к уменьшению числа КЭ по сравнению с аппроксимацией перемещений. Для оболочек не цилиндрической формы применить такой подход не удалось из-за математических трудностей, но в рассматриваемой ниже модели проведен учет перемещений как жесткого тела при построении конечных элементов моментных несущих слоев нерегулярных трехслойных оболочек вращения. С использованием аппроксимаций КЭ несущих слоев получены аппроксимирующие функции перемещений КЭ трехмерного заполнителя. На основе построенных конечных элементов создается блок конечных элементов (БКЭ) для уточненного послойного исследования НДС трехслойных оболочек со сквозными и несквозными вырезами.
Следует отметить, что с помощью рассматриваемой модели и построенных БКЭ можно проводить расчет НДС нерегулярных трехслойных оболочек вращения нулевой кривизны, то есть как оболочек конической, так и цилиндрической формы. Но так как для цилиндрических нерегулярных трехслойных оболочек вращения получена более эффективная модель [38], а для оболочек не цилиндрической формы применить такой подход не удалось из-за математических трудностей, то рассматриваемую здесь модель и построенные БКЭ рекомендуется применять для расчета НДС нерегулярных трехслойных конических оболочек вращения.
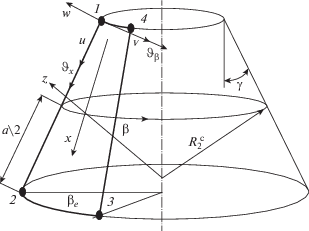
3. Моделирование напряженно-деформированного состояния в тонких моментных несущих слоях трехслойной конической, в общем случае нерегулярной оболочки вращения. Как правило, на практике наиболее распространены трехслойные оболочки с тонкими и жесткими несущими слоями и толстым, но менее жестким заполнителем. Для моделирования напряженно-деформированного состояния в тонких и жестких несущих слоях применим конечные элементы естественной кривизны, построенные на основе классической теории для моментных конических оболочек вращения. В тех случаях, когда гипотезы Кирхгофа–Лява будут несправедливы, несущие слои можно моделировать с помощью конечных элементов заполнителя, построенных на основе соотношений теории упругости.
Для несущих слоев (индекс “c”) вектор обобщенных деформаций состоит из меридиональной ε1, окружной ε2 и сдвиговой γ деформаций, параметров изменения кривизны æ1, æ2 и кручения χ срединной поверхности 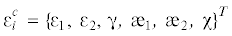 (i = 1, 3, i – номер слоя, начиная с внутренней поверхности оболочки). Запишем соотношения, связывающие
деформации с перемещениями для конических оболочек [51]
(i = 1, 3, i – номер слоя, начиная с внутренней поверхности оболочки). Запишем соотношения, связывающие
деформации с перемещениями для конических оболочек [51]
(3.1)
$\begin{gathered} \varepsilon _{i}^{с } = B_{i}^{с }\delta _{i}^{с } \\ B_{i}^{c} = \left[ {\begin{array}{*{20}{c}} {\frac{\partial }{{\partial x}}}&0&0 \\ {\frac{{\sin \gamma }}{r}}&{\frac{\partial }{{r\partial \beta }}}&{\frac{{\cos \gamma }}{r}} \\ {\frac{\partial }{{r\partial \beta }}}&{\frac{\partial }{{\partial x}} - \frac{{\sin \gamma }}{r}}&0 \\ 0&0&{ - \frac{{{{\partial }^{2}}}}{{\partial {{x}^{2}}}}} \\ 0&{\frac{{\cos \gamma {\text{ }}}}{{{{r}^{2}}}}\frac{\partial }{{\partial \beta }}}&{ - \frac{{{{\partial }^{2}}}}{{{{r}^{2}}\partial {{\beta }^{2}}}} - \frac{{\sin \gamma {\text{ }}}}{r}\frac{\partial }{{\partial x}}} \\ 0&{\frac{{\cos \gamma {\text{ }}}}{r}\frac{\partial }{{\partial x}} - \frac{{\cos \gamma {\text{ }}\sin \gamma }}{{{{r}^{2}}}}}&{ - \frac{{{{\partial }^{2}}}}{{r\partial x\partial \beta }} + \frac{{\sin \gamma }}{{{{r}^{2}}}}\frac{\partial }{{\partial \beta }}} \end{array}} \right] \\ \end{gathered} $Интегрированием соотношений (3.1) при нулевых значениях деформаций определяются функции перемещений как твердого тела (учет которых позволяет увеличить скорость сходимости получаемых результатов), записанные аналогично [37, 38, 41–45, 52, 53] через шесть неопределенных коэффициентов α1, …, α6, являющихся постоянными интегрирования.
Конечные элементы образованы сечением оболочки двумя плоскостями, перпендикулярными оси вращения, и двумя плоскостями, проходящими через ось оболочки. Степенями свободы конечных элементов несущих слоев являются три линейных перемещения $u,\;v,\;w$ и два угла поворота нормали к срединной поверхности вокруг координатных осей x и β(у) в каждом из четырех узлов, т.е. двадцать степеней свободы, из них шесть отвечают за перемещения как твердого тела, оставшиеся четырнадцать – за перемещения, вызванные деформированием оболочки [37, 52, 53]. С помощью четырнадцати неопределенных коэффициентов α7, …, α20 аппроксимируем деформационную (вызванную деформированием оболочки) составляющую перемещения w неполным бикубическим полиномом, а деформационную составляющую перемещений $u$ и $v$ – билинейными полиномами.
Аппроксимирующие функции перемещений рассматриваемого конечного элемента несущих слоев (определяемые в виде суммы жестких и деформационных смещений), записанные в матричной форме, будут выглядеть следующим образом
где $\alpha _{i}^{c}$ – вектор неопределенных коэффициентов α1, …, α20;$T_{i}^{c}$ (3 × 20) – матрица аппроксимирующих функций перемещений КЭ несущих слоев трехслойной конической нерегулярной оболочки вращения. Транспонированная матрица $T_{i}^{c}$ приведена в табл. 1, где приняты следующие обозначения:
r0 – радиус окружности в плоскости, перпендикулярной оси вращения и проходящей через начало местной системы координат конечного элемента конической оболочки. В пустых клеточках таблиц коэффициенты равны нулю.Таблица 1
| u | $\text{v}$ | w | |
|---|---|---|---|
| α1 | c1sinγ | –s1 | c1cosγ |
| α2 | s1sinγ | c1 | s1cosγ |
| α3 | с1r0cosγ | s1xcosγ | –c1(x + r0sinγ) |
| α4 | s1r0sinγ | –c1xcosγ | –s1(x + r0sinγ) |
| α5 | cosγ | –sinγ | |
| α6 | r0+ xsinγ | ||
| α7 | x | ||
| α8 | β | ||
| α9 | xβ | ||
| α10 | β | ||
| α11 | xβ | ||
| α12 | xβ | ||
| α13 | x2 | ||
| α14 | β2 | ||
| α15 | x2β | ||
| α16 | xβ2 | ||
| α17 | x3 | ||
| α18 | β3 | ||
| α19 | x3β | ||
| α20 | xβ3 |
Зная $T_{i}^{c}$, из (3.1) получим выражение для вектора деформаций $\varepsilon _{i}^{c}$, записанное через вектор неопределенных коэффициентов $\alpha _{i}^{c}$
$\Omega _{i}^{c}$ – матрица (6 × 20) аппроксимирующих функций обобщенных деформаций КЭ несущих слоев. Транспонированная матрица $\Omega _{i}^{c}$ без верхних шести строк, коэффициенты которых равны нулю, приведена в табл. 2, где k = 1/r.Таблица 2
| 1 | k x sin γ | ||||
| k β sin γ | k | ||||
| β | k x β sin γ | k x | |||
| k | –k β sin γ | k2cosγ | –βk2cosγsinγ | ||
| kx | β (1– k x sin γ) | k2xcosγ | –xβk2cosγsinγ + βkcosγ | ||
| kxβcosγ | –βksinγ | хk2sinγ – k | |||
| kx2cosγ | –2 | –2xksinγ | |||
| kβ2cosγ | –2k2 | 2βk2sinγ | |||
| kx2βcosγ | –2β | –2xβksinγ | –2kx+ x2k2sinγ | ||
| kxβ2cosγ | –2xk2 – β2ksinγ | 2xβk2sinγ – 2βk | |||
| kx3cosγ | –6 x | –3x2ksinγ | |||
| kβ3cosγ | –6βk2 | 3β2k2sinγ | |||
| kx3βcosγ | –6xβ | –3x2βksinγ | x3k2sinγ – 3x2k | ||
| kxβ3cosγ | –6xβk2 – β3ksinγ | 3xβ2k2sinγ – 3β2k |
Используя физические соотношения, связывающие обобщенные деформации с усилиями и моментами в несущих слоях, по алгоритмам, аналогичным рассмотренным в статье [49], определяются матрицы жесткости КЭ несущих слоев, необходимые для построения общей матрицы жесткости КЭМ трехслойной конической, в общем случае нерегулярной оболочки вращения.
4. Моделирование напряженно-деформированного состояния в слое заполнителя трехслойной конической, в общем случае нерегулярной оболочки вращения. Часто при расчете трехслойных оболочек встречаются случаи (например, при действии локальных радиальных нагрузок), когда необходимо учитывать изменение НДС по толщине заполнителя, или исследовать НДС конструкций с переменными физико-механическими свойствами заполнителя по нормальной к срединной поверхности координате. В этих случаях надо моделировать слой заполнителя не только по меридиональной, окружной, но и по нормальной к поверхности оболочки координате.
Рассмотрим следующий алгоритм построения КЭ слоя заполнителя. За поверхности приведения выберем внутреннюю и внешнюю конические поверхности конечных элементов заполнителя (КЭЗ), в угловых точках которых расположим узлы (узлы находятся на нормалях к этим поверхностям КЭЗ). То есть, у конечных элементов заполнителя на конических поверхностях, по которым сопрягаются КЭЗ с КЭ несущих слоев, будет столько же узлов, сколько их у КЭ несущих слоев, и выбираем на конических поверхностях сопряжения те же обобщенные перемещения и функции формы, что приняты у КЭ несущих слоев.
Такой алгоритм построения КЭ заполнителя позволяет избежать погрешностей, вызванных разрывом обобщенных перемещений на поверхностях раздела несущих слоев и слоя заполнителя.
Так как разрабатывается конечно-элементная модель, позволяющая при необходимости слой заполнителя разбивать и по толщине на требуемое число КЭ, то КЭЗ будут иметь разное число степеней свободы. Степенями свободы в узле конечного элемента слоя заполнителя, который сопрягается по внутренней и внешней коническим поверхностям с конечными элементами несущих слоев, являются три линейных перемещения $u,\;v,\;w$, и углы поворота нормали вокруг координатных осей x и β(у). Конечный элемент в общем случае имеет сорок степеней свободы. Когда конечные элементы слоя заполнителя по толщине оболочки располагаются один за одним, нет смысла учитывать углы поворота нормали (эти степени свободы убираются соответствующей программой). Благодаря этому конечные элементы заполнителя будут иметь вместо сорока двадцать четыре степени свободы, что ведет к уменьшению размерности матрицы жесткости конечно-элементной модели. Таким образом, коническая поверхность, разделяющая эти конечные элементы слоя заполнителя, повышает число степеней свободы КЭМ слоистой оболочки на двенадцать вместо двадцати.
Если конечный элемент слоя заполнителя сопрягается по одной из конических поверхностей с конечным элементом несущих слоев, то эта коническая поверхность конечного элемента слоя заполнителя имеет двадцать степеней свободы. Если по другой конической поверхности стыкуются конечные элементы слоя заполнителя, то эта коническая поверхность КЭ имеет двенадцать степеней свободы – четыре узла по три линейных перемещения $u,\;v,\;w$. Таким образом конечный элемент слоя заполнителя в этом случае имеет 32 степени свободы.
Разбивая в том числе по толщине слой заполнителя на требуемое число КЭ, определяем закон изменения параметров НДС по координатам.
Как отмечалось выше, аппроксимирующие функции перемещений конечных элементов слоя заполнителя строятся на внутренней и внешней конических поверхностях этих КЭ на основе аппроксимаций КЭ несущих слоев. Чтобы использовать аппроксимирующие функции перемещений, полученные для КЭ несущих слоев, переходим в этих КЭ от срединной поверхности, относительно которой получалась матрица жесткости КЭ, к поверхности раздела со слоем заполнителя с помощью матрицы перехода аналогично [34, 54].
Запишем выражения для аппроксимирующих функций полей перемещений конечных элементов слоя заполнителя (индекс f) в местной системе координат, находящейся на срединной поверхности КЭЗ с началом координат, расположенном на пересечении линий, одна из которых проходит на равном расстоянии от криволинейных границ, а другая – на равном расстоянии от прямолинейных границ КЭЗ
(4.1)
$\delta _{{ij}}^{f} = \delta _{{ij}}^{1}\varphi _{{ij}}^{1} + \delta _{{ij}}^{2}\varphi _{{ij}}^{2}$Используя выражения (3.2), запишем (4.1) в виде
где $T_{{ij}}^{f}$ – матрица аппроксимирующих функций перемещений КЭЗ с максимальной размерностью (3 × 40) для случая, когда для моделирования НДС заполнителя применяется один конечный элемент по толщине;$\alpha _{{ij}}^{f}$ – вектор неопределенных коэффициентов для конечных элементов слоя заполнителя, имеющий следующий вид $\alpha _{{ij}}^{f}$ = {$\alpha _{{ij}}^{1}$, $\alpha _{{ij}}^{2}$}T [45].
Рассматривая слой заполнителя как толстостенную коническую оболочку, используем соотношения для трехмерного тела в криволинейных координатах [3] и запишем их в матричном виде
Зная зависимости для перемещений в конечных элементах слоя заполнителя (4.2), легко получить соотношения для деформаций в этих элементах, записанные через вектор неопределенных коэффициентов $\alpha _{{ij}}^{f}$:
где $\Omega _{{ij}}^{f}$ (6 × 40) матрица аппроксимирующих функций обобщенных деформаций КЭЗ с максимальной размерностью (3 × 40) для случая, когда для моделирования НДС заполнителя применяется один конечный элемент по толщине.Напряженное состояние в конечных элементах слоя заполнителя характеризуется компонентами вектора напряжений $\sigma _{{ij}}^{f} = {{\{ \sigma _{{11}}^{{}},\sigma _{{22}}^{{}},\sigma _{{33}}^{{}},\tau _{{12}}^{{}},\tau _{{23}}^{{}},\tau _{{13}}^{{}}\} }^{T}}$.
Используя физические соотношения, связывающие обобщенные деформации с напряжениями, представим
где $D_{{ij}}^{f}$ – матрица упругих констант заполнителя для j-го конечного элемента.Выражение для напряжений в конечных элементах слоя заполнителя, записанное через вектор неопределенных коэффициентов $\alpha _{{ij}}^{f}$с учетом (4.3), (4.4), примет вид
Матрица жесткости КЭ слоя заполнителя и другие вспомогательные матрицы определяются аналогично тому, как это описано в статье [49].
Из рассмотренных двумерных конечных элементов моментных несущих слоев и трехмерных КЭ слоя заполнителя строятся блоки конечных элементов для послойного моделирования НДС трехслойной нерегулярной оболочки нулевой гауссовой кривизны. В зависимости от условий решаемых задач слой заполнителя моделируется по толщине необходимым числом трехмерных КЭ.
5. Исследование напряженно-деформированного состояния трехслойной оболочки с вырезами. При расчете конструкций с помощью МКЭ в варианте метода перемещений важным этапом является выбор или получение аппроксимаций полей перемещений. В настоящее время нет надежных рекомендаций, позволяющих сразу выбрать оптимальный вариант аппроксимирующих выражений для неизвестных функций. Определяющим критерием при выборе аппроксимирующих функций является сравнение приближенных решений, полученных при применении рассматриваемых аппроксимаций искомых функций, с достоверным решением [55].
Достоверность, точность и сходимость результатов, полученных с помощью рассмотренной модели и построенного конечного элемента несущих слоев трехслойной конической оболочки вращения, подтверждена сопоставлением с аналитическим и численными решениями [37, 38], а также экспериментальными данными [56, 57].
Численный пример. Проводится исследование и сравнение напряженно-деформированного состояния трехслойной оболочки со сквозными и несквозными (когда сплошность нарушена только во внутреннем несущем слое) вырезами для тех же параметров, что в статье [57], в которой рассматривались сквозные и закрытые крышками отверстия в трехслойной конической оболочке.
Трехслойные оболочки имели следующие параметры:
L = 1.5 м, R = 1.5 м, H = 5.63 см, γ = 33.69°
– для внутреннего несущего слоя E1 = 2.5 × 105 кг/см2, E2 = 2.2 × 105 кг/см2, G12 = = 0.35 × 105 кг/см2, μ2 = 0.1, h1 = 0.43 см
– для наружного несущего слоя E1 = 2.1 × 105 кг/см2, E2 = 1.9 × 105 кг/см2, G12 = = 0.35 × 105 кг/см2, μ2 = 0.1, h2 = 0.21 см
– для заполнителя: E1 = E2 = E3 = 240 кг/см2, G12 = G13 = G23 = 100 кг/см2
L – длина оболочки, R – внутренний радиус большего основания трехслойной конической оболочки, h1, h2 – толщина внутреннего и наружного несущих слоев, H – толщина трехслойного пакета, γ – угол конусности, Е, G, μ – модули упругости и коэффициент Пуассона.
Оболочка, нагруженная равномерно распределенным внутренним давлением, имеет два диаметрально противоположных “прямоугольных” выреза, находящихся на одинаковом расстоянии от краев оболочки и имеющие длину, равную 1/3 от длины образующей, и угол раствора 30°. Вырезы образованы сечением оболочки двумя плоскостями, проходящими через ось оболочки, и двумя плоскостями, перпендикулярными оси оболочки.
Расчет проводился для 1/4 симметричной в окружном направлении части оболочки, которая разбивалась на 30 блоков конечных элементов в окружном направлении и на 24 блока в меридиональном.
Считается, что граничные условия на торцах оболочки соответствуют случаю жесткой заделки (на торце меньшего диаметра разрешено осевое перемещение).
Анализ результатов расчетов показывает, что НДС оболочки, ослабленной вырезами, характеризуется ярко выраженными краевыми эффектами в окрестности вырезов и, особенно, вблизи угловых точек вырезов, быстро затухающими по мере удаления от них. Наибольшими по абсолютной величине являются мембранные окружные усилия Ту во внутреннем несущем слое в окрестности угловых точек сквозных и несквозных вырезов. Максимальные значения мембранных напряжений в несущих слоях более, чем в 2.5 раза превышают максимальные значения моментных напряжений. Графики на фигурах, относящиеся к оболочке со сквозными вырезами, показаны темными линиями, а графики, относящиеся к оболочке с несквозными вырезами, на фигурах показаны светлыми линиями.
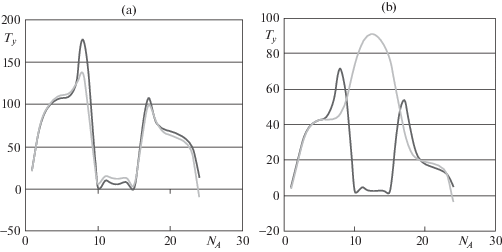
На фиг. 2 представлены графики изменения погонных усилий Ту (кг/см) в несущих слоях (во внутреннем несущем слое – фиг. 2a , во внешнем несущем слое – фиг. 2b ) в сечении плоскостью, проходящей через ось оболочки и меридиональную линию, находящуюся на расстоянии половины размера КЭ в окружном направлении от прямолинейного края выреза (обозначим эту линию А – А) [57]. По оси х (NA) отложены номера КЭ по линии А–А, отсчет ведется от основания конуса с большим диаметром.
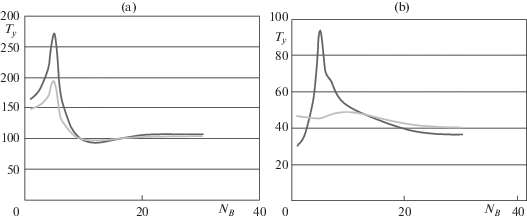
На фиг. 3 представлены графики изменения погонных усилий Ту (кг/см) в несущих слоях (во внутреннем несущем слое – фиг. 3a , во внешнем несущем слое – фиг. 3b ) в сечении плоскостью, перпендикулярной оси оболочки и проходящей через линию, параллельную криволинейному краю выреза c большим диаметром и находящуюся на расстоянии половины размера КЭ от этого края выреза (обозначим эту линию В–В) [57]. По оси х (NB) отложены номера КЭ по линии В–В, отсчет ведется от плоскости симметрии, проходящей через середины криволинейных краев выреза.
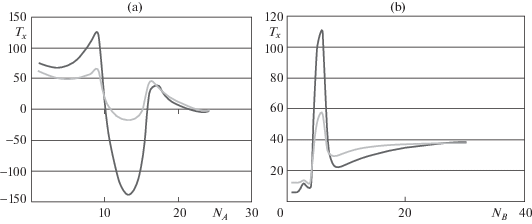
На фиг. 4 представлены графики изменения меридиональных погонных усилий Tx (кг/см) во внутреннем несущем слое по линиям А–А (фиг. 4a ) и В – В (фиг. 4b ) соответственно.
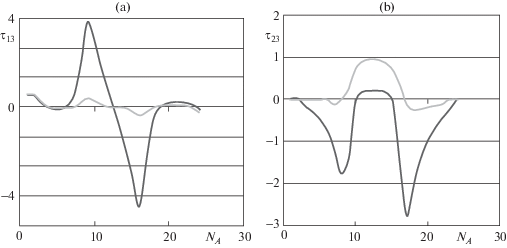
Наибольшими по абсолютной величине в заполнителе трехслойной оболочки со сквозными вырезами являются напряжения τ13, которые более, чем в 2 раза превышают максимальные значения напряжений τ23 и более, чем в 3 раза напряжений σ33, и почти на порядок максимальные значения напряжений τ12, σ11, σ22, которыми в большинстве случаев пренебрегают.
На фиг. 5 а, 5b представлены графики изменения по линии А – А напряжений τ13, τ23 (кг/см2) соответственно.
Из анализа результатов расчетов, представленных на фиг. 2–5 видно, что наличие несквозных вырезов практически не изменяет вид графиков изменения параметров НДС в слоях трехслойной оболочки со сквозными вырезами кроме фиг. 4 b. В случае несквозных вырезов, если сравнивать со сквозными вырезами, значительно сглаживается краевой эффект. При этом максимальные напряжения в слоях уменьшаются и их графики более плавны и сглажены вследствие перераспределения нагрузки, так как значительную ее часть берет на себя внешний несущий слой и частично заполнитель.
Абсолютные величины мембранных погонных усилий в несущих слоях уменьшаются при наличии несквозных вырезов более, чем в 2 раза (фиг. 3, 4 ). На фиг. 2 максимальные значения мембранных погонных усилий в несущих слоях уменьшаются не столь значительно.
Изменение вида графиков мембранных окружных погонных усилий Ту во внешнем несущем слое (фиг. 2b ) вызвано наличием вырезов во внутреннем несущем слое при сохранении сплошности во внешнем несущем слое и в слое заполнителя. Максимальные значения мембранных окружных погонных усилий во внешнем несущем слое наблюдаются в районе середины несквозного выреза, а не вблизи угловых точек вырезов, как для оболочки со сквозными вырезами. Это объясняется действием внутреннего давления, передаваемого на внешний несущий слой.
Наибольшими по абсолютной величине в заполнителе трехслойной оболочки с несквозными вырезами являются напряжения τ13, которые приблизительно в 1.5 раза превышают максимальные значения напряжений τ23, почти в 2 раза максимальные значения напряжений σ33, и почти в 7 раз максимальные значения напряжений σ11, σ22, τ12.
Заключение. На основе блочного конечно-элементного подхода разработана уточненная модель послойного анализа напряженно-деформированного состояния нерегулярных трехслойных оболочек вращения нулевой кривизны. Рассмотренный подход позволяет достаточно точно моделировать неоднородность оболочки и слоя заполнителя, условия закрепления слоев и приложения к ним нагрузок. С использованием аппроксимаций конечных элементов несущих слоев построены аппроксимирующие функции перемещений трехмерного конечного элемента заполнителя и на их основе создана модель для уточненного расчета напряженно-деформированного состояния, позволяющая учесть изменение характеристик материала и параметров напряженного состояния, в том числе по радиальной координате в слое заполнителя. Проведено исследование напряженно-деформированного состояния в слоях трехслойных оболочек со сквозными и несквозными вырезами. Выявлено значительное снижение и сглаживание напряжений краевого эффекта в слоях трехслойных оболочек с несквозными вырезами по сравнению со сквозными вырезами вследствие перераспределения нагрузки, так как значительную ее часть берут на себя слои с ненарушенной сплошностью.
Работа выполнена в рамках государственного задания, номер гос. регистрации АААА-А19-119012290177-0.
Список литературы
Бакулин В.Н., Образцов И.Ф., Потопахин В.А. Динамические задачи нелинейной теории многослойных оболочек: Действие интенсивных термосиловых нагрузок, концентрированных потоков энергии. М.: Наука. Физматлит, 1998. 464 с.
Бакулин В.Н., Острик А.В. Комплексное действие излучений и частиц на тонкостенные конструкции с гетерогенными покрытиями. М.: Физматлит, 2015. 280 с.
Васильев В.В. Механика конструкций из композиционных материалов. М.: Машиностроение, 1988. 272 с.
Григоренко Я.М., Григоренко A.Я. Статические и динамические задачи для анизотропных неоднородных оболочек с переменными параметрами и их числовым решением (обзор) // Прикладная механика. 2013. Т. 49. № 2. С. 3–70.
Паймушин В.Н. Теория среднего изгиба подкрепленных на контуре трехслойных оболочек с трансверсально-мягким заполнителем // Механика композитных материалов. 2017. Т. 53. № 1. С. 3–26.
Григолюк Э.И., Коган Ф.А. Основные математические модели деформирования и прочности многослойных анизотропных оболочек. Прикладные проблемы механики тонкостенных конструкций // Сб. научых статей Ин-та механики МГУ. М.: Изд-во МГУ. 2000. С. 56–109.
Гузь А.Н., Чернышенко И.С., Чехов Вал.Н. и др. Исследования по теории тонких оболочек с отверстиями. Обзор // Прикладная механика 1979. Т. 11. № 15. С. 3–37.
Гузь А.Н., Чернышенко И.С., Чехов Вал.Н., Чехов Вик.Н., Шнеренко К.И. Методы расчета оболочек. Т. 1. Теория тонких оболочек, ослабленных отверстиями. Киев: Наукова думка, 1980. 636 с.
Сало В.А. Краевые задачи статики оболочек с отверстиями. Харьков: НТУ ХПИ. 2003. 216 с.
Бакулин В.Н., Ревенко В.П. Аналитико-численный метод конечных тел решения краевой задачи для цилиндрической ортотропной оболочки с немалым прямоугольным отверстием // Известия вузов. Математика. 2016. № 6. С. 3–14.
Длугач М.И., Гавриленко Г.Д. Расчет ребристых цилиндрических оболочек с большими прямоугольными отверстиями методом сеток // Прикладная механика. 1975. Т. 11. № 12. С. 22–30.
Длугач М.И., Ковальчук Н.В. Метод конечных элементов в применении к расчету цилиндрических оболочек с прямоугольными отверстиями // Прикладная механика. 1973. Т. 9. № 11. С. 35–41.
Морозов В.С. Численный расчет поля смещений консольной цилиндрической оболочки с прямоугольным вырезом при поперечном изгибе. В сб.: Численные и экспериментальные методы исследования прочности, устойчивости и колебаний конструкций ЛА. М.: МАИ. 1983. С. 47–52.
Бакулин В.Н., Репинский В.В. О влиянии размеров прямоугольного выреза на напряженно-деформированное состояние круговой цилиндрической оболочки. Численные методы исследования прочности летательных аппаратов. Тематический сборник научных трудов. М.: Изд-во МАИ. 1988. С. 5–10.
Бакулин В.Н., Снесарев С.Л. Собственные колебания цилиндрических оболочек с прямоугольным вырезом // Изв. вузов. Авиационная техника. Казань. 1988. № 4. С. 3–6.
Пирогов И.М., Юматов В.П., Кутепов С.М. Экспериментальные исследования напряжений в области прямоугольного выреза в стеклопластиковой цилиндрической оболочке. В сб. тр. ВЗПИ – Сопротивление материалов и строительная механика. Вып. 81. М., 1973. С. 189–202.
Воробей В.В. Исследование деформативности стеклопластиковых оболочек, подкрепленных в зоне отверстий // Прикладная механика. 1979. Т. 15. № 1. С. 82–85.
Бакулин В.Н., Мартынович Т.Л., Ревенко В.П. Расчет напряженного состояния цилиндрической композитной оболочки с прямоугольным отверстием // Научно-техническая конференция. Применение композиционных материалов на полимерной и металлической матрицах в машиностроении. Уфа. 1985. С. 80–81.
Преображенский И.Н., Голда Ю.Л., Дмитриев В.Г. Численный метод исследования напряженно-деформированного состояния гибких композитных оболочек вращения, ослабленных вырезами различной формы // Механика композитных материалов. 1985. № 6. С. 1030–1035.
Ревенко В.П. Расчет напряженно-деформированного состояния непологой ортотропной цилиндрической оболочки с эллиптическим отверстием // Прикладная механика. 1988. Т. 24. № 4. С. 57–63.
Бакулин В.Н., Репинский В.В., Снесарев С.Л. Влияние подкрепляющей накладки на напряженно-деформированное состояние ортотропных цилиндрических оболочек с прямоугольным вырезом. Численные и экспериментальные методы исследования прочности конструкций ЛА. Тематический сборник научных трудов МАИ. М.: Изд-во МАИ. 1989. С. 4–6.
Ван Фо Фы Г.А., Савиченко А.А. Напряженное состояние около кругового выреза в трехслойной оболочке // Прикладная механика. 1970. Т. 6. № 8. С. 112–116.
Ван Фо Фы Г.А., Жалило А.И. Равновесие трехслойной сферической оболочки с овальным вырезом. В кн.: Расчет и конструирование изделий из стеклопластиков. Киев: Наукова думка. 1970. С. 79–106.
Ванин Г.А., Савиченко А.А. Исследование взаимодействия двух отверстий на напряженное состояние в трехслойной сферической оболочке // Прикладная механика. 1975. Т. 11. № 12. С. 15–21.
Савиченко А.А. Влияние деформаций сдвига на напряженное состояние трехслойной сферической оболочки, ослабленной отверстием // Прикладная механика. 1976. Т. 12. № 3. С. 47–54.
Пелех Б.Л., Сяський А.А. Распределение напряжений возле отверстий в податливых на сдвиг анизотропных оболочках. Киев: Наукова думка, 1975. 198 с.
Аксентян К.Б., Краснобаев И.А. Основные уравнения изгиба и метод расчета круговой трехслойной цилиндрической оболочки с большим прямоугольным вырезом. В сб.: Теория оболочек и пластин. М.: Наука, 1973. С. 601–605.
Аксентян К.Б., Краснобаев И.А. Расчет круговой трехслойной цилиндрической оболочки с большим прямоугольным вырезом // Изв. вузов. Строительство и архитектура. 1973. № 2. С. 45–51.
Бакулин В.Н., Дячина А.П., Мартынович Т.Л., Осин В.А., Пакош В.А. Экспериментальное и теоретическое исследование задачи об осевом сжатии трехслойной композитной цилиндрической оболочки, ослабленной прямоугольными отверстиями. Всесоюзная конференция “Современные проблемы строительной механики и прочности ЛА”. М.: МАИ, 1983. С. 138.
Алфутов Н.А., Зиновьев П.А., Попов Б.Г. Расчет многослойных пластин и оболочек из композиционных материалов. М.: Машиностроение. 1984. 263 с.
Бакулин В.Н. Метод конечных элементов для исследования напряженно-деформированного состояния трехслойных цилиндрических оболочек. М.: ЦНИИ информ., 1985. 140 с.
Рассказов А.О., Соколовская И.И., Шульга Н.А. Теория и расчет слоистых ортотропных пластин и оболочек. Киев: Вища школа, 1986. 191 с.
Пискунов В.Г., Вериженко В.Е., Присяжнюк В.К. и др. Расчет неоднородных пологих оболочек и пластин методом конечных элементов. Киев: Вища школа, 1987. 200 с.
Бакулин В.Н., Рассоха А.А. Метод конечных элементов и голографическая интерферометрия в механике композитов. М.: Машиностроение, 1987. 312 с.
Рикардс Р.Б. Метод конечных элементов в теории оболочек и пластин. Рига: Зинатне, 1988. 284 с.
Голованов А.И., Тюленева О.Н., Шигабутдинов А.Ф. Метод конечных элементов в статике и динамике тонкостенных конструкций. М.: ФИЗМАТЛИТ, 2006. 392 с.
Бакулин В.Н. Уточненная модель послойного анализа трехслойных нерегулярных конических оболочек // Докл. РАН. 2017. Т. 472. № 3. С. 272–277.
Бакулин В.Н. Эффективная модель послойного анализа трехслойных нерегулярных оболочек вращения цилиндрической формы // Докл. РАН. 2018. Т. 478. № 2. С. 148–152.
Бакулин В.Н. Блочная конечно-элементная модель послойного анализа трехслойных в общем случае нерегулярных оболочек вращения двойной кривизны // Доклады Академии наук. 2019. Т. 484. № 1.
Кантин Д., Клаф Р. Искривленный дискретный элемент цилиндрической оболочки // Ракетная техника и космонавтика. 1968. Т. 6. № 6. С. 82–88.
Бакулин В.Н., Демидов В.И. Трехслойный конечный элемент естественной кривизны // Изв. вузов. Машиностр. 1978. № 5. С. 5–10.
Железнов Л.П., Кабанов В.В. Функции перемещений конечных элементов оболочки вращения как твердых тел // Изв. РАН. МТТ. 1990. № 1. С. 131–136.
Бакулин В.Н. Построение аппроксимаций для моделирования напряженно-деформированного состояния несущих слоев и слоев заполнителя трехслойных неосесимметричных цилиндрических оболочек // Мат. моделир. 2006. Т. 18. № 8. С. 101–110.
Бакулин В.Н. Эффективные модели для уточненного анализа деформированного состояния трехслойных неосесимметричных цилиндрических оболочек // Докл. РАН. 2007. Т. 414. № 5. С. 613–617.
Бакулин В.Н. Построение аппроксимаций и моделей для исследования напряженно-деформированного состояния трехслойных неосесимметричных цилиндрических оболочек // Матем. моделир. 2007. Т. 19. № 12. С. 118–128.
Бакулин В.Н., Каледин Вл.О. О подходе к построению конечно-элементной аппроксимации для эффективного решения задач теории слоистых оболочек // 3 Всесоюзная конференция. Механика неоднородных структур. Львов. Институт прикладных проблем механики и математики АН УССР, 1991. С. 17–18
Каледин Вл.О., Шпиталь С.В. Выбор расчетной схемы при исследовании осесимметричного краевого эффекта в трехслойных цилиндрических оболочках с легким заполнителем // Механика композиционных материалов. 1993. № 5. С. 657–665.
Образцов И.Ф., Бакулин В.Н. Уточненные модели для исследования напряженно-деформированного состояния трехслойных цилиндрических оболочек // Доклады РАН. 2006. Т. 407. № 1. С. 36–39.
Бакулин В.Н. Конечно-элементная модель для анализа напряженно-деформированного состояния трехслойных оболочек // Мат. моделир. 2006. Т. 18. № 1. С. 3–9.
Бакулин В.Н. Тестирование конечно-элементной модели, предназначенной для исследования напряженно-деформированного состояния слоистых нерегулярных оболочек // Матем. моделир. 2009. Т. 21. № 8. С. 121–128.
Новожилов В.В. Теория тонких оболочек. Л.: Судпромгиз, 1951. 344 с.
Репинский В.В. Эффективные конечные элементы для расчета устойчивости тонких анизотропных оболочек вращения // Вопр. оборон. техники. 1997. Сер. 15. Вып. 1 (117). С. 3–7.
Бакулин В.Н. Уточненная модель для расчета напряженно-деформированного состояния трехслойных конических оболочек вращения // Вест. Московского авиационного института. 2011. Т. 18. № 2. С. 211–218.
Бакулин В.Н., Кривцов В.С., Рассоха А.А. Алгоритм получения матрицы жесткости конечного элемента анизотропной оболочки // Изв. вузов. Авиац. техника. 1983. № 4. С. 14–18.
Постнов В.А., Хархурим И.Я. Метод конечных элементов в расчетах судовых конструкций. Л.: Судостроение, 1974. 341 с.
Бакулин В.Н., Репинский В.В. Расчет конических оболочек при локальных нагрузках методом конечных элементов // Материалы ХIХ Международной конференции по вычислительной механике и современным прикладным программным системам, 22–31 мая 2015 г., Алушта. М.: МАИ. 2015. С. 206–208.
Бакулин В.Н. Блочная конечно-элементная модель для послойного анализа напряженно-деформированного состояния трехслойных оболочек с нерегулярной структурой. Изв. РАН. МТТ. 2018. № 4. С. 66–73.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела