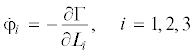Известия РАН. Механика твердого тела, 2019, № 1, стр. 115-140

Введение. В статье решается задача приведения космического аппарата (КА) в положение заданной ориентации оптимальным образом. Способ решения и формализация описания кинематики вращательного движения КА основаны на методе кватернионов [1].

Проблеме управляемых вращений твердого тела вокруг центра масс посвящено достаточно много работ [1–15]. Вопросы создания эффективных режимов и алгоритмов управления ориентацией КА остаются актуальными и сегодня. Наиболее детально задача оптимального управления угловым движением КА решена лишь для двух частных случаев – плоских вращений КА вокруг одной из главных центральных осей инерции [2] и пространственного вращения сферически симметричного тела [1, 3]. Большинство существующих решений задачи пространственного разворота соответствуют вращению вокруг неподвижной оси [1, 2, 4–7]. И хотя принципы оптимизации и алгоритмы управления различны (в том числе, используя прогнозирующие модели [5, 6]), результирующее управление приводит к развороту вокруг оси Эйлера. В то же время разворот в плоскости наименьшего угла разворота во многих практических случаях не является оптимальным, как бы точно он не исполнялся. В работе [7] также описывается построение управлений, стабилизирующих вращение КА вокруг мгновенной оси Эйлера. Однако требование, чтобы КА во время разворота вращался вокруг мгновенной оси Эйлера, – это слишком сильное ограничение на движение КА, делающее процесс переориентации во многих случаях далеким от оптимального.

Как отмечено многими авторами [8, 9], аналитическое решение задачи оптимального разворота в замкнутой форме, если бы оно было найдено, имело бы большой практический интерес, так как позволяет применять на борту КА готовые законы программного управления и изменения оптимальной траектории движения КА (для осесимметричного КА некоторые решения известны [10, 11]). Однако аналитическое решение задачи пространственного разворота для КА с произвольным распределением масс при произвольных граничных условиях по угловому положению КА не найдено; известны лишь некоторые особые случаи решения задачи разворота (например, [1, 9]). Поэтому, в общем случае приходится рассчитывать только на приближенное численное решение задачи. При попытке найти численные решения оптимизационных краевых задач для задач оптимального разворота КА некоторые авторы столкнулись с трудностями, связанными с неоднородностью оптимальной управляющей функции. Часто при проектировании практических (адекватных реальности) алгоритмов управления ориентацией КА за отправную точку берется завершенное решение кинематической задачи разворота. Численное решение задачи оптимального разворота динамически симметричного КА подробно рассмотрено в [11] (авторы [11] решали краевую задачу принципа максимума путем замены переменных и сведением ее к краевой задаче разворота сферически симметричного тела).

Ниже исследуется задача управления переориентацией КА, когда критическим фактором является энергия вращения, которая должна учитываться при формировании оптимального движения (при этом КА считается абсолютно твердым телом). Для решения поставленной задачи используются метод кватернионов и условия оптимальности в форме принципа максимума Л.С. Понтрягина.

1. Уравнения углового движения и постановка задачи управления. Под пространственной переориентацией понимается перевод связанных с корпусом КА осей ОXYZ из одного известного углового положения в другое известное (обычно заданное) угловое положение за конечное время Т. В этом случае параметры разворота (например, компоненты кватерниона разворота) известны заранее, еще до начала маневра; исходные угловые рассогласования могут быть любыми (от нескольких до 180°). При этом угловая ориентация правой системы координат ОXYZ (равно как ее начальное ОX_inY_inZ_in и конечное ОX_fY_fZ_f положения) определяется относительно выбранного опорного базиса I. В работе рассматривается широко распространенный случай, когда опорной является инерциальная система координат ОX_iY_iZ_i (ИСК). В связи с этим исследуется вопрос оптимизации терминального управления, обеспечивающего за конечное время Т совмещение связанной с корпусом КА правой системы координат ОXYZ с программным базисом, положение которого в инерциальном пространстве задано. Предполагается, что управление угловым положением КА осуществляется посредством исполнительных механизмов, создающих моменты относительно всех трех главных центральных осей инерции КА. Для описания пространственного движения КА воспользуемся математическим аппаратом кватернионов (параметров Родрига–Гамильтона). Движение связанного базиса E_SC (связанной системы координат), образованного главными центральными осями инерции КА, относительно опорного базиса I будем задавать кватернионом Λ [1]. Угловое положение начальной и конечной ориентаций КА относительно опорного базиса I определяется кватернионами Λ_in и Λ_f соответственно. Для определенности базис I считается инерциальным. В этом случае имеют место следующие кинематические уравнения:

где L_i , i = 1, 2, 3 − проекции вектора L кинетического момента КА на оси связанного базиса E_SC, J_i – главные центральные моменты инерции КА, λ_j, j = 0, 1, 2, 3 – компоненты кватерниона Λ (λ₀ = sqalΛ – скалярная часть кватерниона Λ; vectΛ = λ₁e₁ + + λ₂e₂ + λ₃e₃ – векторная часть кватерниона Λ; e₁, e₂, e₃ – орты осей связанного базиса E_SC), причем $\left\| \Lambda \right\| = \lambda _{0}^{2} + \lambda _{1}^{2} + \lambda _{2}^{2} + \lambda _{3}^{2} = 1$. Кватернион Λ, задающий текущую ориентацию КА, принят нормированным [1] для удобства ($\left\| \Lambda \right\| = 1$). Запишем краевые условия задачи разворота КА: где Т – время окончания процесса переориентации. Кватернионы Λ_in и Λ_f, задающие ориентацию связанных с КА осей в начальный и конечный моменты времени, имеют произвольные наперед заданные значения, удовлетворяющие условию ||Λ_in|| = ||Λ_f|| = 1 (предполагается, что Λ_in ≠ ±Λ_f). Нередко во время вращений КА приходится ограничивать скоростные параметры движения. Предположим, допустимым считается управление, при котором где Q > 0 – заранее заданная максимально допустимая величина. Эффективность управления будем оценивать по длительности разворота Т, которая определяет степень маневренности КА. Задачу управления пространственной переориентацией сформулируем следующим образом: необходимо КА перевести из положения (1.2) в положение (1.3) в соответствии с уравнениями (1.1) и ограничением (1.4) за минимальное время. При нахождении оптимального закона движения полагаем, что L(t) – кусочно-непрерывная функция времени.

Ограничение в форме (1.4) приходится учитывать довольно часто (из физического смысла Q = 2E_max, где Е_max – максимально допустимая энергия вращения КА). Проблема повышения маневренности КА при ограниченных энергетических возможностях достаточно актуальна (под маневренностью обычно понимают быстроту выполнения маневров). Поэтому сформулированная выше задача управления представляет практический интерес.

2. Решение задачи оптимального управления. Критерий оптимальности в явном виде не зависит от момента М управляющих сил; ограничение (1.4) также не содержит составляющих М_i. Поэтому, искомыми функциями являются компоненты вектора кинетического момента L_i, i = 1, 2, 3, а моменты М_i вычисляются путем подстановки найденных оптимальных функций L_i(t) в динамические уравнения, которые имеют вид:

где М_i, i = 1, 2, 3 – проекции главного момента сил М на главные центральные оси эллипсоида инерции аппарата. Наличие фазового ограничения ||Λ|| = 1 несущественно, так как оно всегда выполняется (при любых движениях КА вокруг центра масс). Переменные ${{\lambda }_{j}}$ (как компоненты кватерниона Λ) обладают характерным свойством – в силу уравнений (1.1) норма ||Λ|| кватерниона Λ есть величина постоянная, $\lambda _{0}^{2} + \lambda _{1}^{2} + \lambda _{2}^{2} + \lambda _{3}^{2}$ = = const. Докажем это утверждение. Возьмем производную по времени левой части указанного равенства

Значит, сделанное утверждение о постоянстве нормы кватерниона Λ, отражающего текущую ориентацию КА, истинно при любых вращениях КА как твердого тела. В начальный момент времени ||Λ(0)|| = ||Λ_in|| = 1, поэтому ||Λ(t)|| = 1 в любой момент времени t ∈ [0, T].

Задача оптимального управления (1.1)–(1.4) рассматривается как классическая кинематическая задача разворота [1] (на угловую скорость граничные условия не накладываются). Вопросы технической реализации оптимального управления с учетом динамики и точности исполнения требуемого (программного) кинетического момента КА – это отдельная проблема, и их проработка требует самостоятельного (и, возможно, достаточно детального) изучения; в рамках кинематической задачи разворота данные вопросы не рассматриваются [1].

Будем решать поставленную задачу управления (1.1)–(1.4), применив принцип максимума Л.С. Понтрягина [16]. Управляющими переменными считаем компоненты кинетического момента L_i. Так как критерий оптимальности не включает позиционных координат λ_j, мы можем использовать универсальные переменные r_i, i = 1, 2, 3 [12], заменяющие сопряженные переменные ψ_j, соответствующие компонентам λ_j кватерниона Λ. Для задачи максимального быстродействия (или максимальной маневренности КА) функция Гамильтона Н равна

Оптимальные функции r_i , как компоненты вектора r, удовлетворяют уравнениям

Функция Гамильтона Н составлена без учета ограничения ||Λ|| = 1 для фазовых переменных в силу равенства ||Λ(0)|| = 1, о чем договорились выше. Вектор r неподвижен относительно инерциального базиса I, из-за чего |r| = const ≠ 0 (постоянство модуля |r| следует из свойств уравнений (2.3)). Решение r(t) системы (2.3) определяется начальным Λ_in и конечным Λ_f положениями КА. Оптимальная функция r(t) вычисляется через кватернион Λ(t) [1, 12]:

(составляющие вектора c_E – проекции вектора r на оси инерциального базиса I). Символ “$ \circ $” – знак умножения кватернионов; $\tilde {\Lambda }$– кватернион, сопряженный кватерниону Λ [1, с. 11–20]. Здесь и далее операция кватернионного умножения на вектор понимается как умножение на кватернион с нулевой скалярной частью; в частности $\Lambda \circ {\mathbf{r}} = \Lambda \circ \Omega $, где Ω – кватернион, у которого sqalΩ = 0, vectΩ = r. Направление вектора c_E зависит от начального и конечного положений КА. Для того, чтобы КА имел требуемую ориентацию на правом конце Λ(T) = Λ_f, необходимо определить вектор c_E (или значение вектора r в начальный момент времени) исходя из получающихся при этом решений системы (1.1). Система уравнений (2.3) совместно с требованием максимальности гамильтониана H и условиями трансверсальности r(0) ≠ 0, r(T) ≠ 0 и Н(Т) = 0 являются необходимыми условиями оптимальности (заметим, что соответствующим выбором оптимального значения |r| всегда можно добиться, чтобы H (T) = 0).

Условия максимума функции H определяют искомое решение L(t); граничные условия по положению (для Λ(0) и Λ(Т)) определяют решения Λ(t) и r(t). Краевая задача принципа максимума заключается в определении значения r(0), при котором решение системы дифференциальных уравнений (1.1), (2.3) с одновременной максимизизацией в каждый момент времени функции Гамильтона Н удовлетворяет условиям разворота Λ(0) = Λ_in и Λ(Т) = Λ_f.

Для нахождения функциональной зависимости оптимальных функций L_i от компонент r_i вектора r введем новые переменные ${{y}_{i}} = {{{{L}_{i}}} \mathord{\left/ {\vphantom {{{{L}_{i}}} {\sqrt {{{J}_{i}}} }}} \right. \kern-0em} {\sqrt {{{J}_{i}}} }}$ и ${{z}_{i}} = {{{{r}_{i}}} \mathord{\left/ {\vphantom {{{{r}_{i}}} {\sqrt {{{J}_{i}}} }}} \right. \kern-0em} {\sqrt {{{J}_{i}}} }}$, i = 1, 2, 3. После замены переменных гамильтониан Н примет вид: H = y₁z₁ + y₂z₂ + y₃z₃ – 1. В условиях ограничения |y|² ≤ Q функция Н максимальна, если векторы y = {y₁, y₂, y₃} и z = {z₁, z₂, z₃} имеют одинаковое направление. Поэтому искомые функции L_i удовлетворяют соотношениям

Задача определения оптимального управления свелась к решению системы уравнений углового движения КА (1.1) и уравнений (2.3) при условии, что управление L выбрано из требования (2.4). Сформулированная задача управления (1.1)–(1.4) решается до формализованной системы уравнений, описывающих оптимальное движение; эта система позволяет обнаружить закономерности оптимального движения в явном виде. Найдем характерные свойства решения задачи (1.1)–(1.4). Поскольку оптимальные функции L_i не зависят от |r|, для удобства перейдем к нормированному вектору р = r/|r| и обозначим r₀ = |r| = const = |r(0)| ≠ 0. Для проекций p_i орта р на оси связанной системы координат справедливы уравнения

В дальнейшем будем использовать компоненты p_i вектора р, а переменные r_i равны r_i = r₀p_i, где r₀ – константа, которую необходимо определить в процессе оптимизации (|p| = 1).

Гамильтониан Н не зависит явно от времени, и длительность Т не фиксирована. Поэтому Н = 0 в любой момент времени t, а не только Н(Т) = 0 в конечный момент времени t = T [17]. Подставив оптимальные значения управляющих функций L_i, вычисленные по соотношениям (2.4), в выражение (2.2) для функции Н с учетом равенств r_i = r₀p_i получим уравнение $r_{0}^{2}Q(p_{1}^{2}{\text{/}}J_{1}^{{}} + p_{2}^{2}{\text{/}}J_{2}^{{}} + p_{3}^{2}{\text{/}}J_{3}^{{}})$ = 1, из которого следует $p_{1}^{2}{\text{/}}J_{1}^{{}} + p_{2}^{2}{\text{/}}J_{2}^{{}} + p_{3}^{2}{\text{/}}J_{3}^{{}}$ = const и ${{r}_{0}} = 1{\text{/}}\left( {С \sqrt Q } \right)$ – оптимальное значение модуля вектора универсальных переменных r, где $C = \sqrt {p_{{10}}^{2}{\text{/}}J_{1}^{{}} + p_{{20}}^{2}{\text{/}}J_{2}^{{}} + p_{{30}}^{2}{\text{/}}J_{3}^{{}}} $; р₁₀, р₂₀, р₃₀ – компоненты вектора р₀ = p(0).

Условия максимума гамильтониана H определили оптимальное решение L(t). Уравнения (1.1) и (2.5) совместно с равенствами (2.4) и r_i = r₀p_i образуют замкнутую систему уравнений. Необходимое условие оптимальности запишем в виде

где b > 0 – скалярная величина. Кинетический момент L и Е_max связаны соотношением

На всем интервале движения 0 < t < Т ограничение (1.4) переходит в строгое равенство и КА вращается с постоянным по модулю кинетическим моментом |L| = const (поэтому во время идеального по маневренности разворота b = const ). Значение параметра С зависит от вектора р(0), который, в свою очередь, определяется граничными значениями Λ(0), Λ(Т) и моментами инерции J₁, J₂, J₃. Оптимальное решение определяется замкнутой системой уравнений (1.1), (2.5), (2.6). Система уравнений (2.5), (2.6) формализует необходимые условия оптимальности для исходной задачи оптимального управления (1.1)–(1.4).

Для получения функциональной зависимости управляющих функций L_i(t) от фазовых координат необходимо решить уравнения (2.5), которые для закона (2.6) принимают вид

где b = const = |L| (в рамках кинематической задачи разворота |L| = const = L_max = = ${{\sqrt Q } \mathord{\left/ {\vphantom {{\sqrt Q } C}} \right. \kern-0em} C}$).

Таким образом, задача построения оптимального управления L(t) состоит, главным образом, в нахождении такого значения вектора p(0), при котором в результате движения КА в соответствии с уравнениями (1.1), (2.5), (2.6) и Λ(0) = Λ_н выполнялось равенство Λ(Т) = Λ_f. Общее решение приведенной системы уравнений найти практически невозможно. Трудность заключается в определении граничных значений p(0) и p(T), которые связаны выражением

или p(Т) = ${{\tilde {\Lambda }}_{{\text{t}}}} \circ $ р(0) $ \circ \,{{\Lambda }_{{\text{t}}}}$ , где ${{\Lambda }_{{\text{t}}}} = {{\tilde {\Lambda }}_{{{\text{in}}}}} \circ {{\Lambda }_{{\text{f}}}}$ – кватернион разворота. Задача оптимального управления с учетом ограничения (1.4) будет решена, если мы найдем решение системы уравнений (1.1), (2.6), (2.7), удовлетворяющее граничным условиям Λ(0) = Λ_in и Λ(Т) = Λ_f. Оптимальный кинетический момент L связан с кватернионом ориентации Λ равенством: где c_Р = const = Λ_in$ \circ $ p₀ $ \circ {{\tilde {\Lambda }}_{{{\text{in}}}}}$. Ключевой искомой характеристикой является значение вектора р₀ = p(0) (напомним р_i0 = р_i(0)). Решение L(t) во время кинематически оптимального разворота (без ограничений на моменты М_i) обладает свойствами (интегралами движения):

Уравнения для управляющих функций L_i формализуются следующим образом:

Они справедливы, так как при развороте за минимальное время при ограничении (1.4) выполняется условие |L| = const (и как следствие b = const). Поскольку искомой функцией принят вектор L кинетического момента КА, то поставленную задачу оптимального управления (кинематическую задачу разворота) можно считать решенной – уравнения (1.1), (2.6) и (2.7) с учетом граничных условий (1.2), (1.3) полностью определяют искомое решение L(t).

Оптимальное управление пространственным разворотом заключается в сообщении КА начальных условий движения (расчетного кинетического момента вначале разворота), поддержании вращения КА с требуемым (программным) изменением кинетического момента L(t), при котором его модуль имеет постоянное значение |L| = const, и сбросе имеющегося кинетического момента до нуля в момент времени t = Т, когда Λ(t) = Λ_f (при достижении КА конечного положения Λ_f). Основная задача – нахождение закона изменения вектора p(t), чтобы в результате решения системы уравнений (1.1), (2.5), (2.6) с начальными условиями Λ(0) = Λ_in граничное условие Λ(T) = Λ_f на правом конце траектории Λ(t) было выполнено (определение вектора p(0) – самостоятельная и достаточно непростая задача).

Теперь определим управляющие моменты М_i, которые обеспечивают оптимальный режим вращения КА в интервале времени 0 < t < T в процессе разворота. Подставим производные функции ${{\dot {L}}_{i}}$, вычисленные по уравнениям (2.11), в динамические уравнения (2.1) и получим М₁ = М₂ = М₃ = 0. Следовательно, идеальным движением (с точки зрения кинематической задачи разворота) является вращение по инерции (движение Эйлера–Пуансо).

Нетрудно показать, что для вращений твердого тела (и, в частности, космического аппарата), удовлетворяющих зависимостям (2.6), в которых b > 0 – скалярная величина, а функции p_i являются решением системы уравнений (2.5) с удовлетворением (2.8), значение интеграла

не зависит от длительности разворота Т и равно [13] где t_pr – прогнозируемое время достижения положения Λ_f (то есть когда выполнится равенство Λ = Λ_f) при вращении твердого тела с кинетическим моментом |L| = K_c из положения Λ(0) = Λ_in в соответствии с уравнениями (1.1), (2.1), в которых М = 0. Характеристика F определяется только условиями разворота Λ_in, Λ_f и инерционными характеристиками КА J₁, J₂, J₃. Длительность оптимального разворота равна T_opt = = ${{FC} \mathord{\left/ {\vphantom {{FC} {\sqrt Q }}} \right. \kern-0em} {\sqrt Q }}$ = F/L_max.

Во многих случаях перед разворотом (когда Λ(t) = Λ_in) L ≠ L_cal, а по завершении разворота (когда Λ(t) = Λ_f) кинетический момент КА должен быть равен нулю. Задача бортовой системы управления заключается в сообщении КА начальных условий движения – расчетного кинетического момента L_cal на момент времени t = 0 и сбросе имеющегося кинетического момента до нуля в момент времени t = Т, когда Λ(t) = Λ_f (при достижении КА конечного положения Λ_f). С момента достижения необходимого начального кинетического момента L_cal и до окончания разворота, когда КА окажется в окрестности требуемого положения Λ_f, момент сил, воздействующих на КА, равен нулю (то есть неуправляемое вращение). Создание начального кинетического момента и ликвидация конечного кинетического момента происходят импульсно (максимально быстро, насколько позволяют это сделать исполнительные органы КА).

3. Построение оптимальной программы пространственного разворота КА. Заметим, что левая часть неравенства (1.4) пропорциональна энергии вращения E = = $(L_{1}^{2}{\text{/}}J_{1}^{{}}\, + \,L_{2}^{2}{\text{/}}J_{2}^{{}}\, + \,L_{3}^{2}{\text{/}}J_{3}^{{}}){\text{/}}2$ и поэтому ограничение (1.4) означает разворот КА с ограниченной энергией (из физического смысла Q = 2E_max). Задача построения оптимального управления сводится к нахождению закона изменения вектора p(t), при котором в результате движения КА согласно уравнениям (1.1), (2.5), (2.6) с начальным условием (1.2) было выполнено граничное условие (1.3). Определяющим в решении задачи оптимального разворота (при построении оптимального программного движения Λ(t)) является нахождение начальных условий p(0) и соответствующего кинетического момента L(0+), равного L(0+) = L_maxp(0). Вектор p(0) зависит от параметров разворота Λ_t и моментов инерции КА J₁, J₂, J₃. Для произвольных значений J₁ ≠ J₂ ≠ J₃ решение поставленной задачи пространственного разворота КА найти достаточно сложно. Трудность состоит в нахождении граничных векторов p(0) и p(T), которые связаны соотношением (2.8). Система уравнений (1.1), (2.5), (2.6) имеет аналитическое решение в элементарных функциях только для динамически симметричного и динамически сферического тел.

Для динамически симметричного КА (когда, например, J₂ = J₃) задача оптимального управления решается до конца. В этом частном случае система (2.7) распадается на две независимые линейные системы дифференциальных уравнений, одна из которых ${{\dot {p}}_{1}} = 0$ (и как следствие р₁ = const = p₁₀), а вторая описывает линейный осциллятор (с параметром р₁₀), у которого переменные р₂ и р₃ – гармонические функции времени. Система (2.11) также разделяется на две автономные системы уравнений, одна из которых ${{\dot {L}}_{1}} = 0$ (если J₂ = J₃), и как следствие L₁ = const = L₁(0), а вторая описывает гармонические колебания функций L₂, L₃. Характеристические уравнения и постоянные времени у систем (2.7) и (2.11) одинаковы; при этом циклическая частота для переменных р₂, р₃ и L₂, L₃ составляет f = |(J₂ – J₁)L₁(0)/J₁J₂. Функции р₁, L₁ соответствуют продольному движению, а функции р₂, р₃ и L₂, L₃ соответствуют поперечному движению. Условие J₂ = J₃ делает как бы независимыми продольное и поперечное движения твердого тела. Такое поведение оптимальных функций р₁, р₂, р₃ и L₁, L₂, L₃ указывает на то, что оптимальный разворот динамически симметричного тела происходит в форме регулярной прецессии. Оптимальное движение в этом частном, но достаточно распространенном случае представляет собой одновременное вращение КА как твердого тела вокруг своей продольной оси ОХ и вокруг некоторого направления η, неподвижного в инерциальном пространстве и составляющего с продольной осью КА определенный постоянный угол. Угловые скорости относительно осей ОХ и η имеют постоянное соотношение. Для динамически симметричного тела (в варианте ${{J}_{1}} \ne {{J}_{2}} = {{J}_{3}}$) решение p(t) запишем следующим образом:

где p₀ = p(0), $\kappa = \dot {\alpha }t$ ($\dot {\alpha } = {\text{const}} = {{L}_{1}}{\text{/}}{{J}_{1}} - {{\sqrt {L_{2}^{2} + L_{3}^{2}} {{p}_{{10}}}} \mathord{\left/ {\vphantom {{\sqrt {L_{2}^{2} + L_{3}^{2}} {{p}_{{10}}}} {\left( {{{J}_{2}}\sqrt {1 - p_{{10}}^{2}} } \right)}}} \right. \kern-0em} {\left( {{{J}_{2}}\sqrt {1 - p_{{10}}^{2}} } \right)}}$ – скорость собственного вращения); ϑ – угол отклонения продольной оси КА от вектора p.

Конкретное значение р₀ определяется исключительно тем, чтобы в результате вращения КА согласно уравнениям (1.1), (2.5), (2.6) выполнялись граничные условия (1.2), (1.3). Программные значения управляющих функций L_i, i = 1, 2, 3 (проекций кинетического момента L на связанные оси) имеют следующий вид:

или где σ₀ = arctg(p₂₀/p₃₀); $\dot {\alpha }$ − угловая скорость собственного вращения (вокруг продольной оси): $\dot {\beta }$ – угловая скорость прецессии (вокруг вектора p). Угловые скорости вращения вокруг осей ОХ и η будут равны: $\dot {\alpha } = \alpha {\text{/}}T$, $\dot {\beta } = \beta {\text{/}}T$ (так как |L| = const, а значит $\dot {\alpha } = {\text{const}}$ и $\dot {\beta } = {\text{const}}$). Для случая регулярной прецессии справедливо соотношение где р₀ = p(0); е₁ – орт продольной оси КА; α – угол поворота КА вокруг своей продольной оси; β – угол поворота КА вокруг вектора р. При этом считается, что |α| ≤ π, 0 ≤ β ≤ π.

В случае динамической симметрии КА (когда J₂ = J₃ = J) соотношения (3.1) совместно с равенствами (3.2) образуют решение системы уравнений (1.1), (2.5) при условии (2.6). Необходимое для синтеза управления решение системы (2.5), (2.6) и (1.1) находится в форме регулярной прецессии. При этом вектор p также описывает конус вокруг продольной оси ОХ в связанной системе координат. При таком типе управления модуль кинетического момента КА сохраняет постоянное значение, а осесимметричное тело движется по “конической траектории”. Перевод КА из положения Λ_in в положение Λ_f осуществляется одновременным поворотом его вокруг вектора c_Е, неподвижного относительно инерциального базиса I, на угол β и вокруг своей продольной оси на угол α. Используя математический аппарат кватернионов для описания поворотов твердого тела вокруг центра масс, получим соотношения, отражающие связь между величинами p₀, α и β. Зависимость оптимальных значений параметров p₀, α , β от граничных угловых положений Λ_in и Λ_f определяется системой уравнений:

где ${{\nu }_{0}}$, ${{\nu }_{1}}$, ${{\nu }_{2}}$, ${{\nu }_{3}}$ – компоненты кватерниона разворота ${{\Lambda }_{{\text{t}}}} = {{\tilde {\Lambda }}_{{{\text{in}}}}} \circ {{\Lambda }_{{\text{f}}}}$; а углы α и β удовлетворяют неравенствам |α| ≤ π, 0 ≤ β ≤ π. Оптимизация в этом частном случае сводится к нахождению значений параметров ϑ , α , β и вектора p₀, удовлетворяющих системе (3.3) (и, соответственно, условиям разворота (1.2), (1.3)). Время маневра переориентации Т пропорционально интегралу (2.12), соответствующему повороту КА из положения Λ_in в положение Λ_f. Когда КА совершает регулярную прецессию интеграл F равен

Время оптимального разворота рассчитывается по формуле

(ϑ – угол между продольной осью КА и вектором p).

Таким образом, кинематическая задача переориентации КА (как твердого тела) полностью решена. Оптимальное управление угловым положением КА реализуется по способу [14]. Оптимальные значения углов α, β и ϑ, удовлетворяющие заданным граничным значениям Λ_in и Λ_f в соответствии с уравнениями (3.3), могут быть определены с помощью устройства [18].

Для сферически симметричного КА (когда J₁ = J₂ = J₃) решение задачи (1.1)–(1.4) значительно упрощается. В этом случае уравнения (2.7) принимают вид ${{\dot {p}}_{i}} \equiv {\text{0}}$ (i = 1, 2, 3), откуда оптимальным является вектор p = const = p₀. Кинематические уравнения (1.1) также приводятся к более простой форме $2\dot {\Lambda } = \Lambda \circ {\mathbf{L}}{\text{/}}{{J}_{1}}$. Условия оптимальности (2.6) выглядят так L = L_maxp₀. Приходим к выводу, что для КА, у которого J₁ = J₂ = J₃, оптимальным разворотом (в смысле быстродействия) является вращение вокруг оси Эйлера в направлении наименьшего угла поворота из положения Λ_in в положение Λ_f; причем оптимальный вектор р₀ совпадает с ортом положительного направления оси Эйлера. Для КА с идеальной симметрией (в форме сферически симметричного твердого тела, у которого J₁ = J₂ = J₃) решение p(t), L(t) есть частный случай регулярной прецессии. В этом варианте сочетания J₁, J₂, J₃ отличительной особенностью оптимального движения является то, что $\dot {\alpha } = 0$ и α = 0; во время оптимального разворота КА вращается вокруг мгновенной оси Эйлера и поэтому

Из вышесказанного запишем решение задачи (1.1)–(1.4) в явном виде:

Задача оптимального разворота сферически симметричного тела рассматривалась неоднократно (в частности, в [1, 3] и в других работах и исследованиях). Так как КА в форме сферически симметричного тела встречаются крайне редко (практически не бывает КА с идеальной симметрией и с одинаковыми моментами инерции относительно всех трех осей), то этот случай управления пространственным разворотом подробно не изучается.

Для произвольного КА (${{J}_{1}} \ne {{J}_{2}} \ne {{J}_{3}}$) решение системы уравнений (1.1), (2.5), (2.6) находится только численными методами (например, методом последовательных приближений). Определение вектора p₀ производится путем решения краевой задачи с граничными условиями (1.2), (1.3) с учетом накладываемых на движение связей (1.1), (2.1), в которых M_i = 0. В результате получим значение кинетического момента в начальный момент времени L_cal, при котором обеспечивается перевод КА из состояния Λ(0) = Λ_in, L(0) = L_cal в состояние Λ(Т) = Λ_f при вращении по инерции (L(Т) при этом принципиального значения не имеет). Значение вектора p₀ связано с найденным L_cal соотношениями p_i0 = L_ical/|L_cal|.

Кватернионы Λ_in и Λ_f, задающие ориентацию связанных с КА осей в начальный и конечный моменты времени, имеют произвольные наперед заданные значения (но при этом ||Λ_in|| = ||Λ_f|| = 1). Разумеется, в моменты времени t = 0 и t = T кинетический момент для номинальной программы вращения КА, определяемый уравнением (2.9), не равен нулю. Следовательно, неизбежны переходные участки: разгон – переход из состояния покоя (когда L = 0) в режим вращения с максимальной энергией E_max = Q/2 и торможение – гашение кинетического момента КА до нуля. Если начальное Λ_in и конечное Λ_f положения и величина L_max таковы, что времена разгона и торможения пренебрежимо малы (по сравнению с временем Т всего разворота), то сообщение КА необходимого кинетического момента L = L_maxр₀, и гашение имеющегося кинетического момента до нуля можно считать импульсным. В этом случае основным будет этап между разгоном и торможением, на котором выполняются условия (2.10). Необходимые условия оптимальности для участка движения с постоянной энергией вращения Е имеют форму (2.5), (2.6). Из динамических уравнений (2.1) следует, что для оптимальных функций L_i(t) управляющие моменты М_i, необходимые для поддержания оптимального режима движения, равны нулю. Определяющим при нахождении оптимальных решений p(t), L(t) является значение вектора p в момент времени t = 0. Решив с учетом уравнений (1.1) и (2.5), в которых соблюдаются соотношения (2.6), кинематическую задачу разворота КА из положения Λ(0) = Λ_in в положение Λ_f , найдем расчетное значение вектора p₀ и соответствующий ему вектор c_Р = const. На участке движения КА с постоянной энергией вращения управляющий момент М = 0 (так как временные функции L_i(t) подчиняются (2.11)).

При оптимальном движении разворот КА из одного углового положения Λ_in в другое положение Λ_f состоит из кратковременного сообщения КА расчетной угловой скорости (номинального кинетического момента), неуправляемого вращения КА и кратковременного (импульсного) гашения угловой скорости до нуля. Для оптимального движения КА время разворота Т и модуль кинетического момента L_max во время вращения КА связаны обратно-пропорциональной зависимостью; то есть для оптимальных значений L_max и Т выполняется соотношение L_maxТ = const.

Ограничение величины располагаемого управляющего момента приводит к появлению ограниченных по времени участков набора и гашения кинетического момента. Следовательно, время разворота Т станет больше, чем Т_opt = K_ct_pr/L_max, которое соответствует идеальному управлению (даже при неизменном значении интеграла (2.12) из-за наличия участков, когда |L(t)| < L_max, длительность разворота увеличивается); напомним, K_ct_pr – значение интеграла (2.12) при вращении КА по инерции. Необходимо, чтобы времена разгона и торможения были минимальными. Если на этапах разгона и торможения модуль момента М постоянен, временные характеристики программы движения могут быть определены достаточно точно.

4. Оптимальное управление разворотом с учетом ограниченности момента сил. Рассмотренный выше случай является предельным и соответствует варианту решения задачи разворота, когда существенным (переходящим в строгое равенство) является лишь ограничение (1.4). Практическое значение имеют задачи, в которых L(0) = L(Т) = 0 (такие условия разворота КА наиболее характерны). Поэтому необходимы этапы раскрутки КА до вращения с максимальным кинетическим моментом L_max и гашения кинетического момента КА до нуля. Между разгоном и торможением выполняются уравнения (2.5) и (2.6), в которых $b = {{L}_{{\max }}} = {{\sqrt Q } \mathord{\left/ {\vphantom {{\sqrt Q } C}} \right. \kern-0em} C} = {\text{const}}$. Если условия разворота Λ_in, Λ_f и время Т таковы, что времена разгона и торможения пренебрежимо малы (по сравнению с длительностью всего разворота), то сообщение КА необходимого кинетического момента L_max и гашение имеющегося кинетического момента до нуля можно считать импульсным, и почти на всем развороте (между разгоном и торможением) |L(t)| = const = L_max с выполнением уравнений (2.5), (2.11) (условие (1.4) переходит в строгое равенство). Определяющим при нахождении оптимальных решений p(t), L(t) является значение вектора р на момент времени t = 0.

Если момент управления М ограничен, то сообщение требуемого кинетического момента до уровня |L| = L_max в начале разворота и гашение имеющегося кинетического момента до нуля в конце разворота занимают некоторое конечное (отличное от нуля) время. Интерес представляет общий случай, когда условия разворота Λ_in и Λ_f таковы (при известных инерционных характеристиках КА J₁, J₂, J₃), что переходными участками (разгоном и торможением) нельзя пренебречь. Пусть управляющий момент М ограничен условием

где u₀ > 0 – некоторая наперед заданная положительная величина (u₀ ≠ 0).

Исследуем оптимальное движение КА на этапах набора и гашения кинетического момента. При решении задач набора и гашения кинетического момента фазовыми переменными будем считать компоненты вектора L кинетического момента. Рассмотрение начнем с гашения угловой скорости КА за минимальное время. Задача формулируется следующим образом: необходимо перевести КА из состояния L(t₀) ≠ 0 в состояние покоя L(Т) = 0 в соответствии с уравнениями (2.1) в условиях ограничения (4.1) за минимальное время; здесь t₀ – момент начала остановки вращения.

Решим задачу наискорейшего гашения исходного кинетического момента L₀, используя принцип максимума Л.С. Понтрягина [16]. Введем сопряженные переменные φ _i, i = 1, 2, 3, соответствующие переменным L_i, и составим функцию Гамильтона

Согласно [16] уравнения для сопряженных функций φ_i таковы:

Сопряженная система уравнений имеет вид

Найдем максимум функции Гамильтона Г по управлению М = {М₁, М₂, М₃} с учетом ограничения (4.1). Для удобства перейдем к переменным ${{u}_{i}} = {{{{M}_{i}}} \mathord{\left/ {\vphantom {{{{M}_{i}}} {\sqrt {{{J}_{i}}} }}} \right. \kern-0em} {\sqrt {{{J}_{i}}} }}$ и перепишем функцию Г в виде $\Gamma = {{u}_{1}}{{\varphi }_{1}}\sqrt {{{J}_{1}}} + {{u}_{2}}{{\varphi }_{2}}\sqrt {{{J}_{2}}} + {{u}_{3}}{{\varphi }_{3}}\sqrt {{{J}_{3}}} + {{\Gamma }_{{{\text{inv}}}}}$, где Г_inv не зависит от искомых функций М_i. В условиях ограничения |u| ≤ u₀ функция Г максимальна, если ${{u}_{i}} = a{{\varphi }_{i}}\sqrt {{{J}_{i}}} $, где а > 0 (здесь u = {u₁, u ₂, u₃}). При оптимальном управлении ограничение (4.1) переходит в строгое равенство; поэтому оптимальными являются функции

Система (2.1), (4.2), (4.3) имеет единственное решение, которое удовлетворяет соотношениям

где ρ – скалярная величина. Подставляя функции φ_i, вычисленные по формулам (4.4), в уравнения (4.2), получаем

Для всех i = 1, 2, 3 имеем ${{\dot {\varphi }}_{i}} = \rho ({{\dot {L}}_{i}} - {{M}_{i}}){\text{/}}{{J}_{i}}$. С другой стороны, из (4.4) следует ${{\dot {\varphi }}_{i}} = (\rho {{\dot {L}}_{i}} + \dot {\rho }{{L}_{i}}){\text{/}}{{J}_{i}}$. Приравнивая оба выражения, получаем ρM_i = –${\dot {\rho }}$L_i. При оптимальном торможении функции L_i(t) и φ_i(t) связаны соотношениями (4.4) (очевидно М ⋅ L < 0). Отсюда с учетом уравнений (4.3), (4.4) и ограничения (4.1) оптимальное управление находится по выражению

Оптимальное решение L(t) для участка торможения определяется условием М || L.

Покажем, что на всем отрезке времени от t = t₀ до t = Т вектор φ = {φ₁, φ₂, φ₃} сопряженных переменных отличен от нуля. Нетрудно видеть, что для функции ρ(t) справедливо уравнение $\dot {\rho }\sqrt {2E} $ – u₀ρ = 0. Его решением будет ρ(t) = $ - {{C}_{1}}{\text{/}}\sqrt {L_{1}^{2}{\text{/}}{{J}_{1}}\, + \,L_{2}^{2}{\text{/}}{{J}_{2}}\, + \,L_{3}^{2}{\text{/}}{{J}_{3}}} $, где С₁ = const > 0 (ρ < 0, так как М ⋅ L < 0). Заметим, что $\sqrt {2E(t)} = {{E}_{0}} - {{C}_{2}}(t - {{t}_{0}})$, где ${{E}_{0}} = \sqrt {2E({{t}_{0}})} $, С₂ = const > 0. Подставив ρ(t) в равенства (4.4) и приняв во внимание зависимости (4.5), получим u₀φ_i = С₁М_i/J_i, $i = \overline {1,3} $. Так как М ≠ 0, то и φ ≠ 0 (потому, что С₁ > 0).

Функция Г не зависит явно от времени, и время остановки вращения Т не фиксировано. Поэтому необходимо выполнение условия Г = 0 [17]. Проверим оптимальность найденного решения (4.4), (4.5) с точки зрения требования Г = 0. Подставим φ_i и М_i, вычисленные по формулам (4.4), (4.5) с учетом оптимальной функции ρ(t), в функцию Г и получим

Значит С₁ = 1/u₀ – оптимальное значение коэффициента С₁. Является доказанным, что функции φ_i(t) и L_i(t), обладающие свойством (4.4), удовлетворяют необходимым условиям оптимальности (системе уравнений (4.2), условию максимума функции Г и условиям трансверсальности φ(0) ≠ 0, φ(T) ≠ 0 и Г(Т) = 0). Таким образом, связь момента сил М с кинетическим моментом L при оптимальном управлении на участке торможения выражается в виде

где J_SC = diag(J₁, J₂, J₃) – тензор инерции КА. В оптимальном движении управляющий момент не меняет своего направления в инерциальной системе координат, а кинетический момент КА составляет с управляющим моментом 180 град. Для энергии вращения E, как функции времени, справедливо уравнение $\dot {E} = - {{u}_{0}}\sqrt {2E} $ (поэтому С₂ = и₀). Учитывая, что L(Т) = 0, находим $\sqrt {2E(t)} = {{E}_{0}}(T - t){\text{/}}(T - {{t}_{0}})$; откуда Е(t) = Е(t₀)(Т – ‒ t)²/(Т – t₀)².

Рассмотренная задача соответствует торможению КА (гашению имеющегося кинетического момента L до нуля) наиболее эффективным образом. Задача сообщения требуемого кинетического момента корпусу КА за минимальное время решается аналогично. Для оптимальной раскрутки КА справедливо то же решение M || L и (4.4), только М ⋅ L > 0 (и поэтому ρ > 0). Оптимальное управление на участке разгона запишем следующим образом:

Как при разгоне, так и при торможении оптимальным по быстродействию является управление, при котором управляющий момент все время параллелен кинетическому моменту КА.

Полученный результат легко объясняется из физического смысла. Исследуем поведение энергии вращения $E = (L_{1}^{2}{\text{/}}{{J}_{1}} + L_{2}^{2}{\text{/}}{{J}_{2}} + L_{3}^{2}{\text{/}}{{J}_{3}}){\text{/}}2$. Производная равна

что соответствует механической мощности. Используя переменные u_i , получим

Величина $\left| {dE{\text{/}}dt} \right|$ максимальна в каждый момент времени (при |u| ≤ u₀), если u_i = = $\mu {{L}_{i}}{\text{/}}\sqrt {{{J}_{i}}} $, где μ – скалярная величина. Откуда M_i = μL_i, то есть M || L. Если μ < 0, то торможение; если μ > 0, то разгон. Управляющие моменты M_i при оптимальном движении L(t) равны

(“+” соответствует разгону, “–” – торможению) или в векторной форме M = = ${{ \pm {{u}_{0}}{\mathbf{L}}} \mathord{\left/ {\vphantom {{ \pm {{u}_{0}}{\mathbf{L}}} {\sqrt {2E} }}} \right. \kern-0em} {\sqrt {2E} }}$.

Функция Е(t) подчиняется дифференциальному уравнению $\dot {E} \pm {{u}_{0}}\sqrt {2E} = 0$ (здесь, в этом уравнении, знак “+” берется для этапа торможения, а знак “–” – для этапа разгона). Его решением будут следующие функции: Е(t) = $u_{0}^{2}$t²/2 (для разгона) и Е(t) = = $u_{0}^{2}$(Т – t)²/2 (для торможения). Вариант Е(t) ≡ 0 не рассматривается, так как функция энергии Е(t) должна быть такой, чтобы Е(t_ac) = Е(τ) ≠ 0 и Е(t_br) ≠ 0, где τ – длительность разгона (торможения); и t_br – момент начала торможения. Заметим, что при любых условиях разворота Е(Т/2) > 0, из-за чего функция Е(t) не может быть тождественно равна нулю. Общее решение таково

На участке разгона Е(t = 0) = 0, а Е(t > 0) > 0; следовательно С_t = 0 и Е(t) = $u_{0}^{2}$t²/2.

На участке торможения Е(t = Т) = 0, а Е(t < Т) > 0; значит С_t = –Т и Е(t) = $u_{0}^{2}$(t – Т)²/2. Отмечаем, что $\sqrt {2E} = {{u}_{0}}(T - t)$, а $\dot {E} = u_{0}^{2}(t - T)$, и поэтому для энергии Е(t) остается справедливым правило $\dot {E} = - {{u}_{0}}\sqrt {2E} $, записанное ранее при решении задачи оптимальной остановки вращения КА.

Запишем динамические уравнения (2.1), подставив в них уравнения (4.8) для моментов M_i , соответствующие оптимальному движению (по критерию максимального быстродействия)

Из (4.8) найдем ${{L}_{i}} = \pm {{M}_{i}}\sqrt {2E} {\text{/}}{{u}_{0}}$, где знак “+” соответствует разгону, а знак “–” – торможению. Далее (после дифференцирования)

так как $d(\sqrt {2E} ){\text{/}}dt = \pm {{u}_{0}}$. С другой стороны (из уравнений (2.1)) ${{\dot {L}}_{1}}$ = M₁ + (J₂ – ‒ J₃)L₂L₃/J₂J₃. Приравняем оба выражения М₁ ± ${{\dot {M}}_{1}}\sqrt {2E} $/u₀ = М₁ + (J₂ – J₃)L₂L₃/J₂J₃; откуда (J₂ – J₃ )L₂L₃/J₂J₃ = ±${{\dot {M}}_{1}}\sqrt {2E} $/u₀. Из (4.8) вычислим L₂L₃/J₃ = ±L₃M₂$\sqrt {2E} $/J₃u₀ и L₂L₃/J₂ = ±L₂M₃$\sqrt {2E} $/J₂u₀. В итоге ±${{\dot {M}}_{1}}\sqrt {2E} $/u₀ = ±(L₃M₂$\sqrt {2E} $/J₃u₀ – L₂M₃$\sqrt {2E} $/J₂u₀). Сокращая на ±$\sqrt {2E} $/u₀, получим уравнение ${{\dot {M}}_{1}}$ = L₃М₂/J₃ – L₂М₃/J₂. Аналогично рассуждая, определим уравнения для переменных М₂, М₃. Окончательный их вид будет таким

Переписав (4.9) в векторной форме, приходим к следующим соотношениям для вектора М:

где ω – вектор абсолютной угловой скорости КА. Из уравнений (4.10) следует равенство |М| = const. А значит и пропорция Е/|L|² остается постоянной на всем этапе разгона (а также торможения); этот вывод следует из формул (4.8), записанных для оптимального управления. Дифференциальные уравнения (4.9) для момента сил М указывают на то, что, изменяясь относительно связанной системы координат КА, оптимальный вектор М остается неизменным относительно инерциальной системы координат. В результате получили, что при оптимальном движении КА во время разгона и торможения управляющий момент М должен быть постоянным (зафиксированным) относительно инерциальной системы координат (и поэтому величина |М| = const). При оптимальном движении (на участках разгона и торможения): поскольку $M = {{ \pm {{u}_{0}}{\mathbf{L}}} \mathord{\left/ {\vphantom {{ \pm {{u}_{0}}{\mathbf{L}}} {\sqrt {2E} }}} \right. \kern-0em} {\sqrt {2E} }}$ ($\dot {E}$ = М ⋅ ω = ${{ \pm {{u}_{0}}\omega \cdot {\mathbf{L}}} \mathord{\left/ {\vphantom {{ \pm {{u}_{0}}\omega \cdot {\mathbf{L}}} {\sqrt {2E} }}} \right. \kern-0em} {\sqrt {2E} }} = \pm {{u}_{0}}\sqrt {2E} $, так как ω ⋅ L = 2E).

Приходим к заключению – как при разгоне, так и при торможении оптимальным по быстродействию является управление, при котором управляющий момент все время параллелен кинетическому моменту КА. Управляющий момент М при оптимальном разгоне (торможении) описывается зависимостями (4.8), в которых знак “+” соответствует участку разгона КА до требуемого кинетического момента, а “–” – участку гашения имеющейся угловой скорости (при торможении ρ < 0, а при разгоне ρ > 0). Если l – орт вектора L кинетического момента КА, то с учетом свойств (4.8), (4.10) и равенства L_i = |L|l_i делаем вывод: на участках разгона и торможения $l_{1}^{2}{\text{/}}{{J}_{1}}\, + \,l_{2}^{2}{\text{/}}{{J}_{2}}\, + \,l_{3}^{2}{\text{/}}{{J}_{3}}$ = = const.

Обозначим ${{m}_{0}} = {{{{u}_{0}}} \mathord{\left/ {\vphantom {{{{u}_{0}}} {\sqrt {l_{1}^{2}{\text{/}}{{J}_{1}} + l_{2}^{2}{\text{/}}{{J}_{2}} + l_{3}^{2}{\text{/}}{{J}_{3}}} }}} \right. \kern-0em} {\sqrt {l_{1}^{2}{\text{/}}{{J}_{1}} + l_{2}^{2}{\text{/}}{{J}_{2}} + l_{3}^{2}{\text{/}}{{J}_{3}}} }}$. Тогда |M| = m₀. Оптимальные управления равны M_i = ±m₀l_i = ±m₀L_i/|L| .

В момент времени t = 0 кинетический момент КА L = 0, и условие (1.4) выполняется при любом М. Поэтому оптимальным по быстродействию будет управление (4.7). Пока 2Е(t) < Q, управляющий момент М = m₀L/|L| будет оптимальным. В момент времени t_p наступает равенство 2Е(t) = Q, и дальнейший рост энергии Е невозможен (управление в виде (4.7) будет недопустимым в силу ограничения (1.4)). Оптимальным по быстродействию будет управление, при котором 2Е(t) = Q и функция Гамильтона Н максимальна. Функция Н принимает максимальное значение в условиях ограничения (1.4) на движениях, удовлетворяющих уравнениям (2.11). Очевидно, что вращение КА с максимальной энергией будет оптимальным по быстродействию, при этом управляющий момент M = 0, что не приводит к нарушению требования (4.1). Так же очевидно, что из-за наличия граничного условия L(Т) = 0 должен существовать такой момент времени t_т, начиная с которого производят гашение кинетического момента с максимальным моментом управления М. Как только 2 Е(t) < Q, так в последующем движении КА ограничение (1.4) становится несущественным и, следовательно, может не учитываться при t > t_т. В силу симметричности участков разгона и торможения оптимальным для наискорейшего гашения кинетического момента является управление М = –m₀L/|L|. Момент времени t_т выбирается с таким расчетом, чтобы к моменту полной остановки L = 0 КА занял требуемое угловое положение Λ_f. Упрощающим обстоятельством является разделение по времени (чередование) участков, когда существенно одно из ограничений (4.1), (1.4) для переменных М_i и L_i. При развороте КА лишь одно из условий (1.4) или (4.1) переходит в строгое равенство; отрезки времени, на которых одно из неравенств (1.4) или (4.1) становится строгим равенством, чередуются. На участках разгона и торможения предельно максимальным является управляющий момент М, строгим равенством становится условие (4.1), а в интервале между разгоном и торможением условие (1.4) выполняется как равенство, предельно максимальной будет энергия вращения Е. Точки излома t_p, t_т модуля кинетического момента – единственные моменты времени, когда оба ограничения (1.4) и (4.1) переходят в строгие равенства.

Таким образом, для нулевых граничных условий L(0) = L(Т) = 0 оптимальный разворот КА включает две фазы, в течение которых действует максимальный по величине управляющий момент – разгон (увеличение угловой скорости) и торможение (гашение угловой скорости до нуля), и фазу неуправляемого вращения, при котором справедливы уравнения (2.11). На участке разгона векторы М и L имеют одинаковое направление, а на участке торможения векторы М и L имеют противоположные направления; вектор кинетического момента L имеет постоянное направление в инерциальном пространстве, но меняется по величине (на участке разгона он увеличивается с нуля до максимального значения L_max, а на участке торможения – уменьшается до нуля). В силу того, что начальная и конечная угловые скорости равны нулю, а величина управляющего момента постоянна |M| = const = m₀, длительность этапов разгона и торможения будет одинакова. В интервале времени между набором и гашением кинетического момента энергия вращения максимальна и постоянна Е = const = = Q/2. Искомое решение L(t) на участке номинального движения (между разгоном и торможением) обладает свойствами (2.10). Максимальное значение L_max модуля кинетического момента равно ${{L}_{{\max }}} = {{\sqrt Q } \mathord{\left/ {\vphantom {{\sqrt Q } C}} \right. \kern-0em} C}$.

Продемонстрируем, что все три участка движения – разгон, неуправляемое вращение, торможение – объединяет одно общее свойство: кинетический момент L на всех отрезках времени [0, t_ac], [t_ac, t_br], [t_br, T] (а значит на всем интервале управления [0, T] ) параллелен одной и той же прямой, неподвижной в инерциальной системе координат (здесь t_ac – момент окончания разгона, t_br – момент начала торможения). На участке разгона ${\mathbf{\dot {l}}}$ = –ω × l и Λ $ \circ $ l $ \circ \,\tilde {\Lambda }$ = const. На участке торможения ${\mathbf{\dot {l}}}$ = –ω × l и Λ $ \circ $ l $ \circ \,\tilde {\Lambda }$ = = const . Между разгоном и торможением ${\mathbf{\dot {p}}}$= –ω × p, Λ $ \circ $ p $ \circ \,\tilde {\Lambda }$ = c_Р = const и p ≡ l . В силу непрерывности функции l (t) заключаем, что ${\mathbf{\dot {l}}}$ = –ω × l, Λ $ \circ $ l $ \circ \,\tilde {\Lambda }$ = const = c_Р и l = p на всем отрезке времени от t = 0 до t = Т. Таким образом, на всем интервале управления t ∈ [0, T] для орта кинетического момента l выполняется условие l = $\tilde {\Lambda } \circ $ c_P$ \circ $ Λ, где c_Р = const . Доказано, что на протяжении всего разворота направление кинетического момента относительно инерциальной системы координат остается постоянным.

Для участка разгона c_I = Λ $ \circ $ l(t) $ \circ \tilde {\Lambda }$ = const . Откуда l (t_ac) = $\tilde {\Lambda }({{t}_{{{\text{ac}}}}}) \circ $ c_I$ \circ $ Λ(t_ac), где t_ac – время начала неуправляемого вращения КА. На участке вращения по инерции [t_ac, t_br] орт кинетического момента совпадает с вектором p, и в момент времени t = t_ac будет p(t_ac) = l(t_ac) = $\tilde {\Lambda }({{t}_{{{\text{ac}}}}}) \circ $ c_I(t_ac) $ \circ $ Λ(t_ac), то есть на время t = t_ac имеем c_I(t_ac) = c_P. В момент начала торможения t = t_br будет p(t_br) = $\tilde {\Lambda }({{t}_{{{\text{br}}}}}) \circ $ c_I(t_ac ) $ \circ $ Λ(t_br), так как c_I(t_br) = c_I(t_ac) (при вращении по инерции направление кинетического момента относительно инерциальной системы координат не меняется). Так как l (t_ac) = p(t_ac), то l (t_br) = p(t_br). При торможении l(t) = $\tilde {\Lambda } \circ $ c_I(t_br) $ \circ $ Λ; причем l(t_br) = p(t_br). Найдем p(t) = $\tilde {\Lambda } \circ $ c_I(t_br) $ \circ $ Λ = l (t), так как c_I(t_br) = c_I(t_ac) = c_P. Поэтому p(Т) = l(Т). Убедились, что на всем отрезке времени [0, T] будет Λ $ \circ $ l(t) $ \circ \tilde {\Lambda }$ = const и p(t) ≡ l(t).

При оптимальном управлении КА вращается по “траектории свободного движения”. Под “траекторией свободного движения” понимается совокупность угловых положений (значений Λ), занимаемых твердым телом в процессе вращения его по инерции. В геометрической интерпретации “траектория свободного движения” есть след изображающей точки Λ(t), где Λ(t) является решением системы дифференциальных уравнений (1.1), (2.1) при M = 0 и L ≠ 0. Вектор p параллелен орту кинетического момента; из чего вытекает равенство модуля управляющего момента на участке разгона и участке торможения, а значит равенство длительности разгона и торможения. Управляющий момент М во время всего разворота от t = 0 до t = Т параллелен кинетическому моменту L или равен нулю. Поэтому направление кинетического момента относительно инерциальной системы координат неизменно. Постоянная c_I, характеризующая “траекторию свободного движения”, одна и та же на всей оптимальной траектории вращения КА во время оптимального разворота (на всем отрезке времени 0 ≤ t ≤ T). На основе указанных свойств оптимального движения L(t), заключаем, что решение краевой задачи и определение вектора р₀ и характеристики F упрощается и совпадает с решением той же краевой задачи для кинематически оптимального разворота, когда |L| = const .

Оценим “проигрыш” по времени (в маневренности) из-за наличия участков разгона и торможения продолжительностью Δt_ac и Δt_br. Для идеального маневра время разворота ${{{{T}_{{{\text{opt}}}}} = FC} \mathord{\left/ {\vphantom {{{{T}_{{{\text{opt}}}}} = FC} {\sqrt Q }}} \right. \kern-0em} {\sqrt Q }}$, а с учетом длительности переходных участков (из-за ограничения (4.1)) время

Так как увеличение длительности разворота ΔТ составляет ΔТ = L_max/m₀ = ${{\sqrt Q } \mathord{\left/ {\vphantom {{\sqrt Q } {{{u}_{0}}}}} \right. \kern-0em} {{{u}_{0}}}}$, то относительный “проигрыш” в маневренности равен $\delta T = \Delta T{\text{/}}{{T}_{{{\text{opt}}}}} = {Q \mathord{\left/ {\vphantom {Q {({{u}_{0}}FC)}}} \right. \kern-0em} {({{u}_{0}}FC)}}$.

Таким образом, для задачи пространственной переориентации определены тип траектории и ключевые свойства оптимального движения КА. Задача оптимального по времени управления разворотом КА в условиях ограничения (1.4) полностью решена. Предельными случаями управления являются: (a) кинематически оптимальный разворот; и (b) управление с одной точкой переключения, при котором отсутствуют интервалы времени, когда М = 0.

Так как при торможении КА момент М направлен строго против кинетического момента L, то момент начала торможения может быть спрогнозирован достаточно точно. Длительность остановки вращения равна $\tau = {{\sqrt {2E} } \mathord{\left/ {\vphantom {{\sqrt {2E} } {{{u}_{0}}}}} \right. \kern-0em} {{{u}_{0}}}}$. Начало участка торможения определяется условием

или где q _j − компоненты кватерниона рассогласования $\tilde {\Lambda }(t) \circ {{\Lambda }_{{\text{f}}}}$ (j = 0, 1, 2, 3); ω_i – проекции вектора угловой скорости КА ω на оси связанной с КА системы координат; К = = |J_SC ⋅ ω| – величина кинетического момента КА (так как τ = |L|/m₀). Предлагаемый закон управления кинетическим моментом улучшает маневренность КА при ограниченной энергии вращения.

Если Q > Q_cr = Fu₀C, то ограничение (1.4) становится несущественным, и время оптимального разворота равно $T = 2\sqrt {FC{\text{/}}{{u}_{0}}} $ (при этом максимальная энергия E_max = Fu₀C/2).

Рассмотренная выше задача управления достаточно актуальна. Не менее важной и интересной является и обратная задача – перевод КА из состояния Λ(Т) = Λ_in, L(0) = 0 в состояние Λ(Т) = Λ_f, L(Т) = 0 за заданное время Т = Т_sp таким образом, чтобы величина

была минимальной. Если бы нам удалось найти связь максимальной энергии вращения E_max с длительностью маневра переориентации Т, то решив задачу максимального быстродействия (1.1)–(1.4), (4.1), в которой Q = 2E_max, мы получим искомое решение L(t) задачи оптимального разворота из состояния Λ(Т) = Λ_in, L(0) = 0 в состояние Λ(Т) = Λ_f, L(Т) = 0 за заданное время Т = Т_sp с минимальной энергией вращения.

Опираясь на ключевые свойства оптимального движения, найдем функциональную зависимость между временем разворота Т и максимальной энергией вращения E_max. Напомним, что для оптимального разворота КА, как вращения по “траектории свободного движения”, когда направление кинетического момента КА неизменно относительно инерциальной системы координат, известна характеристика F (интеграл от модуля кинетического момента за время разворота); она как и вектор р₀ определяется только значениями Λ_in, Λ_f и моментами инерции J₁, J₂, J₃ и не зависит от функции |L(t)|. На основании данного свойства запишем уравнение

(так как длительности разгона и торможения одинаковы и равны τ = L_max/m₀). Отсюда Т = F/L_max + L_max/m₀ при условии L_max ≤ m₀T/2, где m₀ = u₀/C (константа C = = $\sqrt {p_{{10}}^{2}{\text{/}}J_{1}^{{}}\, + \,p_{{20}}^{2}{\text{/}}J_{2}^{{}}\, + \,p_{{30}}^{2}{\text{/}}J_{3}^{{}}} $). Энергия вращения $E = {{\left| L \right|}^{2}}{{(p_{1}^{2}{\text{/}}J_{1}^{{}} + p_{2}^{2}{\text{/}}J_{2}^{{}} + p_{3}^{2}{\text{/}}J_{3}^{{}})} \mathord{\left/ {\vphantom {{(p_{1}^{2}{\text{/}}J_{1}^{{}} + p_{2}^{2}{\text{/}}J_{2}^{{}} + p_{3}^{2}{\text{/}}J_{3}^{{}})} 2}} \right. \kern-0em} 2}$. Используя свойство $p_{1}^{2}{\text{/}}J_{1}^{{}} + p_{2}^{2}{\text{/}}J_{2}^{{}} + p_{3}^{2}{\text{/}}J_{3}^{{}}$ = const, получаем соотношение E_max = = $L_{{\max }}^{2}{{C}^{2}}{\text{/}}2$, связывающее параметры L_max и Е_max оптимального разворота. Следовательно (так как ${{L}_{{\max }}} = {{\sqrt {2{{E}_{{\max }}}} } \mathord{\left/ {\vphantom {{\sqrt {2{{E}_{{\max }}}} } C}} \right. \kern-0em} C}$). Функция F/L_max + L_max/m₀ имеет одну точку экстремума ${{L}_{{{\text{cr}}}}} = \sqrt {{{m}_{0}}F} $ (критическое значение уровня L_max), которой соответствует Е_cr = Fu₀C/2 и время ${{T}_{{{\text{cr}}}}} = 2\sqrt {F{\text{/}}{{m}_{0}}} $. Ранее было показано, что время разворота Т не может быть меньше ${{T}_{{{\text{fast}}}}} = 2\sqrt {FC/{{u}_{0}}} $, где Т_fast – минимально возможное время разворота КА с моментами инерции J₁, J₂, J₃ из положения Λ_in в положение Λ_f с учетом ограничения (4.1) (при определении значения Т_fast ограничение (1.4) игнорируется). Зная взаимозависимость u₀ и m₀ находим T_cr = Т_fast.

Так как при ${{L}_{{\max }}} \leqslant \sqrt {{{m}_{0}}F} = {{L}_{{{\text{cr}}}}}$ время разворота Т – монотонно убывающая функция максимального кинетического момента L_max (значения ${{L}_{{\max }}} \geqslant \sqrt {{{m}_{0}}F} $ не рассматриваются, поскольку должно быть L_max/m₀ ≤ F/L_max, и цель оптимизации управления – минимизация показателя (4.12)), то и обратная функция – зависимость L_max от времени Т – монотонно убывающая функция. Как следствие, G(Т) и Е_max(T) – монотонно убывающие функции длительности разворота Т. Поэтому каждому конкретному значению Т соответствует единственное минимально возможное значение Е_max (и показателя (4.12)). Если время разворота Т задано, то из уравнений (4.13), (4.14) легко найти оптимальные значения L_max и Е_max

Откуда оптимальное (минимально возможное) значение (4.12) равно

На основании свойства оптимального движения, которое заключается в том, что Е_max – монотонно убывающая функция длительности Т, заключаем, что оптимальным разворотом в смысле минимума энергии Е_max (при фиксированном времени Т) является вращение по “траектории свободного движения”, при котором выполняется соотношение

в котором b(t) – скалярная непрерывная кусочно-линейная функция времени с двумя точками излома t = t_ac и t = t_br, причем $\dot {b} = {{m}_{0}}$ при t < t_ac, $\dot {b} = - {{m}_{0}}$ при t > t_br, а на отрезке [t_ac, t_br] имеем b(t) = const и М = 0. Условием реализуемости разворота является требование Т ² ≥ 4F/m₀.

В случае, если Q неограниченно большое и 4F = m₀Т², будет t_ac = t_br = Т/2, в оптимальном развороте участок вращения по инерции отсутствует (|М| = m₀ на всем интервале управления [0, T]), реализуется оптимальный по быстродействию разворот КА (с учетом одного ограничения (4.1)). На всем отрезке времени [0, T] момент М максимально возможный (|M| = const = M_max), но меняет свой знак – первую половину разворота направление момента М совпадает с направлением кинетического момента, а вторую половину разворота (начиная с момента времени t = Т/2) направление момента М противоположно направлению кинетического момента (момент М меняет знак на обратный в момент времени t = Т/2).

Если 4F > m₀Т², то разворот КА (с известными значениями параметров J₁, J₂, J₃) из положения Λ_in в положение Λ_f за отведенное время Т невозможен.

Для заданного времени разворота Т = Т_sp описанное выше управление (раскрутка КА по закону (4.7), вращение по инерции с М = 0, торможение в соответствии с (4.6)) удовлетворяет условию (1.4), если Q ≥ G_opt. Значит, минимально возможная энергия вращения E_opt для разворота КА из состояния Λ(0) = Λ_in, L(0) = 0 в состояние Λ(Т) = = Λ_f, L(Т) = 0 за заданное время Т при ограничении (4.1) равна

Меньшего уровня энергии Е добиться невозможно, так как для Q < 2E_opt на разворот из (1.2) в (1.3) при условии L(0) = L(Т) = 0 и ограничениях (1.4), (4.1) потребуется время Т > Т_sp.

Можно утверждать, что для граничных значений L(0) = L(T) = 0 решение L(t) задачи оптимального разворота из положения (1.2) в положение (1.3) с минимальным значением (4.12) при наличии ограничения (4.1) совпадает с решением L(t) задачи максимального быстродействия (1.1)–(1.4), (4.1) при условии, что Q = 2E_opt, вычисленное по формуле (4.15).

Доказательство. Допустим, существует такое движение L(t), Λ(t) из положения Λ_in в положение Λ_f, удовлетворяющее уравнениям (1.1), (2.1), ограничению (4.1) и граничным условиям (1.2), (1.3), L(0) = L(T) = 0 для заданного времени Т, при котором максимальная энергия вращения Е_max будет меньше, чем при найденном управлении, включающем раскрутку КА в соответствии с законом (4.7), неуправляемое вращение с М = 0 и последующее торможение в соответствии с законом управления (4.6). Тогда мы можем ограничить такое движение условием (1.4), в котором Q = 2Е_max < 2E_opt. Но в этом случае минимально возможное время разворота, определяемое уровнем Q на основе формулы (4.11), окажется больше заданного по условиям разворота значения Т_sp (из-за отрицательности производной dT/dQ всюду в интервале 0 < Q < Q_cr = Fu₀C), что противоречит первоначально сделанному предположению. Следовательно, не существует других решений, кроме описанного выше, и полученное оптимальное управление разворотом КА с минимальной энергией вращения за заданное время – действительно оптимально, так как оно единственное.

Оценим относительный рост энергии Е_max из-за отличного от нуля времени набора и гашения кинетического момента. Для идеального разворота (когда Е(t) = const) энергия вращения будет E_min = F²C²/2T². Если времена разгона Δt_ac и торможения Δt_br не равны нулю, то энергия вращения при оптимальном управлении определяется выражением (4.15). Следовательно, относительное увеличение энергии Е_max (как и показателя G) составляет

Очевидно, значения G и Е_max минимальны, когда Δt_ac + Δt_br = 0. Функция ΔE/E_min возрастает с увеличением длительности переходных участков τ.

В случае, когда u₀ → ∞ (и, соответственно, m₀ → ∞), времена Δt_ac → 0 и Δt_br → 0, что является предельным случаем управления. Другим предельным случаем является управление, при котором τ = Т/2. Этот вариант разворота реализуется, если 4F = m₀T² (напомним, что если момент М ограничен требованием (4.1), то параметр m₀ = = ${{{{u}_{0}}} \mathord{\left/ {\vphantom {{{{u}_{0}}} {\sqrt {l_{1}^{2}{\text{/}}{{J}_{1}} + l_{2}^{2}{\text{/}}{{J}_{2}} + l_{3}^{2}{\text{/}}{{J}_{3}}} }}} \right. \kern-0em} {\sqrt {l_{1}^{2}{\text{/}}{{J}_{1}} + l_{2}^{2}{\text{/}}{{J}_{2}} + l_{3}^{2}{\text{/}}{{J}_{3}}} }}$).

Описанный выше метод управления ориентацией КА применим для ограничения в форме |M| ≤ М₀, если $F = {{K}_{{\text{c}}}}{{t}_{{{\text{pr}}}}} \ll {{M}_{0}}{{T}^{2}}{\text{/}}4$, где М₀ – заданная константа (М₀ > 0). В этом случае все расчетные формулы, приведенные выше, справедливы, если в них заменить m₀ на М₀.

5. Результаты математического моделирования. Приведем численное решение задачи оптимального управления программным разворотом КА. В качестве примера возьмем разворот КА на 180° из начального положения Λ_in, при котором оси КА совмещены (совпадают по направлению) с осями опорного базиса I, в заданное конечное положение Λ_f = Λ_sp. При этом считалось, что начальные и конечные угловые скорости нулевые ω(0) = ω(Т) = 0. Значения элементов кватерниона Λ_sp, характеризующего требуемое угловое положение КА, приняты равными: λ₀ = 0; λ₁ = 0.707107; λ₂ = 0.5; λ₃ = 0.5. Определим оптимальную программу управления кинетическим моментом L(t) для перевода КА из состояния Λ(0) = Λ_in, L(0) = 0 в состояние Λ(Т) = Λ_f, L(Т) = 0. Будем полагать, что главные центральные моменты инерции КА имеют значения, кг ⋅ м²: J₁ = = 63559.2; J₂ = 192218.5; J₃ = 176808.9. Пусть мощность исполнительных органов характеризуется величиной u₀ = 0.0712493 ${\text{H/}}\sqrt {{\text{к г }}} $, а длительность разворота Т = 400 с. Заметим, что принятый кватернион разворота Λ_t соответствует варианту, когда вектор конечного поворота (ось Эйлера) составляет с продольной осью ОХ угол примерно такой же, как с плоскостью, перпендикулярной оси ОХ. Такой разворот отражает достаточно трудный случай пространственного разворота КА, не обладающего сферической симметрией.

Найдем численное решение задачи оптимального управления переориентацией КА с минимальным значением (4.12) за заданное время Т. Краевая задача принципа максимума – определение вектора p₀ для оптимального движения – решается методом последовательных приближений. Поиск расчетного значения вектора p₀ начинаем с решения той же краевой задачи для динамически симметричного КА с моментами инерции J₁ и J, где J – момент инерции относительно поперечной оси, принимаемый равным

В предположении динамической симметричности КА решение p₀ определяется системой (3.3).

Полученные из уравнений (3.3) значения p₀ и β являются начальным приближением к истинному решению. Они уточняются до тех пор, пока не будут удовлетворять системе уравнений (1.1), (2.1), в которых момент сил отсутствует (M = 0), с учетом накладываемых на движение КА ограничений Λ(0) = Λ_in, Λ(t_pr) = Λ_f, а компоненты L_iin начального кинетического момента определяются вектором p₀ и углом β по выражениям:

где Т – время разворота. Прогнозирование “свободного” движения осуществляется интегрированием системы уравнений (1.2), (2.1), описывающих вращение КА, при начальных условиях Λ(0) = Λ_in, L(0) = L_in и с учетом того, что M = 0. Степень приближения найденных р₀ и β к искомому решению характеризуется мерой $\varepsilon = {\text{sqal}}({{\tilde {\Lambda }}_{{{\text{app}}}}} \circ {{\Lambda }_{{\text{f}}}})$, где Λ_app – наиболее близкое к Λ_f положение, полученное в ходе моделирования движения КА около центра масс (согласно уравнений (1.1), (2.1), в которых M_i = 0). Вектор р₀ уточняется до тех пор, пока ε < ε_thr (ε_thr – некоторое близкое к единице пороговое значение, отражающее точность найденного решения). Как только условие ε ≥ ε_thr достигнуто (прогнозируемая ошибка соответствует требуемой точности), истинные значения p₀ и β, удовлетворяющие граничным условиям Λ(0) = Λ_in, Λ(t_pr) = Λ_f, будут найдены, и краевая задача решена. Вектор p₀ уточняется с использованием следующего рекуррентного соотношения где $\Lambda _{{\text{t}}}^{{(k)}}$ – значение кватерниона разворота на k-й итерации, используемое в системе (3.3). “Свободное” движение прогнозируется интегрированием системы уравнений (1.2), (2.1), описывающей вращение КА с начальными условиями Λ(0) = Λ_in, L(0) = L_in и с учетом того, что M = 0. На каждом k-м шаге итераций обновляются элементы кватерниона разворота $\Lambda _{{\text{t}}}^{{(k)}}$ (правые части системы (3.3)), и из уравнений (3.3) мы получаем p₀ и β, а также соответствующий начальный кинетический момент L_in (согласно (5.1)) и прогноз Λ_app. Если ε < ε_thr, то вычисляется кватернион разворота $\Lambda _{{\text{t}}}^{{{\text{(}}k + {\text{1)}}}}$ для следующего (k + 1)-го шага итераций, и процесс уточнения вектора p₀ повторяется. За начальное приближение в правых частях системы (3.3) берутся элементы кватерниона $\Lambda _{{\text{t}}}^{{{\text{(0)}}}} = {{\tilde {\Lambda }}_{{{\text{in}}}}} \circ {{\Lambda }_{{\text{f}}}}$. Итерационный процесс прекращается, когда ε ≥ ε_thr.

Принятая схема итераций аналогична итерационному методу решения уравнения вида x = g(x) для скалярной функции g(x) скалярного (одномерного) аргумента x. В нашем случае, аргумент – гиперкомплексное число (кватернион) Λ_t. Функцией является кватернионная величина ${{\Lambda }_{{\text{t}}}} \circ {{\tilde {\Lambda }}_{{{\text{in}}}}} \circ {{\Lambda }_{{{\text{app}}}}}$, где Λ_f – постоянный (не зависящий от аргумента Λ_t) кватернион; Λ_app зависит от аргумента Λ_t через систему уравнений (3.3), (5.1) посредством модели движения (1.2), (2.1) (в уравнениях (2.1) принимается М_i = 0). С изменением Λ_t изменяются вектор p₀ (в соответствии с (3.3)) и компоненты L_{i in} кинетического момента, а значит изменится и значение Λ_app, что вызовет изменение функции ${{\Lambda }_{{\text{t}}}} \circ {{\tilde {\Lambda }}_{{{\text{in}}}}} \circ {{\Lambda }_{{{\text{app}}}}}$. Как только ${\text{sqal}}({{\tilde {\Lambda }}_{{{\text{app}}}}} \circ {{\Lambda }_{{\text{f}}}}) \geqslant {{\varepsilon }_{{{\text{thr}}}}}$, итерационный процесс прекращается, а решение p₀ считается найденным. Так как ${\text{|vect}}({{\tilde {\Lambda }}_{{\text{f}}}} \circ \Lambda _{{{\text{app}}}}^{{(k)}}){\text{|}} < {\text{|vect}}\Lambda _{t}^{{(k)}}{\text{|}}$ для всех k, то итерационный процесс приближения p₀ к искомому решению сходится. Аналогичный метод определения значения р₀ в решении краевой задачи принципа максимума использовался в известной задаче оптимального управления ориентацией КА [15]. Необходимо отметить, что это лишь один из возможных (но далеко не единственный) итерационных алгоритмов поиска оптимального вектора р₀.

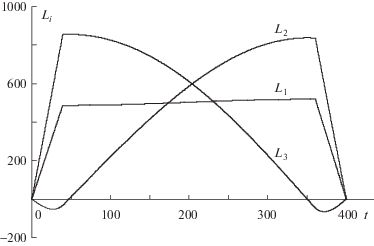
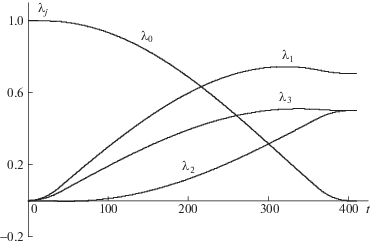
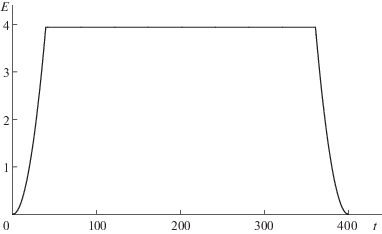
В результате решения краевой задачи разворота из положения Λ(0) = Λ_in в положение Λ(Т) = Λ_f получили расчетные значения вектора p₀ = {0.4953506; –0.1172565; 0.8607431} и интеграла F = 355400 кг ⋅ м². Поэтому максимальная величина управляющего момента равна m₀ = 25.0 Н ⋅ м. Готовое решение (значение вектора р₀ как решение краевой задачи принципа максимума) найдено за три итерации – первое приближение и два шага уточнений (после 2-го уточнения получено решение р₀, удовлетворяющее требуемой точности позиционирования). Исходя из заданного времени разворота Т, по формуле (4.15) вычисляем оптимальную энергию вращения Е_opt и значение Q, которое равно Q = 7.88 Дж. Соответственно номинальные значения $\tau = {{\sqrt Q } \mathord{\left/ {\vphantom {{\sqrt Q } {{{u}_{0}}}}} \right. \kern-0em} {{{u}_{0}}}}$ = 39.4 с и ${{L}_{{\max }}} = {{\sqrt Q } \mathord{\left/ {\vphantom {{\sqrt Q } C}} \right. \kern-0em} C} = 985$ Н⋅м⋅с (константа С зависит только от р₀). Решая задачу оптимального управления (1.1)–(1.4), (2.1) с учетом (4.1) и условия L(0) = = L(T) = 0, получаем оптимальные функции L_i(t), λ_j(t) и p_i(t), приведенные на фиг. 1–3.

Результаты математического моделирования процесса разворота при оптимальном управлении представлены фиг. 1–4. На фиг. 1 изображены графики изменения проекций кинетического момента на оси связанной с КА системы координат L₁(t), L₂(t), L₃(t) по времени (переменные L_i даны в Н⋅м⋅с). Максимальная величина кинетического момента составляет L_max = 985 Н⋅м⋅с, а длительность разгона (торможения) τ = 39.4 с. Соответственно Е_max = 3.94 Дж (так как значение (4.12) равно 7.88 Дж). На фиг. 2 отображены графики изменения компонент кватерниона Λ(t), определяющего текущую ориентацию КА в процессе совершаемого поворотного маневра: λ₀(t), λ₁(t), λ₂(t), λ₃(t). И на фиг. 3 приведена динамика изменения составляющих р₁(t), р₂(t), р₃(t) вектора p во времени (значения р_i, как и λ_j, − безразмерные величины). Характерным является незначительное изменение проекции р₁ (составляющая кинетического момента L₁ на участке номинального вращения также меняется гораздо меньше, чем составляющие кинетического момента L₂ и L₃). Это свидетельствует о том, что ось ОХ – продольная ось КА. Необходимо также отметить, что переменные L₁(t) и р₁(t), соответствующие продольной оси КА, – знакопостоянные функции времени (это свойство наблюдается при любых сочетаниях граничных значений Λ_in и Λ_f). При оптимальном управлении в отличие от кинетического момента L переменные р_i и λ_j являются гладкими функциями времени. Наконец, фиг. 4 демонстрирует поведение энергии вращения во время оптимального разворота (величина Е приведена в Дж). Значение показателя (4.12), отражающего энергетическую экономичность программы L(t) управления кинетическим моментом, составило 7.88 Дж.

Заключение. В статье рассмотрена и решена задача оптимального управления пространственным разворотом КА из произвольного начального в требуемое конечное угловое положение, когда критическим фактором является энергия вращения.

В случае особых требований к энергетике вращения КА для правильного планирования программы полета и корректного назначения приемлемой длительности разворота необходимо решить задачу оптимального быстродействия при наличии ограничений на энергию вращения (чтобы заданное время разворота не было меньше минимально возможного). Постановка задачи имеет традиционную форму, в которой управление положено кусочно-непрерывной функцией времени. Пространственное движение КА относительно центра масс описывается кватернионными переменными, что значительно упрощает расчетные процедуры и существенно снижает вычислительные затраты алгоритма управления, делая его удобным для бортовой реализации. Синтез оптимального управления основан на кватернионном дифференциальном уравнении, связывающем вектор кинетического момента КА с кватернионом ориентации связанной системы координат, в силу чего рассматриваемая задача управления переориентацией приобретает новое качество, а ее решение меняется кардинально (по сравнению с известным решением [1], использующим в качестве управления вектор угловой скорости).

На основании принципа максимума и использовании универсальных переменных r_i [12] получены выражения для оптимального управления, функции Гамильтона и сопряженной системы уравнений для исходной задачи. Определены ключевые свойства оптимального движения и тип траектории, оптимальной по выбранному критерию. Кинематическая задача разворота решена полностью. Найдены необходимые условия оптимальности и определена структура оптимального управления; получены формализованные соотношения для определения программного движения КА. Показано, что оптимальным движением является вращение по инерции. Затем приводится построение программы управления, когда ограничения для управляющего момента становятся существенными (если участками набора и гашения кинетического момента нельзя пренебречь в сравнении с длительностью всего разворота). Задача управления разворотом решена для типовой формы ограничения на управляющий момент. Получена зависимость управляющих переменных от фазовых координат.

Найдена связь между временем разворота и максимальной энергией вращения, позволяющая совершать развороты за заданное время с минимальной энергией вращения. Вопросы оптимального управления с минимумом энергии вращения остаются актуальными и сегодня. Представлены формализованные уравнения и даны расчетные выражения для построения оптимальной программы управления. Описывается процедура реализации оптимального режима управления. Структура построенного управления сравнительно проста, и оно легко может быть реализовано бортовыми системами управления движением КА. Момент начала торможения определяется по фактическим параметрам движения (кватерниону рассогласования и кинетическому моменту), исходя из принципов терминального управления (используются информация об угловом положении и измерения угловой скорости). В статье также дается описание конструктивной схемы решения краевой задачи принципа максимума для произвольных условий разворота и инерционных характеристик КА. Созданные алгоритмы управления позволяют совершать развороты КА за заданное время с минимальной энергией вращения.

Энергетический критерий оптимальности всегда был важен при разработке и оптимизации алгоритмов управления, и поэтому полученное решение представляет особый интерес. Одним из основных свойств оптимального разворота КА является следующее: во все время движения (на всем отрезке времени [0, T]) отношение кинетической энергии вращения к квадрату модуля кинетического момента КА постоянно. Приводятся пример и результаты математического моделирования, которые иллюстрируют характер движения КА при оптимальном управлении пространственным разворотом. Они демонстрируют практическую реализуемость разработанных алгоритмов управления. Для динамически симметричного КА представлено полное решение задачи переориентации в замкнутой форме, выписаны аналитические зависимости для управляющих функций и соотношения для расчета ключевых параметров закона управления; при этом оптимальные значения параметров закона управления могут быть вычислены устройством [18]. Разработанный алгоритм управления пространственной переориентацией КА позволяет применять данный метод на практике, поскольку реальные КА по своим массово-инерционным характеристикам близки к телам с осевой симметрией.