Химическая физика, 2020, T. 39, № 3, стр. 48-52
Точные автономные инварианты химических реакций с участием двух реагентов
В. Х. Федотов 1, *, Н. И. Кольцов 1, П. М. Косьянов 2
1 Чувашский государственный университет им. И.Н. Ульянова
Чебоксары, Россия
2 Филиал Тюменского индустриального университета
Нижневартовск, Россия
* E-mail: fvh@inbox.ru
Поступила в редакцию 25.02.2019
После доработки 13.05.2019
Принята к публикации 20.05.2019
Аннотация
Определены автономные (временны́е) инварианты нелинейных химических реакций, в которых участвуют два реагента. Для динамических моделей таких реакций существуют аналитические решения, которые позволяют найти точные инварианты. Такие инварианты представляют собой соотношения, связывающие неравновесные значения концентраций реагентов, измеренные в двух экспериментах с разными начальными условиями (дуал-экспериментах). Эти соотношения остаются строго постоянными в течение всей реакции. Полученные в работе соотношения применены к исследованию нестационарных свойств одно-, двух- и трехстадийных нелинейных реакций с кинетическим законом действующих масс, протекающих в закрытой системе. Найденные для этих реакций инвариантные кривые сопоставлены с кривыми изменения концентраций реагентов в течение всего переходного процесса. Показано, что зависимости инвариантов от времени остаются строго постоянными (имеют нулевой порядок), в то время как концентрации реагентов претерпевают непрерывные экспоненциальные изменения в ходе переходного процесса. Полученные результаты расширяют представления о характеристиках нелинейных химических реакций и могут быть использованы при решении обратных задач нестационарной химической кинетики и моделировании химических реакторов идеального смешения в изотермических условиях.
ВВЕДЕНИЕ
Одной из актуальных задач нестационарной химической кинетики является определение точных автономных (не зависящих от времени) кинетических инвариантов химических реакций. В настоящее время эта задача решена только для некоторых линейных реакций. Для ее решения использован развиваемый Г.С. Яблонским с соавт. дуал-метод [1–8]. Этот метод основан на анализе двух неравновесных экспериментов с взаимнообратными граничными (“термодинамическими”) начальными условиями и является теоретической базой [3] экспериментальных методов неравновесной кинетики и конструирования химических реакторов − технология временнóго анализа продуктов (temporal analysis of products) [9] и др.
Новые результаты, полученные в этом направлении исследований неравновесной химической кинетики, можно найти в работах [10–16], где изложен мультиметод, обобщающий и расширяющий возможности дуал-метода применительно к нелинейным динамическим системам и химическим реакциям. Мультиметод позволяет по результатам двух и более неравновесных экспериментов с различными начальными условиями (причем необязательно граничными) определить приближенные автономные инварианты (квазиинварианты) нелинейных систем. Квазиинварианты представляют собой комбинации неравновесных концентраций реагентов (температур), которые остаются почти постоянными в течение всей реакции.
Представляет интерес поиск новых неравновесных характеристик нелинейных реакций. Проведем такое исследование и найдем аналитические выражения для точных автономных инвариантов нелинейных химических реакций с участием двух реагентов.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Рассмотрим в общем виде химическую реакцию с участием двух реагентов, А и В, протекающую через стадии вида
(1)
${{a}_{i}}{\text{A}} + {{b}_{i}}{\text{B}} = {{a}_{{ - i}}}{\text{A}} + {{b}_{{ - i}}}{\text{B}},\,\,\,\,i = 1, \ldots ,s;$здесь a±i ≥ 0, b±i ≥ 0 (a±ib±i ≠ 0) − стехиометрические коэффициенты веществ А и В в стадии i. Динамика такой реакции в закрытом безградиентном изотермическом реакторе в рамках закона действующих масс описывается обыкновенными дифференциальными уравнениями (ОДУ):
(2)
$A{\kern 1pt} ' = \sum {({{a}_{{ - i}}} - {{a}_{i}})({{r}_{i}} - {{r}_{{ - i}}}) \equiv f({{k}_{i}},{{k}_{{ - i}}},A,B)} ,$(3)
$B{\kern 1pt} ' = \sum {({{b}_{{ - i}}} - {{b}_{i}})({{r}_{i}} - {{r}_{{ - i}}}) \equiv g({{k}_{i}},{{k}_{{ - i}}},A,B)} ,$где A и B – концентрации реагентов A и B (мольн. доли), соответственно; ri = kiAaiBbi и r−i = = k−iAa −iBb − i – скорости стадий в прямом и обратном направлениях (1/с), ki, k−i − константы скоростей соответствующих стадий (1/с). Начальные условия (н. у.) зададим соотношениями
Координаты равновесий A∞, B∞ реакции (1) определяются из условий
В закрытых системах уравнения равновесия (5) имеют единственное устойчивое решение [17–25] и выполняется нестационарный закон сохранения (тривиальный точный автономный инвариант):
Из (6) следует, что стехиометрические коэффициенты связаны равенством
Соотношения (6), (7) означают, что уравнения (2), (3) зависимы, а система (2)–(3) эквивалентна неоднородному автономному ОДУ:
где a = a(ki, k−i, A0, B0) – вектор параметров.
Для мономолекулярных стадий уравнение (8) запишется следующим образом:
где a ≠ 0, b – параметры. Общее решение этого линейного ОДУ имеет вид
где, согласно (5), A∞ = –b/a. Применим к выражению (10) обобщенный метод расчета нелинейных квазиинвариантов [16]. Для этого зададим н. у. A01 ≠ A02, введем удобные обозначения и найдем инвариант
(11)
$K\left( t \right) \equiv {{\left[ {{{A}_{1}}({{A}_{{02}}} - {{A}_{\infty }}) - {{A}_{2}}({{A}_{{01}}} - {{A}_{\infty }})} \right]} \mathord{\left/ {\vphantom {{\left[ {{{A}_{1}}({{A}_{{02}}} - {{A}_{\infty }}) - {{A}_{2}}({{A}_{{01}}} - {{A}_{\infty }})} \right]} {\left[ {{{A}_{\infty }}({{A}_{{02}}} - {{A}_{{01}}})} \right]}}} \right. \kern-0em} {\left[ {{{A}_{\infty }}({{A}_{{02}}} - {{A}_{{01}}})} \right]}} = 1.$Как видно, хотя K(t) и зависит от неравновесных концентраций реагентов, констант скоростей стадий реакции и н. у., но не зависит от времени, т.е. выражение (11) является точным автономным инвариантом. Пары н. у. A01 = 1, B01 = 0 и A01 = 0, B01 = 1 будем называть “термодинамическими” в том смысле, что они соответствуют взаимнообратным реакциям. Уравнения (9)–(11) могут моделировать только одну обратимую реакцию: A = B.
При наличии бимолекулярных стадий уравнение (8) примет вид
где a, b, c ≠ 0 – параметры. Общее решение этого ОДУ представим в виде
(13)
$\begin{gathered} A\left( t \right) = \\ = {{\left[ { - a + D{\text{tg}}\left( {\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}} \right) + {\text{arctg}}\left( {{{\left( {a + 2{{A}_{0}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{0}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ { - a + D{\text{tg}}\left( {\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}} \right) + {\text{arctg}}\left( {{{\left( {a + 2{{A}_{0}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{0}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} {2c}}} \right. \kern-0em} {2c}}, \\ \end{gathered} $где D = (4bc – a2)1/2. Согласно (5), равновесия определяются выражением A∞ = [–a ± (a2 – 4bc)1/2]/2с. Эти равновесия вещественны при a2 > 4bc, т.е. когда D = i|D| – мнимое число (i – мнимая единица, i2 = −1; |D| – модуль числа) и tg((Dt/2) + arctg((a + + 2A0c)/D)) – комплексное число. Собственное число λ = ∂A'/∂A = 2сA + a в двух равновесиях принимает значения λ1, 2 = ±(a2 – 4bc)1/2, т.е. устойчиво только меньшее (“–”) равновесие [26]. Это равновесие физично (0 < A∞ < 1) при
При a2 = 4bc равновесия сливаются и их устойчивость в линейном приближении не определяется (λ1, 2 = 0). При a2 < 4bc равновесия становятся комплексными (нефизичными).
Применим вновь обобщенный дуал-метод [16]. Решим дважды задачу Коши и запишем решение (13), (14) для н. у. A01 ≠ A02:
(15)
$\begin{gathered} {{A}_{1}}\left( t \right) = \\ = {{\left[ { - a + D{\text{tg}}\left( {\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}} \right) + {\text{arctg}}\left( {{{\left( {a + {\text{ }}2{{A}_{{01}}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + {\text{ }}2{{A}_{{01}}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ { - a + D{\text{tg}}\left( {\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}} \right) + {\text{arctg}}\left( {{{\left( {a + {\text{ }}2{{A}_{{01}}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + {\text{ }}2{{A}_{{01}}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} {2c}}} \right. \kern-0em} {2c}}, \\ \end{gathered} $(16)
$\begin{gathered} {{A}_{2}}\left( t \right) = \\ = {{\left[ { - a + D{\text{tg}}\left( {\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}} \right) + {\text{arctg}}\left( {{{\left( {a + 2{{A}_{{02}}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{{02}}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} \mathord{\left/ {\vphantom {{\left[ { - a + D{\text{tg}}\left( {\left( {{{Dt} \mathord{\left/ {\vphantom {{Dt} 2}} \right. \kern-0em} 2}} \right) + {\text{arctg}}\left( {{{\left( {a + 2{{A}_{{02}}}c} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2{{A}_{{02}}}c} \right)} D}} \right. \kern-0em} D}} \right)} \right)} \right]} {2c}}} \right. \kern-0em} {2c}}. \\ \end{gathered} $Разрешим каждое из этих уравнений относительно времени:
Вычтем из первого уравнения этой системы второе, поделим полученное выражение на его правую часть, введем обозначения и получим
(17)
$K\left( t \right) \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$где
(18)
$\begin{gathered} {{z}_{1}} \equiv {\text{arctg}}\left( {{{\left( {a + 2c{{A}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{1}}} \right)} D}} \right. \kern-0em} D}} \right) = - i{\text{arth}}\left( {{{\left( {a + 2c{{A}_{1}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{1}}} \right)} {\left| D \right|}}} \right. \kern-0em} {\left| D \right|}}} \right), \\ {{z}_{2}} \equiv {\text{arctg}}\left( {{{\left( {a + 2c{{A}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{2}}} \right)} D}} \right. \kern-0em} D}} \right) = - i{\text{arth}}\left( {{{\left( {a + 2c{{A}_{2}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{2}}} \right)} {\left| D \right|}}} \right. \kern-0em} {\left| D \right|}}} \right), \\ {{z}_{{01}}} \equiv {\text{arctg}}\left. {\left( {{{\left( {a + 2c{{A}_{{01}}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{01}}}} \right)} D}} \right. \kern-0em} D}} \right)} \right) = \\ = - i{\text{arth}}\left( {{{\left( {a + 2c{{A}_{{01}}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{01}}}} \right)} {\left| D \right|}}} \right. \kern-0em} {\left| D \right|}}} \right), \\ {{z}_{{02}}} \equiv {\text{arctg}}\left. {\left( {{{\left( {a + 2c{{A}_{{02}}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{02}}}} \right)} D}} \right. \kern-0em} D}} \right)} \right) = \\ = - i{\text{arth}}\left( {{{\left( {a + 2c{{A}_{{02}}}} \right)} \mathord{\left/ {\vphantom {{\left( {a + 2c{{A}_{{02}}}} \right)} {\left| D \right|}}} \right. \kern-0em} {\left| D \right|}}} \right). \\ \end{gathered} $Из (17), (18) следует, что K(t) зависит от неравновесных концентраций реагентов, констант скоростей стадий реакции и н. у., но не зависит от времени, т.е. соотношение (17) является точным нелинейным автономным инвариантом. Этот инвариант выражается через произведения двух мнимых чисел − мнимой единицы (i) и гиперболического арктангенса (arth), и поэтому всегда принимает только действительные значения. Соотношения (12)–(18) могут моделировать шесть одно- и двухстадийных бимолекулярных реакций, включающих стадии A = B, 2A = 2B или A + B = 2B.
При наличии тримолекулярных стадий 3A = = 3B, A + 2B = 3B, 2A + B = 3A, A + 2B = B + 2A, система (2)–(3) принимает вид
и не имеет общего решения. Для таких реакций точные инварианты могут быть найдены только для частных случаев (см. формулы (1.7), (1.8) ниже). Соотношения (9)–(19) моделируют 24 механизма одно-, двух- и трехстадийных моно-, би- и тримолекулярных реакций. Для каждого из них существует множество точных инвариантов, соответствующих разным дуал-экспериментам. Эти инварианты являются дополнительной неравновесной характеристикой механизма исследуемой реакции и могут быть использованы при его реконструкции. Рассмотрим примеры.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Пример 1. Найдем точные инварианты реакции
Примером служит реакция изомеризации бутилена t-C4H8 = c-C4H8, протекающая линейно, если n = 1 [5], или нелинейно, если n > 1. При n = 1 эта реакция описывается уравнением вида (9):
где a = –(k–1 + k1) < 0, b = k–1 > 0. При k1= 4, k–1 = = 1 получим a = –5, b = 1, A∞ = 1/5. Выберем, например, “термодинамические” н. у. A01 = 1, A02 = 0, тогда выражение (11) запишется в следующем виде:
Соотношение (1.3) соответствует горизонтальной линии на графике зависимости K(t) и является линейным автономным инвариантом.
При n = 2 реакция (1.1) описывается уравнением (12):
где c = k–1 − k1 ≠ 0 при k1 ≠ k–1, a = −2k–1 < 0, b = = $k_{{ - 1}}^{2}$ > 0. Условия физичности равновесия (14) выполняются, например, при k1= 4, k–1 = 1. Тогда a = –2, b = 1, c = –3, a2 – 4bc = 16, A∞ = 1/3, D = = (–16)1/2. Выберем “термодинамические” н. у. A01 = 1, A02 = 0, тогда точный инвариант (17), (18) запишется так:
(1.5)
$K\left( t \right) \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$где
Инвариант (1.5) приведен на рис. 1.
Рис. 1.
Решения двух задач Коши и точный инвариант для реакции (1.1) при n = 2, k1= 4, k–1 = 1, A01 = 1, A02 = 0: 1 – A1(t), 2 – A2(t), 3 – K(t).
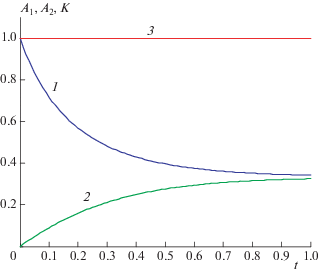
Как видно из рис. 1, зависимость K(t) представляет собой горизонтальную линию, т.е. не зависит от времени, и, следовательно, выражение (1.5) является точным автономным инвариантом.
При n = 3 реакция (1.1) описывается уравнением
которое имеет общее решение только для необратимого случая k−1 = 0:
(1.7)
${{A}_{1}}(t){\text{ }} = {{ \pm 1} \mathord{\left/ {\vphantom {{ \pm 1} {{{{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{0}^{2}}}} \right. \kern-0em} {A_{0}^{2}}} - 2{{k}_{1}}t} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}} \right. \kern-0em} {{{{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{0}^{2}}}} \right. \kern-0em} {A_{0}^{2}}} - 2{{k}_{1}}t} \right)}}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}}}.$Для этого решения, согласно [14–16], искомый инвариант запишется в виде
(1.8)
$K(t) \equiv {{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{1}^{2}}}} \right. \kern-0em} {A_{1}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{2}^{2}}}} \right. \kern-0em} {A_{2}^{2}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{1}^{2}}}} \right. \kern-0em} {A_{1}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{2}^{2}}}} \right. \kern-0em} {A_{2}^{2}}}} \right)} {\left( {{1 \mathord{\left/ {\vphantom {1 {A_{{01}}^{2}}}} \right. \kern-0em} {A_{{01}}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{{02}}^{2}}}} \right. \kern-0em} {A_{{02}}^{2}}}} \right)}}} \right. \kern-0em} {\left( {{1 \mathord{\left/ {\vphantom {1 {A_{{01}}^{2}}}} \right. \kern-0em} {A_{{01}}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{{02}}^{2}}}} \right. \kern-0em} {A_{{02}}^{2}}}} \right)}} = 1.$Здесь, как и в (1.3) и (1.5), k(t) также не зависит от времени и является точным автономным нелинейным инвариантом.
Пример 2. В работе [4] методом граничного дуал-эксперимента (с использованием термодинамических н. у.) исследована двухстадийная реакция
для которой найден только приближенный инвариант, причем в предположении детального баланса. Схема (2.1) для реакции изомеризации бутилена запишется следующим образом: t-C4H8 = c-C4H8, 2с-C4H8 = 2t-C4H8. Покажем, что приведенные выше соотношения позволяют без использования гипотезы детального баланса установить точный автономный инвариант для этой реакции.
Реакция (2.1) описывается нелинейным уравнением вида (12):
(2.2)
$A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}(1 - A) + 2{{k}_{2}}{{(1 - A)}^{2}} - 2{{k}_{{ - 2}}}{{A}^{2}},$где c = 2(k2 – k–2) ≠ 0 при k2 ≠ k–2, a = –(k1 + k–1 + + 4k2) < 0, b = k–1+ 2k2 > 0. Условия физичности равновесия (14) реализуются, например, при k1= 4, k–1 = 1, k2 = 1, k–2 = 0.5. Тогда a = –9, b = 3, c = 1, a2 – 4bc = 69, A∞ ≈ 0.35, D = (–69)1/2. Точный инвариант (17), (18) для реакции (2.1) примет вид
(2.3)
$K(t) \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$где
Инвариант (2.3) показан на рис. 2.
Рис. 2.
Решения двух задач Коши и точный инвариант для реакции (2.1) при k1= 4, k–1 = 1, k2 = 1, k–2 = 0.5, A01 = 0.2, A02 = 0.8: 1 – A1(t), 2 – A2(t), 3 – K(t).
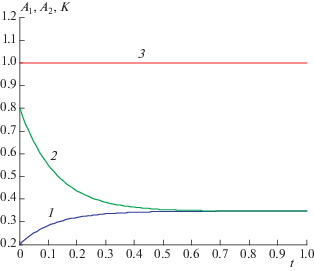
Пример 3. Рассмотрим трехстадийную автокаталитическую реакцию
(3.1)
${\text{A}} = {\text{B}},\,\,\,\,2{\text{B}} = 2{\text{A}},\,\,\,\,{\text{A}} + {\text{B}} = 2{\text{B}},$которая для реакции изомеризации бутилена запишется соответственно в следующем виде: t-C4H8 = = c-C4H8, 2с-C4H8 = 2t-C4H8, t-C4H8 + c-C4H8 = = 2c-C4H8. Реакция (3.1) также описывается нелинейным ОДУ вида (12):
(3.2)
$\begin{gathered} A{\kern 1pt} ' = - {{k}_{1}}A + {{k}_{{ - 1}}}(1 - A) + 2{{k}_{2}}{{(1 - A)}^{2}} - \\ - \,\,2{{k}_{{ - 2}}}{{A}^{2}} - {{k}_{3}}A(1 - A) + {{k}_{{ - 3}}}{{(1 - A)}^{2}}, \\ \end{gathered} $где
Условия физичности равновесия (14) реализуются, например, при k1= 4, k–1 = 1, k2 = 1, k–2 = 1/2, k3 = 1, k–3 = 1. Тогда a = –12, b = 4, c = 3, a2 – 4bc = = 96, A∞ ≈ 0.37, D = (–96)1/2. Точный инвариант (17) для реакции (3.1) примет вид
(3.3)
$K\left( t \right) \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$где
Инвариант (3.3) показан на рис. 3.
Рис. 3.
Решения двух задач Коши и точный инвариант реакции (3.1) при k1= 4, k–1 = 1, k2 = 1, k–2 = 1/2, k3 = 1, k–3 = 1, A01 = 0.3, A02 = 0: 1 – A1(t), 2 – A2(t), 3 – K(t).
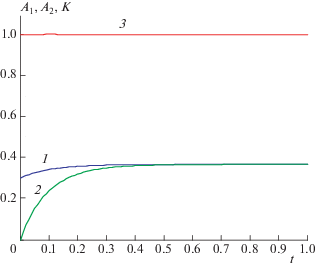
Пример 4. Рассмотрим, как можно использовать инварианты для решения обратных задач химической кинетики. Предположим, что при исследовании реакции (1.1) дуал-методом с н. у. A01 = 1 и A02 = = 0.5 получены две экспериментальные кривые зависимостей A1эксп(t) и A2эксп(t), см. табл. 1. Найдем для этих н. у. инварианты, вычислим их значения при трех разных n и сравним их с теоретическими значениями инвариантов (1.3), (1.5) и (1.8), т.е. с единицей. Для n = 1 инвариант (1.3) примет вид
Таблица 1.
Инварианты реакции nA = nB
| t | A1эксп | A2эксп | K1 | K2 | K3 |
|---|---|---|---|---|---|
| 0 | 1.00 | 0.50 | 1.00 | 1.00 | 1.00 |
| 0.1 | 0.72 | 0.44 | 1.36 | 1.01 | 1.08 |
| 0.2 | 0.57 | 0.4 | 1.49 | 1.05 | 1.06 |
| 0.3 | 0.48 | 0.38 | 1.60 | 0.98 | 0.86 |
| 0.4 | 0.43 | 0.36 | 1.59 | 1.13 | 0.77 |
| 0.5 | 0.40 | 0.35 | 1.60 | 1.23 | 0.64 |
| 0.6 | 0.38 | 0.35 | 1.67 | 0.92 | 0.41 |
| 0.7 | 0.35 | 0.34 | 1.67 | 0.83 | 0.16 |
| 0.8 | 0.35 | 0.34 | 1.67 | 0.83 | 0.16 |
| 0.9 | 0.35 | 0.34 | 1.67 | 0.83 | 0.16 |
| 1.0 | 0.34 | 0.34 | 1.67 | 0.83 | 0.16 |
| Kсред | 1.54 | 0.97 | 0.59 |
При n = 2 инвариант (1.5) запишется в виде
(4.2)
${{K}_{2}} \equiv {{({{z}_{1}} - {{z}_{2}})} \mathord{\left/ {\vphantom {{({{z}_{1}} - {{z}_{2}})} {({{z}_{{01}}} - {{z}_{{02}}})}}} \right. \kern-0em} {({{z}_{{01}}} - {{z}_{{02}}})}} = 1,$где
При n = 3 инвариант (1.8) примет вид
(4.3)
${{K}_{3}} \equiv {{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{2}^{2}}}} \right. \kern-0em} {A_{2}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{1}^{2}}}} \right. \kern-0em} {A_{1}^{2}}}} \right)} \mathord{\left/ {\vphantom {{\left( {{1 \mathord{\left/ {\vphantom {1 {A_{2}^{2}}}} \right. \kern-0em} {A_{2}^{2}}} - {1 \mathord{\left/ {\vphantom {1 {A_{1}^{2}}}} \right. \kern-0em} {A_{1}^{2}}}} \right)} 3}} \right. \kern-0em} 3} = 1.$Результаты расчетов по формулам (4.1)–(4.3) приведены в табл. 1.
Анализ показал, что приведенные в табл. 1 данные одинаково хорошо согласуются с двумя механизмами реакции (1.1) – бимолекулярным и тримолекулярным. Однако среднее значение инвариантов Kср ближе к теоретическому (единице) в случае бимолекулярного механизма, что позволяет считать его наиболее вероятным.
ЗАКЛЮЧЕНИЕ
В работе получены аналитические выражения для определения точных автономных инвариантов химических реакций, протекающих в закрытых изотермических системах с участием двух реагентов в рамках закона действующих масс. Найденные соотношения связывают неравновесные значения концентраций реагентов, измеренные в двух экспериментах с разными начальными условиями (необязательно граничными) и остаются строго постоянными в течение всей реакции. Эти соотношения применены к исследованию неравновесных свойств 24 типов механизмов моно-, би- и тримолекулярных одно-, двух- и трехстадийных реакций. Найденные для этих реакций инвариантные кривые сопоставлены с кривыми изменения концентраций в течение всего переходного процесса. Полученные результаты расширяют представления о неравновесных характеристиках нелинейных химических реакций и могут быть использованы при решении обратных задач химической кинетики и моделировании химических реакторов идеального смешения в закрытых изотермических условиях.
Список литературы
Yablonsky G.S., Constales D., Marin G.B. // Chem. Eng. Sci. 2010. V. 65. P. 6065.
Yablonsky G.S., Gorban A.N., Constales D., Galvita V.V., Marin G.B. // Europhys. Let. 2011. V. 93. № 2. P. 20004.
Constales D., Yablonsky G.S., Galvita V.V., Marin G.B. // Chem. Eng. Sci. 2011. V. 66. P. 4683.
Yablonsky G.S., Constales D., Marin G.B. // Ibid. P. 111.
Constales D., Yablonsky G.S., Marin G.B. // Ibid. 2012. V. 73. P. 20.
Constales D., Yablonsky G.S., Marin G.B. // Comput. and Mathemat. with Applications. 2013. V. 65. № 10. P. 1614.
Yablonsky G.S. // Theor. Found. Chem. Eng. 2014. V. 48. № 5. P. 608.
Branco-Pinto D., Yablonsky G., Marin G., Constales D. // Entropy. 2015. V. 17. № 10. P. 6783.
Gleaves J.T., Ebner J. R. and Kuechler T. C. // Catal. Rev. Sci. Eng. 1988. V. 30. P. 49.
Федотов В.Х., Кольцов Н.И. // Матер. IV Всерос. НПК “Математическое моделирование процессов и систем”. Т. 1. Уфа: БашГУ, 2015. С. 138.
Федотов В.Х., Кольцов Н.И. // Изв. вузов. Химия и хим. технология. 2016. Т. 59. № 5. С. 72.
Федотов В.Х., Кольцов Н.И. // Вестн. технол. ун-та. 2018. Т. 21. № 9. С. 113.
Федотов В.Х., Кольцов Н.И. // Вестн. технол. ун-та. 2018. Т. 21. № 11. С. 195.
Федотов В.Х., Кольцов Н.И., Косьянов П.М. // Вестн. технол. ун-та. 2018. Т. 21. № 12. С. 181.
Федотов В.Х., Кольцов Н.И. // Вестн. технол. ун-та. 2019. Т. 22. № 1. С. 122.
Федотов В.Х., Кольцов Н.И. // Хим. физика. 2019. Т. 38. № 4. С. 23.
Зельдович Я. Б. // ЖФХ. 1938. Т. 11. № 5. С. 685.
Krambeck F.M. // Arc. Rat. Mech. Anal. 1970. V. 38. № 5. P. 317.
Акрамов Т.А., Яблонский Г.С. // ЖФХ. 1975. Т. 49. № 7. С. 1818.
Bykov V.I., Gorban A.N., Dimitrov V.I. // React. Kinet. Catal. Lett. 1979. V. 12. № 1. P. 19.
Zyskin A.G., Snagovskii Yu.S., Slinko M.G. // Ibid. 1981. V. 17. № 3–4. P. 257.
Zyskin A.G., Snagovskii Yu.S., Slinko M.G. // Ibid. P. 263.
Зыскин А.Г., Снаговский Ю.С., Слинько М.Г. // Кинетика и катализ. 1981. Т. 22. № 4. С. 1031.
Gorban A.N., Bykov V.I., Yablonsky G.S. // Taм жe. 1983. T. 24. № 5. C. 1239.
Алексеев Б.В., Кольцов Н.И. // Вестн. Чувашск. ун-та. 2000. № 3–4. С. 34.
Корн Г., Корн Т. Справочник по математике. М.: Наука, 1978.
Дополнительные материалы отсутствуют.
Инструменты
Химическая физика


