1. На главную
  2. Электронные версии
  3. Журнал высшей нервной деятельности им. И.П. Павлова
  4. T. 69, № 6, 2019

Журнал высшей нервной деятельности им. И.П. Павлова, 2019, T. 69, № 6, стр. 768-776

МОДИФИКАЦИЯ МЕТОДА ТЕНЗОРНОГО РАЗЛОЖЕНИЯ PARAFAC ДЛЯ НАХОЖДЕНИЯ БАЗОВЫХ КОМПОНЕНТОВ СПЕКТРОВ ЭЭГ ЧЕЛОВЕКА

В. Ю. Новотоцкий-Власов 1, 2, *, В. П. Ковалев 2, В. А. Тихонов 2

1 Лаборатория высшей нервной деятельности человека, Институт высшей нервной деятельности и нейрофизиологии РАН
Москва, Россия

2 Лаборатория клинической нейрофизиологии, Федеральный медицинский исследовательский центр психиатрии и наркологии им. В.П. Сербского Минздрава России
Москва, Россия

* E-mail: vnovot@mail.ru

Поступила в редакцию 31.01.2019
После доработки 24.04.2019
Принята к публикации 03.06.2019

Полный текст (PDF)

Аннотация

С целью формального описания ЭЭГ представлена модификация метода тензорного разложения PARAFAC для анализа спектров ЭЭГ человека и ее отличия от стандартного алгоритма. Метод позволяет учитывать при описании и анализе индивидуальные особенности ЭЭГ испытуемых. Результаты применения нового метода для анализа модельных спектров свидетельствуют о его высокой точности в воспроизведении компонентов модели. Сравнение результатов факторного и тензорного разложения модельных спектров показало преимущества последнего: однозначность решения из-за отсутствия факторных вращений и большую помехоустойчивость. Результаты анализа реальных спектров ЭЭГ человека показали удовлетворительное согласие с общепринятыми представлениями о ритмах ЭЭГ в области частот от 0 до 15 Гц, а также широкополосность всех спектральных компонентов ЭЭГ.

Ключевые слова: спектр ЭЭГ, ритмы ЭЭГ, тензорное разложение, невязка аппроксимации, нормированные спектры компонентов, нормированная топография компонентов

Понятие “ритма” широко используется в физиологической литературе для компактного описания электроэнцефалограммы (ЭЭГ) при анализе различных функциональных состояний и сравнении разных групп испытуемых. Тем не менее до сих пор в нейрофизиологии отсутствует общепринятое и объективное определение ритмов или базовых компонентов спектров ЭЭГ [Klimesch, 1999; Новотоцкий и др., 2012]. Эти понятия можно считать близкими по смыслу, поскольку известно, что любой периодической составляющей сигнала во временной области соответствует пик в спектре мощности этого сигнала [Марпл мл., 1990].

В современной литературе доминирует представление о пяти общепризнанных частотных диапазонах, соответствующих ритмам дельта (1–4 Гц), тета (4–8 Гц), альфа (8–13 Гц), бета (14–30 Гц) и гамма (30–100 Гц). Такое представление основано на анализе полученных результатов, демонстрирующих качественное своеобразие функциональной активности мозга в этих частотных границах в норме и при патологии мозга [Niedermeyer, 2005]. Принято считать, что эти функционально разные ритмы имеют жесткие частотные границы, но эти границы не только подвижны, но часто в этих границах находятся несколько пересекающихся ритмов [Polich, 1997]. Все описанные в литературе подходы к решению этой проблемы в большей или меньшей степени страдают субъективизмом, будь то (достаточно произвольно) устанавливаемые фиксированные границы диапазонов [Steriade et al., 1990] или адаптивные, подстраиваемые по пиковой частоте альфа-ритма границы диапазонов фиксированной ширины [Klimesch, 1999]. Более подробно достоинства и недостатки как вышеуказанных, так и иных подходов к определению ритмов ЭЭГ были рассмотрены в нашей предыдущей работе [Новотоцкий и др., 2012].

В ней было предложено решение проблемы ритмов на основе факторного анализа спектров ЭЭГ. С его помощью удалось получить результаты, “соответствующие имеющимся представлениям о компонентах ЭЭГ-осцилляций”. Однако в таком решении был элемент субъективизма: именно “соответствием” руководствовались авторы при выборе варианта решения из нескольких альтернатив. Тем не менее полученные таким методом решения подтверждают объективность деления спектров ЭЭГ на компоненты, различающиеся по измеримым параметрам.

Любой вариант факторного анализа позволяет определить только факторное подпространство, но не определенную выделенную систему координат в нем [Харман, 1972]. Т.е. факторное разложение спектров, представленных в виде матрицы, дает решение только с точностью до произвольного вращения факторов.

Кроме того, проверка предложенного в [Новотоцкий и др., 2012] решения на модельных спектрах [Новотоцкий и др., 2009] показала, что предложенный метод искажает спектры компонентов в случае, если последние имеют области, общие для трех и более компонентов. Вращение квартимакс, минимизирующее число факторов, дающих вклад в каждый конкретный элемент данных [Neuhaus, Wrigley, 1954], сохраняет средние частоты компонентов модельных спектров, но сужает их спектральные диапазоны, таким образом сокращая области перекрытий.

Изложенное выше указывает на необходимость поиска метода разложения спектра ЭЭГ на компоненты, свободного от указанных недостатков.

От упомянутой вращательной неопределенности свободно тензорное разложение, известное как PARAFAC (Parallel Factor Analysis – параллельный факторный анализ) [Bro, 1997; Paatero, 1997]. Данное разложение является обобщением факторного анализа на случай массивов, имеющих более двух индексов. Этот метод широко применяется для разделения сигналов и выделения их из шума в различных областях исследований, в том числе в аналитической химии, спектральном анализе, распознавании образов, обработке сигналов и в нейронауке [Colda, Bader, 2009]. В частности, в последней области он используется для удаления мышечных артефактов из ЭЭГ [De Clercq et al., 2005], анализа динамических спектров ЭЭГ [Miwakeichi et al., 2004] и измерения компонентов вызванных потенциалов в единичных реализациях [Vanderperren et al., 2010]. Показано, что в отличие от факторного анализа тензорное разложение при весьма мягких условиях дает в результате не факторное подпространство, а набор конкретных векторов в этом подпространстве (выделенный базис) [Kruskal, 1977; Stegeman, Sidiropoulos, 2007]. Это происходит в результате использования дополнительных связей между элементами многомерных массивов (тензоров). Таким образом, тензорное разложение может дать конкретный набор спектральных компонентов ЭЭГ.

“Платой” за такое преимущество тензорного разложения является отсутствие для последнего алгоритмических методов вычисления и даже методов определения ранга тензора [Bro, Kiers, 2003; Timmerman, Kiers, 2000; Morup, Hansen, 2008]. Найти разложение возможно только численными методами, задав некоторым образом начальные значения факторов и воспользовавшись затем методом градиентного спуска. Примером таких методов является ALS (Alternate Least Squares) – метод наименьших квадратов с последовательно меняющимися аргументами, применяемый также при разложении неотрицательных матриц на неотрицательные составляющие [Lawson, Hanson, 1982].

Кроме того, итерационное решение, использующее различные варианты методов градиентного спуска (к которым относится и ALS), может закончиться в локальном минимуме, поэтому нахождение глобального минимума возможно только путем многократного повторения численных итераций с различными начальными условиями [Paatero, 1997; Timmerman, Kiers, 2000]. Также, поскольку в общем случае получаемые факторы не ортогональны друг другу [Paatero, 1997], такие вычисления надо выполнять для каждого числа факторов из выбранного диапазона отдельно (нельзя, как в случае факторного анализа, найти решение для максимального числа факторов и при необходимости отбрасывать факторы, имеющие малые веса).

Дополнительным ограничением является то, что метод тензорного разложения может быть применен только к данным, допускающим представление в виде как минимум трехмерного массива – тензора третьего порядка (а не в виде матрицы, как для факторного анализа) – и разложение этого массива в сумму элементарных составляющих:

${\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{U} }} = \Sigma {{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}_{p}} + {\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{E} }} \approx \Sigma {{{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }}}_{p}},$
где U – тензор исходных данных, E – погрешность аппроксимации, Xp – составляющие, каждая из которых представима в виде
${\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{X} }} = {\mathbf{a}} \otimes {\mathbf{b}} \otimes {\mathbf{c}},$
где a, b, c – векторы, а ⊗ – знак внешнего (декартова) произведения. Внешнее произведение двух векторов дает матрицу
${\mathbf{a}} \otimes {\mathbf{b}} = \left| {\begin{array}{*{20}{c}} {{{a}_{1}}{{b}_{1}}}&{...}&{{{a}_{1}}{{b}_{m}}} \\ {...}&{...}&{...} \\ {{{a}_{n}}{{b}_{1}}}&{...}&{{{a}_{n}}{{b}_{m}}} \end{array}} \right|,$
а произведение трех и более векторов – тензор соответствующего порядка. Т.е. для применения этого метода базовые составляющие спектров ЭЭГ должны обладать не только постоянным спектральным составом, не зависящим от функциональных состояний, но и постоянной топографией, и изменяться в различных функциональных состояниях только по амплитуде.

Менее формально это условие можно описать следующим образом. Допустим, что в мозгу существуют некоторые постоянные “источники” ритмов, каждый из которых соответствует морфологически определенному ансамблю нейронов (нейросети) и выполняет определенную физиологическую функцию. Независимо от степени своей активности такой ансамбль всегда дает сигнал ЭЭГ постоянного спектрального состава и с одинаковой топографией на скальпе. При выполнении этого предположения данные, описывающие сигнал от такого “источника”, могут быть представлены как прямое произведение трех векторов, отвечающих за спектр, топографию и функциональное состояние.

Целью данной работы является описание адаптации метода тензорного разложения для анализа спектров ЭЭГ человека и поиска их базовых компонентов (ритмов) и проверка этого метода на модельных и реальных спектрах ЭЭГ. Описанный метод является развитием метода факторного анализа спектров ЭЭГ [Новотоцкий и др., 2012] и позволяет объективно (независимо от исследователя) определять характеристики ритмов ЭЭГ – спектральный состав, топографию и реакцию на функциональные нагрузки.

МЕТОДИКА

Подготовка модельных и реальных спектров

Для оценки точности метода в качестве модельных были выбраны спектры, составленные из линейной комбинации 10 спектральных прямоугольных компонентов (рис. 1(б)), имеющих фиксированную топографию и случайное распределение по состояниям, с белым шумом (отношение сигнал/шум ≈ 30 dB) (пример полученных спектров представлен на рис. 1(а)). Выбор конкретного набора компонентов определялся его максимальной “неудобностью” для факторного анализа (9 из 10 компонентов накрывали один и тот же частотный диапазон). Отношение сигнал/шум выбиралось исходя из двух взаимопротиворечащих требований: не портить заметно форму компонентов и одновременно гарантировать тензору полный ранг. Прямоугольная форма компонентов была выбрана для удобства визуального контроля точности воспроизведения их в результате анализа. Всего было построено 256 модельных спектров по 129 точек в каждом (16 отведений × 16 состояний), т.е. массив модельных данных имел размеры 129 × 16 × 16. Частотный диапазон всех спектров (и модельных, и реальных) – 0–100 Гц, частотное разрешение – 0.78 Гц/точка.

Рис. 1.

Модельные спектры, их компоненты и результаты тензорного разложения: (а) – пример спектра из комбинации прямоугольников и шума, (б) – исходные составляющие модельных спектров, (в) – результат тензорного разложения модельных спектров из 10 компонентов с фиксированной топографией, (г) – результат тензорного разложения модельных спектров, составленных из 9 компонентов с фиксированной и 1 компонента со случайной топографией. Ось абсцисс – частота, Гц; ось ординат – спектральная мощность, относительные единицы.

Fig. 1. The model spectra, their components and results of tensor decomposition: (а) – and example of spectrum combined from rectangles and noise, (б) – original components of the model spectra, (в) – the result of tensor decomposition of the model spectra combined of 10 components with fixed topography, (г) – the result of tensor decomposition of the model spectra combined of 9 components with fixed topography and 1 component with stochastic topography. Abscissa – frequency, Hz; ordinate – spectral power, relative units.

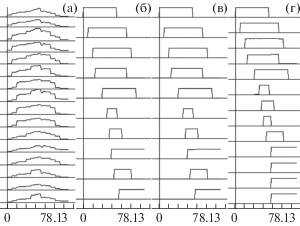
Для оценки устойчивости метода к наличию компонентов, не имеющих структуру тензора первого ранга (не сохраняющих топографию в разных функциональных состояниях), использовались модельные спектры из тех же 10 компонентов, девять из которых имели фиксированную топографию (ту же, что и в предыдущем случае), а один – случайную топографию, т.е. его топография изменялась от состояния к состоянию. Использовались 64 модельных спектра по 129 точек в каждом (16 отведений × 4 состояния). Таким образом проверялась способность метода выявлять и оценивать компоненты, не имеющие тензорной структуры. Эта проверка имеет смысл с точки зрения физиологии, поскольку считается, что топография высокочастотных (корковых) ритмов – бета и гамма – меняется в разных состояниях [McFarland et al., 2000].

В качестве реальных применяли спектры ЭЭГ пилотной группы здоровых испытуемых (6 человек), у каждого из которых ЭЭГ от 19 отведений по системе 10–20 регистрировалась при закрытых глазах в 10 функциональных состояниях (в фоне и при мысленном представлении эмоционально нейтральных, положительных и отрицательных событий; более подробно условия проведения эксперимента и обработки ЭЭГ для получения спектров описаны в [Новотоцкий и др., 2012; Kirenskaya et al., 2011].) Частота квантования – 200 Гц, эпоха анализа для спектрального преобразования – 256 точек (1.28 с), частотное разрешение спектров – 0.78 Гц/точка.

Анализ спектров

Модельные спектры и индивидуальные спектры ЭЭГ испытуемых организовывались в трехмерные массивы с координатами “частота”, “топография” и “состояние”. Эти трехмерные массивы анализировались с помощью тензорного разложения по модифицированному методу ALSA (Alternate Least Squares with Active set – метод наименьших квадратов, применяемый поочередно к каждой из координат массива, с набором активных ограничений) [Kim, Park, 2008].

В связи с большим динамическим диапазоном спектров мощности ЭЭГ стандартный метод ALSA был заменен его модификацией путем использования относительной невязки

$\begin{gathered} Err = {{\sum\limits_{ijk} {\left( {\frac{{{{u}_{{ijk}}} - \sum\limits_p^{} {{{a}_{{ip}}}{{b}_{{jp}}}{{c}_{{kp}}}} }}{{{{u}_{{ijk}}}}}} \right)} }^{2}} = \\ \, = {{\sum\limits_{ijk} {\left( {\frac{{\sum\limits_p^{} {{{a}_{{ip}}}{{b}_{{jp}}}{{c}_{{kp}}}} }}{{{{u}_{{ijk}}}}} - 1} \right)} }^{2}} = \min , \\ \end{gathered} $
где Err – невязка (погрешность аппроксимации), uijk – элемент данных с соответствующими индексами, aip, bjp и ckp – элементы p-го фактора, соответствующие разным модам.

При таком подходе каждая точка спектра вносит в невязку одинаковый вклад (в некоторой степени это эквивалентно использованию корреляционной матрицы в факторном анализе, как в [Новотоцкий и др., 2012]).

Генератор случайных чисел задавал случайные начальные значения искомых факторов, равномерно распределенные по положительному квадранту единичной многомерной сферы, после чего методом последовательных приближений поочередно по каждой из координат уменьшалась суммарная невязка:

$1.\,\,a_{{ip}}^{{}} = \arg {{\min }_{{a \geqslant 0}}}(Err){\kern 1pt} {{|}_{{{\text{bjq,ckq}} = {\text{const}}}}}$,
$2.\,\,b_{{jp}}^{{}} = \arg {{\min }_{{b \geqslant 0}}}(Err){\kern 1pt} {{|}_{{{\text{aiq,ckq}} = {\text{const}}}}}$,
$3.\,\,c_{{kp}}^{{}} = \arg {{\min }_{{c \geqslant 0}}}(Err){\kern 1pt} {{|}_{{{\text{aiq,bjq}} = {\text{const}}}}}$.

Решение в каждом случае получалось поочередным приравниванием к нулю частной производной от невязки по соответствующим переменным

$\partial Err{\text{/}}\partial {\text{A}} = 0,$
$\partial Err{\text{/}}\partial {\text{B}} = 0,$
$\partial Err{\text{/}}\partial {\text{C}} = 0$
и решением получающейся системы линейных уравнений. В случае, если при решении системы какие-то переменные оказывались отрицательными, вступали в силу ограничения: эти переменные приравнивались к нулю, соответствующие им строки и столбцы вычеркивались, и сокращенная система решалась без них. Вычисления повторялись до тех пор, пока для всех не включенных в ограничения переменных не получались неотрицательные итоговые значения. Т.е. одна и та же система линейных уравнений решалась, вообще говоря, многократно с последовательным исключением отрицательных результатов. Цикл по всем трем координатам составлял одну итерацию. Итерации продолжались, пока изменение невязки между последовательными итерациями не становилось меньше заданного порога (в качестве порога использовалось значение 5 × 10–4).

Циклы итераций повторялись по 10 раз с разными начальными условиями для каждого числа факторов (компонентов) из диапазона 1–24. Для каждого числа факторов из 10 полученных решений выбиралось решение с наименьшей итоговой невязкой.

В качестве контрольного метода использовался факторный анализ: модельные спектры (организованные в этом случае в виде матриц размером 129 × 256 элементов для 10 фиксированных факторов и размером 129 × 64 элемента для 9 фиксированных и одного случайного фактора) анализировались также путем факторного разложения NMF (Non-negative Matrix Factorization – разложение неотрицательных матриц на неотрицательные составляющие) [Lee, Seung, 2001] с последующим вращением первичных факторов до получения проекции компонентов модели на подпространство факторов, и полученные результаты сравнивались с результатами тензорного разложения.

Все описанные алгоритмы реализованы в виде программ, написанных на Турбо Паскале для ОС MS-DOS.

РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЙ

Применение описанного метода к модельным спектрам показало, что при задании корректного числа факторов (известного для модели заранее и равного 10) получаемые результаты разложения имеют минимальные отличия от заданных в модели компонентов: менее 4% по спектральным составляющим (фактор 8 – рис. 1(в)) и менее 3% по топографическому распределению (фактор 10 – табл. 1) – и то, и другое касается максимальных отличий решения от модели. Среднее же отличие и по спектру, и по топографии составляло менее 0.5% для всех 10 факторов.

Таблица 1.

Погрешность оценки топографии компонентов модельных спектров, % Table 1. Error of model spectra components’ topography estimates, %

Фактор Код Среднее Максимальное
f1 1 0.11 0.3
  2 0.53 1.4
f2 1 0.03 0.1
  2 0.39 1.2
f3 1 0.04 0.2
  2 0.29 0.8
f4 1 0.09 0.3
  2 0.36 0.9
f5 1 0.04 0.2
  2 0.3 0.6
f6 1 0.11 0.3
  2 0.92 2.7
f7 1 0.23 0.9
  2 0.34 0.7
f8 1 0.49 2.2
  2 0.36 1.2
f9 1 0.11 0.4
  2 0.19 0.4
f10 1 0.76 2.1

Примечания: 1. Код 1 соответствует модели 10 факторов с фиксированной топографией, код 2 – модели 9 факторов с фиксированной и 1 фактора со случайной топографией. 2. Фактор 10 не имеет варианта с кодом 2, поскольку в этом варианте топография данного фактора не фиксировалась.

Notes: 1. Code 1 relates to the model of 10 factors with fixed topography, code 2 – relates to the model of 9 factors with fixed topography and 1 random topography factor. 2. Factor 10 has not code 2 variant, because in this model its topography was not fixed.

Для сравнения на рис. 1 представлены исходные компоненты модели (б) и пример анализируемых спектров (а). Видно, что тензорное разложение правильно определило частотные границы факторов и их форму (прямоугольник).

Анализ спектров, имеющих один компонент со случайной топографией, дал результат, который можно было предположить: число факторов в решении увеличилось на число разных вариантов топографии случайного фактора, т.е. это число было равно числу фиксированных факторов плюс число разных топографий случайного фактора: 9 + 4 = 13 (рис. 1(г)). При этом первые 9 факторов соответствовали таковым в модели, за исключением фактора 8 – он превратился в разность компонентов 8 и 10 модели, сохранив при этом топографию компонента 8 модели. Максимальная погрешность остальных 8 спектральных составляющих – 7.2% – фактор 4, максимальная погрешность топографического распределения по 9 факторам – 2.7% – фактор 6, средняя погрешность по всем факторам – менее 1% и по спектру, и по топографии.

Результат факторного анализа тех же спектров с тем же числом факторов представлен на рис. 2(а). В последнем случае видно, что результат разложения не имеет практически никакого сходства с модельными компонентами, несмотря на то, что суммарная точность приближения модельных спектров в этом случае была лучше, чем при тензорном разложении (величина невязки была на 10% меньше). Последнее связано с тем, что факторный анализ позволил учесть часть наложенного на спектры шума, не имеющего тензорной структуры. Очевидно, что с помощью подходящего факторного вращения можно получить результат, весьма близкий к компонентам модели (они принадлежат близким подпространствам пространства данных) – рис. 2(б). Проблема в том, что это можно сделать, только зная заранее вид требующегося решения.

Рис. 2.

Результаты факторного анализа тех же спектров, что и на рис. 1: (а), (б) – 10 компонентов с фиксированной топографией, (а) – до вращения, (б) – после вращения; (в), (г) – 9 компонентов с фиксированной и 1 компонент со случайной топографией, (в) – до вращения, (г) – после вращения. Оси координат – те же, что на рис. 1.

Fig. 2. The results of factor analysis of the same spectra as in fig. 1: (а), (б) – 10 components with fixed topography, (а) – before the rotation, (б) – after the rotation; (в), (г) – 9 components with fixed topography and 1 component with stochastic topography, (в) – before the rotation, (г) – after the rotation. Coordinate axes – same as in fig. 1.

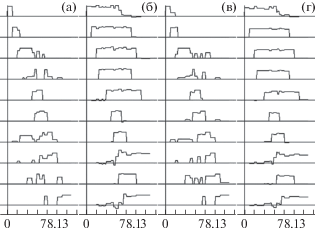
Результаты факторного анализа спектров, имеющих один компонент со случайной топографией, представлены на рис. 2(в) и рис. 2(г). Видно, что результаты анализа спектров, составленных из 10 компонентов с фиксированной топографией (рис. 2(б)) и спектров, имеющих один компонент со случайной топографией (рис. 2(г)), мало различаются – факторный анализ не зависит от постоянства топографии.

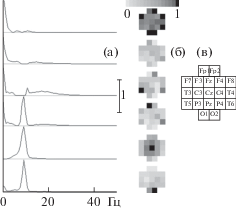
Пример результатов анализа реальных спектров ЭЭГ представлен на рис. 3. Слева на рисунке представлены спектры компонентов (а), а справа – соответствующие им топограммы (б). Видны два класса компонентов: один с максимумом в диапазоне стандартного дельта-ритма (0–4 Гц), другой – в диапазоне стандартного альфа-ритма (8–13 Гц). Интересно, что даже при увеличении числа факторов до 24, большинство компонентов относилось к этим же двум классам и для всех шести испытуемых пилотной группы не возникло ни одного компонента в диапазоне 20–100 Гц. При этом при 6 факторах средняя по группе погрешность аппроксимации (невязка) составляла 2.3 ± 0.62%, а при 24 факторах – 0.6 ± 0.16%.

Рис. 3.

Пример тензорного разложения реальных спектров ЭЭГ человека. (а) – нормированные спектры компонентов, (б) – нормированная топография компонентов (без интерполяции, каждый квадрат отражает значение под соответствующим электродом), (в) – схема расположения электродов. Оси координат (а) – те же, что на рис. 1.

Fig. 3. Example of tensor decomposition of real human EEG spectra. (а) – standardized components’ spectra, (б) – standardized components’ topography (without interpolation, each square reflects the value under corresponding electrode), (в) – electrode layout scheme. Coordinate axes (а) – same as in fig. 1.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Результаты, полученные на модельных спектрах, показывают, что тензорное разложение воспроизводит компоненты модели точнее, чем факторный анализ, даже после вращения. Это может объясняться тем, что факторный анализ может интерпретировать не только дисперсию, связанную с компонентами, но и часть дисперсии шума. Именно поэтому итоговая невязка в факторном анализе получается меньше, чем в тензорном. Необходимо еще раз подчеркнуть, что результаты факторного анализа можно сравнивать с компонентами модели только после неочевидного факторного вращения, тогда как тензорное разложение дает требуемые компоненты непосредственно, без лишних степеней свободы [Stegeman, Sidiropoulos, 2007].

Таким образом, тензорное разложение хорошо воспроизводит компоненты модели, а факторный анализ лучше аппроксимирует модельные спектры. Тензорное разложение более помехоустойчиво за счет использования тензорной структуры данных (дополнительных связей между ними). Получается, что тензорное разложение предпочтительнее для компонентного анализа частотных диапазонов ЭЭГ.

В то же время при наличии в модельных спектрах компонента со случайной топографией факторный анализ аппроксимирует эти спектры тем же числом факторов (10), что и спектры, состоящие полностью из фиксированных компонентов и приблизительно с той же точностью (и приблизительно так же плохо воспроизводит компоненты модели). Тогда как при тензорном разложении этих спектров количество составляющих увеличивается до 13 (число фиксированных факторов плюс число различных топографий случайного фактора). Отличие фактора 8 тензорного разложения от соответствующего компонента модели иллюстрирует редкое исключение из правил, описанных во введении, – когда один компонент представляет часть спектра другого компонента и при этом не имеет фиксированной топографии, в плоскости этих двух компонентов возможно вращение. Это пример невыполнения критерия единственности Краскела [Kruskal, 1977].

В общем, более высокая точность тензорного разложения оплачивается дополнительными ограничениями, накладываемыми на компоненты анализируемых спектров (постоянство не только спектрального состава, но и топографии), а также существенно большей сложностью (и, следовательно, продолжительностью) вычислительных процедур [Bro, 1997].

Результаты применения тензорного разложения для анализа реальных спектров ЭЭГ пилотной группы испытуемых лишь частично соответствуют принятому в литературе (например, [Климеш, 1999]) делению ЭЭГ на ритмы или частотные диапазоны. В то время, как полученные новым методом результаты соответствуют общепринятым в низкочастотной части спектра (0–15 Гц – компоненты дельта-, тета- и альфа-диапазонов), в высокочастотной части самостоятельных компонентов обнаружено не было, несмотря на использование относительной невязки, из-за которого вклад высокочастотной (20–100 Гц) части спектра в суммарную невязку в 4 раза превосходил вклад низкочастотной части (0–20 Гц). Более того, все полученные спектральные компоненты не были локализованы в узкой полосе частот: имея довольно узкий спектральный максимум, все они имели широкие “хвосты”, вплоть до 100 Гц.

Отсутствие самостоятельных компонентов выше 20 Гц может быть связано с сильным загрязнением этого спектрального диапазона электромиограммой [Whitham et al., 2007] и тем, что активность мышц не соответствует тензорной структуре.

Результаты, полученные на пилотной группе испытуемых, дали новое представление о спектральных составляющих ЭЭГ (широкополосность ритмов), которые нуждаются в дальнейшем подтверждении на большей выборке и при иных физиологических состояниях, что будет предметом отдельной работы. В ней также предполагается описать использование результатов тензорного разложения для определения мощности спектральных компонентов ЭЭГ (путем разложения спектров по полученному базису компонентов) и распространения полученных индивидуальных результатов для работы с группами испытуемых.

ВЫВОДЫ

1. Разработана модификация метода тензорного разложения PARAFAC для анализа спектров ЭЭГ человека.

2. Описанный метод решает поставленную задачу определения спектральных и топографических характеристик компонентов ЭЭГ.

3. Результаты анализа модельных спектров свидетельствуют о высокой точности нового метода.

4. Сравнение результатов факторного и тензорного разложения показало преимущество последнего: однозначность решения из-за отсутствия вращений и большая помехоустойчивость (робастность).

5. Результаты анализа реальных спектров ЭЭГ человека показали удовлетворительное согласие с общепринятыми представлениями о ритмах ЭЭГ в области частот от 0 до 15 Гц, что требует дальнейших уточнений.

Список литературы

  1. Марпл мл. С.Л. Цифровой спектральный анализ и его приложения. М.: Мир, 1990. 590 с.

  2. Новотоцкий-Власов В.Ю., Бобрик Г.И., Ковалев В.П. Модельный эксперимент для оценки метода определения частотных характеристик ритмов ЭЭГ. Материалы XV Международного симпозиума “Динамические и технологические проблемы механики конструкций и сплошных сред” им. А.Г. Горшкова, т. 2. М.: Изд-во “Типография “ПАРАДИЗ”, 2009. 107–116.

  3. Новотоцкий-Власов В.Ю., Строганова Т.А., Ковалев В.П. Адаптивный метод разложения спектра ЭЭГ на компоненты. Журн. высш. нерв. деят., 2012. 62 (2): 250–256.

  4. Харман Г. Современный факторный анализ. Пер. с англ. М.: Статистика, 1972. 486 с.

  5. Bro R. PARAFAC. Tutorial and applications. Chemometr. Intell. Lab., 1997. 38: 149–171.

  6. Bro R., Kiers H.A.L. A new efficient method for determining the number of components in PARAFAC models. J. Chemometr., 2003. 17: 274–286.

  7. Colda T.G., Bader B.W. Tensor decompositions and applications. SIAM Review, 2009. 51 (3): 455–500.

  8. De Clercq W., Vergult A., Vanrumste B., Van Hees J., Palmini A., Van Paesschen W., Van Huffel S. A new muscle artifact removal technique to improve the interpretation of the ictal scalp electroencephalogram. Conf. Proc. IEEE Eng. Med Biol. Soc., 2005. 1: 944–947.

  9. Kim H., Park H. Non-negative matrix factorization based on alternating non-negativity constrained least squares and active set method. SIAM J. Matrix Anal. Appl., 2008. 30 (2): 713–730.

  10. Kirenskaya A.V., Novototsky-Vlasov V.Y., Chistyakov A.N., Zvonikov V.M. The relationship between hypnotizability, internal imagery, and efficiency of neurolinguistic programming. Int. J. Clin. Exp. Hypn., 2011. 59 (2): 225–241.

  11. Klimesch W. EEG alpha and theta oscillations reflect cognitive and memory performance: a review and analysis. Brain Res. Rev., 1999. 29: 169–195.

  12. Kruskal J.B. Three-way arrays: rank and uniqueness of trilinear decompositions, with applications to arithmetic complexity and statistics. Linear Algebra Appl., 1977. 18: 95–138.

  13. Lawson C.L., Hanson R.J. Solving least squares problems. Englewood Cliffs, NJ: Prentice-Hall, 1982. 352 p.

  14. Lee D.D., Seung H.S. Algorithms for non-negative matrix factorization. Advances in Neural Information Processing Systems. V. 13, Eds. Leen T.K., Dietterich T.G., Tresp V. The MIT Press. 2001. 556–562.

  15. McFarland D.J., Miner L.A., Vaughan T.M., Wolpaw J.R. Mu and beta rhythm topographies during motor imagery and actual movements. Brain Topogr., 2000. 12 (3): 177–186.

  16. Miwakeichi F., Martinez-Montes E., Valdes-Sosa P.A., Nishiyama N., Mizuhara H., Yamaguchi Y. Decomposing EEG data into space–time–frequency components using Parallel Factor Analysis. NeuroImage, 2004. 22: 1035–1045.

  17. Morup M., Hansen L.K. Automatic relevance determination for multi-way models. J. Chemometr., 2009. 23: 352–363.

  18. Neuhaus J.O., Wrigley C. The quartimax method: An analitical approach to orthogonal simple structure. British J. Math. Statist. Psychol., 1954. 7: 81–91.

  19. Niedermeyer E. The Normal EEG of the Waking Adult. Electroencephalography: Basic Principles, Clinical Applications and Related Fields. Eds Niedermeyer E., Lopes da Silva F.H. Philadelphia PA: Lippincott, Williams & Wilkins. 2005: 167–192.

  20. Paatero P. A weighted non-negative least squares algorithm for three-way ‘PARAFAC’ factor analysis. Chemometr. Intell. Lab., 1997. 38: 223–242.

  21. Polich J. EEG and ERP assessment of normal aging. EEG Clin. Neurophysiol. 1997. 104: 244–256.

  22. Stegeman A., Sidiropoulos N.D. On Kruskal’s uniqueness condition for the Candecomp/Parafac decomposition. Linear Algebra Appl., 2007. 420: 540–552.

  23. Steriade M., Gloor P., Llinas R.R., Lopes da Silva D.H., Mesulam M.-M. Basic mechanisms of cerebral rhythmic activities. EEG Clin. Neurophysiol., 1990. 76: 481–508.

  24. Timmerman M.E., Kiers H.A.L. Tree-mode principal components analysis: Choosing the numbers of components and sensitivity to local optima. Br. J. Math. Stat. Psychol., 2000. 53: 1–16.

  25. Vanderperren K., De Vos M., Mijovic B., Ramautar J.R., Novitskiy N., Vanrumste B., Stiers P., Van den Bergh B.R.H., Wagemans J., Lagae L., Sunaert S., Van Huffel S. PARAFAC on ERP data from a visual detection task during simultaneous fMRI acquisition. Proc. of Intern Biosignal Processing Conference. Berlin, Germany, 2010. 1–4.

  26. Whitham E.M., Pope K.J., Fitzgibbon S.P., Lewis T., Clark C.R., Loveless S., Broberg M., Wallace A., DeLosAngeles D., Lillie P., Hardy A., Fronsko R., Pulbrook A., Willoughby J.O. Scalp electrical recording during paralysis: Quantitative evidence that EEG frequencies above 20 Hz are contaminated by EMG. Clin. Neurophysiol., 2007. 118: 1877–1888.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Журнал высшей нервной деятельности им. И.П. Павлова

Архивы выпусков Информация о журнале Отправить рукопись в журнал