Геохимия, 2021, T. 66, № 11, стр. 1008-1019
Гидродинамическая кавитация как природный процесс формирования зародышей алмазной фазы
С. А. Воропаев a, *, Н. В. Душенко a, А. Ю. Днестровский a, А. В. Кривенко a
a Институт геохимии и аналитической химии им. В.И. Вернадского РАН
119991 Москва, ул. Косыгина, 19, Россия
* E-mail: voropaev@geokhi.ru
Поступила в редакцию 29.03.2021
После доработки 01.04.2021
Принята к публикации 02.04.2021
Аннотация
Рассмотрены особенности формирования углеродных наночастиц при гидродинамической кавитации в природных и лабораторных условиях. Проведено сравнение размеров и структуры продуктов синтеза для различного химического состава углерод-содержащих жидкостей. С помощью методов электронной дифракции и Рамановской спектроскопии выделены и исследованы такие наноформы углерода как наноалмаз, сложные фуллерены и ГЦК-углерод. Изучена возможность легирования синтезируемых наноалмазов примесями азота и кремния, проведена оценка спектров фотолюминесценции наноалмазов. Рассмотрены геохимические приложения результатов к процессам образования минеральных фаз при движении мантийных флюидов.
ВВЕДЕНИЕ
Одной из геологических гипотез академика Э.М. Галимова была оценка важности гидродинамической (ГД) кавитации в качестве природного процесса формирования зародышей алмазной фазы в кимберлитах. Эту идею он развивал в течение нескольких десятилетий, исследуя кавитацию как сложное геофизическое и геохимическое явление, связывающее вместе движение мантийных флюидов, их состав, свойства и процессы образования минеральных фаз в земных недрах.
В данной работе мы суммируем теоретические разработки Э.М. Галимова в этой области и их экспериментальное подтверждение, в которых принимали участие авторы.
РАЗВИТИЕ ИДЕИ
В первых научных публикациях академика Э.М. Галимова в 1971–1973 гг. в журналах Доклады АН СССР, Геохимия и др. (Галимов, 1973, 1974) была высказана гипотеза о том, что образование природных алмазов может происходить не только в статических условиях, но и в динамическом процессе при возникновении кавитации в быстродвижущемся кимберлитовом расплаве.
Принципиально им было рассмотрено два случая:
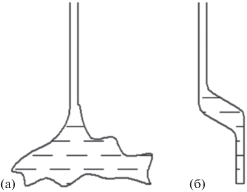
1. Постепенное нарастание давления в подкоровом очаге (рис. 1а). После того как давление превзойдет некоторый критический уровень, происходит прорыв и давление в очаге быстро сбрасывается. Скорость падения давления в очаге зависит от объема и расхода магматического материала через образовавшийся канал. Такой очаг был назван статическим.
2. Непосредственной причиной прорыва кимберлитовой магмы и нарастания давления в очаге, служит движение блоков земной коры (рис. 1б). В этом случае происходит выжимание магмы из очага и давление в процессе извержения поддерживается на первоначальном уровне, благодаря компенсирующему движению блоков. В этом случае характер изменения скоростей и давлений при движении магмы остается практически неизменным во времени и не зависит ни от объема очага, ни от расхода жидкости через канал. Такой очаг был назван динамическим.
Далее Э.М. Галимов рассуждал следующим образом: жидкости, содержащие растворенные газы, склонны к кавитации. Кимберлитовая магма имеет отличительную особенность – высокое газосодержание углекислоты, поскольку реликты этой углекислоты в виде рассеянных карбонатов часто присутствуют в кимберлитах.
Известно, что гидродинамическая (ГД) кавитация возникает в потоке при резкой смене давления. Способность к кавитации принято характеризовать числом кавитации.
где ${{P}_{0}}$ – давление в потоке, ${{P}_{c}}$ – давление, при котором газ полностью растворен (для гомогенной жидкости – давление парообразования), $U$ – скорость потока, $\rho $ – плотность флюида.Сущность явления, по мнению Э.М. Галимова, состояла в следующем. При некотором начальном давлении ${{P}_{0}}$ поток представляет однофазный флюид, в котором газ полностью растворен. Снижение давления ниже критического, например, в результате увеличения скорости потока, приводит к образованию первичных пузырьков газа. Если затем давление возрастает, причем раньше, чем газовые пузырьки объединяются в сплошную фазу, произойдет их схлопывание. При этом вблизи точки, к которой стягивается сферическая поверхность пузырьков, возникают давления, на несколько порядков превосходящие начальное давление в окружающей среде. Одновременно как результат адиабатического сжатия происходит нарастание температуры. Критические значения числа кавитации лежат в диапазоне $0.35 < {{Q}_{i}} < 1.0.$
Роль кавитации как фактора, определяющего синтез природных алмазов, виделась ему в том, что в момент коллапса газового углеродсодержащего пузырька при условиях, существующих в кимберлитовой магме, достигаются давления и температуры, отвечающие термодинамической устойчивости алмаза в точках сжатия согласно Р-Т фазовой диаграмме углерода. Известно, что чем выше скорость движения жидкости, тем больше вероятность возникновения ГД кавитации. Геофизические исследования и вычисления показывали, что скорость расплава может составлять, по меньшей мере, от нескольких десятков до нескольких сотен метров в секунду. По оценкам Э.М. Галимова, в процессе движения такой жидкости на отдельных участках глубинного подводящего канала, который в общем случае имеет неправильную форму и переменное сечение, могут возникать колебания давления, превосходящие несколько гигапаскалей (ГПа), что приводит к возникновению растягивающих напряжений (отрицательных давлений), разрыву жидкости (холодному кипению) и образованию наполненных газом и паром пузырьков и каверн. Это было показано с помощью соотношения Бернулли:
P0 – P = ρ/2u2[(D/d)4 – 1],
где $D$ – средний диаметр магматического канала, $d$ – диаметр сужения, u – средняя скорость движения магмы в канале.
Далее Э.М. Галимов справедливо полагал, что, когда жидкость выйдет из сужения в расширенную часть канала, внешнее давление вновь возрастет, и газ, заполнивший пузырек, испытает сферически сфокусированный гидравлический удар. Иначе говоря, происходит резкое сжатие и схлопывание, в процессе которого могут развиться очень высокие давления. Известно, что даже в средах, находящихся при обычном атмосферном давлении (например, при схлопывании мелких пузырьков в воде) развиваются пиковые давления до 1 ГПа. Это является причиной известного разрушительного действия кавитации на элементы турбин, гребных винтов, насосов, трубопроводов и т.п. Так как энергия схлопывания сферического пузырька прямо пропорциональна начальному давлению:
E = 4/3πR3P0,
то при параметрах кимберлитового процесса она намного превосходит мольную энергию образования новой фазы. Величина возникающего максимального давления (до 5 ГПа) и время его существования (~10–3 с) вполне могут обеспечить образование мелких алмазов, подобно ударному генезису. Далее, как полагал Э.М. Галимов возможно формирование крупных монокристаллов в результате процесса твердофазной рекристаллизации, протекающей уже после завершения сжатия кавитационных пузырьков.
ЭКСПЕРИМЕНТАЛЬНЫЕ ИССЛЕДОВАНИЯ
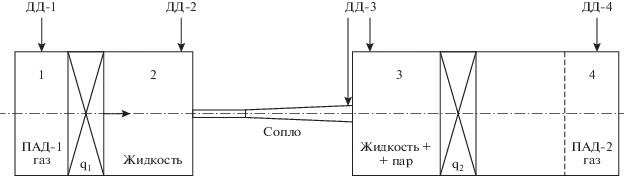
1-й этап, 2000–2006 гг. Предложенная Э.М. Галимовым модель ГД кавитации предлагала оригинальное решение проблемы концентрации рассеянного углерода в мантии, необходимой для формирования зародыша алмаза, и была опубликована в журнале Nature в 1973 году (Galimov, 1974). Однако, выдвинутая гипотеза предполагала прохождение ряда связанных процессов: возбуждения кавитации в расплавах, находящихся под высоким давлением, роста и устойчивости газонаполненных пузырей, динамики их сжатия, и, наконец, всей совокупности проблем, связанных с физико-химической стороной процесса. Необходимо было проверить ее выводы экспериментально, что являлось нетривиальной задачей. Первые экспериментальные и теоретические исследования в рамках рассмотрения выдвинутой гипотезы проводились на малой ГД установке, изготовленной в МГТУ им. Н.Э. Баумана группой проф. В.Н. Скоробогатского (рис. 2) (Галимов и др., 2004).
Сравнение с детонационным методом синтеза алмазов показало, что физико-химические процессы, происходящие в кавитационном пузырьке на последней стадии его сжатия весьма схожи с процессами, происходящими во взрывной камере. Предполагалось, что достигаемые при ГД кавитации давление и температура обеспечивают термодинамическую стабильность и синтез наноалмаза (НА) из возникающей газообразной смеси кластеров углерода и водорода. При этом, контролируемое добавление бор/фосфор-содержащих газов или жидкостей, изменение условий сжатия кавитационных пузырьков позволили бы управлять процессом синтеза легированных нано гетероструктур углерода.
Принципиальная схема первой экспериментальной установки, использованной Э.М. Галимовым для воспроизведения гидродинамической кавитации в углеводородных жидкостях с возможностью создания большого скачка внешнего давления приведена на рисунке 2. Исходную жидкость помещали в камеру (2). В камеры (1) и (4) закладывали пороховой артиллерийский заряд (ПАД), зажигание которого позволяло резко смещать поршни (q), выталкивая рабочую жидкость из одной камеры (2) в другую (3). Давление во всех камерах установки фиксировали датчики давления (ДД). При быстром движении углеводородной жидкости по профилированному каналу в виде сопла Вентури, в жидкости формировались кавитационные полости, которые затем сжимались в рабочей камере (3) при инициируемом резком скачке давления. Скачок давления в ударной волне, достигающий значений 80–90 МПа, обеспечивал близкий к адиабатическому сжатию коллапс кавитационных пузырьков, в ходе которого давление внутри значительно усиливалось. В результате ряда быстропротекающих физико-химических процессов испарения, нагрева и термической диссоциации паров, в кавитационных полостях синтезировалась твердая углеродная фаза, которая затем подвергалась специальной химической процедуре очистки и концентрации.
На малой установке был проведен ряд экспериментов с химически чистыми жидкостями разной молекулярной структуры: бензол (С6H6) (Воропаев и др., 2011), толуол (С6H5CH3) (Воропаев и др., 2012) и смеси этанол–анилин (С2H5OH + С6H5NH2 3%) (Воропаев и др., 2014). Во всех случаях были получены НА различных размеров: 20–30 нм (бензол), 10–15 нм (толуол), 5–10 нм (этанол–анилин). Преимуществом бензола является наилучшее соотношение углерода и водорода, но это вещество повышенного класса опасности и работать с ним в промышленных условиях было бы проблематично. Преимуществом толуола является наличие цикла и дополнительных метильных групп, что могло обеспечить больше структурных элементов (затравок) для алмазной кристаллической решетки и, тем самым, больший выход синтезируемых наночастиц. Наименьшие по размеру НА были получены из смеси этанол-анилин, что подчеркивает особенности формирования зародыша НА из молекулярных фрагментов, а не из пара атомарного углерода.
Весь полученный материал был исследован на просвечивающем электронном микроскопе JEM100CХ11 в ИФТТ РАН Арониным А.С. (табл. 1). На рис. 3 и 4 приведены фотографии образцов и электронные дифрактограммы кавитационных наноалмазов, полученных из химически чистого бензола, толуола и смеси этанол-анилин.
Таблица 1.
Межплоскостные расстояния по результатам обработки электронограмм
| Стандарт | Экспериментальная установка МГТУ им. Н.Э. Баумана | ||||
|---|---|---|---|---|---|
| номер линии | плоскость hkl, индекс Миллера | ГЦК решетка алмаз, Å |
кавитационный алмаз, бензол, Å | кавитационный алмаз, толуол, Å | кавитационный алмаз, этанол–анилин, Å |
| 1 | 111 | 2.06 | 2.06 | 2.06 | 2.06 |
| 2 | 200* | (1.783) | 1.79 | 1.85 | 1.74–1.78 |
| 3 | 220 | 1.261 | 1.26 | 1.26 | 1.25–1.28 |
| 4 | 311 | 1.0754 | 1.08 | 1.076 | 1.08–1.11 |
| 5 | 222 | 1.0297 | – | – | – |
| 6 | 331 | 0.8182 | 0.821 | 0.814 | – |
| 7 | 240* | (0.7976) | – | – | – |
| 8 | 422 | 0.7281 | – | – | – |
| 9 | 115 | 0.6864 | – | – | – |
Рис. 3.
РЭМ-изображения кавитационных алмазов, полученных их бензола (а); толуола (б); смеси этанол + анилин (в).

Рис. 4.
Электронограммы, полученные на просвечивающем электронном микроскопе для алмазов, полученных из бензола (а); толуола (б); смеси этанол–анилин (в).

Расшифровка электронных дифрактограмм показала наличие линий, запрещенных в алмазной решетке (пространственная группа Fd3m), но разрешенных для ГЦК решетки (пространственная группа Fm3m). Запрещенные линии соответствуют отражениям от плоскостей (200) и (240) алмазной ГЦК решетки с постоянной а = 3.563 А: они обозначены звездочкой на рис. 4 и в табл. 1.
Данные кристаллической решетки частиц, синтезированных при ГД кавитации, приведены в табл. 1.
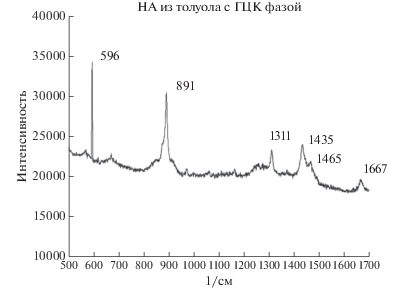
Для получения Рамановских (КР) спектров образцов был использован спектрометр Renishaw InVia Reflex с длиной волны лазера 785 нм, ЦКП МГУ им. М.В. Ломоносова (рис. 5).
Было показано, что наночастицы углерода, полученные на малой экспериментальной установке высокого давления, представляют собой агломераты размером около 10–20 нм со следующими особенностями (Воропаев и др., 2014):
1. Анализ КР спектров образцов полученных из бензола показал характерный пик в интервале 1330–1350 см–1, который указывает на наличие графитовой “шубы” вокруг кристаллических алмазных ядер. Также, заметен пик 1462 см–1, который типичен для ультрадисперсного кристаллического графита, а также деформированных давлением сложных фуллеренов. По-видимому, это продукты меньшего сжатия кавитационных полостей, при которых не достигаются значения давления и температуры, характерные для области термодинамической стабильности алмазной фазы.
2. Анализ КР спектров образов полученных из толуола показывает сдвиг характерного пика с 1332 до 1311 см–1 и сдвиг G-линии с 1590 до 1667 см–1, что является известным размерным эффектом, типичным для кристаллитов размером 3–5 нм. Также, заметны пики 596 и 891 см–1 нетипичные для “чистых” нанокристаллических графита и алмаза и, по видимому, либо являются следствием композитной ГЦК-структуры, либо свидетельствуют о сильной деформации решетки. Пики 1435 и 1465 см–1 типичны для ультрадисперсного кристаллического нанографита, а также деформированных давлением сложных фуллеренов. По-видимому, это продукты меньшего сжатия кавитационных полостей, при которых не достигаются значения давления и температуры, характерные для области термодинамической стабильности алмазной фазы.
3. Анализ КР спектров образов полученных из смеси этанол–анилин показывает сдвиг характерной “алмазной” D-линии с 1332 до 1325 см–1, что является известным размерным эффектом, типичным для кристаллитов размером 3–5 нм. Пики 1338 и 1349 см–1 обусловлены колебательными модами нанографита. Они связаны с краевыми эффектами и указывают на нарушение кристаллической структуры. Детальное исследование КР спектров молекул С60 и С70 было выполнено в работе (Bethune et al., 1990), где спектральное разрешение составляло 9 см–1. Для фуллеренов известно, что основная полоса в КР спектре С60 расположена на частоте 1460–1470 см–1 и соответствует тангенциальной моде колебания пятигранника молекулы. Узкий пик, положение и интенсивность этой полосы указывает на то, что фуллерен С60 состоит из углерода в sp2-состоянии, а также на высокую однородность этой структуры. Напротив, в КР спектре С70 и более сложных фуллеренов присутствует большое число полос в интервале от 1420 до 1460 см–1, обусловленных неэквивалентностью различных атомов углерода и снижением симметрии молекулы. Для С70 в угольной пыли, нанесенной на вольфрамовую фольгу, характерными линиями являются 1568, 1232, 1185, 1062 и 260 см–1. Таким образом, по результатам анализа полученных КР спектров можно с уверенностью предположить, что линии 1234, 1418, 1444, 1452 и 1558 см–1, соответствуют смеси из сложных фуллеренов С70, С78 и С84, уцелевших после химической очистки продуктов синтеза.
На электронных дифрактограммах кавитационных алмазных наночастиц, присутствуют запрещенные в алмазной кристаллической структуре линии (200) и (240). Была выдвинуто предположение о существовании внешней оболочки с гранецентрированной кристаллической решеткой (ГЦК) с параметром решетки, совпадающим с параметром решетки алмаза а = 3.57 Å (Hirai, Kondo, 1991). Сам способ синтеза, предполагающий использование углеродсодержащих органических жидкостей, открывал новые возможности управления размером и внутренней структурой получаемых наноалмазов за счет вариации молекулярной структуры исходного соединения. Особый интерес вызвала возможность получения примесных центров окраски в наноалмазах, в частности, из-за их уникальных квантовых свойств (Jelezko, 2006). Также, особенности спектров люминесценции дефектов алмазной кристаллической решетки азот–вакансия (N–V) и кремний–вакансия (Si–V) позволили бы использовать такие наночастицы в качестве маркеров для целей биомедицинской диагностики.
2-й этап, 2009-2020 гг. К сожалению, малая экспериментальная ГД установка, изготовленная в МГТУ им. Н.Э. Баумана, имела некоторые недостатки: проведение экспериментов требовало аттестованного помещения для взрывных работ, использовались токсичные и канцерогенные углеводородные жидкости, не было возможности использовать непрерывный цикл синтеза. Для дальнейших исследований механизма ГД нуклеации требовались более детальные и точные эксперименты, сочетающие теоретическое и численное моделирование. Так, например, возможность варьирования условий сжатия кавитационных пузырьков, срока их существования и анализ образующихся углеродных наноструктур позволили бы точнее определить условия формирования наноалмазов.
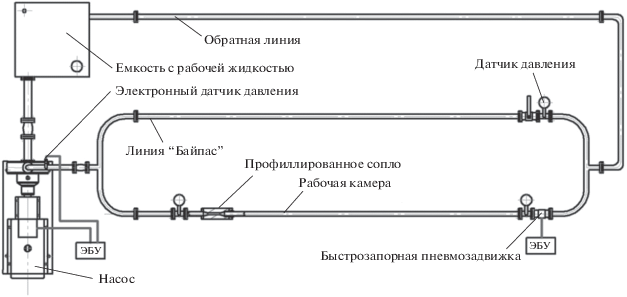
Это привело к разработке в ГЕОХИ РАН, под руководством Э.М. Галимова, новой модифицированной установки кавитационного синтеза наноалмазов (УКНА) с целью приближения метода к промышленной технологии синтеза наночастиц, в которой был применен метод гидроудара по кавитационным пузырькам. Для этого, в первую очередь, потребовалось добиться непрерывного цикла и обеспечить скачок внешнего давления, достаточный для адиабатического коллапса кавитационных пузырьков. Принципиальная схема установки УКНА представлена на рис. 6.
Были проведены серии экспериментов с 3% раствором изопропилового спирта (ИПС, С2Н8О 3%) в дистиллированной воде, которые показали наличие алмазной структуры в некоторых полученных наночастицах при кавитации (Душенко и др., 2016).
Полученный материал был исследован на просвечивающем электронном микроскопе JEM100CХ11 в ИФТТ РАН А.С. Арониным (табл. 2). Принцип действия микроскопа основан на формировании пучка электронов с энергией до 100 кэВ для непосредственного просвечивания объекта измерений. В качестве объектов, прозрачных для электронов с такой энергией, могут исследоваться ультратонкие срезы, напыленные в вакууме реплики, нанесенные на прозрачную для электронов подложку наночастицы и др. Система магнитных линз микроскопа формирует электронно-микроскопическое изображение объекта проходящими электронами (рис. 7).
Таблица 2.
Межплоскостные расстояния в Å, рассчитанные по результатам обработки электронограмм.
| Стандарт | УКНА ГЕОХИ РАН | ||
|---|---|---|---|
| плоскость (hkl, индекс Миллера) | ГЦК решетка алмаз, Å |
Кавитационный алмаз, Н2О (дист) + С2Н8О 3% (ИПС), Å | |
| (а) №52 | (б) №49 | ||
| 111 | 2.06 | 2.06 | 2.06 |
| 200* | (1.783) | 1.782 | – |
| 220 | 1.261 | 1.21 | 1.256 |
| 311 | 1.0754 | – | 1.06 |
| 222 | 1.0297 | 1.04 | – |
| 331 | 0.8182 | – | 0.81 |
| 240* | (0.7976) | 0.79 | – |
| 422 | 0.7281 | 0.744 | 0.724 |
| 115 | 0.6864 | 0.692 | – |
Рис. 7.
Изображение продуктов синтеза: наноалмазы, полученные из Н2О (дистилят) + С2Н8О 3% (ИПС) (увеличение ×100 000, размер частиц 3–5 нм).

Контраст на изображении, т.е. его неравномерная освещенность, возникает из-за того, что рассеяние проходящих электронов зависит от массы атомов просвечиваемого вещества, а также, в случае просвечивания кристаллического вещества, и от ориентации кристаллографических осей относительно электронного луча микроскопа. Соответствующие неоднородности объекта становятся видимыми на электронно-микроскопическом изображении благодаря тому, что электроны, рассеянные на большие углы, задерживаются апертурной диафрагмой и не участвуют в формировании окончательного изображения (рис. 8).
Расшифровка электронных дифрактограмм частиц, синтезированных из ИПС, показала наличие у части из них кристаллической алмазной решетки: данные приведены в табл. 2.
При сопоставлении результатов обработки линий электронограмм с табличными значениями межплоскостных расстояний для частиц наноалмаза для всех случаев наблюдается хорошее соответствие. Но были обнаружены и “лишние” линии, 200 hkl и 240 hkl (образец № 52, рис. 8а), соответствующие межплоскостному расстоянию 1.78 и 0.7976 А. Эти линии запрещены для решетки алмаза (пространственная группа Fd3m), но разрешены для ГЦК решетки (пространственная группа Fm3m). Запрещенные линии соответствуют отражениям от плоскостей (200) и (240) кубической решетки с той же постоянной, что и в решетки алмаза а = 2.563 А. Эти линии присутствуют на многих электронограммах кавитационных алмазов. Из анализа электронограмм различных образцов можно сделать вывод, что запрещенные линии более интенсивны в случае более крупных частиц (на электронограммах присутствуют точечные рефлексы), что подтверждает наличие смеси разных кристаллических фаз – обычной алмазной фазы и фазы ГЦК-углерода. Из табл. 2 также видно, что в основном параметры линий (образец № 49, рис. 8б) совпадают с табличными значениями для алмаза и не содержат запрещенных значений, что говорит о чисто алмазной структуре этого образца.
ТЕОРЕТИЧЕСКИЕ И ЧИСЛЕННЫЕ ИССЛЕДОВАНИЯ
Численные исследования условий зародышеобразования при кавитации проводились для сжатия одиночного пузырька, где исследовались параметры его коллапса. Нульмерное моделирование сжатия одиночного парового пузырька показало, что требование на скачок внешнего давления в малой установке можно ослабить до значений порядка 10 МПа (Днестровский и др., 2011). Одномерное моделирование, с уточненным уравнением состояния бензола, понизило этот порог до 1–1.5 МПа (Днестровский и др., 2016). В этой работе решается система уравнений газовой динамики с учетом теплопроводности в двумерном цилиндрически симметричном приближении со сферической области с подвижной границей. Расчеты проводятся для бензола (C6Н6) с использованием широкодиапазонного уравнения состояния для сверхвысоких давлений и температур (Болотнова, 2007). Среда в пузырьке рассматривается как однофазная, состоящая из смеси молекул бензола (С6Н6), атомарного углерода и водорода:
Уравнения состояния для каждого компонента записываются в форме Ми–Грюнайзена с учетом затрат тепловой энергии на диссоциацию:
где k = m, d соответственно молекулярный и диссоциированный бензол и введены концентрации Xk. здесь K – коэффициент диссоциации.В качестве начальных значений задаются параметры пузырька непосредственно перед стадией прикладывания внешнего давления. Внешнее давление задается в жидкости и является параметром задачи: оно варьируется от 0.1 до 40 МПа. Начальное давление в пузырьке принималось 0.01 МПа, температура пара и жидкости около 300 К, начальный радиус пузырька 100 мкм, расчетная область 1 < r < 200 мкм. Расчеты показали, что при сжатии радиус пузырька достигает значений 5–7 мкм в зависимости от приложенного внешнего давления. Характерной особенностью схлопывания пузырька является наличие ударной волны (УВ). Скорость фронта УВ при скачке внешнего давления 1.5 МПа составляет примерно 4.5 км/с. Фазовый переход пар–жидкость при сжатии не реализуется: из-за быстрого роста температуры давление не достигает значений давления насыщенных паров. На фронте УВ происходит резкий скачок температуры и давления в закритическую область (для бензола Ткрит = 562 К). После прохождения фронта УВ температура и давление продолжают расти, однако в зону формирования алмаза вещество попадает только после отражения волны от внутренней расчетной границы. Как показано, для случая с перепадом внешнего давления ∆Р = 1.5 МПа через 1.2 нс после отражения УВ давление по всему объему пузырька составляет примерно 4–5 ГПа. Таким образом, весь объем пузырька оказывается в зоне формирования алмаза размером 5 нм в течение примерно 1 нс.
Получено, что при внешнем давлении больше 1 МПа при прохождении обратной УВ происходит практически полная диссоциация молекул бензола на атомы по всему объему пузырька. Этот процесс сдерживает рост температуры, которая при достижении внешним давлением 10 МПа еще не достигает температуры плавления алмаза, составляющей примерно 5000 К. При больших внешних давлениях, однако, температура достигает этот порог.
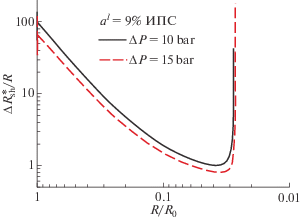
В работе (Днестровский и др., 2020) численно исследовались условия возникновения УВ в углеродосодержащих жидкостях и их водных растворах в нульмерной модели схлопывания одиночного пузырька. Критерием возникновения ударной волны являлось условие пересечения характеристик возмущений, распространяющихся от поверхности пузырька внутрь (Нигматулин, 2014). Если характеристики успевают пересечься внутри пузырька, т.е. параметр $\frac{{\Delta {{R}_{{sh}}}}}{R} < 1$ то возможно образование УВ. На рис. 9 показано изменение этого параметра в ходе сжатия парового пузырька, содержащего пары изопропилового спирта и воды в зависимости от его радиуса для разных внешних давлений. Видно, что этот параметр принимает наименьшее значение незадолго до остановки сжатия, что происходит в момент максимального ускорения стенки пузырька в сторону сжатия.
Рис. 9.
Параметр $\frac{{\Delta {{R}_{{sh}}}}}{R}$ возникновение УВ) в зависимости от размера пузырька в ходе коллапса для случая 9% раствора изопропилового спирта (ИПС) в воде при двух различных внешних давлениях (Днестровский и др., 2016).
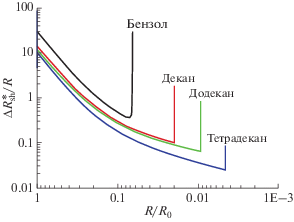
На рис. 10 показаны результаты по решению задачи схлопывания пузырька по указанной методике в чистых жидкостях при температуре 20°С и скачке внешнего давления 1 МПа.
Рис. 10.
Параметр $\frac{{\Delta {{R}_{{sh}}}}}{R}$ возникновение УВ) в зависимости от размера пузырька в ходе коллапса в чистых углеводородных жидкостях: ударная волна возникает при $\frac{{\Delta {{R}_{{sh}}}}}{R} < \,\,1$ (Днестровский и др., 2016).
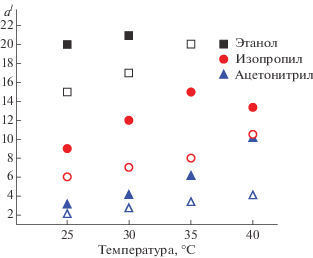
Были проведены расчеты сжатия одиночного пузырька, содержащего смесь водяного пара и пара одного из растворенных углеводородных веществ: C2H5OH (этанол), С2Н8О (изопропанол) и C3H2N (ацетонитрил). Результаты расчета условия образования ударной волны представлены на рис. 11: ударная волна возникает при превышении показанной на рисунке концентрации углеродсодержащего вещества. Повышение температуры жидкости вследствие увеличения начального давления пара р0 приводит к необходимости роста концентрации раствора. При повышении внешнего давления ΔP требуемая концентрация падает. Самая слабая концентрация раствора, которая обеспечивает формирование ударной волны, получается для ацетонитрила (C3H2N).
Рис. 11.
Условия возникновения ударной волны при скачке внешнего давления ΔP = 1 МПа (закрашенные значки) и 1.5 МПа (полые значки) для концентрации водного раствора al этанола (квадраты), изопропила (кружки) и ацетонитрила (треугольники) в зависимости от температуры раствора.
Из расчетов условий возникновения УВ были сделаны следующие выводы:
1. Условие для возникновения УВ перестает выполняться при уменьшении внешнего давления или увеличении температуры жидкости.
2. Для веществ с более высоким молекулярным весом легче обеспечить выполнение условия УВ, т.к. параметр относительного сжатия у них ниже.
Численные расчеты движения жидкости в гидродинамической установке УКНА (Днестровский и др., 2018) проводились для оптимизации параметров течения. Расчеты проводились в среде A-NSYS гидродинамическим модулем CFX для подбора сопла с оптимальным кавитирующим профилем (рис. 12). Результаты расчетов привязывались к данным по давлению, полученным с датчиков. В частности было показано, что схлопывание пузырьков пара происходит под давлением выше 1 МПа, полученным за счет гидроудара. Отметим, что в работе УКНА одним из ключевых управляющих элементов является высокоскоростной запирающий клапан с пневмоприводом, позволяющий за доли секунды полностью перекрыть поток жидкости и обеспечить скачок давления, известный из работ Жуковского Н.Е. как гидроудар (Жуковский, 1898).
Рис. 12.
Развитие кавитационного факела в сопле при разных рабочих режимах: вертикальный разрез, нижняя сторона – ось сопла с цилиндрической симметрией.
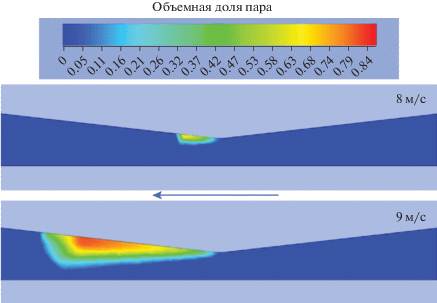
Другим важным элементом является профилированный канал, где происходит кавитация. Ниже приведен пример расчетов структуры кавитационного факела, где указаны доли возникающего пара в объемных процентах, при различных скоростях потока рабочей жидкости (Днестровский и др., 2018). Хорошо заметна “паразитная” область возле боковой стеки сопла с высоким содержанием пара (более 80 об. %), в которой режим схлопывания одиночных пузырьков сильно затруднен. В этой области пузырьки объединяются, формируя единый газопаровой пузырь, ГД удары по которому приводят к частичному разрушению стенок сопла.
В итоге, по результатам численного моделирования процессов движения растворов углеродсодержащих жидкостей были определены такие важные параметры ГД кавитации как оптимальная температура для разрыва жидкости, скорости потока и распределение давления в нем, форма сужения и оптимальная структура кавитационного факела.
ЗАКЛЮЧЕНИЕ
Идея Э.М. Галимова о важной роли ГД кавитации для формирования новых минеральных фаз при движении природных флюидов, изначально обоснованная теоретически, была подтверждена экспериментальными и детальными теоретическими исследованиями. Из ряда углеводородных жидкостей (бензол, толуол, смесь этанола и анилина) с помощью кавитации были синтезированы такие нанофазы углерода как алмаз, графит и сложные фуллерены. При этом был обнаружен неожиданный эффект – рост ГЦК-углерода на поверхности алмазного кристалла. Это позволило лучше понять механизмы зародышеобразования алмазной фазы и построить улучшенную модель формирования новых минеральных фаз в целом. Также, была подтверждена нуклеация алмазной фазы при ГД кавитации в водном растворе, содержащем изопропиловый спирт. Такая возможность изначально была не очевидна из-за неизбежного добавления кислорода при разложении молекул воды в газопаровую среду пузырька. Как известно, микрокристаллический алмаз практически мгновенно сгорает при температуре выше 700°С, для наноалмаза этот порог мог быть существенно ниже.
Мантийные флюиды в зависимости от температуры, давления и окислительно-восстановительных условий состоят в основном из воды и углекислого газа с добавлением CO, CH4 и H2 (Луканин и др., 2020). Сейсмологические измерения показывают, что примерно 70% землетрясений происходит на глубине до 100 км и около 3% на глубинах до 700 км (Жарков, 2012). Как правило, причиной землетрясений является деформация блоков литосферы при их контакте и относительном движении. По достижении критической величины сдвиговых напряжений происходит разрыв сплошности среды, развитие трещины, выделение флюида при разгрузке давления и закрытие трещины по исчерпании накопленной энергии деформации. Происходящий при этом коллапс газовых пузырей, содержащих СH4, СO и CO2, мог приводить к формированию различных кристаллических и аморфных форм углерода с последующей кристаллизацией алмаза в соответствии с его фазовой P-T диаграммой.
При кристаллизации изотопный состав алмаза определялся изотопным составом газа-прекурсора, например, фракционированием изотопов С13/C12 в системе ${\text{C}}{{{\text{H}}}_{4}}--{{{\text{C}}}_{{\sum {\text{CO}}--{\text{C}} - {\text{C}}{{{\text{O}}}_{2}}}}}$. В активных геотектонических зонах данный процесс мог происходить последовательно много раз, на разных глубинах и с различным содержанием флюидов. Известно, например, что на некоторых кимберлитовых полях Якутии встречаются одновременно алмазы различного изотопного состава, габитуса, окраски и др. (Галимов, 1984). Модель ГД кавитации Э.М. Галимова позволяет объяснить и этот природный феномен (Галимов, 1985).
Авторы благодарят чл.-корр. РАН Ф. В. Каминского за просмотр статьи и критические замечания, которые позволили улучшить изложение результатов. Работа была выполнена при поддержке гранта РФФИ (проект 19-05-00554).
Список литературы
Болотнова P.X. (2007) Расширенное уравнение состояния бензола. Труды Института механики. Уфа, УНЦ РАН. 113-120.
Воропаев С.А., Днестровский А.Ю., Скоробогатский В.Н., Аронин А.С., Шкинев В.М., Бондарев О.Л., Страздовский В.В., Елисеев А.А., Зевакин Е.А., Пономарева Е.А., Галимов Э.М. (2011) Синтез углерода с гранецентрированной кристаллической решеткой при кавитационном сжатии. ДАН. 440(3), 326-330.
Воропаев С.А., Шкинев В.М., Днестровский А.Ю., Пономарева Е.А., Аронин А.С., Бондарев О.Л., Страздовский В.В., Скоробогатский В.Н., Елисеев А.А., Спиваков Б.Я., Галимов Э.М. (2012) Особенности синтеза алмазоподобных наночастиц в толуоле при кавитации. ДАН. 446(4), 388-392.
Воропаев С.А., Днестровский А.Ю., Скоробогатский В.Н., Аронин А.С., Шкинев В.М., Бондарев О.Л., Страздовский В.В., Елисеев А.А., Пономарева Е.А., Душенко Н.В., Галимов Э.М. (2014) Экспериментальное изучение процессов образования наноалмазов и фуллеренов при кавитации в смеси этанол анилин. ДАН. 459(2), 162-167.
Воропаев С.А., Душенко Н.В., Скоробогатский В.Н., Аронин А.С., Шкинев В.М., Бондарев О.Л., Страздовский В.В., Елисеев А.А., Пономарева Е.А., Галимов Э.М. (2014) Фотолюминесценция легированных азотом наноалмазов кавитационного синтеза. ДАН. 459(6), 685-590.
Воропаев С.А., Душенко Н.В., Аронин А.С., Шкинев В.М., Галимов Э.М. (2015) Исследование возможности допирования азотом и кремнием кавитационных наноалмазов. Физико-химические аспекты изучения кластеров, наноструктур и наноматериалов. 7, 158-164.
Галимов Э.М., Прохоров В.С., Федосеев Д.В., Варнин В.П. (1973) Гетерогенные изотопные эффекты по углероду при синтезе алмаза и графита из газа. Геохимия. (3), 416-425.
Галимов Э.М. (1974) Кавитация как механизм синтеза природных алмазов. Известия АН СССР. Серия геологическая. 1, 22-37.
Галимов Э.М. (1984) Вариации изотопного состава алмазов и их связь с условиями алмазообразования. Геохимия. (8), 1091-1118.
Галимов Э.М. (1985) Некоторые доказательства реальности кавитационного синтеза алмазов в природе. Геохимия. (4), 456-471.
Галимов Э.М., Кудин А.М., Скоробогатский В.Н., Плотниченко В.Г., Бондарев О.Л., Зарубин Б.Г., Страздовский В.В., Аронин А.С., Фисенко А.В., Буков И.В., Баринов А.Ю. (2004) Экспериментальное подтверждение синтеза алмаза в процессе кавитации. ДАН. 395(2), 187-191.
Душенко Н.В., Воропаев С.А., Пономарева Е.А., Днестровский А.Ю., Шкинев В.М., Аронин А.С., Галимов Э.М. (2016) Кавитационный синтез наноформ углерода гидроударом. Известия высших учебных заведения. Серия: Химия и химическая технология. 59(9), 80-85.
Днестровский А.Ю., Воропаев С.А., Пономарева Е.А. (2011) Моделирование условий образования алмаза при кавитации в бензоле. ДАН. 436(5), 11-14.
Днестровский А.Ю., Воропаев С.А., Забродина Е.А. (2016) Моделирование сжатия кавитационного пузырька в бензоле. ДАН. 469(5), 21-25.
Днестровский А.Ю., Душенко Н.В., Воропаев С.А. (2018) Двухфазное течение в установке для получения кавитационных алмазов. Инженерно-физический журнал. 91(6), 32-37.
Днестровский А.Ю., Воропаев С.А., Душенко Н.В., Наймушин С.Г., Галимов Э.М. (2020) Условия возникновения ударной волны при кавитации в углеродсодержащих растворах. ДАН. 490(1), 24-28.
Жарков В. Н. (2012) Физика земных недр. М.: Изд. Наука и образование, 386 с.
Жуковский Н.Е. (1898) О гидравлическом ударе в водопроводных трубах. М.: Изд. Московского Университета, 134 с.
Луканин О.А., Цехоня Т.И., Колташев В.В., Кононкова Н.Н. (2020) Влияние C–O–H летучих компонентов на распределение Ni, Co и P между силикатным расплавом и жидким металлическим сплавом при 4 ГПа, 1550°С. Геохимия. 65(6), 548-565.
Lukanin O.A., Tsekhonya T.I., Koltashev V.V. and Kononkova N.N. (2020) Influence of C–O–H Volatiles on Ni, Co, and P Partition between Silicate Melt and Liquid Metal Fe Alloy at 4 GPa, 1550°C. Geochem.Int. 58(6), 670-686.
Нигматулин Р.И., Аганин А.А., Топорков Д.Ю., Ильгамов М.А. (2014) Образование сходящихся ударных волн в пузырьке при его сжатии. ДАН. 458(3), 282-286
Федосеев Д.В., Галимов Э.М., Варнин В.П., Прохоров В.С., Дерягин Б.В. (1971) Фракционирование изотопов углерода при физико-химическом синтезе алмаза из газа. ДАН СССР. 201(5), 1149-1158.
Bethune D.S. (1990) The vibrational Raman spectra of purified solid films of C60 and C70. Chem. Phys. Let. 174, 219.
Galimov E.M. (1973) Possibility of natural diamond synthesis under conditions of cavitation, occurring in a fast-moving magnetic melt. Nature. 243, 389.
Galimov E.M. (2001) Isotope fractionation related to kimberlite magmatism and diamond formation. Geochim. et Cosmochim. Acta. 55, 1697.
H. Hirai,K. Kondo. (1991) A New Crystalline Form of Carbon under Shock Compression. Proc. Japan Acad. 67 (Ser. B), 22.
Jelezko. F. (2006) Single defect centres in diamond. Phys. Stat. Solid. A. 203, 3207.
Дополнительные материалы отсутствуют.