Геохимия, 2021, T. 66, № 11, стр. 972-992

Физические свойства и внутреннее строение центральной области Луны

О. Л. Кусков^a, *, Е. В. Кронрод^a, **, Koji Matsumoto^b, c, ***, В. А. Кронрод^a, ****

^a Институт геохимии и аналитической химии им. В.И. Вернадского РАН
119991 Москва, ул. Косыгина, 19, Россия

^b RISE Project, National Astronomical Observatory of Japan
023-0861 Iwate, Oshu, Mizusawa, Hoshigaoka, 2-12, Japan

^c The Graduate University for Advanced Studies, SOKENDAI
240-0193 Kanagawa, Hayama, Shonan Village, Japan

^* E-mail: ol_kuskov@mail.ru
^** E-mail: e.kronrod@gmail.com
^*** E-mail: koji.matsumoto@nao.ac.jp
^**** E-mail: va_kronrod@mail.ru

Поступила в редакцию 30.04.2021
После доработки 04.06.2021
Принята к публикации 10.06.2021

DOI: 10.31857/S0016752521110066

Полный текст (PDF)

Аннотация

Особое место в геохимии и геофизике Луны занимает проблема строения центральной области – ядра и, прилегающего к нему переходного слоя, расположенного на границе между твердой мантией и жидким или частично расплавленным ядром. В настоящем исследовании на основе совместной инверсии прямо не связанных между собой сейсмических, селенофизических и геохимических параметров проведено моделирование химического состава мантии и внутреннего строения центральной области Луны. Решение обратной задачи основано на байесовском подходе с применением алгоритма Монте-Карло по схеме марковских цепей в сочетании с методом минимизации свободной энергии Гиббса. Результаты показывают, что радиус центральной области Луны составляет около 500–550 км. Толщина переходного слоя, радиусы внешнего и внутреннего ядра довольно слабо зависят от валового состава моделей силикатной Луны с разным содержанием тугоплавких оксидов. Силикатная порция Луны обогащена FeO (12–13 мас. %, FeO ~ 1.5 × BSE) и обеднена MgO (магнезиальное число Mg# 79–81) по отношению к валовому составу силикатной Земли (BSE), что отвергает возможность формирования Луны из вещества примитивной мантии Земли и не находит адекватного объяснения в существующих канонических и неканонических моделях происхождения Луны. Концентрации SiO₂ во всех зонах мантии Луны изменяются незначительно и составляют 52–53 мас. %, причем преобладающим минералом верхней мантии является низко кальциевый ортопироксен, а не оливин. В отношении оксида алюминия мантия Луны стратифицирована, с более высоким содержанием Al₂O₃ в нижней мантии по сравнению с вышележащими оболочками. Частично расплавленный переходный слой, окружающий ядро, имеет толщину около 200–250 км. Радиусы твердого внутреннего ядра находятся в пределах 50–250 км, а наиболее вероятные радиусы жидкого внешнего ядра ~300–350 км. Проведено сопоставление физических характеристик лунного ядра с экспериментальными измерениями плотности и скорости звука жидких сплавов Fe(Ni)–S–C–Si. Если сейсмическая модель жидкого внешнего ядра с V_P = 4100 ± 200 м/с (в работе R.C. Weber с соавторами 2011 года) достаточно надежна, то этот диапазон неопределенности лучше всего согласуется со скоростью звука V_P = 3900–4100 м/с жидких Fe(Ni)–S сплавов c содержанием серы до ~10 мас. % и плотностью 6200–7000 кг/м³, а также с инвертированными значениями плотности и скорости звука внешнего ядра. Значения V_P жидких Fe–Ni–C и Fe–N–Si сплавов при 5 ГПа превышают сейсмические оценки скорости звука во внешнем ядре Луны, что указывает на меньшую вероятность вхождения углерода и кремния в состав ядра в качестве доминирующих легких элементов. Внутреннее Fe(Ni)-ядро (возможно, с незначительным содержанием легких элементов – серы, углерода) является предположительно твердым с плотностью 7500–7700 кг/м³. Различие в плотности между внутренним и внешним ядрами Δρ ~ 500–1000 кг/м³ можно объяснить различием в их составе.

Ключевые слова: Луна, скорость звука, плотность, Fe–Ni–S–C–Si-жидкости, переходный слой, мантия, ядро

ВВЕДЕНИЕ

Ключевая для планетологии и геохимии проблема происхождения и состава Луны важна не только сама по себе, но оказывается тесно связанной с до сих пор нерешенной проблемой происхождения системы Земля–Луна (Urey, 1951; Левин, Маева, 1975; Рускол, 1997; Галимов, 1995; Discussion Meeting Issue, 2014; Canup, 2014; Nielsen et al., 2021). В Солнечной системе Луна является единственным космическим телом, кроме Земли, для которого исследованы образцы пород и получены сейсмические данные. Химический состав, внутреннее строение и физическое состояние Луны тесно связаны с моделями ее формирования, теплового режима и крупномасштабной химической и магматической дифференциации. Изучение Луны, начатое более 50 лет назад в XX веке космическими аппаратами Luna, Apollo, Clementine, Lunar Prospector и продолженное в XXI веке зондами LRO (Lunar Reconnaissance Orbiter), GRAIL (Gravity Recovery and Interior Laboratory), Kaguya/SELENE, Chang’ E, Chandrayaan, позволило провести топографическое, минералогическое и гравитационное картирование лунной поверхности и установить особенности строения недр. Полученные сведения позволили сделать исключительно важные выводы для геологии, геохимии и геофизики Луны (Wieczorek et al., 2006; Lognonné, 2005; Khan et al., 2014; Williams et al., 2014; Xiao, Head, 2020), но не дали достоверных аргументов в отношении проблемы происхождения Луны, ее химического состава и внутреннего строения, физического состояния центральной области и размеров ядра. Многие загадки и проблемы в отношении происхождения Луны и ее термохимической эволюции остаются дискуссионными.

Динамические модели формирования Луны противоречивы. Каждая из них (отделения от Земли, захвата, формирования Луны из роя тел, обращающихся вокруг Земли, мегаимпакта, макроимпактов, модель синестии, образования Луны путем фрагментации разреженного протопланетного сгущения) в той или иной степени вносит определенные аргументы в решение проблемы. Однако в целом ни одна из них на дает удовлетворительного объяснения особенностям лунной геохимии из-за отсутствия адекватного решения проблемы совмещения изотопной идентичности ряда элементов (кислород, кремний, титан, вольфрам), обеднения летучими и сидерофильными элементами, достаточно убедительной оценки состава ударника и ударных параметров, соотношения масс ударника и мишени или доли массы, которая захватывается в рой при столкновении двух тел, существенных различий в распространенности FeO и тугоплавких элементов по сравнению с валовым составом силикатной порции Земли (Левин, Маева, 1975; Рускол, 1997; Галимов, 2011, 2019; Hartmann, 2014; Discussion Meeting Issue, 2014; Афанасьев, Печерникова, 2019; Canup, 2014; Hosono et al., 2019; Lock et al., 2019; Nielsen et al., 2021). Геохимическая разработка и компьютерное моделирование эволюции системы Земля–Луна связана с пионерскими работами Э.М. Галимова (Галимов, 1995; Galimov, Krivtsov, 2012). Модель, основана на предположении, что система Земля–Луна образовалась не в результате мегаимпакта, а путем фрагментации массивного газо-пылевого сгущения, которое на заключительной стадии аккреции приводит к относительному обеднению Луны железом, утрате летучих и повышенной концентрации тугоплавких компонентов по сравнению с Землей.

Петролого-геохимические и изотопные исследования лунных образцов, доставленных космическими аппаратами, накладывают слабые ограничения на физические свойства мантии, тогда как измерения тепловых потоков, селенофизические, электромагнитные и сейсмические исследования дают лишь косвенную информацию о составе и температуре лунных недр. Эта проблема осложняется тем фактом, что количество известных параметров меньше числа неизвестных, причем разделение эффектов влияния состава и температуры на физические свойства представляет трудную для решения задачу. Определения количественных ограничений на состав, тепловой режим и внутреннее строение Луны остаются ключевыми проблемами лунной геохимии и геофизики.

Одним из критериев достоверности существующих гипотез может быть валовый химический состав силикатной порции Луны (BSM), выполняющий роль фундаментального геохимического ограничения при тестировании любой космогонической модели ее происхождения. Однако имеющиеся образцы лунного грунта не дают информации о составе Луны в целом. По составу глубинных пород, вынесенных на поверхность в виде ксенолитов, можно, хотя и с оговорками, судить о примитивном веществе мантии Земли. Но для спутника Земли такие данные отсутствуют. В то же время Луна – единственное космическое тело (помимо Земли), для которого известны скорости распространения сейсмических волн до глубин порядка 1200 км, полученные в рамках экспериментов по программе Apollo. Сейсмические данные – своего рода “розеттский камень” – дают важную информацию о внутреннем строении Луны (Lognonné et al., 2003; Garcia et al., 2019), но не отражают особенности ее химического состава, и поэтому требуют дешифровки в терминах химического и минерального состава.

Предполагается, что Луна обеднена летучими (K, Rb, Cs, Tl, Cd, Zn и др.) и сидерофильными (Pt, Re, Ir, Os, Ni, Co и др.) элементами (Taylor et al., 2006; Галимов, 2011), в то время как в отношении содержания основных петрогенных элементов ясности нет. В оценках химического состава Луны используются разные подходы и методы: конденсационные и геохимические модели (Morgan et al., 1978; Dauphas et al., 2014), петрологические эксперименты (Ringwood, 1977; Snyder et al., 1992; Longhi, 2006; Sakai et al., 2014), геофизические инверсии (Kronrod, Kuskov, 2011; Khan et al., 2007; Lognonné et al., 2003). Основные противоречия связаны с оценкой концентраций тугоплавких оксидов CaО и Al₂О₃, а также FeO (рис. 1), имеющих ключевую роль в эволюции Луны и влияющих на количество и устойчивость основных минеральных фаз (плагиоклаза, оливина, пироксенов, граната), физические свойства и момент инерции.

Рис. 1.

Геохимические и геофизические модели валового состава Луны (кора + мантия) по литературным данным в сравнении с составом силикатной порции Земли (звезда). M78 = Morgan et al., 1978; R77 = Ringwood, 1977; TWM = Taylor, 1982; J&D89 = Jones, Delano, 1989; S92 = Snyder, 1992; L03 = Lognonné et al., 2003; LPUM = Longhi, 2006; Kh07 = Khan et al., 2007; D14 = Dauphas et al., 2014; K19/Cold, K19/Hot (холодный и горячий температурный профиль в мантии Луны) = Kuskov et al., 2019a,b.

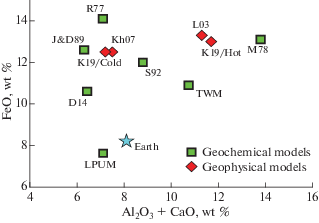
Геофизические модели получены с помощью различных методов обработки данных сейсмического, гравитационного и электромагнитного зондирования в сочетании с расчетами фазовых равновесий (Khan et al., 2007, 2014; Lognonné et al., 2003; Gagnepain-Beyneix et al., 2006; Kuskov et al., 2019a,b; Kronrod et al., 2018, 2019, 2020; Garcia et al., 2019).

Геохимические модели основаны на масс-балансовых соотношениях, анализе зеленых стекол, лунных метеоритов, элементных отношениях Mg/Si, Al/Si, Mg/Al и корреляции между содержаниями Th, U и тугоплавких оксидов (Ringwood, 1977; Snyder et al., 1992; Taylor et al., 2006; Jones, Delano, 1989; Longhi, 2006; Dauphas et al., 2014). В геохимической литературе часто рассматриваются две предельные модели состава Луны: модель TWM (Taylor Whole Moon model), обогащенная (относительно земной мантии) тугоплавкими оксидами примерно на 50% (Taylor, 1982), и модель LPUM (Lunar Primitive Upper Mantle model), имеющая концентрации тугоплавких оксидов, близкие к земным, на уровне ~4% Al₂О₃ (Longhi, 2006). Обе модели по содержанию FeO различаются почти в два раза (рис. 1), то есть в отношении распространенности FeO также нет консенсуса (Kuskov, Kronrod, 2000; Sossi, Moynier, 2017). Неопределенность в оценках концентраций петрогенных элементов позволяет строить модели Луны как близкие по валовому составу к силикатной Земле, так и обогащенные Al₂О₃, CaO. Поскольку скорости сейсмических волн и плотность зависят от химического и минерального состава, то можно ожидать, что модели Луны с различным содержанием FeO и тугоплавких оксидов будут отличаться по распределениям плотности и сейсмических скоростей.

Остаются загадки и нерешенные проблемы в отношении внутреннего строения и физического состояния центральной области Луны с параметрами Т ~ 1700–2000 К, Р ~ 4.5–5 ГПа. Особое место в геофизике Луны занимает проблема изучения ядра и прилегающего к нему переходного слоя – зоны пониженных скоростей/вязкости (LVZ = low-velocity / low-viscosity zone), расположенной на границе между твердой мантией и жидким или частично расплавленным ядром, который условно можно назвать слоем L", аналогично слою D" между ядром и мантией Земли. Определение размеров, состава и физических свойств центральной области необходимо для понимания теплового режима, истории лунного динамо, происхождения и эволюции Луны.

Значительный успех в изучении центральной области Луны был достигнут в результате анализа электромагнитных и селенофизических исследований космическими аппаратами Lunar Prospector, GRAIL, LLR, Kaguya (Hood et al., 1999; Williams et al., 2001, 2014; Khan et al., 2014; Shimizu et al., 2013; Raevskiy et al., 2015). О возможности существования зоны частичного плавления в подошве нижней мантии Луны говорит отсутствие глубокофокусных лунотрясений (Nakamura, 2005), анализ сейсмических данных (Weber et al., 2011), исследования по лазерной локации Луны (Williams et al., 2001) и гравитационному полю (Williams et al., 2014). В работе (Garcia et al., 2011) предложена сейсмическая модель центральной части Луны без частично расплавленного слоя.

Свидетельства, предоставляемые петролого-геохимическим анализом, носят более косвенный характер и часто связаны с идеей лунного магматического океана (lunar magma ocean, LMO). Оценки его мощности охватывают интервал глубин от верхних 500 км до частичного или полного плавления всей Луны (Shearer et al., 2006). Это – один из основных нерешенных вопросов магматической эволюции Луны. От ответа на него во многом зависят состав мантии, существование сейсмических границ и модели формирования Луны, имеющие много свободных параметров. Кристаллизация LMO привела к образованию последовательности кумулятивных слоев, сложенных различными минералогическими ассоциациями, и сопровождалась образованием легкой анортозитовой коры, под которой находился тонкий слой кумулатов с высоким содержанием TiO₂ и FeO, а на больших глубинах – мощный слой пироксен-оливиновых кумулатов (Shearer et al., 2006; Xiao, Head, 2020). Предполагается, что при определенных условиях в этих слоях возникает инверсия плотности (Wieczorek et al., 2006; Yu et al., 2019; Khan et al., 2014). В результате гравитационной нестабильности происходит общемантийный глобальный переворот или овертон (overturn), обусловленный кристаллизацией плотных ильменитсодержащих кумулатов, содержащих радиоактивные элементы (U, Th, K), продуцирующих выделение тепла. Этот процесс способствует образованию глубинного частично расплавленного материала, обогащенного FeO и TiO₂ (van Kan Parker et al., 2012; Khan et al., 2014).

Средняя плотность Луны указывает на сравнительно небольшое металлическое ядро, но его состав, физические свойства и размеры остаются дискуссионными. Вопрос дефицита железа на Луне играет решающую роль при обсуждении происхождения Луны (Галимов, 1995, 2019). Несмотря на то, что сейсмические данные не позволяют надежно выявить структуру ядра, в работах (Garcia et al., 2011; Weber et al., 2011) впервые сообщаются ограничения на радиус лунного ядра. Оценки получены по результатам экспериментов Аpollo с использованием методов обработки массивов сейсмических событий на основе анализа лунных сейсмограмм с учетом отраженных от ядра волн.

В работе (Garcia et al., 2011) в предположении адиабатического сжатия гомогенного материала радиус жидкого ядра Луны составляет 380 ± 40 км со средней плотностью ρ = 5.2 ± 1 г/см³. Скорости волн в жидком ядре не определены; твердое внутреннее ядро не обнаружено, но не исключается. В работе Weber et al. (2011) представлена более детализированная модель центральной области, состоящей из частично расплавленного слоя толщиной около 150 км с вязкостью 2 × 10¹⁶ Pa s (Harada et al., 2014), жидкого внешнего Fe–S ядра, предположительно содержащего ≤6 мас. % серы, радиусом R = 330 ± 20 км и ρ = 5.1 г/см³, и твердого внутреннего ядра (с неопределенным количеством серы) с R = 240 ± 10 км и ρ = 8 г/см³. Столь большие различия между моделями демонстрируют неопределенность в структуре центральной области.

Ядро Земли может содержать значительное количество (до ~10 мас. %) одного или нескольких легких элементов, таких как Si, O, S, C, H (Кусков, 1981; Литасов, Шацкий, 2016). Состав ядер ряда планет земной группы и крупных спутников (Луна, Ио, Европа и Ганимед) часто рассматривается в виде модельного Fe–S сплава (Kuskov, Kronrod, 2000; Khan et al., 2007; Weber et al., 2011; Jing et al., 2014; Лебедев и др., 2016; Morard et al., 2018; Pommier, 2018). Содержание серы изменяется от ∼2% в обыкновенных хондритах и углистых хондритах СО и СV до ∼6 мас. % в энстатитовых и углистых хондритах CI (Jarosewich, 1990). Все легкие элементы в той или иной степени понижают плотность жидких сплавов железа, температура ликвидуса которых, зависящая от концентрации примеси (Si, S, C), составляет менее 1800 К при давлениях лунного ядра.

Экспериментальная информация о физико-химических свойствах Fe-расплавов при Р-Т условиях ядер крупных спутников (~5–10 ГПа, ~1500–2000 К) появилась сравнительно недавно и до сих пор остается крайне ограниченной. Проведены измерения плотности Fe–S–C–Si-расплавов статическими методами (Balog et al., 2003; Morard et al., 2018), скорости звука ультразвуковыми методами (Nishida et al., 2020; Terasaki et al., 2019), а также расчеты твердых и жидких Fe–S растворов методом молекулярной динамики (Belashchenko, 2014; Kuskov, Belashchenko, 2016) с применением потенциала модели погруженного атома (Embedded Atom Model). На основе совокупности методов неупругого рассеяния рентгеновских лучей и рентгеновской дифракции оценены плотности и скорости звука bcc-Fe и fcc-Fe (Antonangeli et al., 2015). Существующие геофизические и экспериментальные данные по оценкам физических свойств указывают на то, что ядро Луны состоит в основном из Fe(Ni) сплава с некоторыми дополнительными легкими элементами S, C, Si (Kuwabara et al., 2016; Terasaki et al., 2019). Однако современное состояние проблемы не позволяет отдать предпочтение какому-либо одному из перечисленных элементов.

Результаты исследования состава и строения многослойной мантии Луны на основе совместной инверсии интегрального набора, напрямую не связанных, гравитационных, сейсмических и петролого-геохимических данных (Kronrod et al., 2018, 2019; Kuskov et al. 2019a,b) использованы в настоящей работе для анализа структурных особенностей наиболее глубоких недр спутника – центральной области Луны. Анализ проблемы основан на байесовском формализме с применением алгоритма Монте-Карло по схеме марковских цепей в сочетании с методом минимизации свободной энергии Гиббса для расчетов равновесного состава минеральных ассоциаций и физических свойств мантии в рамках системы Na₂O–TiO₂–CaO–FeO–MgO–Al₂O₃–SiO₂ (NaTiCFMAS). В качестве основных геофизических граничных условий использованы эксперименты по программе Apollo и данные миссии GRAIL по изучению гравитационного поля Луны (времена пробега сейсмических волн, радиус, масса, момент инерции, число Лява второго порядка и коэффициенты добротности с периодом месяц и год). Особенность настоящей постановки состоит во включении геохимических параметров силикатной порции Луны в качестве наблюденных величин при расчете функции правдоподобия (Khan et al., 2007; Matsumoto et al., 2015; Kronrod et al., 2018). Для этого использованы ограничения на валовый состав Луны: модели с земными значениями CaO и Al₂О₃ (модели Е) и модели с высоким содержанием тугоплавких оксидов (модели М). Ядро Луны моделируется двухкомпонентной системой Fe–S. Проведено сопоставление геофизических моделей ядра с экспериментальными данными по сжимаемости и скорости звука в жидких сплавах железа. Предполагается, что в результате решения обратной задачи будут получены модели внутреннего строения Луны, в некотором смысле наилучшим образом удовлетворяющие сейсмическим, селенофизическим и геохимическим ограничениям.

МОДЕЛЬ ХИМИЧЕСКОГО СОСТАВА И ВНУТРЕННЕГО СТРОЕНИЯ ЛУНЫ

Рассматривается вязкоупругая сферически симметричная Луна (Maxwellian viscoelastic model), дифференцированная на оболочки в результате частичного плавления первоначально однородного тела. Модель Луны состоит из девяти слоев (Kronrod et al., 2018): мегареголит, кора, четырехслойная мантия, переходный слой пониженной скорости/вязкости (LVZ), внешнее жидкое ядро и твердое внутреннее ядро. Входными параметрами являются эксперименты Apollo и GRAIL, а также геохимические ограничения на валовый состав Луны в качестве наблюденных величин при расчете функции правдоподобия (Kronrod et al., 2019).

Граничные условия. Для процедуры инверсии в качестве основных граничных условий задаются следующие селенофизические и сейсмические параметры: масса (7.3463 × 10²² кг), средний радиус (1737.151 км), безразмерный момент инерции (MOI = I_S = (I/MR²) = 0.393112 ± 0.000012), число Лява второго порядка k₂ = 0.02422 ± 0.00022 (Williams et al., 2014), коэффициенты добротности с периодом месяц Q_m = 38 ± 4 и год Q_a = 41 ± 9 (Williams, Boggs, 2015), а также времена пробега сейсмических волн (Lognonné et al., 2003), включающие 177 P-волн и 125 S-волн из 59 источников (24 глубокофокусных и 8 приповерхостных лунотрясений, 19 метеороидных и 8 искусственных воздействий). Поскольку наибольшая неопределенность содержится в сейсмических наблюдениях, предполагается, что увеличение дисперсии σ_τn времен пробега позволит получить решение, удовлетворяющее всем наблюденным геохимическим и геофизическим параметрам. Проведенные численные эксперименты с утроенной ошибкой σ_τn = 3σ_τnL (относительно данных Lognonné et al., 2003) показали удовлетворительное согласование геохимических и сейсмических ограничений (Kronrod et al., 2020). Для всех параметров проявляется нормальное, либо близкое к таковому, распределение. Все результаты расчетов приведены с ошибкой σ_τn = 3σ_τnL. Для расчетов числа Лява используется программный код (Kamata et al., 2015).

Кора. В ранних работах толщина коры в местах посадки Apollo 12, 14, 16 оценивалась около 60 км (Wieczorek et al., 2006). В связи с усовершенствованием методов анализа сейсмической информации Apollo и появлением новых данных GRAIL по гравитационному полю и топографии Луны появились более надежные оценки мощности и плотности коры (Lognonné et al., 2003; Wieczorek et al., 2013), согласно которым средняя толщина коры может варьироваться в пределах 34–43 км. Уменьшение толщины коры в 1.5–2 раза подразумевает и одновременное уменьшение валового содержания оксида алюминия в Луне, что дает дополнительную аргументацию сторонникам одинаковой распространенности тугоплавких элементов в Луне и Земле (Longhi, 2006; Dauphas et al., 2014). Здесь принято, что кора состоит из слоя мегареголита толщиной 1 км и собственно коры толщиной 34 км и средней плотностью ρ_crust = 2590 kg/m³ (Wieczorek et al., 2013). В мегареголите и коре средние величины сейсмических скоростей приняты по модели Weber et al. (2011). Состав коры принят по (Demidova et al., 2007; Taylor, 1982).

Мантия. Поскольку образцы глубинного вещества Луны отсутствуют, то информация о составе и структуре мантии может быть получена только из косвенных источников, таких как анализ базальтов и вулканических стекол, а также на основе совокупности геофизических данных. Существующие геохимические и геофизические модели мантии не всегда равнозначны по детальности и часто взаимно не согласованы, поскольку их построение осуществляется в рамках аксиоматики той или иной методологии и информационной системы данных.

Все опубликованные скоростные разрезы мантии, построенные на основе набора данных по временам пробега P-, S-волн, заметно отличаются друг от друга. Это связано с тем, что обратные задачи, даже с априорными ограничениями, решаются не единственным образом. Обработка сейсмических экспериментов Apollo допускает зональное строение мантии и существование нескольких сейсмических границ в недрах Луны. Ранняя дифференциация Луны с выделением материковой анортозитовой коры и возраст лунных пород привели к гипотезе LMO, под которым обычно понимается внешняя оболочка, прошедшая через стадию частичного плавления (Shearer et al., 2006; Xiao, Head, 2020). Гипотеза LMO использована в качестве дополнительного петрологического ограничения на состав мантии в виде балансовых соотношений для концентраций основных оксидов (Kuskov et al., 2019a,b).

Концепция LMO предполагает, что состав первичной нижней мантии, не затронутой процессами магматической дифференциации, должен быть равен современному составу равномерно перемешанных вышележащих оболочек (коры, верхней и средней мантии), образовавшихся в результате дифференциации LMO вплоть до глубины 750 км, которая соответствует резкой сейсмической границе (Lognonné, 2005; Gagnepain-Beyneix et al., 2006). Предполагается, что эта геофизическая граница, представляющая химический раздел, маркирует подошву LMO, отражающую переход от кумулатов к недифференцированной примитивной мантии, не затронутой процессами частичного плавления. Из этого предположения следует, что состав первичной нижней мантии, идентичный составу магматического океана, должен отражать валовый состав силикатной Луны. Дифференциация до 750 км подразумевает, что алюминий, находящийся в коре, был экстрагирован из равномерно перемешанных верхних оболочек.

В соответствии с моделью (Gagnepain-Beyneix et al., 2006) мантия разделена на четыре слоя (i = 1–4) с фиксированными границами на глубинах 34, 250, 500 и 750 км: верхняя мантия (Mantle 1, 34–250 км), средняя мантия (Mantle 2, 250–500 км + Mantle 3, 500–750 км) и нижняя мантия (Mantle 4), расположенная на глубинах от 750 км до границы с LVZ, и толщина которой определяется в результате решения обратной задачи. Вязкость всех слоев мантии принята равной 10²¹ Pa s. Если процесс эволюции LMO сопровождался конвективным перемешиванием, то это привело к смешению составов верхней и средней мантии, в то время как нижняя примитивная мантия не подвергалась дифференциации. В соответствии с этим предположением будем считать, что a priory неизвестный химический состав трех верхних слоев мантии, будучи одинаковым C(Mantle 1) = C(Mantle 2) = C(Mantle 3), является параметром, то есть изменяется на каждой итерации в расчете (на каждом шаге в цепи). При заданных граничных условиях состав недифференцированной нижней мантии C(Mantle 4), отражающий валовый состав силикатной Луны (BSM), параметром не является, зависит от концентраций оксидов, найденных в вышележащих оболочках (коре и трех верхних слоях мантии), и находится из масс-балансовых соотношений (Kronrod, Kuskov, 2011). Поскольку границы в пределах мантийных слоев фиксированы (250, 500, 750 км), то мощность нижней мантии определяется в ходе расчетов, то есть глубина границы нижняя мантия – LVZ является параметром.

Температура мантии. Несмотря на то, что тепловой истории Луны посвящено множество работ, температура остается одним из наиболее неопределенных и дискуссионных параметров лунных недр. Температуры, восстановленные по сейсмическим моделям, дают значения: на границе кора-мантия Т₄₀ ~ 400°С, на глубинах верхней мантии Т₁₅₀ ~ 500–700°С, Т₅₀₀ ~ 800–1000°С (Kuskov et al., 2014), а на границе ядро – мантия Т ~ 1300–1500°С (Weber et al., 2011; Khan et al., 2007). По совокупности литературных данных диапазон температур в мантии удовлетворяет ограничениям (Karato, 2013; Khan et al., 2014; Kronrod et al., 2019; Kuskov et al., 2019a,b)

(1)

$\begin{gathered} 450 < {{T}_{{150{\text{ км}}}}} < 750^\circ {\text{С}},{\text{ }}750 < {{T}_{{{\text{500 км}}}}} < 1200^\circ {\text{С, }} \\ 950 < {{T}_{{1000{\text{ км}}}}} < 1400^\circ {\text{С}}, \\ \end{gathered} $

показанным на рис. 2, с дальнейшим возрастанием температуры до границы с ядром.

Рис. 2.

Потенциальный диапазон температур в мантии Луны.

В (Kuskov et al., 2019a,b) рассмотрены два сценария термального состояния мантии с холодными и горячими селенотермами, причем на глубинах 1000 км Т < 1400°C, что ниже температуры солидуса пироксенитовой или перидотитовой мантии (Ringwood, Essene, 1970). Из обработки гравитационных данных GRAIL предполагается, что на границе мантия-ядро температуры могут достигать или превышать температуру солидуса (Khan et al., 2014; Williams et al., 2014). Расчеты химического состава и физических свойств мантии в диапазоне температур на рис. 2 проведены в (Kronrod et al., 2019). Здесь, для уменьшения количества неизвестных, температуры на средних глубинах верхней, средней и нижней мантии приняты равными

(2)

$\begin{gathered} {{T}_{{{\text{150 км}}}}} = 595 - 605^\circ {\text{С}},\,\,\,{{T}_{{375{\text{ км}}}}} = 755 - 765^\circ {\text{С}}, \\ {{T}_{{625{\text{ км}}}}} = 930 - 940^\circ {\text{С}},\,\,\,\,{{T}_{{1000{\text{ км}}}}} = 1195 - 1205^\circ {\text{С }}. \\ \end{gathered} $

Геохимические модели состава Луны. Химический состав и физические свойства каждой зоны мантии моделируются в рамках системы Na₂O–TiO₂–CaO–FeO–MgO–Al₂O₃–SiO₂ (NaTiCFMAS); остальные детали изложены в работах (Kuskov et al., 1989; Kuskov, Kronrod, 2009; Kuskov et al., 2014). Скачки состава и физических свойств допускаются лишь на границах зон. В каждой зоне состав, физические свойства и температура считаются постоянными и равными значениям в некоторых средних точках по разрезу мантии в сочетании с естественным требованием отсутствия инверсии плотности (Kronrod, Kuskov, 2011).

Исходя из современного уровня знаний (рис. 1) и геохимических противоречий между концептуальными моделями TWM (Taylor, 1982; Taylor et al., 2006) и LPUM (Longhi, 2006), модели Луны по валовому содержанию оксида алюминия (С(Al₂O₃)) можно разделить на два типа (Kronrod et al., 2018, 2019; Kuskov et al., 2019a,b): модели земного типа 3.5 ≤ C_E(Al₂O₃) ≤ 4.5 мас. % (модели Е, Al₂O₃ ~ 1 × × BSE) и модели, существенно обогащенные тугоплавкими оксидами 4.5 ≤ C_M(Al₂O₃) ≤ 7.7 мас. % (модели M, Al₂O₃ ~ 1.2–1.7 × BSE) по сравнению с валовыми значениями силикатной Земли. Из рис. 1 видно, что за исключением оценок (Dauphas et al., 2014; Longhi, 2006) валовое содержание FeO в Луне находится в пределах 11 ≤ С(FeO) ≤ ≤ 14 мас. %.

Результаты инверсии на основе алгоритма Монте-Карло по схеме марковских цепей позволили оценить валовые концентрации оксидов в силикатной порции Луны. На рис. 3 приведен пример валовых оценок FeO (Kronrod et al., 2018); аналогичные оценки сделаны и для Al₂O₃.

Рис. 3.

Апостериорные вероятности функции плотности для валовых концентраций FeO в силикатной порции Луны (кора + мантия).

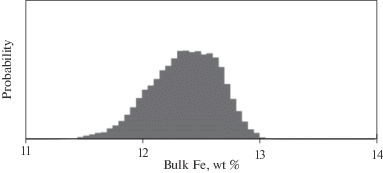
Для обеих моделей BSM средние значения геохимических параметров валового состава силикатной Луны приняты в качестве наблюденных величин при расчете функции правдоподобия (Kronrod et al., 2018):

(3)

$\begin{gathered} {{C}_{{\text{E}}}}\left( {{\text{A}}{{{\text{l}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}} \right) = 4.05 \pm 0.36\% , \\ {{C}_{{\text{M}}}}\left( {{\text{A}}{{{\text{l}}}_{{\text{2}}}}{{{\text{O}}}_{{\text{3}}}}} \right) = 5.91 \pm 0.39\% , \\ {{С}_{{{\text{E,M}}}}}\left( {{\text{FeO}}} \right) = 12.25 \pm 1.33{\text{ мас}}{\text{. }}\% . \\ \end{gathered} $

Концентрации оксидов в верхней, средней и нижней мантии в рамках системы NaTiCFMAS с шагом 1% варьировались в пределах (мас. %):

(4)

$\begin{gathered} 25 \leqslant {\text{MgO}} \leqslant 45\% ,\,\,\,40 \leqslant {\text{Si}}{{{\text{O}}}_{2}} \leqslant 55\% ,{\text{ }} \\ 5 \leqslant {\text{FeO}} \leqslant 15\% ,\,\,\,\,0.1 \leqslant {\text{CaO}},\,\,\,{\text{A}}{{{\text{l}}}_{{\text{2}}}}{{{\text{O}}}_{3}} \leqslant 7\% , \\ \end{gathered} $

причем концентрации Al₂O₃ и CaO связаны хондритовой зависимостью CaO ~ 0.8Al₂O₃ (Ringwood, 1977), а концентрации других оксидов фиксированы на уровне 0.05 мас. % для Na₂O и 0.2 мас. % для TiO₂ (Snyder et al., 1992).

Следует отметить, что вариации концентраций С(FeO) и С(Al₂O₃) сложным образом влияют на физические свойства, в частности, из-за зависимости модуля сдвига от содержания FeO в породе. Так, увеличение С(FeO) и уменьшение С(Al₂O₃) приводит к уменьшению скоростей упругих волн, но может компенсировать изменение плотности (Kuskov et al., 2011). Рост С(FeO) приводит к уменьшению модуля сдвига и V_S, но влечет увеличение плотности породы. Рост С(Al₂O₃) приводит к изменению пропорции фаз и увеличению доли граната, обладающего более высокими значениями плотности и модулей сжатия и сдвига по сравнению с оливином и пироксеном. Одновременное возрастание С(FeO) и С(Al₂O₃) компенсирует изменение скоростей из-за уменьшения модуля сдвига минералов, увеличения доли граната и возрастания плотности породы. Таким образом, вариации С(FeO) и изменение состава от обедненного тугоплавкими элементами до более фертильного вещества оказывает нетривиальное влияние на сейсмические свойства и плотность породы. Кроме того, фертилизация сопровождается изменением пропорции фаз, например, уменьшение доли ортопироксена и увеличение доли граната.

Переходный слой. Существование переходного слоя на границе между твердой мантией и жидким внешним ядром является дискуссионным. Результаты анализа лазерной локации Луны показали, что диссипативные потери, связанные с вращением Луны, могут быть вызваны взаимодействием на топографической границе между твердой мантией и жидким ядром. Об этом косвенно свидетельствуют селенофизические и электромагнитные данные, затухание сейсмических волн в основании нижней мантии (Nakamura, 2005; Khan et al., 2014; Williams et al., 2001; Williams et al., 2014), а также повторный анализ сейсмических данных (Weber et al., 2011). Наличие слоя повышенной диссипации в подошве мантии согласуется с частотной зависимостью Q-факторов (Williams et al., 2014; Matsumoto et al., 2015; Harada et al., 2014), хотя возможны модели Луны без LVZ (Garcia et al., 2011; Matsuyama et al., 2016; Karato et. al., 2013). В постановке задачи слой пониженной вязкости присутствует, а его толщина и физические свойства определяются в результате решения обратной задачи; расчет вязкости производится по (Harada et al., 2014; Matsumoto et al., 2015).

Ядро. Результаты экспериментов Аpollo и их математическая обработка привели к построению целого ряда сейсмических моделей Луны, но не дали прямых сведений о наличии ядра (Lognonné, 2005). Последующие данные, основанные на согласованности в стеках разных типов данных, предполагают, что Луна имеет твердое внутреннее и жидкое внешнее ядро, перекрытое частично расплавленным слоем, толщина которого может иметь неопределенность в несколько десятков километров (Weber et al., 2011; Khan et al., 2014). Поскольку очаги самых глубоких лунотрясений лежат на глубине ~1200 км, то радиус ядра скорее всего не превышает 500 км (Weber et al., 2011; Garcia et al., 2011). Хотя металлическое ядро с радиусом 200–400 км согласуется с геофизическими данными, легкие элементы, такие как сера, углерод и кремний, снижающие плотность и температуру плавления жидкого железа, могли войти в состав ядра в результате аккреции и процесса дифференциации LMO. Здесь предполагается, что ядро Луны состоит из внешнего жидкого ядра (с модулем сдвига μ = 0 Pa и вязкостью 0 Pa s) и твердого внутреннего ядра, сейсмические свойства (V_P, V_S) и размеры которых подлежат определению. Средняя плотность внутреннего Fe-ядра или Fe-ядра с небольшим количеством серы ρ = = 7500 кг/м³ принята по Kuskov, Belashchenko (2016). Плотность внешнего жидкого ядра определяется в результате решения обратной задачи.

Инверсия, метод решения. Определение параметров внутреннего строения Луны, дифференцированной в результате частичного плавления первоначально однородного тела, основано на совместной инверсии вышеперечисленных геохимических, гравитационных и сейсмических ограничений с учетом масс-балансовых соотношений. Задача решается с помощью байесовского подхода с применением алгоритма Монте-Карло по схеме марковских цепей (Markov chain Monte Carlo, MCMC) (Khan et al., 2007; Matsumoto et al., 2015; Kronrod et al., 2018) в сочетании с методом минимизации свободной энергии Гиббса и уравнения состояния Ми–Грюнайзена–Дебая (Kuskov et al., 1983; Kuskov, Kronrod, 2009) для расчетов равновесного состава минеральных ассоциаций и физических свойств мантии в рамках системы NaTiCFMAS на основе базы данных THERMOSEISM с учетом фазовых превращений и ангармонизма; в качестве независимых компонентов приняты оксиды в сухой системе NaTiCFMAS, образующие фазы постоянного и переменного состава (Kuskov et al., 2014; Kuskov et al., 1989). Элементы, присутствующие в малых концентрациях, не рассматриваются. Предполагается, что двухвалентное железо является преобладающей формой железа в мантии Луны, поскольку для восстановительных условий лунных недр фугитивность кислорода близка или ниже буфера IW (Wieczorek et al., 2006; Rai, van Westrenen, 2014).

Как отмечалось выше, некоторые параметры были зафиксированы: химический состав и физические свойства коры, температура и толщина слоев верхней и средней мантии, плотность внутреннего ядра, вязкость твердых слоев, валовые концентрации Na₂O и TiO₂. Концентрация SiO₂ не является параметром, поскольку система NaTiCFMAS нормируется на 100%. Концентрации оксидов в нижней мантии рассчитываются из масс-балансовых соотношений. Общее количество оцениваемых параметров составляет 14: концентрации Al₂O₃, FeO и MgO в дифференцированных слоях мантии (одинаковые для всех трех верхних слоев мантии, Mantle 1–3), толщина LVZ, радиусы внешнего и внутреннего ядра, плотность, модули сжатия и сдвига в LVZ, внутреннем и внешнем ядре (за исключением модуля сдвига в жидком внешнем ядре и плотности во внутреннем ядре), вязкость LVZ.

В верхних слоях мантии концентрации основных оксидов являются параметрами модели, по ним (на каждой итерации в цепочке) с помощью программного комплекса THERMOSEISM рассчитываются упругие параметры (плотности, модули сжатия и сдвига), которые в свою очередь участвуют в расчетах времен пробега и в конечном итоге в расчете функции правдоподобия (LHF), которая в данной постановке записывается в виде (Matsumoto et al., 2015; Kronrod et al., 2018):

(5)

$\begin{gathered} L\left( m \right) \propto \exp \left( { - \frac{{{{{\left( {d_{{obs}}^{{mass}} - d_{{cal}}^{{mass}}\left( m \right)} \right)}}^{2}}}}{{2\sigma _{{mass}}^{2}}}} \right. - \\ - \left. {\,\,\frac{{{{{\left( {d_{{obs}}^{{MOI}} - d_{{cal}}^{{MOI}}\left( m \right)} \right)}}^{2}}}}{{2\sigma _{{MOI}}^{2}}} - \frac{{{{{\left( {d_{{obs}}^{{k2}} - d_{{cal}}^{{k2}}\left( m \right)} \right)}}^{2}}}}{{2\sigma _{{k2}}^{2}}}} \right) \times \\ \times \,\,\exp \left( { - \frac{{{{{\left( {d_{{obs}}^{{Qa}} - d_{{cal}}^{{Qa}}\left( m \right)} \right)}}^{2}}}}{{2\sigma _{{Qa}}^{2}}} - \frac{{{{{\left( {d_{{obs}}^{{Qm}} - d_{{cal}}^{{Qm}}\left( m \right)} \right)}}^{2}}}}{{2\sigma _{{Qm}}^{2}}}} \right. \\ \left. { - \,\,\sum\limits_{n = 1}^{302} {\frac{{{{{\left( {d_{{obs}}^{{\tau n}} - d_{{cal}}^{{\tau n}}\left( m \right)} \right)}}^{2}}}}{{2\sigma _{{Qa}}^{2}}}} } \right) \times \\ \times \,\,\exp \left( { - {\kern 1pt} \frac{{{{{\left( {d_{{obs}}^{{Al~bulk}}\, - \,d_{{cal}}^{{Al~bulk}}\left( m \right)} \right)}}^{2}}}}{{2\sigma _{{Al~bulk}}^{2}}}\, - \,\frac{{{{{\left( {d_{{obs}}^{{Fe~bulk}}\, - \,d_{{cal}}^{{Fe~bulk}}\left( m \right)} \right)}}^{2}}}}{{2\sigma _{{Fe~bulk}}^{2}}}} \right), \\ \end{gathered} $

где d_obs, d_cal(m), σ, τ_n обозначают наблюдаемые данные, данные, рассчитанные по модели m, неопределенность наблюдаемых данных и n-е время пробега сейсмических волн, соответственно. Валовые концентрации Al₂O₃ и FeO обозначены как (Al_bulk) и (Fe_bulk).

Функция правдоподобия показывает меру отклонения теоретических значений от наблюденных с учетом того, что невязка между расчетными и экспериментально определенными величинами не превышает заданной погрешности. Решение для искомых параметров определяется из их апостериорного распределения. Пространство параметров опробовано с помощью 21 × ${{10}^{6}}$ итераций MCMC с десятью параллельными цепочками. Длина каждой цепочки составляет 3 миллиона, и первые 30% образцов отбрасываются при обработке. В результате инверсии получаем вероятную модель Луны, которая, в определенном смысле, наилучшим образом удовлетворяет совокупности геофизических и геохимических ограничений.

РЕЗУЛЬТАТЫ И ОБСУЖДЕНИЕ

Задача формулируется следующим образом. При заданных селенофизических, сейсмических и геохимических условиях на модель внутреннего строения Луны, которые выбраны в качестве наблюденных величин при расчете функции правдоподобия, требуется найти химический состав мантии, физические свойства (скорости P-, S‑волн и плотности) мантии и центральной области, а также толщину переходного слоя и размеры Fe–S ядра. Все перечисленные параметры определяются в процессе решения обратной задачи при геохимических ограничениях на валовый состав C_E,M(Al₂O₃) и С_E,M(FeO) по (3) в рамках интервала концентраций (4) с учетом ограничений на распределение температуры (2).

Мантия

Содержания FeO для всех успешных моделей Е и М во всех зонах мантии и в силикатной Луне (кора + мантия) характеризуются практически постоянными значениями на уровне 12–13 мас. %. Узкий диапазон FeO согласуется с предыдущими результатами (Kuskov, Kronrod, 2000; Lognonné et al., 2003; Khan et al., 2007; Sakai et al., 2014; Kronrod et al., 2019; Kuskov et al., 2019a,b), что указывает на робастность результатов инверсии геофизических данных в термины химического состава. Напротив, геохимические и космохимические оценки BSM показывают широкий разброс: от 7.6% FeO (Longhi, 2006) до 13–14% FeO (Morgan et al., 1978; Taylor et al., 2006).

Концентрации SiO₂ во всех зонах мантии Луны изменяются незначительно и составляют 52–53 мас. % для моделей E и M. Большое количество SiO₂ и, следовательно, высокое содержание пироксена являются геохимическим следствием инверсии геофизических данных. Наиболее надежный результат относится к верхней мантии, состоящей в основном из оливин-содержащего пироксенита, в котором преобладающим минералом является низко кальциевый ортопироксен, а не оливин. Этот результат согласуется с инверсией сейсмических данных Apollo (Lognonné et al., 2003; Khan et al., 2006; Kuskov, Kronrod, 2019a,b), петрологическими (Ringwood, Essene 1970; Moriarty et al., 2021) и спектральными наблюдениями по данным миссий Kaguya и Chang’E (Li et al., 2019; Lemelin et al., 2019).

Напротив, в отношении Al₂O₃ мантия стратифицирована, с более высокой концентрацией Al₂O₃ в нижней мантии (= BSM) по сравнению с вышележащими оболочками (Kronrod et al., 2019). Для модели E С_E(Al₂O₃)_{low mantle} = = С_E(Al₂O₃)_bulk ~ 4.2 мас. % (Al₂O₃ ~ 1 × BSE), что близко к оценкам (Khan et al., 2007; Kronrod, Kuskov, 2011). Для модели M С_M(Al₂O₃)_{low mantle} = = С_M(Al₂O₃)_bulk ~ 5.6 мас. % (Al₂O₃ ~ 1.4 × BSE), что близко к оценкам (Lognonné et al., 2003; Kuskov et al., 2019a,b). Содержание граната с приблизительным минеральным составом Py₇₀Al₂₅Gr₅ в нижней мантии может достигать 10% для модели E и 15 мас. % для модели М.

Переходный слой

Толщина и физические свойства частично расплавленного слоя с пониженной вязкостью или жесткостью для геохимических моделей E и M показаны на рис. 4, 5 . Видно, что различия в химическом/минеральном составе, следовательно, и в плотности мантии для моделей E и M мало влияют на параметры LVZ. Область LVZ толщиной около 200–250 км (рис. 4) расположена на глубинах от ~1200 до ~1400 км. Трудно определить более узкий диапазон значений, поскольку толщина LVZ может иметь отрицательную корреляцию с радиусом внешнего ядра (Matsumoto et al., 2015). Имеющиеся оценки толщины LVZ составляют 150-200 км (Weber et al., 2011; Khan et al., 2014).

Рис. 4.

Результаты инверсии для определения толщины LVZ для геохимических моделей E и M с σ_τn = 3σ_τnL – утроенной ошибкой времен пробега сейсмических волн по Lognonné et al. (2003).

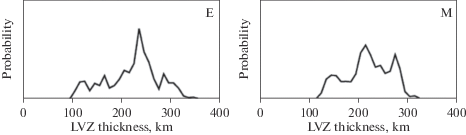
Рис. 5.

Двухмерные апостериорные вероятности функции плотности, полученные инверсией сейсмических, селенофизических и геохимических (модели E и M) ограничений в распределения скоростей P-, S-волн и плотности в переходном слое с утроенной ошибкой времен пробега σ_τn = 3σ_τnL. Пунктирные вертикальные линии показывают значения модели Weber et al. (2011).

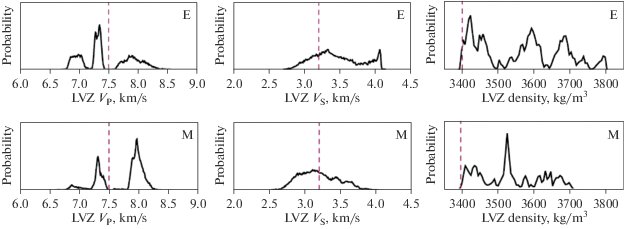
Параметры слоя LVZ (толщина, вязкость, плотность, упругие модули) варьировались в широких пределах. В большинстве удачных решений слой LVZ присутствует, хотя полученные распределения физических свойств LVZ (рис. 5) далеки от нормального и находятся в широком диапазоне параметров. Для обеих моделей E и M вероятные скорости сейсмических волн находятся в диапазоне 7.3–8 км/с для V_P и 3–3.5 км/с для V_S (рис. 5), что находится в разумном согласии с (Weber et al., 2011; Matsumoto et al., 2015). По данным Williams et al. (2014) V_P = 7.16 км/с и V_S = 2.7 км/с.

В ряде работ на основе интерпретации данных по лазерной локации Луны, экспериментов Apollo и GRAIL (Williams et al., 2001, 2014; Weber et al., 2011; Harada et al., 2014) предполагается присутствие частично расплавленного слоя, перекрывающего жидкое ядро. Наличие такого слоя согласуется с моментом инерции, приливным числом Лява и добротностью. Matsumoto et al. (2015) обнаружили, что наличие низкоскоростной зоны толщиной более 170 км необходимо для соответствия данным наблюдений. О потенциально возможном существовании области повышенной диссипации в подошве мантии на границе с ядром свидетельствует интерпретация геофизических данных (Khan et al., 2014). Полученные данные (рис. 5) позволяют предположить существование переходного слоя L'' в основании мантии Луны, обладающего низкой скоростью поперечных волн. Williams et al. (2014) также связывают эту зону с низкой скоростью поперечных волн, в то время как Harada et al. (2014) предлагают сверхнизкую вязкость в подошве мантии. Raevskiy et al. (2015) на основе совместной инверсии сейсмических и гравитационных данных выяснили, что согласование модельных и экспериментально определенных чисел Лява возможно, если в подошве мантии допустить уменьшение модуля сдвига, что можно интерпретировать наличием зоны частичного плавления вещества мантии в окрестности ядра.

Напротив, Nimmo et al. (2012) предполагают наличие вязкоупругого диссипативного слоя без плавления в подошве мантии. Matsuyama et al. (2016) получили ограничения на плотность переходного слоя в диапазоне от 3500 до 5090 кг/м³, но полагают, что данных наблюдения недостаточно, чтобы продемонстрировать наличие или отсутствие переходного слоя. Karato et al. (2013) пришли к выводу, что частичное плавление мантии маловероятно. В работе Garcia et al. (2011) слой L'' не обнаружен.

Плотность LVZ имеет решающее значение для понимания устойчивости слоя, то есть обладает ли слой положительной, отрицательной или нейтральной плавучестью по отношению к валовой плотности моделей E и M. Результаты инверсии показывают, что плотность слоя LVZ (рис. 5) превышает 3400 кг/м³, что удовлетворительно согласуется с геофизическими оценками (Matsumoto et al., 2015; Weber et al., 2011; Khan et al., 2014). Для геохимических моделей E и M значения плотности мантии на глубинах от 750 км до границы с LVZ варьируют в диапазоне от 3398 кг/м³ для моделей Е до 3409 кг/м³ для моделей М и находятся на нижнем пределе плотности LVZ (рис. 5), что хорошо согласуется с экспериментальными результатами (van Kan Parker et al., 2012), показывающими, что расплавы лунных черных стекол с содержанием ~16 мас. % TiO₂ и плотностью около 3400 кг/м³, обладают нейтральной плавучестью на границе мантии с ядром. Khan et al. (2014) также пришли к выводу, что в глубоких недрах Луны имеется частично расплавленный слой толщиной 150–200 км, обогащенный FeO и TiO₂ с плотностью 3250–3450 кг/м³, характерной для плотности лунных магм с умеренным и высоким содержанием TiO₂ (<15 мас. % TiO₂). Наличие такого частичного расплавленного материала, обогащенного радиоактивными элементами, предотвращающими охлаждение ядра, позволяет поддерживать внешнюю часть ядра в жидком состоянии, что вытекает из анализа данных LLR (Williams et al., 2001).

Ядро

Результаты инверсии по определению параметров лунного ядра показаны на рис. 6. Для геохимических моделей E и M приведены радиус и плотность жидкого внешнего ядра (R_oc, ρ_oc), а также радиус твердого внутреннего ядра (R_ic) при фиксированной плотности ρ_ic = 7500 кг/м³. Можно видеть, что различия в химическом составе и плотности моделей E и M мало влияют на параметры ядра. Это связано с тем, что физические свойства мантии для моделей E и M определены из соответствия имеющимся данным по временам пробега P-, S-волн в мантии лишь до ~1200 км (Lognonné et al., 2003; Weber et al., 2011), поскольку сейсмические источники на больших глубинах отсутствуют.

Рис. 6.

Двухмерные апостериорные вероятности функции плотности, полученные инверсией сейсмических (σ_τn = 3σ_τnL) и селенофизических ограничений и геохимических моделей E и M для радиусов и плотности внешнего флюидного ядра и радиусов внутреннего твердого ядра. Горизонтальные полосы для моделей E и M показывают размеры ядра по данным GRAIL (Williams et al., 2014) и Apollo (Weber et al., 2011; Garcia et al., 2011); вертикальные пунктирные линии с закрашенной областью показывают значения модели Weber et al. (2011). Средняя плотность внутреннего Fe-ядра или Fe-ядра с небольшим количеством легкого элемента ρ = 7500 кг/м³ принята по Kuskov, Belashchenko (2016).

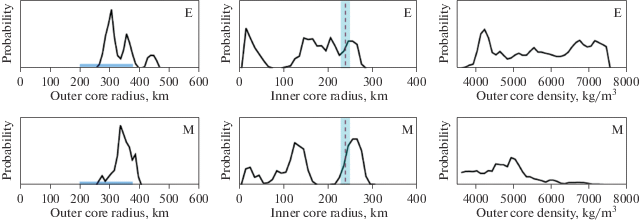
Для обеих моделей E и M вероятные радиусы внешнего ядра R_oc ~ 300–350 км (рис. 6) согласуются с результатами обработки экспериментов Apollo R_oc = 330 ± 20 (Weber et al., 2011) и R_oc = 380 ± ± 40 км (Garcia et al., 2011). Плотность и скорость звука внешнего ядра составляют ρ = 4500–7500 кг/м³ и V_P = 4000–5000 м/с, что находится в диапазоне инверсий (Matsumoto et al., 2015). Радиусы твердого внутреннего ядра, существование которого не вытекает непосредственно из сейсмических и селенофизических данных, – R_ic ~ ~ 50–250 км (рис. 6). Согласно моделям по данным GRAIL и Apollo (Weber et al., 2011; Williams et al., 2014) для флюидного ядра R_oc = 200–380 км, а для твердого внутреннего ядра R_ic = 0–280 км. Полученные данные, указывая на неоднородности в строении ядра, позволяют установить ограничения на размеры внешнего и внутреннего ядер, но не дают возможности для надежного определения их плотности.

Поэтому плотность вещества ядра, зависящая от состава, температуры и давления, остается плохо обусловленным параметром и может быть уточнена из других соображений. Несмотря на то, что экспериментальных данных по физическим свойствам расплавов на основе Fe при Р-Т условиях ядра Луны довольно мало, полезно сравнить их с сейсмическими оценками. Результаты экспериментов по измерению плотности и скорости звука Fe-расплавов, а также влияния термального состояния на размеры ядра Луны приведены на рис. 7–9 .

Рис. 7.

Гистограммы радиусов Fe–S ядра со средней плотностью 7.1 г/см³ и содержанием серы 6–10 ат. % (3.5–6 мас. %) для двух моделей термального состояния Луны. Расчеты проведены для двух профилей температур на средних глубинах (км) мантийных резервуаров: холодная модель T₁₅₀ = 600°С, T₅₀₀ = 900°С, T₁₀₀₀ = 1100°С, горячая модель T₁₅₀ = 700°С, T₅₀₀ = 1100°С, T₁₀₀₀ = 1300°С (по Kuskov et al., 2019b).

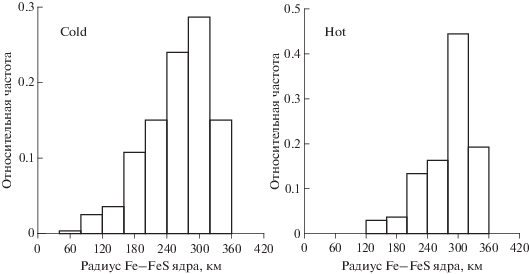
Рис. 8.

Плотность Fe(Ni)–S расплавов (все концентрации в ат. %) в сравнении с модельной плотностью ядра Луны. Открытые и залитые звезды – плотности твердого внутреннего (ρ = 8 г/см³) и жидкого внешнего (ρ = 5.1 г/см³) ядра по (Weber et al., 2011). Обозначения экспериментов: M18 = Morard et al. (2018), Fe–10 ат. % S (6 мас.% S)/1900 K; N16 = = Nishida et al. (2016), Fe–0% S (чистое железо), Fe–20 ат. % S (13 мас. % S)/1923 K; Ter19 = Terasaki et al. (2019), Fe₇₃Ni₁₀S₁₇ (10 мас. % S)/1900–2000 K; J14 = Jing et al. (2014), Fe–16 ат. % S (10 мас. % S)/1923 K; B03 = Balog et al. (2003), Fe–16 ат. % S (10 мас. % S)/1773–2123 K; D14 = Dorogokupets et al. (2014), bcc-Fe/1811 K; C14 = Chen et al. (2014), FeS расплав/1650 K. Расчеты плотности до 14 ГПа проведены методом молекулярной динамики (Kuskov, Belashchenko, 2016) при 2000 К и концентрациях серы 0% (пунктирная линия), 10% (6 мас. % S, штриховая линия) и 16% (10 мас. % S, сплошная линия).

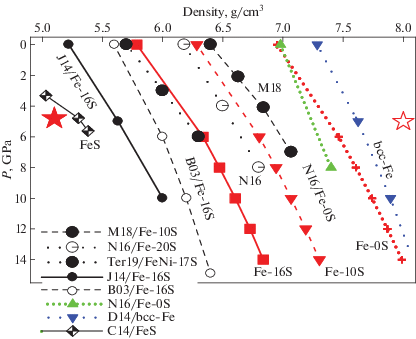
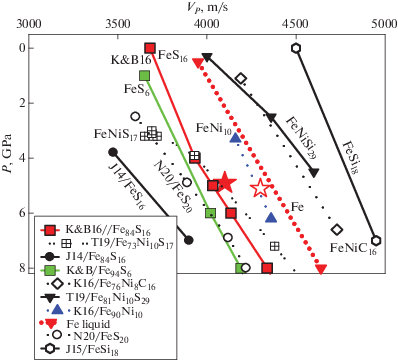
Рис. 9.

Сравнение скорости звука (V_P) жидкостей Fe(Ni)–S–C–Si (все концентрации в ат. %) с сейсмическими данными Apollo V_P = 4100 м/с для внешнего (залитая звезда) и V_P = 4300 м/с для внутреннего (не залитая звезда) ядра Луны по модели Weber et al. (2011). Значения V_P ультразвуковых экспериментов при 1700–2000 K: J14 = Jing et al. (2014), Fe₈₄S₁₆ (10 мас. % S); N20 = Nishida et al. (2020), Fe₈₀S₂₀ (13 мас. % S); T19 = Terasaki et al. (2019), Fe₇₃Ni₁₀S₁₇ (10.5 мас. % S); T19 = Terasaki et al. (2019), Fe₆₁Ni₁₀Si₂₉ (17 мас. % Si); K16 = Kuwabara et al. (2016), Fe_75.4Ni_8.3C_16.3 (Ni = = 10 мас. %, C = 4 мас. %) и Fe_90.4Ni_9.6 (Ni ~ 10 мас. %); J15 = Jing et al. (2015), Fe₈₂Si₁₈ (10 мас. % Si). V_P для жидкого Fe (точечная линия) по (Jing et al., 2014; Nishida et al., 2016, 2020). K&B16 = Kuskov, Belashchenko (2016), расчет методом молекулярной динамики для расплава Fe–S при 2000 K и концентрациях серы 6 ат. % (3.5 мас. %) и 16 ат. % (10 мас. %).

На рис. 7 показаны гистограммы радиусов жидкого Fe–S ядра с содержанием 3.5–6 мас. % серы в виде частотных распределений, средние значения которых соответствуют решениям, удовлетворяющим заданным условиям на толщину и плотность коры, массу и момент инерции Луны, скорости распространения P-, S-волн в мантии, а также ограничениям на химический состав мантии, ее минералогию и плотность (Kuskov et al., 2019b). Плотность расплава Fe–S рассчитана методом молекулярной динамики (Kuskov, Belashchenko, 2016). Как можно видеть из рис. 7, размеры ядра довольно слабо зависят от теплового режима и соответствуют интервалу 250–350 км, что находится в отличном согласии с результатами инверсии сейсмических и селенофизических данных (риc. 6).

В табл. 1 приведены модели ядра Луны, полученные в результате обработки гравитационных, электромагнитных и сейсмических наблюдений, в сопоставлении с теоретическими оценками, основанными на совместном обращении данных по скоростям сейсмических волн, моменту инерции и массе Луны. Можно видеть, что радиус ядра зависит от его состава (плотности), интерпретации сейсмических и селенофизических данных.

Таблица 1.

Модели ядра Луны

Состав внешнего ядра Луны	Радиус внешнего ядра, км	Плотность внешнего ядра, кг/м³	Метод	Литературный источник
Не известен Не известен	340±90 290–400	Не известна Не известна	Электромагнитные данные Lunar Prospector, Kaguya	Hood et al. (1999) Shimizu et al. (2013)
Fe Fe–FeS–эвтектика	≤352 ≤374	Плотность Fe Плотность Fe-FeS	Лазерная локация Луны, LLR	Williams et al. (2001)
Fe– ≤6 мас. % S	330 ± 20	5100	Интерпретация данных Apollo	Weber et al. (2011)
Не известен	380±40	5171	Интерпретация данных Apollo	Garcia et al. (2011)
Не известен	200–380	Не известна	Миссия GRAIL	Williams et al. (2014)
Не известен	200–410	4700–7500	Инверсия данных GRAIL, LLR, LOLA*	Matsuyama et al. (2016)
Не известен	220–395 330–380	5500–4500 4500–5000	Инверсия гравитационных, сейсмических и электромагнитных данных (M, I/MR², k₂, T_P, T_S, Q, ρ_a(ω))	Matsumoto et al. (2015) Khan et al. (2014) Garcia et al. (2019)
Fe–10 мас. % S Fe	340 ± 30 290–340	5700 8000		Kronrod, Kuskov (2011) Kuskov, Kronrod, (2000)
Fe(Ni)–S (до ~10 мас. % S)	300–350	6200–7000	Инверсия сейсмических, селенофизических и геохимических моделей Е и М ((FeO)_bulk), (Al₂O₃)_bulk, M, I/MR², T_P, T_S, k₂, Q) с учетом данных по плотности жидких Fe(Ni)-S сплавов	Настоящая работа

* GRAIL – the Gravity Recovery and Interior Laboratory, LLR – Lunar Laser Ranging, LOLA – Lunar Orbiter Laser Altimeter

На первый взгляд из табл. 1 кажется, что радиусы и плотности ядра в пределах погрешности определений находятся в разумном соответствии друг с другом. Однако это согласие не вполне очевидное, поскольку состав ядра не известен, а значения его плотности при Р-Т параметрах центральной области (5 ± 0.5 ГПа/1800–2000 К) могут изменяться в широких пределах.

В сейсмологических работах (Weber et al., 2011; Garcia et al., 2011) принята плотность внешнего ядра ρ = 5.1–5.2 г/см³, что соответствует плотности FeS расплава при 4.5 ГПа/1650 K (Chen et al., 2014), но значительно ниже плотности bcc-Fe, fcc-Fe и жидких сплавов Fe–S–C–Si при высоких давлениях (Tsujino et al., 2013; Dorogokupets et al., 2014; Antonangeli et al., 2015; Nishida et al., 2016). Плотность внешнего ядра около 5 г/см³ (Chen et al., 2014) достигается лишь при содержании серы 50 ат. %, что намного превышает распространенность серы в веществе метеоритов (Jarosewich, 1990). Из этого обсуждения следует, что плотность внешнего ядра Луны по сейсмическим моделям не соответствует экспериментальным измерениям плотности жидких Fe сплавов при высоких давлениях

Из рис. 8, на котором представлены экспериментальные данные по плотности расплавов Fe–S, видно, что при 5 ГПа значения изменяются от ρ ~ ~ 5 г/см³, что соответствует плотности жидкого сульфида железа (Chen et al., 2014; Nishida et al., 2016) до 6 г/см³ для Fe–29 ат. % S (Morard et al., 2018) и до 6.2–6.9 г/см³ для Fe–16–10 ат. % S (Kuskov, Belashchenko, 2016; Morard et al., 2018; Terasaki et al., 2019). Для чистого жидкого железа и Fe–10% Ni ρ ~ 7.2–7.4 г/см³ (Jing et al., 2015; Antonangeli et al., 2015; Nishida et al., 2016; Kuskov, Belashchenko, 2016; Kuwabara et al., 2016). При 5 ГПа плотности двойных Fe–S (до ~13 мас. % S), Fe–C (3.5 мас. % C), Fe–Si (10 мас. % Si) и тройных жидких сплавов Fe–C–Si (3.6 мас. % C и 7.2 мас. % Si) (Shimoyama et al., 2013; Nishida et al., 2016; Knibbe et al., 2021), Fe₉₀Ni₁₀–3–5 мас. % C (Zhu et al., 2021) попадают в интервал ρ ~ 6.2–7.2 г/см³, что лучше всего соответствует модели Е для плотности внешнего ядра (рис. 6), но на 20% выше плотности внешнего ядра по сейсмическим моделям (Garcia et al., 2011; Weber et al., 2011).

Состав сплава/расплава на основе железа важен не только, как геохимическая характеристика ядра, но и становится критическим параметром при определении его радиуса, поскольку определение размеров ядра зависит от плотности материала, слагающего ядро (табл. 1). Из лабораторных измерений и численных экспериментов методом молекулярной динамики следует, что средняя плотность внешнего жидкого ядра не может быть значительно выше ~7.2 г/см³ и существенно ниже ~6.2 г/см³ (рис. 8), что соответствует жидкому Fe–Ni сплаву, легированному легкими элементами до ~10 мас. %, но с неопределенностью относительно точного состава. Гипотетически, альтернативой металлическому Fe–Ni–S ядру может быть плотное подплавленное силикатное ядро, обогащенное FeO и TiO₂ и имеющее высокую электропроводность.

Более тонкий вопрос – какой легкий элемент(ы) и в каком количестве присутствует в лунном ядре. Сера является сидерофильным элементом и является ведущим кандидатом в качестве легкой примеси в ядре. Было высказано предположение, что обедненность лунной мантии сидерофильными элементами можно объяснить вхождением серы в ядро, причем рассматривались варианты богатой и бедной серой природе ядра (Rai and van Westrenen, 2014; Steenstra et al., 2016; Jing et al., 2014; Antonangeli et al., 2015; Nishida et al., 2016; Morard et al., 2018). Кроме того, сульфиды железа встречаются повсеместно в железных метеоритах. Другие модели не исключают вхождение углерода и кремния в состав ядра (Righter et al., 2017; Kuwabara et al., 2016; Steenstra et al., 2016; Terasaki et al., 2019; Deng et al., 2019; Knibbe et al., 2021).

Помимо плотности, важным ограничением на состав и структуру ядра являются экспериментальные измерения скоростей продольных волн жидких сплавов Fe, позволяющие провести сопоставление со скоростью звука в центральной части Луны по данным Apollo. Состав ядра остается неизвестным, поэтому необходимо рассмотреть ряд элементов-кандидатов (рис. 9).

Все легкие элементы в той или иной степени понижают плотность расплавов железа. В отношении скорости звука (V_P) дело обстоит сложнее. В последнее время V_P жидких Fe–Ni, Fe–S, Fe–C и Fe–Si были измерены в статических экспериментах при высоких давлениях ультразвуковым методом ниже 10 ГПа и с помощью неупругого рассеяния рентгеновских лучей выше 10 ГПа. Эти результаты показывают, что S, C и Ni снижают V_P жидкого Fe при давлениях ниже 10 ГПа, а S и C увеличивают V_P жидкого Fe выше 10 ГПа (Jing et al., 2014; Kuwabara et al., 2016; Nishida et al., 2016; Shimoyama et al., 2016; Nakajima et al., 2015). Вероятное объяснение этой тенденции, возможно, связано с изменением структуры и электронных свойств жидкого Fe–S. В целом, экспериментальные данные показывают, что наличие как C, так и Si увеличивает V_P жидкого Fe по крайней мере в интервале до 20 ГПа (Jing et al., 2015; Terasaki et al., 2019; Knibbe et al., 2021) в отличие от эффекта S (Nishida et al., 2020).

Рис. 9 показывает, что значения V_P жидких сплавов Fe(Ni)–S–C–Si зависят от легирующего элемента и его концентрации. При 5 ГПа измеренные значения колеблются в диапазоне V_P ~ ~ 3700 м/с для Fe–10 мас. % S (Jing et al., 2014), до V_P ~ 3900–4100 м/с для Fe–3–13 мас. % S (Kuskov, Belashchenko, 2016; Nishida et al., 2016, 2020; Terasaki et al., 2019), до V_P ~ 4200 м/с для Fe–Ni и ~4400 м/с для Fe (Kuwabara et al., 2016; Nishida et al., 2016, 2020), до V_P ~ 4500 м/с для Fe(Ni)–3–5 мас. % C (Nakajima et al., 2015; Kuwabara et al., 2016; Zhu et al., 2021) и до V_P ~ 4700 м/с для Fe–Si и Fe(Ni)–10–17 мас. % Si жидких сплавов (Jing et al., 2015; Terasaki et al., 2019). Присутствие небольших количеств углерода в Fe–Si расплаве не оказывают заметного влияния на указанную тенденцию, кроме того, растворимость C в жидком металле снижается с увеличением концентрации Si (Knibbe et al., 2021) и, вероятно, Ni. Растворимость S, C и Si в жидком Fe сильно зависит от окислительно-восстановительных условий в недрах планетарного тела. Поскольку фугитивность кислорода в мантии Луны оценивается на уровне ΔIW ~ −2 (Wieczorek et al., 2006; Rai, van Westrenen 2014), то вхождение кремния в состав Fe-ядра во время его формирования считается менее вероятным (Steenstra et al., 2016), нежели в ядро Меркурия, для которого fO₂ находится в интервале от 3.2 до 7.3 логарифмических единиц ниже буфера Fe–FeO (Knibbe et al., 2021).

Сравним теперь сейсмические оценки скорости звука в жидком ядре с ультразвуковыми измерениями жидких сплавов (рис. 9). В работе (Garcia et al., 2011) скорости волн в жидком ядре не определены. В работе (Weber et al., 2011) скорость звука для жидкого внешнего ядра принята равной V_P = 4100 ± 200 м/с (±5%) на основании экспериментальных измерений физических свойств расплавов железа. Тогда при 5 ГПа скорость звука жидкостей Fe–10% Ni и Fe всего на 5–7% выше, чем для внешнего ядра (рис. 9). Скорость звука (V_P ~ 4500–4700 м/с) для жидких Fe(Ni)–3–5 мас. % C и Fe(Ni)–10–17 мас.% Si выше, чем V_P для жидких Fe и Fe–Ni (Kuwabara et al., 2016; Terasaki et al., 2019; Knibbe et al., 2021; Jing et al., 2015; Zhu et al., 2021).

Таким образом, скорость звука расплавов Fe–Ni–C и Fe–Ni–Si характеризуется значениями, превышающими 4500 м/с (рис. 9), что на 10% выше, чем V_P для внешнего ядра по Weber et al. (2011). Если сейсмическая модель достаточно точна, то жидкие сплавы Fe(Ni) с добавкой C (и тем более Si) в качестве легкого элемента маловероятны и могут быть исключены из рассмотрения с определенной степенью достоверности как на основе ультразвуковых измерений Fe(Ni)–C и Fe(Ni)–Si жидкостей, так и по причинам слишком окислительных условий при формировании лунного ядра в отношении Fe(Ni)–Si.

Только V_P ~ 3900–4100 м/с (Kuskov, Belashchenko, 2016; Nishida et al., 2016, 2020; Terasaki et al., 2019) жидких сплавов Fe(Ni)–S (до ~16 ат. % S/~10 мас. % S) попадает в этот диапазон неопределенности, что согласуется с 6–8 мас. % S в лунном ядре по данным распределения сидерофильных элементов между силикатным расплавом и жидким металлическим сплавом (Rai, van Westrenen 2014; Steenstra et al., 2016). Однако скорость звука жидкости Fe–10% Ni в пределах погрешностей согласуется с сейсмической оценкой модели Weber et al. (2011).

Если сера (с некоторой неопределенностью относительно ее количества) является единственным легким элементом в жидком внешнем ядре, то его плотность и скорость звука находятся в диапазоне 6200–7000 кг/м³ (рис. 6, 8 ) и 3900–4100 м/с (рис. 9). При 5 ГПа плотность твердого bcc-Fe при 1811 К ρ = 7620 кг/м³ (Dorogokupets et al., 2014). Если твердое внутреннее ядро состоит из bcc-Fe, fcc-Fe, Fe(Ni) сплава или Fe(Ni) сплава с небольшой примесью легких элементов (S или C), то его плотность должна находиться в интервале 7500–7700 кг/м³ (Antonangeli et al., 2015; Dorogokupets et al., 2014; Kuskov, Belashchenko, 2016) немного более низкой, нежели принято в сейсмической модели Weber et al. (2011), рис. 8. Изменение плотности на 500–1000 кг/м³ можно объяснить различием в составе внутреннего и внешнего ядра, что вероятно должно приводить к сильному отражению от границы внутреннего ядра с радиусом 240 ± 10 км, согласно Weber et al. (2011).

ЗАКЛЮЧЕНИЕ

На основе совместной инверсии прямо не связанных между собой сейсмических, селенофизических и геохимических (M, I/MR², T_P, T_S, k₂, Q, (FeO)_bulk, (Al₂O₃)_bulk) параметров проведено моделирование химического состава мантии и внутреннего строения центральной области Луны с радиусом около 500–550 км. Результаты работы позволяют связать набор геофизических, геохимических и физико-химических параметров на фундаментальном уровне, установить более надежные ограничения на внутреннее строение центральной зоны, а также на химический состав, физические свойства и размеры лунного ядра.

Результаты показывают, что толщина частично расплавленного слоя, радиусы внешнего и внутреннего ядра довольно слабо зависят от валового состава моделей силикатной порции Луны. Концентрации FeO для моделей Е и М унифицированы и характеризуются практически постоянными значениями на уровне 12–13 мас. % во всех зонах мантии. Силикатная порция Луны (кора + + мантия) обогащена FeO (12–13 мас. %, FeO ~ ~ 1.5 × BSE) и обеднена MgO (Mg# 79–81) по отношению к BSE (FeO ~ 8% и Mg# 89). Этот, по-видимому, неопровержимый факт отвергает возможность формирования Луны из вещества примитивной мантии Земли без привлечения дополнительных ad hoc гипотез (Hosono et al., 2019) и не находит адекватного объяснения в канонических и неканонических моделях происхождения Луны в рамках гипотезы гигантского удара (the Giant Impact) - мегаимпакта (Discussion Meeting Issue, 2014; Canup, 2014).

Концентрации SiO₂ во всех зонах мантии Луны изменяются незначительно и составляют 52–53 мас. %, причем преобладающим минералом верхней мантии является низко кальциевый ортопироксен, а не оливин. Напротив, мантия стратифицирована в отношении оксида алюминия с более высокой концентрацией Al₂O₃ в нижней мантии по сравнению с вышележащими оболочками. Увеличение содержания Al в нижней мантии приводит к увеличению доли граната по отношению к шпинели и ортопироксену.

Поскольку различие в содержании FeO между Землей и Луной столь существенно, то возникает вопрос о механизме обогащения Луны закисным железом. Согласно канонической модели мегаимпакта (Canup, 2004), Луна образовалась в результате столкновения Земли с небесным телом, получившем название Тейя (Theia), с размером порядка Марса, причем большая часть лунного материала получена из ударника. В этом случае Луна в изотопном отношении должна отражать вещество Theia. Эта гипотеза сталкивается с определенными трудностями, прежде всего геохимического характера (Галимов, 2011, 2019), поскольку ударное тело, образовавшееся в своем изотопном резервуаре Солнечной системы, имело изотопный состав, отличный от земного, а в этом случае состав лунных и земных образцов должен быть также различным. Однако измерения показывают высокую степень изотопного сходства между лунными и земными породами, то есть изотопные составы Земли и гипотетической протопланеты Theia по целому ряду элементов (кислород, кремний, хром, титан, вольфрам) очень близки (Armytage et al., 2012; Dauphas et al., 2014), что противоречит предсказаниям канонической модели происхождения Луны в результате мегаимпакта, согласно которой основная масса Луны была сформирована именно из Theia, и приводит к гипотезе о том, что Луна состоит из материала, в основном полученного из мантии прото-Земли (Ringwood, 1977), или из материала ударного тела, идентичного Земле по изотопному составу (Dauphas et al., 2014).

С другой стороны, как показано в настоящем исследовании, обогащение Луны закисным железом исключает возможность формирования Луны из вещества примитивной мантии Земли, что подтверждается предыдущими данными (Kuskov, Kronrod, 2000; Lognonné et al., 2003; Khan et al., 2007; Kronrod, Kuskov, 2011; Sakai et al., 2014; Kuskov et al., 2019a,b) и, следовательно, предполагает, что 12–13 мас. % FeO в лунном веществе унаследовано преимущественно от массивной протопланеты – Theia с более высоким содержанием FeO и подразумевает, что ударное тело и прото-Земля в основном формировались из общего изотопного резервуара во внутренней Солнечной системе (Nielsen et al., 2021). В любом случае, обогащение Луны FeO имеет фундаментальное значение и должно приводить к дополнительным ограничениям при анализе космогонических концепций происхождения Луны и моделировании динамических процессов формирования системы Земля–Луна.

Переходный слой, окружающий ядро, расположенный на глубинах ~1200–1400 км, имеет толщину около 200–250 км с плотностью ≥3400 кг/м³, характерной для плотности лунных черных стекол с высоким содержанием FeO и TiO₂ (van Kan Parker et al., 2012; Khan et al., 2014). Радиусы предположительно твердого внутреннего ядра R_ic ~ 50–250 км, а наиболее вероятные радиусы жидкого внешнего ядра, слабо зависящие от термального состояния Луны, составляют 300–350 км (~1% от массы Луны), что соответствует геофизическим ограничениям (Weber et al., 2011; Garcia et al., 2011; Williams et al., 2014; Matsumoto et al., 2015).

Сопоставление физических характеристик ядра с экспериментальными измерениями плотности показывает, что при 5 ГПа плотности жидких сплавов железа с содержанием до ~10 мас. % легкого элемента (S, C, Si) составляют 6200–7000 кг/м³, что находится в интервале инвертированных значений плотности внешнего ядра (рис. 6), но на 20–40% выше плотности внешнего ядра (рис. 8) по сейсмическим моделям (Garcia et al., 2011; Weber et al., 2011).

Другое важное ограничение на состав и физические свойства ядра Луны – скорость звука. При давлениях ядра измеренные ультразвуковыми методами значения варьируют от V_P ~ 3900–4100 м/с для Fe(Ni)–S, до V_P ~ 4200–4400 м/с для Fe–Ni и до V_P ~ 4500–4700 м/с для жидких сплавов Fe(Ni)–C и Fe(Ni)–Si (рис. 9). Если предположить, что сейсмическая модель (Weber et al., 2011) достаточно точна и ошибка в V_P = 4100 ± 200 м/с составляет 5%, то при 5 ГПа только скорость звука жидких сплавов Fe(Ni)–S (до ~10 мас. % S) и, возможно, Fe–10% Ni попадает в этот диапазон неопределенности (Kuwabara et al., 2016; Kuskov, Belashchenko, 2016; Terasaki et al., 2019; Nishida et al., 2016, 2020), что согласуется с 6–8 мас. % S в лунном ядре по данным металл-силикатного распределения сидерофильных элементов (Rai and van Westrenen, 2014; Steenstra et al., 2016). Инвертированные в настоящем исследовании значения V_P = = 4000–5000 м/с для внешнего ядра с определенной степенью достоверности попадают в пространство измерений скорости звука жидких сплавов Fe(Ni)–S.

Значения V_P жидких Fe–Ni–C и Fe–N–Si сплавов превышают сейсмические оценки скорости звука в жидком внешнем ядре Луны. Поскольку растворимость S, C и Si в жидком Fe зависит от фугитивности кислорода, которая оценивается на уровне ΔIW ~ −2 в недрах Луны, то жидкие сплавы Fe(Ni) с добавкой C (и тем более Si) в качестве легкого элемента в составе внешнего ядра маловероятны и могут быть исключены из рассмотрения как на основе ультразвуковых измерений Fe(Ni)–C и Fe(Ni)–Si жидкостей, так и по причинам слишком окислительных условий при формировании ядра в отношении Fe(Ni)–Si. По этой же причине можно исключить Fe–Si сплав в качестве основы для твердого внутреннего ядра. Это согласуется со значением изотопной сигнатуры Si (δ³⁰Si) Луны (Armytage et al., 2012), идентичной таковой для Земли, что позволяет исключить вхождение Si в лунное ядро. Согласно (Xia et al., 2019), изотопное содержание Cu в BSM исключает углерод в качестве значимого легкого элемента в ядре. Присутствие кислорода в ядре Луны маловероятно из-за слишком восстановительных условий при его формировании.

Внутреннее Fe–Ni-ядро (возможно, с незначительным содержанием серы) является предположительно твердым с плотностью 7500–7700 кг/м³. Различие в плотности между внутренним и внешним ядрами Δρ ~ 500–1000 кг/м³ можно объяснить различием в их составе. В работе (Weber et al., 2011), помимо V_P (рис. 9), сообщается V_S = = 2300 м/с для внутреннего ядра. Экспериментальные определения V_P и V_S для твердых сплавов на основе железа при Р-Т параметрах лунного ядра отсутствуют. Такие данные существуют при подходящих давлениях, но недостаточно высоких температурах до 800–1200 К (Deng et al., 2019 и ссылки в этой работе). В работе (Deng et al., 2019) были измерены V_P и V_S для сплава Fe₅Si (9 мас. % Si) в ОЦК структуре при 2.6 ГПа/800–1150 К и 3–7 ГПа/300 К, которые трудно сравнивать с сейсмическими данными из-за несоответствия Р-Т параметров эксперимента и ядра Луны. Можно лишь отметить, что твердое внутреннее ядро на основе такого сплава маловероятно из-за недостаточно восстановительных условий в недрах Луны (относительно высоких значений fO₂, ΔIW ~ –2) по сравнению с таковыми в недрах Меркурия.

В заключение отметим, что размеры лунного ядра заметно зависят от плотности Fe-сплава (концентрации серы и/или других легких примесей), но слабо зависят от петрологических моделей мантии и термального режима Луны (Kuskov et al., 2019a,b; Kronrod et al., 2020). Полностью закристаллизованное ядро не удовлетворяет анализу данных LLR и GRAIL (Williams et al., 2001, 2014). Наличие сравнительно небольшого плотного, электропроводящего и частично расплавленного Fe(Ni)–S ядра Луны с радиусом 300–350 км, умещающегося в “прокрустово ложе” данных электромагнитного зондирования Lunar Prospector (Hood et al., 1999; Shimizu et al., 2013) и геофизических ограничений (Garcia et al., 2011; Weber et al., 2011; Williams et al., 2014; Matsumoto et al., 2015), согласуется с наличием частично расплавленного слоя с высокой диссипацией (Williams, Boggs, 2015; Weber et al., 2011; Khan et al., 2014), геохимическими наблюдениями по обеднению пород Луны сидерофильными элементами и металл/силикатному распределению Ni, Co, W, Mo, P и др. (Rai, van Westrenen, 2014; Steenstra et al., 2016), экспериментальными измерениями плотности и скорости звука расплавов Fe(Ni)–S (Nishida et al., 2016, 2020; Terasaki et al., 2019; Kuskov, Belashchenko, 2016) и совместимы с моделированием механизма генерации лунного динамо ~3–4 млрд лет назад, обусловленного процессами взаимодействия между твердой силикатной мантией и жидким ядром или кристаллизацией внутреннего ядра (Williams et al., 2001; Breuer et al., 2015).

Статья посвящается светлой памяти академика Эрика Михайловича Галимова, который был инициатором исследований в области геохимии и эволюции системы Земля–Луна.

Работа выполнена в рамках госзадания Института геохимии и аналитический химии им. В.И. Вернадского РАН № 0137-2019-0004.

Список литературы

Афанасьев В.Н., Печерникова Г.В. (2019) О вероятности захвата планетезималей в протолунный рой в процессе формирования системы Земля–Луна / Динамические процессы в геосферах. Сборник научных трудов ИДГ РАН 11, 80-91.
Галимов Э.М. (1995) Проблема происхождения Луны. Основные направления геохимии. К 100-летию со дня рождения А.П.Виноградова / Ред. Галимов Э.М. М.: Наука, 8-43.
Галимов Э.М. (2011) Образование Луны и Земли из общего супрапланетного газо-пылевого сгущения (доклад на XIX Всеросс. Симпозиуме по геохимии изотопов 16 ноября 2010 г.) Геохимия (6), 563-580.
Galimov E.M. (2011) Formation of the Moon and the Earth from a Common Supraplanetary Gas Dust Cloud. Lecture Presented at the XIX All-Russia Symposium on Isotope Geochemistry, November 2010. Geochem. Int. 49(6), 537-554.
Галимов Э.М. (2019) Особые черты геохимии Луны и Земли, определяемые механизмом образования системы Земля–Луна (Доклад на 81-й Международной метеоритной конференции, Москва, июль 2018). Геохимия 64 (8), 762-776.
Galimov E.M. (2019) Features of the geochemistry of the Moon and the Earth, determined by the mechanism of formation of the Earth – Moon system (report at the 81st international meteorite conference, Moscow, july 2018). Geochem. Int. 57 (8), 762-776.
Кусков О.Л. Химический состав ядра Земли (1981) Геохимия (9), 1267-1292.
Лебедев Е.Б., Аверин В.В., Луканин О.А., Рощина И.А., Кононкова Н.Н., Зевакин Е.Е. (2016) Влияние окислительно-восстановительных условий на сегрегацию железной металлической фазы при экспериментальном моделировании формирования ядра Луны с использованием высокотемпературной центрифуги. Геохимия (7), 623-632.
Lebedev E.B., Averin V.V., Lukanin O.A., Roshchina I.A., Kononkova N.N., Zevakin E.A. (2016) Effect of redox conditions on iron metal phase segregation during experimental high-temperature centrifuge modeling of the origin of the Moon’s core. Geochem. Int. 54 (7), 609-617.
Левин Б.Ю., Маева С.В. (1975) Загадки происхождения и термической истории Луны. Космохимия Луны и планет/ Ред. Виноградов А.П. М.: Наука, 283-298.
Литасов К.Д., Шацкий А.Ф. (2016) Состав и строение ядра Земли. Изд-во СО РАН, Новосибирск, 304 с.
Рускол Е.Л. (1997) Происхождение системы Земля-Луна. М.: ОИФЗ РАН, 16 с.
Antonangeli D., Morard G., Schmerr N.C., Komabayashi T., Krisch M., Fiquet G., Fei Y. (2015) Toward a mineral physics reference model for the Moon’s core. PNAS 112, 3916-3919.
Armytage R.M.G., Georg R.B., Williams H.M., Halliday A.N. (2012) Silicon isotopes in lunar rocks: implications for the Moon’s formation and the early history of the Earth. Geochim. Cosmochim. Acta 77, 504-514.
Balog P.S., Secco R.A., Rubie D.C., Frost D.J. (2003) Equation of state of liquid Fe–10 wt % S: Implications for the metallic cores of planetary bodies. J. Geophys. Res. 108.
Belashchenko D.K. (2014) Estimation of the thermodynamic characteristics of the Earth’s core using the Embedded Atom Model. Geochem. Int. 52 (6), 456-466.
Breuer D., Rueckriemen T., Spohn T. (2015) Iron snow, crystal floats, and inner-core growth: modes of core solidification and implications for dynamos in terrestrial planets and moons. Progress Earth Planet. Sci. 2 (1), 39.
Canup R.M. (2014) Lunar-forming impacts: processes and alternatives. Phil. Trans. R. Soc. A 372: 20130175.
Chen J., Yu T., Huang S., Girard J., Liu X. (2014) Compressibility of liquid FeS measured using X-ray radiograph imaging. Phys. Earth Planet. Inter. 228, 294-299.
Dauphas N., Burkhardt C., Warren P.H., Fang-Zhen T. (2014) Geochemical arguments for an Earth-like Moon-forming impactor. Phil. Trans. R. Soc. A. 372, 20130244.
Demidova S.I., Nazarov M.A., Lorenz C.A., Kurat G., Brandstätter F., Ntaflos Th. (2007) Chemical composition of lunar meteorites and the lunar crust. Petrology 15, 386-407.
Deng L., Kono Y., Shen G. (2019) Sound wave velocities of Fe₅Si at high-pressure and high-temperature conditions: Implications to lunar and planetary cores. Amer. Mineral. 104, 291-299.
Discussion Meeting Issue ‘Origin of the Moon: challenges and prospects’ organised and edited by David J. Stevenson and Alex N. Halliday. Phil. Trans. R. Soc. A. 372 (2014).
Dorogokupets P.I., Sokolova T.S., Litasov K.D. (2014) Thermodynamic properties of bcc-Fe to melting temperature and pressure to 15 GPa. Geodyn. Tectonophys. 5, 1033-1044.
Gagnepain-Beyneix, J., Lognonné, P., Chenet, H., Lombardi, D., Spohn, T. (2006) A seismic model of the lunar mantle and constraints on temperature and mineralogy. Phys. Earth Planet. Inter. 159, 140-166.
Galimov E.M., Krivtsov A.M. (2012) Origin of the Moon. New concept. Geochemistry and dynamics. De Gruyter, 168 pp.
Garcia R.F., Gagnepain-Beyneix J., Chevrot S., Lognonné P. (2011) Very preliminary reference Moon model. Phys. Earth Planet. Inter. 188, 96-113.
Garcia R.F., Khan A., Drilleau M., Margerin L., Kawamura T., Sun D., Wieczorek M.A., Rivoldini A., Nunn C., Weber R.C., Marusiak A.G., Lognonné P., Nakamura Y., Zhu P. (2019) Lunar Seismology: An Update on Interior Structure Modelsч. Space Sci. Rev. 215(50).
Harada Y., Goossens S., Matsumoto K., Yan J., Ping J., Noda H., Haruyama J. (2014). Strong tidal heating in an ultralow-viscosity zone at the core-mantle boundary of the Moon. Nat. Geosci. 7, 569-572.
Hartmann W.K. The giant impact hypothesis: past, present (and future?) (2014) Phil. Trans. R. Soc. A. 372: 20 130 249.
Hood L.L., Mitchell D.L., Lin R.P., Acuña M.H., Binder A.B. (1999) Initial measurements of the lunar induced magnetic dipole moment using lunar prospector magnetometer data. Geophys. Res. Lett. 26, 2327-2330.
Hosono N., Karato S., Makino J., Saitoh T.R. (2019) Terrestrial magma ocean origin of the Moon. Nature Geoscience. https://doi.org/10.1038/s41561-019-0354-2
Jarosewich E. (1990) Chemical analyses of meteorites: A compilation of stony and iron meteorite analyses. Meteoritics 25, 323-337.
Jing Z., Han J., Yu T., Wang Y. (2015) Sound velocity and equation of state of iron-silicon and iron-carbon liquids under planetary core conditions. 46th Lunar Planet. Sci. Conf., LPI Contrib. No. 2921.
Jing Z., Wang Y., Kono Y., Yu T., Sakamaki T., Park C., Rivers, M.L., Sutton, S.R., Shen, G. (2014) Sound velocity of Fe–S liquids at high pressure: Implications for the Moon’s molten outer core. Earth Planet. Sci. Lett. 396, 78-87.
Jones J.H., Delano J.W. (1989) A three component model for the bulk composition of the Moon. Geochim. Cosmochim. Acta. 53, 513-527.
Kamata S., Matsuyama I., Nimmo F. (2015) Tidal resonance in icy satellites with subsurface oceans. J. Geophys. Res. Planets 120, 1528-1542.
Karato S.-I. (2013) Geophysical constraints on the water content of the lunar mantle its implications for the origin of the Moon. Earth Planet. Sci. Lett. 384, 144-153.
Khan A., Connolly J.A.D., Olsen N., Mosegaard K. (2006) Constraining the composition and thermal state of the Moon from an inversion of electromagnetic lunar day-side transfer functions. Earth Planet. Sci. Lett. 248, 579-598.
Khan A., Connolly J.A.D., Maclennan J., Mosegaard K. (2007) Joint inversion of seismic and gravity data for lunar composition and thermal state. Geophys. J. 168, 243-258.
Khan A., Connolly J.A.D., Pommier A., Noir J. (2014) Geophysical evidence for melt in the deep lunar interior and implications for lunar evolution. J. Geophys. Res. Planets 119, 2197-2221.
Knibbe J.S., Rivoldini A., Luginbuhl S.M., Namur O., Charlier B., Mezouar M., Sifre D., Berndt J., Kono Y., Neuville D.R., van Westrenen W., Van Hoolst T. (2021) Mercury’s interior structure constrained by density and P-wave velocity measurements of liquid Fe–Si–C alloys. J. Geophys. Res.: Planets 126, e2020JE006651.
Kronrod E., Kuskov O. Matsumoto K., Kronrod V. (2020) Estimation of the probable size of the lunar core based on geophysical and geochemical data. J. Phys.: Conf. Ser. 1705 012 024.
Kronrod E., Matsumoto K., Kuskov O., Kronrod V., Yamada R., Kamata S. (2019) The effect of temperature distribution in the lunar mantle on joint inversion of geochemical (bulk chemical composition), seismic and selenodetic (GRAIL and LLR) data. J. Phys.: Conf. Ser. 1301 012001.
Kronrod E., Matsumoto K., Kuskov O., Kronrod V., Yamada R., Kamata S. (2018) Joint inversion of geophysical (seismic and selenodetic) and geochemical data for internal structure and composition of the Moon. IOP Conf. Ser.: Mater. Sci. Eng. 468 012015.
Kronrod V.A., Kuskov O.L. (2011) Inversion of seismic and gravity data for the composition and core sizes of the Moon. Izv. Phys. Solid Earth 47, 711-730.
Kuskov O.L., Belashchenko D.K. (2016) Thermodynamic properties of Fe-S alloys from molecular dynamics modeling: Implications for the lunar fluid core. Phys. Earth Planet. Inter. 258, 43-50.
Kuskov O.L., Fabrichnaya O.B., Galimsyanov R.F., Truskinovsky L.M. (1989) Computer simulation of the phase diagram for the MgO–SiO₂ system at P–T parameters of the mantle transition zone. Phys. Chem. Minerals 16, 442-454.
Kuskov O.L., Galimzyanov R.F., Truskinovsky L.M., Pil’chenko V.A (1983) Reliability of thermodynamic calculations of chemical and phase-equilibria at high-pressures and temperatures. Geokhimiya 6, 849-871.
Kuskov O.L., Kronrod V.A. (2000) Resemblance and difference between the constitution of the Moon and Io. Planet. Space Sci. 48, 717-726.
Kuskov O.L., Kronrod V.A. (2009) Geochemical constraints on the model of the composition and thermal conditions of the Moon according to seismic data. Izv. Phys. Solid Earth 45, 753-768.
Kuskov O.L., Kronrod E.V., Kronrod V.A. (2019a) Thermo-chemical constraints on the lunar bulk composition and the structure of a three-layer mantle. Phys. Earth Planet. Inter. 286, 1-12.
Kuskov O.L., Kronrod E.V., Kronrod V.A. (2019b) Effect of thermal state on the mantle composition and core sizes of the Moon. Geochem. Int. 57, 605-620.
Kuskov O.L., Kronrod V.A., Kronrod E.V. (2014) Thermo-chemical constraints on the interior structure and composition of the lunar mantle. Phys. Earth Planet. Inter. 235, 84-95.
Kuskov O.L., Kronrod V.A. Prokof’ev A.A. (2011) Thermal structure and thickness of the lithospheric mantle underlying the Siberian Craton from the Kraton and Kimberlit superlong seismic profiles. Izv. Phys. Solid Earth 47, 155-175.
Kuwabara S., Terasaki H., Nishida K., Shimoyama Y., Takubo Y., Higo Y., Shibazaki Y., Urakawa S., Uesugi K., Takeuchi A., Kondo T. (2016) Sound velocity and elastic properties of Fe–Ni and Fe–Ni–C liquids at high pressure. Phys. Chem. Min. 43, 229–236.
Lemelin M., Lucey P.G., Miljkovic K., Gaddis L.R., Hare T., Ohtake M., 2019. The compositions of the lunar crust and upper mantle: Spectral analysis of the inner rings of lunar impact basins. Planet. Space Sci. 165, 230–243.
Li C., Liu D., Liu B., Ren X., Liu J., He Z., Zuo W., Zeng X., Xu R., Tan X., Zhang X., Chen W., Shu R., Wen W., Su Y., Zhang H., Ouyang Z., 2019. Chang’E-4 initial spectroscopic identification of lunar far-side mantle-derived materials. Nature 569, 378-382.
Lock S.J., Stewart S.T., Petaev M.I., Jacobsen S.B. (2019) A terrestrial synestia: a new environment for formation of the Moon. 50th Lunar Planet. Sci. Conf., LPI Contrib. No. 2132.
Lognonné P. (2005) Planetary seismology. Annu. Rev. Earth Planet. 33, 571-604.
Lognonné P., Gagnepain-Beyneix J., Chenet H. (2003) A new seismic model of the Moon: implications for structure, thermal evolution and formation of the Moon. Earth Planet. Sci. Lett. 211, 27-44.
Longhi J. (2006) Petrogenesis of picritic mare magmas: Constraints on the extent of early lunar differentiation. Geochim. Cosmochim. Acta 70, 5919-5934.
Matsumoto K., Yamada R., Kikuchi F., Kamata S., Ishihara Y., Iwata T., Hanada H., Sasaki S. (2015) Internal structure of the Moon inferred from Apollo seismic data and selenodetic data from GRAIL and LLR. Geophys. Res. Lett. 42. https://doi.org/10.1002/2015GL065335
Matsuyama I., Nimmo F., Keane J.T., Chan N.H., Taylor G.J., Wieczorek M.A., Kiefer W.S., Williams J.G. (2016) GRAIL, LLR, and LOLA constraints on the interior structure of the Moon. Geophys. Res. Lett. 43, 8365-8375.
Moriarty D.P., Watkins R.N., Valencia S.N., Kendall J.D., Evans A.J., Dygert N., Petro N.E. (2021). Evidence for a stratified upper mantle preserved within the south pole–Aitken Basin. J. Geophys. Res.: Planets 121, e2020JE006589.
Morard G., Bouchet J., Rivoldini A., Antonangeli D., Roberge M., Boulard E., Denoeud A., Mezouar M. (2018) Liquid properties in the Fe-FeS system under moderate pressure: Tool box to model small planetary cores. Amer. Mineral. 103, 1770-1779.
Morgan J.W., Hertogen J., Anders E. (1978) The Moon: composition determined by nebula processes. Moon and Planets 18, 465-478.
Nakajima Y., Imada S., Hirose K., Komabayashi T., Ozawa H., Tateno S., Tsutsui S., Kuwayama Y., Baron A.Q.R. (2015) Carbon-depleted outer core revealed by sound velocity measurements of liquid iron–carbon alloy. Nature Comm. 6, 8942.
Nakamura Y. (2005) Farside deep moonquakes and deep interior of the Moon. J. Geophys. Res. 110. https://doi.org/10.1029/2004JE002332
Nielsen S.G., Bekaert D.V., Auro M. (2021) Isotopic evidence for the formation of the Moon in a canonical giant impact. Nat. Comm. 12:1817. https://doi.org/10.1038/s41467-021-22155-7
Nimmo F., Faul U.H., Garnero E.J. (2012) Dissipation at tidal and seismic frequencies in a melt-free Moon. J. Geophys. Res. 117, E09005.
Nishida K., Shibazaki Y., Terasaki H., Higo Y., Suzuki A., Funamori N., Hirose K. (2020) Effect of sulfur on sound velocity of liquid iron under Martian core conditions. Nat. Comm. 11, 1954. https://doi.org/10.1038/s41467-020-15755-2
Nishida K., Suzuki A., Terasaki H., Shibazaki Y., Higo Y., Kuwabara S., Shimoyama Y., Sakurai M., Ushioda M., Takahashi E., Kikegawa T., Wakabayashi D., Funamori N. (2016) Towards a consensus on the pressure and composition dependence of sound velocity in the liquid Fe–S system. Phys. Earth Planet. Inter. 257, 230-239.
Pommier A. (2018) Influence of sulfur on the electrical resistivity of a crystallizing core in small terrestrial bodies. Earth Planet. Sci. Lett. 496, 37-46.
Raevskiy S.N., Gudkova T.V., Kuskov O.L., Kronrod V.A. (2015) On reconciling the models of the interior structure of the Moon with gravity data. Izv., Phys. Solid Earth 51(1), 134-142.
Rai N., van Westrenen W. (2014) Lunar core formation: New constraints from metal–silicate partitioning of siderophile elements. Earth Planet. Sci. Lett. 388, 343-352.
Righter K., Go B.M., Pando K.A., Danielson L., Ross D.K., Rahman Z., Keller L.P. (2017) Phase equilibria of a low S and C lunar core: Implications for an early lunar dynamo and physical state of the current core. Earth Planet. Sci. Lett. 463, 323-332.
Ringwood A.E. (1977) Basaltic magmatism and the bulk composition of the Moon. I. Major and heat-producing elements. The Moon 16, 389-423.
Ringwood A.E., Essene E. (1970) Petrogenesis of Apollo 11 basalts, internal constitution and origin of the Moon. Proc. Apollo 11 Lunar Sci. Conf. 1, 769-799.
Sakai R., Nagahara H., Ozawa K., Tachibana S. (2014) Composition of the lunar magma ocean constrained by the conditions for the crust formation. Icarus 229, 45-56.
Shearer C.K., Hess P.C., Wieczorek M.A., Pritchard M.E., Parmentier E.M., Borg L.E., Longhi J., Elkins-Tanton L.T., Neal C.R., Antonenko I., Canup R.M., Halliday A.N., Grove T.L., Hager B.H., Lee D.C., Wiechert U. (2006) Thermal and magmatic evolution of the Moon // New views of the Moon: Rev. Mineral. Geochem. 60(1), 365-518.
Shimizu H., Matsushima M., Takahashi F., Shibuya H., Tsunakawa H. (2013) Constraint on the lunar core size from electromagnetic sounding based on magnetic field observations by an orbiting satellite Icarus 222, 32-43.
Shimoyama Y., Terasaki H., Ohtani E., Urakawa S., Takubo Y., Nishida K., Suzuki A., Katayama Y. (2013) Density of Fe–3.5 wt % C liquid at high pressure and temperature and the effect of carbon on the density of the molten iron. Phys. Earth Planet. Inter. 224, 77-82.
Snyder G.A., Taylor L.A., Neal C.R. (1992) A chemical model for generating the source of mare basalts: Combined equillibrium and fractional crystallization of the lunar magmasphere. Geochim. Cosmochim. Acta 56, 3809-3823.
Sossi P.A., Moynier F., 2017. Chemical and isotopic kinship of iron in the Earth and Moon deduced from the lunar Mg-Suite. Earth Planet. Sci. Lett. 471, 125–135.
Steenstra E.S., Rai N., Knibbe J.S., Lin Y.H., van Westrenen W. (2016) New geochemical models of core formation in the Moon from metal–silicate partitioning of 15 siderophile elements. Earth Planet. Sci. Lett. 441, 1-9.
Taylor S.R. (1982) Planetary Science: A Lunar Perspective, Lunar Planet. Inst., Houston, 481 pp.
Taylor S.R., Taylor G.J., Taylor L.A. (2006) The Moon: A Taylor perspective. Geochim. Cosmochim. Acta 70, 594-598.
Terasaki H., Rivoldini A., Shimoyama Y., Nishida K., Urakawa S., Maki M., Kurokawa F., Takubo Y., Shibazaki Y., Sakamaki T., Machida A., Higo Y., Uesugi K., Takeuchi A., Watanuki T., Kondo T. (2019) Pressure and composition effects on sound velocity and density of core-forming liquids: Implication to core compositions of terrestrial planets. J. Geophys. Res.: Planets, 124(8), 2272-2293.
Tsujino N., Nishihara Y., Nakajima Y., Takahashi E., Funakoshi K., Higo Y. (2013) Equation of state of γ‑Fe: Reference density for planetary cores. Earth Planet. Sci. Lett. 375, 244-253.
Urey H.C. (1951) The origin and development of the earth and other terrestrial planets. Geochim. Cosmochim. Acta 1 (4-6), 209-277.
van Kan Parker M., Sanloup C., Sator N., Guillot B., Tronche E.J., Perrillat J.-P., Mezouar M., Rai N., van Westrenen W. (2012) Neutral buoyancy of titanium-rich melts in the deep lunar interior, Nat. Geosci. 5, 186-189.
Weber R.C., Lin P., Garnero E.J., Williams Q., Lognonné P. (2011) Seismic detection of the lunar core. Science 331, 309-312.
Wieczorek M.A., Jolliff B.J., Khan A., Pritchard M.E., Weiss B.J., Williams J.G., Hood L.L., Righter K., Neal C.R., Shearer C.K., McCallum I.S., Tompkins S., Hawke B.R., Peterson C., Gillis J.J., Bussey B. (2006) The constitution and structure of the lunar interior. Rev. Mineral. Geochem. 60, 221-364.
Wieczorek M.A., Neumann G.A., Nimmo F., Kiefer W.S., Taylor G.J., Melosh H.J., Phillips R.J., Solomon S.C., Andrews-Hanna J.C., Asmar S.W., Konopliv A.S., Lemoine F.G., Smith D.E., Watkins M.M., Williams J.G., Zuber M.T. (2013) The crust of the Moon as seen by GRAIL. Science 339, 671-675.
Williams J.G., Boggs D.H. (2015) Tides on the Moon: theory and determination of dissipation. J. Geophys. Res.: Planets 120, 689-724.
Williams J.G., Boggs D.H., Yoder C.F., Ratcliff J.T., Dickey J.O. (2001) Lunar rotational dissipation in solid body and molten core. J. Geophys. Res. 106, 27933–27968.
Williams J.G., Konopliv A.S., Boggs D.H., Park R.S., Yuan D-N., Lemoine F.G., Goossens S., Mazarico E., Nimmo F., Weber R.C., Asmar S.W., Melosh H.J., Neumann G.A., Phillips R.J., Smith D.E., Solomon S.C., Watkins M.M., Wieczorek M.A., Andrews-Hanna J.C., Head J.W., Kiefer W.S., Matsuyama I., McGovern P.J., Taylor G.J., Zuber M.T. (2014) Lunar interior properties from the GRAIL mission. J. Geophys. Res.: Planets, 119 (7), 1546-1578.
Xia Y., Kiseeva E.S., Wade J., Huang F. (2019) The effect of core segregation on the Cu and Zn isotope composition of the silicate Moon. Geochem. Persp. Lett. 12, 12-17.
Xiao L., Head J.W. (2020) Geological characteristics of the Moon. Oxford Research Encyclopedias, Planetary Science. https://doi.org/10.1093/acrefore/9780190647926.013.90
Yu S., Tosi N., Schwinger S., Maurice M., Breuer D., Xiao L. (2019) Overturn of ilmenite-bearing cumulates in a rheologically weak lunar mantle. J. Geophys. Res.: Planets 124, 418–436.
Zhu F., Lai X., Wang J., Amulele G., Kono Y., Shen G., Jing Z., Manghnani M.H., Williams Q., Chen B. (2021) Density of Fe-Ni-C liquids at high pressures and implications for liquid cores of Earth and the Moon. J. Geophys. Res.: Solid Earth, 126, e2020JB021089.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Геохимия

Архивы выпусков Информация о журнале Отправить рукопись в журнал